A New Method for Free Vibration Analysis of Triangular Isotropic and Orthotropic Plates of Isosceles Type Using an Accurate Series Solution
Abstract
:1. Introduction
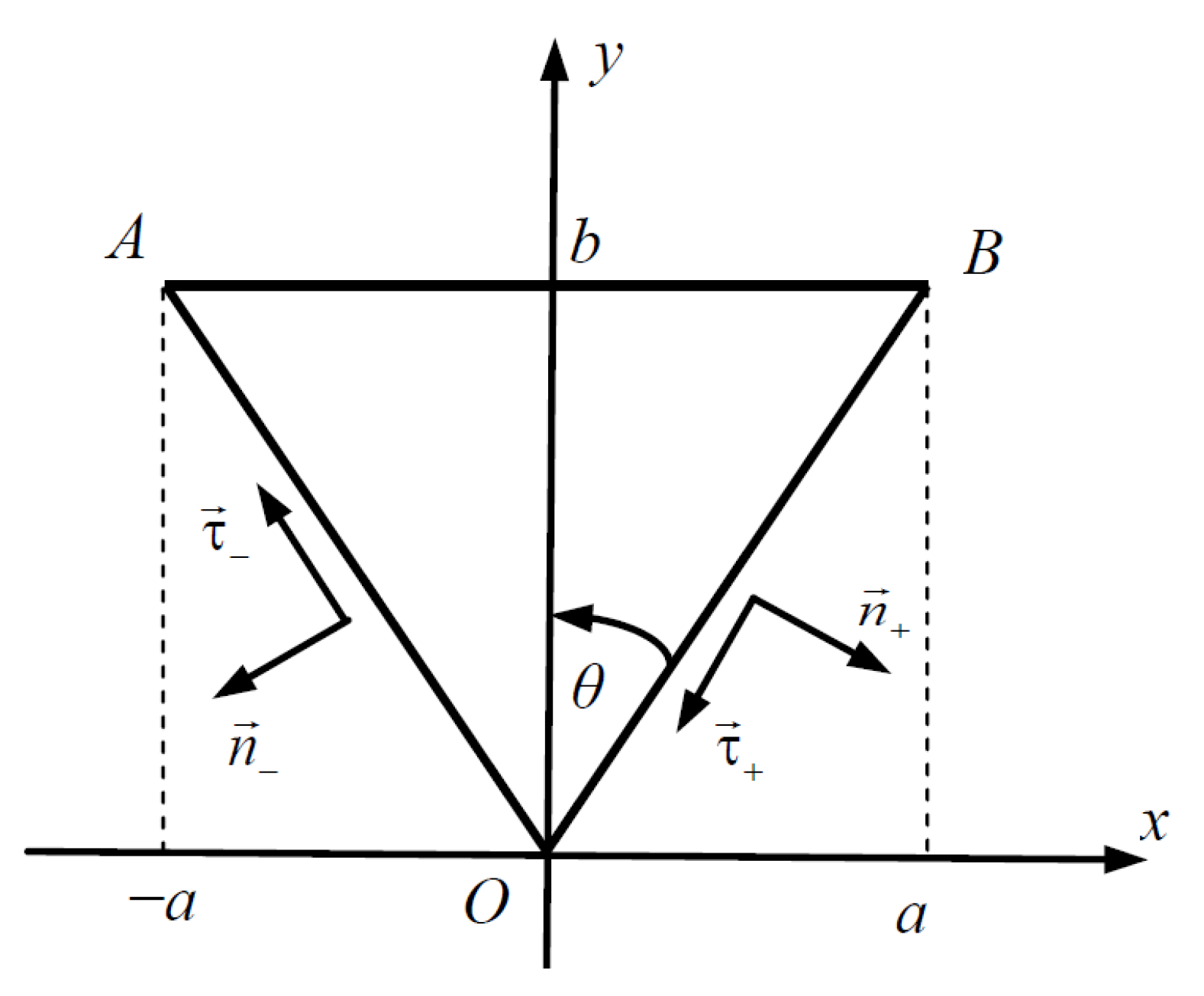
2. Theory Formulation
2.1. Governing Differential Equation and Boundary Value Problem
2.2. Construction of General Solution
2.3. Infinite System of Linear Algebraic Equations
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Leissa, A.W. Vibration of Plates (NASA SP-160); US Government Printing Office: Washington, DC, USA, 1969. [Google Scholar]
- Cox, H.L.; Klein, B. Fundamental frequencies of clamped triangular plates. J. Acoust. Soc. Am. 1955, 27, 266–268. [Google Scholar] [CrossRef]
- Ota, T.; Hamada, M.; Tarumoto, T. Fundamental frequency of an isosceles-triangular plate. Bull. JSME 1961, 4, 478–481. [Google Scholar] [CrossRef] [Green Version]
- Reid, W.P. Vibrating triangular plate. Appl. Sci. Res. 1967, 17, 291–295. [Google Scholar] [CrossRef]
- Koerner, D.R.; Snell, R.R. Vibration of Cantilevered Right Triangular Plates. J. Struct. Div. 1967, 93, 561–566. [Google Scholar] [CrossRef]
- Gorman, D.J.; Leissa, A. Free vibration analysis of rectangular plates. J. Appl. Mech. 1982, 49, 683. [Google Scholar] [CrossRef] [Green Version]
- Gorman, D. A highly accurate analytical solution for free vibration analysis of simply supported right triangular plates. J. Sound Vib. 1983, 89, 107–118. [Google Scholar] [CrossRef]
- Gorman, D. Free vibration analysis of right triangular plates with combinations of clamped-simply supported boundary conditions. J. Sound Vib. 1986, 106, 419–431. [Google Scholar] [CrossRef]
- Gorman, D. Accurate free vibration analysis of right triangular plates with one free edge. J. Sound Vib. 1989, 131, 115–125. [Google Scholar] [CrossRef]
- Kim, C.; Dickinson, S. The free flexural vibration of right triangular isotropic and orthotropic plates. J. Sound Vib. 1990, 141, 291–311. [Google Scholar] [CrossRef]
- Kim, C.; Dickinson, S. The free flexural vibration of isotropic and orthotropic general triangular shaped plates. J. Sound Vib. 1992, 152, 383–403. [Google Scholar] [CrossRef]
- Singh, B.; Chakraverty, S. Transverse vibration of triangular plates using characteristic orthogonal polynomials in two variables. Int. J. Mech. Sci. 1992, 34, 947–955. [Google Scholar] [CrossRef]
- Pradhan, K.K.; Chakraverty, S. Natural frequencies of equilateral triangular plates under classical edge supports. Symp. Stat. Comput. Model. Appl. 2016, 30–34. [Google Scholar]
- Leissa, A.; Jaber, N. Vibrations of completely free triangular plates. Int. J. Mech. Sci. 1992, 34, 605–616. [Google Scholar] [CrossRef]
- Irie, T.; Yamada, G.; Narita, Y. Free Vibration of Clamped Polygonal Plates. Bull. JSME 1978, 21, 1696–1702. [Google Scholar] [CrossRef]
- Sakiyama, T.; Huang, M. Free-vibration analysis of right triangular plates with variable thickness. J. Sound Vib. 2000, 234, 841–858. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, C.M. Vibration of triangular plates: Point supports, mixed edges and partial internal curved supports. J. Sound Vib. 1994, 172, 527–537. [Google Scholar] [CrossRef]
- Abrate, S. Vibration of point supported triangular plates. Comput. Struct. 1996, 58, 327–336. [Google Scholar] [CrossRef]
- Haldar, S.; Sengupta, D.; Sheikh, A.H. Free Vibration Analysis of Composite Right Angle Triangular Plate Using a Shear Flexible Element. J. Reinf. Plast. Compos. 2003, 22, 229–255. [Google Scholar] [CrossRef]
- Cheung, Y.; Zhou, D. Three-dimensional vibration analysis of cantilevered and completely free isosceles triangular plates. Int. J. Solids Struct. 2002, 39, 673–687. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W. Vibration of arbitrarily-shaped triangular plates with elastically restrained edges. J. Sound Vib. 2015, 357, 195–206. [Google Scholar] [CrossRef] [Green Version]
- Lv, X.; Shi, D. Free vibration of arbitrary-shaped laminated triangular thin plates with elastic boundary conditions. Results Phys. 2018, 11, 523–533. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, F.; Liu, T.; Qin, B.; Yu, H. Free vibration analysis of moderately thick composite materials arbitrary triangular plates under multi-points support boundary conditions. Int. J. Mech. Sci. 2020, 184, 105789. [Google Scholar] [CrossRef]
- Kaur, N.; Khanna, A. On vibration of bidirectional tapered triangular plate under the effect of thermal gradient. J. Mech. Mater. Struct. 2021, 16, 49–62. [Google Scholar] [CrossRef]
- Cai, D.; Wang, X.; Zhou, G. Static and free vibration analysis of thin arbitrary-shaped triangular plates under various boundary and internal supports. Thin-Walled Struct. 2021, 162, 107592. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, Y.; Ma, X.; Linghu, S.; Zhang, G. Free transverse vibration analysis of general polygonal plate with elastically restrained inclined edges. J. Sound Vib. 2022, 536, 117151. [Google Scholar] [CrossRef]
- Wittrick, W.; Williams, F. Buckling and vibration of anisotropic or isotropic plate assemblies under combined loadings. Int. J. Mech. Sci. 1974, 16, 209–239. [Google Scholar] [CrossRef]
- Wittrick, W.H.; Williams, F.W. A general algorithm for computing natural frequencies of elastic structures. Q. J. Mech. Appl. Math. 1971, 24, 263–284. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Williams, F.W. Clamped-clamped natural frequencies of a bending torsion coupled beam. J. Sound Vib. 1994, 176, 301–306. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration of sandwich beams using the dynamic stiffness method. Comput. Struct. 2003, 81, 1915–1922. [Google Scholar] [CrossRef]
- Banerjee, J. Dynamic stiffness formulation for structural elements: A general approach. Comput. Struct. 1997, 63, 101–103. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Dynamic stiffness formulation for composite Mindlin plates for exact modal analysis of structures. Part I: Theory. Comput. Struct. 2012, 96–97, 61–73. [Google Scholar] [CrossRef]
- Fazzolari, F.A. A refined dynamic stiffness element for free vibration analysis of cross-ply laminated composite cylindrical and spherical shallow shells. Compos. Part B Eng. 2014, 62, 143–158. [Google Scholar] [CrossRef]
- Nefovska-Danilovic, M.; Petronijevic, M. In-plane free vibration and response analysis of isotropic rectangular plates using the dynamic stiffness method. Comput. Struct. 2015, 152, 82–95. [Google Scholar] [CrossRef]
- Banerjee, J.; Papkov, S.; Liu, X.; Kennedy, D. Dynamic stiffness matrix of a rectangular plate for the general case. J. Sound Vib. 2015, 342, 177–199. [Google Scholar] [CrossRef]
- Papkov, S.; Banerjee, J. Dynamic stiffness formulation for isotropic and orthotropic plates with point nodes. Comput. Struct. 2022, 270, 106827. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Krylov, V.L. Approximate Methods of Higher Analysis; Noordhooff: Groningen, The Netherlands, 1964. [Google Scholar]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Pergamon Press: Oxford, UK, 1982. [Google Scholar]


| N = 18 | |||||||
|---|---|---|---|---|---|---|---|
| Diaplacement and rotation W, ϕ | l (See Column 1 of the Table) | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | Prescribed B.C (exact) | |
| 1.00001 | 0.99999 | 1.00001 | 0.99995 | 0.99953 | 1.00092 | 1 | |
| 1.00000 | 1.00000 | 1.00000 | 0.99995 | 1.00002 | 1.00092 | 1 | |
| 0.00000 | −0.00002 | 0.00005 | 0.00030 | 0.00081 | 0.00913 | 0 | |
| N = 24 | |||||||
| Diaplacement and rotation W, ϕ | l (See Column 1 of the Table) | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | Prescribed B.C (exact) | |
| 1.00002 | 1.00000 | 0.99997 | 0.99992 | 1.00005 | 1.00021 | 1 | |
| 1.00000 | 1.00000 | 1.00000 | 1.00001 | 1.00002 | 1.00021 | 1 | |
| 0.00000 | −0.00002 | 0.00002 | 0.00030 | 0.00089 | 0.00891 | 0 | |
| θ | |||
|---|---|---|---|
| Ref. [1] | 13.646 | 8.626 | 6.841 |
| Present | 13.686 | 8.618 | 6.839 |
| Method | Non-Dimensional Natural Frequency () | ||||
|---|---|---|---|---|---|
| Present | 8.6177 | 11.9063 | 11.9061 | 14.8814 | 15.3748 |
| Ref [12] | 8.6178 | 11.9075 | 11.9128 | 14.9210 | 15.4150 |
| Ref [13] | 8.6166 | 11.9039 | 11.9039 | 14.9137 | 15.4068 |
| θ | Non-Dimensional Natural Frequency () | |||||||
|---|---|---|---|---|---|---|---|---|
| 12.6923 | 15.6017 | 18.6982 | 19.1273 | 19.5364 | 22.3531 | 25.3006 | 25.6629 | |
| 7.6432 | 10.3031 | 10.7894 | 12.8591 | 13.6279 | 13.8966 | 15.4193 | 16.2192 | |
| 5.8533 | 7.7661 | 8.3775 | 9.6595 | 10.3058 | 10.9457 | 11.5676 | 12.1677 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papkov, S.; Banerjee, J.R. A New Method for Free Vibration Analysis of Triangular Isotropic and Orthotropic Plates of Isosceles Type Using an Accurate Series Solution. Mathematics 2023, 11, 649. https://doi.org/10.3390/math11030649
Papkov S, Banerjee JR. A New Method for Free Vibration Analysis of Triangular Isotropic and Orthotropic Plates of Isosceles Type Using an Accurate Series Solution. Mathematics. 2023; 11(3):649. https://doi.org/10.3390/math11030649
Chicago/Turabian StylePapkov, Stanislav, and Jnan Ranjan Banerjee. 2023. "A New Method for Free Vibration Analysis of Triangular Isotropic and Orthotropic Plates of Isosceles Type Using an Accurate Series Solution" Mathematics 11, no. 3: 649. https://doi.org/10.3390/math11030649




