Weighted Radial Basis Collocation Method for the Nonlinear Inverse Helmholtz Problems
Abstract
1. Introduction
2. Approximation of Radial Basis Functions
3. Formulations for the Inverse Helmholtz Problem of Identifying Parameter
3.1. Discretization of the Governing Equation as Well as Boundary Conditions and Known Conditions
3.2. Least-Squares Solution
4. Numerical Solutions of Some Representative Examples
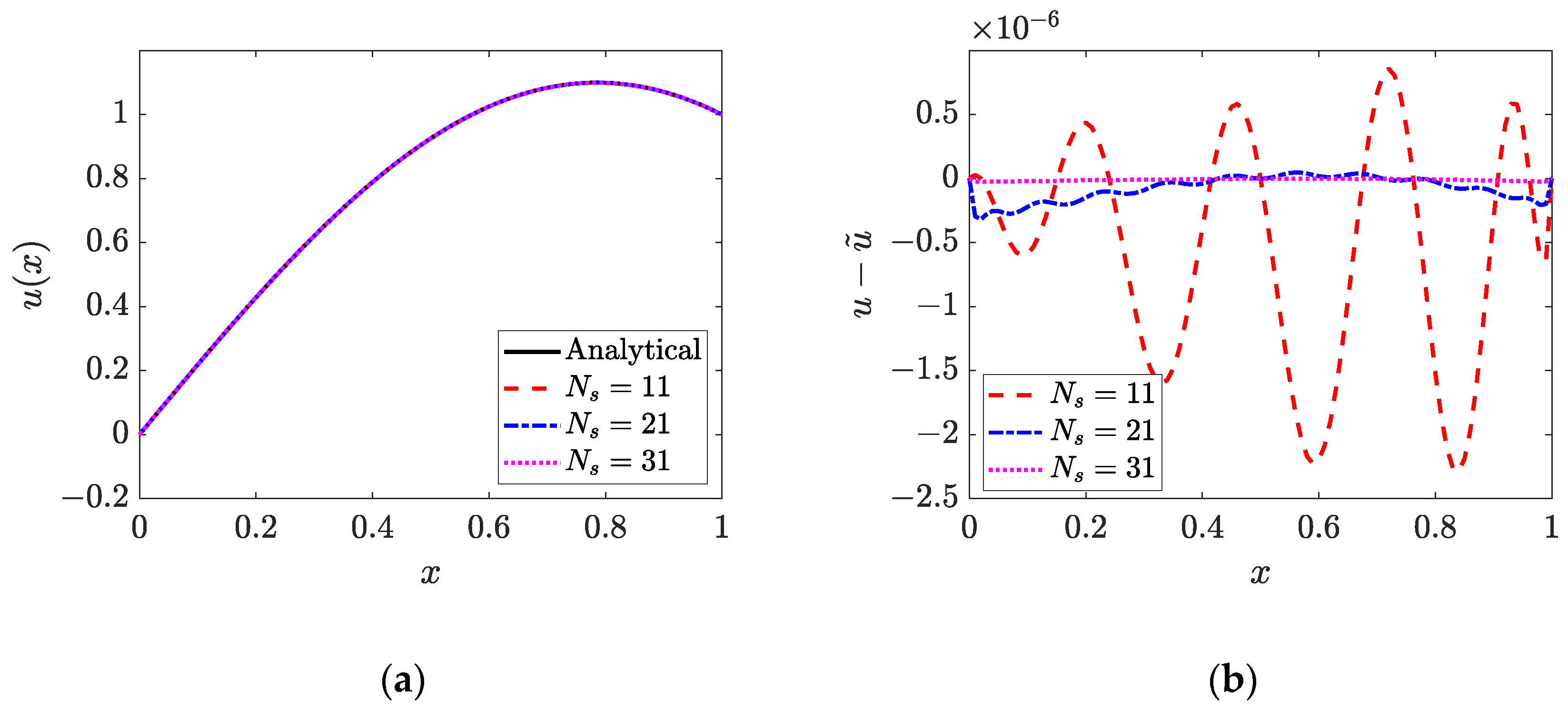
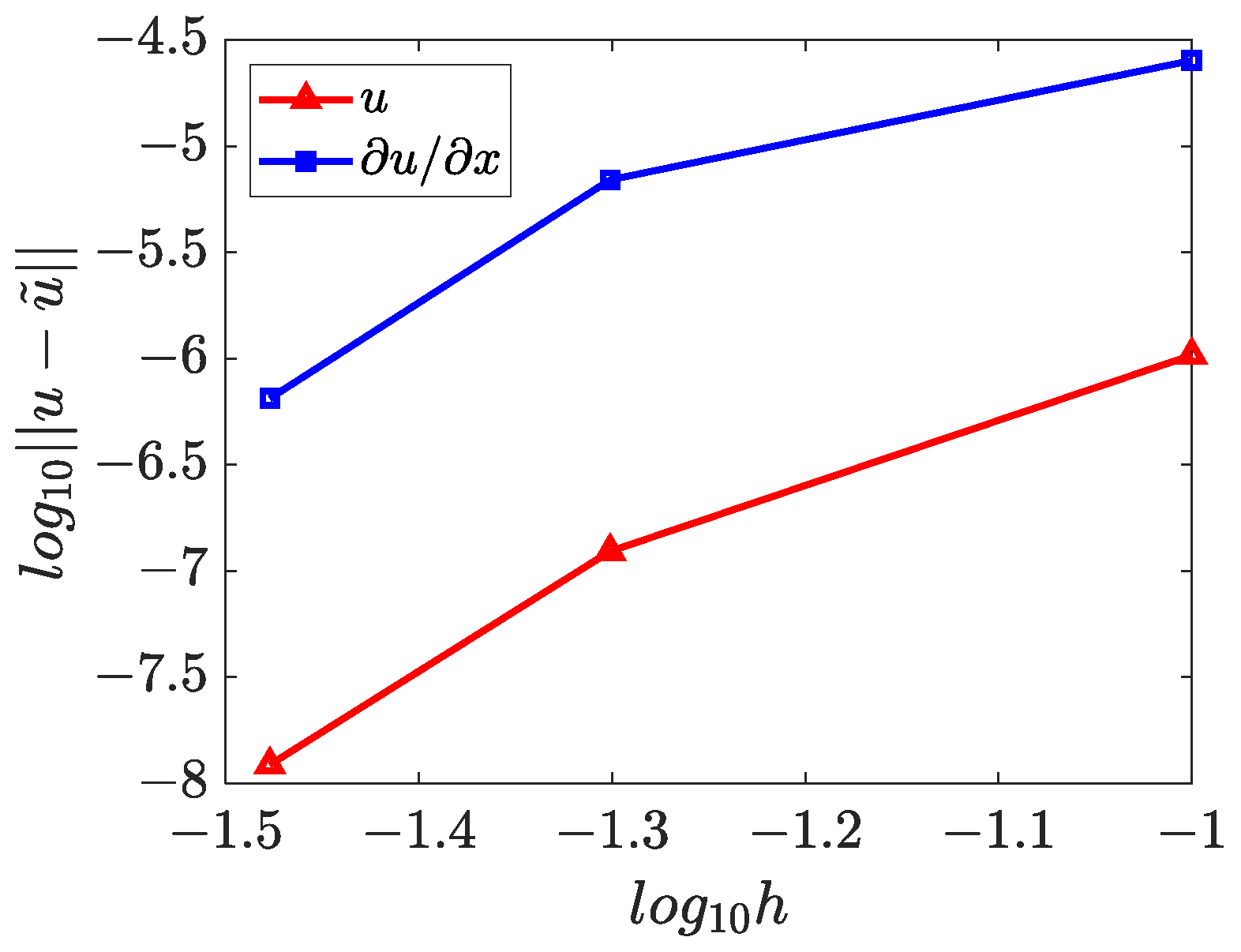
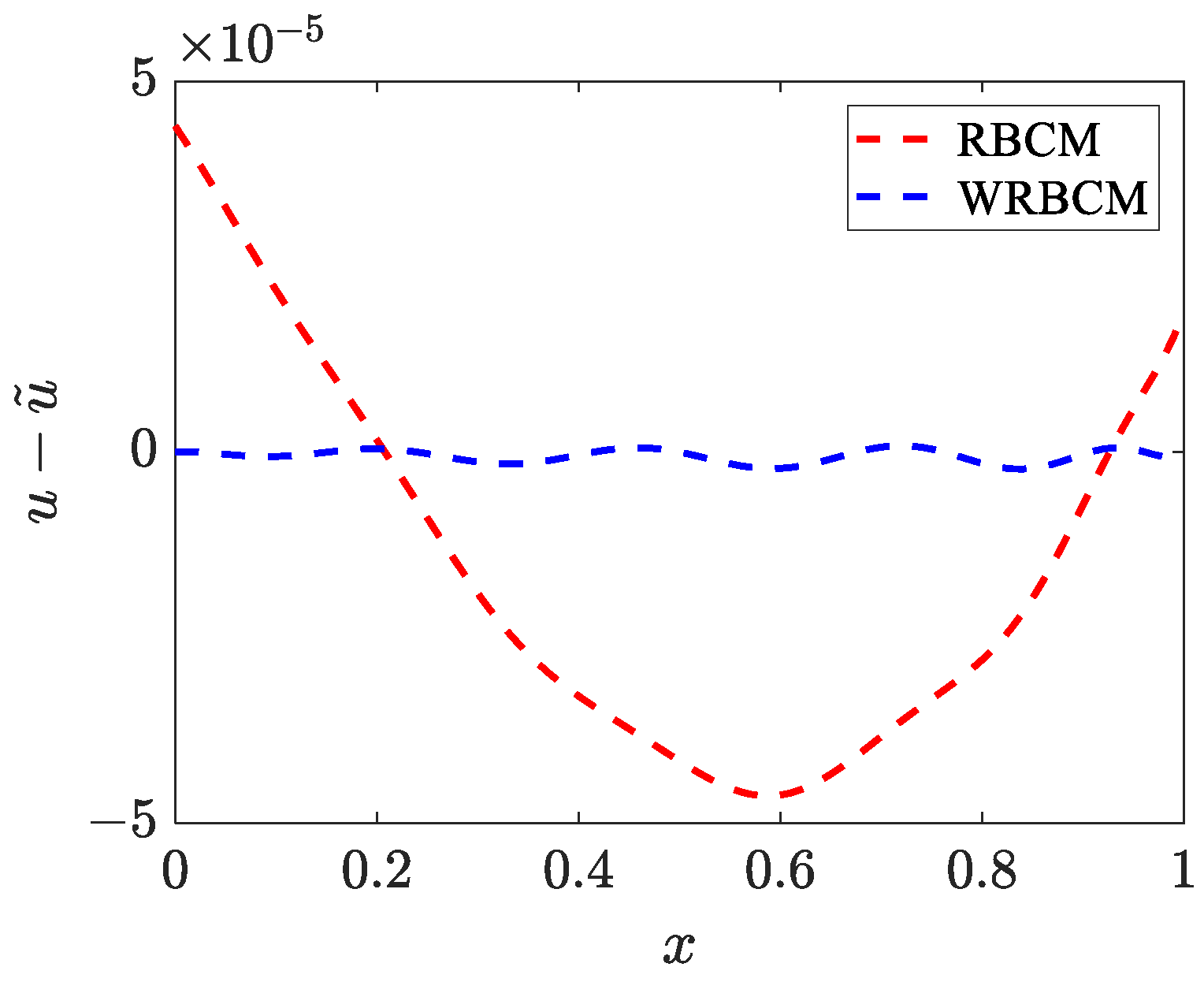
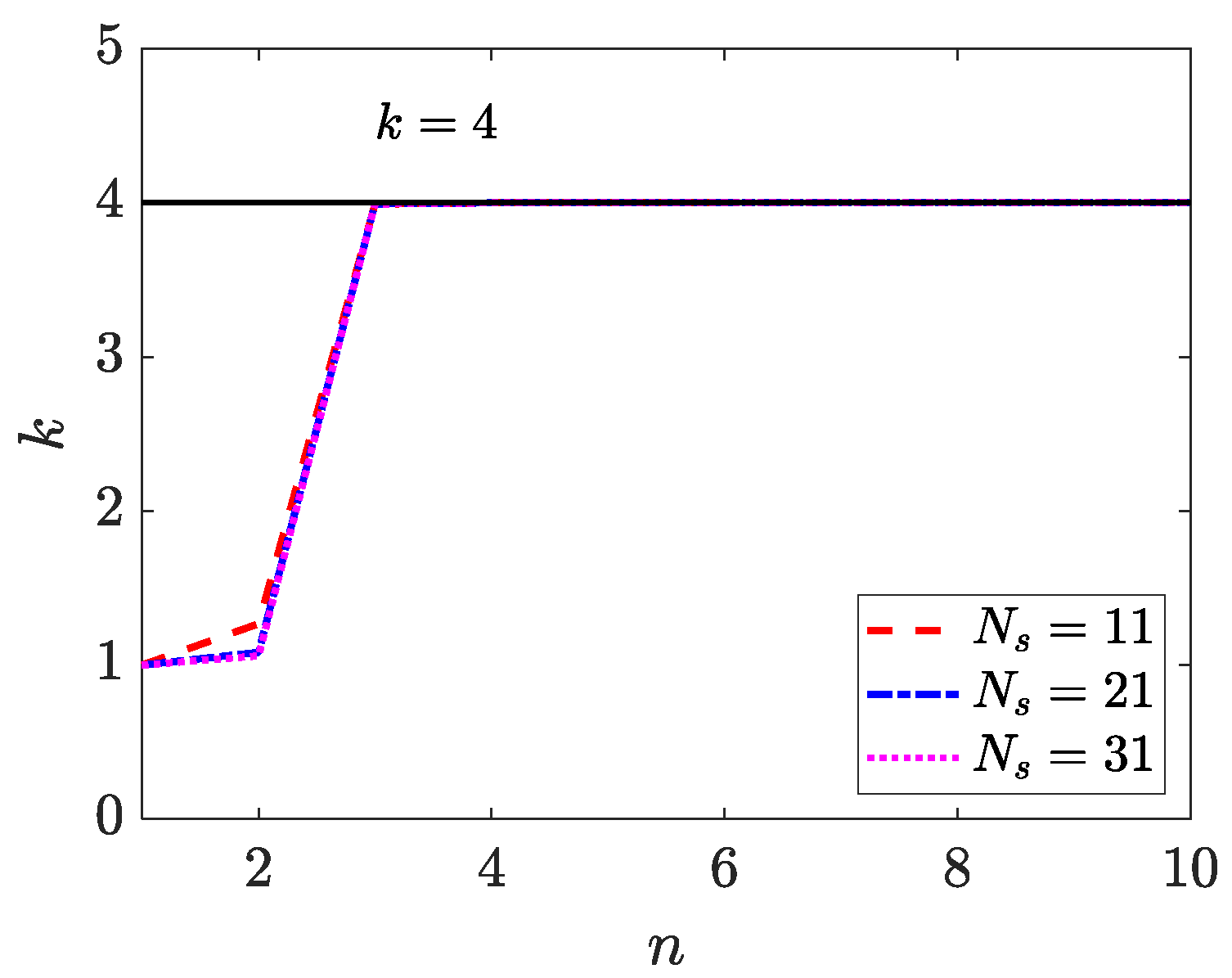
4.1. One-Dimensional Inverse Helmholtz Problem of Constant Parameter Identification
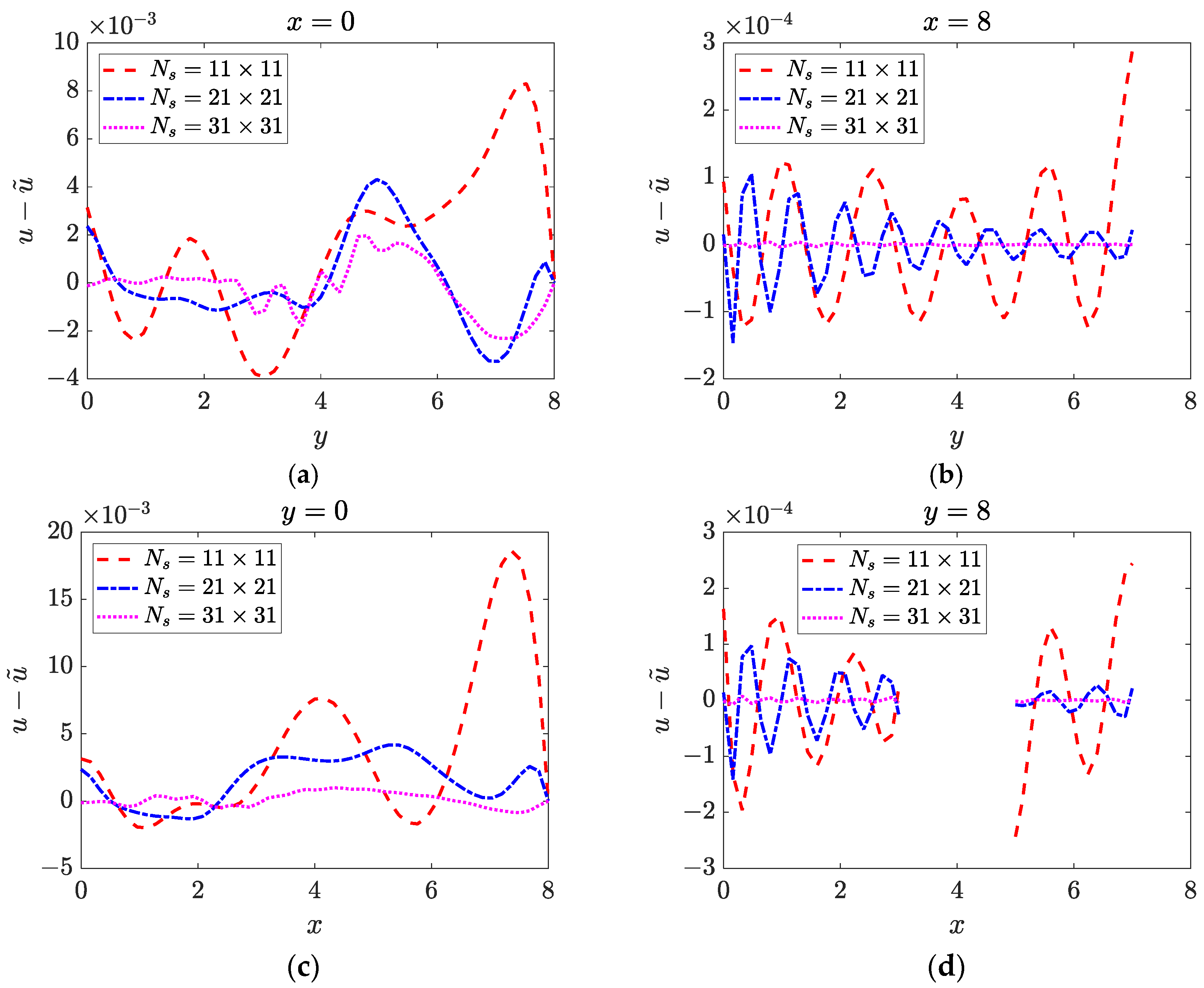
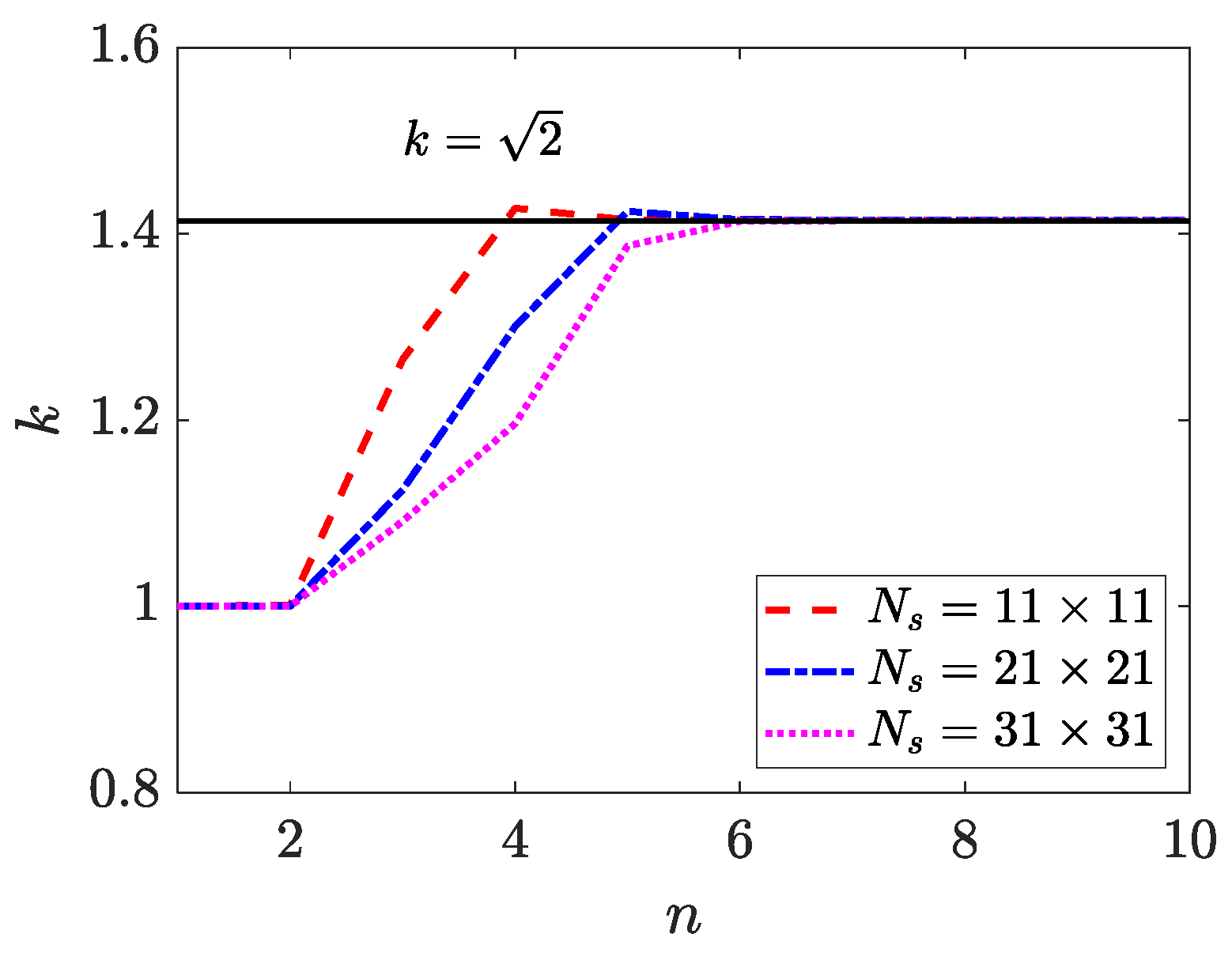
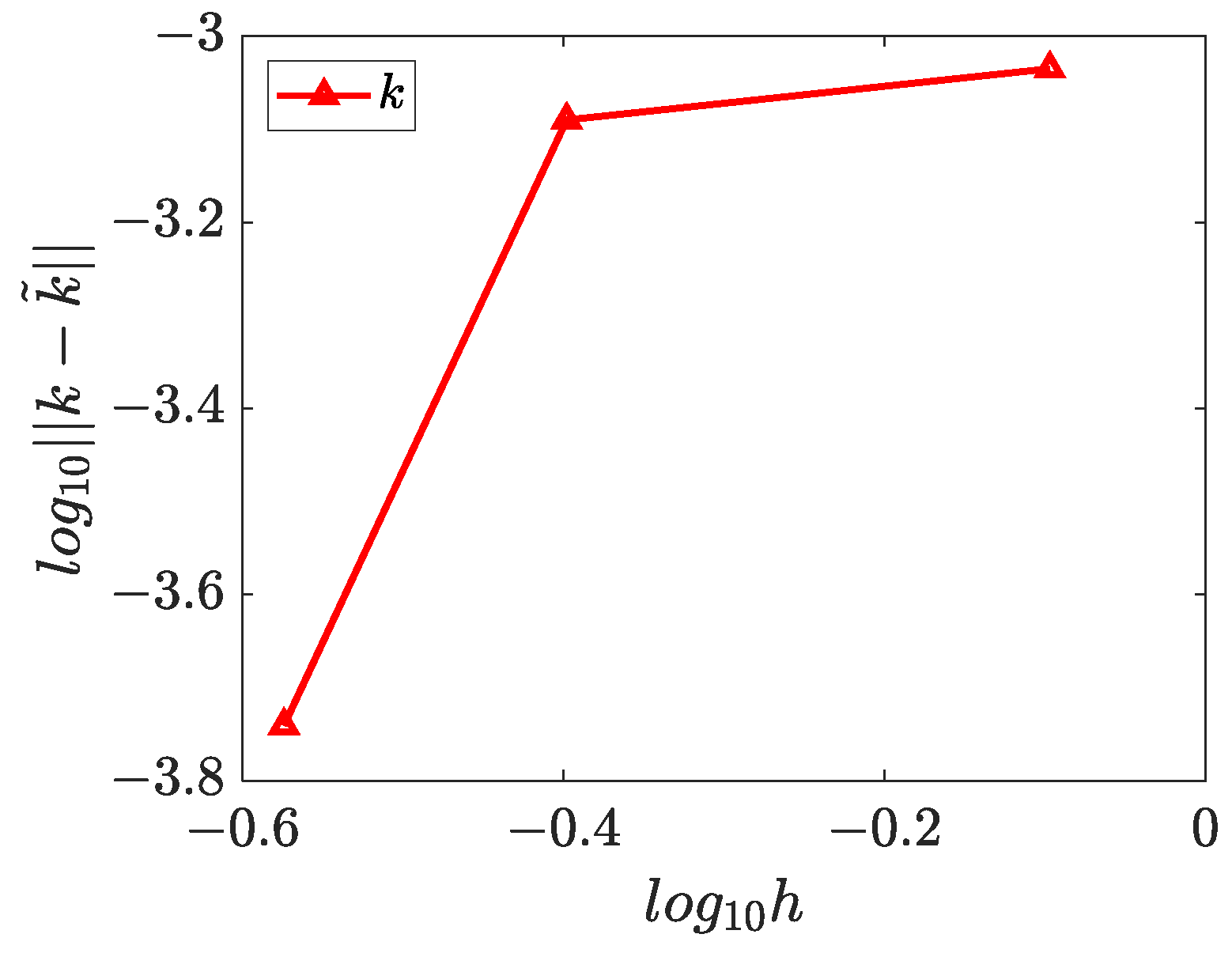
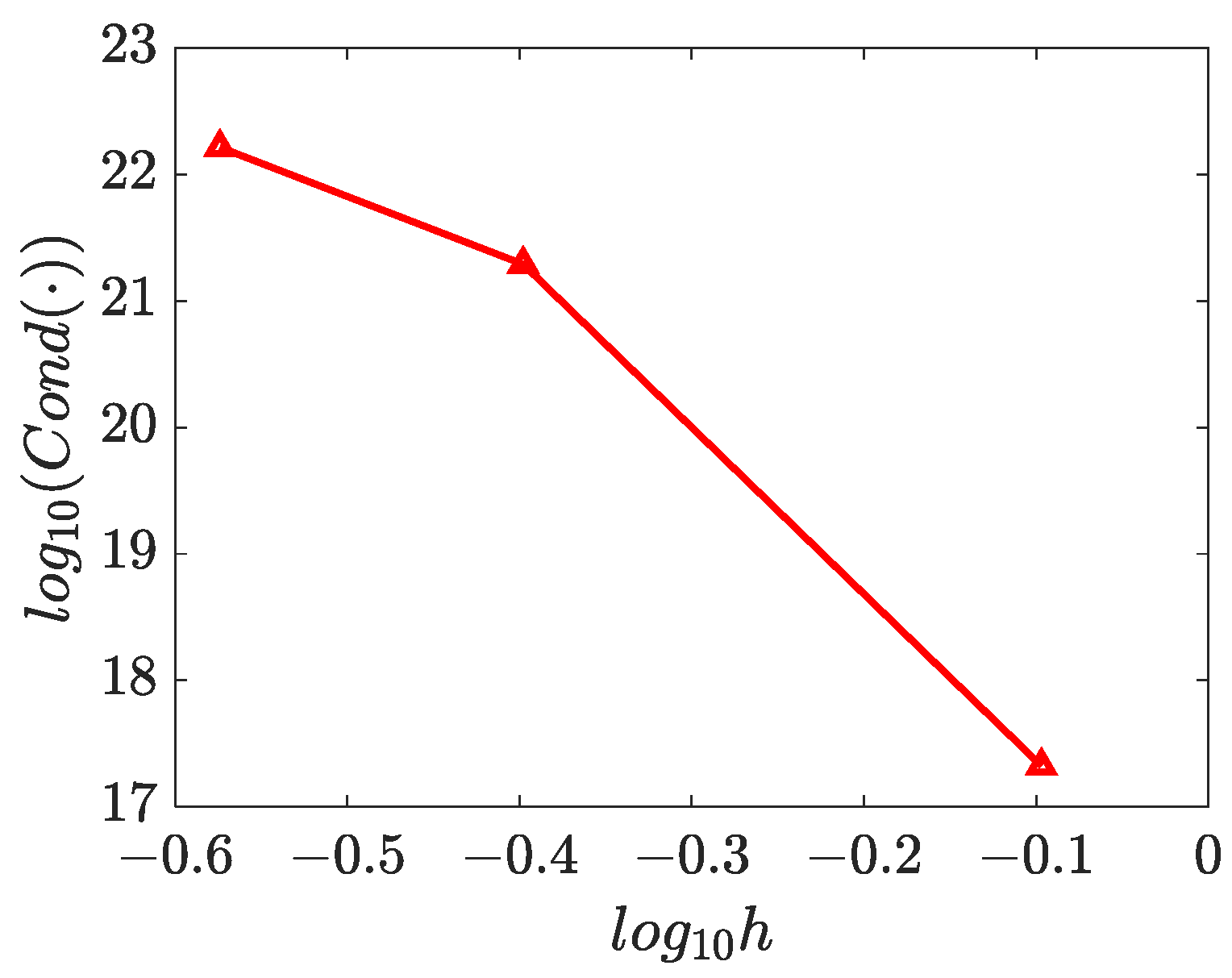
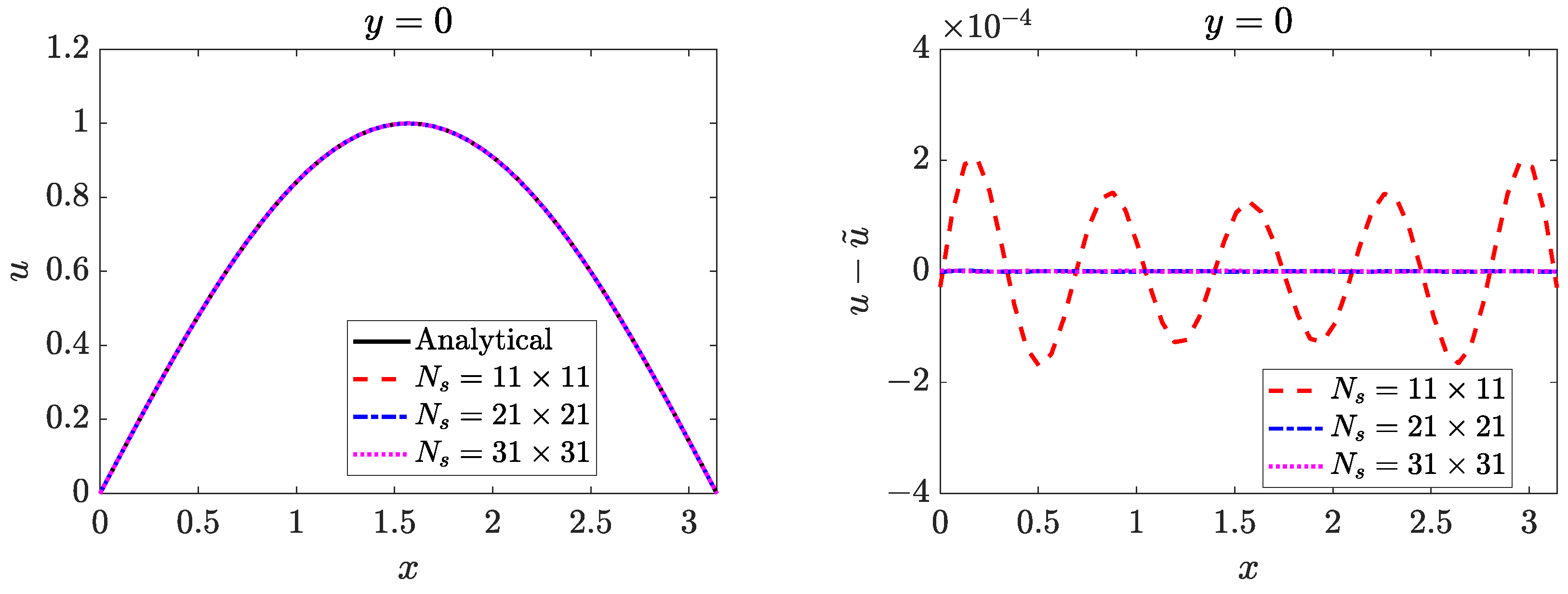
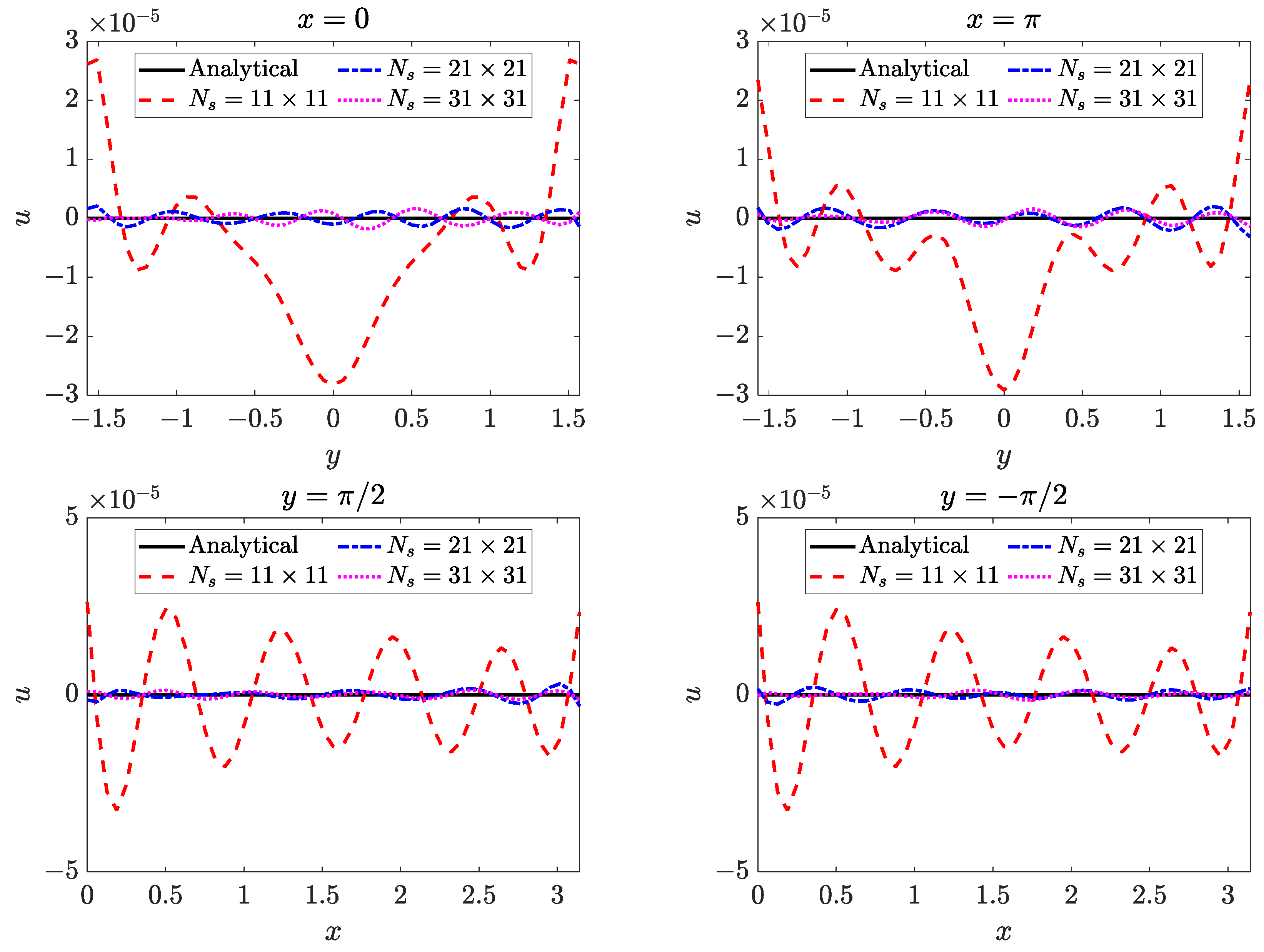
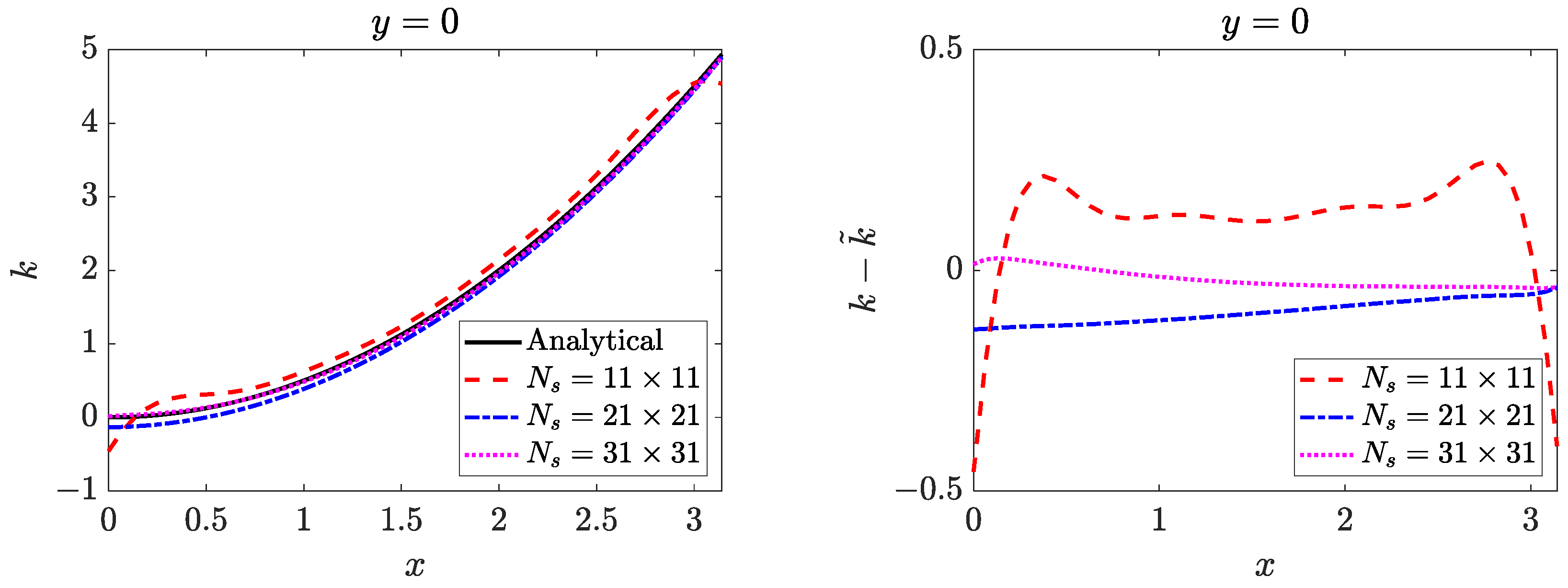
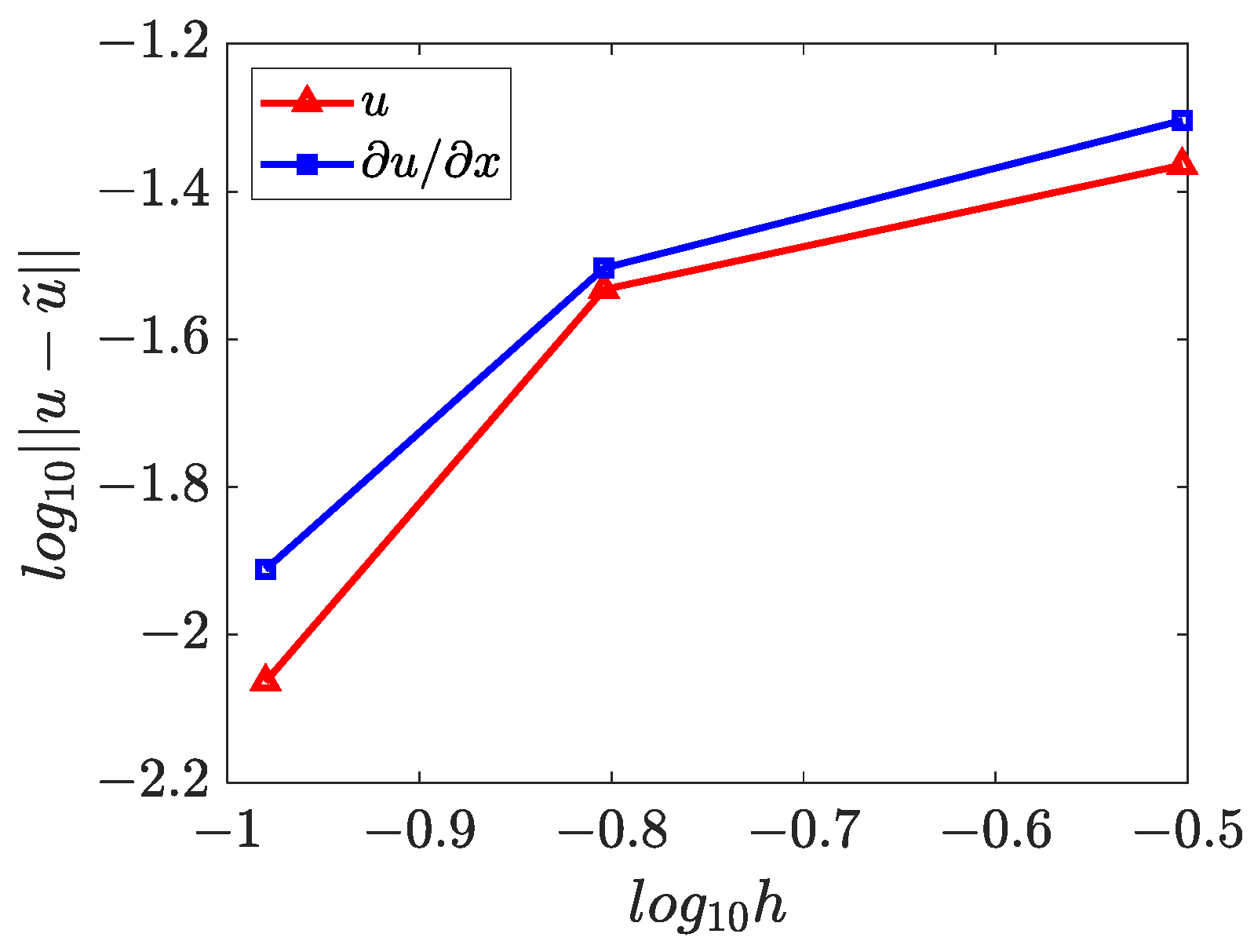
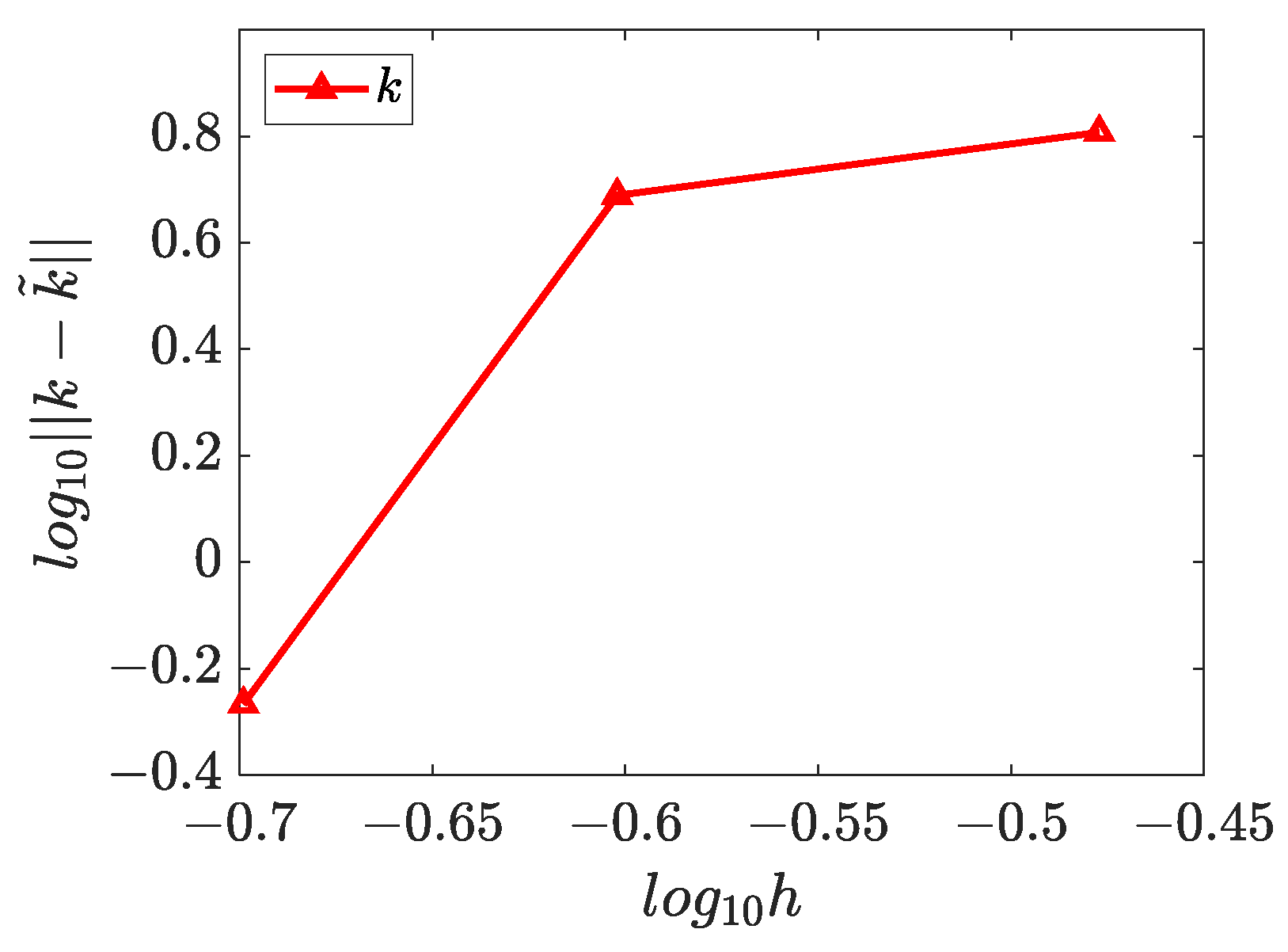
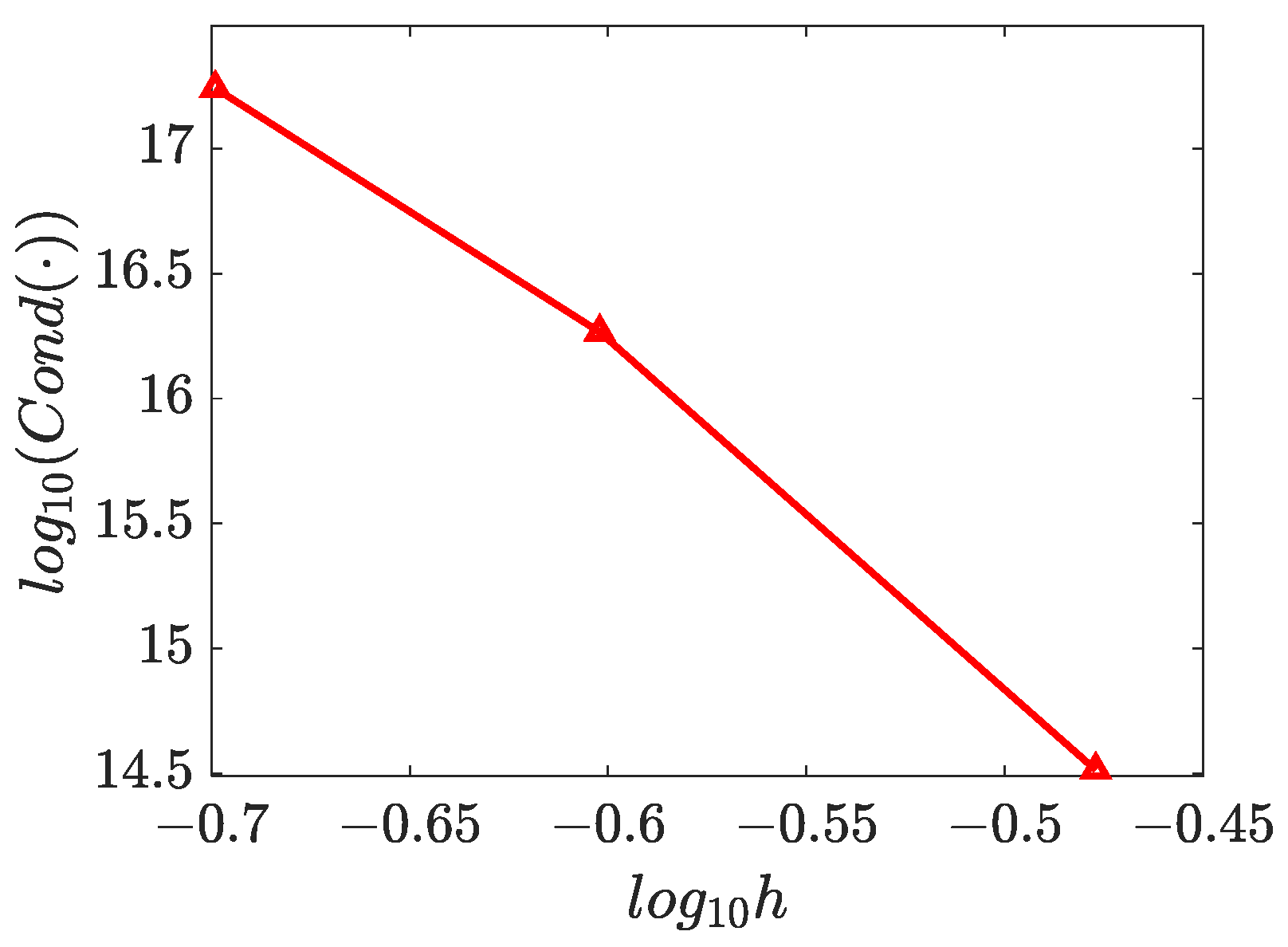
4.2. Two-Dimensional Inverse Helmholtz Problem of Constant Parameter Identification in Irregular Geometry
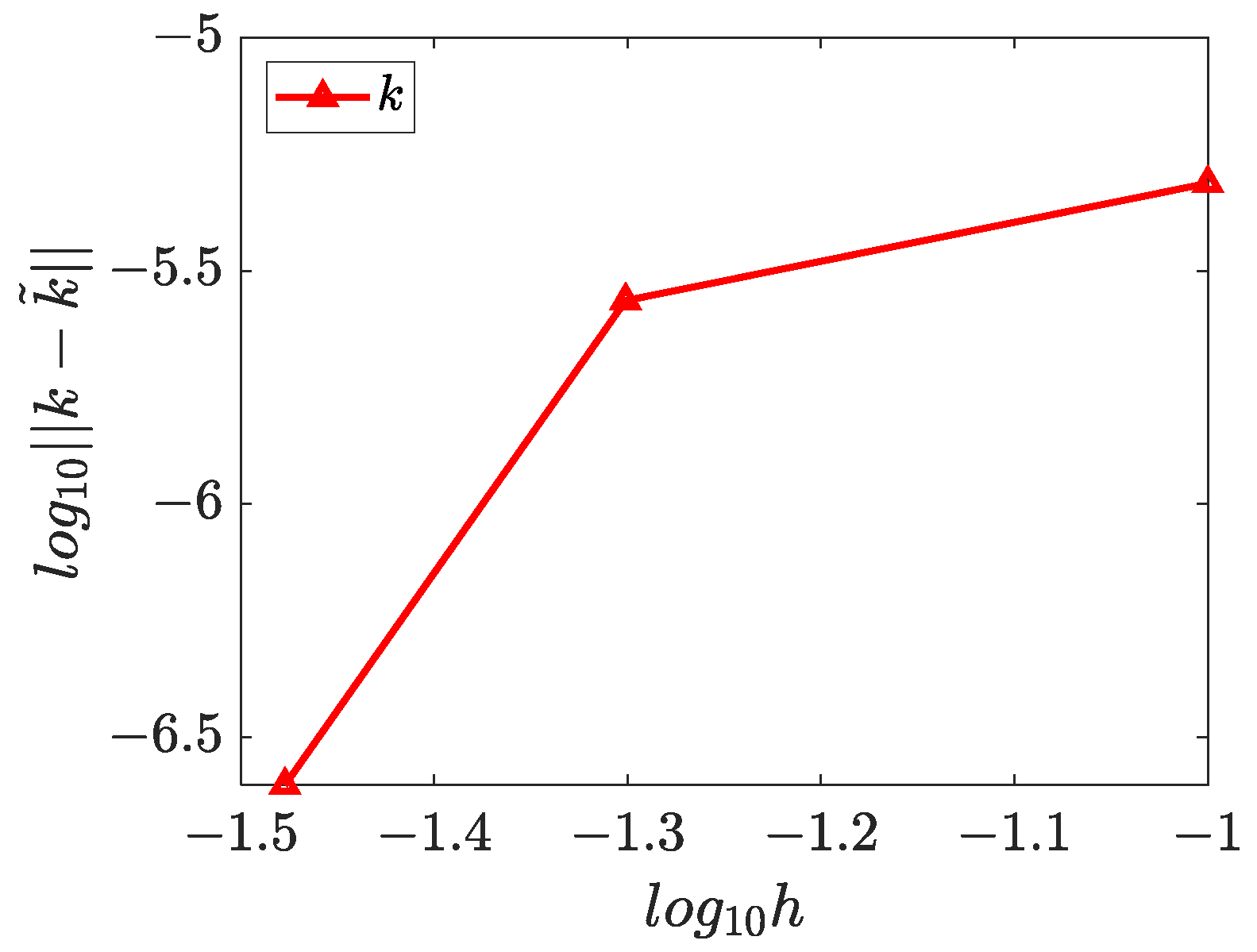
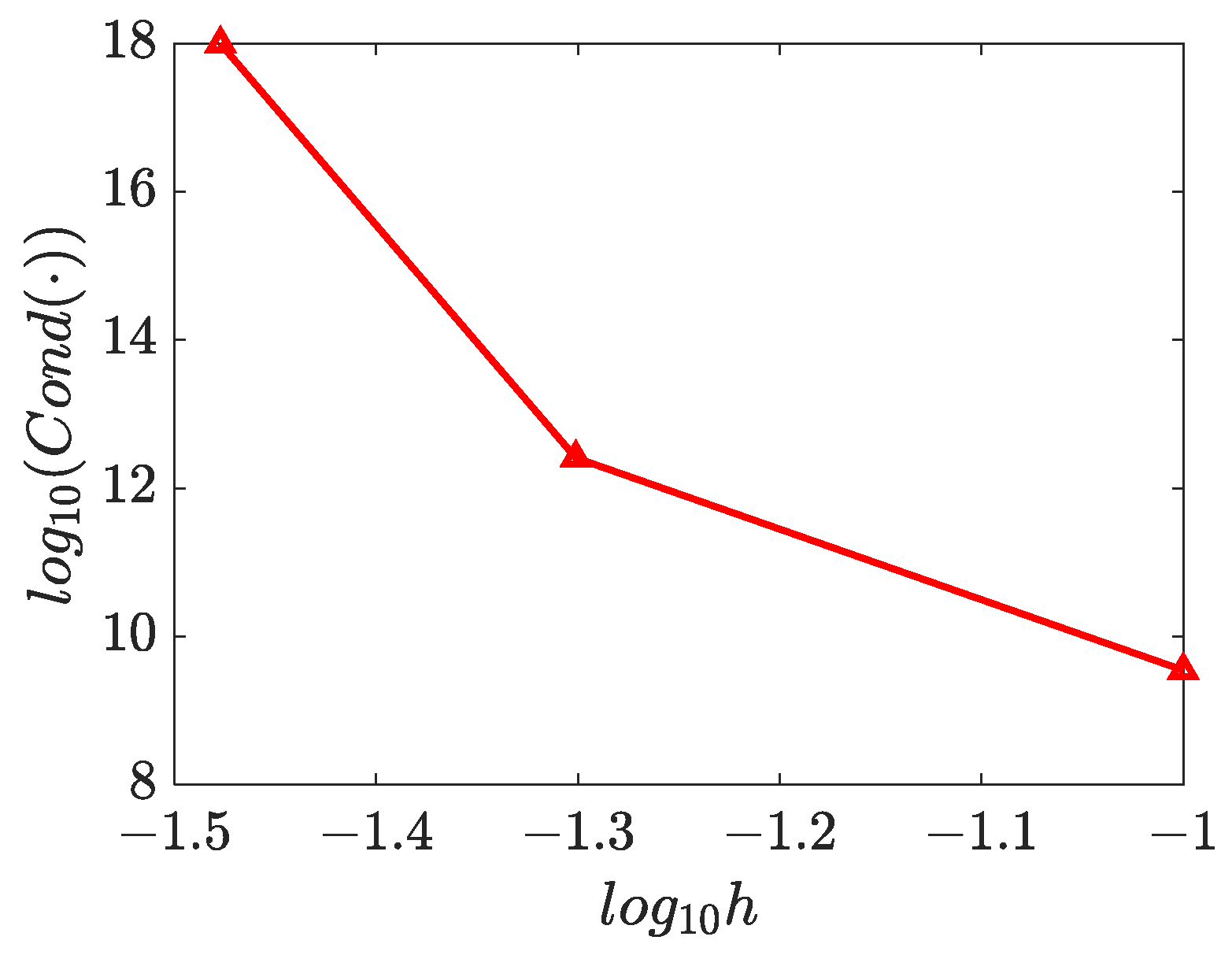
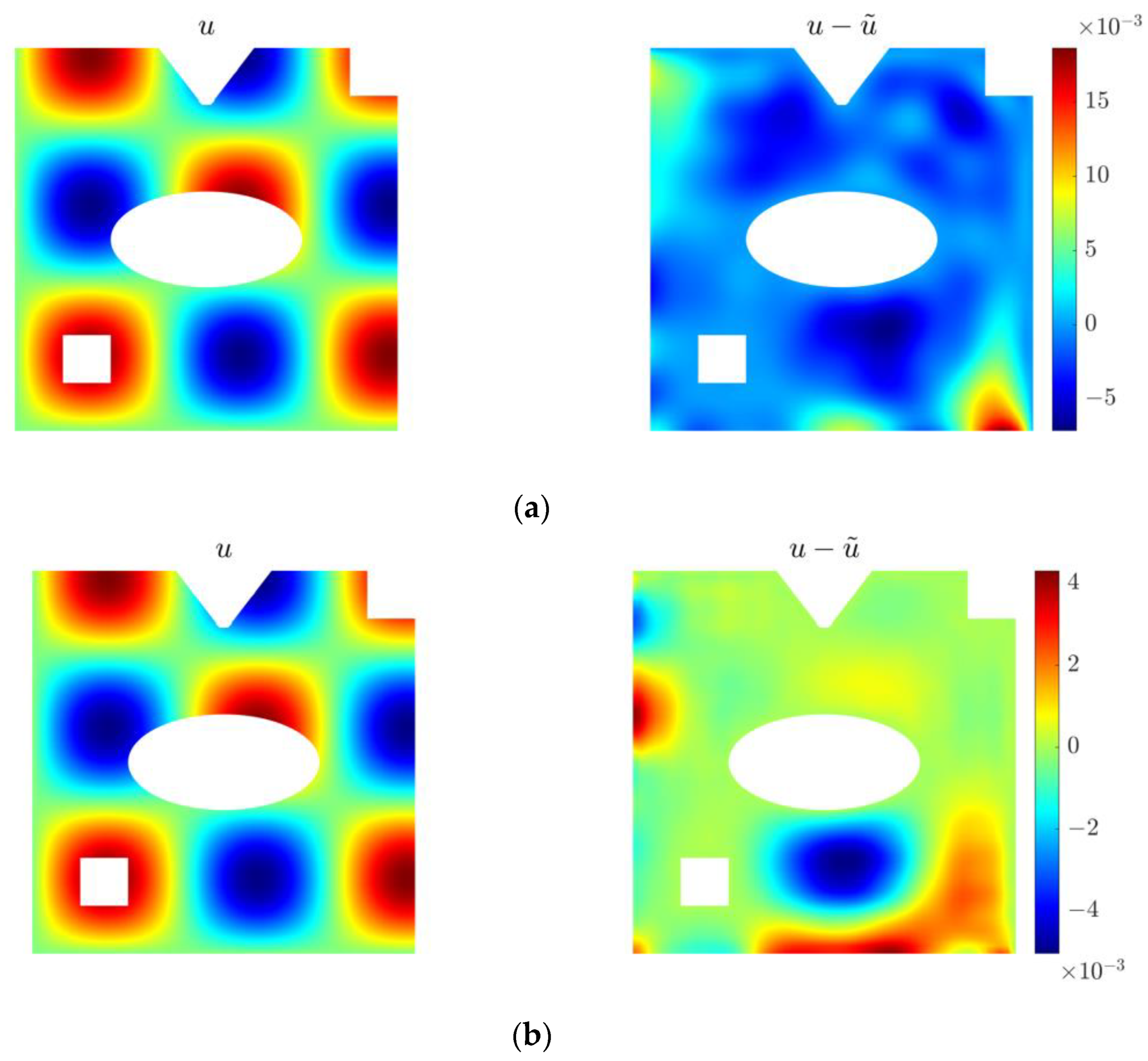
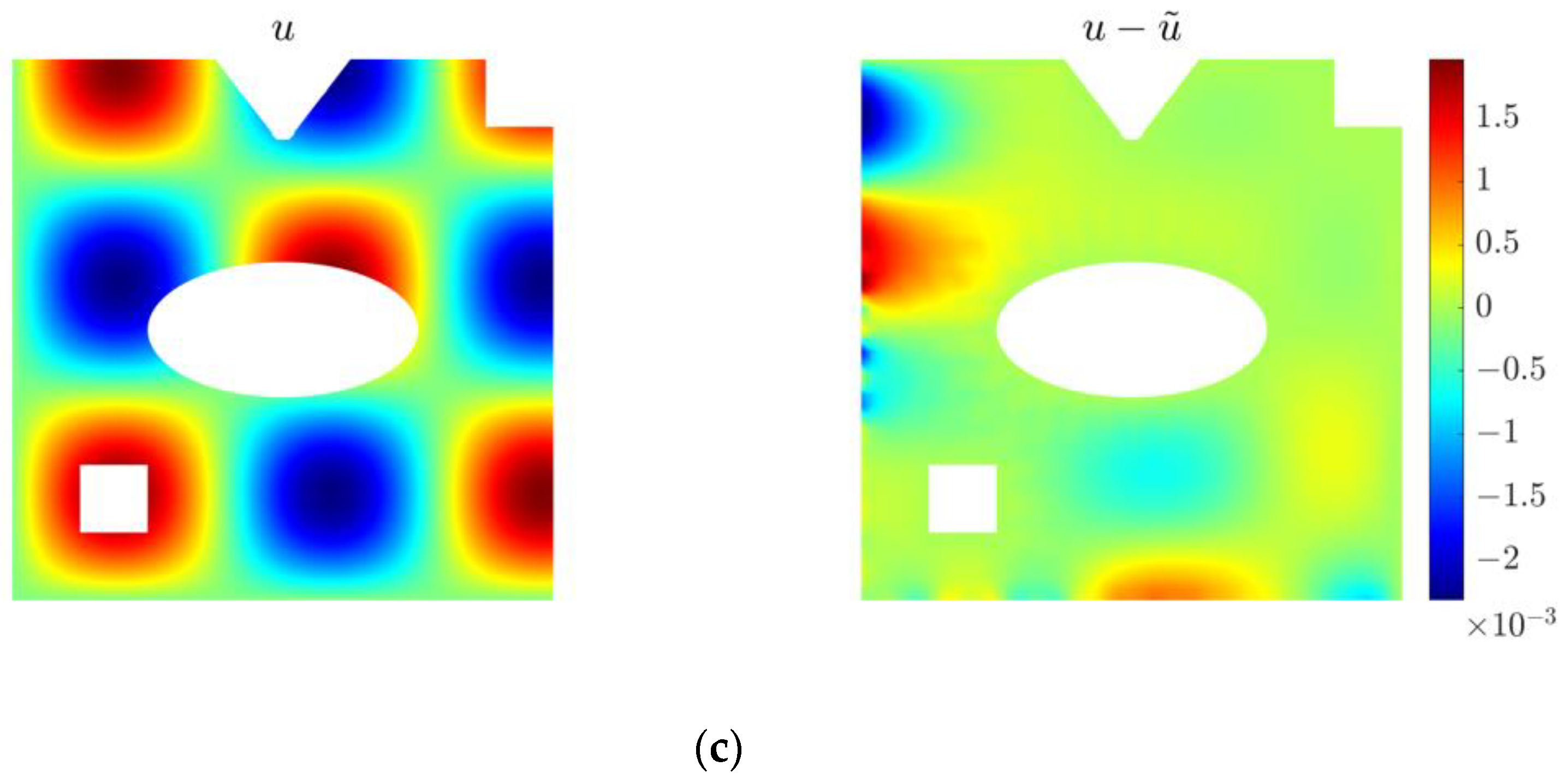
4.3. Two-Dimensional Inverse Helmholtz Problem of Parameter Identification
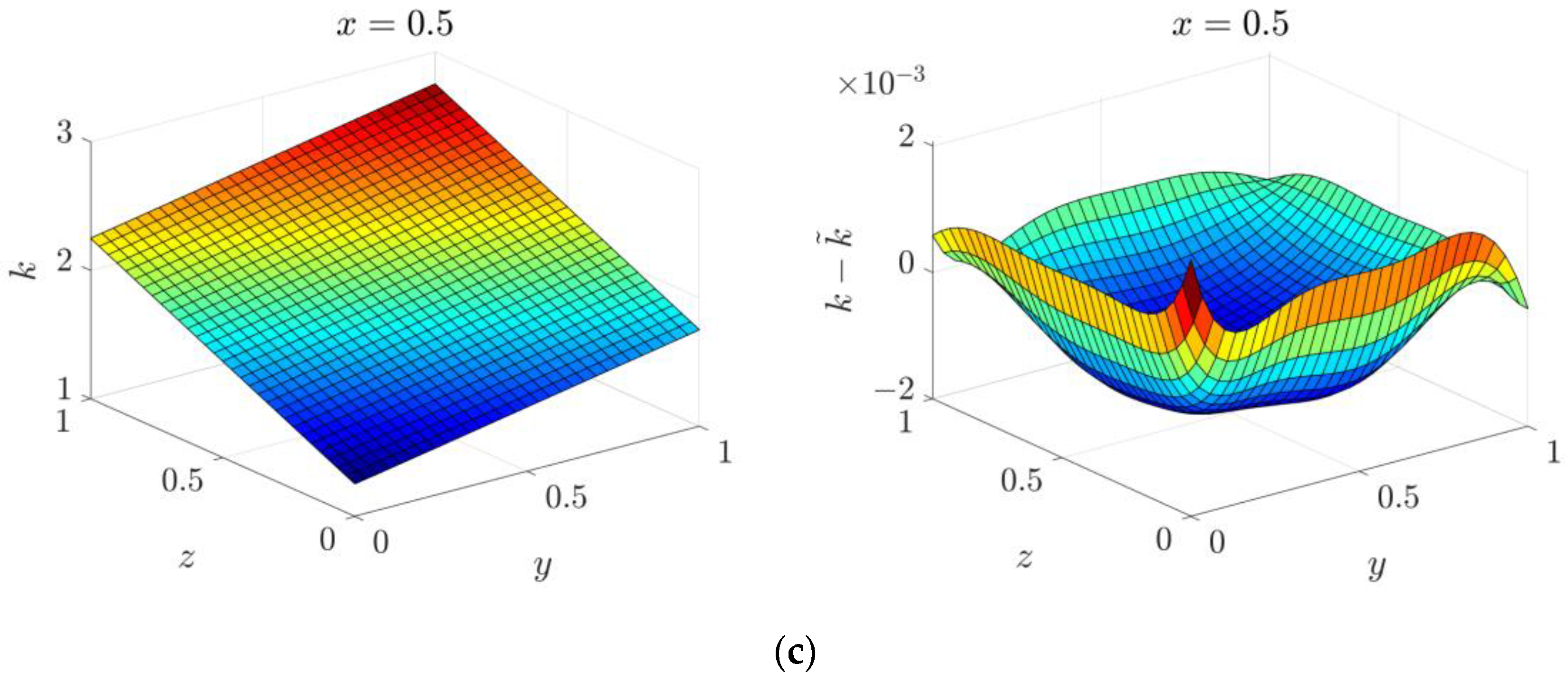
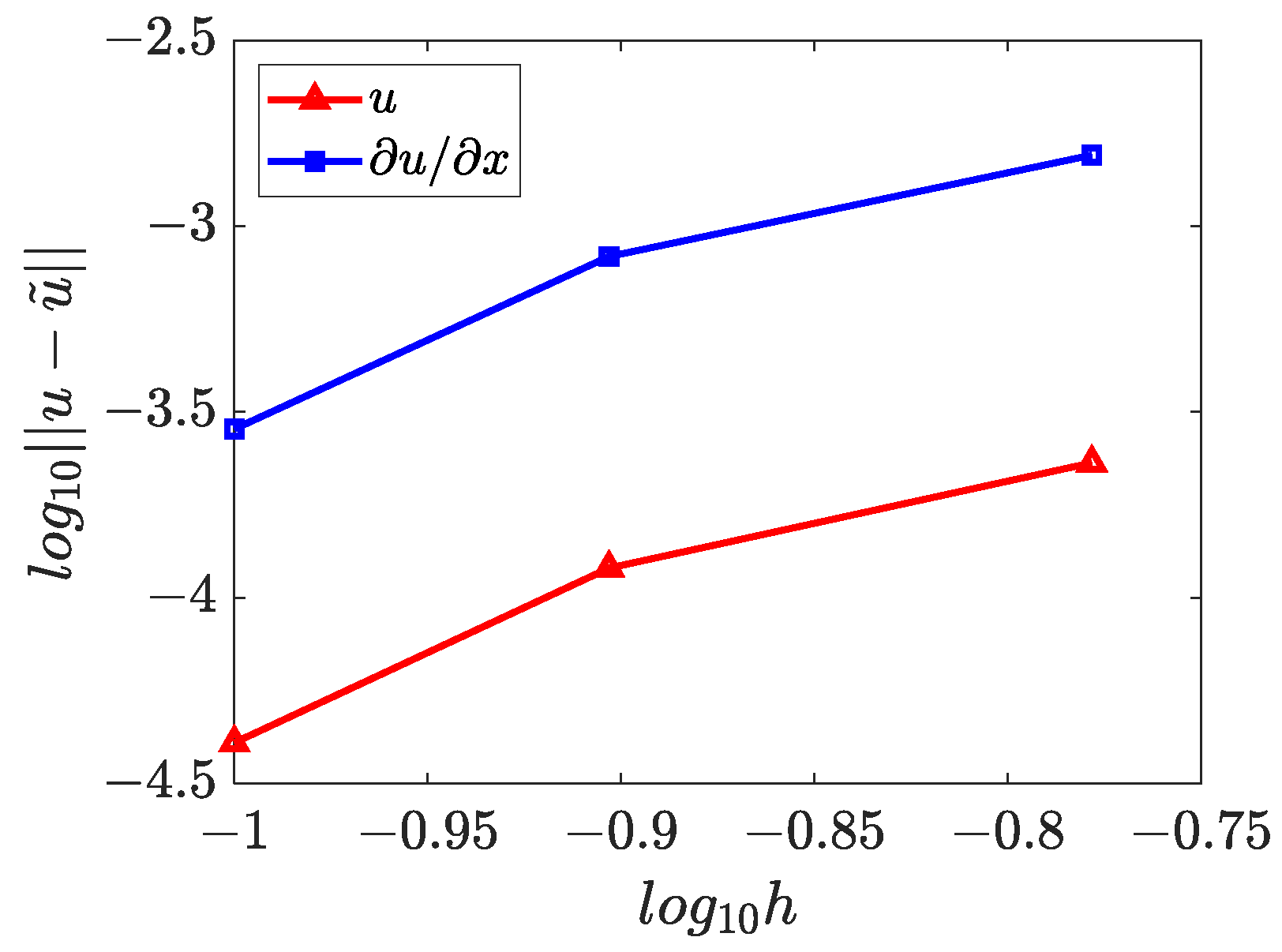
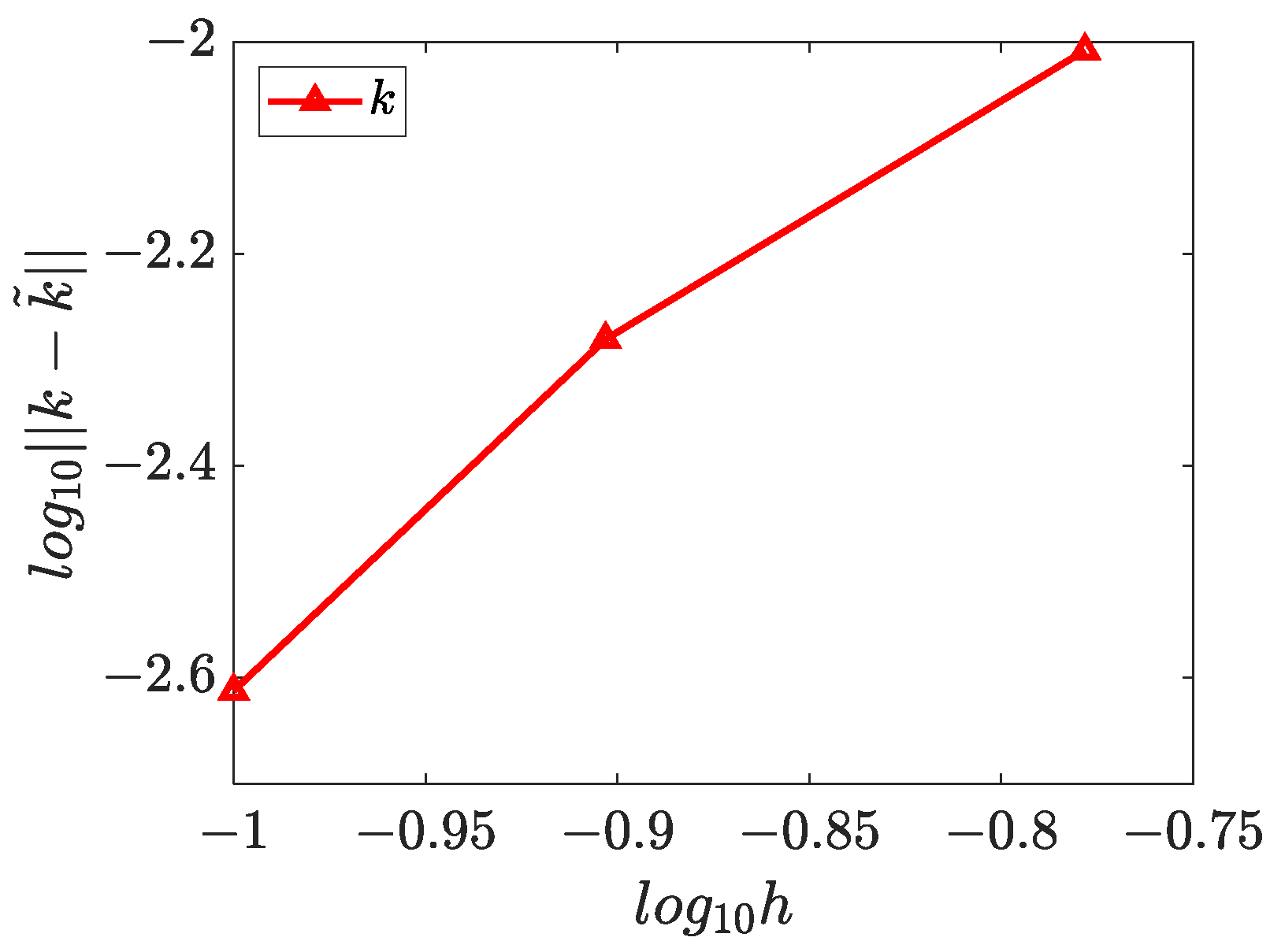
4.4. Three-Dimensional Inverse Helmholtz Problem of Parameter Identification in Cubic Domain
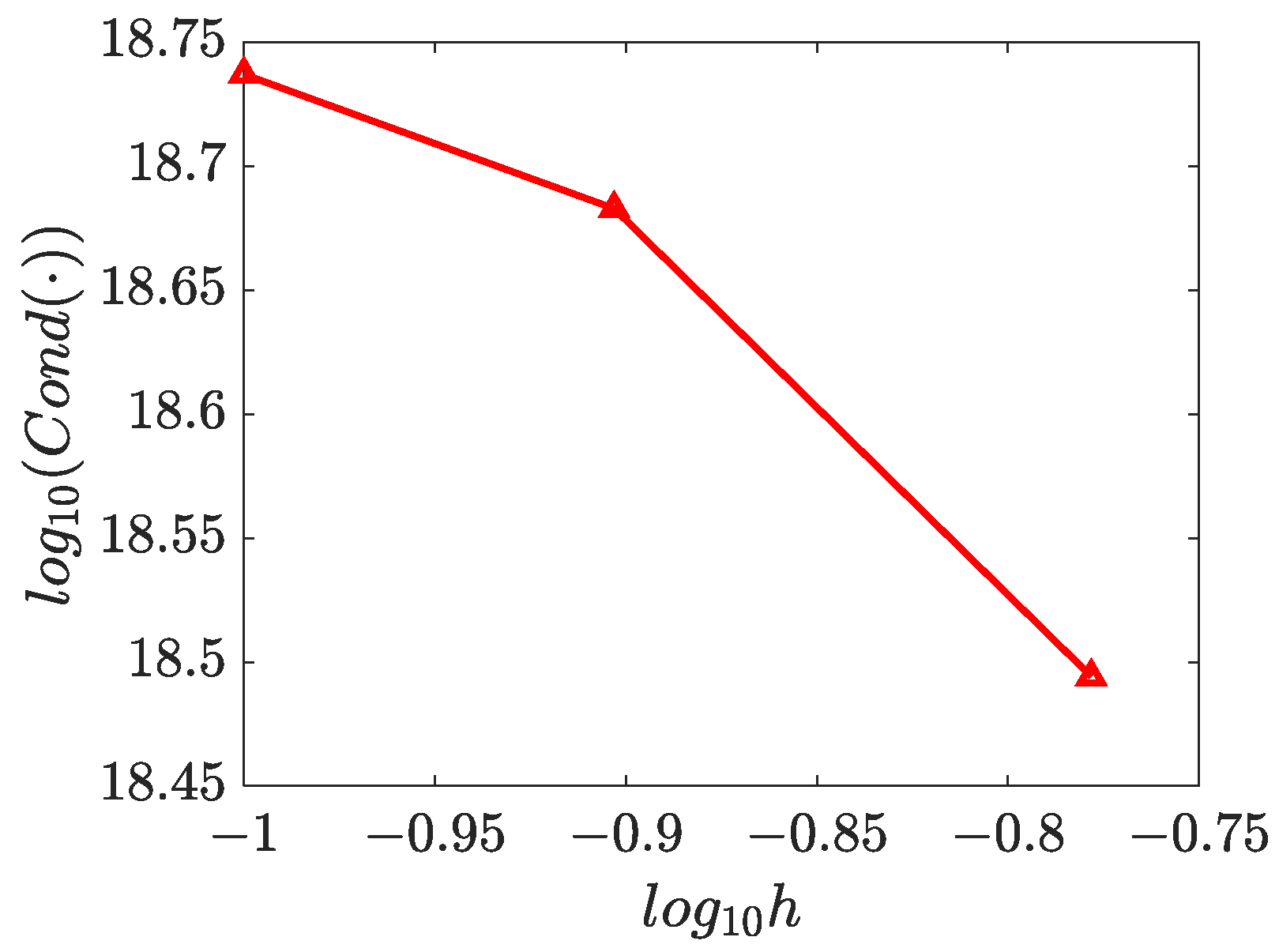
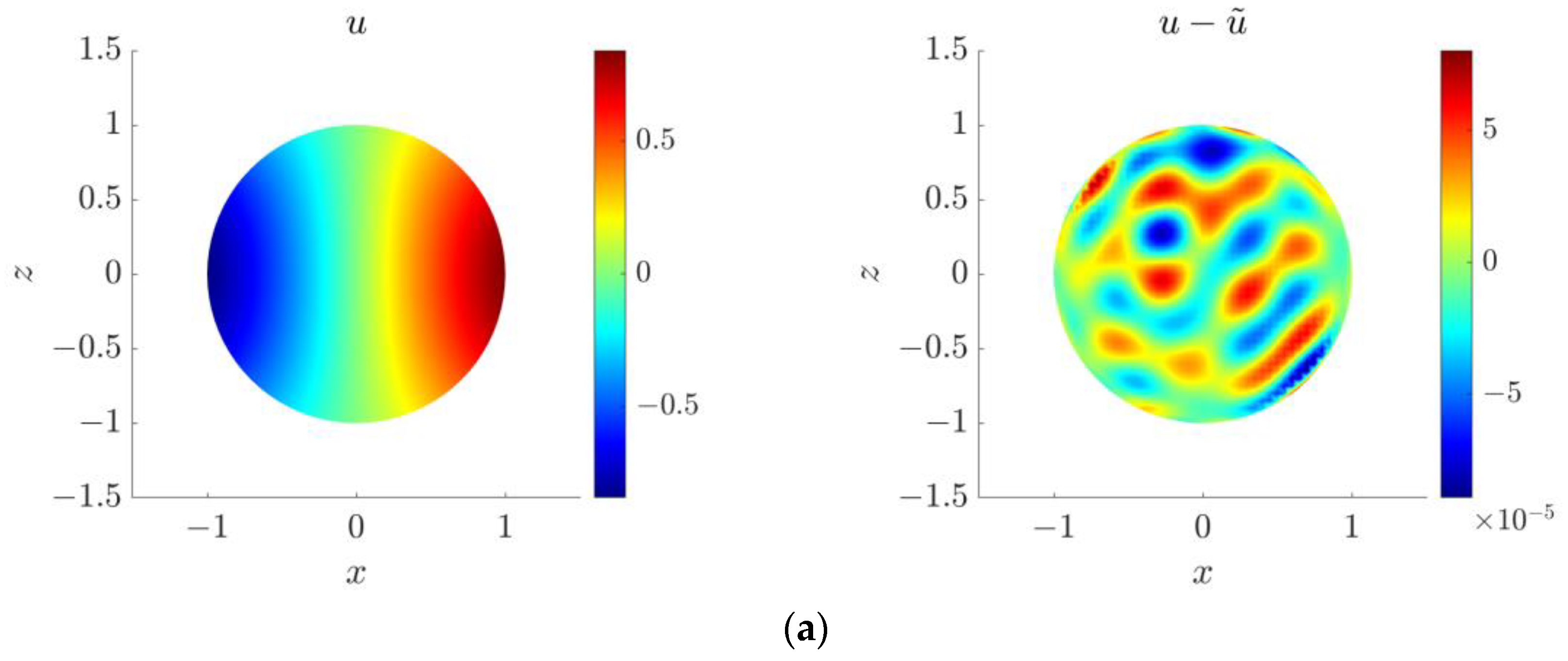
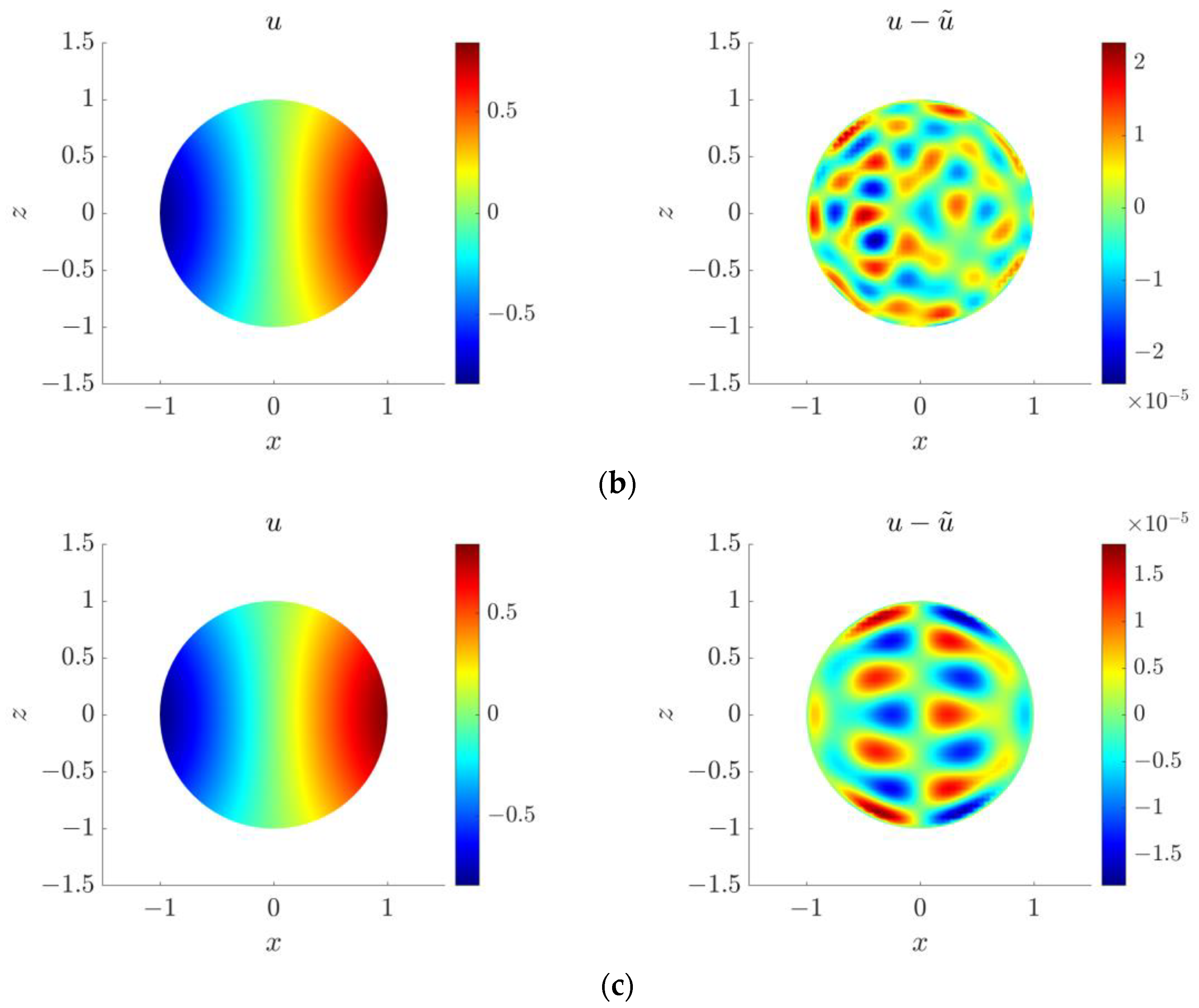
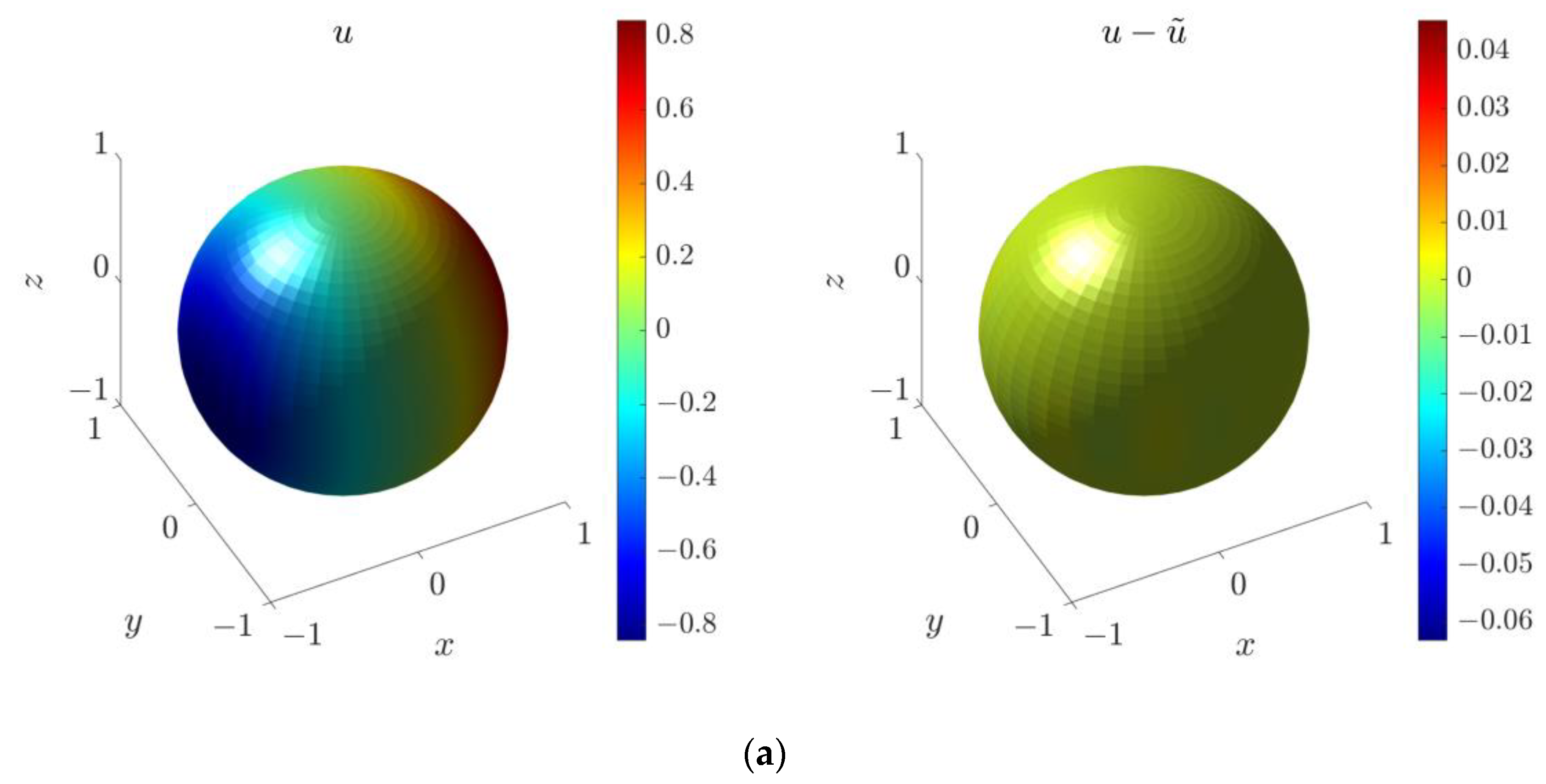
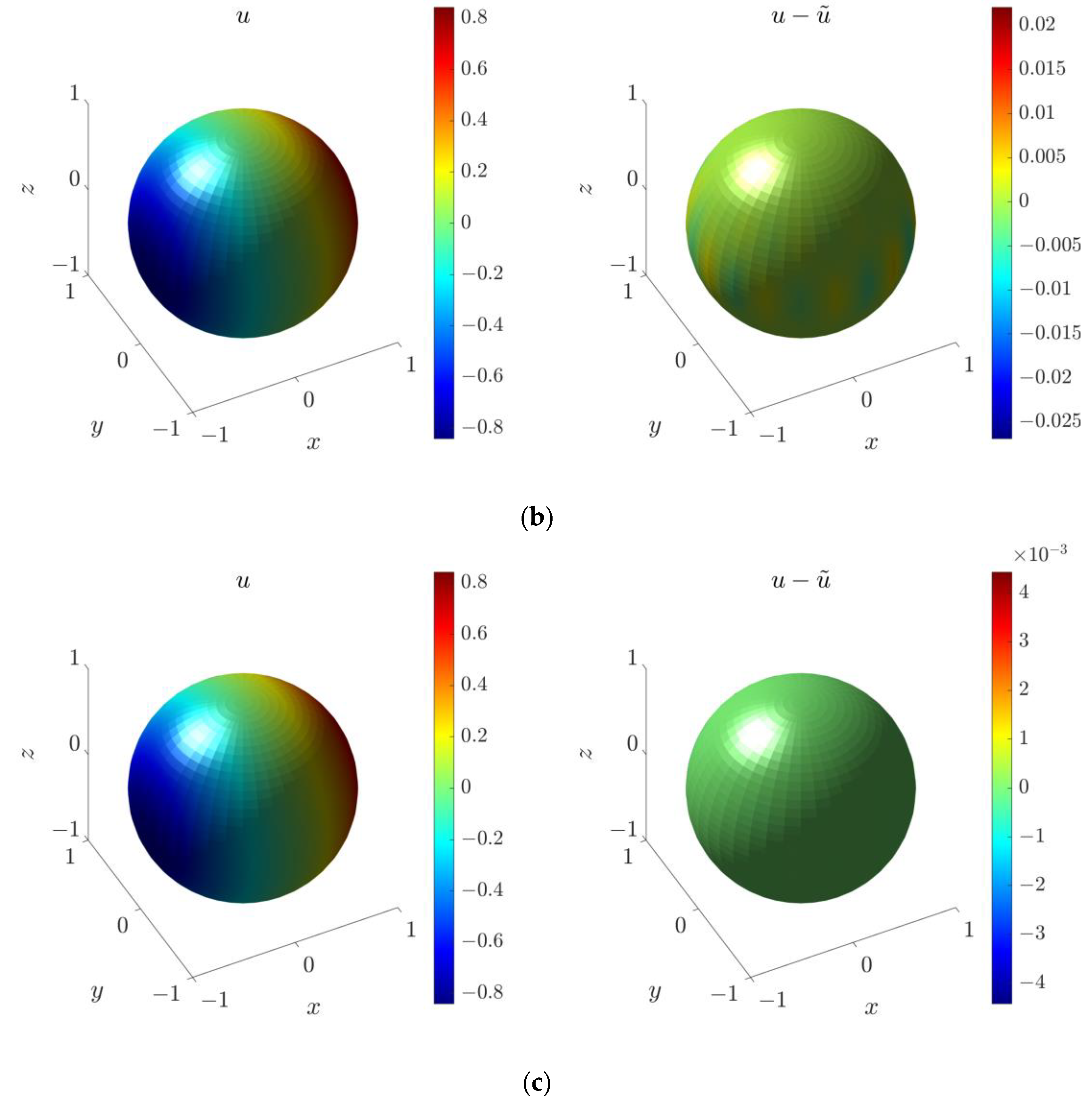
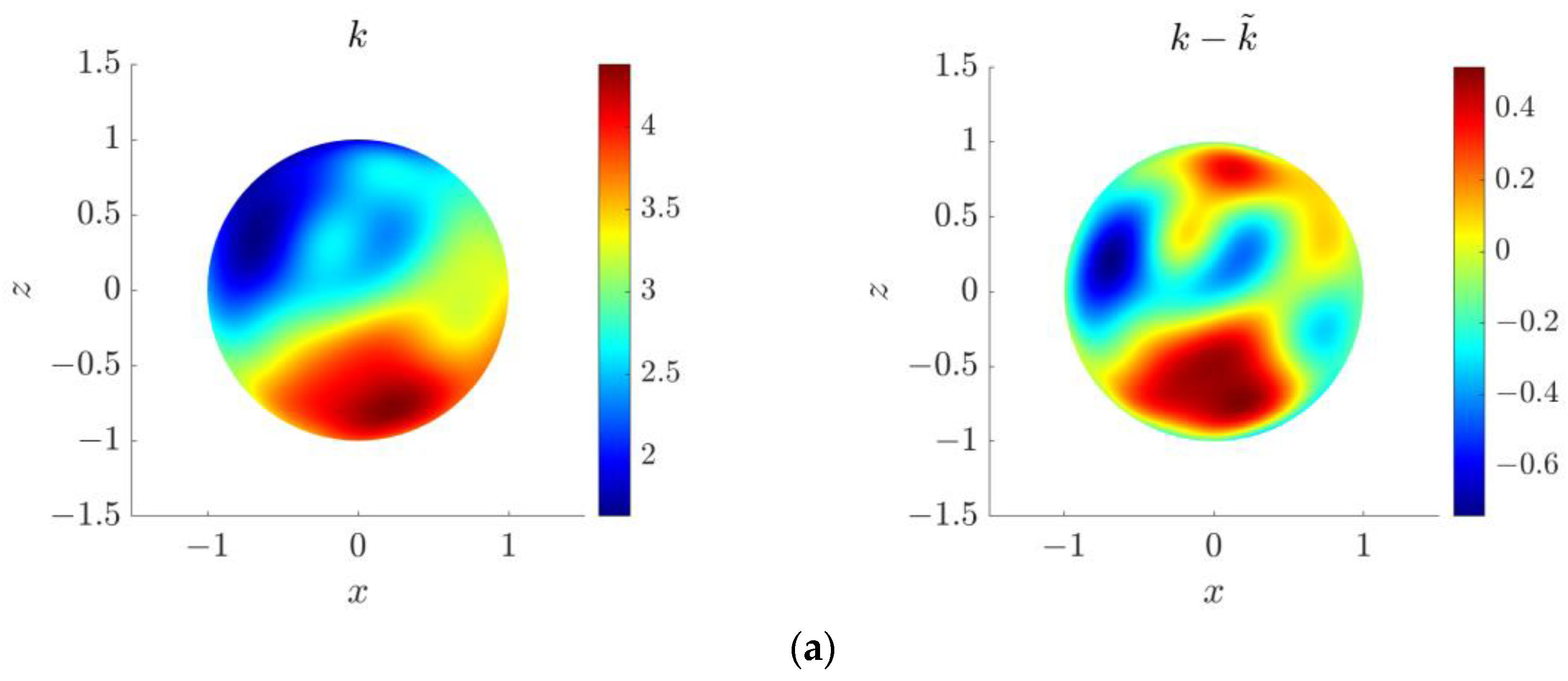
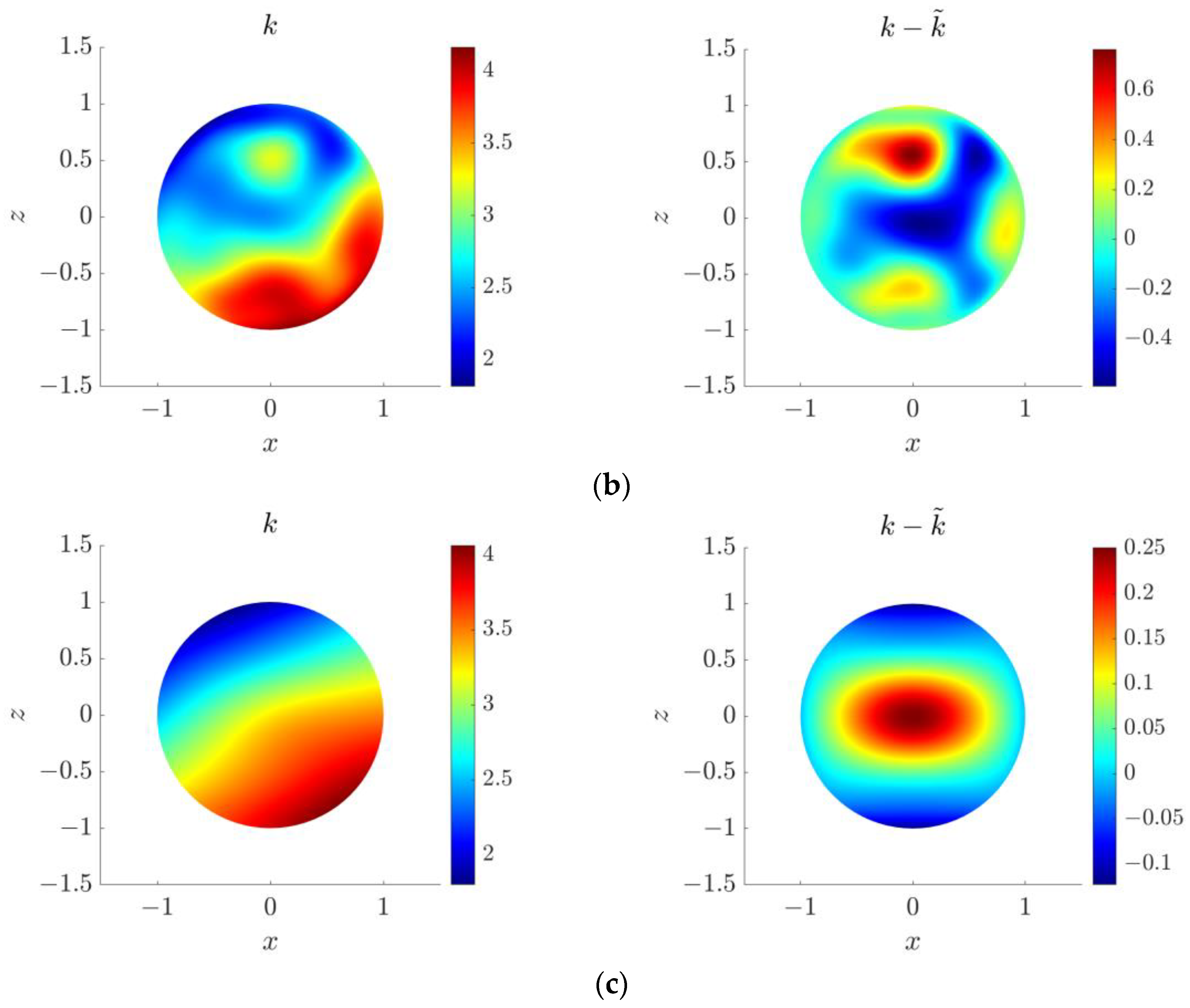
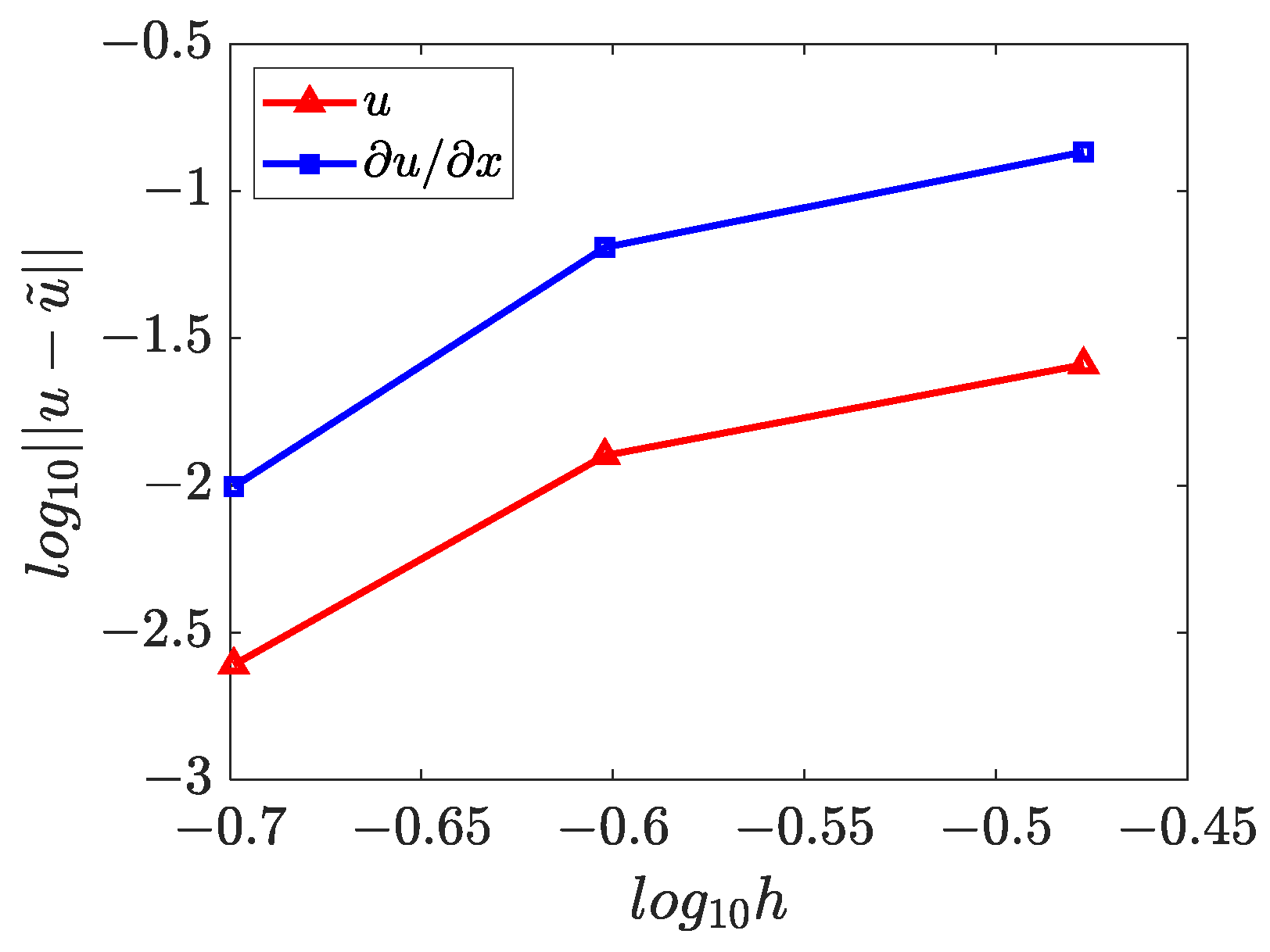
4.5. Three-Dimensional Inverse Helmholtz Problem of Parameter Identification in Spherical Domain
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beskos, D.E. Boundary element methods in dynamic analysis: Part II (1986–1996). Appl. Mech. Rev. 1997, 50, 149–197. [Google Scholar] [CrossRef]
- Hall, W.S.; Mao, X.Q. A boundary element investigation of irregular frequencies in electromagnetic scattering. Eng. Anal. Bound. Elem. 1995, 16, 245–252. [Google Scholar] [CrossRef]
- Chen, J.T.; Wong, F.C. Dual formulation of multiple reciprocity method for the acoustic mode of a cavity with a thin partition. J. Sound Vib. 1998, 217, 75–95. [Google Scholar] [CrossRef]
- Wood, A.S.; Tupholme, G.E.; Bhatti, M.I.H.; Heggs, P.J. Steady-state heat transfer through extended plane surfaces. Int. Commun. Heat Mass Transf. 1995, 22, 99–109. [Google Scholar] [CrossRef]
- Shojaei, A.; Galvanetto, U.; Rabczuk, T.; Jenabi, A.; Zaccariotto, M. A generalized finite difference method based on the Peridynamic differential operator for the solution of problems in bounded and unbounded domains. Comput. Methods Appl. Mech. Eng. 2019, 343, 100–126. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C. Achievements and some unsolved problems of the finite element method. Int. J. Numer. Methods Eng. 2000, 47, 9–28. [Google Scholar] [CrossRef]
- Onishi, K.; Kobayashi, K.; Ohura, Y. Numerical solution of a boundary inverse problem for the Laplace equation. Theor. Appl. Mech. 1996, 45, 257–264. [Google Scholar]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Liu, W.K.; Chen, Y.; Jun, S.; Chen, J.S.; Belytschko, T.; Pan, C.; Uras, R.A.; Chang, C. Overview and applications of the reproducing kernel particle methods. Arch. Comput. Methods Eng. 1996, 3, 3–80. [Google Scholar] [CrossRef]
- Oñate, E.; Perazzo, F.; Miquel, J. A finite point method for elasticity problems. Comput. Struct. 2001, 79, 2151–2163. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y. A point interpolation method for two-dimensional solids. Int. J. Numer. Methods Eng. 2001, 50, 937–951. [Google Scholar] [CrossRef]
- Cheng, A.D.; Cabral, J.J.S.P. Direct solution of ill-posed boundary value problems by radial basis function collocation method. Int. J. Numer. Methods Eng. 2005, 64, 45–64. [Google Scholar] [CrossRef]
- Wang, L.; Qian, Z. A meshfree stabilized collocation method (SCM) based on reproducing kernel approximation. Comput. Methods Appl. Mech. Eng. 2020, 371, 113303. [Google Scholar] [CrossRef]
- Wang, L.; Hu, M.; Zhong, Z.; Yang, F. Stabilized Lagrange Interpolation Collocation Method: A meshfree method incorporating the advantages of finite element method. Comput. Methods Appl. Mech. Eng. 2023, 404, 115780. [Google Scholar] [CrossRef]
- Wang, L. Radial basis functions methods for boundary value problems: Performance comparison. Eng. Anal. Bound. Elem. 2017, 84, 191–205. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Zhou, Y.; Yang, F. Static and dynamic analysis of thin functionally graded shell with in-plane material inhomogeneity. Int. J. Mech. Sci. 2021, 193, 106165. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Q. A Multiscale RBF Collocation Method for the Numerical Solution of Partial Differential Equations. Mathematics 2019, 7, 964. [Google Scholar] [CrossRef]
- Dehghan, M.; Shokri, A. A meshless method for numerical solution of the one-dimensional wave equation with an integral condition using radial basis functions. Numer. Algorithms 2009, 52, 461–477. [Google Scholar] [CrossRef]
- Wang, L.; Chu, F.; Zhong, Z. Study of radial basis collocation method for wave propagation. Eng. Anal. Bound. Elem. 2013, 37, 453–463. [Google Scholar] [CrossRef]
- Hu, H.Y.; Chen, J.S.; Hu, W. Weighted radial basis collocation method for boundary value problems. Int. J. Numer. Methods Eng. 2007, 69, 2736–2757. [Google Scholar] [CrossRef]
- Zhang, X.; Song, K.Z.; Lu, M.W.; Liu, X. Meshless methods based on collocation with radial basis functions. Comput. Mech. 2000, 26, 333–343. [Google Scholar] [CrossRef]
- Liu, X.; Liu, G.R.; Tai, K.; Lam, K. Radial point interpolation collocation method (RPICM) for partial differential equations. Comput. Math. Appl. 2005, 50, 1425–1442. [Google Scholar] [CrossRef]
- Chen, J.S.; Hillman, M.; Chi, S.W. Meshfree methods: Progress made after 20 years. J. Eng. Mech. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Wang, L.; Zhong, Z. Radial basis collocation method for nearly incompressible elasticity. J. Eng. Mech. 2013, 139, 439–451. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, C.; Wang, Y.; Chen, W.; Sladek, J.; Sladek, V. A local RBF collocation method for band structure computations of 2D solid/fluid and fluid/solid phononic crystals. Int. J. Numer. Methods Eng. 2017, 110, 467–500. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Roque, C.M.C.; Jorge, R.M.N. Free vibration analysis of symmetric laminated composite plates by FSDT and radial basis functions. Comput. Methods Appl. Mech. Eng. 2005, 194, 4265–4278. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Fasshauer, G.E. Computation of natural frequencies of shear deformable beams and plates by an RBF-pseudospectral method. Comput. Methods Appl. Mech. Eng. 2006, 196, 134–146. [Google Scholar] [CrossRef]
- Chu, F.; Wang, L.; Zhong, Z.; He, J. Hermite radial basis collocation method for vibration of functionally graded plates with in-plane material inhomogeneity. Comput. Struct. 2014, 142, 79–89. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Roque, C.M.C.; Polit, O. Analysis of laminated shells by a sinusoidal shear deformation theory and radial basis functions collocation, accounting for through-the-thickness deformations. Compos. Part B Eng. 2011, 42, 1276–1284. [Google Scholar] [CrossRef]
- Chen, J.S.; Wang, L.; Hu, H.Y.; Chi, S.W. Subdomain radial basis collocation method for heterogeneous media. Int. J. Numer. Methods Eng. 2009, 80, 163–190. [Google Scholar] [CrossRef]
- Zerroukat, M.; Power, H.; Chen, C. A numerical method for heat transfer problems using collocation and radial basis functions. Int. J. Numer. Methods Eng. 1998, 42, 1263–1278. [Google Scholar] [CrossRef]
- Wang, L.; Chen, J.S.; Hu, H.Y. Subdomain radial basis collocation method for fracture mechanics. Int. J. Numer. Methods Eng. 2010, 83, 851–876. [Google Scholar] [CrossRef]
- Hon, Y.C.; Chen, W. Boundary knot method for 2D and 3D Helmholtz and convection–diffusion problems under complicated geometry. Int. J. Numer. Methods Eng. 2003, 56, 1931–1948. [Google Scholar] [CrossRef]
- Marin, L.; Lesnic, D. The method of fundamental solutions for the Cauchy problem associated with two-dimensional Helmholtz-type equations. Comput. Struct. 2005, 83, 267–278. [Google Scholar] [CrossRef]
- Marin, L. A meshless method for the numerical solution of the Cauchy problem associated with three-dimensional Helmholtz-type equations. Appl. Math. Comput. 2005, 165, 355–374. [Google Scholar] [CrossRef]
- Jin, B.; Zheng, Y. A meshless method for some inverse problems associated with the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 2006, 195, 2270–2288. [Google Scholar] [CrossRef]
- Hon, Y.C.; Wei, T. A fundamental solution method for inverse heat conduction problem. Eng. Anal. Bound. Elem. 2004, 28, 489–495. [Google Scholar] [CrossRef]
- Shojaei, A.; Boroomand, B.; Soleimanifar, E. A meshless method for unbounded acoustic problems. J. Acoust. Soc. Am. 2016, 139, 2613–2623. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Seleson, P.; Cyron, C.J. Dirichlet absorbing boundary conditions for classical and peridynamic diffusion-type models. Comput. Mech. 2020, 66, 773–793. [Google Scholar] [CrossRef]
- Hermann, A.; Shojaei, A.; Steglich, D.; Höche, D.; Zeller-Plumhoff, B.; Cyron, C.J. Combining peridynamic and finite element simulations to capture the corrosion of degradable bone implants and to predict their residual strength. Int. J. Mech. Sci. 2022, 220, 107143. [Google Scholar] [CrossRef]
- Li, M.; Jiang, T.; Hon, Y.C. A meshless method based on RBFs method for nonhomogeneous backward heat conduction problem. Eng. Anal. Bound. Elem. 2010, 34, 785–792. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, X.; Zhang, H.; Zhang, Q. The Solution of Backward Heat Conduction Problem with Piecewise Linear Heat Transfer Coefficient. Mathematics 2019, 7, 388. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Qian, Z. A meshfree method for inverse wave propagation using collocation and radial basis functions. Comput. Methods Appl. Mech. Eng. 2017, 322, 311–350. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Qian, Z.; Gao, Y.; Zhou, Y. Direct collocation method for identifying the initial conditions in the inverse wave problem using radial basis functions. Inverse Probl. Sci. Eng. 2018, 26, 1695–1727. [Google Scholar] [CrossRef]
- Wang, L.; Qian, Z.; Wang, Z.; Gao, Y.; Peng, Y. An efficient radial basis collocation method for the boundary condition identification of the inverse wave problem. Int. J. Appl. Mech. 2018, 10, 1850010. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Hardy, R.L. Research results in the application of multiquadratic equations to surveying and mapping problems. Surv. Mapp. 1975, 35, 321–332. [Google Scholar]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Madych, W.R.; Nelson, S.A. Multivariate interpolation and conditionally positive definite functions. II. Math. Comput. 1990, 54, 211–230. [Google Scholar] [CrossRef]
- Li, Z.C.; Lu, T.T.; Hu, H.Y.; Cheng, A.H. Trefftz and Collocation Methods; WIT Press: Boston, MA, USA, 2008. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Wang, L.; Yang, F.; Zhou, Y. Weighted Radial Basis Collocation Method for the Nonlinear Inverse Helmholtz Problems. Mathematics 2023, 11, 662. https://doi.org/10.3390/math11030662
Hu M, Wang L, Yang F, Zhou Y. Weighted Radial Basis Collocation Method for the Nonlinear Inverse Helmholtz Problems. Mathematics. 2023; 11(3):662. https://doi.org/10.3390/math11030662
Chicago/Turabian StyleHu, Minghao, Lihua Wang, Fan Yang, and Yueting Zhou. 2023. "Weighted Radial Basis Collocation Method for the Nonlinear Inverse Helmholtz Problems" Mathematics 11, no. 3: 662. https://doi.org/10.3390/math11030662
APA StyleHu, M., Wang, L., Yang, F., & Zhou, Y. (2023). Weighted Radial Basis Collocation Method for the Nonlinear Inverse Helmholtz Problems. Mathematics, 11(3), 662. https://doi.org/10.3390/math11030662






