Statistical Method Based Waveform Optimization in Collocated MIMO Radar Systems

Abstract

Multiple-input multiple-output (MIMO) radar has acquired considerable attention as it offers an additional degree of freedom which results in performance gains when contrasted with the regular single antenna element radar system. Waveform optimization in MIMO radar is essential as it can offer tremendous improvements in target detection which are quantified in terms of reductions in the symbol error rate and improvements in target detection probability. In this work, we foster a strategy for the optimization of transmitter and receiver waveform in a collocated MIMO radar by only considering the second order statistics, thus relaxing the information of the instantaneous target states. Our contributions are primarily two-fold. First, we find a closed-form expression of the outage probability of an unknown target under clutter environment. For this prospect, we model the signal-to-interference-plus-noise ratio in a canonical quadratic structure, and then utilize the modern residue theory approach to characterize the distribution function. Secondly, we propose constrained and unconstrained optimization problems for the reduction in outage probability using algorithmic techniques such as interior-point, sequential-quadratic programming, and the active-set method for the optimization of the transmitter and receiver waveform. We also provide simulated re-enactments to validate our hypothetical deductions.

1. Introduction

Mainly, multiple-input and multiple-output (MIMO) radar can be grouped into two classes: collocated MIMO radar and MIMO radar with widely separated antennas. The former utilizes numerous independently transmitted signals by exciting closely separated antennas to obtain the assorted waveform; therein, all the transmitting antenna elements identically detect the target radar cross sections [1]. The latter notices a target at multiple angles to achieve spatial diversity [2], hence increasing the detection probability [3] and angle of estimation [4]. Unlike the conventional phased array radars with a single transmitting beam, waveform diversity empowers MIMO radar with several advantages including parameter identification, interference rejection capability, and flexible beam pattern design [5]. Designing an aggregated transmitted signal is either based on the direct way or the indirect way. While the direct way is based on designing each sample of a transmitted waveform, the indirect method is more concerned with the synthesis of transmitted signal and statistical parameters such as covariance matrices [6,7,8].

There is a myriad of research directed towards achieving better performance metrics vis-à-vis the waveform optimization of MIMO radar systems. For instance, Quasi-orthogonal waveform designing methods have been proposed in [9,10,11] and they deal with the minimization of auto-correlation and cross-correlation of the waveform. Furthermore, authors in [12,13,14,15,16,17] deliberate on the waveform synthesis in creating beam patterns, and several works including [18,19,20,21] deal with the maximization of the signal-to-interference-plus-noise-ratio (SINR). It is becoming evident that unlocking the true possibilities offered by modern collocated MIMO radars is achieved via waveform designs as well as detection and estimation approaches [22]. While the last decade has seen a greater interest and thus greater research output in the MIMO radar, there exist significant challenges which are need to be thoroughly addressed. Firstly, the assumption of a known target in [18,23] is rather limiting. Secondly, the randomization procedure can often require undesirably large computational resources [18,24]. Moreover, the exact characterization and minimization of outage probability for the collocated MIMO radar is rather involved [18,25,26,27]. Lastly, several existing works utilize the SINR statistics where signal and interference powers are evaluated separately by assuming both the target and interferers as either moving slowly or completely still [24,28,29].

Motivated by the aforementioned discussion, we investigate herein the probability of outage based on the waveform optimization of collocated transmit antenna MIMO radar systems by relaxing the assumption of a known target and removing the constraint of the slow-moving or stationary target and interferers. We also provide a unified characterization methodology for the system by employing recent advancements in the indefinite quadratic forms (IQF) approach [30,31,32,33]. The IQF approach enables us to achieve a closed-form expression for the cumulative density function (CDF) and the corresponding probability density function (PDF) in a simple form. Next, using the closed-form expression of the CDF, also referred to as the outage probability, we define several non-linear constrained and unconstrained waveform optimization techniques for collocated MIMO radar and reflect on the convergence, time complexity, and, most importantly, outage probability minimization.

Table 1. Related works on collocated MIMO radars.

Paper	SINR Formulation	Outage Probability	Optimization Approach
[18]	✓	×	Chen & Vaidyanathan iterative method
[22]	✓	×	Machine learning & deep learning techniques
[34]	✓	×	Cyclic optimization algorithm
[35]	✓{Indirectly}	×	Minorization- maximization based method
[36]	✓	×	Rao-based detector
Proposed	✓	✓	Interior-Point based approach

provides selected papers on collocated MIMO radar and describes the key contrasting features of the proposed work. This work opens doors for several other exhaustive search techniques by casting the outage probability expression as an objective function.

Following the introduction in Section 1, Section 2 deals with the mathematical built-up for the system model of collocated MIMO radar for target and clutter waveform. Section 3 outlines the analysis of outage probability using the IQF approach. Section 4 deals with the waveform design vis-à-vis two distinct optimization algorithms. Results and Conclusions follows thereafter.

Notations: Matrices, vectors, and scalar quantities are denoted by bold uppercase, bold lower case, and italicized letters, respectively. (·)${}^T$, (·)${}^H$, and (·)${}^{\frac{H}{2}}$ indicate the transpose, conjugate transpose, and sort representation of ((·)${}^{\frac{1}{2}}$)${}^H$, respectively. *, ⊗, $sign(.)$, and $u(.)$ are used to express the convolution operator, Kronecker product, signum function, and unit step function, respectively. Moreover, ${∥\mathbf{x}∥}_{\mathbf{A}}^2\triangleq {\mathbf{x}}^{\mathbf{H}}\mathbf{A}\mathbf{x}$.

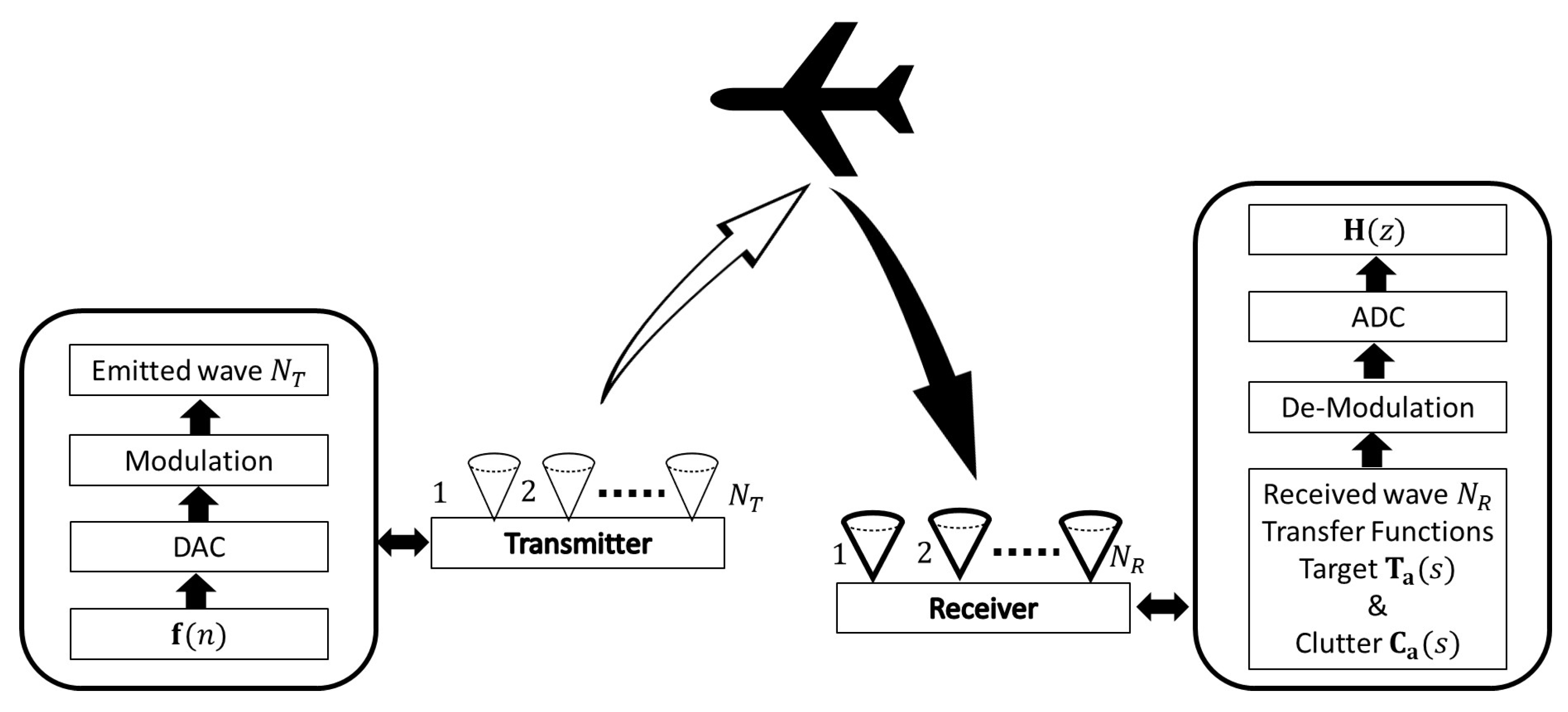
2. System Model

The collocated MIMO radar considered herein is adopted from [18], where a MIMO radar with $N_T$ and $N_R$ collocated to transmit and receive antenna elements, respectively, are employed as shown in Figure 1. At inception, a finite signal $\mathbf{f}\left(n\right)$ of dimension $N_T\times 1$ duration passes through a digital to analog converter (DAC) filter, modulated and transmitted through $N_T$ antenna elements. At the reflection from target, the subsequent waveform is transformed by the transfer function of both the target and clutter, i.e., ${\mathbf{T}}_{\mathbf{a}}\left(s\right)$ and ${\mathbf{C}}_{\mathbf{a}}\left(s\right)$, respectively. At the receiver end, an $N_R\times 1$ waveform is acquired and thereby passed through a demodulator and analog-to-digital converter (ADC) filter to achieve a received signal $\mathbf{r}\left(n\right)$. Thus, the receive filter $\mathbf{H}\left(z\right)$ processes the acquired signal $\mathbf{r}\left(n\right)$ to extract meaningful information for the existence of an unknown random target through an Lth order FIR filter $\mathbf{T}\left(z\right)$ given by

$$\mathbf{T}\left(z\right)=\sum _{n=0}^L\mathbf{t}\left[n\right]z^{-n},$$

(1)

where $\mathbf{t}\left[n\right]\sim \mathcal{CN}(\mathbf{0},{\mathbf{R}}_{\mathbf{T}});\in {\mathbb{C}}^{N_R\times N_T}$ represents the impulse response of target with covariance ${\mathbf{R}}_{\mathbf{T}}$.

Similarly, the transfer function of clutter $\mathbf{C}\left(z\right)$ is the bilateral z-Transform of the clutter impulse response, i.e., $\mathbf{c}\left[n\right]\sim \mathcal{CN}(\mathbf{0},{\mathbf{R}}_{\mathbf{C}});\in {\mathbb{C}}^{N_R\times N_T}$ with ${\mathbf{R}}_{\mathbf{C}}$ as the covariance matrix. Hence, after ADC the received waveform $\mathbf{r}\left[n\right]$ of dimension $N_R\times 1$ is expressed as

$$\mathbf{r}\left[n\right]=\left[\mathbf{f}\left[n\right]\ast \left[\mathbf{t}\left[n\right]+\mathbf{c}\left[n\right]\right]\right]+\mathbf{g}\left[n\right],$$

(2)

where the convolution sum runs from 0 to $L_T$ and $L_T$ denotes the order of $\mathbf{f}\left[n\right]$. Moreover, $\mathbf{g}\left[n\right]$ represent the additive white noise in the receiver. Furthermore, the received baseband waveform is

$$\mathbf{r}\triangleq {\left[\mathbf{r}{\left(0\right)}^T\mathbf{r}{\left(1\right)}^T\cdots \mathbf{r}{\left(L_R\right)}^T\right]}^T\in {}^{N_R(L_R+1)\times 1},$$

(3)

where $L_R$ denotes the order of $\mathbf{H}\left(z\right)$; hence, the received waveform is simplified as

$$\mathbf{r}=\mathbf{f}\times \left[\mathbf{T}+\mathbf{C}\right]+\mathbf{g}.$$

(4)

Here, $\mathbf{f}\in {}^{N_T(L_T+1)\times 1}$ and $\mathbf{g}\in {}^{N_R(L_R+1)\times 1}$ are the accumulated vectors containing all the available terms of $\mathbf{f}\left[n\right]$ and $\mathbf{g}\left[\mathbf{n}\right]$. Moreover, $\mathbf{T}$ and $\mathbf{C}$ in (4) are block Toeplitz matrices given in [18] and they incorporate all the multi-path vectors $\mathbf{t}\left[n\right]$ and $\mathbf{c}\left[n\right]$, respectively. These matrices are formulated as follows  

$$\begin{array}{ccc}\hfill \mathbf{T}\triangleq & \left[\begin{array}{cccc}\mathbf{t}\left(0\right)& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{t}\left(1\right)& \mathbf{t}\left(0\right)& \ddots & ⋮\\ ⋮& \mathbf{t}\left(1\right)& \ddots & \mathbf{0}\\ \mathbf{t}\left(L\right)& ⋮& \ddots & \mathbf{t}\left(0\right)\\ \mathbf{0}& \mathbf{t}\left(L\right)& \ddots & \mathbf{t}\left(1\right)\\ ⋮& \ddots & \ddots & ⋮\\ \mathbf{0}& \cdots & \mathbf{0}& \mathbf{t}\left(L\right)\end{array}\right];\mathbf{C}\triangleq \hfill & \hfill \left[\begin{array}{cccc}\mathbf{c}\left(0\right)& \mathbf{c}(-1)& \cdots & \mathbf{c}(-L_T)\\ \mathbf{c}\left(1\right)& \mathbf{c}\left(0\right)& \ddots & ⋮\\ ⋮& \mathbf{c}\left(1\right)& \ddots & ⋮\\ ⋮& \ddots & \ddots & \mathbf{c}\left(0\right)\\ ⋮& \ddots & \ddots & \mathbf{c}\left(1\right)\\ ⋮& \ddots & \ddots & ⋮\\ \mathbf{c}\left(L_R\right)& \mathbf{c}(L_R-1)& \cdots & \mathbf{c}\left(L\right)\end{array}\right]\end{array}$$

Hence, the receiving filter output, i.e., y formulates as

$$y=\mathbf{h}\mathbf{r}=\mathbf{h}\mathbf{T}\mathbf{f}+\mathbf{h}\mathbf{C}\mathbf{f}+\mathbf{h}\mathbf{g},$$

(5)

where vector $\mathbf{h}$ of dimension $1\times N_R(L_R+1)$ includes the impulse response of $\mathbf{H}\left(z\right)$. The first term in (5) represents the desired signal, the second term is the clutter received, while the third term is noise.

Using (5), the SINR (denoted for notation simplicity as $\eta$) is a function of $\mathbf{f}$ and $\mathbf{h}$, defined as:

$$\eta (\mathbf{f},\mathbf{h})\triangleq \frac{{\left|\mathbf{h}\mathbf{T}\mathbf{f}\right|}^2}{{\left|\mathbf{h}\mathbf{g}\right|}^2+{\left|\mathbf{h}\mathbf{C}\mathbf{f}\right|}^2}.$$

(6)

Next, we use a Kronecker-structured correlation matrix formulation in which the transmit correlation ${\mathbf{R}}_{tx}$ and receive correlation ${\mathbf{R}}_{rx}$ for both target ${\mathbf{R}}_T$ and clutter ${\mathbf{R}}_C$ are represent as [32]:

$$\begin{array}{ccc}\hfill {\mathbf{R}}_T& =& {\mathbf{R}}_{Ttx}^T\otimes {\mathbf{R}}_{Trx},\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathbf{R}}_C& =& {\mathbf{R}}_{Ctx}^T\otimes {\mathbf{R}}_{Crx}.\hfill \end{array}$$

(8)

Furthermore, whitening transformation of $\mathbf{T}$ and $\mathbf{C}$ are $\mathbf{T}={\mathbf{R}}_{Trx}^{\frac{1}{2}}\overline{\mathbf{T}}{\mathbf{R}}_{Ttx}^{\frac{1}{2}}$ and $\mathbf{C}={\mathbf{R}}_{Crx}^{\frac{1}{2}}\overline{\mathbf{C}}{\mathbf{R}}_{Ctx}^{\frac{1}{2}}$, respectively. Here, elements of $\overline{\mathbf{T}}$ and $\overline{\mathbf{C}}$ are independent and identically distributed (i.i.d.) $\mathcal{CN}(0,1)$. Hence, the SINR reformulates to

$$\begin{array}{cc}\hfill \eta (\mathbf{f},\mathbf{h})\triangleq & \frac{|\mathbf{h}{\mathbf{R}}_{Trx}^{\frac{1}{2}}\overline{\mathbf{T}}{\mathbf{R}}_{Ttx}^{\frac{1}{2}}{\mathbf{f}|}^2}{\left(\mathbf{h}\mathbf{g}\right){\left(\mathbf{h}\mathbf{g}\right)}^T+{\left|\mathbf{h}{\mathbf{R}}_{Crx}^{\frac{1}{2}}\overline{\mathbf{C}}{\mathbf{R}}_{Ctx}^{\frac{1}{2}}\mathbf{f}\right|}^2}.\hfill \end{array}$$

(9)

Next, $\overline{\mathbf{T}}$ and $\overline{\mathbf{C}}$ are vectorized as $\overline{\mathbf{t}}$ = vec($\overline{\mathbf{T}}$) and $\overline{\mathbf{c}}$ = vec($\overline{\mathbf{C}}$), respectively, with dimensions $N_R(L_R+1)N_T(L_T+1)\times 1$. To further simplify, we express the composite channel and waveform terms of target and clutter parts of the above expression as $\overline{\mathbf{T}}{\mathbf{R}}_{Ttx}^{\frac{1}{2}}\mathbf{f}$ = $(\mathbf{I}\otimes {\left({\mathbf{R}}_{\mathbf{Ttx}}^{\frac{\mathbf{1}}{\mathbf{2}}}\mathbf{f}\right)}^{\mathbf{T}})\overline{\mathbf{t}}$ and $\overline{\mathbf{C}}{\mathbf{R}}_{Ctx}^{\frac{1}{2}}$ = $(\mathbf{I}\otimes {\left({\mathbf{R}}_{\mathbf{Ctx}}^{\frac{\mathbf{1}}{\mathbf{2}}}\right)}^{\mathbf{T}})\overline{\mathbf{c}}$, respectively. Such a transformation enables us to express the SINR in a quadratic form given by

$$\begin{array}{cc}\hfill \eta (\mathbf{f},\mathbf{h})\triangleq & \frac{{∥\overline{\mathbf{t}}∥}_{\mathbf{A}}^2}{{\sigma }^2{∥\mathbf{h}∥}^2+{∥\overline{\mathbf{c}}∥}_{\mathbf{B}}^2},\hfill \end{array}$$

(10)

where the weight matrices of target and clutter components are $\mathbf{A}$ and $\mathbf{B}$, respectively, while $\mathbf{A}={\mathbf{a}}^H\mathbf{a}$, and the vectors are $\mathbf{B}={\mathbf{b}}^H\mathbf{b}$, and $\mathbf{a}=\mathbf{h}{\mathbf{R}}_{Trx}^{\frac{1}{2}}(\mathbf{I}\otimes {\left({\mathbf{R}}_{\mathbf{Ttx}}^{\frac{\mathbf{1}}{\mathbf{2}}}\mathbf{f}\right)}^{\mathbf{T}})$; $\mathbf{b}=\mathbf{h}{\mathbf{R}}_{\mathbf{Crx}}^{\frac{\mathbf{1}}{\mathbf{2}}}(\mathbf{I}\otimes {\left({\mathbf{R}}_{\mathbf{Ctx}}^{\frac{\mathbf{1}}{\mathbf{2}}}\mathbf{f}\right)}^{\mathbf{T}})$. Hence, such formulation makes both $\mathbf{A}$ and $\mathbf{B}$ unit-rank Hermitian matrices.

3. Characterization of Outage Probability

This section deals with the exact characterization of outage probability for the collocated antenna MIMO radar system. The notion of outage probability herein is that the instantaneous value of SINR expression, which is a random variable, falls below a predefined threshold value, thus resulting is a monotonic CDF function of SINR. Hence, we proceed by imposing a condition on the CDF of SINR given in (10), i.e., $Pout\left(\gamma \right|\zeta )=Pr\left(\eta (\mathbf{f},\mathbf{h})<\gamma \right)$, where $\zeta ={∥\overline{\mathbf{c}}∥}_{\mathbf{B}}^2$ defines the condition and $\gamma$ is a predefined threshold value. Hence, the outage probability is expressed as:

$$\begin{array}{cc}\hfill Pout\left(\gamma \right|\zeta )=& Pr\left(\frac{\left|\right|\overline{\mathbf{t}}{\left|\right|}_{\mathbf{A}}^{\mathbf{2}}}{{\sigma }^2{∥\mathit{h}∥}^2+\zeta }<\gamma \right),\hfill \\ \hfill =& Pr\left(({\sigma }^2{∥\mathit{h}∥}^2+\zeta )\gamma -\left|\right|\overline{\mathbf{t}}{\left|\right|}_{\mathbf{A}}^{\mathbf{2}}>0\right),\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }f\left(\overline{\mathbf{t}}\right)u\left(({\sigma }^2{∥\mathit{h}∥}^2+\zeta )\gamma -\left|\right|\overline{\mathbf{t}}{\left|\right|}_{\mathbf{A}}^{\mathbf{2}}\right)d\overline{\mathbf{t}},\hfill \end{array}$$

(11)

where $f\left(\overline{\mathbf{t}}\right)$ is the PDF of an L-dimensional {$L=N_R(L_R+1)N_T(L_T+1)$} circular white Gaussian random vector $\overline{\mathbf{t}}$, mathematically, $f\left(\overline{\mathbf{t}}\right)=\frac{1}{{\pi }^L}{e}^{-\left|\right|\overline{\mathbf{t}}{\left|\right|}^{\mathbf{2}}}$. Moreover, using the Fourier representation of unit step function as in [30], the CDF in (11) is expressed as

$$\begin{array}{ccc}\hfill Pout\left(\gamma \right|\zeta )& =& \frac{1}{2{\pi }^{}}{\int }_{-\infty }^{\infty }\times \frac{1}{{\pi }^L}{\int }_{-\infty }^{\infty }\frac{e^{({\sigma }^2{∥\mathit{h}∥}^2+\zeta )\gamma (j\omega +\beta )}}{(j\omega +\beta )}{e}^{-{\left|\right|\overline{\mathbf{t}}\left|\right|}_{\mathbf{I}+\mathbf{A}(j\omega +\beta )}^2}d\overline{t}dw,\hfill \\ & =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{({\sigma }^2{∥\mathit{h}∥}^2+\zeta )\gamma (j\omega +\beta )}}{(j\omega +\beta )|\mathbf{I}+{\Lambda }_A(j\omega +\beta )|}dw,\hfill \\ & =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{({\sigma }^2{∥\mathit{h}∥}^2+\zeta )\gamma (j\omega +\beta )}}{(j\omega +\beta )(1+{\lambda }_A(j\omega +\beta ))}dw,\hfill \end{array}$$

(12)

where we achieve the second equality by using the multi-dimensional Gaussian integral solution, and ${\Lambda }_A$ is a diagonal matrix having eigenvalues of matrix $\mathbf{A}$ as elements. The third equality is obtained owing to rank one of matrix A; thus, such a matrix has only one eigenvalue which is denoted as ${\lambda }_A$.

Next, we remove the condition in (11) by evaluating the CDF, i.e., $F\left(\zeta \right)$ by using the quadratic formulation as

$$\begin{array}{ccc}\hfill F\left(\zeta \right)& =& Pr\left({∥\overline{\mathbf{c}}∥}_{\mathbf{B}}^2<\zeta \right),\hfill \\ & =& Pr\left(\zeta -{∥\overline{\mathbf{c}}∥}_{\mathbf{B}}^2>0\right),\hfill \\ & =& {\int }_{-\infty }^{\infty }f\left(\overline{\mathbf{c}}\right)u\left(\zeta -{∥\overline{\mathbf{c}}∥}_{\mathbf{B}}^2\right)d\overline{\mathbf{t}},\hfill \\ & =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{\zeta (j\omega +\beta )}}{(j\omega +\beta )|\mathbf{I}+{\Lambda }_B(j\omega +\beta )|}dw,\hfill \end{array}$$

(13)

where $f\left(\overline{\mathbf{c}}\right)$ is the PDF of $\overline{\mathbf{c}}$. As in other notable works [37,38], clutter is considered as a Gaussian random vector.

Now, differentiation of $F\left(\zeta \right)$ yields the PDF $f\left(\zeta \right)$ which is simplified using the indefinite quadratic forms approach [30] as follows

$$\begin{array}{ccc}\hfill f\left(\zeta \right)& =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{\zeta (j\omega +\beta )}}{|\mathbf{I}+{\Lambda }_B(j\omega +\beta )|}dw,\hfill \\ & =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{\zeta (j\omega +\beta )}}{\left(1+{\lambda }_B(j\omega +\beta )\right)}dw,\hfill \\ & =& \frac{1}{{\lambda }_B}{e}^{-\frac{\zeta }{{\lambda }_B}}u\left(\frac{\zeta }{{\lambda }_B}\right),\hfill \end{array}$$

(14)

where ${\Lambda }_B$ is the diagonal matrix containing the eigenvalues of Hermitian matrix B, ${\lambda }_B$ is the only non-zero eigenvalue resulting in second equality, whereas the third equality is from the definition of residue theory [39], i.e.,

$$\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{\beta j\omega }}{(\alpha +j\omega )}d\omega =sign\left(\alpha \right)e^{-\alpha \beta }\mathit{u}\left(\alpha \beta \right).$$

(15)

Next, the outage probability with the aforementioned aspects simplifies to

$$\begin{array}{cc}\hfill Pout\left(\gamma \right)=& {\int }_{-\infty }^{\infty }Pout\left(\gamma \right|\zeta )f\left(\zeta \right)d\zeta ,\hfill \\ \hfill =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{{\sigma }^2{∥\mathit{h}∥}^2\gamma (j\omega +\beta )}}{(j\omega +\beta )(1+{\lambda }_A(j\omega +\beta ))}\frac{1}{{\lambda }_B}\times {\int }_{-\infty }^{\infty }{e}^{\frac{-\zeta }{{\lambda }_B}+\zeta \gamma (j\omega +\beta )}u\left(\frac{\zeta }{{\lambda }_B}\right)d\zeta dw.\hfill \end{array}$$

(16)

Since B is a positive semi-definite matrix, ${\lambda }_B$ will have a non-negative value. Therefore, the inner integral of variable $\zeta$ is solved as follows

$$\begin{array}{c}\hfill {\int }_{-\infty }^{\infty }{e}^{\frac{-\zeta }{{\lambda }_B}+\zeta \gamma (j\omega +\beta )}u\left(\frac{\zeta }{{\lambda }_B}\right)d\zeta ={\int }_0^{\infty }{e}^{-\zeta (\frac{1}{{\lambda }_B}-\gamma (j\omega +\beta ))}d\zeta =\frac{1}{\frac{1}{{\lambda }_B}-\gamma (j\omega +\beta )}.\end{array}$$

(17)

$$\begin{array}{ccc}\hfill Pout\left(\gamma \right)=\frac{1}{{\lambda }_B}& \times & \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\underset{D1}{\underbrace{\frac{1}{(j\omega +\beta )\left(1+{\lambda }_A(j\omega +\beta )\right)\left(\frac{1}{{\lambda }_B}-\gamma (j\omega +\beta )\right)}}}\hfill \\ & \times & e^{{\sigma }^2{∥\mathit{h}∥}^2\gamma (j\omega +\beta )}dw,\hfill \end{array}$$

(18)

where we employ partial fraction expansion on the under-brace term $D1$ as

$$\begin{array}{cc}\hfill D1=& {\lambda }_B\frac{1}{(j\omega +\beta )}-\frac{{\lambda }_B\gamma }{1+\frac{{\lambda }_A}{{\lambda }_B\gamma }}\frac{1}{\left((j\omega +\beta )-\frac{1}{{\lambda }_B\gamma }\right)}-\frac{{\lambda }_B}{1+\frac{{\lambda }_B\gamma }{{\lambda }_A}}\frac{1}{\left((j\omega +\beta )-\frac{1}{{\lambda }_A}\right)}.\hfill \end{array}$$

(19)

Next, by plugging (19) in (18), we obtain

$$\begin{array}{ccc}\hfill Pout\left(\gamma \right)& =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{1}{(j\omega +\beta )}{e}^{{\sigma }^2{∥\mathit{h}∥}^2\gamma (j\omega +\beta )}dw\hfill \\ & -& \frac{\gamma }{1+\frac{{\lambda }_A}{{\lambda }_B\gamma }}\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{1}{\left((j\omega +\beta )-\frac{1}{{\lambda }_B\gamma }\right)}{e}^{{\sigma }^2{∥\mathit{h}∥}^2\gamma (j\omega +\beta )}dw\hfill \\ & -& \frac{1}{1+\frac{{\lambda }_B\gamma }{{\lambda }_A}}\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{1}{\left((j\omega +\beta )+\frac{1}{{\lambda }_A}\right)}{e}^{{\sigma }^2{∥\mathit{h}∥}^2\gamma (j\omega +\beta )}dw.\hfill \end{array}$$

(20)

Eventually, applying the residue theory (15), yields a closed-form expression for the CDF of collocated antenna MIMO radar system for an unknown random target as follows

$$\begin{array}{cc}\hfill Pout\left(\gamma \right)=& 1-\left[\frac{\gamma }{1+\frac{{\lambda }_A}{{\lambda }_B\gamma }}{e}^{\frac{{\sigma }^2{∥\mathit{h}∥}^2}{{\lambda }_B}}u\left(-\frac{{\sigma }^2{∥\mathit{h}∥}^2}{{\lambda }_B}\right)+\frac{1}{1+\frac{{\lambda }_B\gamma }{{\lambda }_A}}{e}^{-\frac{{\sigma }^2{∥\mathit{h}∥}^2\gamma }{{\lambda }_A}}u\left(\frac{{\sigma }^2{∥\mathit{h}∥}^2\gamma }{{\lambda }_A}\right)\right].\hfill \end{array}$$

(21)

4. Algorithms for Waveform Optimization

The availability of closed-form expressions derived in the previous section enables us to perform an unsupervised constrained optimization and thus decrease the probability of outage given in (21) for the collocated MIMO radar. In what follows, we break down this section into first outlining a sub-optimal, albeit closed-form, solution of the optimization variable. Next, we use the closed-form expression as an initialized vector and perform the outage probability minimization using heuristic approaches.

4.1. Closed-Form Solution of Transceiver Waveform

For the closed-form solution, a candidate algorithm is the so-called Match Filter Bound given in [40], a well-known optimization algorithm. Herein, we optimize the transmit filters and the receive filter is matched with the transmitted waveform. The upper bound of the SINR for fixed transmit filters is obtained by $\mathbf{h}=\nu {\mathbf{R}}_v^{-1}\mathbf{T}\mathbf{f}$, where $\nu$ is a scalar constraint for the power. Consequently, the optimization problem is expressed as

$$\begin{array}{cc}\hfill \underset{\mathbf{f}}{max}& {\mathbf{f}}^{†}{\mathbf{T}}^{†}{\mathbf{R}}_v^{-1}\mathbf{T}\mathbf{f}\hfill \\ \hfill \mathrm{subj}.\mathrm{to}& {\parallel \mathbf{f}\parallel }^2\le 1.\hfill \end{array}$$

(22)

This is a notable Rayleigh quotient given in [40]. The optimization solution of vector $\mathbf{f}$ is reported in [18] and it is the principal component of ${\mathbf{T}}^{†}{\mathbf{R}}_v^{-1}\mathbf{T}$ and the maximization of the objective function which is achieved by the dominant eigenvalue of ${\mathbf{T}}^{†}{\mathbf{R}}_v^{-1}\mathbf{T}$, denoted as ${\lambda }_1\left({\mathbf{T}}^{†}{\mathbf{R}}_v^{-1}\mathbf{T}\right).$

4.2. Heuristic Solution of Transceiver Waveform

Since the match filter bound gives a sub-optimal solution, we leverage by setting it as an initialized solution and propose minimization methods with and without constraints on the transmitted wave.

Unconstrained Minimization Method (UMM): Unconstrained optimization is viable given that the transmit power protocols are not enforced. Hence, UMM is proposed for the minimization problem of outage probability, and formulates as follows:

$$\begin{array}{cc}\hfill \underset{\mathbf{f}}{min}& Pout(\mathbf{f},\mathbf{h},\gamma )\hfill \end{array}$$

(23)

Constrained Minimization Method (CMM): This method extends the UMM by constraining the allocated power of the transmitted wave. Thus, we cast the CMM as follows:

$$\begin{array}{cc}\hfill \underset{\mathbf{f}}{min}& Pout(\mathbf{f},\mathbf{h},\gamma )\hfill \\ \hfill \mathrm{subj}.\mathrm{to}& {\left|\right|\mathbf{f}\left|\right|}^2\le 1\hfill \end{array}$$

(24)

Herein, the objective functions presented in (23) and (24) can be solved using several off-the-shelf non-linear algorithms such as interior-point, sequential quadratic programming, and  active-set routines incorporated to achieve the desired minimization. Algorithm 1 gives the pseudo-code of a heuristic search-enabled beamformer design. At the inception stage, we formulate a random transmitted waveform from the Gaussian code-book and then employ the match filter bound to achieve sub-optimal solution of the transmitted waveform. We set the sub-optimal solution as ${\mathbf{f}}^{init.}$, i.e., initialization vector in Algorithm 1. Furthermore, we employ the algorithm nesting approach which desires the optimization variables in a scalar and vector form. To this end, we segregate the real and complex terms as $\mathbf{f}=[\Re \left(\mathbf{f}\right)\Im (\mathbf{f}\left)\right]$ which makes the number of optimization variables as $2N_T$. In line 11 of Algorithm 1, $ϵ$ is the optimality tolerance set as ${10}^{(-6)}$ and it defines the convergence criterion. Moreover, $i_{max}$ is the maximum number of iterations which are allowed for convergence and it is set as 400. Furthermore, the inequality constraints are enforced for CMM and its tolerance, i.e., the constraint violation is a positive scalar set as ${10}^{(-6)}$. Algorithm 1 terminates based on the stopping criterion defined in step 14.

Algorithm 1 Build of Heuristic Search enabled Waveform Design

1: Input: $N_T$, $N_R$, $L_T$, $L_R$, ${\mathbf{f}}^{init.}$, and ${\mathbf{h}}^{init.}$. 2: Output: $P_{out}\left(\zeta \right)$, ${\mathbf{f}}^{opt.}$, and ${\mathbf{h}}^{opt.}$. 3: Set maximum allowable iterations ($i_{max}$), and  the precision upper bound ($ϵ$). 4: i = 1 5: Compute $P_{out}^{\left(i\right)}\left(\zeta \right)$ in (21) using ${\mathbf{f}}^{init.}$ and ${\mathbf{h}}^{init.}$. 6: repeat 7:       $i=i+1$ 8:       Compute $P_{out}^{\left(i\right)}\left(\zeta \right)$ in (21) using (23) or (24). 9:       Update ${\mathbf{f}}^{opt.}$ using algorithm sub-routines. 10:     Compute ${\mathbf{h}}^{opt.}\leftarrow \nu {\mathbf{R}}_v^{-1}\mathbf{T}{\mathbf{f}}^{opt.}$. 11:     if $\left\{\right|P_{out}^{\left(i\right)}\left(\zeta \right)-P_{out}^{(i-1)}\left(\zeta \right)|\le ϵ\}\&\&\{i_{}=i_{max}\}$ then 12:         set Condition = true. 13:     end if 14: until {Condition = true}

5. Simulation Results and Discussions

In this section, we validate the closed-form expressions given in (3) and (21), and then we cast the later expression in the proposed algorithm of outage probability minimization. In the considered experimental set-up, we consider distinct transmissions and receive correlation matrices of target and clutter waveform denoted, respectively, as, ${\mathbf{R}}_{Tt}$, ${\mathbf{R}}_{Tr}$, ${\mathbf{R}}_{Ct}$ and ${\mathbf{R}}_{Cr}$. Furthermore, the correlation matrices are constructed using correlation coefficient $\eta$ such that ${\mathbf{R}}_{a,b}$ = ${\eta }^{|a-b|}$, and $0<\eta <1$. The SNR value considered throughout is 2 dB.

5.1. Validation of Closed-Form Expressions

For the purpose of validating the theoretical results, we set Monte Carlo simulation runs as ${10}^5$. Moreover, we investigate the performance of MIMO radar system and quantify the effect of number of transmitter and receiver antenna elements and filter order. The validation of our work and its analysis is given in the following three ways.

• Validation of the outage probability expression in (21) is showcased using Figure 2a. Therein, the values of $\mathbf{f}$ and $\mathbf{h}$ are obtained using the match filter bound. We increase the order of $N_T$ and $N_R$ from single-input single-output (SISO) cases to MIMO cases of 2 and 8. It is observed that a great degree of gain is achieved by increasing the antenna order of transceiver units, e.g., there is a 16.7% reduction in outage probability by moving from SISO to MIMO case by setting antenna order of 8 at $\gamma =1$. From the validation prospective, it is observed that a perfect degree of match exits across the $\gamma$ range for all the considered antenna diversity orders;
• Validation of clutter signal PDF, i.e., $f\left(\zeta \right)$ in (3) is presented using Figure 2b. The aforementioned network configurations are considered herein as well. Due to the large values at low $\zeta$, a log scale axis is used. Again, a perfect match is observed between the analytical and closed-form expression;
• Validation of (21) by altering the transmit and receive filter order is demonstrated using Figure 3. Herein, we consider the case $N_T=N_R=2$. Initially, we consider a single order filter at transmitter and receiver ends. There is a marked decrease of about 10% in the outage probability if the filter order of 2 is used as compared to 1 at $\gamma =1$. Furthermore, increasing the filter order further to 4 results only in a marginal change. Hence, in the remainder of the work, we consider a filter order of 2. Again, the Monte Carlo simulation ascertains the theoretical results across the $\gamma$ range.

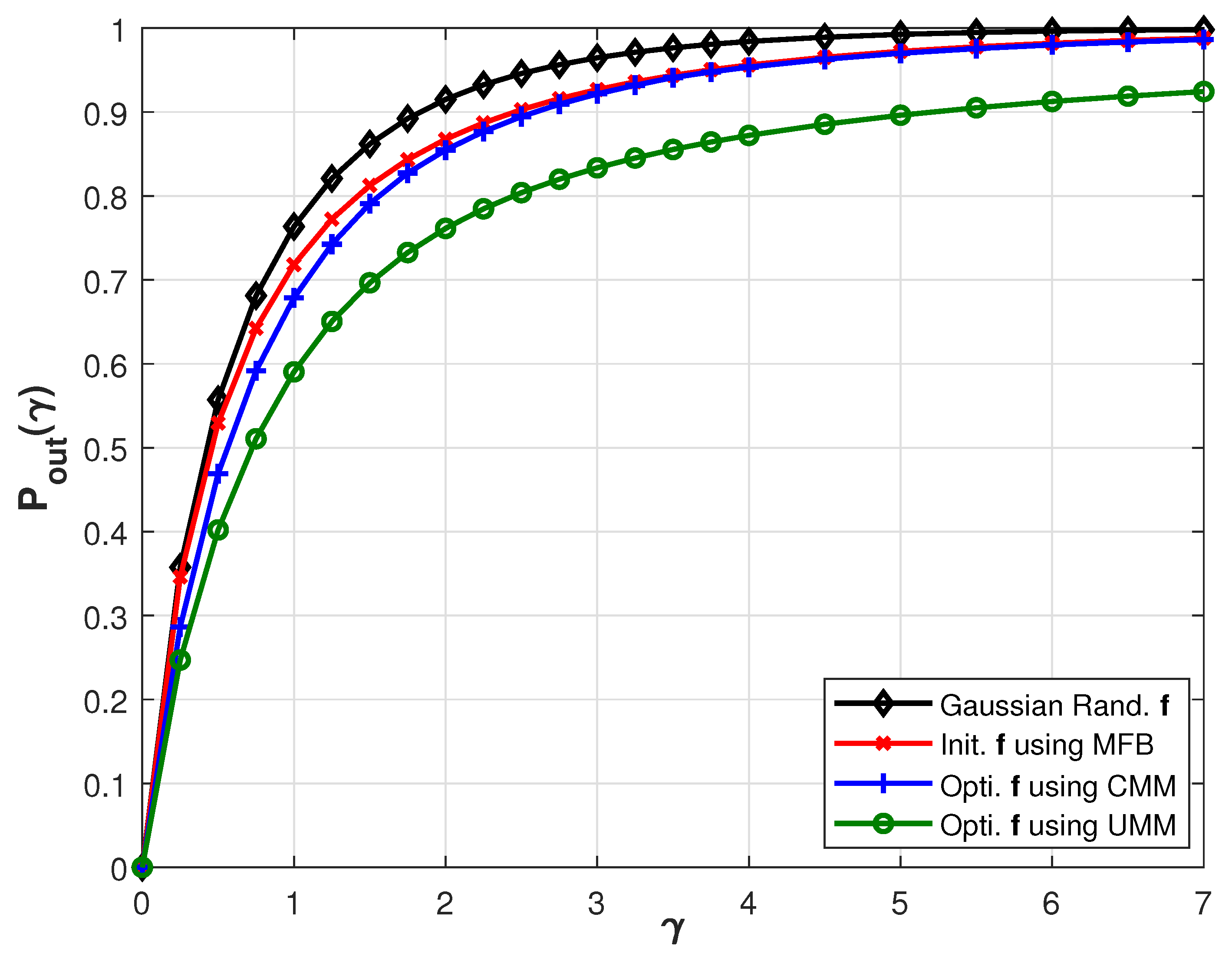
5.2. Minimization of $P_{out}\left(\gamma \right)$

In order to test the effectiveness of Algorithm 1 given in Section 4, we optimize transmit and receive waveform. The network configurations are kept as in Section 5.1. The results are given in the following three ways:

• Using Figure 4, we reflect on the performance while selecting a specific $\mathbf{f}$. Initially, we select $\mathbf{f}$ using random complex Gaussian vector and normalize it to have power 1. Next, we employ a match filter bound and achieve local solutions of $\mathbf{f}$ and also link it to obtain $\mathbf{h}$. This solutions shows consistent improvement across the gamma range and it reflects on the effectiveness of such a solution over a random selection of $\mathbf{f}$ and $\mathbf{h}$. We set the local solution of $\mathbf{f}$, referred in Figure 4 as, `Init. $\mathbf{f}$ using MFB’, as an initialization vector and perform CMM and UMM optimization using Algorithm 1. While the improvement is for both methods, the later, i.e., unconstrained approach finds excellent solutions across the $\gamma$ range. Hence, in the forthcoming analysis, only UMM is considered while CMM shall have similar results;
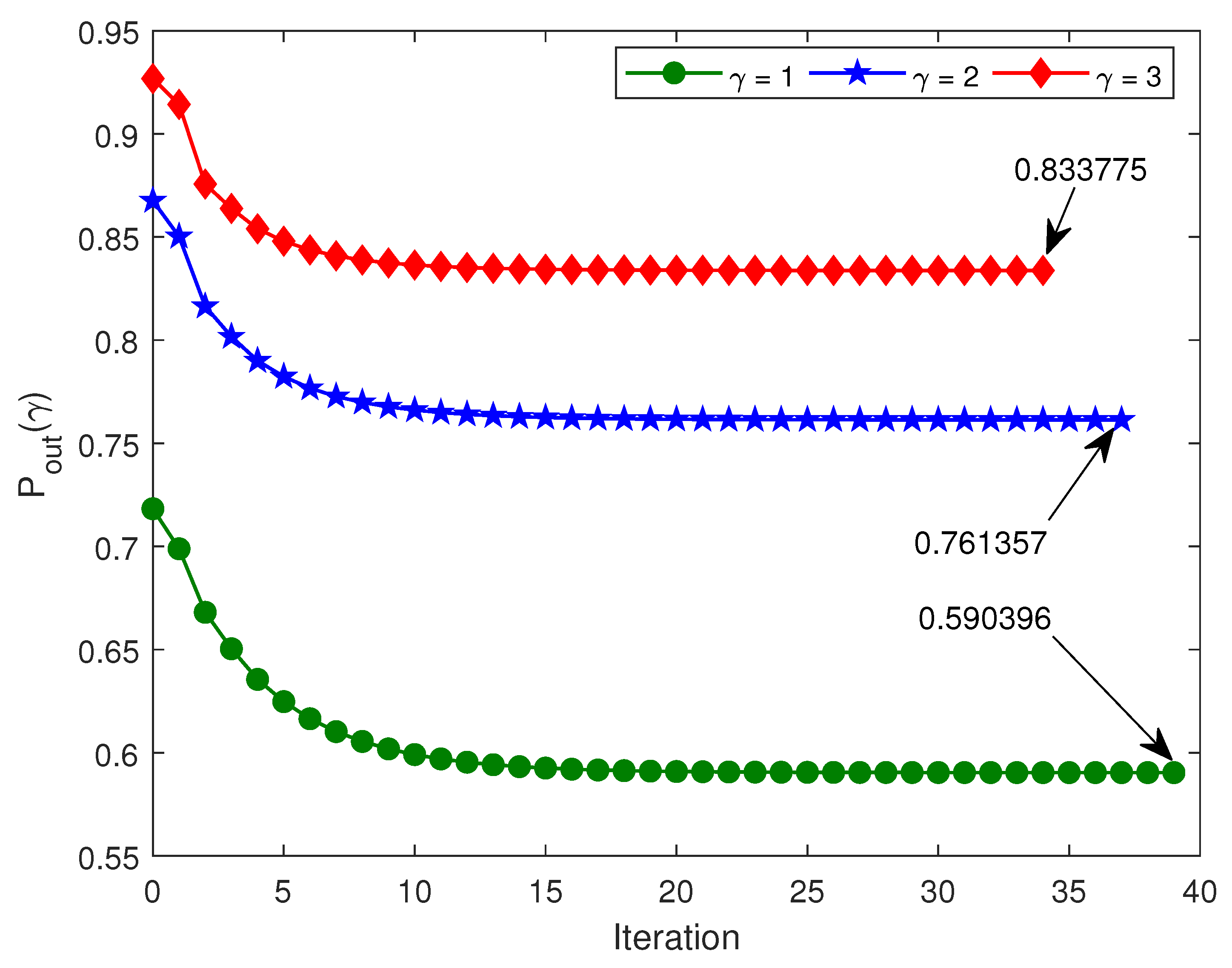
• Using Figure 5, we indicate the convergence of Algorithm 1 at three different values of $\gamma$, i.e., at 1, 2, and 3 respectively. The plot shows that the convergence is achieved at the 39th, 37th, and 34th iteration, having terminal values of 0.590396, 0.761357, and 0.833775, for $\gamma =$ 1, 2, and 3 respectively. Hence, a faster convergence at higher values of threshold is observed. Note that the convergence is based on the objective function (outage probability), which is non-decreasing in a viable direction to within the the optimality tolerance threshold set as ${10}^{(-6)}$;
• Using Figure 6, we demonstrate the time complexity for three sub-routines of Algorithm 1, namely, interior-point, sequential quadratic programming, and active-set approach. It is observed that the convergence of each of the three schemes is exactly the same and hence they find identical solutions; however, the time taken for each approach is different, hence the need for this analysis. The processor considered for this task is Intel(R) Core(TM) m7-6Y75 CPU 1.20 GHz 1.50 GHz with 16 GB RAM. Figure 6a is the scatter plot of the three sub-routines and it is observed that the `active-set’ method is finding solutions faster compared to its counterparts. The marked difference is especially notable at high threshold values where `active-set’ method is consuming just 0.05 s as compared with 0.6 s required for other methods. Figure 6b shows the box plot for the three sub-routines indicating the mean value and standard deviation with respect to time in seconds. Again, the `active-set’ method fairs better.

6. Conclusions

This work provided an in depth analysis of the collocated MIMO radar system under the relaxed assumption of instantaneous target states of target and clutter. Specifically, a key performance metric, i.e., the outage probability, is derived for generic settings and then synthesized based on the eigenvalues of clutter and transmitting weight matrices under the ratio of indefinite quadratic forms and by considering the characteristics of the channel environment as circular convolution. The presented solution is for the central Gaussian random variable; investigating the non-central case shall be an interesting extension of this work. We optimized the transceiver waveform under CMM and UMM approaches, which resulted in marked decrease of the probability of outage. Of the sub-routines used, the active-set method showed faster convergence and it can be used in the joint optimization of both $\mathbf{f}$ and $\mathbf{h}$ as an extension. Moreover, outage probability can be minimized by investigating the covariance shaping based receiver waveform design. Although, the work presented in this paper has been applied on a collocated MIMO radar system, it can also be applied on distributed MIMO Radar system with multi-target considerations.