Analysis of Error and Stability of Nanofluid over Horizontal Channel with Heat/Mass Transfer and Nonlinear Thermal Conductivity
Abstract
1. Introduction
2. Mathematical Modeling
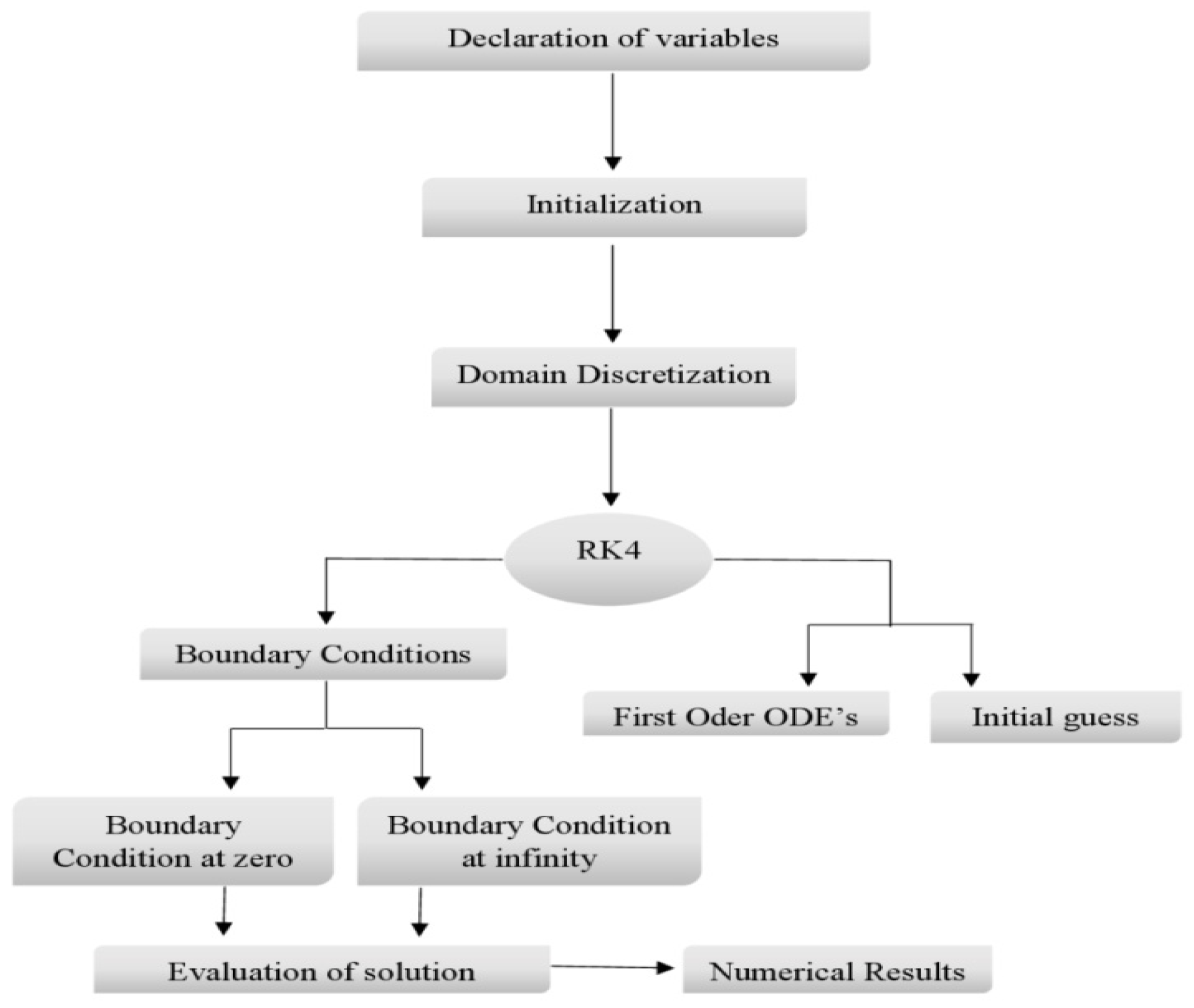
3. Numerical Procedure and Stability Analysis
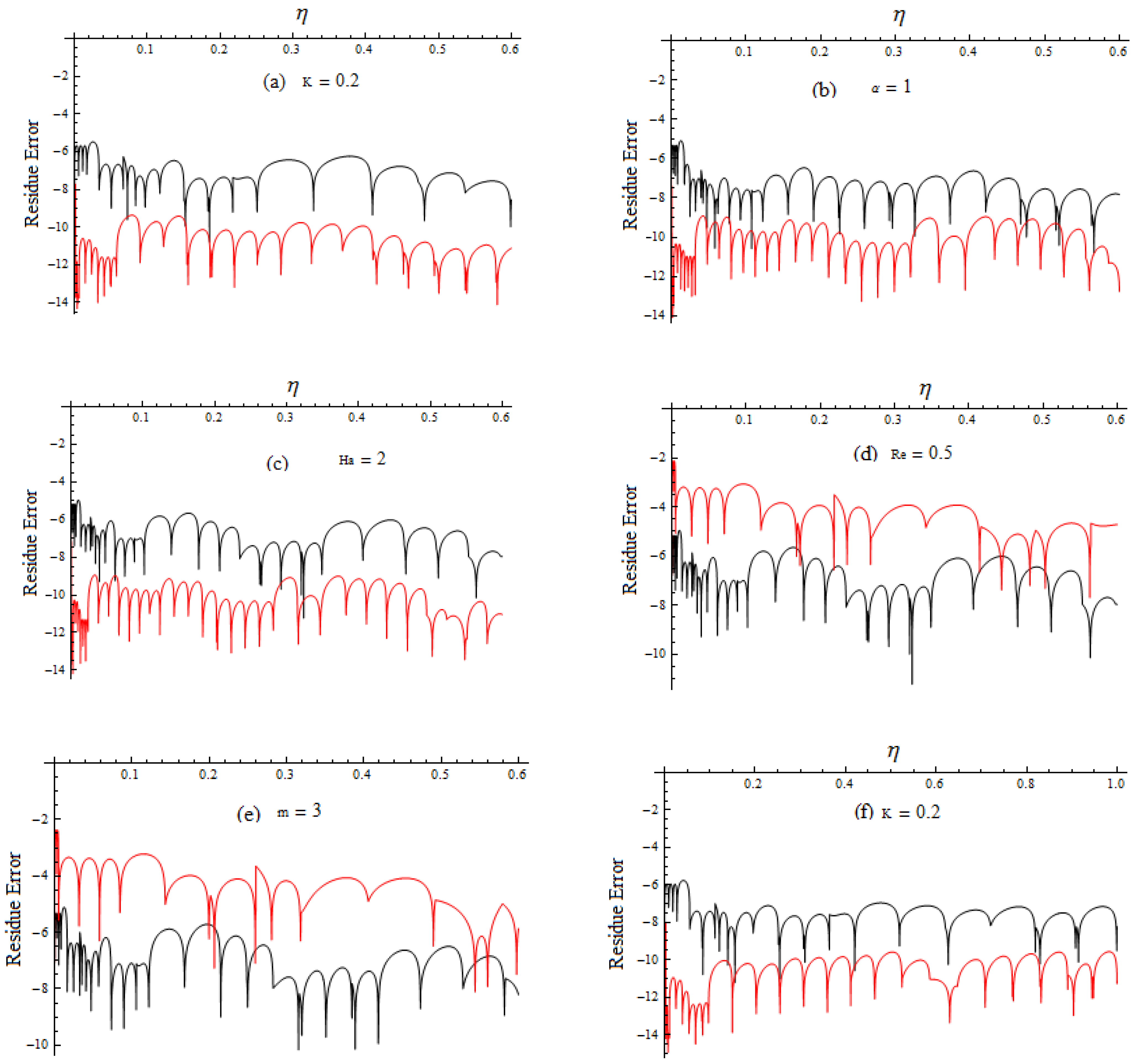
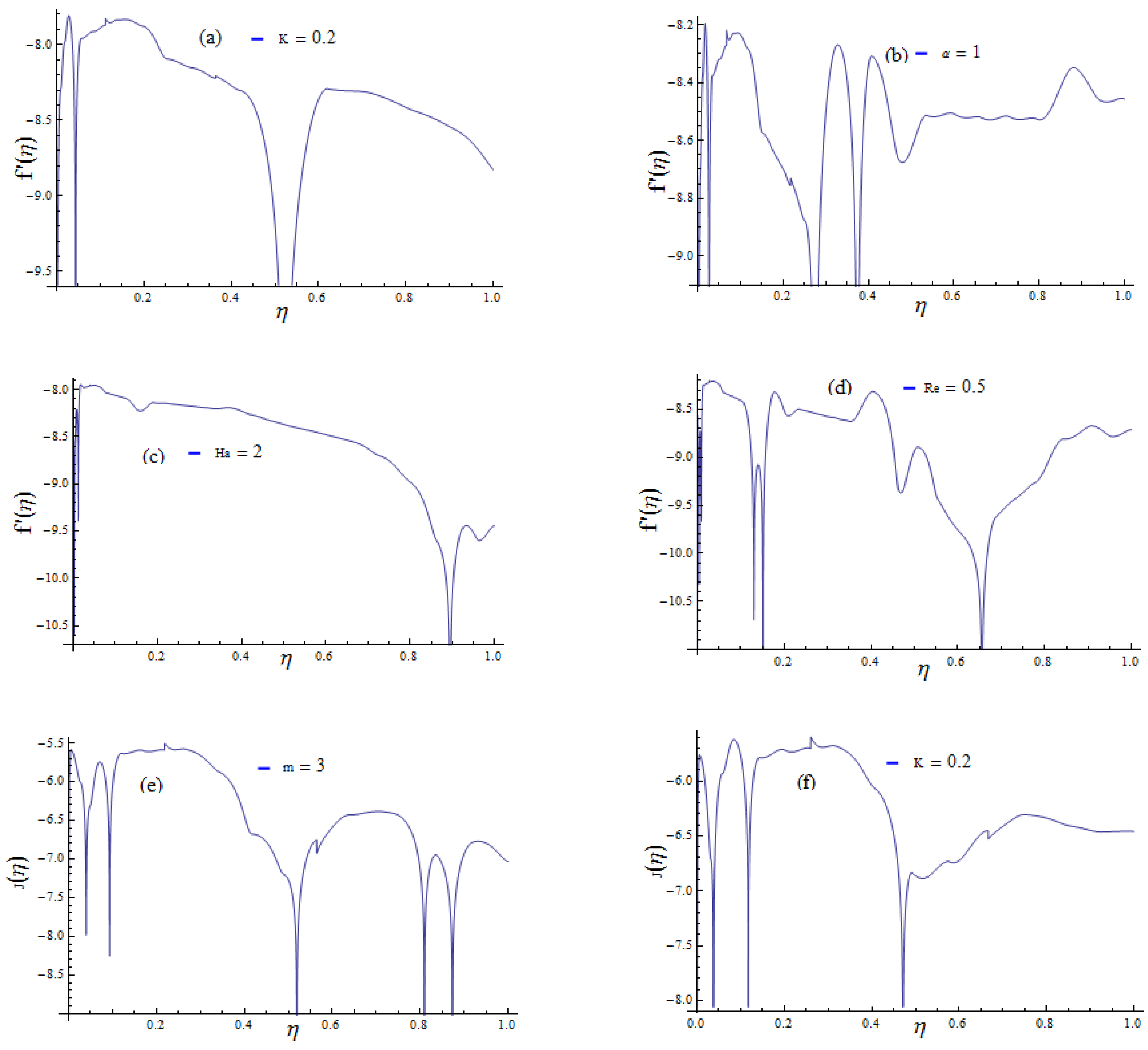
4. Error Analysis and Confirmation of RK4 Method
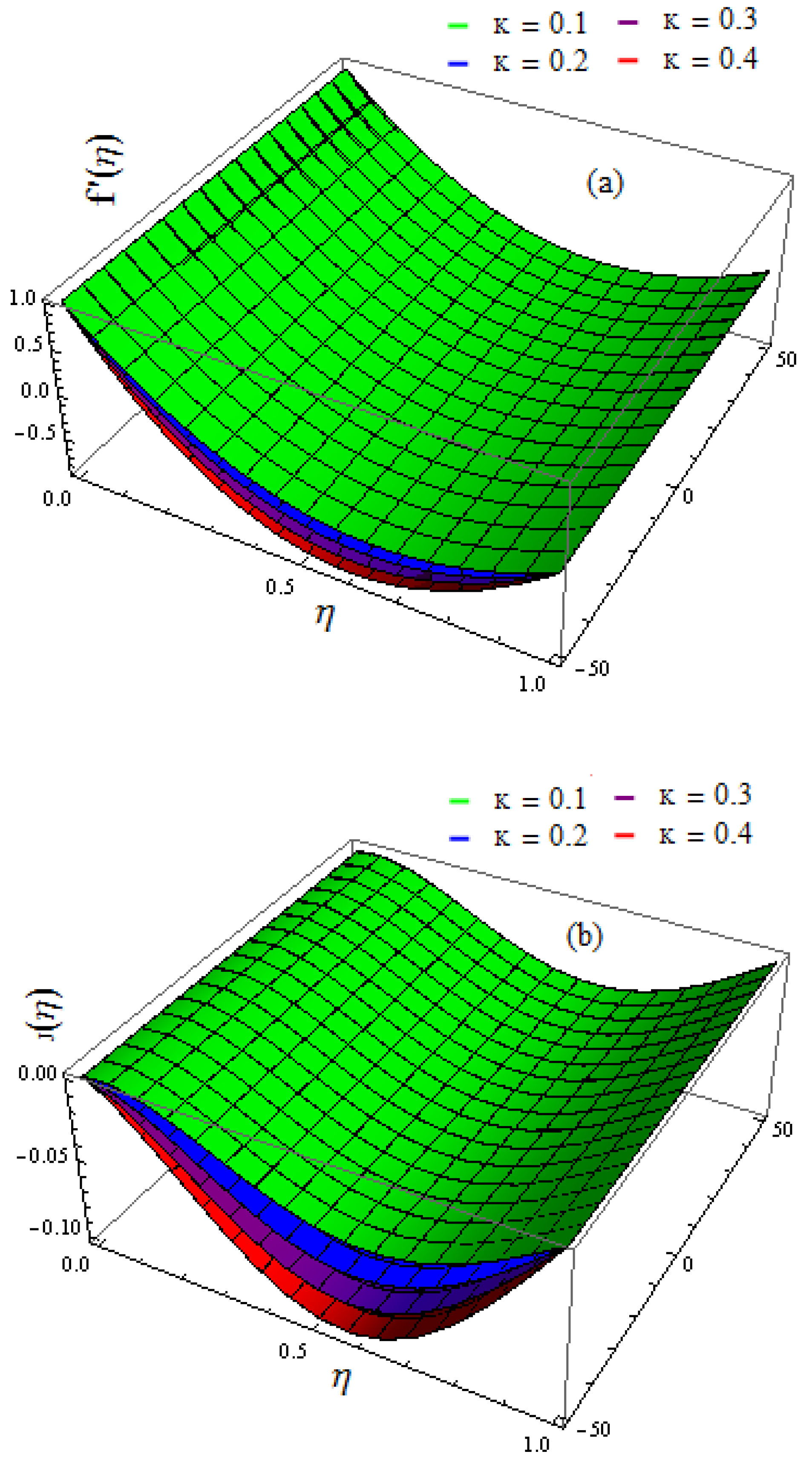
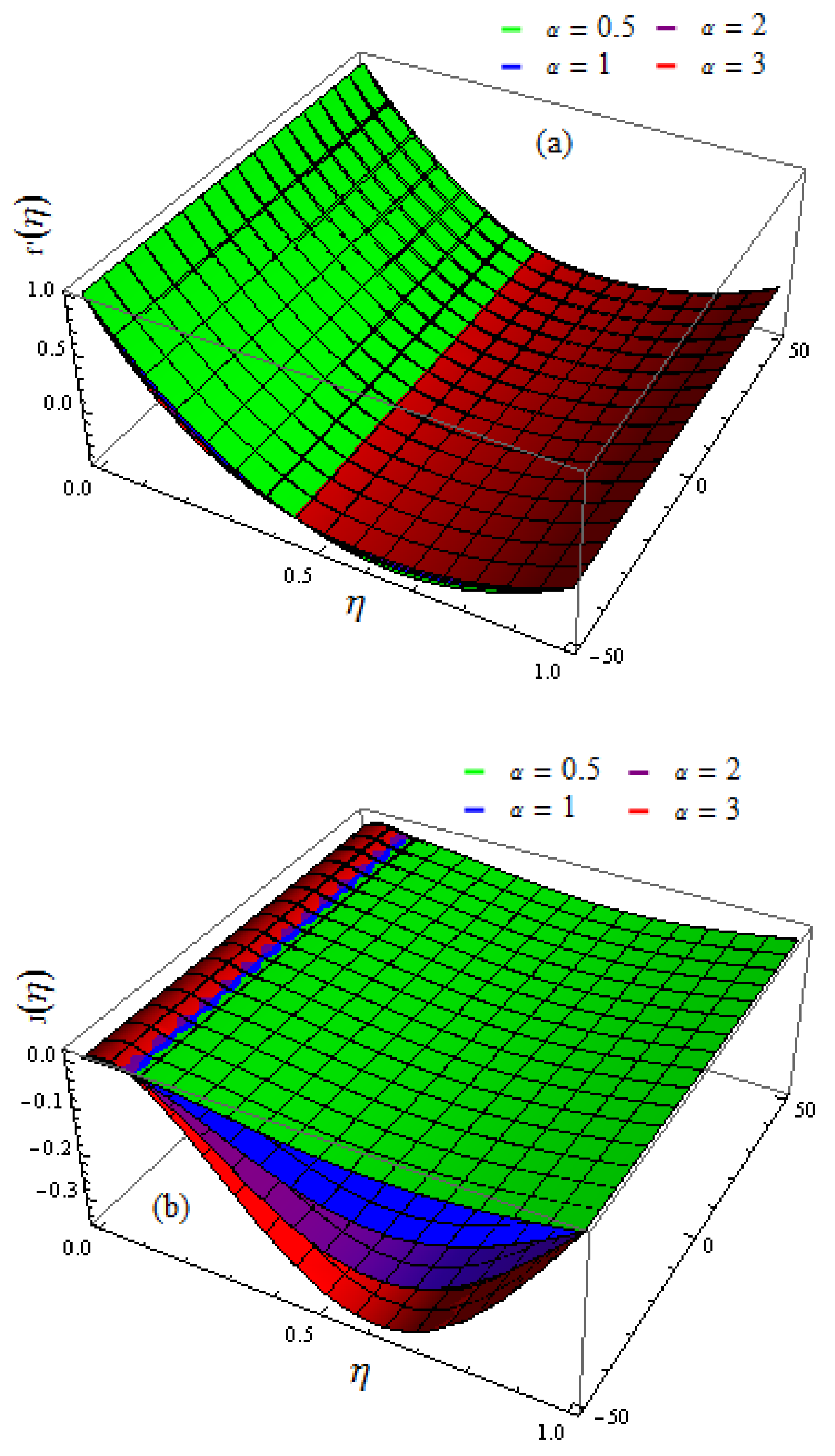
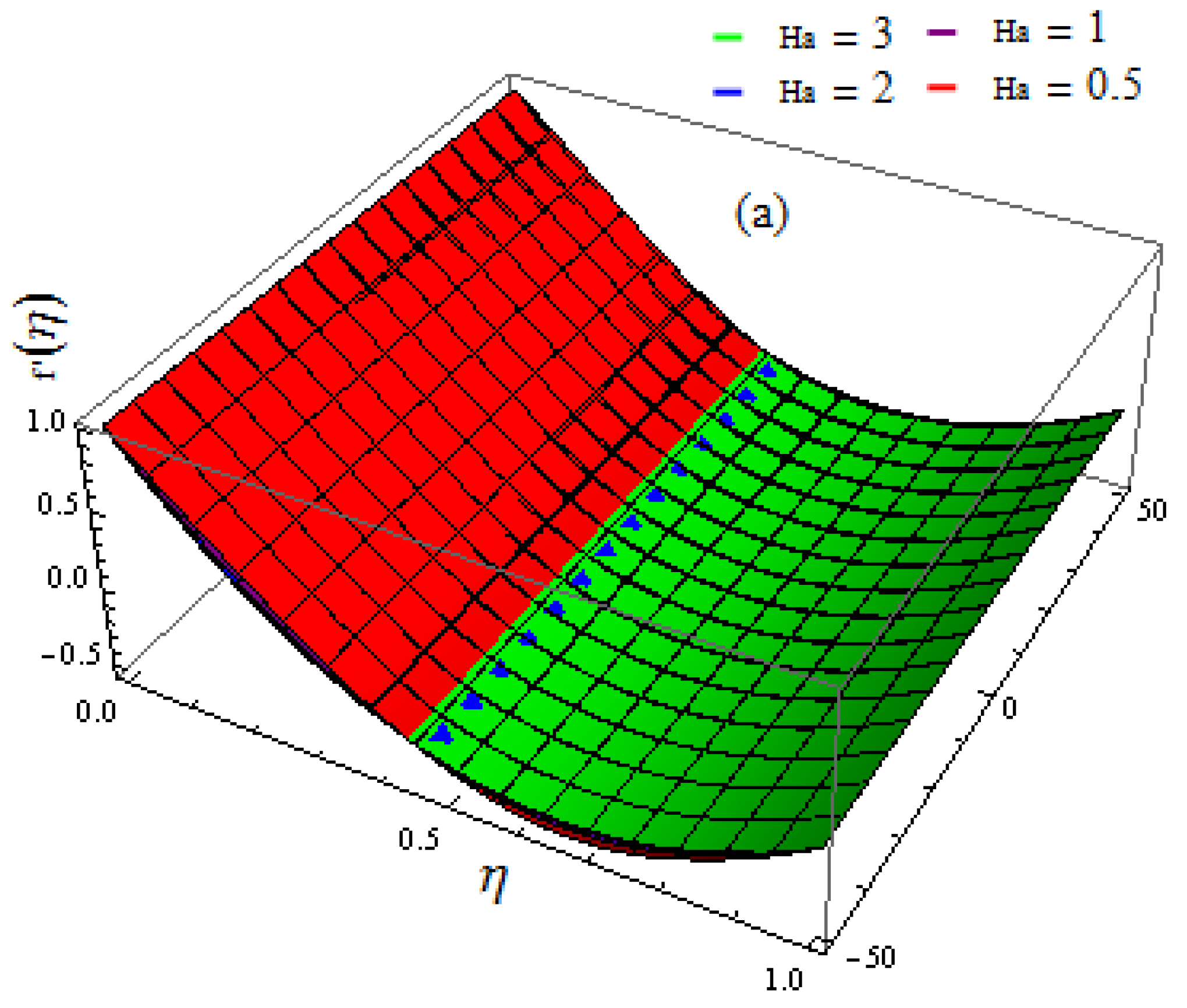
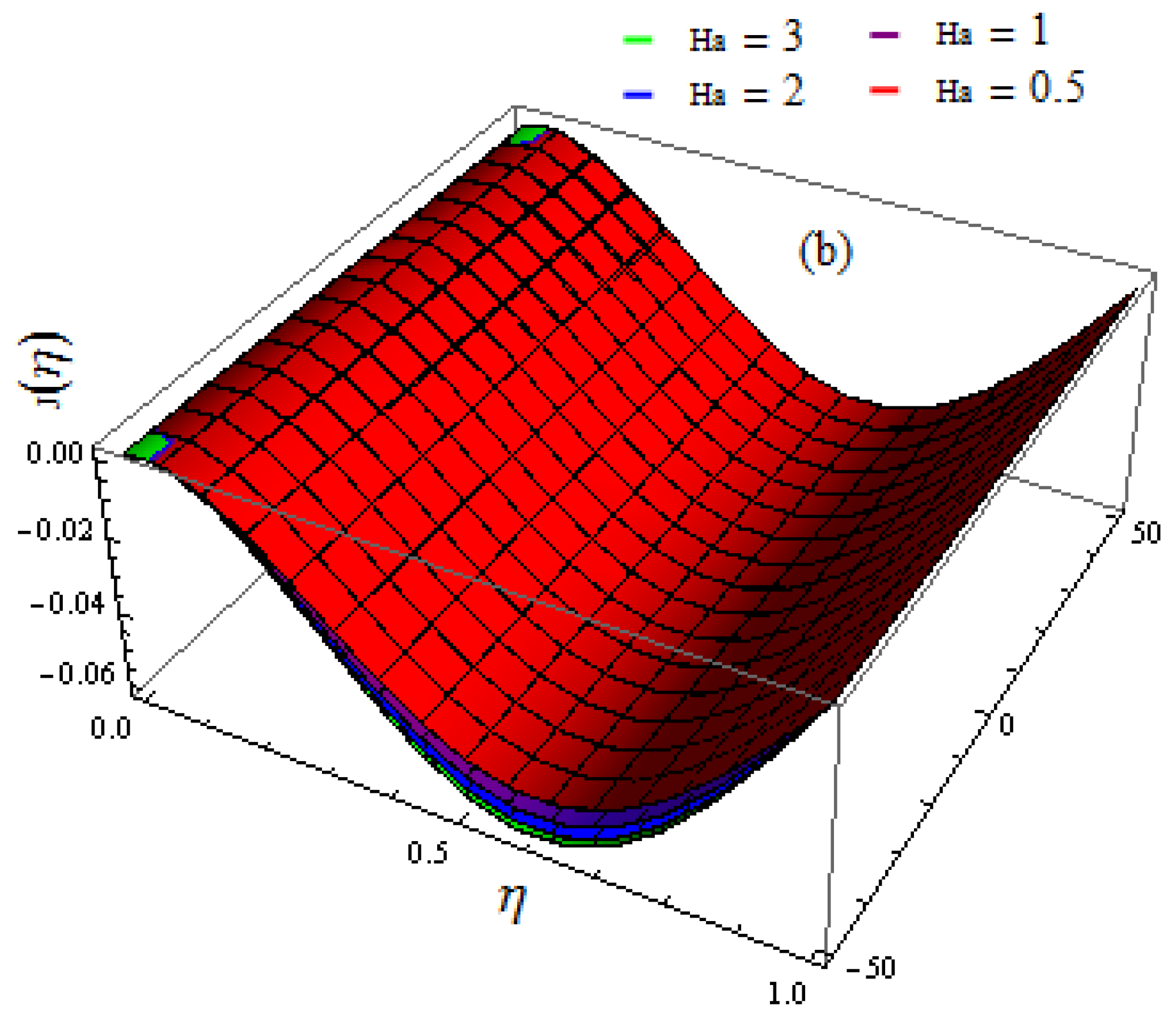
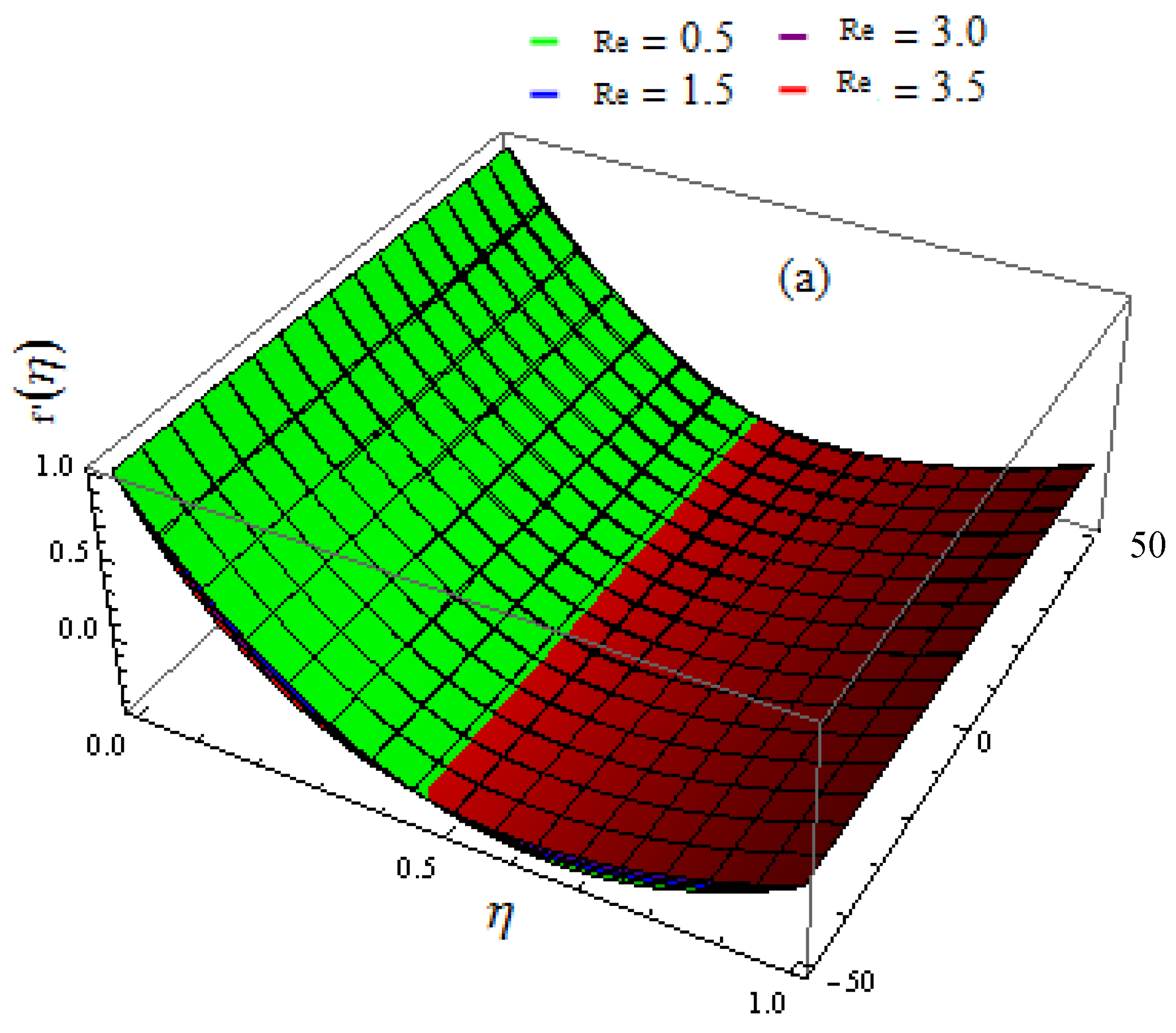
5. Results and Discussion
6. Conclusions
- It is observed that the velocity profiles decline with the increasing values of the suction factor;
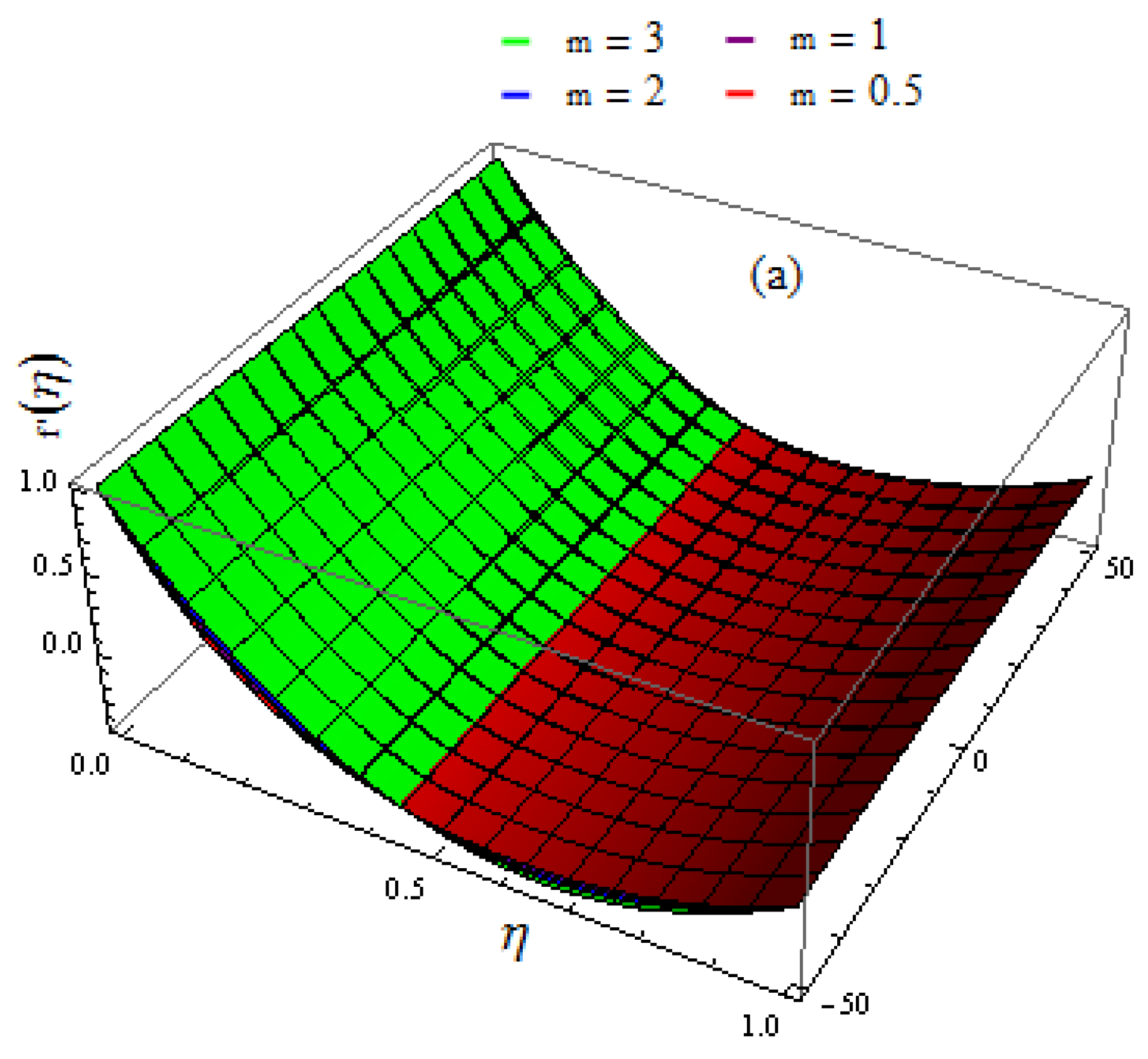
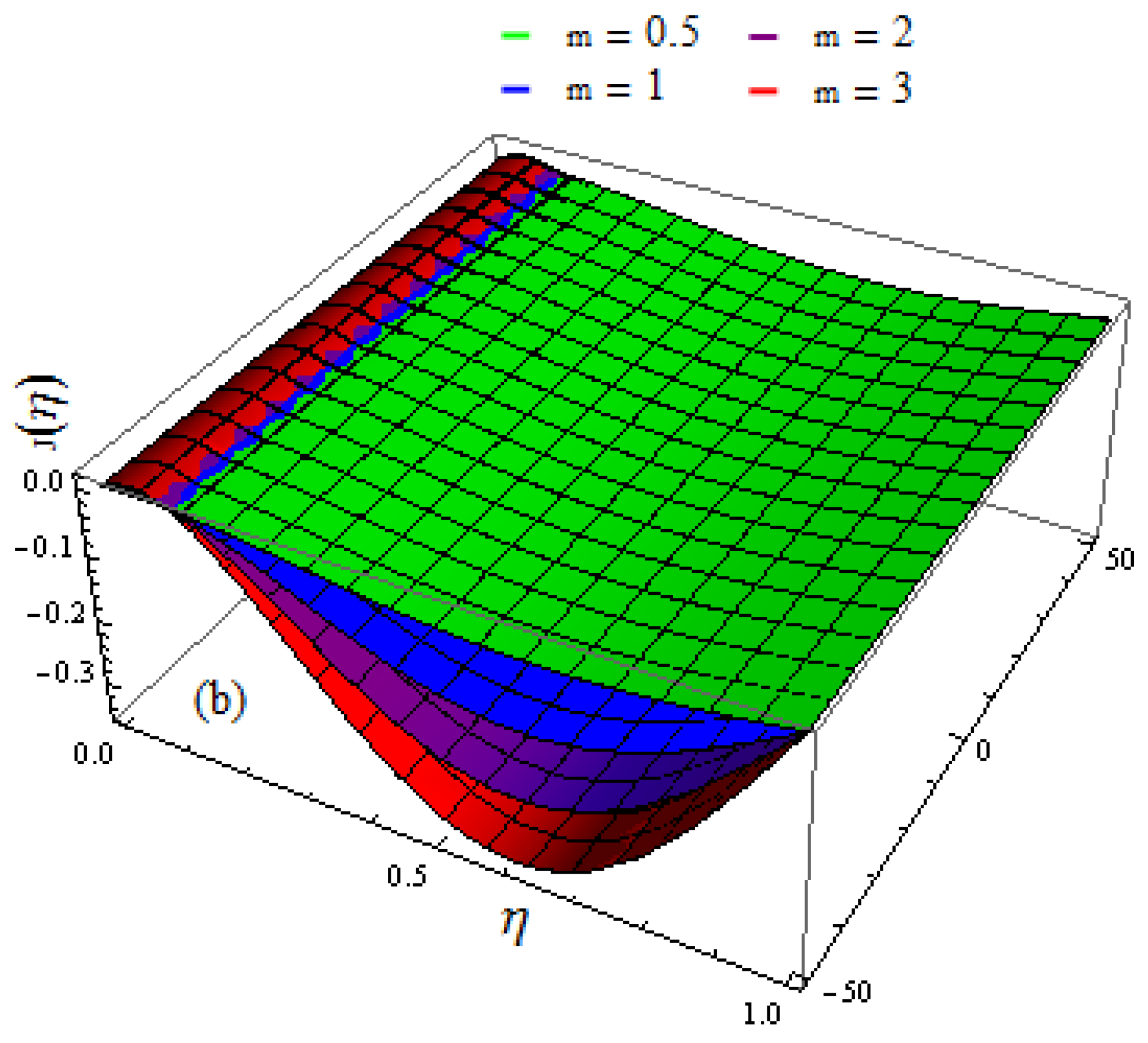
- The velocity profile increases when the values of the rotation factor are increased;
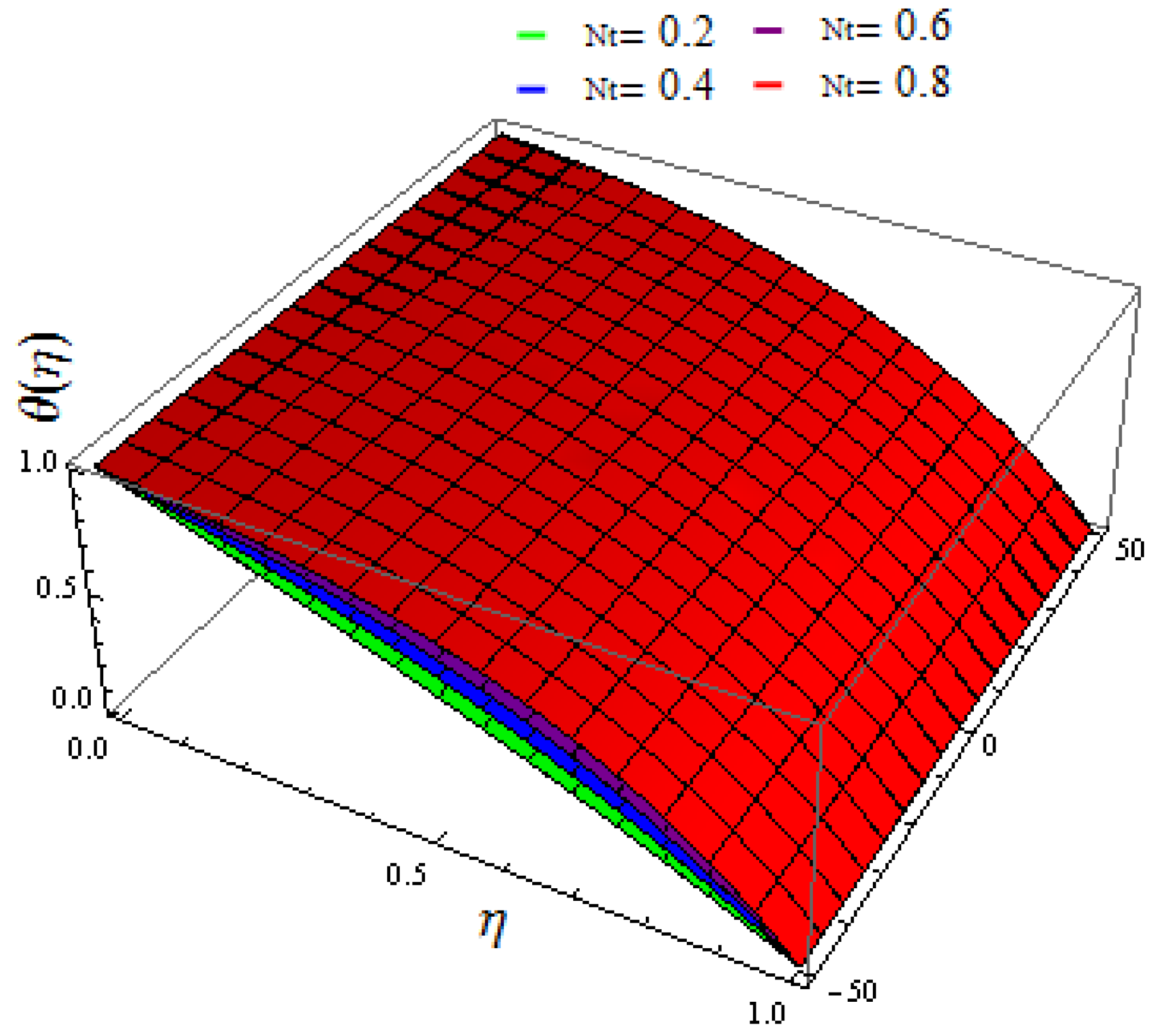
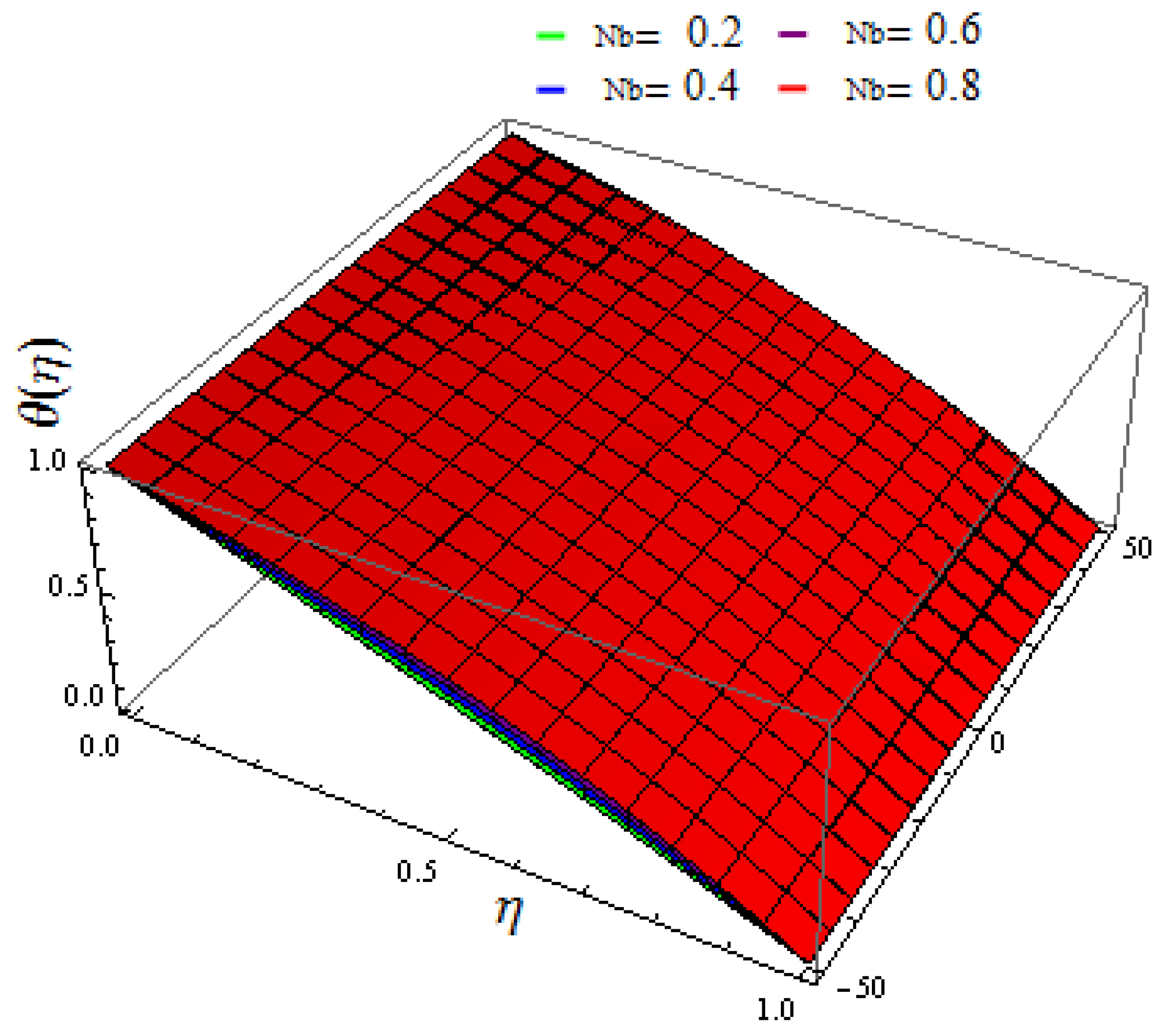
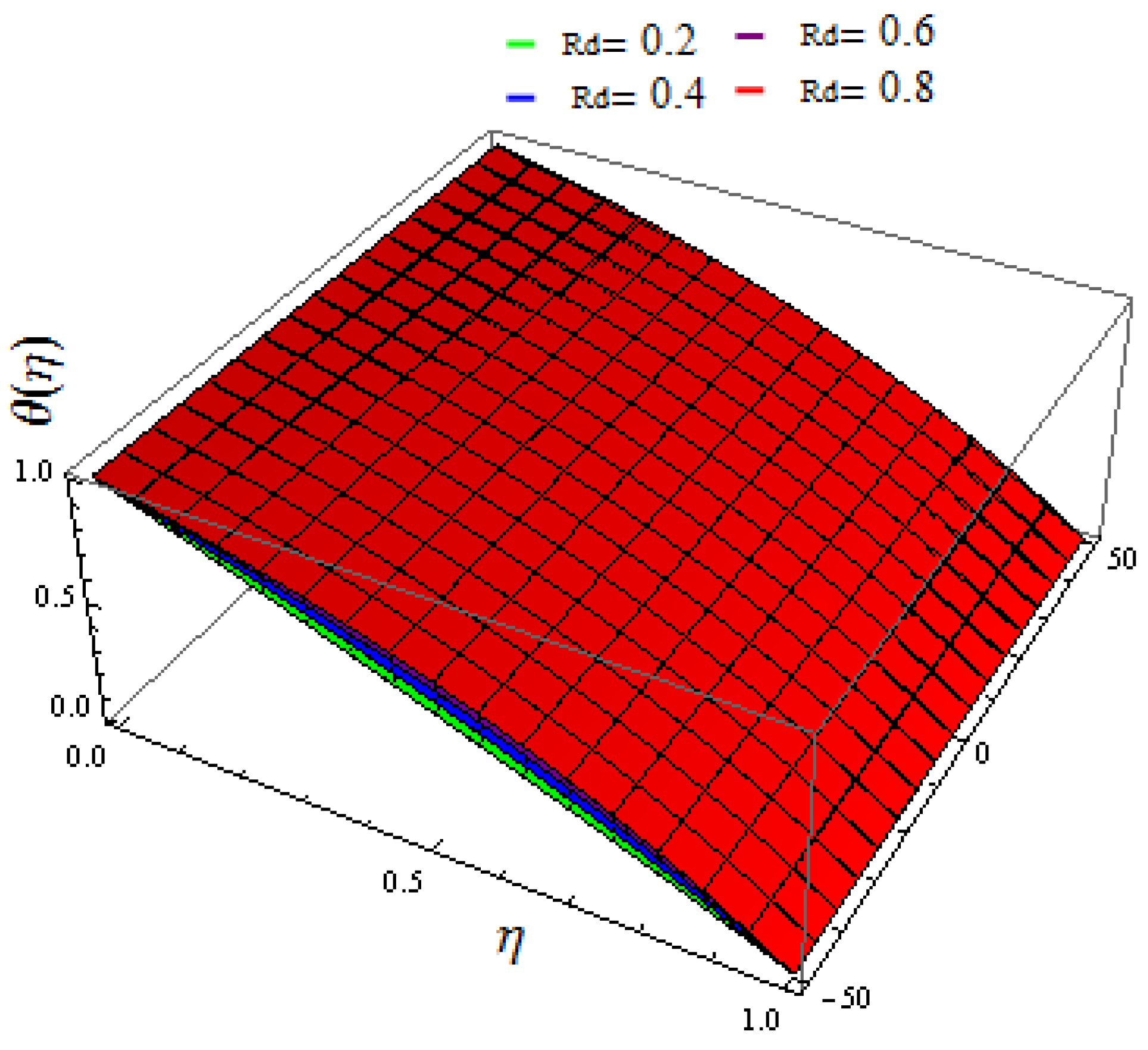
- The temperature field exhibits a rising behavior for increasing values of the thermophoresis factor, Brownian motion, and thermal radiation factor;
- The concentration profile decreases when the values of Brownian and thermophoresis numbers are increased;
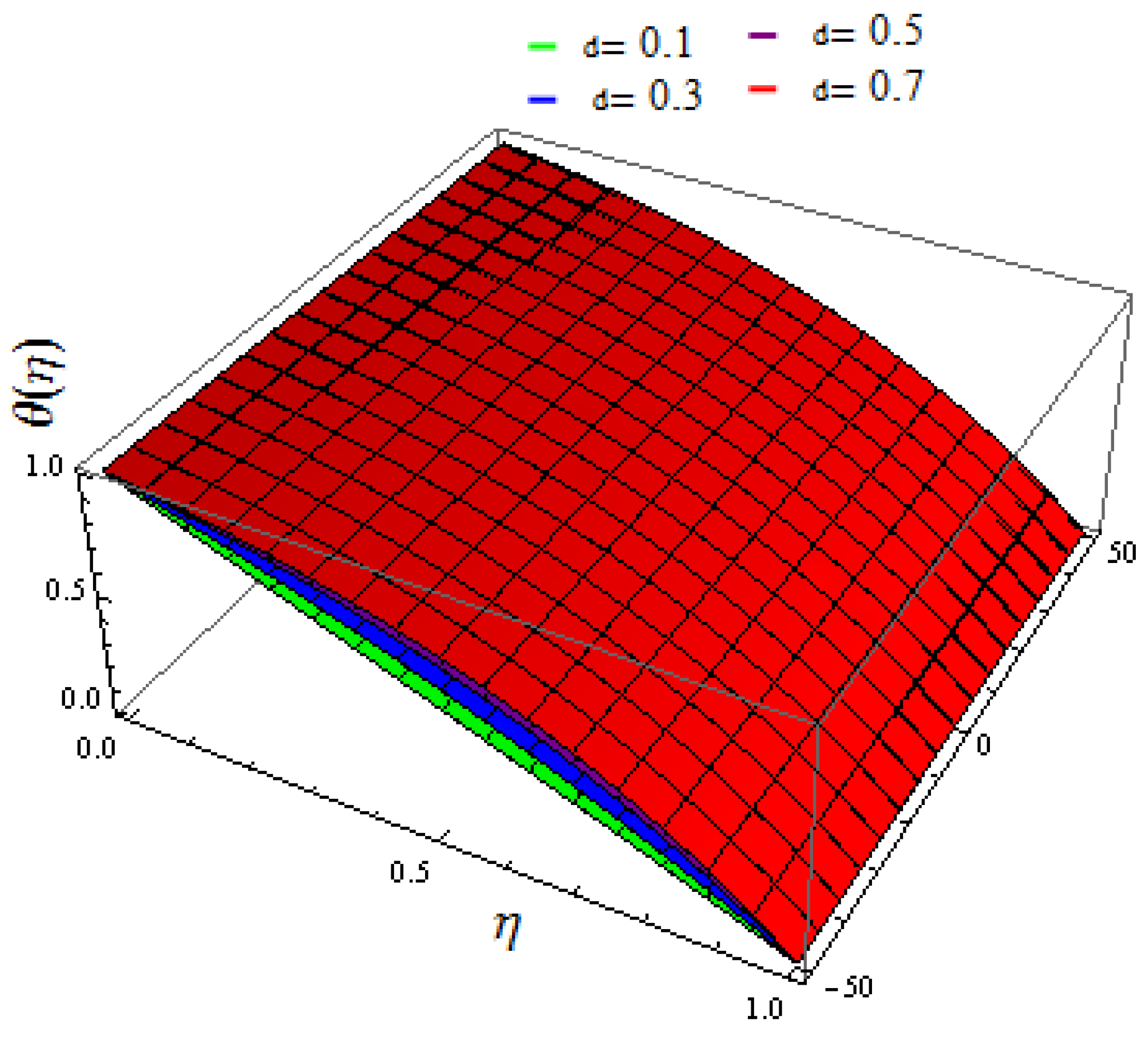
- It is analyzed that the concentration field declines with the variation of and δ.
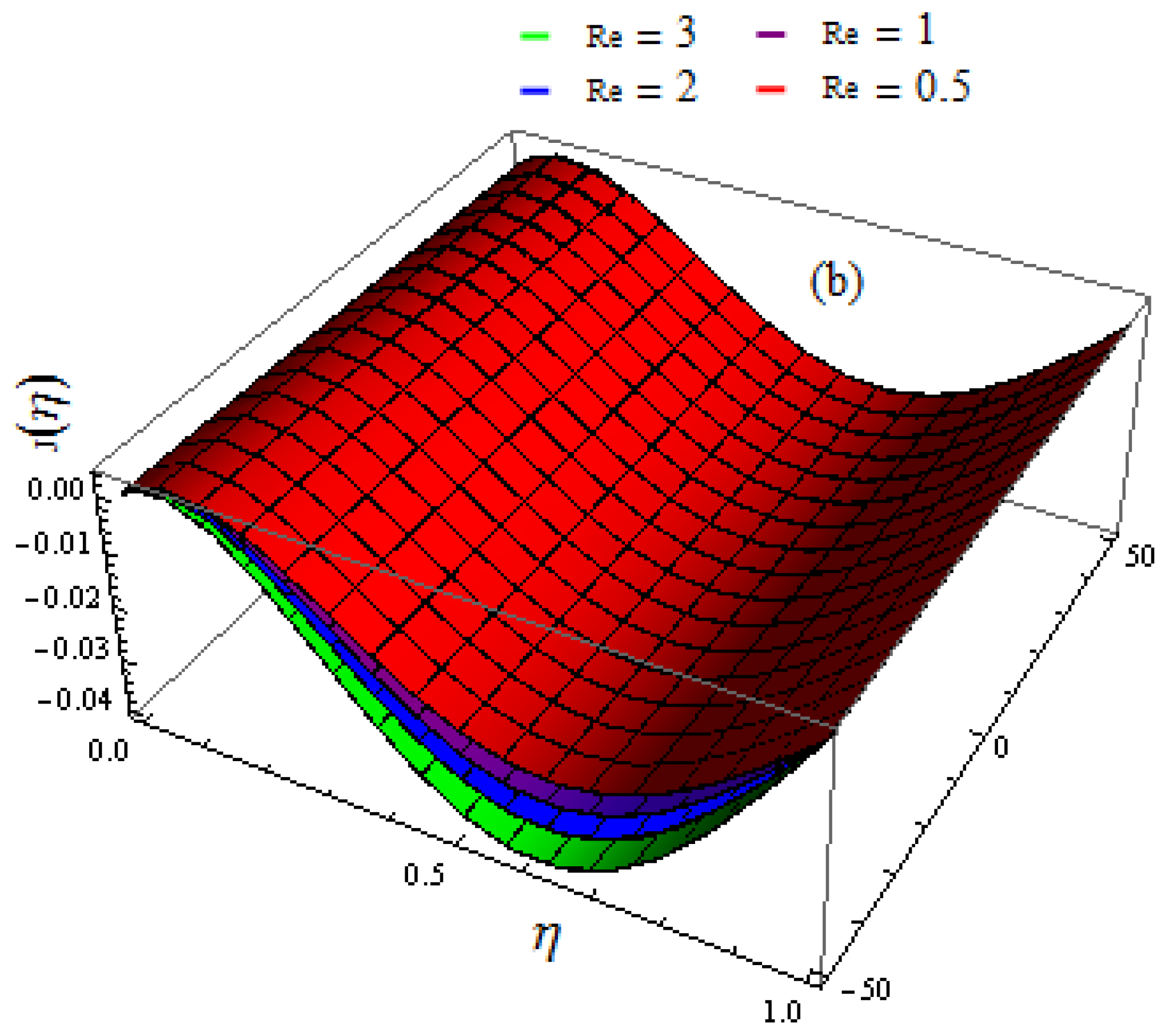
- Shear stress at the upper wall increases when the rotation variable and suction variable are amplified;
- Heat transmission escalates at the bottom wall when , and are increased.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938, CONF-951135-29; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transfer 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Rafati, M.; Hamidi, A.A.; Niaser, M.S. Application of nanofluids in computer cooling systems (heat transfer performance of nanofluids). Appl. Therm. Eng. 2012, 45–46, 9–14. [Google Scholar] [CrossRef]
- Xian, H.W.; Sidik, N.A.C.; Najafi, G. Recent state of nanofluid in automobile cooling systems. J. Therm. Anal. Calorim. 2019, 135, 981–1008. [Google Scholar] [CrossRef]
- Sheikhpour, M.; Arabi, M.; Kasaeian, A.; Rokn Rabei, A.; Taherian, Z. Role of nanofluids in drug delivery and biomedical technology: Methods and applications. Nanotechnol. Sci. Appl. 2020, 13, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, P.K.; Subramani, J.; Suyambazhahan, S.; Sathyamurthy, R. Nanofluids for solar collector applications: A review. Energy Procedia 2014, 61, 2416–2434. [Google Scholar] [CrossRef]
- Motsumi, T.G.; Makinde, O.D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Phys. Scr. 2012, 86, 045003. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Sandeep, N.; Ashwinkumar, G.P. Impact of nanoparticle shape on magnetohydrodynamic stagnation-point flow of carreau nanoliquid: A comparative study. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 236, 1004–1012. [Google Scholar] [CrossRef]
- Sandeep, N.; Ranjana, B.; Samrat, S.P.; Ashwinkumar, G.P. Impact of nonlinear radiation on magnetohydrodynamic flow of hybrid nanofluid with heat source effect. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 1616–1627. [Google Scholar] [CrossRef]
- Samrat, S.P.; Ashwinkumar, G.P.; Sandeep, N. Simultaneous solutions for convective heat transfer in dusty-nano-and dusty-hybrid nanoliquids. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 236, 473–479. [Google Scholar] [CrossRef]
- Chalavadi, S.; Madde, P.; Naramgari, S.; Gangadhar Poojari, A. Effect of variable heat generation/absorption on magnetohydrodynamic sakiadis flow of casson/carreau hybrid nanoliquid due to a persistently moving needle. Heat Transfer. 2021, 50, 8354–8377. [Google Scholar] [CrossRef]
- Mabood, F.; Ashwinkumar, G.P.; Sandeep, N. Effect of nonlinear radiation on 3D unsteady MHD stagnancy flow of Fe3O4/graphene–water hybrid nanofluid. Int. J. Ambient Energy 2020, 43, 3385–3395. [Google Scholar] [CrossRef]
- Mabood, F.; Ashwinkumar, G.P.; Sandeep, N. Simultaneous results for unsteady flow of MHD hybrid nanoliquid above a flat/slendering surface. J. Therm. Anal. Calorim. 2021, 146, 227–239. [Google Scholar] [CrossRef]
- Tlili, I.; Nabwey, H.A.; Ashwinkumar, G.P.; Sandeep, N. 3-D magnetohydrodynamic AA7072-AA7075/methanol hybrid nanofluid flow above an uneven thickness surface with slip effect. Sci. Rep. 2020, 10, 4265. [Google Scholar] [CrossRef]
- Nehad, A.S.; Abderrahim, W.; Essam, R.E.; Thirupathi, T.; Se-Jin, Y.; Ashwinkumar, G.P. Heat transfers Thermodynamic activity of a second-grade ternary nanofluid flow over a vertical plate with Atangana-Baleanu Time-Fractional integral. Alex. Eng. J. 2022, 12, 10045–10053. [Google Scholar]
- Raju, C.S.K.; Ameer, N.A.; Kiran, S.; Nehad, A.S.; Se-jin, Y.; Dinesh, M.K. Nonlinear linear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable Darcy Walls with different shapes and densities: Simple linear regression. Int. Commun. Heat Mass Transfer 2022, 135, 106110. [Google Scholar] [CrossRef]
- Ghulam, R.; Nehad, A.S.; Essam, R.E.; Abderrahim, W. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022, 1–20. [Google Scholar]
- Tlili, I.; Nabwey, H.A.; Samrat, S.P.; Sandeep, N. 3D MHD nonlinear radiative flow of CuO-MgO/methanol hybrid nanofluid beyond an irregular dimension surface with slip effect. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Alotaibi, H.; Althubiti, S.; Eid, M.R.; Mahny, K.L. Numerical treatment of mhd flow of casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Continua 2020, 66, 229–245. [Google Scholar] [CrossRef]
- Yu, B.; Ramzan, M.; Riasat, S.; Kadry, S.; Chu, Y.M.; Malik, M.Y. Impact of autocatalytic chemical reaction in an Ostwald-de-Waele nanofluid flow past a rotating disk with heterogeneous catalysis. Sci. Rep. 2021, 11, 15526. [Google Scholar] [CrossRef] [PubMed]
- Shaheen, N.; Ramzan, M.; Alshehri, A.; Shah, Z.; Kumam, P. Soret–Dufour impact on a three-dimensional Casson nanofluid flow with dust particles and variable characteristics in a permeable media. Sci. Rep. 2021, 11, 14513. [Google Scholar] [CrossRef] [PubMed]
- Bilal, M.; Ramzan, M.; Mehmood, Y.; Kbiri Alaoui, M.; Chinram, R. An entropy optimization study of non-Darcian magnetohydrodynamic Williamson nanofluid with nonlinear thermal radiation over a stratified sheet. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1883–1889. [Google Scholar] [CrossRef]
- Liu, C.; Khan, M.U.; Ramzan, M.; Chu, Y.M.; Kadry, S.; Malik, M.Y.; Chinram, R. Nonlinear radiative Maxwell nanofluid flow in a Darcy–Forchheimer permeable media over a stretching cylinder with chemical reaction and bioconvection. Sci. Rep. 2021, 11, 9391. [Google Scholar] [CrossRef]
- Bashir, S.; Ramzan, M.; Chung, J.D.; Chu, Y.M.; Kadry, S. Analyzing the impact of induced magnetic flux and Fourier’s and Fick’s theories on the Carreau-Yasuda nanofluid flow. Sci. Rep. 2021, 11, 9230. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.M.; Yang, Z. Study of nanofluid forced convection heat transfer in a bent channel by means of lattice Boltzmann method. Phys. Fluids 2018, 30, 032001. [Google Scholar] [CrossRef]
- Zhang, Y.; Shahmir, N.; Ramzan, M.; Alotaibi, H.; Aljohani, H.M. Upshot of melting heat transfer in a Von Karman rotating flow of gold-silver/engine oil hybrid nanofluid with cattaneo-christov heat flux. Case Stud. Therm. Eng. 2021, 26, 101149. [Google Scholar] [CrossRef]
- Riasat, S.; Ramzan, M.; Sun, Y.L.; Malik, M.Y.; Chinram, R. Comparative analysis of Yamada-Ota and Xue models for hybrid nanofluid flow amid two concentric spinning disks with variable thermophysical characteristics. Case Stud. Therm Eng. 2021, 26, 101039. [Google Scholar] [CrossRef]
- Zeeshan; Rasheed, H.U.; Khan, W.; Khan, I.; Alshammari, N.; Hamadneh, N. Numerical computation of 3D Brownian motion of thin film nanofluid flow of convective heat transfer over a stretchable rotating surface. Sci. Rep. 2022, 12, 2708. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.U.; Khan, I.; Abu-Zinadah, H.; Aldahlan, M.A. Mathematical Simulation of Casson MHD Flow through a Permeable Moving Wedge with Nonlinear Chemical Reaction and Nonlinear Thermal Radiation. Materials 2022, 15, 747. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Khan, I.; Weera, W.; Mohamed, A. Heat transfer analysis of Cu and Al2O3 dispersed in ethylene glycol as a base fluid over a stretchable permeable sheet of MHD thin-film flow. Sci. Rep. 2022, 12, 8878. [Google Scholar]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Weera, W. Insight into significance of bioconvection on MHD tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Chung, J.D. Micropolar dusty fluid: Coriolis force effects on dynamics of MHD rotating fluid when lorentz force is significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Qasem, N.A.A.; Younis, O.; Marzouki, R.; Mourad, A.; Chung, J.D. MHD hybrid nanofluid mixed convection heat transfer and entropy generation in a 3-D triangular porous cavity with zigzag wall and rotating cylinder. Mathematics 2022, 10, 769. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Saleem, A.; Malik, M.Y.; Issakhov, A.; Alharbi, F.M. Models base study of inclined MHD of hybrid nanofluid flow over nonlinear stretching cylinder. Chin. J. Phys. 2021, 69, 109–117. [Google Scholar] [CrossRef]
- Fourier, J.; Baptiste, J. Théorie Analytique de la Chaleur; Chez Firmin Didot, père et fils: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti. Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Zeeshan; Ahammad, N.A.; Rasheed, H.U.; El-Deeb, A.A.; Almarri, B.; Shah, N.A. A Numerical Intuition of Activation Energy in Transient Micropolar Nanofluid Flow Configured by an Exponentially Extended Plat Surface with Thermal Radiation Effects. Mathematics 2022, 10, 4046. [Google Scholar] [CrossRef]
- Rehman, S.; Zeeshan; Rasheed, H.U.; Islam, S. Visualization of multiple slip effects on the hydromagnetic Casson nanofluid past a nonlinear extended permeable surface: A numerical approach. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L.; Liu, L. MHD viscoelastic flow and heat transfer over a vertical stretching sheet with Cattaneo-Christov heat flux effects. J. Mol. Liq. 2016, 221, 19–25. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Abbasi, F.M.; Hayat, T.; Ahmad, B. Cattaneo-Christov heat flux model for third-grade fluid flow towards exponentially stretching sheet. Appl. Math. Mech. 2016, 37, 761–768. [Google Scholar] [CrossRef]
- Rehman, S.U.; Fatima, N.; Ali, B.; Imran, M.; Ali, L.; Shah, N.A.; Chung, J.D. The Casson Dusty Nanofluid: Significance of Darcy–Forchheimer Law, Magnetic Field, and Non-Fourier Heat Flux Model Subject to Stretch Surface. Mathematics 2022, 10, 2877. [Google Scholar] [CrossRef]
- Sui, J.; Zheng, L.; Zhang, X. Boundary layer heat and mass transfer with Cattaneo–Christov double diffusion in upper-convected Maxwell nanofluid past a stretching sheet with slip velocity. Int. J. Therm. Sci. 2016, 104, 461–468. [Google Scholar] [CrossRef]
- Acharya, N.; Das, K.; Kundu, P.K. Cattaneo–Christov intensity of magnetised upper-convected Maxwell nanofluid flow over an inclined stretching sheet: A generalised Fourier and Fick’s perspective. Int. J. Mech. Sci. 2017, 130, 167–173. [Google Scholar] [CrossRef]
- Nagendramma, V.; Raju, C.S.K.; Mallikarjuna, B.; Shehzad, S.A.; Leelarathnam, A. 3Dcasson nanofluid flow over slendering surface in a suspension of gyrotactic microorganisms with Cattaneo-Christov heat flux. Appl. Math. Mech. 2018, 39, 623–638. [Google Scholar] [CrossRef]
- Rauf, A.; Mushtaq, A.; Shah, N.A.; Botmart, T. Heat transfer and hybrid ferrofluid flow over a nonlinearly stretchable rotating disk under the influence of an alternating magnetic field. Sci. Rep. 2022, 12, 17548. [Google Scholar] [CrossRef]
- Ullah, K.S.; Ali, N.; Hayat, T.; Abbas, Z. Heat transfer analysis based on Cattaneo-Christov heat flux model and convective boundary conditions for flow over an oscillatory stretching surface. Therm. Sci. 2019, 23, 443–455. [Google Scholar] [CrossRef]
- Lv, Y.P.; Gul, H.; Ramzan, M.; Chung, J.D.; Bilal, M. Bioconvective Reiner–Rivlin nanofluid flow over a rotating disk with Cattaneo–Christov flow heat flux and entropy generation analysis. Sci. Rep. 2021, 11, 15859. [Google Scholar] [CrossRef]
- Abid, N.; Ramzan, M.; Chung, J.D.; Kadry, S.; Chu, Y.M. Comparative analysis of magnetized partially ionized copper, copper oxide–water and kerosene oil nanofluid flow with Cattaneo–Christov heat flux. Sci. Rep. 2020, 10, 19300. [Google Scholar] [CrossRef]
- Li, Y.X.; Shah, F.; Khan, M.I.; Chinram, R.; Elmasry, Y.; Sun, T.C. Dynamics of cattaneo- Christov double diffusion (CCDD) and arrhenius activation law on mixed convective flow towards a stretched Riga device. Chaos Solitons Fractals 2021, 148, 111010. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Kadry, S.; Chu, Y.M. Role of bioconvection in a three dimensional tangent hyperbolic partially ionized magnetized nanofluid flow with cattaneo-Christov heat flux and activation energy. Int. Commun. Heat Mass Transfer 2021, 120, 104994. [Google Scholar] [CrossRef]
- Tlili, I.; Hamadneh, N.N.; Khan, W.A.; Atawneh, S. Thermodynamic analysis of MHD Couette-Poiseuille flow of water-based Nano fluids in a porous channel with radiation and Hall effects. J. Term. Anal. Calorim. 2018, 132, 1899–1912. [Google Scholar] [CrossRef]



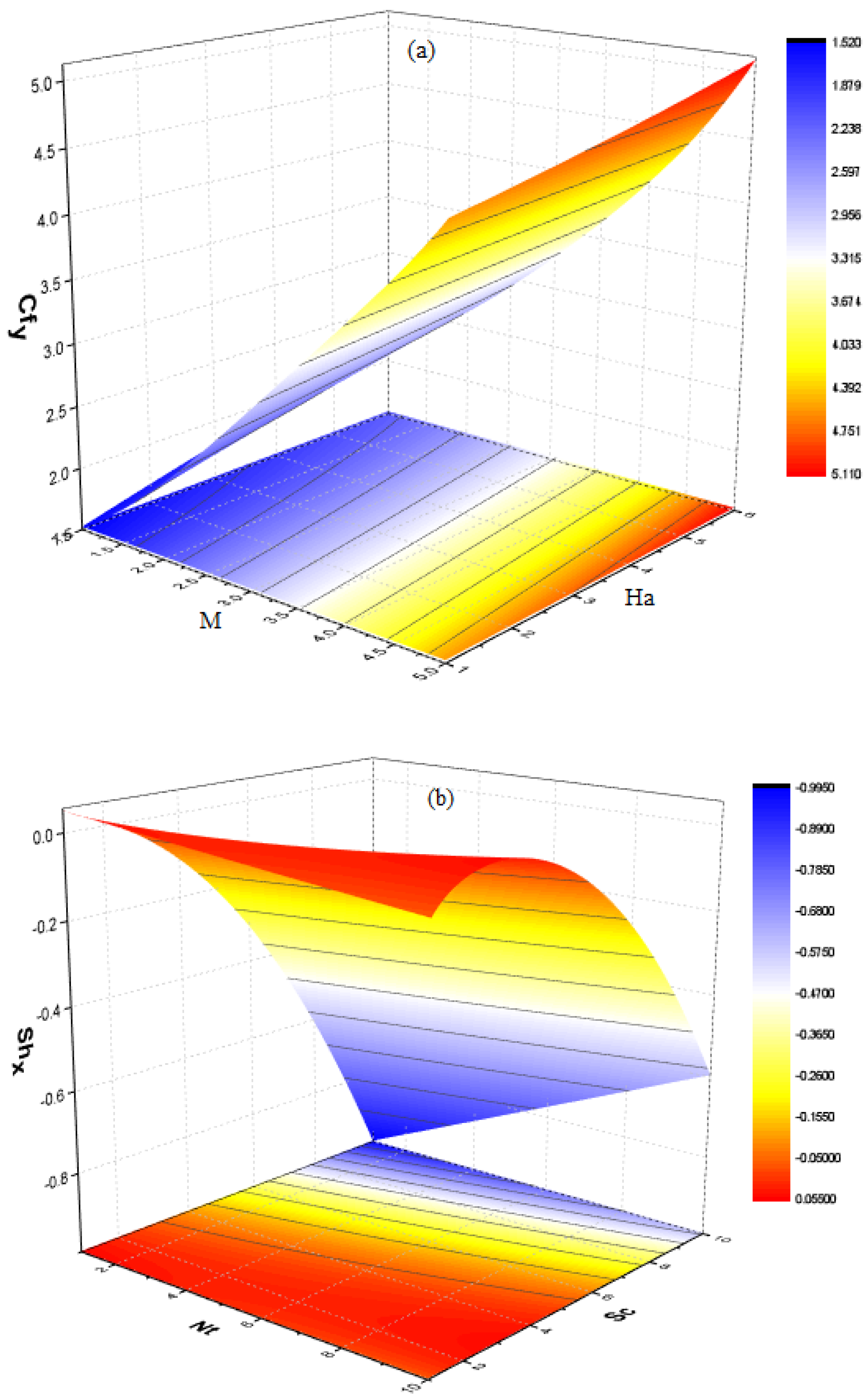
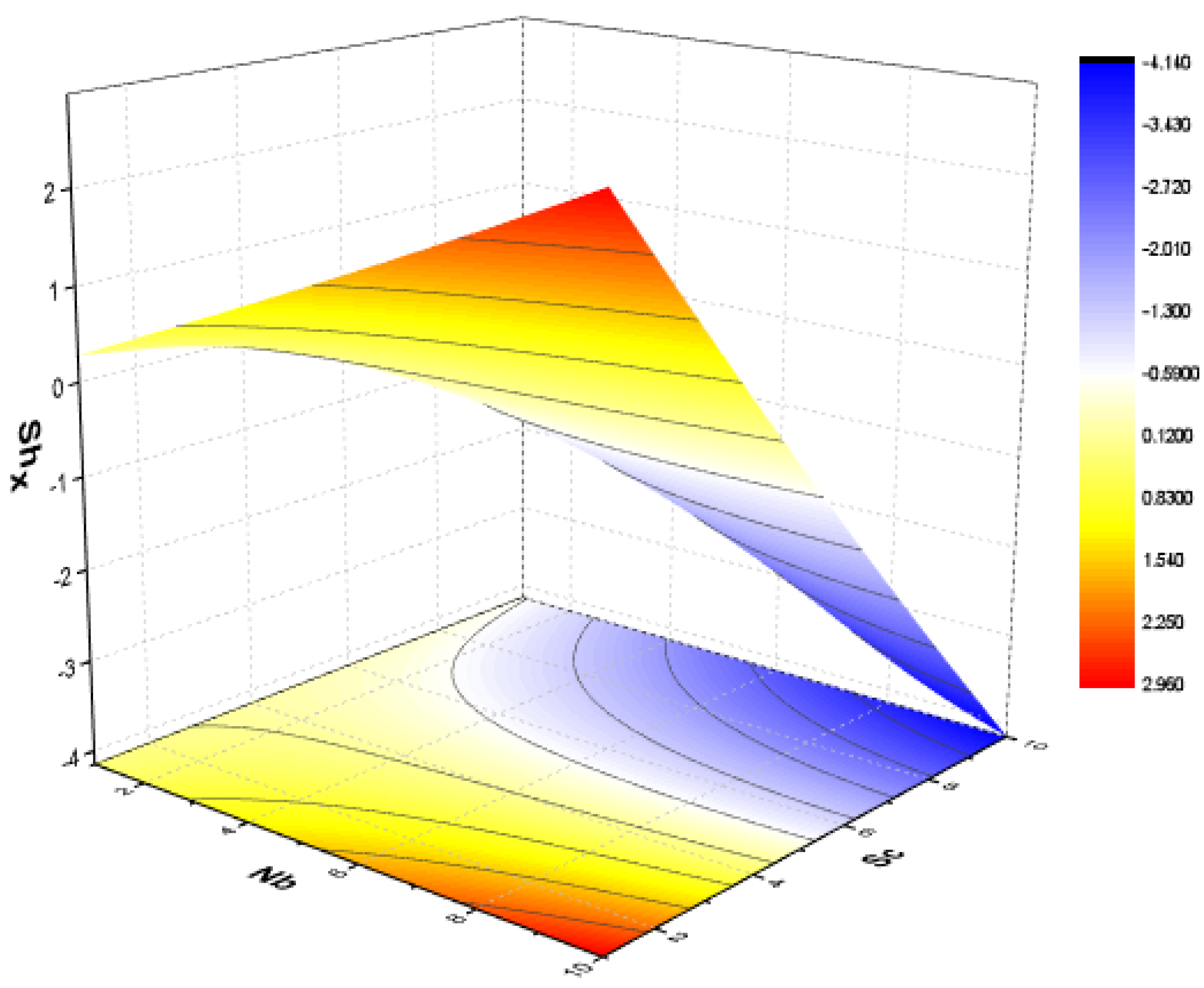
| Tili et al. [55] | Current | Tili et al. [55] | Current | |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 |
| 0.1 | 0.7568230 | 0.7568230 | 0.6160560 | 0.6160560 |
| 0.3 | 0.6071153 | 0.6071151 | 0.3736382 | 0.3736381 |
| 0.5 | 0.4046126 | 0.4046123 | 0.1671527 | 0.1671527 |
| 0.7 | 0.1718404 | 0.1718401 | 0.0026777 | 0.0026777 |
| 1 | 0 | 0 | 0 | 0 |
| Ha | ||||||
|---|---|---|---|---|---|---|
| 0.4 | 1 | 0.2 | −3.8262455 | 0.22541159 | 3.5926925 | 0.54849149 |
| 0.6 | −3.7983194 | 0.22937296 | 3.5992994 | 0.58998432 | ||
| 0.8 | −3.7619566 | 0.23142925 | 3.5987119 | 0.64987973 | ||
| 0.3 | 1 | 0.4 | −3.7988799 | 0.28672762 | 3.5953999 | 0.97287839 |
| 3 | −3.9971633 | 0.37866375 | 3.6589899 | 1.5282953 | ||
| 5 | −4.4167316 | 0.43814944 | 3.7469865 | 1.9585998 | ||
| 0.4 | 1 | 0.1 | −4.5444949 | −0.1333518 | 3.9993977 | 0.67772693 |
| 0.3 | −5.9429682 | −0.3575427 | 4.9899783 | 0.93912785 | ||
| 0.5 | −7.6632682 | −0.5299198 | 5.9943565 | 1.1715158 |
| Pr | Rd | |||
|---|---|---|---|---|
| 1 | 0.5 | 0.2 | 2.9693338 | 3.3797674 |
| 4 | 3.1232217 | 3.4167495 | ||
| 7 | 3.1763599 | 3.6592875 | ||
| 3 | 0.2 | 0.1 | 2.6937456 | 2.9846985 |
| 0.4 | 2.9717172 | 3.3412984 | ||
| 0.6 | 3.2393369 | 3.5999498 | ||
| 3 | 0.5 | 0.2 | 3.1792415 | 3.6889439 |
| 0.4 | 3.3259978 | 3.1497378 | ||
| 0.6 | 3.4679672 | 4.6419175 |
| Sc | Nt | Nb | E | |||
|---|---|---|---|---|---|---|
| 0.5 | 0.2 | 0.4 | 0.2 | 0.5 | 1.2682748 | 0.8782798 |
| 1.0 | 1.3569924 | 0.8331143 | ||||
| 1.4 | 1.4471383 | 0.7999553 | ||||
| 1.0 | 0.1 | 1.8912389 | 3.7326718 | |||
| 0.3 | 1.7123892 | 3.9118486 | ||||
| 0.5 | 1.5379884 | 4.2974655 | ||||
| 0.1 | 0.6 | 1.2446956 | 0.8882515 | |||
| 1.2 | 1.2747579 | 0.8771941 | ||||
| 1.4 | 1.2944949 | 0.8663445 | ||||
| 0.2 | 1.9955616 | 3.4693693 | ||||
| 0.4 | 1.6926893 | 3.9924682 | ||||
| 0.6 | 1.3628933 | 4.5733221 | ||||
| 1 | 1.1981187 | 0.8961844 | ||||
| 2 | 1.1853191 | 0.8999332 | ||||
| 3 | 1.1791132 | 0.9129878 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeeshan; Ahammad, N.A.; Shah, N.A.; Chung, J.D.; Attaullah; Rasheed, H.U. Analysis of Error and Stability of Nanofluid over Horizontal Channel with Heat/Mass Transfer and Nonlinear Thermal Conductivity. Mathematics 2023, 11, 690. https://doi.org/10.3390/math11030690
Zeeshan, Ahammad NA, Shah NA, Chung JD, Attaullah, Rasheed HU. Analysis of Error and Stability of Nanofluid over Horizontal Channel with Heat/Mass Transfer and Nonlinear Thermal Conductivity. Mathematics. 2023; 11(3):690. https://doi.org/10.3390/math11030690
Chicago/Turabian StyleZeeshan, N. Ameer Ahammad, Nehad Ali Shah, Jae Dong Chung, Attaullah, and Haroon Ur Rasheed. 2023. "Analysis of Error and Stability of Nanofluid over Horizontal Channel with Heat/Mass Transfer and Nonlinear Thermal Conductivity" Mathematics 11, no. 3: 690. https://doi.org/10.3390/math11030690
APA StyleZeeshan, Ahammad, N. A., Shah, N. A., Chung, J. D., Attaullah, & Rasheed, H. U. (2023). Analysis of Error and Stability of Nanofluid over Horizontal Channel with Heat/Mass Transfer and Nonlinear Thermal Conductivity. Mathematics, 11(3), 690. https://doi.org/10.3390/math11030690






