Dynamic Analysis and FPGA Implementation of a New, Simple 5D Memristive Hyperchaotic Sprott-C System
Abstract
:1. Introduction
2. A Simple 4D Hyperchaotic System
2.1. Equilibrium Point and Stability
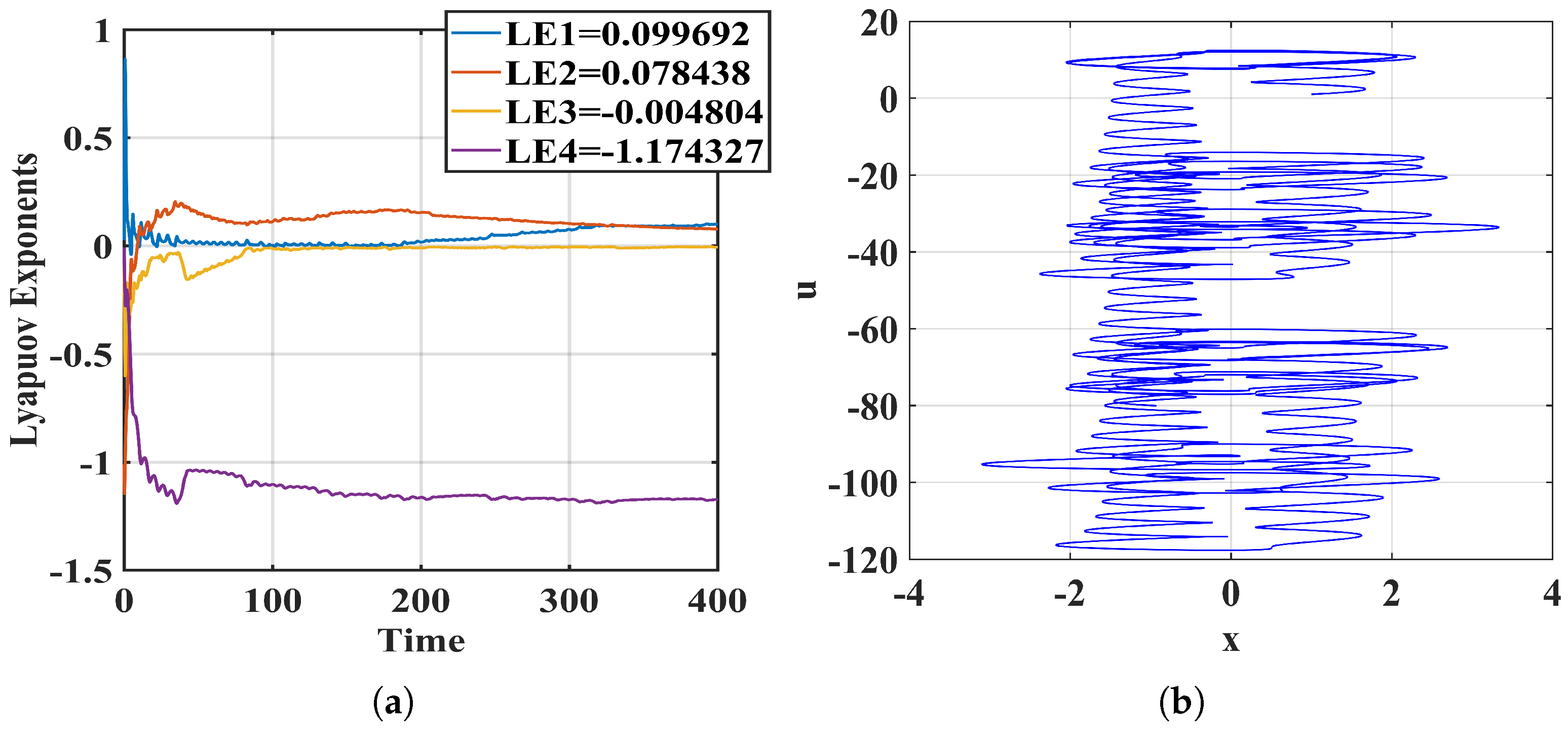
2.2. Lyapunov Exponents
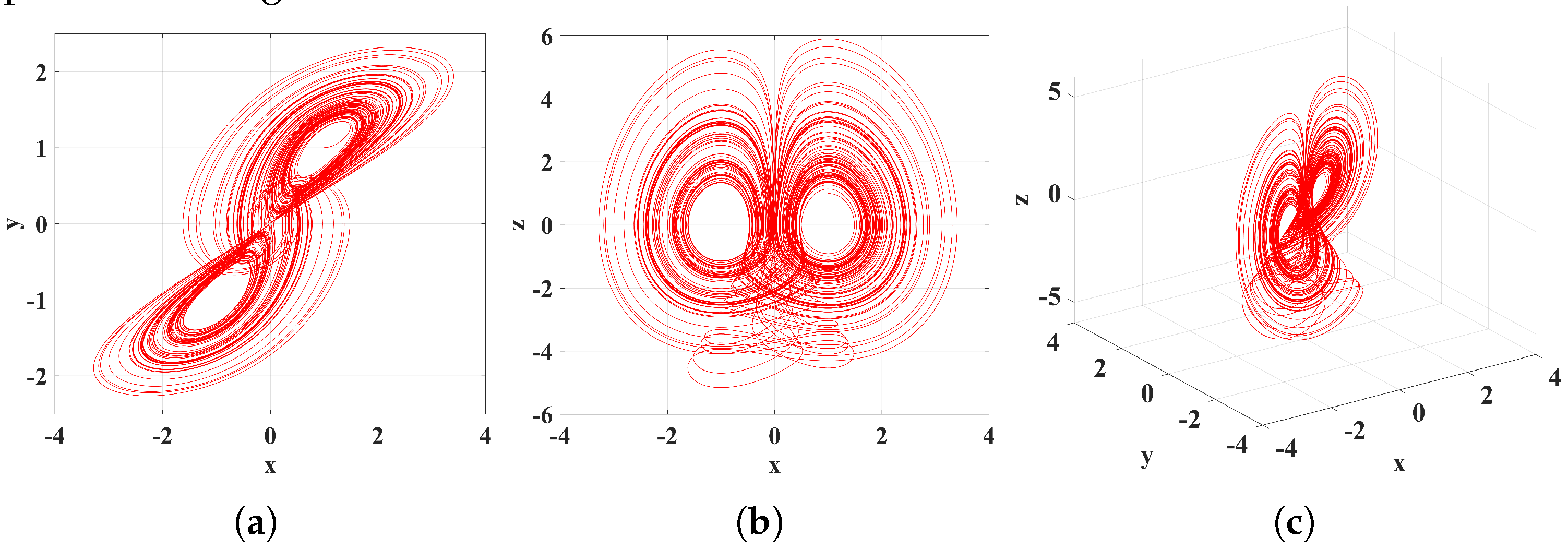
2.3. Nonlinear Dynamic Behavior Analysis
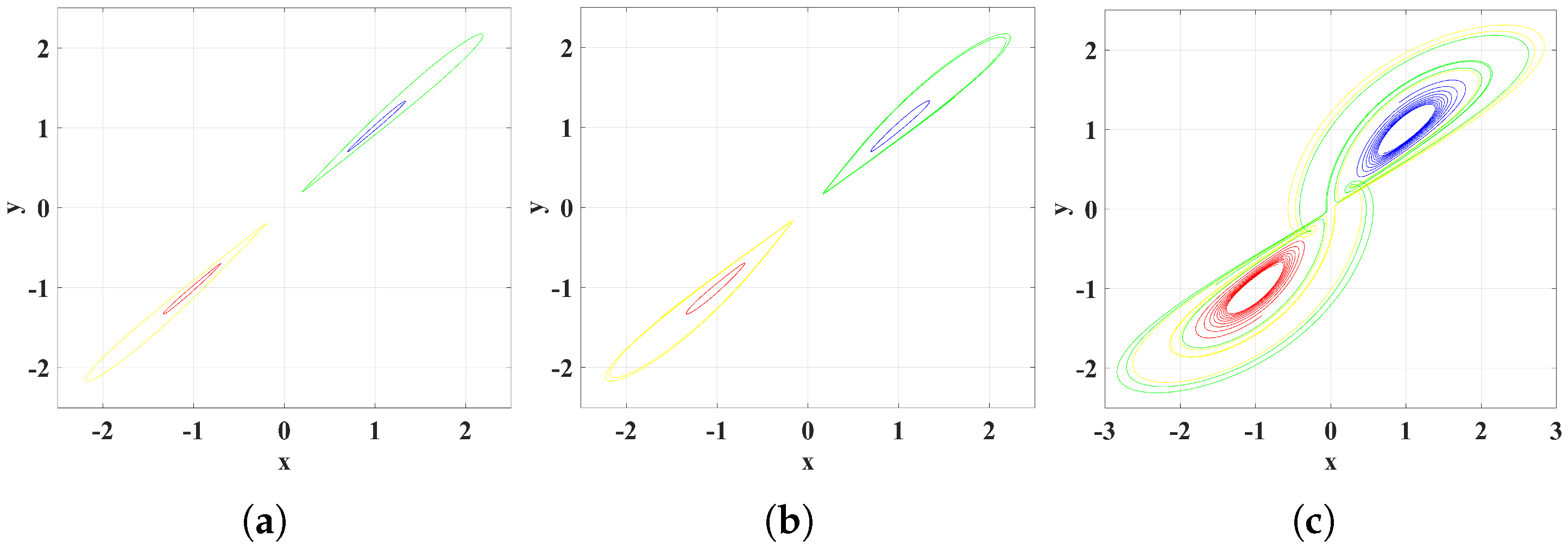
3. Sprott-C Hyperchaotic System Based on Memristor
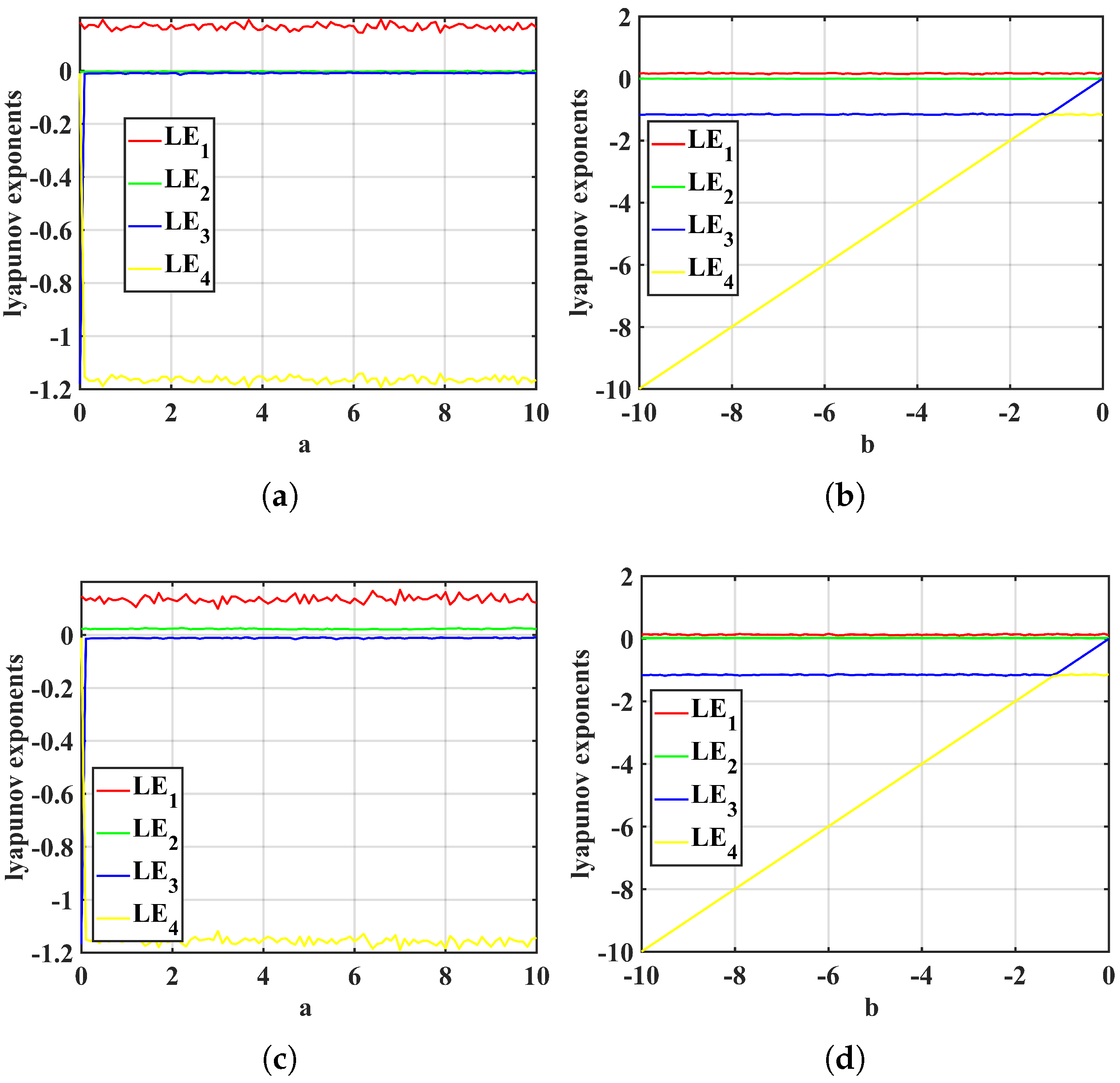
3.1. Divergence and Lyapunov Exponents
3.2. Equilibrium Points and Stability
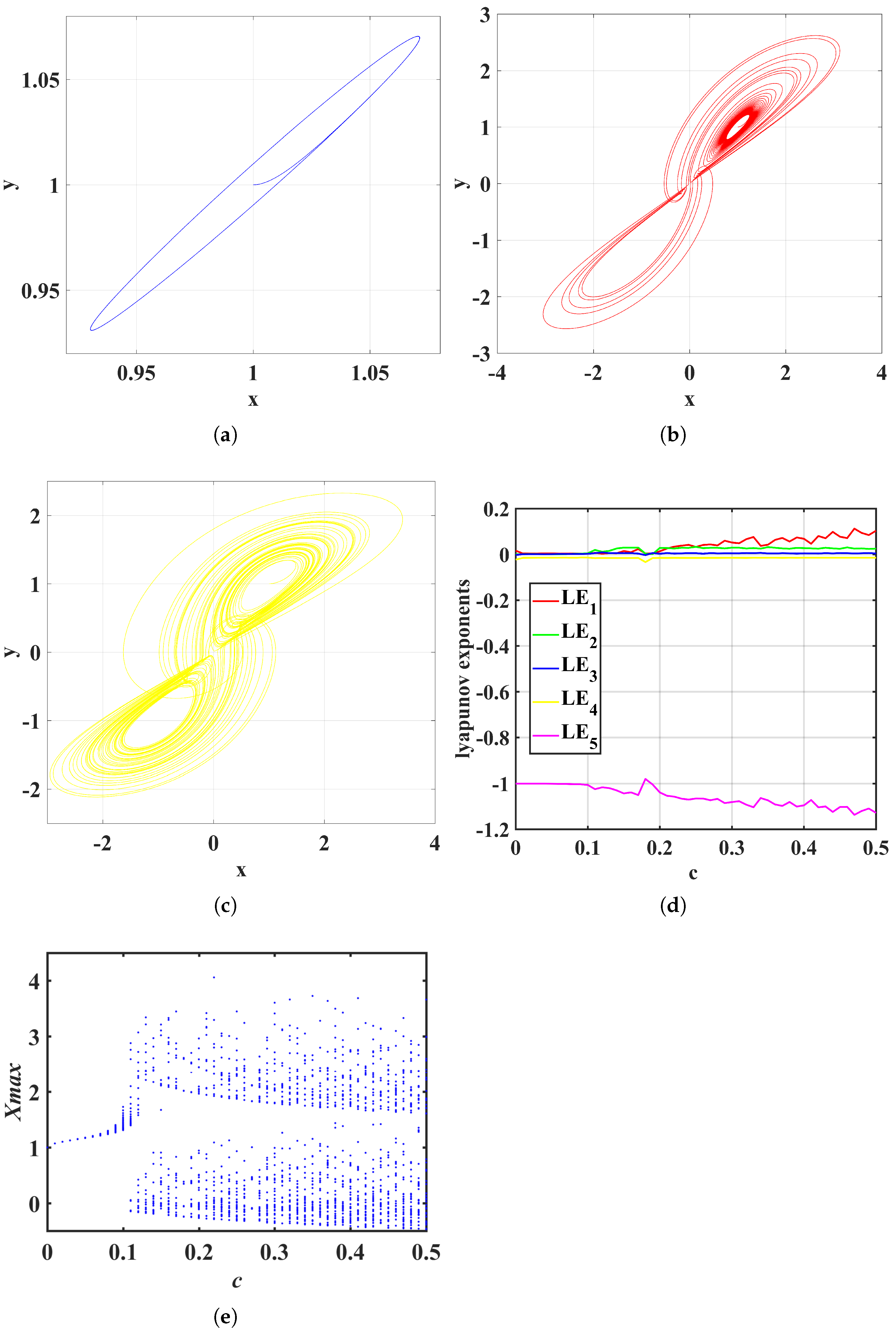
3.3. Abundant Dynamic Behavior
3.4. Coexistence of Attractors
4. FPGA Implementation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wan, Q.; Yan, Z.; Li, F.; Chen, S.; Liu, J. Complex dynamics in a Hopfield neural network under electromagnetic induction and electromagnetic radiation. Chaos 2022, 32, 073107. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Yu, F.; Kong, X.; Mokbel, A.A.M.; Wang, C.; Cai, S. Dynamics study on the effect of memristive autapse distribution on Hopfield neural network. Chaos 2022, 32, 083133. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, Y.; Wang, T. Generating n-scroll chaotic attractors from a memristor-based magnetized hopfield neural network. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 311–315. [Google Scholar] [CrossRef]
- Shen, H.; Yu, F.; Wang, C.; Sun, J.; Cai, S. Firing mechanism based on single memristive neuron and double memristive coupled neurons. Nonlinear Dyn. 2022, 110, 3807–3822. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, C.; Deng, Q.; Lin, H. Regulating memristive neuronal dynamical properties via excitatory or inhibitory magnetic field coupling. Nonlinear Dyn. 2022, 110, 3823–3835. [Google Scholar] [CrossRef]
- Lu, Y.M.; Wang, C.H.; Deng, Q.L.; Xu, C. The dynamics of a memristor-based Rulkov neuron with the fractional-order difference. Chin. Phys. B 2022, 31, 060502. [Google Scholar] [CrossRef]
- Ma, M.; Lu, Y.; Li, Z.; Sun, Y.; Wang, C. Multistability and Phase Synchronization of Rulkov Neurons Coupled with a Locally Active Discrete Memristor. Fractal Fract. 2023, 7, 82. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, C.; Yao, W.; Lin, H. Observer-based synchronization of memristive neural networks under DoSattacks and actuator saturation and its application to image encryption. Appl. Math. Comput. 2022, 425, 127080. [Google Scholar]
- Ma, M.; Xiong, K.; Li, Z.; Sun, Y. Dynamic Behavior Analysis and Synchronization of Memristor-Coupled Heterogeneous Discrete Neural Networks. Mathematics 2023, 11, 375. [Google Scholar] [CrossRef]
- Long, M.; Chen, Y.; Peng, F. Simple and accurate analysis of BER performance for DCSK chaotic communication. IEEE Commun. Lett. 2011, 15, 1175–1177. [Google Scholar] [CrossRef]
- Yu, F.; Yu, Q.; Chen, H.; Kong, X.; Mokbel, A.A.M.; Cai, S.; Du, S. Dynamic analysis and audio encryption application in IoT of a multi-scroll fractional-order memristive Hopfield neural network. Fractal Fract. 2022, 6, 370. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, Hardware implementation and Image encryption application. Integration 2021, 81, 71–83. [Google Scholar] [CrossRef]
- Li, X.; Zhou, L.; Tan, F. An image encryption scheme based on finite-time cluster synchronization of two-layer complex dynamic networks. Soft Comput. 2022, 26, 511–525. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Mokbel, A.A.M.; Yao, W.; Cai, S. Complex Dynamics, Hardware Implementation and Image Encryption Application of Multiscroll Memeristive Hopfield Neural Network with a Novel Local Active Memeristor. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 326–330. [Google Scholar] [CrossRef]
- Korolj, A.; Wu, H.T.; Radisic, M. A healthy dose of chaos: Using fractal frameworks for engineering higher-fidelity biomedical systems. Biomaterials 2019, 219, 119363. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Xu, C.; Yu, F. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Yu, Q.; Kong, X.; Sharma, P.K.; Cai, S. Privacy Protection of Medical Data Based on Multi-Scroll Memristive Hopfield Neural Network. IEEE Trans. Netw. Sci. Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, C.; Lin, H.; Sun, Y. A Memristive Spiking Neural Network Circuit with Selective Supervised Attention Algorithm. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Momani, S.; Almatroud, O.A.; Al-Sawalha, M.M.; Boulaaras, S.M.; Pham, V.T. Special Fractional-Order Map and Its Realization. Mathematics 2022, 10, 4474. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Liu, W.; Bao, B. Discrete memristive neuron model and its interspike interval-encoded application in image encryption. Sci. China Sci. 2021, 64, 2281–2291. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Chen, H.; Yu, Q.; Cai, S.; Huang, Y.; Du, S. A 6D fractional-order memristive hopfield neural network and its application in image encryption. Front. Phys. 2022, 10, 847385. [Google Scholar] [CrossRef]
- Azam, A.; Aqeel, M.; Sunny, D.A. Generation of Multidirectional Mirror Symmetric Multiscroll Chaotic Attractors (MSMCA) in Double Wing Satellite Chaotic System. Chaos Solitons Fractals 2022, 155, 111715. [Google Scholar] [CrossRef]
- Ai, W.; Sun, K.; Fu, Y. Design of multiwing-multiscroll grid compound chaotic system and its circuit implementation. Int. J. Mod. Phys. C 2018, 29, 1850049. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Kong, X.; Yu, Q.; Cai, S.; Huang, Y.; Du, S. Dynamic analysis and application in medical digital image watermarking of a new multi-scroll neural network with quartic nonlinear memristor. Eur. Phys. J. Plus 2022, 137, 434. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, Q. Dynamical analysis of the generalized Sprott C system with only two stable equilibria. Nonlinear Dyn. 2012, 68, 543–554. [Google Scholar] [CrossRef]
- Wei, Z.; Moroz, I.; Liu, A. Degenerate Hopf bifurcations, hidden attractors, and control in the extended Sprott E system with only one stable equilibrium. Turk. J. Math. 2014, 38, 672–687. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Mou, J.; Jahanshahi, H.; Cao, Y.; Bu, F. A new set of hyperchaotic maps based on modulation and coupling. Eur. Phys. J. Plus 2022, 137, 523. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Banerjee, S.; Wang, Z.; Cao, Y. Design and DSP implementation of a fractional-order detuned laser hyperchaotic circuit with applications in image encryption. Chaos Solitons Fractals 2022, 159, 112133. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Liu, Y. Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos Solitons Fractals 2022, 165, 112781. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, W.; Wang, J.; Zhou, Z.; Chen, J.; Zhong, G. Secure communication based on microcontroller unit with a novel five-dimensional hyperchaotic system. Arab. J. Sci. Eng. 2022, 47, 813–828. [Google Scholar] [CrossRef]
- Yan, S.; Li, L.; Gu, B.; Cui, Y.; Wang, J.; Song, J. Design of hyperchaotic system based on multi-scroll and its encryption algorithm in color image. Integration 2023, 88, 203–221. [Google Scholar] [CrossRef]
- Goufo, E.F.D. Linear and rotational fractal design for multiwing hyperchaotic systems with triangle and square shapes. Chaos Solitons Fractals 2022, 161, 112283. [Google Scholar] [CrossRef]
- Al-hayali, M.A.; Al-Azzawi, F.S. A 4D hyperchaotic Sprott S system with multistability and hidden attractors. J. Phys. Conf. Ser. 2021, 1879, 032031. [Google Scholar] [CrossRef]
- Ojoniyi, O.S.; Njah, A.N. A 5D hyperchaotic Sprott B system with coexisting hidden attractors. Chaos Solitons Fractals 2016, 87, 172–181. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Xu, C.; Zhang, X.; Iu, H.H. A memristive synapse control method to generate diversified multi-structure chaotic attractors. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022. [Google Scholar] [CrossRef]
- Wan, Q.; Yan, Z.; Li, F.; Liu, J.; Chen, S. Multistable dynamics in a Hopfield neural network under electromagnetic radiation and dual bias currents. Nonlinear Dyn. 2022, 109, 2085–2101. [Google Scholar] [CrossRef]
- Ramadoss, J.; Almatroud, O.A.; Momani, S.; Pham, V.T.; Thoai, V.P. Discrete memristance and nonlinear term for designing memristive maps. Symmetry 2022, 14, 2110. [Google Scholar] [CrossRef]
- Ma, M.; Yang, Y.; Qiu, Z.; Peng, Y.; Sun, Y.; Li, Z.; Wang, M. A locally active discrete memristor model and its application in a hyperchaotic map. Nonlinear Dyn. 2022, 107, 2935–2949. [Google Scholar] [CrossRef]
- Ramadoss, J.; Ouannas, A.; Tamba, V.K.; Grassi, G.; Momani, S.; Pham, V.T. Constructing non-fixed-point maps with memristors. Eur. Phys. J. Plus 2022, 137, 211. [Google Scholar] [CrossRef]
- Yu, F.; Qian, S.; Chen, X.; Huang, Y.; Liu, L.; Shi, C.; Cai, S.; Song, Y.; Wang, C. A new 4D four-wing memristive hyperchaotic system: Dynamical analysis, electronic circuit design, shape synchronization and secure communication. Int. J. Bifurc. Chaos 2020, 30, 2050147. [Google Scholar] [CrossRef]
- Kamdem Kuate, P.D.; Lai, Q.; Fotsin, H. Complex behaviors in a new 4D memristive hyperchaotic system without equilibrium and its microcontroller-based implementation. Eur. Phys. J. Spec. Top. 2019, 228, 2171–2184. [Google Scholar] [CrossRef]
- Yu, F.; Xu, S.; Xiao, X.; Yao, W.; Huang, Y.; Cai, S.; Yin, B.; Li, Y. Dynamics analysis, FPGA realization and image encryption application of a 5D memristive exponential hyperchaotic system. Integration 2023, 90, 58–70. [Google Scholar] [CrossRef]
- Yu, F.; Liu, L.; Qian, S.; Li, L.; Huang, Y.; Shi, C.; Cai, S.; Wu, X.; Du, S.; Wan, Q. Chaos-based application of a novel multistable 5D memristive hyperchaotic system with coexisting multiple attractors. Complexity 2020, 2020, 8034196. [Google Scholar] [CrossRef] [Green Version]
- Ramamoorthy, R.; Rajagopal, K.; Leutcho, G.D.; Krejcar, O.; Namazi, H.; Hussain, I. Multistable dynamics and control of a new 4D memristive chaotic Sprott B system. Chaos Solitons Fractals 2022, 156, 111834. [Google Scholar] [CrossRef]
- Koyuncu, İ.; Tuna, M.; Pehlivan, İ.; Fidan, C.B.; Alçın, M. Design, FPGA implementation and statistical analysis of chaos-ring based dual entropy core true random number generator. Analog Integr. Circuits Signal Process. 2020, 102, 445–456. [Google Scholar] [CrossRef]
- Ding, S.; Wang, N.; Bao, H.; Chen, B.; Wu, H.; Xu, Q. Memristor synapse-coupled piecewise-linear simplified Hopfield neural network: Dynamics analysis and circuit implementation. Chaos Solitons Fractals 2023, 166, 112899. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Jin, J.; Du, S. Design and FPGA implementation of a pseudo-random number generator based on a Hopfield neural network under electromagnetic radiation. Front. Phys. 2021, 9, 690651. [Google Scholar] [CrossRef]
- Chen, H.; He, S.; Pano Azucena, A.D.; Yousefpour, A.; Jahanshahi, H.; López, M.A.; Alcaraz, R. A multistable chaotic jerk system with coexisting and hidden attractors: Dynamical and complexity analysis, FPGA-based realization, and chaos stabilization using a robust controller. Symmetry 2020, 12, 569. [Google Scholar] [CrossRef] [Green Version]
- Shah, D.K.; Chaurasiya, R.B.; Vyawahare, V.A.; Pichhode, K.; Patil, M.D. FPGA implementation of fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 245–257. [Google Scholar] [CrossRef]
- Koyuncu, I.; Ozcerit, A.T.; Pehlivan, I. Implementation of FPGA-based real time novel chaotic oscillator. Nonlinear Dyn. 2014, 77, 49–59. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Said, L.A.; Radwan, A.G. Reconfigurable fpga realization of fractional-order chaotic systems. IEEE Access 2021, 9, 89376–89389. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Zhang, X.; Koyuncu, I.; Bonny, T.; Tuna, M.; Alçin, M.; Zhang, S.; Sulaiman, I.M.; Awwal, A.M.; et al. A novel 3D chaotic system with line equilibrium: Multistability, integral sliding mode control, electronic circuit, FPGA implementation and its image encryption. IEEE Access 2022, 10, 68057–68074. [Google Scholar] [CrossRef]
- Lai, Q.; Wang, Z.; Kuate, P.D.K. Dynamical analysis, FPGA implementation and synchronization for secure communication of new chaotic system with hidden and coexisting attractors. Mod. Phys. Lett. B 2022, 36, 2150538. [Google Scholar] [CrossRef]
- Chen, W.; Jin, J.; Chen, C.; Yu, F.; Wang, C. A Disturbance Suppression Zeroing Neural Network for Robust Synchronization of Chaotic Systems and Its FPGA Implementation. Int. J. Bifurc. Chaos 2022, 32, 2250210. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Du, S. FPGA implementation and image encryption application of a new PRNG based on a memristive Hopfield neural network with a special activation gradient. Chin. Phys. B 2022, 31, 020505. [Google Scholar] [CrossRef]
- Sheet, A.T.; Al-Azzawi, S.F. A New Simple 4D Hyperchaotic Sprott-B System with Seven-Terms. In Proceedings of the 2022 International Conference on Computer Science and Software Engineering (CSASE), Duhok, Iraq, 15–17 March 2022; pp. 65–70. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Wang, C.; Li, Y. Dynamic Analysis and FPGA Implementation of a New, Simple 5D Memristive Hyperchaotic Sprott-C System. Mathematics 2023, 11, 701. https://doi.org/10.3390/math11030701
Yu F, Zhang W, Xiao X, Yao W, Cai S, Zhang J, Wang C, Li Y. Dynamic Analysis and FPGA Implementation of a New, Simple 5D Memristive Hyperchaotic Sprott-C System. Mathematics. 2023; 11(3):701. https://doi.org/10.3390/math11030701
Chicago/Turabian StyleYu, Fei, Wuxiong Zhang, Xiaoli Xiao, Wei Yao, Shuo Cai, Jin Zhang, Chunhua Wang, and Yi Li. 2023. "Dynamic Analysis and FPGA Implementation of a New, Simple 5D Memristive Hyperchaotic Sprott-C System" Mathematics 11, no. 3: 701. https://doi.org/10.3390/math11030701
APA StyleYu, F., Zhang, W., Xiao, X., Yao, W., Cai, S., Zhang, J., Wang, C., & Li, Y. (2023). Dynamic Analysis and FPGA Implementation of a New, Simple 5D Memristive Hyperchaotic Sprott-C System. Mathematics, 11(3), 701. https://doi.org/10.3390/math11030701









