Approximations for Secular Variation Maxima of Classical Orbital Elements under Low Thrust
Abstract
:1. Introduction
2. Gauss’s Variational Equations and Simplifying Assumptions
2.1. Gauss’s Variational Equations for Classical Orbital Elements
2.2. Simplifying Assumptions
- The fuel consumption is small and ignored due to the low magnitude of the thrust compared to the total mass of the spacecraft. Consequently, the magnitude of the propulsive acceleration becomes constant because of the constant low-thrust magnitude . Thus, the following equation holdsThe thrust magnitude is modeled as a function of the maximum thruster input power and specific impulse as [40]where denotes the thruster efficiency, whose value together with are selected from [40]. They are assumed to be constant in this paper to obtain a constant low-thrust magnitude. Meanwhile, is the standard gravitational acceleration.
- The variation of the true anomaly caused by the three components of can be ignored because its maximum is much smaller than the central gravitational acceleration [34].In Equation (9), the approximation of the Equation (6) can be derived when the effect on caused by the low thrust is small enough compared to the term (a similar approximation can also obtained in [36,41]).Divided by Equation (9), Gauss’s variational equations of classical orbital elements are transformed into the following differential equations in terms of the true anomaly
3. Secular Variation Maximum of Single Classical Orbital Element
3.1. Secular Variation Maximum of Semi-Major Axis
| Algorithm 1: Iterative algorithm. |
| Input: Initial orbital elements , and For each loop iteration of each subsection:
Stopping conditions: The time of flight reaches the given value. Output: Approximations for the variation of the orbital elements |
3.2. Secular Variation Maximum of Eccentricity
3.3. Secular Variation Maximum of Inclination
3.3.1. Strategy 1
3.3.2. Strategy 2
3.4. Secular Variation Maximum of Right Ascension of the Ascending Node
3.5. Secular Variation Maximum of Argument of Periapsis
4. Numerical Simulations
4.1. Simulations for Variation Maximum of Each Orbital Element
4.2. Estimation of the Velocity Increment
5. Discussion
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| a | Semi-major axis |
| e | Eccentricity |
| i | Inclination |
| Right ascension of ascending node | |
| Argument of periapsis | |
| f | True anomaly |
| h | Magnitude of specific angular momentum |
| Gravitational constant | |
| Propulsive acceleration vector | |
| Variation group of the classical orbital elements over one orbital revolution | |
| Values of the orbital elements after N orbital revolutions | |
| Thrust magnitude | |
| Mean equatorial radius of the Earth | |
| Second order zonal harmonic of the Earth’s gravitational potential | |
| Velocity increment | |
| Group of the orbital elements | |
| Thrust vector | |
| u | Engine thrust ratio |
| Unit vector of thrust direction | |
| Time of flight | |
| Lagrange multiplier associated with state, i.e., costate | |
| H | Hamiltonian |
| AU | Astronomical unit |
| Combination of shooting functions | |
| m | Instantaneous mass of spacecraft |
| Out-of-plane (yaw) steering angle | |
| In-plane thrust-steering angle | |
| Subscripts | |
| Low thrust | |
| perturbation | |
| P | Proposed method |
| I | Indirect method |
| N | N-th orbital revolution |
| 0 | Initial time |
| f | Final time |
References
- Rayman, M.D.; Williams, S.N. Design of the first interplanetary solar electric propulsion mission. J. Spacecr. Rocket. 2002, 39, 589–595. [Google Scholar] [CrossRef]
- Benkhoff, J.; Van Casteren, J.; Hayakawa, H.; Fujimoto, M.; Laakso, H.; Novara, M.; Ferri, P.; Middleton, H.R.; Ziethe, R. BepiColombo—Comprehensive exploration of Mercury: Mission overview and science goals. Planet. Space Sci. 2010, 58, 2–20. [Google Scholar] [CrossRef]
- Alemany, K.; Braun, R. Survey of Global Optimization Methods for Low-Thrust, Multiple Asteroid Tour Missions. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Sedona, AZ, USA, 28 January–1 February 2007. [Google Scholar]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]
- Chen, Y.; Baoyin, H.; Li, J. Accessibility of main-belt asteroids via gravity assists. J. Guid. Control Dyn. 2014, 37, 623–632. [Google Scholar] [CrossRef]
- Liu, E.; Yan, Y.; Yang, Y. Analysis and determination of capture area for space debris removal based on reachable domain. Adv. Space Res. 2021, 68, 1613–1626. [Google Scholar] [CrossRef]
- Dahl, J.; de Campos, G.R.; Olsson, C.; Fredriksson, J. Collision avoidance: A literature review on threat-assessment techniques. IEEE Trans. Intell. Veh. 2018, 4, 101–113. [Google Scholar] [CrossRef]
- Holzinger, M.; Scheeres, D. Applied reachability for space situational awareness and safety in spacecraft proximity operations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6096. [Google Scholar]
- Xu, Z.; Chen, X.; Huang, Y.; Bai, Y.; Chen, Q. Collision prediction and avoidance for satellite ultra-close relative motion with zonotope-based reachable sets. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 3920–3937. [Google Scholar] [CrossRef]
- Lee, S.; Hwang, I. Reachable set computation for spacecraft relative motion with energy-limited low-thrust. Aerosp. Sci. Technol. 2018, 77, 180–188. [Google Scholar] [CrossRef]
- Battin, R.H. An Introduction to the Mathematics and Methods of Astrodynamics; Revised Edition; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999. [Google Scholar]
- Xue, D.; Li, J.; Baoyin, H.; Jiang, F. Reachable Domain for Spacecraft with a Single Impulse. J. Guid. Control Dyn. 2010, 33, 934–942. [Google Scholar] [CrossRef]
- Li, X.H.; He, X.S.; Zhong, Q.F. Investigation on Reachable Domain of Satellite with a Single Impulse. Adv. Mater. Res. 2012, 433–440, 5759–5766. [Google Scholar] [CrossRef]
- Wen, C.; Peng, C.; Gao, Y. Reachable domain for spacecraft with ellipsoidal Delta-V distribution. Astrodynamics 2018, 2, 265–288. [Google Scholar] [CrossRef]
- Vinh, N.X.; Gilbert, E.G.; Howe, R.M.; Sheu, D.; Lu, P. Reachable domain for interception at hyperbolic speeds. Acta Astronaut. 1995, 35, 1–8. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, X.; Ma, G. Reachable domain of spacecraft with a single tangent impulse considering trajectory safety. Acta Astronaut. 2013, 91, 228–236. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, J.; Wang, W.; Wang, J. Reachable domain of spacecraft with a single normal impulse. Aircr. Eng. Aerosp. Technol. 2019, 91, 977–986. [Google Scholar] [CrossRef]
- Li, X.; He, X.; Zhong, Q.; Song, M. Reachable domain for satellite with two kinds of thrust. Acta Astronaut. 2011, 68, 1860–1864. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Russell, R.P. Primer vector theory applied to global low-thrust trade studies. J. Guid. Control Dyn. 2007, 30, 460–472. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Chen, H. Interplanetary transfer optimization using cost function with variable coefficients. Astrodynamics 2019, 3, 173–188. [Google Scholar] [CrossRef]
- Liu, X.; Lu, P.; Pan, B. Survey of convex optimization for aerospace applications. Astrodynamics 2017, 1, 23–40. [Google Scholar] [CrossRef]
- Vasile, M.; Minisci, E.; Locatelli, M. Analysis of some global optimization algorithms for space trajectory design. J. Spacecr. Rocket. 2010, 47, 334–344. [Google Scholar] [CrossRef] [Green Version]
- Topputo, F.; Zhang, C. Survey of Direct Transcription for Low-Thrust Space Trajectory Optimization with Applications. Abstr. Appl. Anal. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Tang, G.; Jiang, F.; Li, J. Low-thrust trajectory optimization of asteroid sample return mission with multiple revolutions and moon gravity assists. Sci. China Phys. Mech. Astron. 2015, 58, 114501. [Google Scholar] [CrossRef]
- Hudson, J.S.; Scheeres, D.J. Orbital targeting using reduced eccentric anomaly low-thrust coefficients. J. Guid. Control Dyn. 2011, 34, 820–831. [Google Scholar] [CrossRef]
- Ko, H.C.; Scheeres, D.J. Essential thrust-Fourier-coefficient set of averaged Gauss equations for orbital mechanics. J. Guid. Control Dyn. 2014, 37, 1236–1249. [Google Scholar] [CrossRef]
- Caruso, A.; Bassetto, M.; Mengali, G.; Quarta, A.A. Optimal solar sail trajectory approximation with finite Fourier series. Adv. Space Res. 2021, 67, 2834–2843. [Google Scholar] [CrossRef]
- Taheri, E.; Abdelkhalik, O. Initial three-dimensional low-thrust trajectory design. Adv. Space Res. 2016, 57, 889–903. [Google Scholar] [CrossRef]
- Huo, M.; Zhang, G.; Qi, N.; Liu, Y.; Shi, X. Initial trajectory design of electric solar wind sail based on finite Fourier series shape-based method. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3674–3683. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, D.; Jiang, F.; Zhou, H. A New 3D Shaping Method for Low-Thrust Trajectories between Non-Intersect Orbits. Aerospace 2021, 8, 315. [Google Scholar] [CrossRef]
- Nie, T.; Gurfil, P. Long-term evolution of orbital inclination due to third-body inclination. Celest. Mech. Dyn. Astron. 2021, 133, 1–33. [Google Scholar] [CrossRef]
- Colombo, C.; Vasile, M.; Radice, G. Semi-Analytical Solution for the Optimal Low-Thrust Deflection of Near-Earth Objects. J. Guid. Control Dyn. 2009, 32, 796–809. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Kluever, C. Analytic orbital averaging technique for computing tangential-thrust trajectories. J. Guid. Control Dyn. 2005, 28, 1320–1323. [Google Scholar] [CrossRef]
- Gonzalo, J.L.; Bombardelli, C. Multiple scales asymptotic solution for the constant radial thrust problem. Celest. Mech. Dyn. Astron. 2019, 131, 37. [Google Scholar] [CrossRef]
- Carlo, M.D.; da Graça Marto, S.; Vasile, M. Extended analytical formulae for the perturbed Keplerian motion under low-thrust acceleration and orbital perturbations. Celest. Mech. Dyn. Astron. 2021, 133, 13. [Google Scholar] [CrossRef]
- Izzo, D.; Märtens, M.; Pan, B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2019, 3, 287–299. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Chung, S.J.; Slotine, J.J. Learning-based Adaptive Control via Contraction Theory. arXiv 2021, arXiv:2103.02987. [Google Scholar]
- Gaudet, B.; Linares, R.; Furfaro, R. Deep reinforcement learning for six degree-of-freedom planetary landing. Adv. Space Res. 2020, 65, 1723–1741. [Google Scholar] [CrossRef]
- Gao, Y.; Kluever, C. Engine-switching strategies for interplanetary solar-electric-propulsion spacecraft. J. Spacecr. Rocket. 2005, 42, 765–767. [Google Scholar] [CrossRef]
- Henninger, H.C.; Biggs, J.D. Near time-minimal Earth to L1 transfers for low-thrust spacecraft. J. Guid. Control Dyn. 2017, 40, 2999–3004. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964; Volume 55.
- Kluever, C.A. Simple guidance scheme for low-thrust orbit transfers. J. Guid. Control Dyn. 1998, 21, 1015–1017. [Google Scholar] [CrossRef]
- Petropoulos, A.E. Simple Control Laws for Low-Thrust Orbit Transfers; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2003. [Google Scholar]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Locally-optimal electric sail transfer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 166–179. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 12. [Google Scholar]
- Sidi, M.J. Spacecraft Dynamics and Control: A Practical Engineering Approach; Cambridge University Press: Cambridge, UK, 1997; Volume 7. [Google Scholar]
- Rao, A.V.; Benson, D.A.; Darby, C.; Patterson, M.A.; Francolin, C.; Sanders, I.; Huntington, G.T. Algorithm 902: Gpops, a matlab software for solving multiple-phase optimal control problems using the gauss pseudospectral method. ACM Trans. Math. Softw. (TOMS) 2010, 37, 1–39. [Google Scholar] [CrossRef]
- Jiang, F.; Baoyin, H.; Li, J. Practical Techniques for Low-Thrust Trajectory Optimization with Homotopic Approach. J. Guid. Control Dyn. 2012, 35, 245–258. [Google Scholar] [CrossRef]
- Hull, D.G. Optimal Control Theory for Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. User Guide for MINPACK-1; Argonne National Laboratory: Argonne, IL, USA, 1980; ANL-80-74. [Google Scholar]


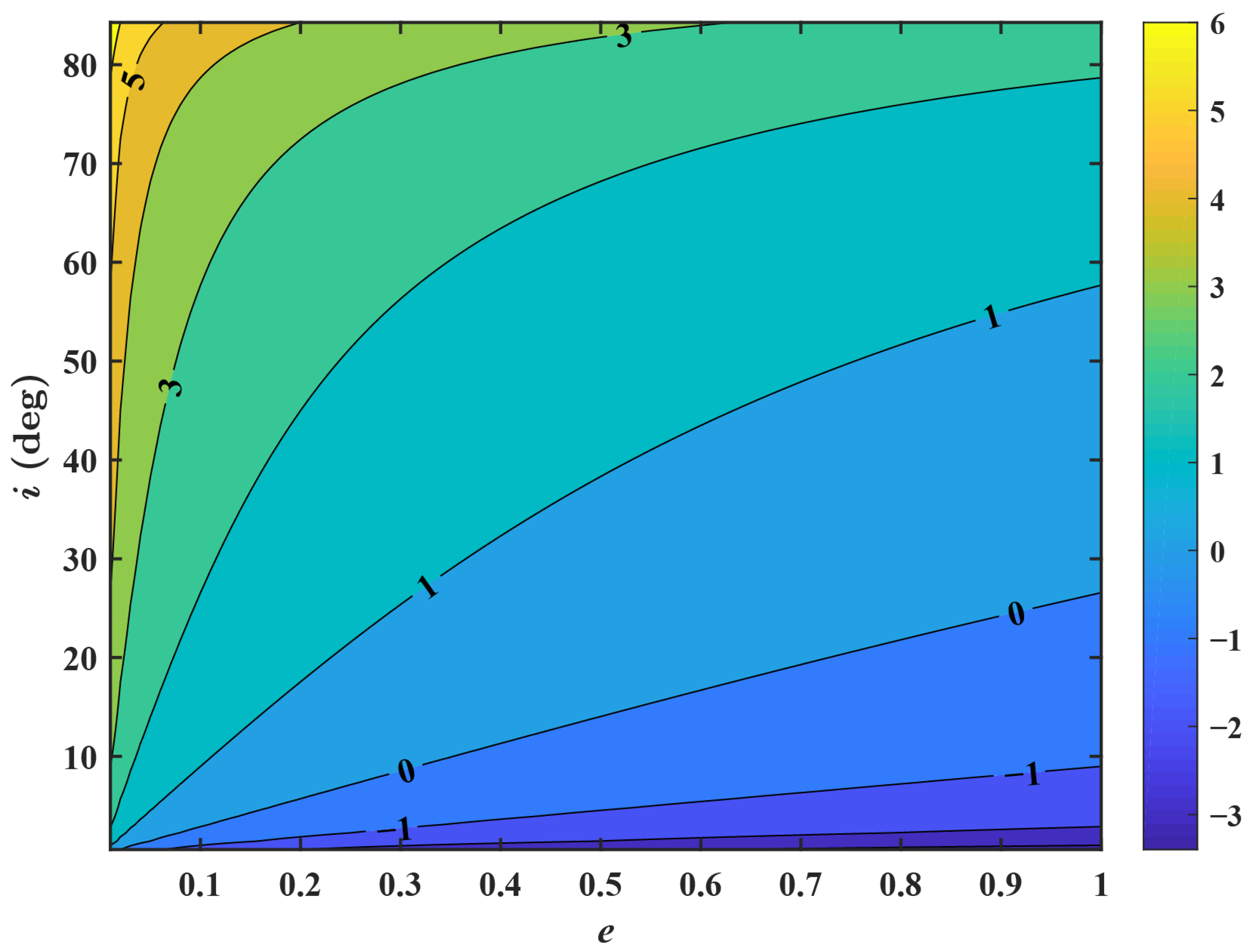

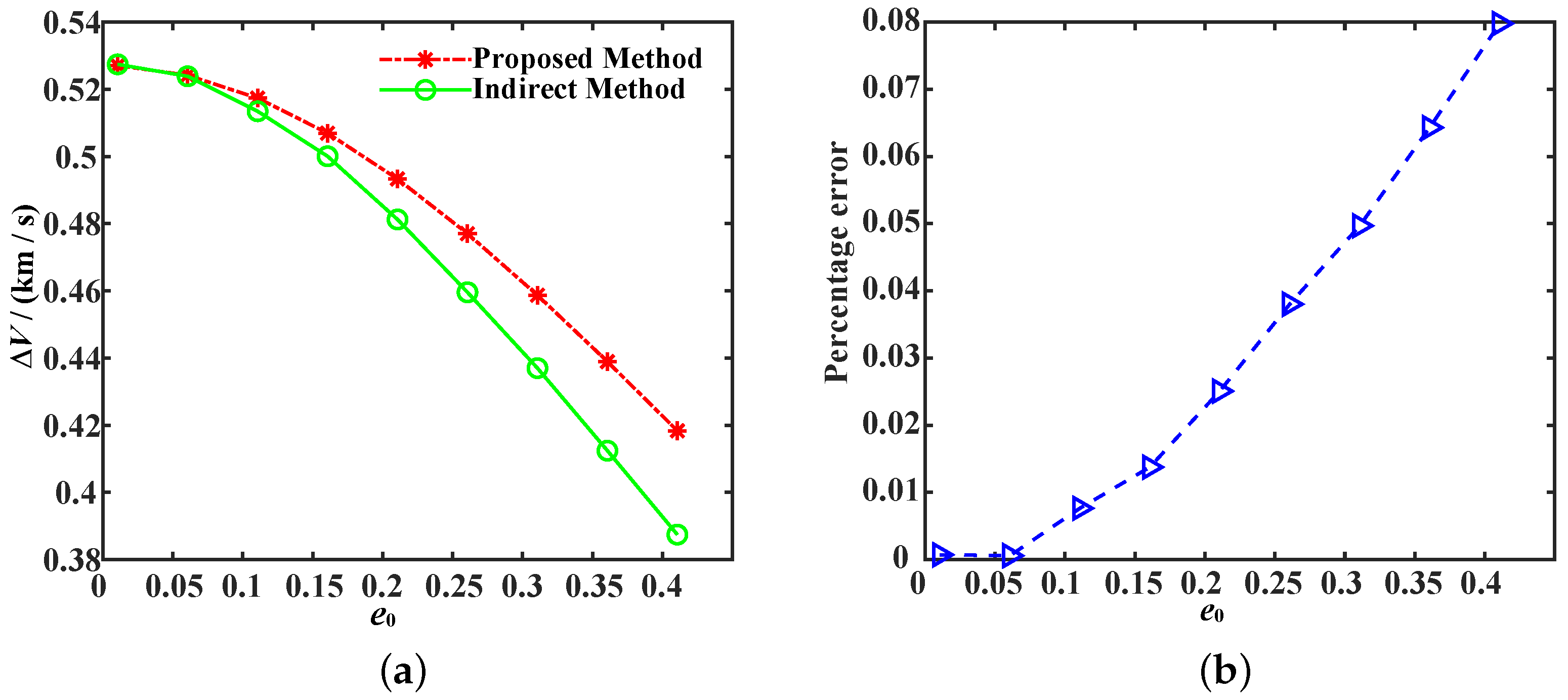
| Case | , deg | , deg | , deg | , deg | ||
|---|---|---|---|---|---|---|
| 1 | 1.1759, | 0.001 | 10 | 30 | 10 | 0 |
| 2 | 3.9196, | 0.5 | 55 | 150 | 130 | 0 |
| 3 | 5.8011, | 0.3 | 100 | 270 | 250 | 0 |
| 4 | 1.0, AU | 0.0167 | 5 | 30 | 50 | 0 |
| Case 3 | , | , deg | , deg | , deg | |
|---|---|---|---|---|---|
| Indirect method | 7.6628 | 0.4875 | 104.9775 | 275.8517 | 291.4525 |
| GPOPS | 7.6775 | 0.4837 | 105.0753 | 275.8700 | 290.1070 |
| Percentage error | 1.9 × 10−3 | 7.8 × 10−3 | 9.3 × 10−4 | 6.6 × 10−5 | 4.6 × 10−3 |
| Proposed Method | Indirect Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case | ||||||||||
| 1 | 6.2 | 7.3 | S1: 0.08 | S1: 0.04 | / | 25.64 | 4.58 | 150.73 | 6.91 | / |
| S2: 20 | S2: 19 | |||||||||
| 2 | 1.1 | 1.2 | S1: 0.05 | S1: 0.06 | 10 | 10.19 | 71.48 | 1.51 | 5.84 | 16.07 |
| S2: 3.3 | S2: 3.2 | |||||||||
| 3 | 1.0 | 0.7 | S1: 0.09 | S1: 0.08 | 20 | 1.44 | 15.65 | 1.15 | 9.02 | 27.67 |
| S2: 1.9 | S2: 1.9 | |||||||||
| 4 | 0.093 | 0.016 | 0.011 | 0.083 | / | 0.036 | 0.032 | 0.082 | 0.367 | / |
| Proposed | Indirect Method | Percentage Error | ||
|---|---|---|---|---|
| Case 1 | , | 1.3287 | 1.3297 | 8.2 |
| 0.0923 | 0.0928 | 6.3 | ||
| , deg | S1: 12.1615 | 12.1647 | 2.6 | |
| S2: 12.1615 | 2.6 | |||
| , deg | S1: 42.4473 | 42.6318 | 4.3 | |
| S2: 42.4287 | 4.7 | |||
| Case 2 | , | 4.8558 | 4.8658 | 2.1 |
| 0.6369 | 0.6376 | 1.1 | ||
| , deg | S1: 59.9658 | 60.1101 | 2.4 | |
| S2: 59.9955 | 1.9 | |||
| , deg | S1: 156.6328 | 156.9221 | 1.8 | |
| S2: 156.8552 | 1.6 | |||
| (), deg | 152.2657 | 152.8683 | 3.9 | |
| , deg | 147.5200 | 147.9650 | 3.0 | |
| (), deg | 147.5433 | 147.9809 | 2.9 | |
| Case 3 | , | 7.6366 | 7.6628 | 3.4 |
| 0.4863 | 0.4875 | 2.4 | ||
| , deg | S1: 104.9113 | 104.9775 | 6.3 | |
| S2: 104.9107 | 6.4 | |||
| , deg | S1: 275.6966 | 275.8517 | 5.6 | |
| S2: 275.6077 | 8.8 | |||
| (), deg | 275.8296 | 276.0224 | 6.9 | |
| , deg | 287.4059 | 291.4525 | 13 | |
| (), deg | 287.3791 | 290.9265 | 12 | |
| Case 4 | , AU | 1.2387 | 1.2684 | 2.6 |
| 0.1952 | 0.2081 | 6.2 | ||
| , deg | 9.2333 | 9.5141 | 2.9 | |
| , deg | 78.5656 | 84.9038 | 7.5 |
| Example 1 | Example 2 | |||
|---|---|---|---|---|
| Orbit Elements | Initial Orbit | Target | Initial Orbit | Target |
| Semi-major axis, km | 27,906 | 27,906 | 27,906 | 30,906 |
| Eccentricity | 0.0106–0.4106 | free | ||
| Inclination, deg | 40 | 42–56 | 40 | 45 |
| Average Computational Time | Example 1 | Example 2 |
|---|---|---|
| Proposed method, | ||
| Indirect method, | 82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cheng, L.; Jiang, F. Approximations for Secular Variation Maxima of Classical Orbital Elements under Low Thrust. Mathematics 2023, 11, 744. https://doi.org/10.3390/math11030744
Wang Z, Cheng L, Jiang F. Approximations for Secular Variation Maxima of Classical Orbital Elements under Low Thrust. Mathematics. 2023; 11(3):744. https://doi.org/10.3390/math11030744
Chicago/Turabian StyleWang, Zhaowei, Lin Cheng, and Fanghua Jiang. 2023. "Approximations for Secular Variation Maxima of Classical Orbital Elements under Low Thrust" Mathematics 11, no. 3: 744. https://doi.org/10.3390/math11030744
APA StyleWang, Z., Cheng, L., & Jiang, F. (2023). Approximations for Secular Variation Maxima of Classical Orbital Elements under Low Thrust. Mathematics, 11(3), 744. https://doi.org/10.3390/math11030744








