The History of a Lemma from Archimedes to Newton

Abstract

In this work, we identify some traces of the history of Archimedes’ straight line, a lemma introduced by Archimedes within the solution of prop. II 4 of On the Sphere and Cylinder, in which it is asked to cut a sphere with a plane in order to obtain two spherical segments such that their ratio is equal to a given ratio. In the course of solving this proposition with the method of analysis, assuming given what is required, as specified in this method, Archimedes traces the path along which one goes in search of the final point, from which what is required comes, expressed in a lemma which in history is referred to as Archimedes’ straight line or the square problem. The Syracusan mathematician promised to later give a solution to the lemma, but he did not keep his promise. The lemma was taken up again by Eutocius of Ascalon towards the end of the Hellenistic period, it had considerable resonance among some Arab mathematicians, who traced a specific line of research around it, finally finding attention in the Latin tradition up to Newton within the first part of the history of the path of the analytic method.

1. Introduction

At the conclusion of the solution with the method of the analysis of prop. II 4 of On the Sphere and Cylinder, in which it is asked to cut a sphere with a plane in order to obtain two spherical segments such that their ratio is equal to a given ratio, Archimedes recalls a lemma which is the strong point of the solution itself. Throughout history, it has been indicated in various ways: Archimedes’ straight line, the parallelogram problem, the rhombus problem, and, finally, the square problem. During the solution Archimedes promises to give the solution of this lemma “at the end”, but he doesn’t keep his promise since neither a solution of his can be found, either at the conclusion of the proposition or the end of book II, nor there are manuscripts that contain it.

Towards the end of the Hellenistic period, we find a single mention of this question in the commentary of Eutocius of Ascalon on this proposition of On the Sphere and Cylinder. In it, the author notes that he has found traces of a solution obtained by Archimedes by means of intersections between conics in an illegible, corrupted, and difficult-to-interpret manuscript [1,2,3].

In this work, after having identified the lemma within the proof of the Archimedean proposition, we outline the history of Archimedes’ straight line whose extreme points of reference are Eutocius’ comment on prop. II 4 of On the Sphere and Cylinder and the Géométrie by René Descartes [4,5], in book III, simply presents the problem of the square expressed by means of a quadratic equation, of which he seeks the general solution, and some pages of The Mathematical Papers of Isaac Newton [6], while the central part of the story is drawn from the writings of some Arab mathematicians.

Following the historical evolution of the proof of Archimedes’ lemma is important, not only in the history of mathematics, but also because it characterizes a research line regarding the construction of regular polygons inscribed into a circle, in particular the regular heptagon, which has a clear didactical value. Moreover, since the solution to the problem under study requires the use of conics, it also supplies some possible ideas for didactic insights.

2. The Prop. II 4 of On the Sphere and Cylinder

Among the problems chosen by Archimedes and inserted in book II of On the Sphere and Cylinder, the following proposition finds its place [1,2,3]:

Prop. II 4. Cut a given sphere with a plane so that the volumes of the [spherical] segments [obtained] have a ratio to each other equal to a given ratio.

Let us follow the articulated speech of Archimedes in the solution with the method of analysis.

This method, as it has been attested since ancient times, begins with assuming given or granted what is required to find in the statement, to reconstruct the different steps until one gets to understand what is the ultimate mathematical reality that the truth of the statement is based on.

Suppose the sphere $ABCD$ with center $K$ and diameter $BD$ is given (Figure 1).

The plane $AC$ intersects $BD$ at $X$ and divides the sphere into the two spherical segments $ADC$ and $ABC$, which are in a given ratio to each other.

We intersect the sphere with another plane passing through $K$ and perpendicular to the plane $AC$, obtaining as a section the great circle $ABCD$ with center $K$ and diameter $BD$.

Before starting with the proof of Prop. II 4 given by Archimedes, which is quite complicated, we summarize here the logical structure of his way of arguing.

Archimedes begins the demonstration by extending the diameter $BD$ on both sides and choosing two points on the extension of $BD$ ($L$ on $D$ and $P$ on the side of $B$) in such a way as to construct two opposite cones having as bases the circle identified by the same circular section of the two spherical segments $ADC$ and $ABC$. By appropriately choosing these points, the two cones have volumes (and, therefore, heights) that are in the same ratio as the volumes of the two spherical segments. By applying the properties of proportions, Archimedes obtains a relation that binds the ratios between the segments identified by the chosen points and by the ends of the diameter of the sphere and the diameter itself. Then, Archimedes chooses two new points, $F$ and $G$, such that $BF$ equals the radius of the sphere and $GF$ is to this radius as one of the heights of the cones is to the sum of the two. In this way, he arrives at determining a relationship between the distances of point $X$ from points $F$ and $D$ as a function of other known segments. Unfortunately, this relation, which Archimedes states as a lemma, is not a linear relation and, as such, its solution is not immediate. However, he claims to have solved this final step of the problem and promises to provide the solution “at the end”. However, no trace of such a solution has arrived to us.

Let us follow the details of the proof of Archimedes’ proposition. To make it easier to read, we write the proportions in the form of fractions.

We extend the diameter $BD$ on both sides and on its extensions, we take point $L$ on the side of $D$ and the point $P$ on the side of $B$ so that it is

$$\frac{DK+DX}{DX}=\frac{XP}{XB}$$

(1)

and

$$\frac{KB+XB}{XB}=\frac{LX}{DX}$$

(2)

Finally, we trace $AL$, $CL$, $AP$, and $CP$.

For the prop. II 2 (a spherical segment is equal to the cone having a base equal to that of the segment and for height, the straight line which, with respect to the height of the segment, has the same ratio that the sum of the radius of the sphere and the height of the remaining segment has with respect to the height of the remaining segment), since the cones $ALC$ and $ABC$ have the same base, the ratio between their volumes is equal to the ratio between their respective heights: $\frac{V_{cono ALC}}{V_{cono APC}}=\frac{LX}{XP}$. Then $\frac{LX}{XP}$ is given.

By factoring (1) we get: $\frac{DK+DX-DX}{DX}=\frac{XP-XB}{XB}$, that is $\frac{DK}{DX}=\frac{BP}{XB}$.

Since $DK=KB$, because radii of the great circle, then $\frac{KB}{DX}=\frac{BP}{XB}$ which becomes $\frac{KB}{BP}=\frac{DX}{XB}$.

Operating in the same way with (2), this is transformed first into $\frac{KB}{XB}=\frac{LD}{DX}$ and then into $\frac{KB}{LD}=\frac{XB}{XD}$ and into $\frac{LD}{KB}=\frac{DX}{XB}$, i.e., into $\frac{LD}{DK}=\frac{DX}{XB}$.

The result is then $\frac{KB}{BP}=\frac{LD}{DK}$ which becomes $\frac{BP}{KB}=\frac{DK}{LD}$, from which we obtain $\frac{BP+KB}{KB}=\frac{DK+LD}{LD}$, that is $\frac{KP}{KB}=\frac{LK}{LD}$.

Since $DK=KB$, the previous relation becomes $\frac{KP}{DK}=\frac{LK}{LD}$ which we can write as $\frac{KP}{LK}=\frac{DK}{LD}$, from which we obtain $\frac{KP+LK}{LK}=\frac{DK+LD}{LD}$, that is $\frac{LP}{LK}=\frac{LK}{LD}$.

From this last relation we get $LP·LD=L{K}^2$ and $\frac{LP}{LD}=\frac{L{K}^2}{L{D}^2}$.

From $\frac{LD}{DK}=\frac{DX}{XB}$ we have $\frac{XB}{DX}=\frac{DK}{LD}$ from which we obtain $\frac{DX+XB}{DX}=\frac{LD+DK}{LD}$, i.e., $\frac{DB}{DX}=\frac{LK}{LD}$.

On the extension of the diameter we take the point $F$ so that it is $BF=KB$.

It is evident that $F$ lies beyond $P$, since $\frac{DX}{XB}=\frac{KB}{BP}$ and, being $DX>XB$, it results $KB=BF>BP$.

Since $KB=BF$, (2) transforms into $\frac{XB+BF}{XB}=\frac{LX}{DX}$, i.e., $\frac{XF}{XB}=\frac{LX}{DX}$, which becomes $\frac{XF}{XF-XB}=\frac{LX}{LX-DX}$, i.e., $\frac{XF}{BF}=\frac{LX}{LD}$.

Being given $BF$ and the ratio $\frac{XF}{BF}$, $\frac{LX}{LD}$ is also given.

Since $\frac{LD}{LX}$ is given, $\frac{LP}{LX}$ is also given, being $\frac{LP}{LX}=\frac{LP}{LD} \frac{LD}{LX}$.

But: $\frac{LP}{LD}=\frac{LD+DB+BP}{LD}$ and $DB=2DK$, therefore, deriving $BP$ and $LD$ respectively from $\frac{DK}{DX}=\frac{BP}{XB}$ and from $\frac{LD}{DK}=\frac{DX}{XB}$ we obtain $\frac{LP}{LD}=\frac{D{B}^2}{D{X}^2}$.

Furthermore, since $\frac{LD}{LX}=\frac{BF}{XF}$, we have $\frac{LP}{LX}=\frac{D{B}^2}{D{X}^2} \frac{BF}{XF}$.

We take $G$ between $B$ and $P$ so that $\frac{LP}{LX}=\frac{BF}{GF}$.

Since $\frac{LP}{LX}$ is given, $\frac{BF}{GF}$ is also given, and, since $BF$ equals the radius of the sphere, which is given, $GF$ is also given.

Therefore, $\frac{BF}{GF}=\frac{D{B}^2}{D{X}^2} \frac{BF}{XF}$ and, since $\frac{BF}{GF}=\frac{BF}{XF} \frac{XF}{GF}$, it results $\frac{XF}{GF}=\frac{D{B}^2}{D{X}^2}$.

Here, Archimedes said that the solution of this last relation, therefore, how to determine the point $X$, would have been given “at the end”, but this solution of his never reached us.

Interpreting the last relation geometrically, a given segment $DF$ must be cut in $X$ in such a way that the ratio between the square of $DB$ and the square of $DX$ is equal to the ratio between $XF$ and $GF$.

Thus, $\frac{XF}{GF}=\frac{D{B}^2}{D{X}^2}$ expresses the lemma known in history as Archimedes’ straight line and is the proportion on which the solution with the method of analysis is based.

At this point, Archimedes observes that the problem formalized with this proportion in a general form, without any limitation that allows the problem of prop. II 4 to have acceptable solutions:

If the problem is proposed in this general form [without conditions], it needs a diorism, [that is, its limits of possibility must be specified]; then, if the conditions that exist in this case are added, i.e., that$DB=2BF$ and that $BF>GF$ , [then], after the analysis, there is no need for diorism.

For this reason, he reformulates the problem, stated in the lemma, in the following terms:

Given two segments $DB$and$BF$, such that $DB=2BF$, and given the point $G$on$BF$, cut the segment $DB$at the point $X$so that the square of $DB$is to the square of $DX$, as $XF$is to $GF$.

Each of these problems will be solved by means of analysis and synthesis in the end.

From the statement, it is deduced that on the segment $DF$, made up of the adjacent segments $DB$ and $BF$ such that $DB=2BF$, taking the point $G$ between the points $B$ and $F$, we must find the point $X$ between $D$ and $B$, such that the stated proportion is satisfied. From this, we deduce that while $D$, $B$, and $F$ are determined and $G$ is chosen between $B$ and $F$, $X$ must be determined between $D$ and $B$ so that the proportion is satisfied.

The problematic point of the lemma consists in finding a way to express the relationship between $G$ and $X$, as can be deduced from the historical traces, in which one reflects on the lemma.

Furthermore, the solution given above to prop. II 4 is the one that Archimedes develops according to the method of analysis, following the style given to this method before him, generally applied to the solution of geometric problems. Even if we read its formulation in a text of a period subsequent to the one of Archimedes (beginning of book VII of the Mathematical Collection [7,8] of Pappus of Alexandria dating back to the II, III century AD), in fact, the method had been already formulated and applied in the period of Plato and Aristotle. Finally, it must not be confused with the analytical method based on the existence of algebra and symbolic algebra.

In the statement of the prop. II 4 one is asked to find a sphere that satisfies the given conditions. With the method of analysis, it is assumed that the sphere exists and that the conditions set are satisfied. By reasoning around them and explaining them in a geometric sense, in successive steps, one searches for where they originate from and on which geometric foundation, they find consistency. Archimedes finds their foundation to be in the lemma.

He promises to give the solution “at the end” but does not keep his promise since this solution is not found either at the conclusion of the proposition or at the end of book II and there are no manuscripts, as far as we know, containing it.

Ultimately, we can say, in a more modern language, that the solution of the prop. II 4, passes through the demonstration of Archimedes’ lemma, which requires the solution of a third-degree equation.

In fact, since the quantities $DB$ and $GF$ are given, the problem of the demonstration of the lemma will be traced back to find $X$ such that: $D{X}^2·XF=q$, being $q$ a known quantity. Placing $DB=2a$, $DX=x$, taking into account the fact that $XF=DF-x$, since $DF=3a$ and therefore $XF=3a-x$, we will have: $x^3-3a{x}^2+q=0$.

Thus, we are faced with a third-degree equation to be solved. This problem will be addressed, as will be seen below, geometrically by Arab Mathematicians, then from Descartes and Newton through algebra.

3. Traces of Archimedes’ Straight Line in the Hellenistic Period

As previously mentioned, Archimedes promised to give a solution to the lemma but, leafing through any edition of his writings, we find no trace of this solution nor do we find any reference to it in writings by previous mathematicians, coeval, or later, with the exception of what we read in the commentary on proposition II 4 of On the Sphere and Cylinder made by Eutocius of Ascalon (VI century AD), in which the reflections on the Archimedean proposition of the mathematicians Dionysodorus and Diocles are gathered.

We have no historical evidence regarding the formulation of the lemma, while it is transmitted that it, known as Archimedes’ straight line, was studied by Apollonius of Perga, Dionysodorus of Caunus (Caria, currently in Turkey), and Diocles of Káristos (Euboea), and is easily connected to a typical insertion problem linked to the existence of a quadrilateral (parallelogram, rhombus, rectangle, square) in which, between the extension of a side and another side contiguous to the extended one, it is possible to insert a given segment. For this connection, it is advisable to read some pages of book VII of Pappo’s Mathematical Collection, in which the writing On the inclinations, by Apollonius, is presented. The manuscript was lost and reconstructed only from the beginning of the seventeenth century. This paper testifies that Apollonius dealt with the parallelogram problem, limiting the attention to the simple insertion of a segment and giving it a formulation, which is the simplest, of the type: given a parallelogram and one of its sides prolonged, insert in the angle outside a straight line equal to another given straight line.

In Eutocius’ commentary, the names of Dionysodorus and Diocles appear. This Dionysodorus can be connected to Dionysodorus who solved cubic equations by means of the intersection between a parabola and a hyperbola, as attested in a Herculaneum papyrus. The name of Diocles was transmitted to later mathematicians because he was the author of the essay On Burning Mirrors, in which three different questions are presented: the first on the construction of burning mirrors, the second around the solution of Archimedes’ straight line, and the third on the solution of the problem of the duplication of the cube, obtained through the curve called cissoid.

Eutocius speaks of them in the commentary on prop. II 4 of On the Sphere and Cylinder, reporting their solutions to the problem posed in the proposition, within which Archimedes’ straight line is solved. We have no writing by Dionysodorus in Greek or any other ancient language and we have no sources that present his solution before the pages of Eutocius. Of Diocles’ writing, On Burning Mirrors, we do not have any manuscripts in Greek. We have an Arabic translation in a volume by G. J. Toomer from 1976 [9] and in one by R. Rashed from 2002 [10].

Eutocius opens the speech by reporting Archimedes’ words, commenting on them in these terms, and also mentioning what he finds in the course of his research:

[Archimedes] promised that he would give the solution of what he stated at the end, but in no codex what he promised can be found. [In the course of our research] we have found that Dionysodorus, who desired the same things and could not devise the premised lemma, introduced another explanation of the whole problem; Diocles himself, in that book entitled On Burning Mirrors, in search of what Archimedes had promised and not having found it, tried to make up for what [that was not there]: we now register his effort, since he himself has nothing in common with [Archimedes’] premises, however, like Dionysodorus, he approached the problem with another solution.

From his words, it is clear that Dionysodorus and Diocles, given the difficulty of the lemma, do without it and give a solution to the problem proposed by Archimedes in the proposition by following a path in which the lemma does not appear.

Let us take up the words of Eutocius:

[Furthermore], since in an ancient book, without having neglected to look for many things, I came across some theorems written in an obscure form by present errors and by wrong figures, [these theorems] retained what we were looking for, [which in] part [were written in] the Dorian language, [in which Archimedes spoke], and they were written with the names used in the ancient discipline of these things, since the parabola is called the section of the right-angled cone, the hyperbola the section of the obtuse cone. The suspicion arose that these things were what [Archimedes] had promised to write at the end. Therefore, applying myself with great care, since I found that the words themselves, as they are written, were obscure from the great number of errors, as [above] I said, I rewrote the individual sentences of the speech according to the more current use and as clearly as I could.

Referring to an “ancient book”, in which he reads theorems that present errors and are illustrated with wrong figures, where conics were sections of particular cones [11] and not sections of the same cone [12,13], Eutocius gives extraordinary news, since he speaks of a text which, hypothetically, could be traced back to Archimedes for the language adopted and for the solution of the lemma through the intersection of a parabola with a hyperbola. Could that ancient text be the one attributed to Archimedes in the first period of the golden age of Arab mathematics (9th century)?

What did Eutocius find in that illegible manuscript written in the Doric dialect (that of the writings of Archimedes)? We can only assume that he found some element with which to reconstruct or divine (according to the language of the 16th and 17th centuries) the solution.

As he did in the commentary on prop. II 1 of the same paper, in which he collected the solutions of the construction of the double proportional mean, in the commentary on prop. II 4 Eutocius presented his own solution of the lemma and of the proposition, which he followed up with the solutions of Dionysodorus and Diocles.

Eutocius reformulated the Archimedean lemma in these terms:

Lemma. Given two straight lines $AB$and $AC$and an area $D$, on $AB$find a point $E$such that $\frac{AE}{AC}=\frac{D}{E{B}^2}$.

Even if Eutocius claimed to have found hints of a solution in a corrupted manuscript of the Archimedean writings, we can consider his solution to be the first complete solution of the lemma.

It is an unconvincing and weak claim of his to have found a text full of errors, the wrong figures, etc., in a corrupt manuscript, even if this is probable. Perhaps this is a ploy or a literary pretext not to say that the solution of the lemma is entirely and explicitly his work, and it is the result of his reflection. Subtly, he dares to put together and on the same level, what belongs to the Syracusan mathematician and what belongs to him, bearing in mind that Archimedes’ fame passes from century to century wrapped up in a mythological language, being difficult to distinguish what is history from what is a myth. Perhaps later mathematicians, who study the writings of Archimedes, with which they associate the commentary of Eutocius, see beyond his statement, considering one (the writings) and the other (the commentary) in a single block. In one case or another, Eutocius does a great service to the mathematics of the VI and of the following centuries, so as to consider his pages indispensable for the reading of the Archimedean writings.

In the mathematicians considered so far, the lemma and the parallelogram/rhombus/square problem are solved without any connection with any applications. For other mathematicians, they will become useful tools for solving further problems, as will happen for the square problem in solving the problem of constructing the side of a regular heptagon in a circle.

4. Archimedes’ Straight Line Becomes Object of Research in the Arab World of the IX-XIII Centuries

By comparing the pages of writings of the Hellenistic period that present the lemma and the problem of the parallelogram/rhombus/square with writings by Arabic-speaking mathematicians who lived between the first decades of the IX century and the first decades of the XIII century, we observe that, while in the Hellenistic period, these problems remain secondary in the development of mathematical ideas and the elaborations of mathematicians, despite the efforts of Pappus and, above all, of Eutocius in recovering and transmitting them, in the first two hundred years of the Arab mathematical tradition the interest in the same problems is so strong that it has become a specific line of research. Among the mathematicians who deal with it are Thābit ibn Qurra, Ibn Sahl, Al-Qūhī, Al-Saghani, Al-Sijzī, Ibn al-Haytham, Al-Shannī, Kamal al-Dīn ibn Yūnus.

Among the writings that make up the Riyāda Collection, Dār al-Kutub, ms. 41, of Cairo there is the Book of the construction of the circle divided into seven equal parts by Archimedes in the Arabic translation of Thābit ibn Qurra. This writing does not appear among the writings of Archimedes that have come down to us, it is simply attributed to him (it is, therefore, a pseudo-Archimedean text), as attested by the bookseller Al-Nadīm in the Kitāb al-fihrist (Book of the Index), of 988 [14]. The Collection Riyāda is copied by Mustafā Sidqī between 1733 and 1740, within which the Book occupies fol. 105^r–110^r.

Concerning this writing, the scribe Mustafā Sidqī wrote:

When I set out to transcribe this book, I found nothing but a deteriorated and altered copy due to the copyist’s ignorance and lack of understanding. I have gone to great lengths in the effort to verify problems, in summarizing analyzes [solutions], and in ordering propositions in easy and accessible terms; and I introduced some proofs of the moderns.

These statements pose some preliminary problems regarding the reliability and authorship of the text, as we do not have any elements of comparison with other possible editions. Thus, we must take the text as the copyist delivered it to us and, starting from this copy, put forward some hypotheses on how the text came out of the hands of Thābit ibn Qurra, who predictably translates it from Greek into Arabic.

Taking Sidqī’s statement as valid, the text at our disposal was revised by him and integrated with propositions, some solutions of which have been attributed to Arab mathematicians considered more “modern”. We are unable to pinpoint with certainty who these “moderns” are in Sidqī’s view of the development of mathematics. Following common sense, we can assume that the “moderns” are the Arab mathematicians who studied the texts elaborated by previous mathematicians, whose fame and whose writings are transmitted to subsequent generations.

In 2000, R. Rashed edited the Book in Arabic, translated it into French, and commented in the context of modern mathematics [15]. In the last century, this text was translated into German by C. Schoy and included in Die trigonometrischen Lehren des Persichen Astronomen Abū’l Raihān Muhammad ibn Ahmad al-Bīrūnī (The trigonometric teaching of the Persian astronomer Abū’l Raihān Muhammad ibn Ahmad al-Bīrūnī) of 1927. It was also translated into Russian by B. Rosenfeld and published in Archimed -socinenja by J. N. Weselowskii in 1962 [16].

In the paper, we find 18 propositions concerning the squares of segments (Propositions 1–2), some properties of right triangles (Propositions 3–8), the relationship between the right triangle and the circle (Propositions 9–14), the division of the arc subtended by a chord (Proposition 15,16), the insertion of a segment between one side of a square and the extension of another side (Proposition 17) and the construction of a regular heptagon in a circle (Proposition 18).

We observe that, while the first propositions have no connection with the subsequent ones, the last two are strictly connected to each other, being able to consider prop. 17 as a lemma for the solution of prop. 18. This makes us wonder how many propositions both the original pseudo-Archimedean text and Thābit’s translation were made up of. It also makes us wonder in what period and by whom the other propositions were added, and if the solutions of some of these can be traced back to Al-Hubūbī and Al-Shannī, who were mathematicians after Thābit.

In the passage from one generation to another, the translation that came out of Thābit’s hands is subject to additions. However, we do not have elements or news to state when these integrations took place, whether all at the same time or at successive times. Nor can we argue that the additions are the work exclusively of one or more copyists or whoever discovers the manuscript last. They are the material instrument through which the transmission of the text takes place. Presumably, it can be excluded that the additions are the work of copyists, since these, in general, had good skills on the different writing characters, which sometimes varied from one place to another, on the material on which the writing took place, and on the presentation of a text of any content, but they were not recognized as having specific knowledge about the content of a text, except in rare cases. We are not even able to say precisely which parts the editor of the Arabic edition inserts at our disposal today.

Since the text (presumably in Greek) that Thābit translates is essentially anonymous (hence the attribution to Archimedes), we can hypothesize that initially, it consisted of only the last two propositions of the current text.

Expressed by the Proposition 17 is an insertion problem around a square, which goes down in history as the square problem. The square problem, which in itself is a simple insertion problem, affirms the truth of relations, starting from which one easily arrives at a proportion very similar to that which solves the problem of Archimedes’ straight line. Thus, we detect a very close connection between Archimedes’ straight line and the problem of the square.

It is appropriate to see the wording of Proposition 17, and from the relations present in the statement deduce the connection between the problem of the square and Archimedes’ straight line.

The square problem is stated as follows:

Prop. 17. Let the square $ABCD$be given; we extend the side $AB$from the side of $A$to the point $E$; we draw the diagonal $BC$and place a line so that it has one end point at $D$and the other end point at $AE$, such that, intersecting $AE$at $G$, $AC$at $H$and $BC$at $I$, the triangles $GAH$and $CID$are equal; finally, we draw $KIL$parallel to $AC$; then $AB·BK=A{G}^2$, $KG·KA=B{K}^2$and $BK>KA$and $AG>KA$.

With a simple construction (Figure 2), we realize that having built the square $ABCD$, after having extended the side $AB$ on the side of $A$ and after having taken the point $E$ along this extension, on the segment $BE$ we find the points $B$, $K$, $A$, $G$, $E$, dividing it into parts. Taking into consideration the first four points, which divide the segment $BG$ into three parts, and bearing in mind the relationships between these parts of the statement, we can see that between these parts there exists a proportion, in which the terms of the first relationship are areas, while the terms of the second ratio are segments, between the extremes of which are the points $K$ and $G$.

This proportion is similar to that which characterizes Archimedes’ straight line. Thus, the problem of the square and the straight line of Archimedes are closely linked, since the problem of the square is the way to understand the straight line of Archimedes.

In fact, expressing the conditions found by Thābit in a modern algebraic language, we can set $AG=x$, $BK=y$, $BA=a$, so: $KG=BG-BK=a+x-y$ and $KA=AB-BK=a-y$, and the relations $AB·BK=A{G}^2$ and $KG·KA=B{K}^2$ can be expressed in the form: $ay=x^2$ and $\left(a+x-y\right)\left(a-y\right)=y^2$.

By eliminating the unknown $y$ in the two relations, we arrive at an equation of the form: $x^3+2a{x}^2-a^{2}x-a^3=0$, which is a third-degree equation which, once solved, gives the position of the point $G$ and point $K$ on segment $BE$. This equation, eliminating the linear term with a transformation, is analogous to the third-degree equation obtained starting from the condition of Archimedes’ lemma.

We can therefore state that the solution of the square problem given by Thābit corresponds to a geometric solution of the third-degree equation.

Considering that Proposition 17 has not been altered during the transmission (we know the statement in the text copied in 1740), if we pay attention to the relations that solve the problem of the square, we are faced with a question about which we can make some hypotheses.

We can hypothesize, for example, that the propositions that allow us to familiarize ourselves with mathematical relations concerning the distance between points of the same segment have been introduced gradually over time. In this perspective, it is possible to read the first 16 propositions, taking into account only the relative geometric constructions and the solutions obtained. We can thus pass from Propositions 1,2, in which we are dealing with squares of segments belonging to the same straight line, at props. 3–8, where the relationships between the sides of a right triangle are read as relationships between segments of the same straight line, at props. 9-15, in which some issues concerning the right-angled triangle are considered in relation to the inscribed circle, finally arriving at props. 15 and 16, in which the discussion expands to the consideration of triangles within a semicircle.

In light of this hypothesis, we can conclude that originally the writing attributed to Archimedes could have been formed only by the props. 17 and 18 of the text. Predictably, this is the text that arrived in the hands of Thābit and has been translated by him. Subsequently and gradually other mathematicians or mathematics enthusiasts added other propositions, making sure that the writing is intelligible and didactically effective. If this hypothesis of ours were true, we would pass from a short reading to a long reading, from an older reading, because it is shorter, to a more recent reading because it is longer, making our own the terminology expressed in the laws of hermeneutics, applicable in matters in which one tries to date a text. This hypothesis would explain the existence of the writing copied and increased by Sidqī, at his pleasure, after that of others.

If then, within a strictly mathematical discourse, we concentrate on how to obtain four points on a segment in order to satisfy a fixed relation, we are led to look for the possible relation existing between the straight line, which Archimedes uses in the solution of prop. II 4 of On the Sphere and Cylinder, and prop. 17 of Thābit’s translation. That is the relation between Archimedes’ straight line and the problem of the square, in which, on one side of a square and on its extension, there exist four points satisfying a given relationship. This takes us away from the structure of the text translated by Thābit, copied and integrated by Sidqī in 1740, leading us to study the context in which Thābit’s translation is transmitted, at least in the first 150 years. The attempt to justify it leads us to study the other treatises on the construction of the regular heptagon, drawn up during the X century and in the first half of the XI century, analyzing the structure and organization of the mathematical discourse. They are specifically due to Ibn Sahl, Al-Qūhī, Al-Sijzī, and Ibn al-Haytham [17,18]. In these treatises the construction of that square is in turn the necessary and indispensable lemma for the construction of the regular heptagon, that is, it is an integral part of the line of research around the construction of this regular polygon. On the other hand, in the same period, we find another line of research around Archimedes’ straight line, separate from the first one, as it is recorded in the writings of Ibn Sahl, Al-Qūhī, and Ibn al-Haytham, where the Archimedean line is resolved through the parallelogram problem or through the square problem.

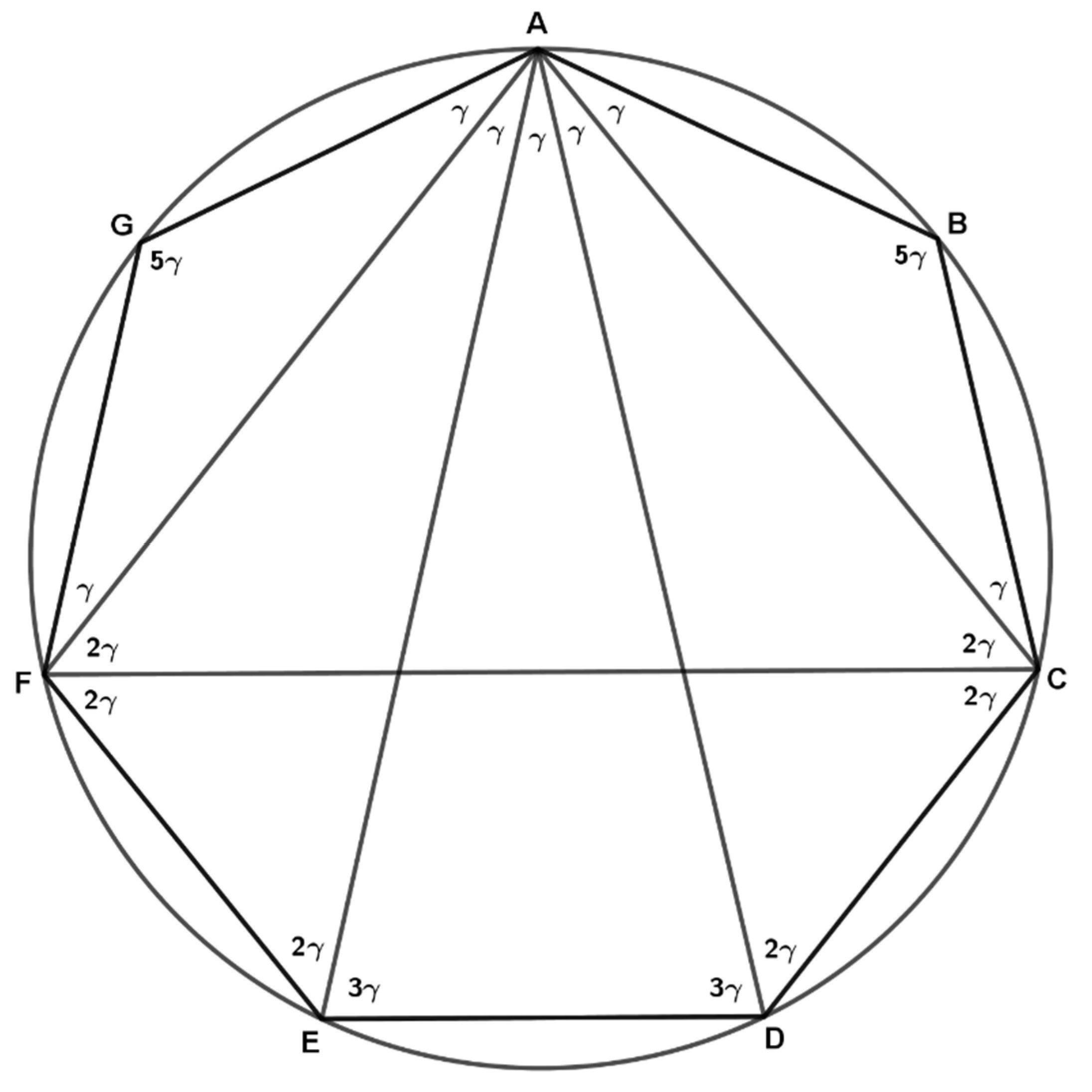
To understand the relationship between the square problem and the construction of the regular heptagon let us consider a regular heptagon $ABCDEFG$, inscribed in a circle (Figure 3), each side of which corresponds to an angle to the circumference $\gamma =\frac{\pi }{7}$.

The chords $AC$, $AD$, $AE$, $AF$, and $CF$ identify the following triangles: $ABC$ and $AGF$, equal to each other, having angles ($\gamma$, 5$\gamma$, $\gamma$); $ADC$ and $AEF$, equal to each other, having angles ($\gamma$, 2$\gamma$, 4$\gamma$); $ADE$, of angles ($\gamma$, 3$\gamma$, 3$\gamma$); $ACF$, of angles (3$\gamma$, 2$\gamma$, 2$\gamma$).

Let us now consider (Figure 4) a segment $BA$ and two points $D$ and $C$ on it such that they satisfy the relations: $B{D}^2=AD·CD$ and $A{C}^2=CB·BD$. Such relations are similar to those obtained as a result of Prop. 17, the solution of the square problem.

Finally, let us consider (Figure 5) a point $E$ external to $BA$ and such that $DE=DB$ and $CE=CA$. We obtain four triangles $EDC$, $EDB$, $ECA$, and $BAE$, corresponding to the triangles $ADC$ and $AEF$, $ACF$, $ABC$ and $AGF$, $ADC$, and $AEF$.

Therefore, by subdividing the segment $BA$ according to the solution of Prop. 17, we obtain triangles from which we can construct a regular heptagon inscribed in a circle [15].

In the written Book of the synthesis of the problems analyzed by Abū Sa’d al-’Alā ibn Sahl, whose content is by Ibn Sahl while the editing is by Al-Shannī, the path that leads to the solution of the construction of the regular heptagon begins by giving space to the solution of the parallelogram problem and presenting the preliminaries necessary to obtain the construction of the heptagon. In this paper, Archimedes’ straight line and the parallelogram problem are not distinct mathematical realities, without any element in common, but the parallelogram problem is a means of solving Archimedes’ straight line. The parallelogram problem becomes the square problem, which plays the role of lemma for the construction of the heptagon, as we have already said for Thābit’s paper. With Ibn Sahl, read following the editing of Al-Shannī, the goal of solving the parallelogram problem is achieved, in which, in particular, the areas of two triangles are related to each other as two given segments. The same problem, formulated for particular cases, first becomes the problem of the rectangle and then the problem of the square.

Al-Qūhī’s argument relating to Archimedes’ lemma is very advanced compared to the contents of the text of Eutocius and the texts of other Arab mathematicians. The author demonstrates great fluency in bringing together algebra and geometry and in using the language of geometry, even when he thinks in an algebraic way.

Al-Qūhī dedicates his Lemma on the division of Archimedes’ straight line to the exclusive treatment of Archimedes’ lemma, probably because, once given an unequivocal solution of the lemma, it can constitute an important step or premise in the search for the solution of other problems. The solution of the lemma takes place around the geometric figure of the square, without being faced with the problem of the square, whose fundamental character is that of being an insertion problem. From this choice, we can conclude that the square problem constitutes the geometric situation in which to obtain the division of a segment corresponding to Archimedes’ straight line.

In the Treatise on the construction of the side of the regular heptagon in the circle, Al-Qūhī shows that, through the division of the segment in the manner of Archimedes’ straight line, the construction of the regular heptagon is obtained. Opening the treatise, we are faced with praise of Archimedes and his writings, among which explicit reference is made to the one on the construction of the regular heptagon. Thus, we note that Al-Qūhī is witness to the passage from the “news” of the writing attributed to Archimedes to the “certainty” that he is undoubtedly its author.

The treatise opens with these words:

Mathematicians agree in recognizing the eminence of Archimedes and his supremacy over the other Ancients, observing how he solved beautiful and distant things and difficult and hidden propositions, in the precious demonstrative sciences; this is clearly testified by the existence of his books, such as the book The Centers of Gravity, the book On the Sphere and Cylinder and other books, each of which occupies a vertex, beyond which there is nothing. Thus, they [the mathematicians] believed that what he [Archimedes] tried to solve, and that he did not obtain, nobody would find the path to get there, and nobody else would find another way to accomplish it. This is what they believed concerning the construction of the side of the regular heptagon inscribed in the circle, after what resulted from the book that he composed on this subject. This is a subtle book, in which he has not obtained what he set out to do nor achieved his goal in determining the heptagon by only one way, let alone several ways.

Al-Qūhī speaks with certainty of the writing, which is a “thin book”, in which, however, Archimedes does not achieve the result. From these words, it can be hypothesized that the purpose that Al-Qūhī sets for himself by reflecting on this issue, is to go beyond what Archimedes expressed.

His proposal is enclosed in seven propositions, logically and closely linked to each other, from whose study the close link between Archimedes’ straight line and the construction of the heptagon clearly emerges. From his speech, it is clear that, for the construction of the regular heptagon in a circle, it is crucial to identify a segment that is divided into three parts, which we can easily accoast to Archimedes’ straight line. Furthermore, the latter, in this treatise, is not linked in any way to the problem of the parallelogram or the problem of the square.

In the same environment and the same period as Al-Qūhī, Al-Saghani works, who addresses a letter to the Caliph Al-Dawla in which we read his elaboration of knowledge around the construction of the regular heptagon, bearing in mind what has been received from tradition, i.e., that it is possible to solve the problem of the chord of the heptagon starting from a lemma stated by Archimedes. In this letter, we find a path, in which the relationship between Archimedes’ straight line and the problem of the square is explored, similar to that of Al-Qūhī in the Treatise on the construction of the regular heptagon in the circle.

From reading Al-Saghani’s treatise we get the impression that the author, at the time he writes the letter to the Caliph, has his own notes on the subject and Al-Qūhī’s treatise at hand. We get this impression, especially in relation to the props. 3, 4, and 5 of Al-Qūhī, which Al-Saghani explains in didactically simpler terms in the props. 3, 4, 5, and 6, and in the first part of prop. 7.

While in Al-Qūhī’s text, we have to struggle a bit to find what makes us identify the terms with which Archimedes’ line and the problem of the square are presented, in Al-Saghani’s text everything is made simple, since the elements in the construction lead to these geometrical realities are clearly spelled out, allowing us to read the geometrical situations as specific to a classic insertion problem.

Indeed, the writings of Al-Qūhī and the letter of Al-Saghani lead to the same conclusion: the construction of the regular heptagon is easily achieved if one is able to construct a triangle whose angles are proportional according to a double ratio. This is possible to the extent that a given segment can be divided into three parts such that the ratio of the parts satisfies the property of the Archimedean line.

In the paper, On the construction of the regular heptagon and on the trisection of the angle, Al-Sijzī resumes and deepens the path followed in other works by mathematicians of the same historical period, where the problems of the construction of the regular heptagon and the trisection of the angle are addressed together. This paper opens with some reflections on the sense of the solution of Archimedes’ straight line, emphasizing the mathematical importance of the writings of Archimedes, Heron, and Apollonius, and this with the aim of contesting the approach given by Al-Jūd to Archimedes’ straight line.

Al-Sijzī’s aim is to find a geometric solution, i.e., a solution obtained by means of geometric figures among which conic sections are also present. The solution given to the problem of the heptagon, which has Archimedes’ straight line as lemma, interferes with that of Abū al-Jūd Muhammad ibn al-Layth (of whom we have news only through Al-Sijzī), expressed in the manuscript Book on the construction of the heptagon in the circle, sent to Abū al-Hasan ibn Muhammad ibn Ishāq al Ghādī, and in a letter addressed to Abū Muhammad ‘Abd Allāh ibn ‘Ali al-Hāsīb, in which the methods of Al-Qūhī and Al-Sāghānī on the construction of the regular heptagon are analyzed.

In the introduction to the Book on the construction of the heptagon in the circle, Al-Jūd traces the path followed in the discussion. From this paper, it emerges that the reference point of the author’s reflections is a construction attributed by a “certain geometer” to Al-Qūhī as well as the treatise that he draws upon the construction of the heptagon based on Archimedes’ lemma. Al-Jūd states that the treatise of Al-Qūhī is his term of comparison and that the novelty he brings is related to the division of the requested segment.

It clearly emerges that the real problematic point of the question concerns the division of the segment into two parts by means of a single point and not into three parts by means of two points.

The second writing of Al-Jūd, which is a letter, opens with the affirmation of having received two letters between the very eminent master Al-Qūhī and his master the surveyor Al-Saghani which dealt with the determination of the seventh part of the circle.

Both mathematicians took a look at the proposition that Archimedes introduced in his letter on the construction of the heptagon, trying to correct and prove it. Specifically, Al-Jūd takes up what he expressed in the Book mentioned above by introducing the novelty of dividing the straight line into only two parts, and not into three parts, taking his cue from the way in which Euclid in props. IV 10–14 (resumed, then, in props. XIII 7, 8, 10, and 11) of the Elements constructs the regular pentagon in the circle, assuming the existence of an isosceles triangle in which each of the angles at the base is double the third angle, and this is one-fifth of a straight angle. The focal point of the letter revolves around the question of dividing a segment into two parts and through this division arriving at the construction of the regular heptagon in the circle.

After observing that Al-Qūhī and Al-Saghani, who followed the Archimedean way, rectifying his lemma and basing the construction of the heptagon on it, worked well, Al-Jūd states:

The division of a given segment into two parts, as I have done, is more immediate than the division into three parts, as they have done; and the analogy I used to construct the isosceles triangle, in which each of the angles at the base is three times the other angle, holds for all polygons, each of which has an odd number of sides, but their [of Al -Qūhī and by Al-Saghani] analogy does not hold for all polygons: we can, in fact, find an isosceles triangle such that each of the angles at the base is five times the other angle; then we obtain the eleven-sided polygon inscribed in the circle; and there is no triangle in which three angles follow each other according to any double ratio such as to obtain a polygon of eleven sides inscribed in the circle. The same thing happens for most regular polygons, whose number of sides is odd.

In these terms, Al-Jūd presents his position on the division of the segment and the construction of the heptagon. It is clearly an alternative to the solution which, according to tradition, can be traced back to Archimedes in the pseudo-Archimedean writing on the construction of the regular heptagon in the circle and which is expressed by some mathematicians who reflect on this division. Faced with one or the other division, from what has been said so far it can be deduced that the construction of a regular heptagon in a circle is obtained if one has Archimedes’ straight line as a lemma.

We can imagine that Al-Sijzī has read, studied, and meditated on the writing of Al-Jūd, to which he thinks he will give an adequate answer with the composition of the Book... on the construction of the regular heptagon in the circle and on the trisection of the rectilinear angle. Speaking of Al-Jūd’s mathematical elaboration, Al-Sijzī criticizes the division of Archimedes’ straight line obtained by him, showing that his premises are “corrupt” and its construction is “fallacious”, and states that in this treatment of his the reference points are Archimedes, Apollonius, and Ibn Sahl.

While Al Sijzī claims unconditional loyalty to Archimedes (but to which Archimedes, if the writing on the construction of the heptagon is simply attributed to him?), Al-Jūd emphasizes that the expression gone down as Archimedean can be evaluated in a different context, in which the intersection of conics does not intervene and in which we simply speak of the division of a segment into two parts and not into three parts.

In the incipit of the essay, On the division of the straight line used by Archimedes in the second book of On the Sphere and Cylinder Ibn al-Haytham refers to Archimedes’ way of proceeding in the solution with the method of analysis of the prop. II 4 of On the Sphere and Cylinder, expressing his intention to deal in his writing with the division of the straight line according to the ratio supposed by Archimedes, highlighting this possibility. In the context of the method of analysis (the same context in which Archimedes invokes the lemma), Archimedes’ straight line is solved through the intersection between a parabola and a hyperbola. The construction of this straight line occurs around a rectangle, without interfering with the square problem, which is a classic example of an insertion problem. This choice of his puts him in a critical position with respect to the tradition formed among the mathematicians who preceded him, from which it can be deduced that the two problems, Archimedes’ straight line and the problem of the square, are closely linked, the problem of the square being the via to solve Archimedes’ straight line, i.e., to make sure that on a segment there are five points which divide it into four parts between which the proportion indicated by Archimedes occurs.

In the writing A lemma on the side of the heptagon, Ibn al-Haytham, keeping the construction of the heptagon in the background, focuses on the problem of the square. The incipit of the text is as follows:

Archimedes founded the side of the heptagon on the square he introduced, without showing how to construct the square according to the property he requested. Indeed, if he did not show this, it is because the construction of the square according to the required property is obtained by means of the conic sections. Since he did not mention anything about conic sections in his book, at the end of which he built the heptagon, thinking not to mix in this book what does not belong to the same genus, then he took this square as given and based on it the side of the heptagon.

From this, we deduce that it is certain that Archimedes left a writing in which he presented the construction of the heptagon in the circle, obtained by assuming the existence of a square in which, between one side and the extension of another side, a segment is inserted (a classic insertion problem). We are thus faced with triangles of equal area, around which relations are expressed that make sense if obtained through the intersection of conic sections. This conclusion is held to be fundamental by Ibn al-Haytham. In this elaboration of him, he shows how to act around the square, what to build and what results to obtain in order to be able to build the heptagon. Since the results around the square are obtained through the intersection of conics, this causes the problem of the square to be associated with Archimedes’ straight line.

Reading Ibn al-Haytham’s writing makes us ask some questions.

The first question concerns what Ibn al-Haytham knows about the Archimedean text on the construction of the heptagon. From his words, it is clear that there is no doubt about the attribution to Archimedes of a text that presents this theme. Indeed, from his words and those of other mathematicians of the period, it seems that this text is enveloped in that halo of mythological classicism in which Archimedes’ writings are read.

The second question relates to the relationship between the square problem and Archimedes’ straight line, a question that has been asked several times over the years. The answer comes gradually, reaching the highest level of clarity with this writing by Ibn al-Haytham, solving the problem of the square both in sight and as a way to obtain the division of Archimedes’ straight line. In this paper, the construction of that triangle which allows the construction of the heptagon in the circle is certainly important. We are convinced, at the same time, that this is not the reason why the author wrote it, being entirely concentrated on unraveling the question of the relationship between Archimedes’ straight line and the problem of the square.

The writing, On the construction of the heptagon in the circle by Ibn al-Haytham, constitutes the third level in his path toward the construction of a regular heptagon in a circle, after reflecting on Archimedes’ straight line (first writing) and having studied its relationship with the square problem (second writing). In the introduction, the author confirms the news that Archimedes traces the construction of the heptagon in the circle, prepared in turn by the lemma, Archimedes’ straight line, without providing a solution. He states that

Some ancient [mathematicians] and some contemporary [mathematicians] have successfully arrived at [the construction of the regular heptagon in the circle], although this success contains some errors. For the ancients it was Archimedes who built it; in truth, he wrote a treatise to determine the side of the heptagon, but he chose a lemma for its determination, without giving its proof.

While referring to the attribution of the solution of the problem to Archimedes by the ancients, Ibn al-Haytham speaks of the Archimedean treatise without expressing any doubts, freely showing his point of view on the chosen lemma, and affirming that he has given a solution with a written dedicated to it. He also refers to two previous writings, the first of which is dedicated to the straight line of Archimedes, of which he does not indicate the author (nor can we say with certainty who he is). In the second writing, which is by Al-Qūhī, the problem of the construction of the heptagon in the circle is solved. With respect to all this tradition, from the oldest to the one closest to him, he expresses a very precise judgment of merit with the following words:

We have not found a treatise [in which it is] sufficiently explained by some of the ancients and contemporaries, in which the different ways by which one can arrive at the construction of the heptagon are contained [...], we have carefully examined the construction of the heptagon and we have demonstrated all the ways through which to arrive at the construction of the heptagon, proceeding by analysis and synthesis.

In this way, Ibn al-Haytham expresses a project that is much broader than that of the ones who have reflected on the same problem. Thus, he places himself at the pinnacle of research on the problem of the square, Archimedes’ straight line, and the construction of a regular heptagon in a circle.

The elaboration marks three moments that follow each other.

In the first moment, his reflection is aimed at clarifying the nature and characterization of Archimedes’ straight line. Thus, a segment is divided into three parts which appear in the proportion expressed by Archimedes in the lemma.

In the second moment, the study is concentrated on the relationship between Archimedes’ straight line and the problem of the square, arriving at the conclusion that the problem of the square is the way and the means to study and understand the meaning of Archimedes’ straight line.

In the third moment, one reflects around the construction of a regular heptagon in a circle, obtained through the construction of a triangle, which presupposes the existence of the Archimedean line. In this phase, the path that leads from the problem of the square to Archimedes’ straight line becomes clear, from the latter to the construction of a triangle whose sides are the parts into which the segment of the Archimedean straight line is divided and, finally, from this triangle to the construction of the heptagon in the circle.

In following this path and considering the three moments, we have the impression of having before us pages in which a reflection that has reached full maturity is expressed. The point at which this impression becomes certainty is when, after having constructed in the circle the triangle whose sides are the parts into which Archimedes’ straight line is divided, Ibn al-Haytham considers the different possible triangles: an isosceles triangle in which the angles at the base have a width three times that of the angle at the vertex; an isosceles triangle in which the base angles are formed by two parts and the vertex angle by three parts of a straight angle; an isosceles triangle in which the base angles are formed by one part and the apex angle by five parts of a straight angle; a scalene triangle in which the vertex angle consists of one part, one base angle consists of two parts, and the other base angle consists of four parts of a flat angle. The problem of the construction of the heptagon is solved for each type of triangle examined, so as not to leave any unresolved element.

Beyond the example taken from prop. II 4 of On the Sphere and Cylinder of Archimedes and of the other that is found in the treatise attributed to him on the construction of the heptagon, there are no other examples in which it is shown what the Archimedean lemma is for and what it leads to.

Considering the continuation of the history of these topics, we are led to affirm that the line of research on them opens and closes with these Arab mathematicians, reaching levels of excellence in mathematical discourse and that subsequent references to the same problems are only a reflection of the elaboration expressed by the mathematicians considered here. This line of research initially concentrated on the lemma, Archimedes’ straight line, then expands with the study of the relationship between this straight line and the problem of the square, considering how many parts (whether into three or two parts) a segment has to be divided in so that the proportion indicated by Archimedes in the lemma can occur. Setting aside the division into two parts, relying on the division into three parts, obtained through the intersection of conics (a parabola and a hyperbola or two hyperbolas), a triangle is constructed with these parts, starting from which we have the cultural and operational tools to build a regular heptagon in a circle.

Only some of the Arab mathematicians considered have presented Archimedes’ straight line without linking it to the construction of the heptagon, while those who have presented this construction are more numerous, increasingly accrediting the pseudo-Archimedean writing on the construction of this regular polygon.

Alongside the writings whose authors, Thābīt ibn Qūrrā, Ibn Sahl, Al-Qūhī, Al-Sijzī, and Ibn al-Haytham, are pillars of mathematical research “tout court” in the centuries IX and X, let us not overlook the existence of three writings by contemporary or later mathematicians: Book on the discovery of Abū al-Jūd regarding two lemmas for constructing heptagon by Al-Shannī; Summary of the analysis of the lemma of the regular heptagon inscribed in the circle by an anonymous author; On the proof of the lemma which Archimedes neglected in his book on the construction of the heptagon inscribed in the circle and how it must be done by Ibn Yunus. These writings confirm the central role of the construction of regular polygons in the circle [19], addressing the more complicated problem relating to the construction of the regular heptagon and what it is necessary to prefix (the lemmas) to arrive at this construction.

What of all this passes into the West and filters into the Latin tradition that is formed over the centuries? In the next section, we will try to highlight what is happening around this issue in Europe.

5. Slight Traces of Archimedes’ Straight Line in the Latin Tradition

The formation of the Latin tradition, which begins with the translation by European scholars of texts from the Greek and Arabic languages into the Latin language, takes place gradually and with different connotations. Translations from Greek to Latin are a constant that accompanies the formation of schools from the IX century onwards (monastic schools, schools around great masters, the first universities), while the translations from Arabic to Latin are typical of some centuries (XI–XII centuries), becoming more sporadic in the following centuries. The study of these translations constitutes the first level of an in-depth reflection by Latin-speaking scholars which leads to new elaborations.

Among the Latin translations of Archimedes’ writings and the translations and elaborations which, even indirectly, refer to some of Archimedes’ texts, an important place is occupied by the translation of On the Sphere and Cylinder, as attested by M. Clagett in the five volumes Archimedes in the Middle Ages [20], published between 1964 and 1984.

The first writing that contains the Latin translation of contents that refer to Archimedes’ On the Sphere and Cylinder is entitled Verba filiorum, a very widespread text in the Latin Middle Ages. This writing is the translation of a text attributed to the three Banū Mūsā brothers, edited by Gherardo or Gerardo da Cremona. This paper contains 19 propositions, the statements of which refer to the contents of The measure of the circle, Heron’s theorem for areas, the solution of the double proportional mean, to contents of On the Sphere and Cylinder, and the first Latin solution of the problem of the trisection of an angle. However, there is no reference to prop. II 4 of On the Sphere and Cylinder.

In the history of translations of Archimedean writings, the translations of William of Moerbeke of a certain number of writings occupy a central and decisive place, including that of On the Sphere and Cylinder, to which the commentary by Eutocius of Ascalon is associated. After this choice by William, the translation of the Eutocian commentary generally accompanies the translation of this Archimedean work. We also point out the translation of the Archimedean writings by Iacopo da San Cassiano da Cremona during the fifteenth and early sixteenth centuries, which does not seem to be done on known and transmitted manuscripts. Finally, we note the passages translated by Giorgio Valla from On the Sphere and Cylinder and from the commentary by Eutocio in the posthumous writing De expetendis et fugiendis rebus… opus of 1501 [21].

Among the mathematical writings of the Middle Ages, the Renaissance, and Humanism we find a proposition from the Liber de triangulis by Giordano Nemorario or Giordano di Nemore or Nemi in which, in synthetic form, the problem of constructing a heptagon in a circle is solved. The lemma that we have indicated as the problem of the square, expressed in Archimedes’ straight line, is recalled within the solution.

In full humanism, Johann Werner collected in a Libellus [22], published in 1522, his interests around the conic sections, the solution of the duplication of the cube (specified as “paraphrastica enarratio”), the solutions of Dionysodorus and Diocles to the problem posed from Archimedes in prop. II 4 of On the Sphere and Cylinder, to which he follows his own solution, and the motion of the eighth sphere.

In the seventeenth century, the square problem, from its more general formulation as a rhombus problem to the specific one concerning the square, aroused the attention of some mathematicians, the first of whom was Marino Ghetaldi, who resumed the tradition that refers to the texts of Apollonius [23]. In the prop. 3 of Apollonius redivivus. Seu, restituta Apollonii Pergaei inclinationum geometria [24] of 1607, which is the reconstruction of book I of the essay On the inclinations of Apollonius, the problem of the rhombus is solved with the method of synthesis. The problem is taken up by Ghetaldi in the posthumous writing De resolutione & compositione mathematica libri quinque [25] of 1630, where, in prop. V 1 of chap. IV of book V, De resolutione & compositione problematum, quae sub algebram non cadunt, the problem is solved. This chapter is of particular importance for the history of problem-solving methods since it presents eight problems of plane geometry considered by Ghetaldi to be insoluble by means of algebra, the first of which is the rhombus problem. These pages are historically not negligible since they bear witness to the discussion around which problems can be solved by means of algebra and which cannot be solved, before the introduction of the analytic method.

In the second decade of the seventeenth century, Albert Girard, in the Invention nouvelle en algèbre [26] of 1629, discussed the meaning to give to negative solutions in geometric problems, after saying that a negative solution in geometry can be explained by “going backwards” and that a positive solution is explained “going forward”. He shows this by presenting a problem of inclination, which is the problem of the square, of which he exhibits for the first time the algebraic solution in a particular case, obtaining what Ghetaldi had denied. This problem did not escape the attention of René Descartes (1590-1650) who, in book III of Géométrie of 1637, gave the first algebraic solution, which we could consider general, within the treatment of solutions of fourth-degree equations.

We underline the fact that Descartes chooses as unknowns of the problem, not the segments that would immediately lead to writing a third-degree equation, but those segments that lead him to formulate the problem, after a suitable transformation, in the form of a fourth-degree equation, expressible with the product of two second-degree polynomials. In order to realize the latter, he needs to solve a biquadratic equation of sixth-degree for a new unknown. So the problem is reconducted to the solution of a new third-degree equation. The advantage of this procedure lies in the fact that the latter can be lowered to a second-degree equation through a simple division between polynomials. Therefore, by solving the two quadratic equations separately, Descartes arrives at determining all the possible solutions to the problem.

Here below, we report some further details concerning the rather complicated procedure followed by Descartes to arrive at the solution to the problem.

Through a suitable choice of the variables (the length of the segments in the geometric construction), Descartes finds that the solution to the problem can be cast in the form of a fourth-degree equation:

$$x^4-2a{x}^3+\left(2a^2-c^2\right)x^2-2a^{3}x+a^4=0$$

where $x$ is the unknown and $a$ and $c$ are known parameters. This equation can be transformed in another equation of the same degree without the cubic term through the transformation:

$$x=z+\frac{a}{2}$$

(3)

In this way, Descartes obtains the following equation for $z$:

$$z^4+\left(\frac{1}{2}{a}^2-c^2\right)z^2-\left(a^3+a{c}^2\right)z+\frac{5}{16}{a}^4-\frac{1}{4}{a}^2{c}^2=0$$

(4)

that, once solved, gives the solution for $x$.

Now, Descartes shows that it is possible to break the fourth-degree polynomial at the left-hand side into the product of two second-degree polynomials in the form:

$$z^4+\left(\frac{1}{2}{a}^2-c^2\right)z^2-\left(a^3+a{c}^2\right)z+\frac{5}{16}{a}^4-\frac{1}{4}{a}^2{c}^2=\left(z^2-yz+n\right)\left(z^2+yz+m\right)$$

and therefore, the fourth-degree Equation (4) is reconducted into two separate equations of second-degree that can be easily solved. However, in order to arrive at the latter form, the newly introduced parameters $n$, $m$, and $y$, are to be obtained. Working out the products on the right-hand side and comparing them with the terms on the left-hand side, one obtains the following relations:

$$\{\begin{array}{c}m+n=\frac{1}{2}{a}^2-c^2+y^2\\ n-m=-\frac{a^3+a{c}^2}{y}\\ mn=\frac{5}{16}{a}^4-\frac{1}{4}{a}^2{c}^2\end{array}$$

By making explicit the values of $m$ and $n$ as a function of $y$ from the first two relations, one gets to:

$$m=\frac{y^3+\left(\frac{a^2}{2}-c^2\right)y+\left(a^3+a{c}^2\right)}{2y} \mathrm{and} n=\frac{y^3+\left(\frac{a^2}{2}-c^2\right)y-\left(a^3+a{c}^2\right)}{2y}$$

(5)

and, using the third relation, we get a third-degree equation for $y^2$:

$$y^6+\left(a^2-2c^2\right)y^4+\left(-a^4+c^4\right)y^2+\left(-a^6-2a^4{c}^2-a^2{c}^4\right)=0$$

The advantage of this procedure is that now the latter can be written in the form:

$$\left[y^2-\left(a^2+c^2\right)\right]\left[y^4+\left(2a^2-c^2\right)y^2+a^4+a^2{c}^2\right]=0.$$

(6)

Hence, by separately solving the two (first and second order in $y^2$, respectively) equations obtained from (6), we obtain the possible solutions for the variable $y$ and, by using the (5), for $m$ and $n$. As a consequence, we have found the decomposition that allows us to cast Equation (4) as the product of two second-degree polynomials in the unknown $z$. Once all the solutions for $z$ are found, we finally arrive at the solutions for $x$ by using the (3).

Worthy of note is the appendix Problematum quorundam illustrium constructiones to the text De circuli magnitudine inventa [27] by Christiaan Huygens of 1654. In this text, eight problems are stated and solved, including the square problem (probl. 4), of which Huygens gives a different solution than the one given by Pappus in prop. VII 72 of the Mathematical Collection (see chap. I). Closely connected to this problem are also problems 5, 6, and 7 (the last two present the rhombus problem). In Huygens’ manuscripts, we find the algebraic solution of these problems. These pages represent the attempt to move from the geometric solution to the algebraic solution to a problem and are a living testimony of the reflection of mathematicians around the analytic method and its expressions.

Finally, Isaac Newton, on several occasions and in different periods of his intellectual activity, refers to the problem of the square and both its algebraic and geometric solution, as attested in The Mathematical Papers of Isaac Newton [6], published by Thomas Whiteside in eight volumes between 1967 and 1981.

In particular, we recall three points in which Newton refers to the problem of the square.

The first point is within the notes that Newton draws up in the month of May 1665 in which many reflections are expressed, on different questions, which are found in part III of vol. I of [6] under the title The theory and construction of equations. These notes talk about equations and the relationship between roots, taking up the problem of the square as it is presented in book III of the Géométrie. In the context of the search for solutions to fourth-degree equations, Newton focused his attention on the equation that solves the problem of the square, constructed in relation to the problem of inclinations.

The second point is recorded in three different pages of the notes which, only much later, will form the treatise Arithmetica universalis.

The first page is found within a chapter entitled by Whiteside Newton’s lectures on algebra during 1673–1683: the copy later deposited in the Cambridge archives, which is in part I of vol. V of [6].

When Newton indicates what to do to pass from the statement of a problem to its equation, among the given examples he also presents an Apollonian problem (probl. 13), which is that of inserting a segment into an external angle of a square.

The second and third pages are found within the manuscript Arithmeticae universalis liber primus, which is in part II of the same volume. This manuscript was probably composed in the spring of 1684.

The third point is in the last pages of the notes of Geometriae liber primus, which is in part II of vol. VII of [6]. In these pages the Apollonian problem is taken up again, that is the problem of the square and the problem of the rhombus. The composition of this writing is placed around 1693.

While in the first point, Newton follows quite closely the algebraic solution provided by Descartes, in the following points he experiments with the various equations and formulations of the problem that are obtained by choosing various combinations of the unknowns, identifying the algebraically more convenient ones.

Ultimately, although we do not know the solution to the lemma given by Archimedes, since we have not received it, we can assume that it was a solution of a geometric type, therefore analogous to the one subsequently given by Thābit. In the 17th century, with the advent of Descartes and Newton, the problem assumed purely algebraic characteristics and, in fact, became an opportunity to speculate on the solution of fourth-degree equations.

Considering the way in which these mathematicians tackled and solved the problem, noting that the attention of seventeenth-century mathematicians was directed to the pages of Book VII of Pappo’s Mathematical Collection without any reference to the reflections of Arab mathematicians, we can assume, as concluded, the history of the problem.

6. Conclusions

In this work we have tried to identify the origins of Archimedes’ straight line and the parallelogram/rhombus/square problem, tracing the historical development of this problem. The ancient pages begin with Archimedes’ solution of prop. II 4 of On the Sphere and Cylinder, in which the lemma is presented and used, called Archimedes’ straight line, which is only stated in this proposition. They then continue with the pages of Pappo’s Mathematical Collection on the parallelogram problem, a necessary prerequisite for tackling the solution of the trisection of an angle (book IV), and on Apollonius’ treatise On inclinations, with the addition of lemmas that allow a simplified reading of the text, reducing problems of insertion to easy problems on the plane (book VII). Finally, they come to Eutocio’s comment on prop. II 4 of On the Sphere and Cylinder in which the latter provides the solution to the lemma and presents the solutions of Dionysodorus and Diocles of the Archimedean proposition to the readers. In the three solutions of the lemma (of Eutocius, Dionysodorus, and Diocles), we find a point of intersection between a parabola and a hyperbola or between an ellipse and a hyperbola which is projected onto a given segment AB. Three points, aligned with the extremes A and B of the segment, divide it into parts between which it is possible to find the proportion which expresses Archimedes’ straight line and the one which expresses the parallelogram/rhombus/square problem, which is a classic problem of insertion. Thus, mathematicians are offered a tool (a lemma) useful for solving other problems, such as that of constructing the side of a regular heptagon in a circle, which the Arab tradition dates back to Archimedes himself, even if we have no historical reference about this.

The cited writings of the Arab mathematicians testify a keen interest in Archimedes’ straight line and its expressions, while fully accrediting the pseudo-Archimedean writing on the construction of the heptagon. Two lines of research are highlighted: the first around Archimedes’ straight line and the second on the construction of the side of a regular heptagon in a circle, which has the problem of the square as its essential premise. The one that directly deals with the division of Archimedes’ straight line highlights epistemological and resolutive aspects not addressed by Archimedes in completing prop. II 4 and as a premise for the construction of a regular heptagon in a circle. The other deals directly with the construction of the regular heptagon, giving space to his epistemological and mathematical premises. From reading the considered writings, we have the impression of being faced with points of intersection of the two lines of research.

The formation of the Latin tradition in relation to these problems takes place very slowly. We record that the reflection around Archimedes’ straight line, explicitly mentioned, disappears and that the attention of mathematicians is concentrated on the parallelogram problem, the rhombus problem, and the square problem.

During the Middle Ages, the translation of Archimedes’ writings and Eutocius’ commentary on some of them makes this problem known. William of Moerbeke’s translation and Giorgio Valla’s use of sources bear witness to this. At the same time, we note that some translations of elaborations by Arab mathematicians are beginning to pass, such as the one reported by Giordano Nemorario, which refers to some sheets translated from Arabic by Gerardo da Cremona.

Significant is the testimony of Johann Werner, who knows the state of the question through the comment of Eutocius, and revises the solutions of Dionysodorus and Diocles of prop. II 4 of On the Sphere and Cylinder and presents its own solution.

As far as we know today, the discussion of the question around Archimedes’ writing ends with him.

The testimony recorded in Christian Huygens in relation to the Archimedean proposition itself is not central to his interests, even if he pays attention to it by giving his own solution in the 1654 paper. Starting from this period much interest is directed to the writing of Pappus and to the recovery of the writings of Apollonius, of which Pappus himself is a witness in book VII of the Mathematical Collection.

The tracts by Marino Ghetaldi highlight that the rhombus problem attracts the attention of mathematicians. In the 1607 paper, book I of Apollonius’ paper On inclinations is reconstructed, in which the problem of the rhombus is presented as a problem of insertion, while in the posthumous paper of 1630, the same problem is considered one of the elements of demarcation between the problems solvable through algebra and those that cannot be solved through algebra.

This is a new problem in the context of lovers of geometry, lovers of the relationship between geometry and algebra, and lovers of the new algebra. We must assume that there are reflections and debates around this question, if Albert Girard presents the first algebraic solution to the problem of the square by solving the problem of inclinations, albeit in a particular case. This problem is constantly revived up to Newton.

In the context of algebra and the analytical method, one wonders whether it is possible to have a general solution to the problem of the square, because only in that case can it be said that the problem can be solved by means of algebra. Certainly, we can consider Descartes’ solution as a general one, because the particular case of Girard has been overcome, while observing that the equation that solves the problem of the square is chosen as a simple example of a fourth-degree equation expressible as the product of two quadratic equations. Due to this, the problem, of which this equation is an expression, is classified as a plane problem. Franz van Schooten, commenting on Descartes’ solution to quadratic equations, takes up Girard’s problem of inclinations, retraces the steps towards the solution, and gives a general formulation, classifying it as an insertion problem. At his school, there is the young Christian Huygens who, during his training at the University of Leiden, is urged by van Schooten to study the methods of the ancients, to become familiar with them, and to study and become accustomed to the use of the new instruments deriving from algebra and the analytic method. His notes of 1652, in which the problem of the rhombus is solved algebraically, as well as geometrically, and the printed appendix of 1654, in which the solution to the problem proposed by Archimedes in his prop. II 4 of On the Sphere and Cylinder, the problem of the square and the problem of the rhombus, are presented geometrically, and represent a living testimony of the reflections on these problems during these years.

We can say that Newton completes a path around the problem of the square and the problem of the rhombus. He recovers and adopts Pappus’ pages on these problems and, at the same time, tackles the solution of quadratic equations starting from the example of the problem of inclinations, read as a problem solved by means of a specific section. The initial closeness between Descartes and Newton soon becomes the distance between the two since, once he has taken note of Descartes’ observations around this problem, Newton gives precise indications on what and how to solve it in a simpler way.