Efficient and Privacy-Preserving Categorization for Encrypted EMR

Abstract

Electronic Health Records (EHRs) must be encrypted for patient privacy; however, an encrypted EHR is a challenge for the administrator to categorize. In addition, EHRs are predictable and possible to be guessed, although they are in encryption style. In this work, we propose a secure scheme to support the categorization of encrypted EHRs, according to some keywords. In regard to the predictability of EHRs, we focused on guessing attacks from not only the storage server but also the group administrator. The experiment result shows that our scheme is efficient and practical.

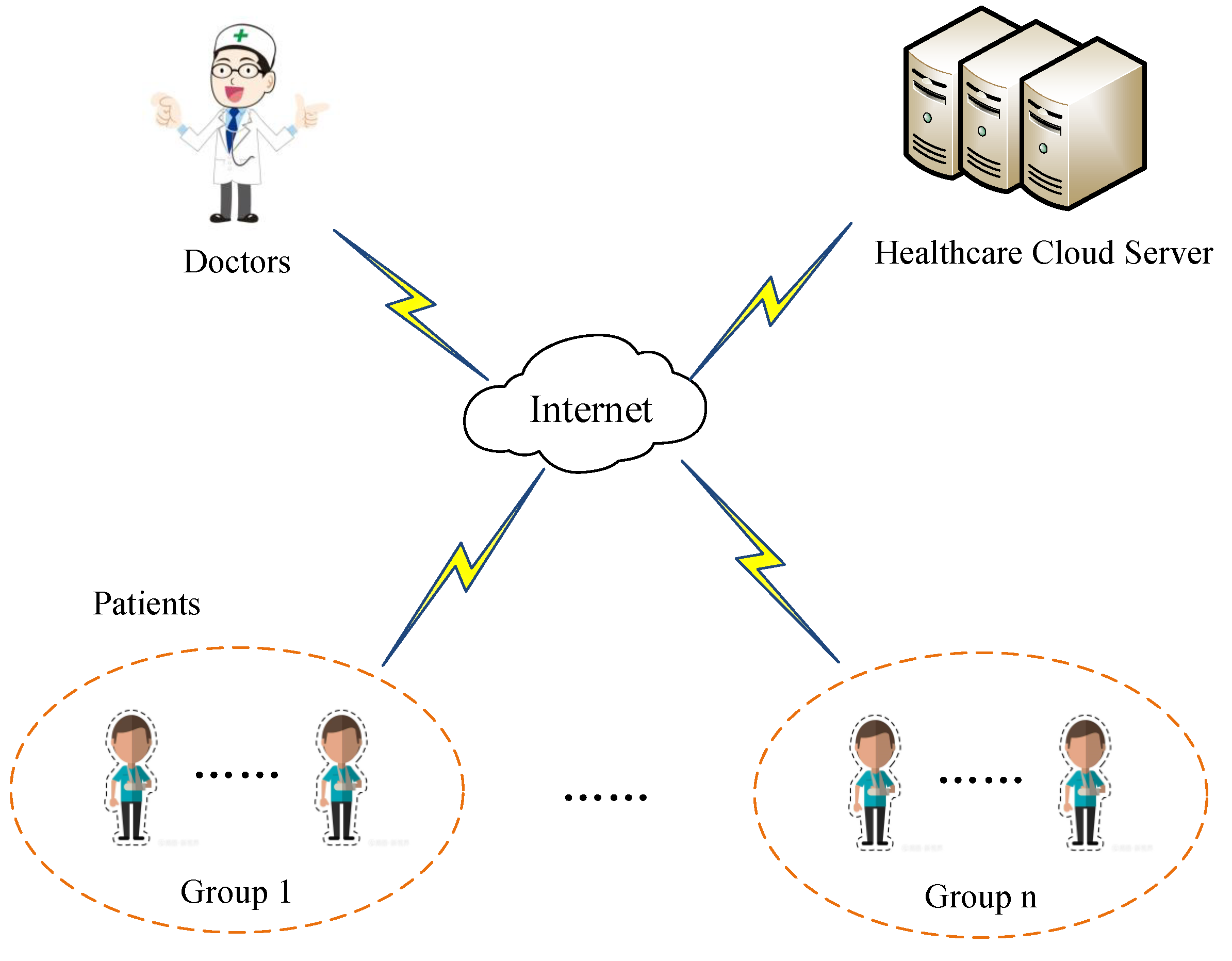
1. Introduction

With the tremendous benefits of cloud computing, more and more data are being outsourced to the cloud by data owners, and shared with authorized users [1,2,3]. Outsourcing electronic health records (EHRs) to a third party is the most common practice in health systems, providing both computational cost savings and quality service.

An electronic health record (EHR) is a technical tool for recording a patient’s health in a smart healthcare system. The EHR contains all information related to the patient’s health, including sensitive information, such as personal medical history, health reports, and medication records. Due to the sensitive patient data contained in EHRs, and the large storage space required for the data, cloud storage technology has been proposed for data storage management [4,5]; however, cloud service providers are not entirely trustworthy: for example, cloud servers can be curious [6], and for some reason can steal users’ data or compromise the integrity of the data.

To prevent sensitive data from being disclosed to cloud servers, patients encrypt the EHRs before uploading to the cloud server [7]; however, medical staff have to download and decrypt the data prior to searching, which makes the overhead cost much higher. To solve this problem, researchers have proposed public-key-encryption-based searchable encryption (PEKS), which allows servers to search encrypted data without revealing plaintext data (see [7,8,9,10,11]): for example, the public key searchable encryption scheme first proposed by Boneh et al. [8] has been applied to mail routing, where the mail server retrieves the data and sends the ciphertext of the message containing the keywords to the recipient. Khader et al. proposed a public key searchable encryption scheme based on K-Resilient IBE [11], which not only proved to be secure under the standard model, but also without using the bilinear pair, resulting in a significant improvement in operational efficiency.

However, searchable encryption (SE) only allows for searching on ciphertexts that have been encrypted under the same public keys, which makes it unsuitable for scenarios with different public key encryption. To solve this issue, a public key encryption with an equality test (PKEET) ([12,13]) was proposed, which was used to check whether two ciphertexts that were encrypted by different public keys contained the same plaintext. To reduce the storage cost of trapdoors, and the communication cost, Ling et al. [14] proposed the concept of group public key encryption with an equality test; however, Ling’s scheme failed to resolve the guessing attack from the group administrators in the system, which led to the security risk of data leakage. We have built on Ling’s results, to further improve the security of the scheme, and to combine it with the smart healthcare system.

In the traditional PKEET application scenario, any user can generate encrypted files, upload the ciphertext to the server, and wait for the result after the server test. The application of smart medical scenarios can lead to the privacy leakage of patient medical data. In order to solve this problem, we introduced a group-oriented PKEET into the medical scenario shown in Figure 1, taking the hospital as a group, with the patients uploading their encrypted electronic health records to the hospital. The third-party server could then perform an equality test on the ciphertexts within the group, after authorization, to determine whether the patient was suffering from the same symptoms, while the health records outwith the group could not be compared with the health records within the group: this ensured that external malicious attackers could not guess the internal patient’s health records, thus avoiding the leakage of patient privacy. When the server returned the test results to the doctor, the doctor could classify the patients in the group, according to their symptoms, to conduct better research for the disease.

1.1. Our Contributions

To support the efficient management of EMR, we introduced the notion of group-oriented PKEET. The main contributions of this scheme can be summarized as follows.

• We improved the group-oriented PKEET proposed in [14], to be resistant to guessing attack even by the group administrator: in this way, patient privacy was enhanced.
• We applied our group-oriented PKEET to the healthcare system, so that the EMR were managed efficiently and securely.

1.2. Related Work

Public key encryption with keyword search.

The concept of public key encryption with keyword search (PKE-KS) was first proposed by Boneh [8]. In the scheme, the receiver sends a trapdoor to the server, so that the server can search for specific keywords contained in the ciphertext.

Public key encryption with equality testing. Public key encryption with equality testing (PKEET) was introduced by Yang et al. [12]. In the scheme, the tester can arbitrarily check whether two ciphertexts encrypted with different public keys contain the same plaintext, without decrypting the ciphertext. To impose authorization mechanisms on PKEET, Tang proposed a strengthened PKEET (FG-PKEET) [13] to support fine-grained authorization. In the scheme, two users were required to jointly generate a token, and to authorize the tester to perform the equality test. In addition, Tang [15] presented an all-or-nothing PKEET (AoN-PKEET), which developed a fine-grained authorization mechanism that specified the users who performed the equality test. Ma et al. [16] proposed a public key encryption scheme to support the delegation equality test (PKE-DET), in which only the delegated party was required to handle the work in a practical multi-user environment: however, due to a large number of bilinear mapping operations, it could not be used in real scenarios. Huang et al. [17] proposed a public key encryption scheme with an authorization equality test (PKE-AET). In the PKE-AET, the protocol method was divided into receiver warrants and cipher warrants, to improve privacy protection.

Group encryption with equality testing. The concept of group encryption with equality testing was first proposed by Ling et al. [14]. The authors combined group mechanism with PKEET, and enabled equality testing on different users’ ciphertexts within a group, which reduced the storage cost of trapdoors and computation; however, Ling’s scheme was unable to resist a guessing attack from the group administrator, which was a serious privacy threat, especially in the healthcare system.

1.3. Organization

In the following, we briefly introduce some preliminaries in Section 2; we present the system definition and security model of the scheme in Section 3; in Section 4, we describe our scheme’s construction; in Section 5, we propose a formal security analysis; the comparison and performance evaluation are shown in Section 6; finally, we present this paper’s conclusion in Section 7.

2. Preliminaries

In this part, we give a brief introduction to the basic mathematical background, the bilinear map, the building block, and the cryptographic tool used.

2.1. Mathematical Background

Bilinear Map: Let G and $G_T$ be two multiplicative cyclic groups of prime order p. Suppose that g is G group’s generator. A bilinear map $\widehat{\mathit{e}}:$ G × G → $G_T$ has the following properties:

• bilinear: for any g ∈ G and $\mathit{a}$, $\mathit{b}$ ∈ Z${}_p^{*}$, $\widehat{\mathit{e}}$(g${}^a$,g${}^b$) = $\widehat{\mathit{e}}$(g,g)${}^{ab}$;
• non-degenerate: $\widehat{\mathit{e}}$(g,g) ≠ 1;
• computable: there is an effective algorithm for computing $\widehat{\mathit{e}}$(g,g) for any g ∈ G.

Computational Diffie–Hellman Problem (CDH) [18]: Let G be a group of prime order p. The CDH problem is as follows: we represent by $\stackrel{R}{⟵}$ the process of uniformly sampling a random element; if, given 3-tuple (g,g^a,g^b) ∈ G${}^3$ as input and $a,b$$\stackrel{R}{⟵}$ Z${}_p^{*}$, we can say that the CDH problem is hard in G, any probabilistic polynomial time algorithm $\mathcal{A}$ computes g${}^{ab}$ with negligible advantage $ϵ$:

$${\mathsf{Adv}}_{\mathcal{A},\mathrm{G}}^{\mathrm{CDH}}\stackrel{def}{=}Pr\left[\mathcal{A}\left(g,g^a,g^b\right)=g^{ab}\right]\le ϵ$$

2.2. Building Block

G-PKEET is the building block to construct our security [14]. The system model of G-PKEET is shown in Figure 2, which includes four entities: Group Administrator (GA); Sender; Receiver; and Cloud Server (CS).

• Group Administrator (GA) is responsible for generating the group secret key, $gsk$, and the group public key, $gpk$, of the system; then, it keeps the $gsk$, and sends the $gpk$ to the patient.
• Sender: the patient encrypts the electronic medical record with the group public key (gpk) and with the patient’s own secret key (sk), to generate the ciphertext C, then stores it in the cloud server.
• Cloud Server (CS): with the authorization, the cloud server is in charge of performing the equality test, and returns the result to the doctor.
• Receiver: upon receiving the result from the cloud server, the receiver can classify the based on the result.
  The receiver can use their own private key to decrypt the ciphertext at the same time.

3. System Definition and Security Model

3.1. The Syntax of PKEET

Public key encryption with equality testing consists of the following algorithms ($\mathtt{Gen},\mathtt{Enc},\mathtt{Dec},\mathtt{Test}$) operating over plaintext $\mathcal{M}$, ciphertext space $\mathcal{C}$, and key space $\mathcal{K}:$

• $\mathtt{Gen}$($1^{\lambda }$): the algorithm inputs a security parameter, $\lambda$, and outputs a public/secret key pair ($pk,sk$);
• $\mathtt{Enc}(\mathtt{pk},\mathtt{M})$: the algorithm inputs message M, the receiver’s public key, $pk$, and outputs a ciphertext, C;
• $\mathtt{Dec}(\mathtt{sk},\mathtt{C})$: the algorithm inputs a ciphertext, C, the receiver’s secret key, $sk$, and outputs a message, M;
• $\mathtt{Test}({\mathtt{C}}_{\mathtt{1}},{\mathtt{C}}_{\mathtt{2}})$: the algorithm inputs two ciphertexts, $C_1,C_2$, and outputs 1, if $C_1$ and $C_2$ are encrypted from the same plaintexts, and 0 otherwise.

3.2. The Syntax of G-PKEET

As an improvement, the group public key encryption with equality testing consists of the following algorithms ($\mathtt{Setup}$, ${\mathtt{KeyGen}}_{\mathtt{user}}$, ${\mathtt{KeyGen}}_{\mathtt{g}\mathtt{roup}}$, $\mathtt{Join},\mathtt{Enc},\mathtt{Dec},\mathtt{Aut},\mathtt{Test}$) operating over plaintext $\mathcal{M}$, ciphertext space $\mathcal{C}$, and key space $\mathcal{K}:$

• $\mathtt{Setup}$$(\lambda )$: the algorithm inputs a security parameter, $\lambda$, and outputs $pp$ as a system parameter;
• ${\mathtt{KeyGen}}_{\mathtt{user}}(\mathtt{pp})$: the algorithm inputs system parameter $pp$, and outputs (pk${}_i$,sk${}_i$) as a public/secret key pair;
• ${\mathtt{KeyGen}}_{\mathtt{g}\mathtt{roup}}(\mathtt{pp})$: the algorithm inputs system parameter $pp$, and outputs $gsk$ as a group secret key; it is run by GA;
• $\mathtt{Join}(\mathtt{gsk},{\mathtt{pk}}_{\mathtt{i}})$: the algorithm inputs a group secret key, $gsk$, a public key, $p{k}_i$, and outputs $gp{k}_i$ as a group public key for group user $U_i$; it is run by GA;
• $\mathtt{Enc}({\mathtt{gpk}}_{\mathtt{i}},{\mathtt{sk}}_{\mathtt{i}},{\mathtt{pk}}_{\mathtt{j}},\mathtt{M})$: the algorithm inputs a group public key, $gpk$, and a secret key, $s{k}_i$, of the group user $U_i$, a public key, $p{k}_j$, of the group user $U_j$, and a message, m, where $U_i$ and $U_j$ represent the receiver and sender, respectively, and outputs C${}_{ij}$ as a ciphertext;
• $\mathtt{Dec}({\mathtt{gpk}}_{\mathtt{i}},{\mathtt{sk}}_{\mathtt{j}},{\mathtt{C}}_{\mathtt{i},\mathtt{j}})$: the algorithm inputs a group public key, $gp{k}_i$ of the group user $U_i$, a secret key, $s{k}_j$, of the group user $U_j$, where $U_i$ and $U_j$ represent the receiver and sender, respectively, and outputs message M;
• $\mathtt{Aut}(\mathtt{gsk})$: the algorithm inputs a group secret key, gsk, and outputs a group trapdoor gtd; it is run by GA;
• $\mathtt{Test}({\mathtt{C}}_{\mathtt{i},\mathtt{j}},{\mathtt{C}}_{{\mathtt{i}}^{\prime },{\mathtt{j}}^{\prime }},\mathtt{gtd})$: the algorithm inputs two ciphertexts, $C_{i,j},C_{i^{\prime },j^{\prime }}$, a group trapdoor, gtd, and outputs 1, if $C_{i,j}$ and $C_{i^{\prime },j^{\prime }}$ are encrypted from the same plaintexts, and 0 otherwise.

3.3. Security Models

To simplify the security analysis, we defined the following games and adversaries for the security model:

• Type-I Adversary: the attacker authorized by GA cannot retrieve a message from the challenge ciphertext;
• Type-II Adversary: the attacker unauthorized by GA cannot determine by which plaintext the challenge ciphertext is encrypted.

OW-CCA security against Type-I adversary.

Game 1: Let ${\mathcal{A}}_1$ be a Type-I adversary.

1.

Setup: With a security parameter, $\lambda$, challenger ${\mathcal{C}}_1$ runs the $Setup$ algorithm to generate public parameter pp; then, it runs the $KeyGe{n}_{user}$ algorithm to generate n group users’ public/secret key pair ($p{k}_i,s{k}_i$) ($1\le i\le n$); it runs the $KeyGe{n}_{group}$ algorithm, to generate a group secret key, gsk; it runs the $Join$ algorithm, to generate n group user’s group public key, $gp{k}_i$ ($1\le i\le n$); and it runs the $Aut$ algorithm, to generate a group trapdoor, $gtd$; finally giving $pp$, all $p{k}_i$, $gp{k}_i$, and $gtd$ to the adversary ${\mathcal{A}}_1$.

2.

Phase 1: ${\mathcal{A}}_1$ makes the following queries for polynomial times:

• ${\mathcal{O}}_{Key}$ query $〈i〉:$${\mathcal{A}}_1$ sends $p{k}_i$, and gets $s{k}_i$ from the oracle;
• ${\mathcal{O}}_{Enc}$ query $〈i,j,M〉:$${\mathcal{A}}_1$ sends ($gp{k}_i,s{k}_i,p{k}_j,M$), and gets the encryption result of M from the oracle;
• ${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉:$${\mathcal{A}}_1$ sends ($gp{k}_i,s{k}_j,C_{i,j}$), and gets the decryption result of $C_{i,j}$ from the oracle.

3.

Challenge: The challenge ${\mathcal{C}}_1$ randomly selects a message, M, runs $Enc(gp{k}_{i^{*}},s{k}_{i^{*}},p{k}_{j^{*}},M)$, and sends the output ${\widehat{C}}_{i^{*},j^{*}}$ to ${\mathcal{A}}_1$.

4.

Phase 2: ${\mathcal{A}}_1$ issues queries, as in Phase 1: the constraint is that ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$.

5.

Guess: ${\mathcal{A}}_1$ outputs a guess, $M^{*}$: if $M^{*}=M$, ${\mathcal{A}}_1$ wins the game.

We define the advantage of ${\mathcal{A}}_1$ in the Game 1 as

$${\mathbf{Adv}}_{{\mathcal{A}}_1}^{\mathit{OW}-\mathit{CCA}}(\lambda )=\mathit{Pr}[M^{*}=M]$$

Definition 1.

The improved G-PKEET scheme is OW-CCA-secure if ${\mathit{Adv}}_{{\mathcal{A}}_1}^{\mathit{OW}-\mathit{CCA}}$ is negligible for any probabilistic polynomial time OW-CCA adversary in the security parameters.

IND-CCA security against Type-II adversary.

Game 2: Let ${\mathcal{A}}_2$ be a Type-II adversary.

1.

Setup: With a security parameter, $\lambda$, challenger ${\mathcal{C}}_2$ runs the $Setup$ algorithm to generate public parameter PP; then, it runs the $KeyGe{n}_{user}$ algorithm to generate n group users’ public/secret key pair, ($p{k}_i,s{k}_i$) ($1\le i\le n$); it runs the $KeyGe{n}_{group}$ algorithm to generate a group secret key, gsk; it runs the $Join$ algorithm to generate n group user’s group public key, $gp{k}_i$ ($1\le i\le n$); and it runs the $Aut$ algorithm to generate a group trapdoor, $gtd$; finally, it gives $pp$, all $p{k}_i$, $gp{k}_i$, and $gtd$ to the adversary, ${\mathcal{A}}_2$.

2.

Phase 1: ${\mathcal{A}}_2$ makes the following queries for polynomial times:

• ${\mathcal{O}}_{Key}$ query $〈i〉:$ ${\mathcal{A}}_2$ sends $p{k}_i$, and gets $s{k}_i$ from the oracle;
• ${\mathcal{O}}_{Enc}$ query $〈i,j,M〉$: ${\mathcal{A}}_2$ sends ($gp{k}_i,s{k}_i,p{k}_j,M$), and gets the encryption result of M from the oracle;
• ${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉:$ ${\mathcal{A}}_2$ sends ($gp{k}_i,s{k}_j,C_{i,j}$), and gets the decryption result of $C_{i,j}$ from the oracle.

3.

Challenge: ${\mathcal{A}}_2$ randomly selects two messages, $m_0,m_1$, and sends them to challenge ${\mathcal{C}}_2$; then, ${\mathcal{C}}_2$ randomly selects $\sigma \stackrel{R}{\leftarrow }\{0,1\}$, runs $Enc(gp{k}_{i^{*}},s{k}_{i^{*}},p{k}_{j^{*}},M)$, and sends ${\widehat{C}}_{i^{*},j^{*}}$ to ${\mathcal{A}}_2$.

4.

Phase 2: ${\mathcal{A}}_2$ issues queries, as in Phase 1. The constraint is that ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$.

5.

Guess: ${\mathcal{A}}_2$ returns a guess, ${\sigma }^{*}$. If ${\sigma }^{*}=\sigma$, ${\mathcal{A}}_2$ wins the game.

We define the advantage of ${\mathcal{A}}_2$ in the Game 2 as

$${\mathbf{Adv}}_{{\mathcal{A}}_2}^{\mathit{INC}-\mathit{CCA}}(\lambda )=\left|\mathrm{Pr}\left[{\sigma }^{*}=\sigma \right]-\frac{1}{2}\right|$$

Definition 2.

The improved G-PKEET scheme is IND-CCA-secure if ${\mathit{Adv}}_{{\mathcal{A}}_2}^{\mathit{IND}-\mathit{CCA}}$ is negligible for any probabilistic polynomial time IND-CCA adversary in the security parameters.

4. Construction

• $Setup(\lambda )$: this algorithm is performed by Key Generation Center (KGC). KGC inputs security parameter $\lambda$, and outputs public parameters $pp=\{G,G_T,p,g,e,H_1,H_2,H_3,H_4\}$. $H_1,H_2,H_3,H_4$ are four collision-resistant hash functions:

  -

  H${}_1$:${\{0,1\}}^{l_1}$ → G,

  -

  H${}_2$:G → G,

  -

  H${}_3$:G → ${\{0,1\}}^{l_1+l_2}$,

  -

  H${}_4$:${\{0,1\}}^{*}\to {\{0,1\}}^{\lambda }$, where l${}_1$ and l${}_2$ represent the length of message and the length of Z${}_p$.

• $KeyGe{n}_{user}(pp)$: this algorithm is performed by the patient, who randomly selects $x_i,y_i\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and outputs a public/secret key pair, $\left(p{k}_i,s{k}_i\right)$

$$\left(p{k}_i,s{k}_i\right)=((g^{x_i},g^{y_i}),(x_i,y_i)).$$

• $KeyGe{n}_{group}(pp)$: this algorithm is performed by the GA (for example, the hospital director), who randomly selects s${}_1$, s${}_2$$\stackrel{}{\leftarrow }{\mathbb{Z}}_p^{*}$, and: (1) outputs a group secret key, gsk = (s${}_1$, s${}_2$); (2) sets the group trapdoor, gtd = s${}_2$.
• $Join(gsk,p{k}_i)$: this algorithm is performed by GA, and outputs a group public key for group patients, U${}_i$:
  $${\mathit{gpk}}_i=\left(g^{x_i{s}_1},g^{s_2}\right)$$
• $Enc(gp{k}_i,s{k}_i,p{k}_j,M)$: this algorithm is performed by patient i. To encrypt $EHRs$, say $M\in {\{0,1\}}^{*}$, patient i randomly chooses two random numbers, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and uses doctor j’s public key, $p{k}_j$, to set the ciphertext, C = (C${}_1$,C${}_2$,C${}_3$,C${}_4$,C${}_5$), as follows:
  $$\begin{array}{c}{C}_1=g^{\frac{x_i}{y_i}{s}_1{\zeta }_1},C_2=H_1{(M)}^{\frac{x_i}{y_i}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ C_3=g^{{\zeta }_2},C_4=H_3(g^{x_j{\zeta }_2})\oplus \left(M\parallel g^{{\zeta }_1}\right),\\ C_5=H_4\left(C_1∥C_2∥C_3∥C_4∥M\parallel g^{{\zeta }_1}\right).\end{array}$$
• $Dec(gp{k}_i,s{k}_j,C_{i,j})$: this algorithm is performed by a doctor, and computes ($M^{\prime }\left|\right|g^{{\zeta }_1^{\prime }}$) ← $C_4\oplus H_3(C_3^{x_j})$, then decides if the following equation holds:
  $$\begin{array}{c}\widehat{e}(C_1,g^{y_i})=\widehat{e}(g^{x_i{s}_1},g^{{\zeta }_1^{\prime }}),\\ C_5=H_4\left(C_1∥C_2∥C_3∥C_4∥M^{\prime }\parallel g^{{\zeta }_1^{\prime }}\right);\end{array}$$
  if yes, then the doctor obtains the EHRs’ $M^{\prime }$.
  In the decryption step, a verification operation is performed, to prevent attackers from decrypting the modified ciphertext to obtain the plaintext; data security is ensured.
• $Aut(gsk)$: this algorithm is performed by GA, and outputs a group gtd = $s_2$ to the cloud server, for the next testing step.
• $Test(C_{i,j},C_{i^{\prime },j^{\prime }},gtd)$: the algorithm is performed by tester (cloud server). Given ciphertexts, group trapdoor, the algorithm outputs 1 if the following equation holds:
  $$\widehat{e}(C_1,C_2^{\prime }/H_2({(C_3^{\prime })}^{s_2}))=\widehat{e}(C_1^{\prime },C_2/H_2(C_3^{s_2})).$$
  Note: We presented a detailed construction for the G-PKEET scheme as above, and compared it to Ling et al.’s scheme [14]. We made some improvements to the encryption part, by using a pair of generated private keys to encrypt the EHRs, so that only the server could test the ciphertext if it got the group trapdoor.

5. Security Analysis

In this section, we show that our improved G-PKEET scheme is OW-CCA-secure against a Type-I adversary, and IND-CCA-secure against a Type-II adversary with the random oracles.

Theorem 1.

The improved G-PKEET scheme is OW-CCA-secure against a Type-I adversary, based on the CDH problem in the random oracle model.

Proof. 

Let ${\mathcal{A}}_1$ be a probabilistic polynomial time (PPT) adversary attacking the OW-CCA security. Assuming that ${\mathcal{A}}_1$ makes, at most, $q_{H_1}$ > 0 $H_1$ hash queries, $q_{H_2}$ > 0 $H_2$ hash queries, $q_{H_3}$ > 0 $H_3$ hash queries, $q_{H_4}$ > 0 $H_4$ hash queries, $q_K$ > 0 secret key queries, $q_{Enc}$ > 0 encryption queries, $q_{Dec}$ > 0 decryption queries, and $q_{Aut}$ > 0 authorization queries. Let ${\mathrm{Adv}}_{{\mathcal{A}}_1}^{\mathit{OW}-CCA}$($\lambda$) represent the advantage of ${\mathcal{A}}_1$ in the following games. We will demonstrate the security proof through a series of games. □

Game 1.0:

1.

$pp\leftarrow \left(p,\mathbb{G},{\mathbb{G}}_T,\widehat{e},g\right)$, $\forall 1\le i\le n$, $(x_i,y_i)\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, sk${}_i$ = ($x_i,y_i$), pk${}_i$ = ($g^{x_i},g^{y_i}$), $s_1,s_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, gsk = (s${}_1$, s${}_2$), gpk${}_i$ = (g${}^{x_i{s}_1}$, g${}^{s_2}$), gtd = s${}_2$. H${}_1$, H${}_2$, H${}_3$, and H${}_4$ are random oracles. H-query. The challenger prepares four hash tables, to record and respond to queries.

${\mathcal{O}}_{H_1}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger randomly selects $u\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, computes $h_1=g^u\in \mathbb{G}$, saves ($v_1,u,h_1$) into $T_1$, and sends $h_1$ to ${\mathcal{A}}_1$.

${\mathcal{O}}_{H_2}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger chooses a compatible random value, $h_2$, and saves ($v_1,h_2$) into $T_2$ for ${\mathcal{O}}_{H_2}$.

${\mathcal{O}}_{H_3}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger chooses a compatible value, $h_3$, uniformly from the set ${\{0,1\}}^{l_1+l_2}$ that is returned, and saves ($v_1,h_3$) into $T_3$ for ${\mathcal{O}}_{H_3}$.

${\mathcal{O}}_{H_4}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger chooses a compatible value, $h_4$, uniformly from the set ${\{0,1\}}^{\lambda }$ that is returned, and saves ($v_1,h_4$) into $T_4$ for ${\mathcal{O}}_{H_4}$.

2.

state ← ${\mathcal{A}}_1^{O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}(PP,{\{p{k}_i,gp{k}_i\}}_{i=1}^n,gtd,i^{*},j^{*}),$ where the oracles are simulated as follows, and $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}$ oracle:

${\mathcal{O}}_{Key}$ query $〈i〉:$ input index i; the challenger sends ($x_i,y_i$) to ${\mathcal{A}}_1$;

${\mathcal{O}}_{Enc}$ query $〈i,j,M〉:$ input two indexes, i, j, and a plaintext M; the challenger runs the $Enc$ algorithm, and returns $C_{i,j}$ = $Enc(gp{k}_i,s{k}_i,p{k}_j,M)$;

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉:$ input two indexes, i,j, and a ciphertext, $C_{i,j}$; the challenger runs the $Dec$ algorithm, and returns M = $Dec(gp{k}_i,s{k}_j,C_{i,j})$.

3.

$M\stackrel{R}{\leftarrow }$${\{0,1\}}^{l_1}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*},{\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$, and computes:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=H_3(g^{x_{j^{*}}{\zeta }_2})\oplus \left(M\parallel g^{{\zeta }_1}\right),\\ {\widehat{C}}_5=H_4\left({\widehat{C}}_1∥{\widehat{C}}_2∥{\widehat{C}}_3∥{\widehat{C}}_4∥M\parallel g^{{\zeta }_1}\right).\end{array}$$

4.

$M^{\prime }\leftarrow {\mathcal{A}}_1^{O_{(H_1,H_2,H_3,H_4)},O_{(Key,Enc,Dec)}}(state,{\widehat{C}}_{i^{*},j^{*}}).$ The constraint is that ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$, and $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}.$

Let $S_{1.0}$ denote the event $M^{\prime }=M$ in Game 1.0. Thus, the advantage of ${\mathcal{A}}_1$ is as follows:

$$\begin{array}{c}{\mathsf{Adv}}_{{\mathcal{A}}_1}^{\mathit{OW}-\mathit{CCA}}(q_{H_1},q_{H_2},q_{H_3},q_{H_4},q_{Key},q_{Enc},q_{Dec})\\ =Pr\left[S_{1.0}\right]\end{array}$$

(1)

Game 1.1: In this game, the performance of the challenger is the same as in Game 1.0, except for the following:

1.

${\mathcal{O}}_{Enc}$ query $〈i,j,M〉$: the challenge ${\mathcal{C}}_1$ selects ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and returns a ciphertext, $C_{i,j}$, to ${\mathcal{A}}_1$, then computes

$$C_1=g^{\frac{x_i}{y_i}{s}_1{\zeta }_1},C_3=g^{{\zeta }_2};$$

it executes a query on ${\mathcal{O}}_{H_1}$, with input M to return $h_1$, a query on ${\mathcal{O}}_{H_2}$, with input $g^{s_2{\zeta }_2}$ to return $h_2$, and a query on ${\mathcal{O}}_{H_3}$, with input $g^{x_j{\zeta }_2}$ to return $h_3$; then, it computes

$$C_2=h_1^{\frac{x_i}{y_i}{\zeta }_1}·h_2,C_4=h_3\oplus (M||g^{{\zeta }_1}).$$

and, finally, it executes a query on ${\mathcal{O}}_{H_4}$ with input $(C_1|\left|C_2\right|\left|C_3\right|\left|C_4\right|\left|M\right||g^{{\zeta }_1})$ to return $h_4$; then, it sets

$$C_5=h_4.$$

The challenger saves ($v_1,h_1$), ($v_1,h_2$), ($v_1,h_3$), ($v_1,h_4$) to $T_1,T_2,T_3,T_4$, and returns $C_{i,j}$ to ${\mathcal{A}}_1.$

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉$: the challenger executes a query on ${\mathcal{O}}_{H_3}$ on input $C_3^{x_j}$, and gets the answer $h_3$; it then computes $C_4\oplus h_3$, to get $M^{\prime }\left|\right|g^{{\zeta }_1^{\prime }}$, and checks if the following equations hold:

$$\begin{array}{c}{C}_1=g^{\frac{x_i}{y_i}{s}_1{\zeta }_1^{\prime }},\\ C_5=H_4\left(C_1∥C_2∥C_3∥C_4∥M^{\prime }\parallel g^{{\zeta }_1^{\prime }}\right).\end{array}$$

If either fails to be maintained, the challenger sends ⊥ to ${\mathcal{A}}_1$; otherwise, it sends $M^{\prime }$ to ${\mathcal{A}}_1$.

2.

$M\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $W^{*}\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$ computes

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2});\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W_{1.1}^{*}\oplus \left(M\parallel g^{{\zeta }_1}\right);\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the challenger saves the tuple $(g^{x_{j^{*}}{\zeta }_2},W_{1.1}^{*})$ into tables $T_3$ for ${\mathcal{O}}_{H_3}$.

Let $S_{1.1}$ denote the event $M^{\prime }=M$ in Game 1.1. Given the idealness of the random oracle, Game 1.1 is the same as Game 1.0, and we have

$$Pr\left[S_{1.1}\right]=Pr\left[S_{1.0}\right]$$

(2)

Game 1.2: In this game, the performance of the challenger is the same as in Game 1.1, except for the following:

1.

${\mathcal{O}}_{H_3}$ query $〈v_1〉$ is the same as that in Game 1.1; in addition, if ${\mathcal{A}}_1$ asks ${({\widehat{C}}_3)}^{x_{j^{*}}}$, denote this event by E${}_1$;

2.

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉$ is the same as that in Game 1.1; in addition, if ${\mathcal{A}}_1$ requests the decryption of (${\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4^{\prime },{\widehat{C}}_5$) after receiving the challenge ciphertext ${\widehat{C}}_{i^{*},j^{*}}$, where ${\widehat{C}}_4^{\prime }\ne {\widehat{C}}_4$, the challenger sends ⊥ to ${\mathcal{A}}_1;$

3.

$M\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $W_{2.1}^{*}\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$ is defined as follows:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W_{2.1}^{*},\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the tuple $(g^{x_{j^{*}}{\zeta }_2},W_{2.1}^{*}\oplus (M||g^{{\zeta }_1}))$ is saved into tables $T_3$ for ${\mathcal{O}}_{H_3}$.

Let S${}_{1.2}$ denote the event that $M=M^{\prime }$ in Game 1.2. The challenge ciphertext generated in Game 1.1 is identically distributed to that in Game 1.2, as ${\widehat{C}}_4$ is a random value in both Game 1.1 and Game 1.2; therefore, if event E${}_1$ does not happen, Game 1.2 is identical to Game 1.1, and we have

$$\begin{array}{c}\left|Pr\left[{\mathbf{S}}_{1.2}\right]-Pr\left[{\mathbf{S}}_{1.1}\right]\right|\le Pr\left[{\mathbf{E}}_1\right].\hfill \end{array}$$

(3)

Next, we show that the event (3) holds.

Lemma 1.

Event E₁ happens in Game 1.2 with negligible probability if the CDH problem is intractable.

Proof. 

Suppose that Pr[E${}_1$] is non-negligible. We construct a PPT algorithm, ${\mathcal{B}}_1$, to break the CDH assumption. Given a tuple, ($G,G_T,p,\widehat{e},g,g^{\alpha },g^{\beta }$), it runs ${\mathcal{A}}_1^{\prime }$, and works as follows: □

1.

${\mathcal{B}}_1$ sets PP = ($G,G_T,p,g,\widehat{e}$); it chooses two random values, $s_1,s_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $1\le i^{*},j^{*}\le n$, and sets gsk = $(s_1,s_2)$, $s{k}_{j^{*}}=\alpha$, $p{k}_{j^{*}}=g^{\alpha }$, and $gp{k}_{j^{*}}=({(g^{\alpha })}_1^s,g_2^s)$. Then, it chooses random value $x_i\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and sets $s{k}_i=x_i,p{k}_i=g_i^x,gp{k}_i=(g^{x_i{s}_1},g^{s_2})$, and gtd = $s_2$. $H_1,H_2,H_3,H_4$ are four random oracles. H-query. ${\mathcal{B}}_1$ prepares four hash tables to record and respond to queries, where all the hash tables are initialized to empty:

${\mathcal{O}}_{H_1}$ query $〈v_1〉$: same as that in Game 1.1;

${\mathcal{O}}_{H_4}$ query $〈v_1〉$: same as that in Game 1.1;

${\mathcal{O}}_{H_3}$ query $〈v_1〉$: same as that in Game 1.1;

${\mathcal{O}}_{H_2}$ query $〈v_1〉$: same as that in Game 1.1, except that if ${\mathcal{A}}_1^{\prime }$ asks ${({\widehat{C}}_3)}^{x_{j^{*}}}=g^{\alpha \beta }$, we denote this event by ${\mathbf{E}}_1^{\prime }.$

2.

state ← ${\mathcal{A}}_1^{O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}(pp,{\{p{k}_i,gp{k}_i\}}_{i=1}^n,gtd,i,j),$ where the oracles are simulated as follows:

${\mathcal{O}}_{Key}query〈i〉$: same as that in Game 1.1;

${\mathcal{O}}_{Enc}query〈i,j,M〉$: same as that in Game 1.1, except that if query $〈i,j^{*},M〉$, ${\mathcal{B}}_1$ chooses random values, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and outputs a ciphertext, $C_{i,j}=(C_1,C_2,C_3,C_4,C_5)$, defined as

$$C_1={(g^{\alpha })}^{s_1{\zeta }_1},C_3=g^{{\zeta }_2},$$

then it executes a query on ${\mathcal{O}}_{H_1}$, with input M to return $(v_1,u_M,h_1)$, a query on ${\mathcal{O}}_{H_2}$, with input $g^{s_2{r}_2}$ to return $h_2$, and a query on ${\mathcal{O}}_{H_3}$, with input $g^{x_j{\zeta }_2}$ to return $h_3$; then, it computes

$$C_2={(g^{\alpha })}^{u_M{\zeta }_1}·h_2,C_4=h_3\oplus (M||g^{{\zeta }_1});$$

finally, it executes a query on ${\mathcal{O}}_{H_4}$, with input $(C_1|\left|C_2\right|\left|C_3\right|\left|C_4\right|\left|M\right||g^{{\zeta }_1})$ to return $h_4$, and sets $C_5=h_4.$

The challenger saves $(v_1,h_1)$ to table $T_1$ for ${\mathcal{O}}_{H_1}$, $(v_1,h_2)$ to table $T_2$ for ${\mathcal{O}}_{H_2}$, $(v_1,h_3)$ to table $T_3$ for ${\mathcal{O}}_{H_3}$, $(v_1,h_4)$ to table $T_4$ for ${\mathcal{O}}_{H_4}$, and returns $C_{i,j}$ to ${\mathcal{A}}_1^{\prime }$.

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉$: same as that in Game 1.1. In addition to query $〈i,j^{*},C_{i,j}〉$, if ${\mathcal{A}}_1^{\prime }$ asks the decryption of (${\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4^{\prime },{\widehat{C}}_5$) after obtaining the challenger ciphertext ${\widehat{C}}_{i^{*},j^{*}}$, and ${\widehat{C}}_4^{\prime }\ne {\widehat{C}}_4$, the challenger sends ⊥ to ${\mathcal{A}}_1$. For the tuple ($v_1,h_3$), ${\mathcal{B}}_1$, after computing $M^{\prime }\left|\right|g^{{\zeta }_1^{\prime }}=C_4\oplus h_3$, verifies if $C_1=g^{\frac{x_i}{y_i}{s}_1{\zeta }_1^{\prime }}$; otherwise, it returns ⊥; then, it inputs $(C_1|\left|C_2\right|\left|C_3\right|\left|C_4\right|\left|M^{\prime }\right||g^{{\zeta }_1^{\prime }})$ to get $h_4$, and verifies if $C_5=h_4$: if so, it returns M; if a compatible tuple does not exist, it returns ⊥.

3.

$M\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1}$, ${\zeta }_1\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, ${(W^{*})}^{\prime }\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$, defined as follows:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2({(g^{\beta })}^{s_2}),\\ {\widehat{C}}_3=g^{\beta },{\widehat{C}}_4={(W^{*})}^{\prime }\oplus \left(M\parallel g^{{\zeta }_1}\right),\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M\left|\right|g^{{\zeta }_1});\end{array}$$

finally, it saves the tuple ($\Delta ,C_4^{\prime }$) into table $T_3$, where $\Delta$ Indicates that the value is unknown.

4.

$M^{\prime }\leftarrow {\mathcal{A}}_1^{O_{(H_1,H_2,H_3,H_4)},O_{(Key,Enc,Dec)}}(state,{\widehat{C}}_{i^{*},j^{*}})$. The constraints are that $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}$, and ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$.

Indistinguishable simulation. Based on the setting of the simulation, the correctness and randomness of the simulation hold, given a ciphertext $C_{i,j}=(C_1,C_2,C_3,C_4,C_5)$ for a decryption query, if $j\ne j^{*}$, ${\mathcal{B}}_1$ is able to execute decryption simulation; if $j=j^{*}$, we have the following scenarios:

• $C_3^{\alpha }$ has been queried to ${\mathcal{O}}_{H_3}$ before decryption query is asked: in this case, $C_4$ is uniquely determined after $C_3^{\alpha }$ is queried to ${\mathcal{O}}_{H_3}$; then, the decryption oracle is perfectly simulated;
• $C_3^{\alpha }$ has never been queried to ${\mathcal{O}}_{H_3}$ when the decryption query is asked: in this case, ⊥ is returned by the decryption oracle if the simulation fails; however, the idealness of the random oracle happens with probability $1/2^{l_1+l_2}$.

${\mathbf{E}}_2$ denotes the event that a valid ciphertext is refused in the simulation: then, we have $Pr\left[{\mathbf{E}}_2\right]\le q_D/2^{l_1+l_2}$, which is negligible, so that ${\mathcal{B}}_1$ executes the decryption simulation correctly, but with negligible probability. The simulation is indistinguishable from Game 1.2.

Probability of successful simulation. If the simulated game is not aborted, then the probability of successful simulation is 1.

Analysis. As ${\mathcal{A}}_1^{\prime }$ queries ${({\widehat{C}}_3)}^{\alpha }$ with probability $Pr\left[{\mathbf{E}}_1^{\prime }\right]$, ${\mathcal{B}}_1$ is able to solve the CDH problem with probability $Pr\left[{\mathbf{E}}_1^{\prime }\right]$, and we have $Pr\left[{\mathbf{E}}_1^{\prime }\right]$ = ${\mathbf{Adv}}_{{\mathcal{A}}_1}^{\mathrm{CDH}}$. In addition, if ${\mathbf{E}}_2$ does not occur, we have $Pr\left[{\mathbf{E}}_1^{\prime }\mid \neg {\mathbf{E}}_2\right]=Pr\left[{\mathbf{E}}_1\right]$.

$$\begin{array}{cc}Pr\left[{\mathbf{E}}_1^{\prime }\right]\hfill & =Pr\left[{\mathbf{E}}_1^{\prime }\mid {\mathbf{E}}_2\right]Pr\left[{\mathbf{E}}_2\right]+Pr\left[{\mathbf{E}}_1^{\prime }\mid \neg {\mathbf{E}}_2\right]Pr\left[\neg {\mathbf{E}}_2\right]\hfill \\ & \ge Pr\left[{\mathbf{E}}_1^{\prime }\mid \neg {\mathbf{E}}_2\right]Pr\left[\neg {\mathbf{E}}_2\right]=Pr\left[{\mathbf{E}}_1\right]\left(1-Pr\left[{\mathbf{E}}_2\right]\right)\hfill \\ & \ge Pr\left[{\mathbf{E}}_1\right]-Pr\left[{\mathbf{E}}_2\right].\hfill \end{array}$$

Therefore, according to ${\mathbf{Adv}}_{{\mathcal{A}}_1}^{\mathrm{CDH}}\ge Pr\left[{\mathbf{E}}_1\right]-q_D/2^{l_1+l_2}$, we have

$$\begin{array}{c}Pr\left[{\mathbf{E}}_1\right]\le {\mathbf{Adv}}_{{\mathcal{A}}_1}^{\mathrm{CDH}}+q_D/2^{l_1+l_2},\hfill \end{array}$$

(4)

which is negligible. This completes the proof of Lemma 1.

Finally, in Game 1.2, we analyze the challenge ciphertext ${\widehat{C}}_{i^{*},j^{*}}$:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W^{*}\oplus \left(M\parallel g^{{\zeta }_1}\right),\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M\left|\right|g^{{\zeta }_1}).\end{array}$$

Note that ${\widehat{C}}_1$, ${\widehat{C}}_3$, and ${\widehat{C}}_4$ are independent from the message M. Given the one-wayness of hash functions, ${\mathcal{A}}_1$ can figure out M from ${\widehat{C}}_2$ and ${\widehat{C}}_5$ with a negligible probability $\epsilon$; thus, we have

$$Pr\left[{\mathbf{S}}_{1.2}\right]\le \epsilon$$

(5)

According to (1)–(5), we have

$${\mathsf{Adv}}_{{\mathcal{A}}_1}^{\mathit{OW}-\mathit{CCA}}(q_{H_1},q_{H_2},q_{H_3},q_{H_4},q_{Key},q_{Enc},q_{Dec})\le {\mathbf{Adv}}_{{\mathcal{A}}_{\mathcal{1}}}^{\mathrm{CDH}}+q_D/2^{l_1+l_2}+\epsilon ,$$

which is negligible. This completes the proof of Theorem 1.

Theorem 2.

The improved G-PKEET scheme is IND–CCA-secure against a Type-II adversary based on the CDH problem in the random oracle model.

Proof. 

Let ${\mathcal{A}}_2$ be a probabilistic polynomial time (PPT) adversary attacking the IND-CCA security. Assuming that ${\mathcal{A}}_2$ makes, at most, $q_{H_1}$ > 0 $H_1$ hash queries, $q_{H_2}$ > 0 $H_2$ hash queries, $q_{H_3}$ > 0 $H_3$ hash queries, $q_{H_4}$ > 0 $H_4$ hash queries, $q_K$ > 0 secret key queries, $q_{Enc}$ > 0 encryption queries, $q_{Dec}$ > 0 decryption queries, and $q_{Aut}$ > 0 authorization queries, let $\mathrm{Ad}{v}_{{\mathcal{A}}_2}^{\mathrm{IND}-CCA}$($\lambda$) represent the advantage of ${\mathcal{A}}_2$ in the following games. We will demonstrate the security proof through a series of games. □

Game 2.0:

1.

$pp\leftarrow \left(p,\mathbb{G},{\mathbb{G}}_T,\widehat{e},g\right)$, $\forall 1\le i\le n$, $(x_i,y_i)\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, sk${}_i$ = ($x_i,y_i$), pk${}_i$ = ($g^{x_i},g^{y_i}$), $s_1,s_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, gsk = (s${}_1$, s${}_2$), gpk${}_i$ = (g${}^{x_i{s}_1}$, g${}^{s_2}$), gtd = s${}_2$. H${}_1$, H${}_2$, H${}_3$, and H${}_4$ are random oracles. H-query. The challenger prepares four hash tables, to record and respond to queries:

${\mathcal{O}}_{H_1}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger randomly selects $u\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, computes $h_1=g^u\in \mathbb{G}$, saves ($v_1,u,h_1$) into $T_1$, and sends $h_1$ to ${\mathcal{A}}_2$;

${\mathcal{O}}_{H_2}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger chooses a compatible random value $h_2$, and saves ($v_1,h_2$) into $T_2$ for ${\mathcal{O}}_{H_2}$;

${\mathcal{O}}_{H_3}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger chooses a compatible value $h_3$ uniformly from the set ${\{0,1\}}^{l_1+l_2}$ that is returned, and saves ($v_1,h_3$) into $T_3$, for ${\mathcal{O}}_{H_3}$;

${\mathcal{O}}_{H_4}$ query $〈v_1〉:$ given a $v_1\in \mathbb{G}$, the challenger chooses a compatible value $h_4$ uniformly from the set ${\{0,1\}}^{\lambda }$ that is returned, and saves ($v_1,h_4$) into $T_4$, for ${\mathcal{O}}_{H_4}$;

2.

($M_0,M_1$) ← ${\mathcal{A}}_2^{O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}(PP,{\{p{k}_i,gp{k}_i\}}_{i=1}^n,gtd,i,j)$, where the oracles are simulated as follows:

${\mathcal{O}}_{Enc}$ query $〈i,j,M〉:$ input two indexes, i, j, and a plaintext M; the challenger runs $Enc$ algorithm, and returns $C_{i,j}$ = $Enc$($gp{k}_i,s{k}_i,p{k}_j,M$);

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉:$ input two indexes, i, j, and a ciphertext, $C_{i,j}$; the challenger runs a $Dec$ algorithm, and returns M = $Dec$($gp{k}_i,s{k}_j,C_{i,j}$).

3.

$b\stackrel{R}{\leftarrow }\{0,1\}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$ computes:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M_b)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=H_3(g^{x_{j^{*}}{\zeta }_2})\oplus \left(M_b\parallel g^{{\zeta }_1}\right),\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M_b\left|\right|g^{{\zeta }_1}).\end{array}$$

4.

$b^{\prime }\leftarrow {\mathcal{A}}_2^{O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}({\widehat{C}}_{i^{*},j^{*}})$. The constraints are that $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}$, and ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$.

Let $S_{2.0}$ denote the event $b^{\prime }=b$ in Game 2.0. Thus, the advantage of ${\mathcal{A}}_2$ is as follows:

$$\begin{array}{c}{\mathsf{Adv}}_{{\mathcal{A}}_2}^{\mathit{IND}-\mathit{CCA}}(q_{H_1},q_{H_2},q_{H_3},q_{H_4},q_{Key},q_{Enc},q_{Dec})\\ =|Pr\left[S_{2.0}\right]-1/2|\end{array}$$

Game 2.1: In this game, the performance of challenger is the same as in Game 2.0, except for the following:

1.

${\mathcal{O}}_{Enc}$ query $〈i,j,M〉:$ the challenger chooses two random values, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and returns a ciphertext, $C_{i,j}$, then computes

$$C_1=g^{\frac{x_i}{y_i}{s}_1{\zeta }_1},{\mathbb{C}}_3=g^{{\zeta }_2}.$$

It executes a query on ${\mathcal{O}}_{H_1}$ with input M to return $h_1$, a query on ${\mathcal{O}}_{H_2}$ with input $g^{s_2{\zeta }_2}$ to return $h_2$, and a query on ${\mathcal{O}}_{H_3}$ with input $g^{x_j{\zeta }_2}$ to return $h_3$; then, it computes

$$C_2=h_1^{\frac{x_i}{y_i}{\zeta }_1}·h_2,{\mathbb{C}}_4=h_3\oplus (M||g^{{\zeta }_1}),$$

and, finally, executes a query on ${\mathcal{O}}_{H_4}$, with input $(C_1|\left|C_2\right|\left|C_3\right|\left|C_4\right|\left|M\right||g^{{\zeta }_1})$ to return $h_4$, then sets: $C_5=h_4.$

The challenger saves ($v_1,h_1$), ($v_1,h_2$), ($v_1,h_3$), ($v_1,h_4$) to $T_1,T_2,T_3,T_4$, and returns $C_{i,j}$ to ${\mathcal{A}}_2.$

2.

$b\stackrel{R}{\leftarrow }\{0,1\}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $W^{*}\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$ computes:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W^{*}\oplus \left(M_b\parallel g^{{\zeta }_1}\right),\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M_b\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the tuple $(g^{x_{j^{*}}{\zeta }_2},W^{*})$ is saved into tables, $T_3$, for ${\mathcal{O}}_{H_3}$.

3.

$b^{\prime }\leftarrow {\mathcal{A}}_2^{O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}({\widehat{C}}_{i^{*},j^{*}})$. The constraints are that $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}$, and ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$.

• Let $S_{1.1}$ denote the event $b^{\prime }=b$ in Game 2.1. The idealness of the random oracle, Game 2.1, is the same as Game 1.0, and we have

$$\begin{array}{c}Pr\left[S_{2.1}\right]=Pr\left[S_{2.0}\right].\hfill \end{array}$$

(6)

• Game 2.2: in this game, the performance of the challenger is the same as in Game 2.1, except for the following:

1.

${\mathcal{O}}_{H_3}$ query $〈v_1〉:$ same as that in Game 2.1, except that if ${\mathcal{A}}_2$ asks ${({\widehat{C}}_3)}^{x_j^{*}}$, we denote this event by ${\mathbf{E}}_1$.

2.

${\mathcal{O}}_{Dec}query〈i,j,C_{i,j}〉:$ same as that in Game 2.1, except that if ${\mathcal{A}}_2$ asks the decryption of (${\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4^{\prime },{\widehat{C}}_5$) after receiving the challenge ciphertext ${\widehat{C}}_{i^{*},j^{*}}$, where ${{\widehat{C}}_4}^{\prime }\ne {\widehat{C}}_4$, the challenger sends ⊥ to ${\mathcal{A}}_2$.

3.

$b\stackrel{R}{\leftarrow }\{0,1\}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $W_{2.1}^{*}\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$, defined as follows:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·H_2(g^{s_2{\zeta }_2}),\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W_{2.1}^{*},\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M_b\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the tuple $(g^{x_{j^{*}}{\zeta }_2},W_{2.1}^{*}\oplus (M_b\left|\right|g^{{\zeta }_1})$ is saved into tables $T_3$.

Let S${}_{2.2}$ denote the event that $b=b^{\prime }$ in Game 2.2. The challenge ciphertext generated in Game 2.1 is identically distributed to that in Game 2.2, as ${\widehat{C}}_4$ is a random value in both Game 2.1 and Game 2.2; therefore, if event E${}_1$ does not happen, Game 1.2 is equal to Game 2.1, and we have

$$\begin{array}{c}Pr\left[{\mathbf{E}}_1\right]\le {\mathbf{Adv}}_{{\mathcal{A}}_2}^{\mathrm{CDH}}+q_D/2^{l_1+l_2}.\hfill \end{array}$$

(7)

Game 2.3: In this game, the performance of the challenger is the same as in Game 2.2, except for the following:

1.

$b\stackrel{R}{\leftarrow }\{0,1\}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $W_{3.1}^{*}\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, $W_{3.2}^{*}\stackrel{R}{\leftarrow }G$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$, defined as follows:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=H_1{(M)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1}·W_{3.2}^{*},\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W_{3.1}^{*},\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M_b\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the tuple $(g^{x_{j^{*}}{\zeta }_2},W_{3.1}^{*}\oplus (M_b\left|\right|g^{r_1}))$, $(g^{s_2{\zeta }_2},W_{3.2}^{*})$ is saved into table $T_3$, $T_2$.

Let $S_{2.3}$ denote the event $b^{\prime }=b$ in Game 2.3. Given the idealness of the random oracle, Game 2.3 is the same as Game 2.2, and we have

$$Pr\left[S_{2.3}\right]=Pr\left[S_{2.2}\right].$$

Game 2.4: In this game, the performance of the challenger is the same as in Game 2.3, except for the following:

1.

${\mathcal{O}}_{H_2}$ query $〈v_1〉:$ same as that in Game 2.3, except that if ${\mathcal{A}}_2$ asks ${({\widehat{C}}_3)}^{s_2}$, we denote this event by ${\mathbf{E}}_3$;

2.

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉:$ same as that in Game 2.3, except that if ${\mathcal{A}}_2$ asks the decryption of (${\widehat{C}}_1,{\widehat{C}}_2^{\prime },{\widehat{C}}_3,{\widehat{C}}_4^{\prime },{\widehat{C}}_5$) after receiving the challenge ciphertext ${\widehat{C}}_{i^{*},j^{*}}$, where ${\widehat{C}}_2^{\prime }\ne {\widehat{C}}_2$ and ${\widehat{C}}_4^{\prime }\ne {\widehat{C}}_4$, the challenger sends ⊥ to ${\mathcal{A}}_2$;

3.

$b\stackrel{R}{\leftarrow }\{0,1\}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, $W_{4.1}^{*}\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, $W_{4.2}^{*}\stackrel{R}{\leftarrow }G$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$, defined as follows:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2=W_{4.2}^{*},\\ {\widehat{C}}_3=g^{{\zeta }_2},{\widehat{C}}_4=W_{4.1}^{*},\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M_b\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the tuple $(g^{x_{j^{*}}{\zeta }_2},W_{4.1}^{*}\oplus (M_b\left|\right|g^{{\zeta }_1}))$, $(g^{s_2{\zeta }_2},W_{4.2}^{*}/H_1{(M_b)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1})$ is saved to table $T_3$, $T_2$.

Let S${}_{2.4}$ denote the event that $b=b^{\prime }$ in Game 2.4. The challenge ciphertext generated in Game 2.3 is equally distributed to that in Game 2.4, as $C_4^{*}$ is a random value in both Game 2.3 and Game 2.4; therefore, if event E${}_3$ does not happen, Game 2.4 is the same as Game 2.3, and we have

$$\begin{array}{c}\left|Pr\left[{\mathbf{S}}_{2.4}\right]-Pr\left[{\mathbf{S}}_{2.3}\right]\right|\le Pr\left[{\mathbf{E}}_3\right].\hfill \end{array}$$

(8)

Next, we show that the event (8) holds.

Lemma 2.

Event ${\mathit{E}}_3$ happens in Game 2.4 with negligible probability if the $\mathit{CDH}$ problem is intractable.

Proof. 

Suppose that Pr[E${}_3$] is non-negligible. We construct a PPT algorithm, ${\mathcal{B}}_2$, to break the CDH assumption. Given a tuple ($G,G_T,p,\widehat{e},g,g^{\alpha },g^{\beta }$), it runs ${\mathcal{A}}_2^{\prime }$, and works as follows. □

1.

${\mathcal{B}}_2$ sets PP = ($G,G_T,p,g,e$); it chooses two random values $(x_i,y_i)\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and sets $s{k}_i=(x_i,y_i)$, $p{k}_i=(g^{x_i},g^{y_i})$, $1\le i,j\le n$; it chooses a random value, $s_1\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, and sets $gsk=(s_1,\top )$, $gp{k}_i=(g^{x_i{s}_1},g^{\alpha })$, $1\le i,j\le n$, and gtd = ⊤. $H_1,H_2,H_3,H_4$ are four random oracles.

H-query. ${\mathcal{B}}_2$ prepares four hash tables to record and respond to queries, where all the hash tables are initialized to empty:

${\mathcal{O}}_{H_1}$ query $〈v_1〉$: same as that in Game 2.3;

${\mathcal{O}}_{H_2}$ query $〈v_1〉$: same as that in Game 2.3;

${\mathcal{O}}_{H_4}$ query $〈v_1〉$: same as that in Game 2.3;

${\mathcal{O}}_{H_3}$ query $〈v_1〉$: same as that in Game 2.3, except that ${\mathcal{A}}_2^{\prime }$ asks ${({\widehat{C}}_3)}^{s_2}=g^{\alpha \beta }$, and we denote this event by ${\mathbf{E}}_3^{\prime }$.

2.

state ← ${\mathcal{A}}_2^{\prime O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}(PP,{\{p{k}_i,gp{k}_i\}}_{i=1}^n,i^{*},j^{*})$, where the oracles are simulated as follows, and $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}$:

${\mathcal{O}}_{Key}$ query $〈i〉$: same as that in Game 2.3;

${\mathcal{O}}_{Enc}$ query $〈i,j,M〉$: same as that in Game 2.3;

${\mathcal{O}}_{Dec}$ query $〈i,j,C_{i,j}〉$: same as that in Game 2.3.

3.

$b\stackrel{R}{\leftarrow }\{0,1\}$, ${\zeta }_1,{\zeta }_2\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$, ${W_{4.1}^{*}}^{\prime }\stackrel{R}{\leftarrow }{\{0,1\}}^{l_1+l_2}$, ${W_{4.2}^{*}}^{\prime }\stackrel{R}{\leftarrow }G$, ${\widehat{C}}_{i^{*},j^{*}}=({\widehat{C}}_1,{\widehat{C}}_2,{\widehat{C}}_3,{\widehat{C}}_4,{\widehat{C}}_5)$, defined as follows:

$$\begin{array}{c}{\widehat{C}}_1=g^{\frac{x_{i^{*}}}{y_{i^{*}}}{s}_1{\zeta }_1},{\widehat{C}}_2={W_{4.2}^{*}}^{\prime },\\ {\widehat{C}}_3=g^{\beta },{\widehat{C}}_4={W_{4.1}^{*}}^{\prime },\\ {\widehat{C}}_5=H_4({\widehat{C}}_1\left|\right|{\widehat{C}}_2\left|\right|{\widehat{C}}_3\left|\right|{\widehat{C}}_4\left|\right|M_b\left|\right|g^{{\zeta }_1}).\end{array}$$

Finally, the tuple $({(g^c)}^{x_{j^{*}}},{W_{4.1}^{*}}^{\prime }\oplus (M_b\left|\right|g^{{\zeta }_1}))$ is saved into table $T_3$ for ${\mathcal{O}}_{H_3}$, and the tuple $(\top ,{W_{4.2}^{*}}^{\prime }/H_1{(M_b)}^{\frac{x_{i^{*}}}{y_{i^{*}}}{\zeta }_1})$ into table $T_2$ for ${\mathcal{O}}_{H_2}$.

4.

$b^{\prime }\leftarrow {\mathcal{A}}_2^{O_{H_1},O_{H_2},O_{H_3},O_{H_4},O_{Key},O_{Enc},O_{Dec}}({\widehat{C}}_{i^{*},j^{*}})$. The constraints are that $j^{*}$ cannot appear in ${\mathcal{O}}_{Key}$, and ($i^{*},j^{*},{\widehat{C}}_{i^{*},j^{*}}$) cannot appear in ${\mathcal{O}}_{Dec}$.

Indistinguishable simulation. Based on the setting of the simulation, the correctness and randomness of the simulation hold, and we have the following scenarios:

• $C_3^{\alpha }$ has been queried to ${\mathcal{O}}_{H_3}$ before decryption query is asked: in this case, $C_4$ is uniquely determined after $C_3^{\alpha }$ is queried to ${\mathcal{O}}_{H_3}$; then, the decryption oracle is perfectly simulated.
• $C_3^{\alpha }$ has never been queried to ${\mathcal{O}}_{H_3}$ when the decryption query is asked: in this case, ⊥ is returned by the decryption oracle if the simulation fails. The idealness of the random oracle happens with probability $1/p$.

${\mathbf{E}}_4$ denotes the event that a valid ciphertext is refused in the simulation: then we have $Pr\left[{\mathbf{E}}_4\right]\le q_D/p$, which is negligible, so that ${\mathcal{B}}_2$ executes the decryption simulation correctly, except with negligible probability. The simulation is indistinguishable from Game 2.4.

Probability of successful simulation. If the simulated game is not aborted, then the probability of successful simulation is 1.

Analysis. As ${\mathcal{A}}_2^{\prime }$ queries ${({\widehat{C}}_3)}^{\alpha }$ to ${\mathcal{O}}_{H_2}$ with probability $Pr\left[{\mathbf{E}}_3^{\prime }\right]$, then ${\mathcal{B}}_2$ is able to solve the CDH problem with probability $Pr\left[{\mathbf{E}}_3^{\prime }\right]$. We have $Pr\left[{\mathbf{E}}_3^{\prime }\right]$ = ${\mathbf{Adv}}_{\mathcal{A}}^{\mathrm{CDH}}$. In addition, if ${\mathbf{E}}_2$ does not occur, the simulated game is indistinguishable from Game 2.4. We have $Pr\left[{\mathbf{E}}_3^{\prime }\mid \neg {\mathbf{E}}_4\right]=Pr\left[{\mathbf{E}}_3\right].$

$$\begin{array}{cc}Pr\left[{\mathbf{E}}_3^{\prime }\right]\hfill & =Pr\left[{\mathbf{E}}_3^{\prime }\mid {\mathbf{E}}_4\right]Pr\left[{\mathbf{E}}_4\right]+Pr\left[{\mathbf{E}}_3^{\prime }\mid \neg {\mathbf{E}}_4\right]Pr\left[\neg {\mathbf{E}}_4\right]\hfill \\ & \ge Pr\left[{\mathbf{E}}_3^{\prime }\mid \neg {\mathbf{E}}_4\right]Pr\left[\neg {\mathbf{E}}_4\right]=Pr\left[{\mathbf{E}}_3\right]\left(1-Pr\left[{\mathbf{E}}_4\right]\right)\hfill \\ & \ge Pr\left[{\mathbf{E}}_3\right]-Pr\left[{\mathbf{E}}_4\right].\hfill \end{array}$$

Therefore, according to ${\mathbf{Adv}}_{\mathcal{A}}^{\mathrm{CDH}}\ge Pr\left[{\mathbf{E}}_1\right]-q_D/2^{l_1+l_2}$, we have

$$\begin{array}{c}Pr\left[{\mathbf{E}}_3\right]\le {\mathbf{Adv}}_{\mathcal{A}}^{\mathrm{CDH}}+q_D/p,\hfill \end{array}$$

(9)

which is negligible. This completes the proof of Lemma 2.

6. Comparison and Performance Evaluation

In this section, we compare the theoretical analysis of our scheme with four other schemes [13,16,19,20] and we analyze the performance evaluation of the scheme.

6.1. Comparison

We compare these schemes in terms of computational and storage overhead, and the data details are shown as follows. The computational cost of an exponentiation and a bilinear pairing operation are denoted by Exp and P, respectively. We show the efficiency comparison and security comparison in

Table 1. Comparison of Computational Cost.

Schemes	Enc	Dec	Test	Security
[13]	5Exp	3Exp	2P	OW-CCA
[19]	6Exp	5Exp	2P + 2Exp	OW/IND-CCA
[16]	1P + 5Exp	1P + 4Exp	4P + 2Exp	OW/IND-CCA
[20]	6Exp	5Exp	2P + (6n − 2)Exp	OW/IND-CCA
Ours	5Exp	1P + 2Exp	2P + 4Exp	OW/IND-CCA

.

According to Table 1, the computation cost in our scheme for Enc is 5Exp. Compared with [16,19,20], we have less computation cost. In the Dec phase, although the computation is slightly higher than other schemes, we need to do an integrity check on the message, when decrypting, to guarantee the security of the user data. Finally, the computation cost of the Test in our scheme is 2P + 4Exp lower than the scheme in [16]. In addition, regarding security, as with [16,19,20], our scheme also satisfies OW-CCA and IND-CCA against the adversary.

6.2. Performance Evaluation

To obtain the running time of the experiment in our scheme, we set up the following environment. The host operating system was Windows 10 for 64 bit, with an Intel(R) Core(TM) i7-10875H [email protected] GHz CPU and 16 GB RAM. Java 1.8 was the execution language. The public parameter data for the experiment was obtained from Charm. The cycle group G was based on a non-supersingular elliptic curve over a finite field with a 512-bit length prime number.

The experiment focused on evaluating the computing overheads, including encryption time, decryption time, and equality test time.

Figure 3 shows the relationship between the number of the encrypted file and the encryption time. Although it seemed to take longer to encrypt, we could use the offline encryption method, where some encryption steps that were not related could be computed beforehand. In this way, we could reduce the amount of time spent online. For this simulation experiment, we performed a rigorous linear fit to the data, and derived a value of linear K, K = 14.736.

Figure 4 shows the relationship between the size of the decryption file and the decryption time. As the recipient has to check the integrity of the encrypted data after retrieving it from the cloud server, to ensure that it has not been tampered with, it is inevitably more time-consuming than other solutions, but at the same time, we ensure the integrity of the user’s data, so that the medical staff can make an accurate diagnosis. For this simulation experiment, we performed a rigorous linear fit to the data, and derived a value of linear K, K = 4.04.

Figure 5 shows that the length of time for testing increased with the number of files. For this simulation experiment, we performed a rigorous linear fit to the data, and derived a value of linear K, K = 11.164.

7. Conclusions

In this paper, we propose the scheme named G-PKEET, to categorize patients’ EHRs without privacy leakage, and to prove the computational and performance efficiency of this scheme. Our scheme could apply to group scenarios: only a group trapdoor needs to be generated and authorized to the cloud server for the equality test. We undertook a security analysis. We proved that our scheme can resist a guessing attack not only from the storage server but also from the group administrator. A performance evaluation demonstrated our scheme’s lower overheads compared to other, related schemes. This paper combines G-PKEET with Smart Healthcare; in real life, we can also apply this technology to private set intersection (PSI), firewall filtering, mail system filtering, encrypted databases, etc.

Finally, users need to pay attention to the fact that the number of comparisons grew with the number of ciphertexts in the two-comparison test, and that it took a lot of time to compare a large number of ciphertexts. In the future, we will study how to use efficient batch equality testing to improve testing efficiency.