Authentication of Counterfeit Hundred Ringgit Malaysian Banknotes Using Fuzzy Graph Method
Abstract
:1. Introduction
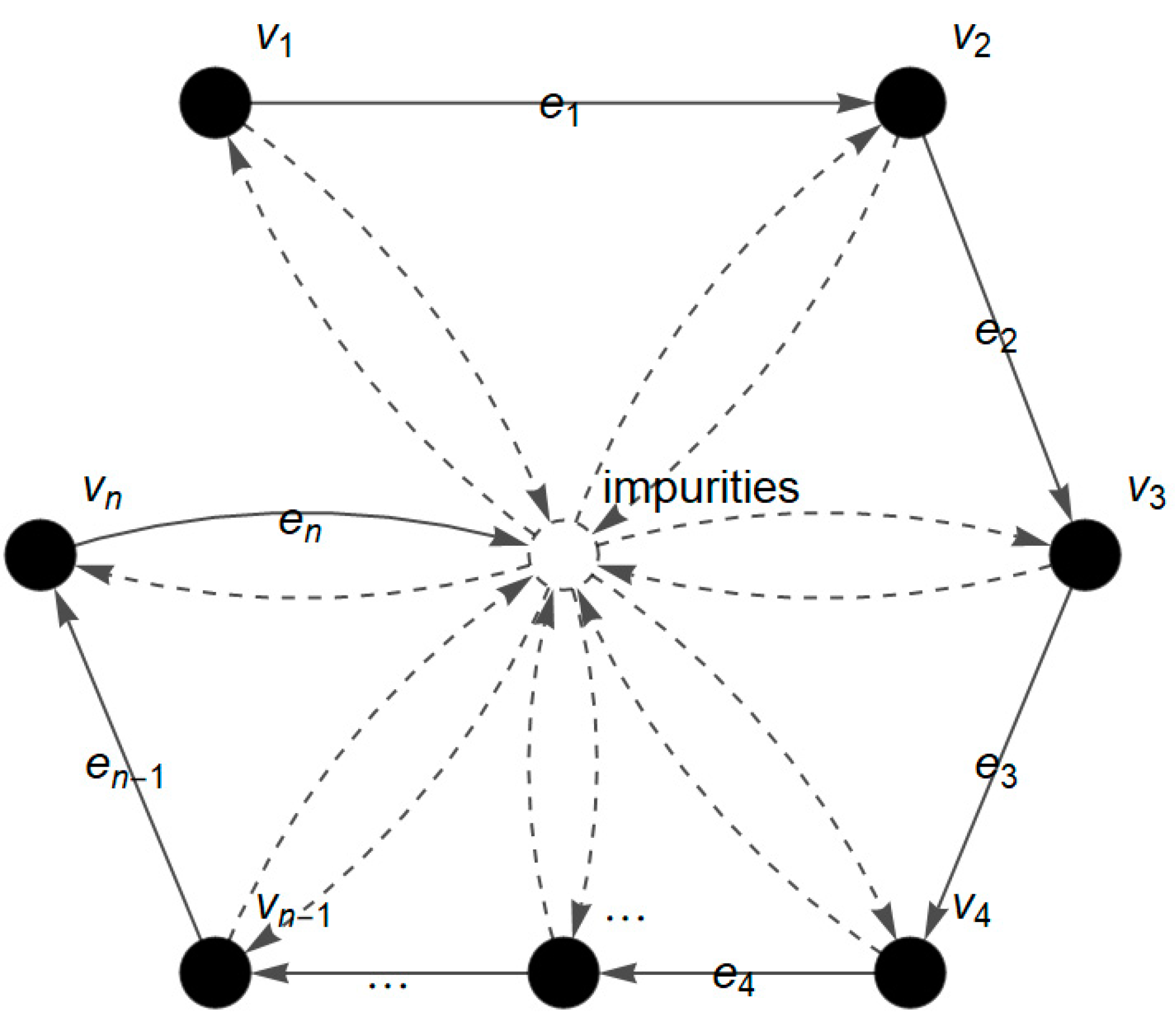
2. Definitions, Methods, and Algorithm
| Algorithm 1 The coordinated c-FACS algorithm |
|
3. Samples, Instrument, and Acquisition
4. Results and Discussion
4.1. FTIR Analysis
4.2. c-FACS Analysis
4.3. Principal Component Analysis (PCA)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spearlea, P.S.M. Economic and financial crime: Challenges for sustainable development. Soc. Econ. Debates 2021, 10, 56–63. [Google Scholar]
- Brici, I. New tendency of economic and financial crime in the context of digital age: Literature Review. DIEM Dubrov. Int. Econ. Meet. 2022, 7, 130–141. [Google Scholar] [CrossRef]
- Finlay, R.; Francis, A. A Brief History of Currency Counterfeiting; Reserve Bank of Australia Bulletin; Reserve Bank of Australia: Sydney, Australia, 2019; pp. 10–19. [Google Scholar]
- Williams, M.M.; Anderson, R.G. Currency Design in the United States and Abroad: Counterfeit Deterrence and Visual Accessibility. Rev.-Fed. Reserve Bank St. Louis 2007, 89, 371. [Google Scholar]
- Bruna, A.; Farinella, G.M.; Guarnera, G.C.; Battiato, S. Forgery detection and value identification of Euro banknotes. Sensors 2013, 13, 2515–2529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sonnex, E.; Almond, M.J.; Baum, J.V.; Bond, J.W. Identification of forged Bank of England £20 banknotes using IR spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 118, 1158–1163. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.S.; Das, P.P.; Roney, M.S.A. Image-Based Approach for the Detection of Counterfeit Banknotes of Bangladesh. In Proceedings of the 2016 5th International Conference on Informatics, Electronics, and Vision (ICIEV), Dhaka, Bangladesh, 3–14 May 2016. [Google Scholar]
- Baek, S.; Choi, E.; Baek, Y.; Lee, C. Detection of counterfeit banknotes using multispectral images. Digit. Signal Process. 2018, 78, 294–304. [Google Scholar] [CrossRef]
- Itrić, K.; Vukoje, M.; Banić, D. FT-IR Spectroscopy as a discrimination Method for establishing Authenticity of Euro Banknotes. Acta Graph. J. Print. Sci. Graph. Commun. 2018, 29, 27–30. [Google Scholar] [CrossRef] [Green Version]
- Ajid, N.F.D.; How, F.K.; Mahat, N.A.; Desa, W.N.S.M.; Kamaluddin, M.R.; Huri, M.A.M.; Maarof, H.; Ismail, D. Counterfeit one hundred Malaysian ringgit banknotes discrimination using chemical imaging inspection and pattern recognition. Aust. J. Forensic Sci. 2021, 54, 695–709. [Google Scholar] [CrossRef]
- Hassan, N.; Ahmad, T.; Mahat, N.A.; Maarof, H.; How, F.K. Counterfeit fifty Ringgit Malaysian banknotes authentication using novel graph-based chemometrics method. Sci. Rep. 2022, 12, 4826. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Singapore, 1996; Volume 6. [Google Scholar]
- Harary, F. Graph Theory; Addison Wesley Publishing Company: Berkeley, CA, USA, 1969. [Google Scholar]
- Jain, S.; Krishna, S. Autocatalytic Sets and the growth of complexity in an evolutionary model. Phys. Rev. Lett. 1998, 81, 5684–5687. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, T.; Baharun, S.; Arshad, K.A. Modeling a clinical incineration process using Fuzzy Autocatalytic Set. J. Math. Chem. 2010, 47, 1263–1273. [Google Scholar] [CrossRef]
- Ashaari, A.; Ahmad, T.; Mohamad, W.M.W. Transformation of Pressurized Water Reactor (AP1000) to Fuzzy Graph. MATEMATIKA 2018, 34, 235–244. [Google Scholar] [CrossRef] [Green Version]
- Hassan, N.; Ahmad, T.; Zain, N.M.; Awang, S.R. A Fuzzy Graph Based Chemometrics Method for Gelatin Authentication. Mathematics 2020, 8, 1969. [Google Scholar] [CrossRef]
- Hassan, N.; Ahmad, T.; Ashaari, A.; Awang, S.R.; Mamat, S.S.; Mohamad, W.M.W.; Fuad, A.A.A. A fuzzy graph approach analysis for COVID-19 outbreak. Results Phys. 2021, 25, 104267. [Google Scholar] [CrossRef] [PubMed]
- Livingstone, D.J. A Practical Guide to Scientific Data Analysis; John Wiley & Sons: West Sussex, UK, 2009. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, N.; Ahmad, T.; Mahat, N.A.; Maarof, H.; Abdullahi, M.; Ajid, N.F.D.; Jasmi, Z.S.; How, F.K. Authentication of Counterfeit Hundred Ringgit Malaysian Banknotes Using Fuzzy Graph Method. Mathematics 2023, 11, 1002. https://doi.org/10.3390/math11041002
Hassan N, Ahmad T, Mahat NA, Maarof H, Abdullahi M, Ajid NFD, Jasmi ZS, How FK. Authentication of Counterfeit Hundred Ringgit Malaysian Banknotes Using Fuzzy Graph Method. Mathematics. 2023; 11(4):1002. https://doi.org/10.3390/math11041002
Chicago/Turabian StyleHassan, Nurfarhana, Tahir Ahmad, Naji Arafat Mahat, Hasmerya Maarof, Mujahid Abdullahi, Nur Farah Dina Ajid, Zarith Sofia Jasmi, and Foo Keat How. 2023. "Authentication of Counterfeit Hundred Ringgit Malaysian Banknotes Using Fuzzy Graph Method" Mathematics 11, no. 4: 1002. https://doi.org/10.3390/math11041002
APA StyleHassan, N., Ahmad, T., Mahat, N. A., Maarof, H., Abdullahi, M., Ajid, N. F. D., Jasmi, Z. S., & How, F. K. (2023). Authentication of Counterfeit Hundred Ringgit Malaysian Banknotes Using Fuzzy Graph Method. Mathematics, 11(4), 1002. https://doi.org/10.3390/math11041002






