A 3D Numerical Study of the Surface Dielectric Barrier Discharge Initial Phase

Abstract

This study presents the results of the numerical modeling of surface dielectric barrier discharge in planar configuration with the strips active electrode. A positive half-period of the sinusoidal driving voltage and the two-species case is assumed in this study. Currently, many numerical models of surface dielectric barrier discharge deal with different electrode geometries, longer timescales, or discharge energizations. However, the main innovation presented in this study is developing a three-dimensional numerical model for the initial phase of the discharge phenomenon and a deeper focus on the numerical theory behind it. Based on the fluid model, this study presents a detailed mathematical and numerical formulation of the problem, stable numerical reconstruction of ion and electron velocity fields and an explanation of the need for linear approximation of ionization rate. Finally, it computes the potential and electric field distributions, electron and ion densities, and their velocities. The obtained results of a numerical simulation showing trajectories and velocities of electrons and ions reflect the active region of the discharge. A numerical simulation demonstrates the method in a three-dimensional domain inspired by a real-life experiment. The model can be used to optimize the electrode geometry of the discharge.

1. Introduction

The usage of surface dielectric barrier discharge (SDBD) [1] is on the rise in many applications, such as active particles, ozone, and ultraviolet generation [2], pollution control [3], surface treatment [4,5], plasma-chemical vapor deposition [6], in biological and chemical applications [7], and air-flow control [8,9]. Surface discharges are generated on the surface of a dielectric. Regarding the configuration of electrodes, two types of discharges are distinguished—surface barrier discharges and coplanar barrier discharges. Our attention was focused on surface dielectric barrier discharges. SDBD has been frequently studied within a planar experimental configuration [10], where an active electrode, cut out of a thin foil made of an electrically conductive material (copper, aluminum, stainless steel, special steel), connected to an alternating high voltage power supply system and serving as a high-voltage (active) electrode, is applied to one side of a planar dielectric plate (barrier) by means of screen printing, steaming, and dusting or, eventually, is glued by conductive glue. A grounded electrode, often made of the same material in an oblong or square shape and overlapping the active electrode surface by several mm, is located on the lower (opposite) side. The actual shape of the active electrode is usually selected in keeping with the purpose to be served by the designed generator of active particles and ozone (it can also be a source of ultraviolet irradiation). The configuration frequently features thin parallel strips, circles, and segments in the shape of a honeycomb, but it can also take the form of a mesh [11,12,13]. The recent articles offer a predominance of studies describing the origin and behavior of dielectric barrier discharge from an experimental point of view [14,15,16,17,18], while phenomena characterized by physical-mathematical models are treated less frequently [19,20,21,22,23,24]. The past few decades have seen the development of mathematical models describing—with a certain, smaller, or greater precision and success rate—the specific configuration of the phenomenon being modeled [25,26,27,28,29]. The authors of Refs. [14,17,30,31] classify such models into simplified (phenomenological) ones and first-principles ones that employ mathematical approaches to solving the given task. The category of simplified models comprises, for instance, Electrostatic models, Linearized force models, or Potential flow models. For their part, first-principles-based models include Kinetics models and Fluid models [21,32,33]. The latter ones, in particular, are the subject of our studies.

Our main goal is to expose the numerical theory to the community focused on the SDBD studies in much more detail than usual. In alignment with this particular chief objective, we will focus heavily on the proper formulation of the problem, the description of the critical issues, and the complications.

The presented mathematical model deals with the surface dielectric barrier discharge. Therefore, it should reflect the physics of the discharge. As long as our research is oriented toward the discharge generation of various active species such as ozone [34], the critical quantity which determines the efficiency of this generation is the dimension of the active volume in which the processes of species generation occur. In the case of SDBD, the discharge develops along the dielectric surface. At critical field strength, a set of microdischarges appears on the dielectric surface, which is accompanied by the luminosity of the discharge near the strip electrodes. This luminosity area and, consequently, the active discharge volume, do not cover the whole area of the dielectric. The physics of the discharge, leading to the formation of the active volume, is rather complex; therefore, we had to make essential simplifications. Thus, we restricted ourselves to the positive half-period of the driving voltage only, used only one type of positive ions-electrons model, and restricted ourselves to a time interval of $T=46$ ns. This assumption is associated with the processes of electron production from the electrodes. In the case of the strip electrode’s positive polarity, the photoemission current plays a decisive role. The ion emission current plays a minor role [35]. According to this paper, the photoemission starts after more than $T=15$ ns. In fact, for the negative polarity of the strip electrode, the photoemission current reaches a maximum at about $T=6$ ns. Thus, the photoemission and the ion emission from electrodes in the chosen simulation time interval can be neglected. Besides, this time interval limitation allows us to neglect the heating of electrodes, gas heating, and heat-related effects on electrodes and gas properties.

For the assumptions mentioned above, we present a numerical method based on the Finite Elements Method (FEM) and our results from the respective numerical experiment [34]. The experiment is implemented in a FEniCS environment (see fenicsproject.org, accessed on 15 January 2023), its mesh consisting of approximately 600,000 tetrahedrons generated in tetgen (see tetgen.org, accessed on 15 January 2023), using a predefined set of vertices [34].

Presently, a variety of models of the SDBD deal with complex chemistry, electrode geometries, and longer timescales. However, the main innovation presented in our paper is developing a 3D numerical model for the initial phase of the SDBD.

2. Introducing the Models

Let us start with the definition of mathematical models describing the physical entities that appear in the SDBD phenomena.

Since we present numerical results of an experiment motivated by a real-life experiment [34], we will restrict ourselves to a small extent and formulate the problem on a specific domain. Otherwise, we will try to keep the problem on a general level.

Thus, let $\Omega \subset {\mathbb{R}}^3$ be a bounded domain and $T>0$ a given time. We set $Q_T=\Omega \times [0,T]$ and by $\partial \Omega$, we denote the boundary of $\Omega$. Further, let $\Omega$ be a composition of two disjoint domains, $\Omega ={\Omega }_{Die}\cup {\Omega }_{Gas}$, and $\partial \Omega$ consist of several disjoint parts, $\partial \Omega ={\Gamma }_{Grnd}\cup {\Gamma }_{Walls}$, where ${\Gamma }_{Walls}={\Gamma }_{BottomWalls}\cup {\Gamma }_{TopWalls}$ (see Figure 1 and Figure 2 in Section 2). Next, let the interface between ${\Omega }_{Die}$ and ${\Omega }_{Gas}$ consist of two disjoint parts, $\partial {\Omega }_{Die}\cap \partial {\Omega }_{Gas}={\Gamma }_{GasToDie}\cup {\Gamma }_{Strip}$.

The SDBD Phenomena

The presented article uses a two-species model with electrons and one type of ions, notably for positive ions. Moreover, we restrict ourselves to the initial phase of the positive half-period of the applied voltage and neglect different ionic reactions.

Therefore, the definition of the model follows from Refs. [24,29,34,36,37,38]. Hence, we first model the relation between the electric field $\mathbf{E}:Q_T\to {\mathbb{R}}^3$ and the electric potential $\Phi :Q_T\to \mathbb{R}$ by means of the Poisson equation as follows

$$\begin{array}{c}\hfill \mathbf{E}=-\nabla \Phi \mathrm{in}{Q}_T,\end{array}$$

(1)

where ∇ represents the gradient with respect to the space variable. Further, we assume the electric potential to be decomposed into two parts: $\varphi :Q_T\to \mathbb{R}$ being induced by the external electric field and $\phi :{\Omega }_{Air}\times (0,T)\to \mathbb{R}$ being induced by the net charge density in the plasma, i.e., $\Phi =\varphi +\phi$ and

$$\begin{array}{cc}\hfill \nabla ·\left({\epsilon }_{Air}{\epsilon }_0\nabla \phi \right)& =-{\mathit{e}}_c({\mathit{n}}_{\mathit{e}}-{\mathit{n}}_{\mathit{i}})\mathrm{in}{\Omega }_{Air}\times (0,T),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \nabla ·\left({\epsilon }_r{\epsilon }_0\nabla \varphi \right)& =0\mathrm{in}{Q}_T,\hfill \end{array}$$

(3)

where ∇ represents the divergence operator, n_e$:{\Omega }_{Air}\times (0,T)\to \mathbb{R}$ denotes the electron density, n_i$:{\Omega }_{Air}\times (0,T)\to \mathbb{R}$ denotes the ion density, ${\epsilon }_0$ is the vacuum permittivity, ${\epsilon }_r$ is a piecewise constant function denoting the relative permittivity of air (${\epsilon }_r={\epsilon }_{Air}$ on ${\Omega }_{Air}$) and dielectric material (${\epsilon }_r={\epsilon }_{Die}$ on ${\Omega }_{Die}$) and ${\mathit{e}}_c$ is the elementary charge.

Further, the time evolution of electrons and ions concentrations are determined by the continuity equations where the ionic reactions are defined using the Townsend coefficients [39], i.e., the time evolution equations are described as follows

$$\begin{array}{cc}\hfill \frac{\partial {\mathit{n}}_{\mathit{i}}}{\partial t}+\nabla ·({\mathit{n}}_{\mathit{i}}{\mathbf{V}}_i)& =A{p}_{c}exp\{-\frac{B{p}_c}{∥\mathbf{E}∥}\}\Vert {\mathit{n}}_{\mathit{e}}{\mathbf{V}}_e\Vert -r_{i\leftrightarrow e}{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{e}}\hfill \end{array}$$

(4)

in ${\Omega }_{Air}\times (0,T)$.

Summing up, the used assumptions, including chosen simulation time interval, allowed us to write a continuity equation for electrons in the form of (5),

$$\begin{array}{cc}\hfill \frac{\partial {\mathit{n}}_{\mathit{e}}}{\partial t}+\nabla ·({\mathit{n}}_{\mathit{e}}{\mathbf{V}}_e)& =A{p}_{c}exp\{-\frac{B{p}_c}{∥\mathbf{E}∥}\}\Vert {\mathit{n}}_{\mathit{e}}{\mathbf{V}}_e\Vert -r_{i\leftrightarrow e}{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{e}},\hfill \end{array}$$

(5)

in ${\Omega }_{Air}\times (0,T)$, where ${\mathbf{V}}_i:{\Omega }_{Air}\times (0,T)\to {\mathbb{R}}^3$ is the ion velocity field, ${\mathbf{V}}_e:{\Omega }_{Air}\times (0,T)\to {\mathbb{R}}^3$ is the electron velocity field, $p_c$ is the constant air pressure, $r_{i\leftrightarrow e}$ denotes the electron-ion recombination rate, A and B are pre-exponential and exponential constants, respectively. For the sake of completeness, let us note that $\parallel ·\parallel$ represents the usual Euclidean norm.

Remark: Let us comment on the assumption of constant air pressure. Since we will work within a very small time range (≈ns), it seems reasonable to assume the air pressure to be constant. Although it is still by no means obvious that this simplification is insignificant, we are also not able to compute the approximate solution without this assumption as of yet.

Further, using the so-called Drift-Diffusive model (see Refs. [39,40]), we can rewrite the electronic and ionic fluxes as

$$\begin{array}{cc}\hfill {\mathit{n}}_{\mathit{i}}{\mathbf{V}}_i& ={\mathit{n}}_{\mathit{i}}{\mu }_i\mathbf{E}-D_i\nabla {\mathit{n}}_{\mathit{i}}\mathrm{in}{\Omega }_{Air}\times (0,T),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\mathit{n}}_{\mathit{e}}{\mathbf{V}}_e& =-{\mathit{n}}_{\mathit{e}}{\mu }_e\mathbf{E}-D_e\nabla {\mathit{n}}_{\mathit{e}}\mathrm{in}{\Omega }_{Air}\times (0,T),\hfill \end{array}$$

(7)

where ${\mu }_e$ and ${\mu }_i$ are the electron and ion mobility coefficients, respectively, and $D_e$ and $D_i$ are the electron and ion diffusion coefficients, respectively.

Now we observe that the numerical solution of Equation (3) can be computed independently of the remaining equations. Therefore, by substituting (1), (6), and (7) into (4) and (5) and using the results of (3), we can reduce the remaining equations to three scalar equations for three scalar unknowns $(\phi ,$n_i,n_e) and compute the remaining entities afterward. In total, we therefore, focus on finding a solution $\left(\varphi \right)$ of Equation (3) in $Q_T$ and solution $(\phi ,$n_i,n_e) for Equation (2) coupled with the following equations

$$\begin{array}{cc}\hfill \frac{\partial {\mathit{n}}_{\mathit{i}}}{\partial t}& +\nabla ·(-{\mathit{n}}_{\mathit{i}}{\mu }_i\nabla (\varphi +\phi )-D_i\nabla {\mathit{n}}_{\mathit{i}})\hfill \\ \hfill & =A{p}_{c}exp\{-\frac{B{p}_c}{∥\nabla (\varphi +\phi )∥}\}\Vert {\mathit{n}}_{\mathit{e}}{\mu }_e\nabla (\varphi +\phi )-D_e\nabla {\mathit{n}}_{\mathit{e}}\Vert \hfill \\ \hfill & -r_{i\leftrightarrow e}{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{e}}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \frac{\partial {\mathit{n}}_{\mathit{e}}}{\partial t}& +(\nabla ·{\mathit{n}}_{\mathit{e}}{\mu }_e\nabla (\varphi +\phi )-D_e\nabla {\mathit{n}}_{\mathit{e}})\hfill \\ \hfill & =A{p}_{c}exp\{-\frac{B{p}_c}{∥\nabla (\varphi +\phi )∥}\}\Vert {\mathit{n}}_{\mathit{e}}{\mu }_e\nabla (\varphi +\phi )-D_e\nabla {\mathit{n}}_{\mathit{e}}\Vert \hfill \\ \hfill & -r_{i\leftrightarrow e}{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{e}},\hfill \end{array}$$

(9)

in ${\Omega }_{Air}\times (0,T)$.

Thus, formulating the initial and boundary conditions for $\left(\varphi \right)$ and $(\phi ,$n_i,n_e) remains. We assume the following setting [34]

$$\begin{array}{cc}\hfill & \varphi (x,0)=0\mathrm{in}\Omega ,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & \varphi (x,t)=0\mathrm{on}{\Gamma }_{Grnd}\times (0,T),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \varphi (x,t)=U_{amp}sin\left(\omega t\right)=:{\varphi }_{Strip}(x,t)\mathrm{on}{\Gamma }_{Strip}\times (0,T)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \frac{\partial \varphi }{\partial \mathit{n}}(x,t)=0\mathrm{on}{\Gamma }_{Walls}\times (0,T)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \phi (x,0)=0,\mathrm{in}{\Omega }_{Air},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & \phi (x,t)=0\mathrm{on}{\Gamma }_{Strip}\times (0,T),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \frac{\partial \phi }{\partial \mathit{n}}(x,t)=0\mathrm{on}{\Gamma }_{TopWalls}\cup {\Gamma }_{AirToDie}\times (0,T),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\mathit{n}}_{\mathit{i}}(x,0)=n_i^0\left(x\right)\mathrm{in}{\Omega }_{Air},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & {\mathit{n}}_{\mathit{i}}(x,t)=0,\mathrm{on}{\Gamma }_{Strip}\times (0,T),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & \frac{\partial {\mathit{n}}_{\mathit{i}}}{\partial \mathit{n}}(x,t)=0\mathrm{on}{\Gamma }_{TopWalls}\cup {\Gamma }_{AirToDie}\times (0,T),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\mathit{n}}_{\mathit{e}}(x,0)=n_e^0\left(x\right)\mathrm{in}{\Omega }_{Air},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \frac{\partial {\mathit{n}}_{\mathit{e}}}{\partial \mathit{n}}(x,t)=0\mathrm{on}\partial {\Omega }_{Air}\times (0,T),\hfill \end{array}$$

(21)

where ${\varphi }_{Strip}:{\Gamma }_{Strip}\times (0,T)\to \mathbb{R}$ is an electric potential boundary function, $\mathit{n}$ denotes the outer unit normal vector to $\partial \Omega$, $n_i^0:{\Omega }_{Air}\to \mathbb{R}$ and $n_e^0:{\Omega }_{Air}\to \mathbb{R}$ is the initial ion density and electron density, respectively, $U_{Amp}$ is the discharge voltage, $\omega =2\pi f$ is the angular velocity, and f is the frequency.

Remark 1.

Let us comment on the boundary conditions for ions and electrons. Although there are several theories regarding a proper setting of boundary conditions for them [21,41], we prefer to assume the homogeneous Neumann condition on the whole boundary. An exception will be for the ${\Gamma }_{Strip}$ for ions, where it is clear and physically reasonable to assume a homogeneous Dirichlet condition for the positive half-period of the discharge. Since there is uncertainty in the proper setting of those boundary conditions, we instead implement the general condition even though, numerically, it brings worse stability to the computations.

3. Problem Formulation

In this section, we start with the process of partial non-dimensionalization and then introduce the weak formulations of the studied problems. The partial non-dimensionalization is motivated by better numerical stability due to the appropriate rescaling of the quantities we are simulating.

Non-Dimensionalization and Weak Formulations

Inspired by the non-dimensionalization scheme presented in Ref. [26], we introduce new variables and new dimensionless quantities as follows

$$\begin{array}{cc}\hfill \tau =\frac{t}{t_0},z_i& =\frac{x_i}{L},i=1,2,3,\hfill \\ \hfill {\mathit{N}}_{\mathit{e}}=\frac{{\mathit{n}}_{\mathit{e}}}{n_0},{\mathit{N}}_{\mathit{i}}& =\frac{{\mathit{n}}_{\mathit{i}}}{n_0},{\Phi }_{nd}=\frac{{\mathit{e}}_c}{k_B{T}_e}\Phi ,\hfill \end{array}$$

(22)

where $t_0$ is the reference time, L is the characteristic length, $n_0$ is the reference particle density, $k_B$ is the Boltzmann’s constant, and $T_e$ is the electron temperature.

Let us now define

$$\begin{array}{cc}\hfill {\mathcal{D}}^G& =\{\tilde{\varphi }\in H^1(\Omega ):\tilde{\varphi }=0\mathrm{on}{\Gamma }_{Grnd}\}\hfill \\ \hfill {\mathcal{D}}^{SG}& =\{\tilde{\varphi }\in H^1(\Omega ):\tilde{\varphi }=0\mathrm{on}{\Gamma }_{Strip}\cup {\Gamma }_{Grnd}\}\hfill \\ \hfill {\mathcal{D}}_{Air}^S& =\{\tilde{\phi }\in H^1\left({\Omega }_{Air}\right):\tilde{\varphi }=0\mathrm{on}{\Gamma }_{Strip}\}\hfill \end{array}$$

and assume there exists ${\varphi }_{Strip}^{*}\in \mathcal{C}(0,T;{\mathcal{D}}^G)$ such that ${\varphi }_{Strip}$ is its trace on ${\Gamma }_{Strip}\times (0,T)$. Now we are ready to introduce the weak formulation of the problem governed by Equation (3) and boundary conditions (10)–(13). Let us denote this weak formulation as (SDBD-0): Find $\varphi \in L^2(0,T;{\mathcal{D}}^G)$ so that it holds:

$$\begin{array}{cc}\hfill \varphi -\frac{{\mathit{e}}_c}{k_B{T}_e}{\varphi }_{Strip}^{*}& \in L^2(0,T;{\mathcal{D}}^{SG}),\hfill \\ \hfill a(\varphi ,\tilde{\varphi })& =0\mathrm{for}\mathrm{a}.\mathrm{e}.t\in (0,T),\forall \tilde{\varphi }\in {\mathcal{D}}^{SG},\hfill \\ \hfill \underset{t\to 0}{lim}{\parallel \varphi (·,t)\parallel }_{L^2(\Omega )}& =0,\hfill \end{array}$$

(23)

where

$$\begin{array}{cc}\hfill a(\varphi ,\tilde{\varphi })& ={\epsilon }_{Air}{\int }_{{\Omega }_{Air}}\nabla \varphi \nabla \tilde{\varphi }dx+{\epsilon }_{Die}{\int }_{{\Omega }_{Die}}\nabla \varphi \nabla \tilde{\varphi }dx.\hfill \end{array}$$

(24)

Further, let us also introduce the weak formulation to a problem governed by Equations (2), (8) and (9) and conditions (14)–(21). Let $\varphi \in L^2(0,T;{\mathcal{D}}^G)$ be a weak solution of problem (SDBD-0). We denote the weak formulation as (SDBD-1): Find $\phi \in L^2(0,T;{\mathcal{D}}_{Air}^S)$, N_i $\in L^2(0,T;{\mathcal{D}}_{Air}^S)$ and N_e $\in L^2(0,T;H^1\left({\Omega }_{Air}\right))$ such that for a.e. $t\in (0,T)$, ∀$\tilde{\phi }\in {\mathcal{D}}_{Air}^S$, ∀${\tilde{N}}_i\in {\mathcal{D}}_{Air}^S$ and ∀${\tilde{N}}_e\in {\mathcal{H}}^1\left({\Omega }_{Air}\right)$

$$\begin{array}{cc}\hfill a_{Air}(\phi ,\tilde{\phi })& =L({\mathit{N}}_{\mathit{i}},{\mathit{N}}_{\mathit{e}},\tilde{\phi }),\hfill \\ \hfill {\int }_{{\Omega }_{Air}}\frac{\partial {\mathit{N}}_{\mathit{i}}}{\partial \tau }{\tilde{N}}_{i}dx& +{\mu }_{i}c({\mathit{N}}_{\mathit{i}},\phi ,\varphi ,{\tilde{N}}_i)+D_{i}d({\mathit{N}}_{\mathit{i}},{\tilde{N}}_i)\hfill \\ \hfill & -f_e({\mathit{N}}_{\mathit{e}},\phi ,\varphi ,{\tilde{N}}_i)=R({\mathit{N}}_{\mathit{i}},{\mathit{N}}_{\mathit{e}},{\tilde{N}}_i),\hfill \\ \hfill {\int }_{{\Omega }_{Air}}\frac{\partial {\mathit{N}}_{\mathit{e}}}{\partial \tau }{\tilde{N}}_{e}dx& -{\mu }_{e}c({\mathit{N}}_{\mathit{e}},\phi ,\varphi ,{\tilde{N}}_e)+D_{e}d({\mathit{N}}_{\mathit{e}},{\tilde{N}}_e)\hfill \\ \hfill & -f_e({\mathit{N}}_{\mathit{e}},\phi ,\varphi ,{\tilde{N}}_e)=R({\mathit{N}}_{\mathit{i}},{\mathit{N}}_{\mathit{e}},{\tilde{N}}_e),\hfill \end{array}$$

(25)

and

$$\begin{array}{c}\hfill \underset{t\to 0}{lim}{\parallel \phi (·,t)\parallel }_{L^2\left({\Omega }_{Air}\right)}=0,\\ \hfill \underset{t\to 0}{lim}{\parallel {\mathit{N}}_{\mathit{i}}(·,t)-\frac{1}{n_0}{n}_i^0(·)\parallel }_{L^2\left({\Omega }_{Air}\right)}=0,\\ \hfill \underset{t\to 0}{lim}{\parallel {\mathit{N}}_{\mathit{e}}(·,t)-\frac{1}{n_0}{n}_e^0(·)\parallel }_{L^2\left({\Omega }_{Air}\right)}=0,\end{array}$$

where (for $N,\tilde{N}\in {\mathcal{H}}^1\left({\Omega }_{Air}\right)$)

$$\begin{array}{cc}\hfill a_{Air}(\phi ,\tilde{\phi })& ={\int }_{{\Omega }_{Air}}\nabla \phi \nabla \tilde{\phi }dx,\hfill \\ \hfill c(N,\phi ,\varphi ,\tilde{N})& =\frac{k_B{T}_e{t}_0}{{\mathit{e}}_{c}L}{\int }_{{\Omega }_{Air}}N(\nabla \phi +\nabla \varphi )\nabla \tilde{N}dx,\hfill \\ \hfill d(N,\tilde{N})& =\frac{t_0}{L}{\int }_{{\Omega }_{Air}}\nabla N\nabla \tilde{N}dx,\hfill \\ \hfill & ·\parallel \frac{{\mu }_i{k}_B{T}_e{t}_0}{{\mathit{e}}_{c}L}N(\nabla \phi +\nabla \varphi )+\frac{D_i{t}_0}{L}\nabla N\parallel ·\tilde{N}dx,\hfill \\ \hfill f_e(N,\phi ,\varphi ,q)& =A{p}_c{\int }_{{\Omega }_{Air}}exp\{-\frac{B{p}_c{\mathit{e}}_{c}L}{k_B{T}_e\parallel \nabla \phi +\nabla \varphi \parallel }\}\hfill \\ \hfill & ·\parallel \frac{{\mu }_e{k}_B{T}_e{t}_0}{{\mathit{e}}_{c}L}N(\nabla \phi +\nabla \varphi )-\frac{D_e{t}_0}{L}\nabla N\parallel ·\tilde{N}dx,\hfill \\ \hfill L({\mathit{N}}_{\mathit{i}},{\mathit{N}}_{\mathit{e}},\tilde{\phi })& =\frac{{\mathit{e}}_c^2{L}^2{n}_0}{{\epsilon }_{Die}{k}_B{T}_e}{\int }_{{\Omega }_{Air}}\tilde{\phi }({\mathit{N}}_{\mathit{i}}-{\mathit{N}}_{\mathit{e}})dx,\hfill \\ \hfill R({\mathit{N}}_{\mathit{i}},{\mathit{N}}_{\mathit{e}},\tilde{N})& =-r_{i\leftrightarrow e}{n}_0{t}_0{\int }_{{\Omega }_{Air}}\tilde{N}{\mathit{N}}_{\mathit{i}}{\mathit{N}}_{\mathit{e}}dx.\hfill \end{array}$$

4. Discretization

We suppose that the domain $\Omega$ is polyhedral with the Lipschitz boundary. By ${\mathcal{T}}_h$, we denote a regular partition of the domain $\Omega$, and by ${\mathcal{T}}_h^{Air}\subset {\mathcal{T}}_h$, we denote a regular partition of the domain ${\Omega }_{Air}$. Let us define

$$\begin{array}{cc}\hfill {\mathcal{D}}_h^G& =\{{\tilde{\varphi }}_h\in {\mathcal{D}}^G:{\tilde{\varphi }}_h{\mid }_K\in P_r\left(K\right),K\in {\mathcal{T}}_h\},\hfill \\ \hfill {\mathcal{D}}_h^{SG}& =\{{\tilde{\varphi }}_h\in {\mathcal{D}}^{SG}:{\tilde{\varphi }}_h{\mid }_K\in P_r\left(K\right),K\in {\mathcal{T}}_h\},\hfill \\ \hfill {\mathcal{D}}_{Air,h}^S& =\{{\tilde{N}}_h\in {\mathcal{D}}_{Air}^S:{\tilde{N}}_h{\mid }_K\in P_r\left(K\right),K\in {\mathcal{T}}_h^{Air}\},\hfill \\ \hfill {\mathcal{D}}_{Air,h}& =\{{\tilde{N}}_h\in H^1\left({\Omega }_{Air}\right):{\tilde{N}}_h{\mid }_K\in P_r\left(K\right),K\in {\mathcal{T}}_h^{Air}\},\hfill \\ \hfill {\mathit{L}}_h& =\{{\mathbf{E}}_h\in L^2{(\Omega )}^3:{\mathbf{E}}_h{\mid }_K\in P_{r-1}{\left(K\right)}^3,K\in {\mathcal{T}}_h\},\hfill \\ \hfill {\mathit{L}}_h^{Air}& =\{{\mathbf{V}}_h\in L^2{\left({\Omega }_{Air}\right)}^3:{\mathbf{V}}_h{\mid }_K\in P_{r-1}{\left(K\right)}^3,K\in {\mathcal{T}}_h^{Air}\},\hfill \end{array}$$

where $P_r\left(K\right)$, $P_s\left(K\right)$ and $P_q\left(K\right)$ denote the space of all polynomials on K of a degree less or equal to r, s and q, respectively. Moreover, we assume $r\ge 2$, $s\ge 1$ and $q\ge 1$.

For the time discretization of (SDBD-0) and (SDBD-1) we consider a uniform partition of the time interval $[0,T]$ formed by the time instants $t_j=j\Delta t$, $j=0,1,\dots ,j_{max}$, with a time step $\Delta t=T/j_{max}$.

4.1. Approximate Solution for (SDBD-0)

Let ${\mathit{g}}_h^j\in {\mathcal{D}}_h^G\approx U_{amp}sin\left(\omega t_j\right)$ on ${\Gamma }_{Strip}$, $j=0,\dots ,j_{max}$. We define the approximate solution of (SDBD-0) problem obtained by the Finite Elements Method as a set of functions ${\varphi }_h^j\in {\mathcal{D}}_h^G$, $j=0,\dots ,j_{max}$, satisfying

$$\begin{array}{cc}\hfill {\varphi }_h^j-{\mathit{g}}_h^j& \in {\mathcal{D}}_h^{SG}\forall j=0,\dots ,j_{max},\hfill \\ \hfill a({\varphi }_h^j,{\tilde{\varphi }}_h)& =0\forall j=0,\dots ,j_{max},\forall {\tilde{\varphi }}_h\in {\mathcal{D}}_h^{SG}\hfill \\ \hfill \parallel {\varphi }_h^0{\parallel }_{L^2(\Omega )}& =0.\hfill \end{array}$$

(26)

4.2. Approximate Solution for (SDBD-1)

Let ${\left\{{\varphi }_h^j\right\}}_{j=0}^{j_{max}}$ be an approximate solution of (SDBD-0). We define the approximate solution of the (SDBD-1) problem obtained by the BDF-2 method (BDF stands for Backward differentiation formula) and the Finite Elements Method as functions $({\phi }_h^j,$N_i${}_h^j,$N_e${}_h^j)\in {\mathcal{D}}_{Air,h}^S\times {\mathcal{D}}_{Air,h}^S\times {\mathcal{D}}_{Air,h}$, $j=0,\dots ,j_{max}$, satisfying for all $j=1,\dots ,j_{max}$

$$\begin{array}{cc}\hfill a_{Air}({\phi }_h^j,{\tilde{\phi }}_h)& =L({\mathit{N}}_{\mathit{e}}{}_h^j,{\mathit{N}}_{\mathit{i}}{}_h^j,{\tilde{\phi }}_h)\forall {\tilde{\phi }}_h\in {\mathcal{D}}_{Air,h}^S\hfill \\ \hfill \frac{1}{\Delta \tau }& {\int }_{{\Omega }_{Air}}({\mathit{N}}_{\mathit{i}}{}_h^j-\frac{4}{3}{\mathit{N}}_{\mathit{i}}{}_h^{j-1}+\frac{1}{3}{\mathit{N}}_{\mathit{i}}{}_h^{j-2}){\tilde{N}}_{i,h}dx\hfill \\ \hfill & =\frac{2}{3}{\mathbf{F}}_i({{\mathit{N}}_{\mathit{i}}}_h^j,{\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\mathit{N}}_{\mathit{i}}{}_h^{j-1},{\phi }_h^{j-1},{\varphi }_h^{j-1},{\tilde{N}}_{i,h})\hfill \\ \hfill & \forall {\tilde{N}}_{i,h}\in {\mathcal{D}}_{Air,h}^S,\hfill \\ \hfill \frac{1}{\Delta \tau }& {\int }_{{\Omega }_{Air}}({\mathit{N}}_{\mathit{e}}{}_h^j-\frac{4}{3}{\mathit{N}}_{\mathit{e}}{}_h^{j-1}+\frac{1}{3}{\mathit{N}}_{\mathit{e}}{}_h^{j-2}){\tilde{N}}_{e,h}dx\hfill \\ \hfill & =\frac{2}{3}{\mathbf{F}}_e({\mathit{N}}_{\mathit{i}}{}_h^j,{\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\mathit{N}}_{\mathit{e}}{}_h^{j-1},{\phi }_h^{j-1},{\varphi }_h^{j-1},{\tilde{N}}_{e,h})\hfill \\ \hfill & \forall {\tilde{N}}_{e,h}\in {\mathcal{D}}_{Air,h},\hfill \end{array}$$

(27)

where $\Delta \tau =\frac{\Delta t}{t_0}$, $({\phi }_h^0,$N_i${}_h^0,$N_e${}_h^0)$ and $({\phi }_h^{-1},$N_i${}_h^{-1},$N_e${}_h^{-1})$ are defined as the $L^2(\Omega )$ projections of the initial data $(0,\frac{n_i^0}{n_0},\frac{n_e^0}{n_0})$ and $(0,0,0)$, respectively, on ${\mathcal{D}}_{Air,h}^S\times {\mathcal{D}}_{Air,h}^S\times {\mathcal{D}}_{Air,h}$ and

$$\begin{array}{cc}\hfill {\mathbf{F}}_i({\mathit{N}}_{\mathit{i}}{}_h^j,& {\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\mathit{N}}_{\mathit{i}}{}_h^{j-1},{\phi }_h^{j-1},{\varphi }_h^{j-1},{\tilde{N}}_{i,h})\hfill \\ \hfill & ={\mu }_{i}c({\mathit{N}}_{\mathit{i}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\tilde{N}}_{i,h})-D_{i}d({\mathit{N}}_{\mathit{i}}{}_h^j,{\tilde{N}}_{i,h})\hfill \\ \hfill & +{\tilde{f}}_e({\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\mathit{N}}_{\mathit{e}}{}_h^{j-1},{\phi }_h^{j-1},{\varphi }_h^{j-1},{\tilde{N}}_{i,h})\hfill \\ \hfill & +R({\mathit{N}}_{\mathit{i}}{}_h^j,{\mathit{N}}_{\mathit{e}}{}_h^j,{\tilde{N}}_{i,h})\hfill \\ \hfill {\mathbf{F}}_e({\mathit{N}}_{\mathit{i}}{}_h^j,& {\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\mathit{N}}_{\mathit{e}}{}_h^{j-1},{\phi }_h^{j-1},{\varphi }_h^{j-1},{\tilde{N}}_{e,h})\hfill \\ \hfill & =-{\mu }_{e}c({\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\tilde{N}}_{e,h})-D_{e}d({\mathit{N}}_{\mathit{e}}{}_h^j,{\tilde{N}}_{e,h})\hfill \\ \hfill & +{\tilde{f}}_e({\mathit{N}}_{\mathit{e}}{}_h^j,{\phi }_h^j,{\varphi }_h^j,{\mathit{N}}_{\mathit{e}}{}_h^{j-1},{\phi }_h^{j-1},{\varphi }_h^{j-1},{\tilde{N}}_{e,h})\hfill \\ \hfill & +R({\mathit{N}}_{\mathit{i}}{}_h^j,{\mathit{N}}_{\mathit{e}}{}_h^j,{\tilde{N}}_{e,h})\hfill \end{array}$$

where ${\tilde{f}}_e$ is the linear approximation of $f_e$, defined in the following Section 4.2.

Linear Approximation of Ionization Rate

Even though it might seem that we should directly use the Newton method to solve the presented non-linear problem, we would rather introduce a linear approximation of ionization rate separately and with extra care. As we will show below, it is necessary to carefully treat the possibility of division by zero and problems with finite machine precision. Most importantly, identical problems have to be overcome even if we skip the linearization process and directly use the Newton method since the derivatives performed in the Newton method will introduce similar “controversial” terms.

Let us define the following operator f acting on ${\mathcal{D}}_{Air,h}\times {\mathcal{D}}_{Air,h}$

$$\begin{array}{cc}\hfill f({\phi }_h,N_h)& =\alpha exp\{-\frac{\beta }{\parallel \nabla {\phi }_h\parallel }\}\parallel \gamma N_h\nabla {\phi }_h-\delta \nabla N_h\parallel :\Omega \to \mathbb{R},\hfill \end{array}$$

(28)

where $\alpha ,\beta ,\gamma ,\delta$ are generic constants. It is obvious that $f({\phi }_h,N_h)$ is not defined on set $\Theta =\{\mathit{x}\in {\Omega }_{Air}:\parallel \nabla {\phi }_h\left(x\right)\parallel =0\}$ for given ${\phi }_h\in {\mathcal{D}}_{Air,h}$. Nevertheless, we can set $f({\phi }_h,N_h)\equiv 0$ on $\Theta$ and then for such $f({\phi }_h,N_h)$ holds that $f({\phi }_h,N_h)\in \mathcal{C}\left({\Omega }_{Air}\right)$.

Now, we present the linearization of the operator (28) for any $({\phi }_h,N_h)\in {\mathcal{D}}_{Air,h}\times {\mathcal{D}}_{Air,h}$ from which one can easily deduce the linear approximation of ionization rate.

Let ${\overrightarrow{\psi }}_h={\left\{{\psi }_h^i\right\}}_{i=1}^{m_d}$ be the basis of space ${\mathcal{D}}_{Air,h}$, $m_d=dim\left({\mathcal{D}}_{Air,h}\right)$. Now, any ${\phi }_h\in {\mathcal{D}}_{Air,h}$ can be uniquely represented as ${\phi }_h=\overrightarrow{\Psi }·{\overrightarrow{\psi }}_h={\sum }_{i=1}^{m_d}{\Psi }_i{\psi }_h^i$, where $\overrightarrow{\Psi }\in {\mathbb{R}}^{m_d}$.

Consequently, operator f can be understood as an operator acting on ${\mathbb{R}}^{m_d}\times {\mathbb{R}}^{m_d}$, i.e.,

$$\begin{array}{cc}\hfill & f({\phi }_h,N_h)=f({\overrightarrow{\Psi }}_{\phi },{\overrightarrow{\Psi }}_N)\hfill \\ \hfill & =\alpha exp\{-\frac{\beta }{\parallel {\overrightarrow{\Psi }}_{\phi }·\nabla {\overrightarrow{\psi }}_h\parallel }\}\parallel \gamma {\overrightarrow{\Psi }}_N·{\overrightarrow{\psi }}_h{\overrightarrow{\Psi }}_{\phi }·\nabla {\overrightarrow{\psi }}_h-\delta {\overrightarrow{\Psi }}_N·\nabla {\overrightarrow{\psi }}_h\parallel \hfill \end{array}$$

Using the Taylor series, we introduce a linear approximation of $f({\overrightarrow{\Psi }}_{\phi },{\overrightarrow{\Psi }}_N)$ near point $({\overrightarrow{\Psi }}_{\phi }^0,{\overrightarrow{\Psi }}_N^0)\in ({\mathbb{R}}^{m_d}\times {\mathbb{R}}^{m_d})$ as follows

$$\begin{array}{cc}\hfill f({\overrightarrow{\Psi }}_{\phi },{\overrightarrow{\Psi }}_N)\approx f({\overrightarrow{\Psi }}_{\phi }^0,{\overrightarrow{\Psi }}_N^0)& +\frac{\partial f}{\partial {\overrightarrow{\Psi }}_{\phi }}({\overrightarrow{\Psi }}_{\phi }^0,{\overrightarrow{\Psi }}_N^0)·({\overrightarrow{\Psi }}_{\phi }-{\overrightarrow{\Psi }}_{\phi }^0)\hfill \\ \hfill & +\frac{\partial f}{\partial {\overrightarrow{\Psi }}_N}({\overrightarrow{\Psi }}_{\phi }^0,{\overrightarrow{\Psi }}_N^0)·({\overrightarrow{\Psi }}_N-{\overrightarrow{\Psi }}_N^0),\hfill \end{array}$$

where using marking $\mathbb{J}=\gamma {\overrightarrow{\Psi }}_N^0{\overrightarrow{\psi }}_h{\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h-\delta {\overrightarrow{\Psi }}_N^0\nabla {\overrightarrow{\psi }}_h$

$$\begin{array}{cc}\hfill \frac{\partial f}{\partial {\overrightarrow{\Psi }}_{\phi }}({\overrightarrow{\Psi }}_{\phi }^0,{\overrightarrow{\Psi }}_N^0)& =\nabla {\overrightarrow{\psi }}_h\left[\alpha exp\{-\frac{\beta }{\parallel {\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h\parallel }\}\gamma {\overrightarrow{\Psi }}_N^0{\overrightarrow{\psi }}_h\frac{\mathbb{J}}{2\parallel \mathbb{J}\parallel }\right.\hfill \\ \hfill & \left.+\parallel \mathbb{J}\parallel \beta exp\{-\frac{\beta }{\parallel {\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h\parallel }\}\frac{{\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h}{2\parallel {\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h{\parallel }^3}\right]\hfill \\ \hfill \frac{\partial f}{\partial {\overrightarrow{\Psi }}_N}({\overrightarrow{\Psi }}_{\phi }^0,{\overrightarrow{\Psi }}_N^0)& =\left[\alpha exp\{-\frac{\beta }{\parallel {\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h\parallel }\}\frac{\mathbb{J}}{2\parallel \mathbb{J}\parallel }\right]\hfill \\ \hfill & ·\left(\gamma {\overrightarrow{\Psi }}_{\phi }^0\nabla {\overrightarrow{\psi }}_h·{\overrightarrow{\psi }}_h-\delta \nabla {\overrightarrow{\psi }}_h\right),\hfill \end{array}$$

under the assumption that every term on the right-hand side makes sense.

Here, we can observe that we should take care of possible divisions by zero and potential problems introduced by the machine precision limitations, as mentioned earlier.

Let us now switch back to the equivalent representation of operator f by (28). We finally present the approximation of f at the point $({\phi }_h,N_h)\in {\mathcal{D}}_{Air,h}\times {\mathcal{D}}_{Air,h}$ near point $({\phi }_h^0,N_h^0)\in {\mathcal{D}}_{Air,h}\times {\mathcal{D}}_{Air,h}$

$$\begin{array}{cc}\hfill f({\phi }_h,N_h)& \approx \tilde{f}({\phi }_h,N_h,{\phi }_h^0,N_h^0)\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & ={\tilde{f}}_{00}({\phi }_h^0,N_h^0)+{\tilde{f}}_{10}({\phi }_h^0,N_h^0)·\nabla ({\phi }_h-{\phi }_h^0)\hfill \\ \hfill & +{\tilde{f}}_{01}({\phi }_h^0,N_h^0)·\left[\gamma \nabla {\phi }_h^0(N_h-N_h^0)-\delta \nabla (N_h-N_h^0)\right],\hfill \end{array}$$

(30)

where using marking $\mathbb{K}=\gamma N_h^0\nabla {\phi }_h^0-\delta \nabla N_h^0$

$$\begin{array}{cc}\hfill {\tilde{f}}_{00}({\phi }_h^0,N_h^0)& =0,\mathrm{if}\parallel \nabla {\phi }_h^0\parallel <\frac{{10}^{-2}}{\beta },\hfill \\ \hfill & =\alpha exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\parallel \mathbb{K}\parallel ,\mathrm{else}\hfill \\ \hfill {\tilde{f}}_{10}({\phi }_h^0,N_h^0)& =0,\mathrm{if}\parallel \nabla {\phi }_h^0\parallel <\frac{{10}^{-2}}{\beta },\hfill \\ \hfill & =\parallel \mathbb{K}\parallel \beta exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\frac{\nabla {\phi }_h^0}{2\parallel \nabla {\phi }_h^0{\parallel }^3},\hfill \\ \hfill & \mathrm{if}\parallel \nabla {\phi }_h^0\parallel \ge \frac{{10}^{-2}}{\beta },\parallel \mathbb{K}\parallel <\frac{1}{2}\alpha \gamma exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\hfill \\ \hfill & =\alpha exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\gamma N_h^0\frac{\mathbb{K}}{2\parallel \mathbb{K}\parallel }\hfill \\ \hfill & +\parallel \mathbb{K}\parallel \beta exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\frac{\nabla {\phi }_h^0}{2\parallel \nabla {\phi }_h^0{\parallel }^3},\mathrm{else}\hfill \\ \hfill {\tilde{f}}_{01}({\phi }_h^0,N_h^0)& =0,\hfill \\ \hfill & \mathrm{if}\parallel \nabla {\phi }_h^0\parallel <\frac{{10}^{-2}}{\beta }\mathrm{or}\parallel \mathbb{K}\parallel <\frac{1}{2}\alpha exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\hfill \\ \hfill & =\alpha exp\{-\frac{\beta }{\parallel \nabla {\phi }_h^0\parallel }\}\frac{\gamma N_h^0\nabla {\phi }_h^0-\delta \nabla N_h^0}{2\parallel \gamma N_h^0\nabla {\phi }_h^0-\delta \nabla N_h^0\parallel },\mathrm{else}.\hfill \end{array}$$

It is clear that $\tilde{f}$ is linear. Taking here ${\phi }_h^j+{\varphi }_h^j$ instead of ${\phi }_h$, N_e ${}_h^j$ instead of $N_h$, ${\phi }_h^{j-1}+{\varphi }_h^{j-1}$ instead of ${\phi }_h^0$, N_e ${}_h^{j-1}$ instead of $N_h^0$ and by proper choice of $\alpha ,\beta ,\gamma$ and $\delta$, one easily gets the linear approximation of the ionization rate.

4.3. The Reconstruction of $\mathbf{E}$, ${\mathbf{V}}_i$ and ${\mathbf{V}}_e$

In order to reconstruct the entities $\mathbf{E}$, ${\mathbf{V}}_i$ and ${\mathbf{V}}_e$, we use Equations (1), (6) and (7), respectively. First, we define the approximate solution to (1) as a projection of $(\nabla ({\varphi }_h^j+{\phi }_h^j))$ on ${\mathit{L}}_h$, i.e., as a function ${\mathbf{E}}_h^j\in {\mathit{L}}_h$, $j=0,\dots ,j_{max}$, satisfying for all ${\tilde{\mathbf{E}}}_h\in {\mathit{L}}_h$

$$\begin{array}{c}\hfill {\int }_{\Omega }{\mathbf{E}}_h^j{\tilde{\mathbf{E}}}_{h}dx=-\frac{k_B{T}_e}{{\mathit{e}}_{c}L}({\int }_{\Omega }\nabla {\varphi }_h^j{\tilde{\mathbf{E}}}_{h}dx+{\int }_{{\Omega }_{Air}}\nabla {\phi }_h^j{\tilde{\mathbf{E}}}_{h}dx),\end{array}$$

where ${\varphi }_h^j$ is the approximate solution of (SDBD-0) and ${\phi }_h^j$ is the first component of the approximate solution of (SDBD-1).

Now, the reconstruction of ${\mathbf{V}}_i$ and ${\mathbf{V}}_e$ has to be more cautious. Since the precomputed particle densities N_i ${}_h^j$ and N_e ${}_h^j$ may be of zero value, Equations (6) and (7) become meaningless at some parts of the domain (there might be no particles to track). To make the method worse, since we work within computer arithmetic, the values might not be equal to zero but just close to the machine epsilon. This may lead to absurd values of particle velocities.

Therefore, we employ a simple heuristic: “where there are a few particles, there is no movement”. We define a minimal amount of particle coefficient $N_{min}$. Further, we define the approximate solution to (6) as a function ${\mathbf{V}}_i^{hj}\in {\mathit{L}}_h^{Air}$, $j=0,\dots ,j_{max}$, satisfying for all ${\tilde{\mathbf{E}}}_h\in {\mathit{L}}_h^{Air}$ and for all $K\in {\mathcal{T}}_h^{Air}$

$$\begin{array}{cc}\hfill {\int }_K{\mathbf{V}}_i^{hj}{\tilde{\mathbf{E}}}_{h}dx& ={\int }_K\left({\mu }_i{\mathbf{E}}_h^j-\frac{D_i}{L}(\nabla \right.{\mathit{N}}_{\mathit{i}}{}_h^j/{\mathit{N}}_{\mathit{i}}{}_h^j){\tilde{\mathbf{E}}}_{h}dx,\hfill \\ \hfill & \mathrm{if}{\int }_K{\mathit{N}}_{\mathit{i}}{}_h^{j}dx>N_{min}\hfill \\ \hfill & =0,\hfill \\ \hfill & \mathrm{if}{\int }_K{\mathit{N}}_{\mathit{i}}{}_h^{j}dx<=N_{min}.\hfill \end{array}$$

Analogously, we define the approximate solution to (7) as the function ${\mathbf{V}}_e^{hj}\in L_h^{Air}$, $j=0,\dots ,j_{max}$.

5. Numerical Scheme

As stated in the introduction, we carried out the implementation in FEniCS environment, and we will describe the numerical scheme using pseudocode based on FEniCS libraries.

We start by describing the numerical solution (SDBD-0) and (SDBD-1). First, let us note that all the presented discrete problems are equivalent to a system of linear algebraic equations.

SDBD-0

We use the FEniCS in-built GMRES (Generalized Minimal RESidual) iteration method with ILU preconditioner to solve the system of linear algebraic equations. The absolute convergence criterion (based on the norm of residuum) for GMRES is set to ${10}^{-9}$ with a maximum of 200 iterations [34].

SDBD-1

We use a similar setting as for (SDBD-0), i.e., we use the FEniCS in-built GMRES iteration method with ILU preconditioner with the same criterion settings.

Reconstructions

Using the FEniCS method project (from dolfin.fem.projection), we implement the reconstruction algorithms and obtain approximative solutions.

Pseudocode of the Main Scheme

Now the main algorithm scheme is as follows:

${\mathrm{timestamp}}_{\mathrm{SDBD}}=\Delta \tau$

while ${\mathrm{timestamp}}_{\mathrm{SDBD}}\le T$:

Solve (SDBD-0) at ${\mathrm{timestamp}}_{\mathrm{SDBD}}$

Compute coefficients for ${\tilde{f}}_e$

Solve (SDBD-1) at ${\mathrm{timestamp}}_{\mathrm{SDBD}}$

Compute reconstructions at ${\mathrm{timestamp}}_{\mathrm{SDBD}}$

${\mathrm{timestamp}}_{\mathrm{SDBD}}+=\Delta \tau$

6. Numerical Experiment Simulation

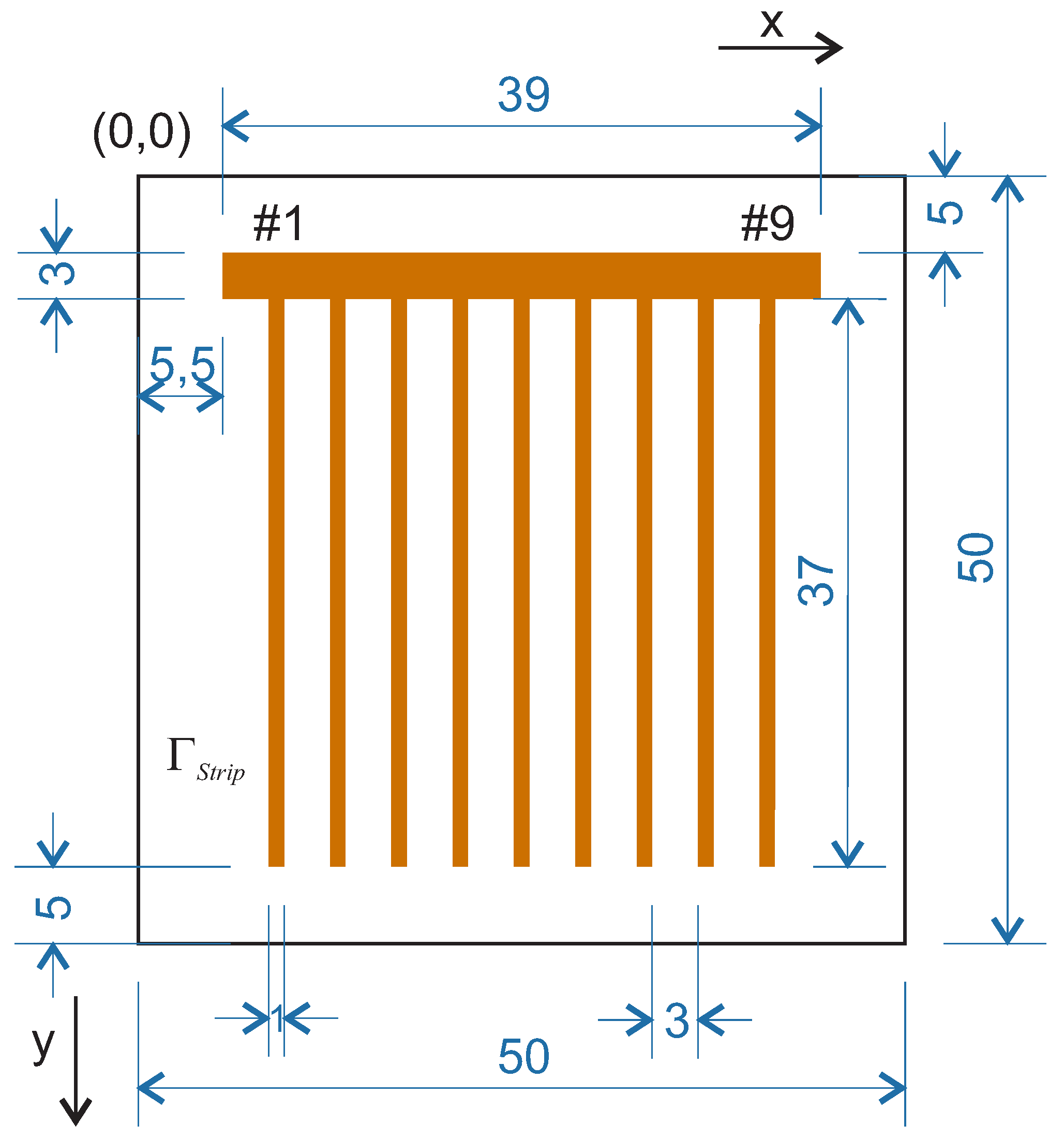
Let us start with the definition of the domain $\Omega$ and its mesh. Note that we use the meter as a unit for distance in the following definitions.

The domain $\Omega$ is defined as a cuboid. In particular, $\Omega =\{\mathit{x}\in {\mathbb{R}}^3:x_1\in (0,0.05),x_2\in (0,0.05),x_3\in (0,0.005715)\}$, i.e., $\Omega$ is an open cuboid of the size $50\times 50\times 5.715$ mm. Next, ${\Omega }_{Air}=\{\mathit{x}\in {\mathbb{R}}^3:x_1\in (0,0.05),x_2\in (0,0.05),x_3\in (0.000635,0.005715)\}$ and ${\Omega }_{Die}=\{\mathit{x}\in {\mathbb{R}}^3:x_1\in (0,0.05),x_2\in (0,0.05),x_3\in (0,0.000635)\}$. Further, ${\Gamma }_{Strip}=\{\mathit{x}\in {\mathbb{R}}^3:(x_1,x_2)\in {\mathbf{S}}_{xy},x_3=0.000635\}$, where ${\mathbf{S}}_{xy}\subset {\mathbb{R}}^2$ is a closed set, defined in Figure 1 as the orange area.

Furthermore, ${\Gamma }_{Grnd}=\{\mathit{x}\in {\mathbb{R}}^3:(x_1,x_2)\in {\mathbf{G}}_{xy},x_3=0\}$, where ${\mathbf{G}}_{xy}\subset {\mathbb{R}}^2$ is a closed set, defined in Figure 2 as the orange area.

Finally, with the help of Figure 3 and Figure 4, we define the remaining parts of boundaries as ${\Gamma }_{AirToDie}=(\partial {\Omega }_{Air}\cap {\Omega }_{Die})\backslash {\Gamma }_{Strip}$ (light grey color), ${\Gamma }_{BottomWalls}=\partial {\Omega }_{Die}\backslash (\partial {\Omega }_{Air}\cup {\Gamma }_{Grnd})$ (dark purple color,) and ${\Gamma }_{TopWalls}=\partial {\Omega }_{Air}\backslash (\partial {\Omega }_{Die})$ (green color).

Further, the mesh consists of approximately $\mathrm{600,000}$ tetrahedrons [34]. It was generated in tetgen (see tetgen.org) using a predefined set of vertices. The predefined set of vertices divides the domain into cubes adaptively refined near electrodes (${\Gamma }_{Strip}$ and ${\Gamma }_{Grnd}$). There are four levels of refinement, and the smallest cube is of the size $0.00025\times 0.00025\times 0.0003175$ m, i.e., $0.25\times 0.25\times 0.3175$ mm.

Now we proceed to the parameters settings. We first specify the physical coefficients. Hence, we set the vacuum permittivity ${\epsilon }_0=8.85\times {10}^{-12}$ Fm${}^{-1}$, the air permittivity coefficient ${\epsilon }_{Air}=1.0006$, the dielectric permittivity coefficient ${\epsilon }_{Die}=9.6$, the elementary charge $e_c=1.6022\times {10}^{-19}$ C, and the exponential and pre-exponential coefficients are set to $A=1.5\times {10}^3$ m${}^{-1}$torr${}^{-1}$ and $B=3.56\times {10}^4$ V m${}^{-1}$torr${}^{-1}$, respectively.

Furthermore, we set the ion and electron mobility coefficients ${\mu }_i=0.145/\pi$ m${}^2$s${}^{-1}$V${}^{-1}$ and ${\mu }_e=44/\pi$ m${}^2$s${}^{-1}$V${}^{-1}$, respectively, the ion and electron diffusion coefficients $D_i=(k_B/e_c)T_i{\mu }_i$ m${}^2$s${}^{-1}$ and $D_e=(k_B/e_c)T_e{\mu }_e$ m${}^2$s${}^{-1}$, respectively, Boltzmann’s constant is $k_B=1.3806488\times {10}^{-23}$ m${}^2$kgs${}^{-2}$K${}^{-1}$, the ion and electron temperature $T_i=300$ K and $T_e=$ 60,000 K, respectively, the reference particle density $n_0=2\times {10}^{15}$ m${}^{-3}$. Further, we define the initial ion/electron particle densities $n_i^0\left(x\right)=n_e^0\left(x\right)=n_0$ and set $U_{amp}=3000$ V, $\omega =2\pi f$ and $f=10.9\times {10}^3$ Hz. Moreover, we choose the reference time $t_0=1/\omega$ s, the characteristic length $L=0.05$ m, and the characteristic velocity $V_0=1\times {10}^{-6}$ ms${}^{-1}$.

Finally, the degrees of polynomial approximations are set to $r=2$, $s=2$ and $q=1$, respectively. The problem is solved for $T=\frac{1}{2f}\times {10}^{-3}$ s, i.e., $T\approx 46$ ns, with time step $\Delta \tau =0.1$ ns, i.e., $j_{max}=460$. The minimal amount of particles coefficient is set to $N_{min}=10$.

The Results

The presented experiment took about a day on a standard personal computer. In the following, we present the visualization of several key numerical simulation results using the open-source software ParaView (see https://www.paraview.org/, accessed on 15 January 2023).

Firstly, we show the top view of the difference in ions and electrons densities $n_i-n_e$ at various instants of time close to the tip of the strips; see Figure 5, Figure 6, Figure 7 and Figure 8. These figures show that close to the strip electrode, the density of electrons exceeds the density of positive ions. On the other hand, the situation is the opposite, farther from the strip electrode. This conclusion agrees with the results presented in Ref. [24], and our analysis is for the positive half-period of the driving voltage.

Depending on the discharge conditions, the lifetime of the microdischarges ranges to several tens of nanoseconds, which is why we used for our numerical experiment the time scale $T=46$ ns [35]. The distribution of electron density is narrower than that of the positive ions. This outcome agrees with the results presented in Figure 5, Figure 6, Figure 7 and Figure 8.

Secondly, in Figure 9, Figure 10, Figure 11 and Figure 12, we show the trajectories of electrons and ions at two instants of time, $T=18$ ns and $T=46$ ns, with the corresponding $V_i$ and $V_e$ velocities. The color of the individual parts of the trajectories expresses the magnitude of the velocity. For better readability, only trajectories between two neighboring strips are shown close to their tips. It should be pointed out that these trajectories represent the situation in the initial phase of the positive half-period of the driving voltage only. From the comparison of the trajectories of electrons and ions, it can be concluded that the electrons do not extend as much from the edge of the strips as the ions.

This trajectory of these particles could be associated with the luminous region around the strip electrode, which represents the active volume of the discharge. Therefore, this result could be used to optimize the distance among neighboring strips. This would have a strong impact on the design of the electrode system.

7. Conclusions

We developed a 3D numerical model for the initial phase of the surface dielectric barrier discharge in planar configuration with the strips active electrode. We assume a positive half-period of the sinusoidal driving voltage and the two-species model. Based on the fluid model, we present the following

• Mathematical formulation of the problem;
• Detailed formulation of the numerical model;
• Linear approximation of the ionization rate;
• Stable reconstruction of ion and electron velocity fields;
• Simulations showing trajectories and velocities of electrons and ions.

In contrast with the preceding models mentioned in existing literature, the main innovation presented in our paper is developing a 3D numerical model of the initial phase of the surface dielectric barrier discharge. We have paid particular attention to the proper formulation of the problem, description of the key issues, and possible numerical complications. Overall, we exposed the numerical theory in much more detail and laid down a good theoretical foundation for further research of the SDBD.

For future development of the model, we consider involving additional ionic effects on the electrodes so that it could be used for negative half-periods of the driving voltage. For simulations of extended periods, other techniques for stabilization need to be adopted.

Our model can be used to optimize the electrode geometry of the discharge. We believe the presented deeper mathematical insight into the problems will help predict and understand the experimental results in a better way.