Regional Consensus Control for Multi-Agent Systems with Actuator Saturation
Abstract
:1. Introduction
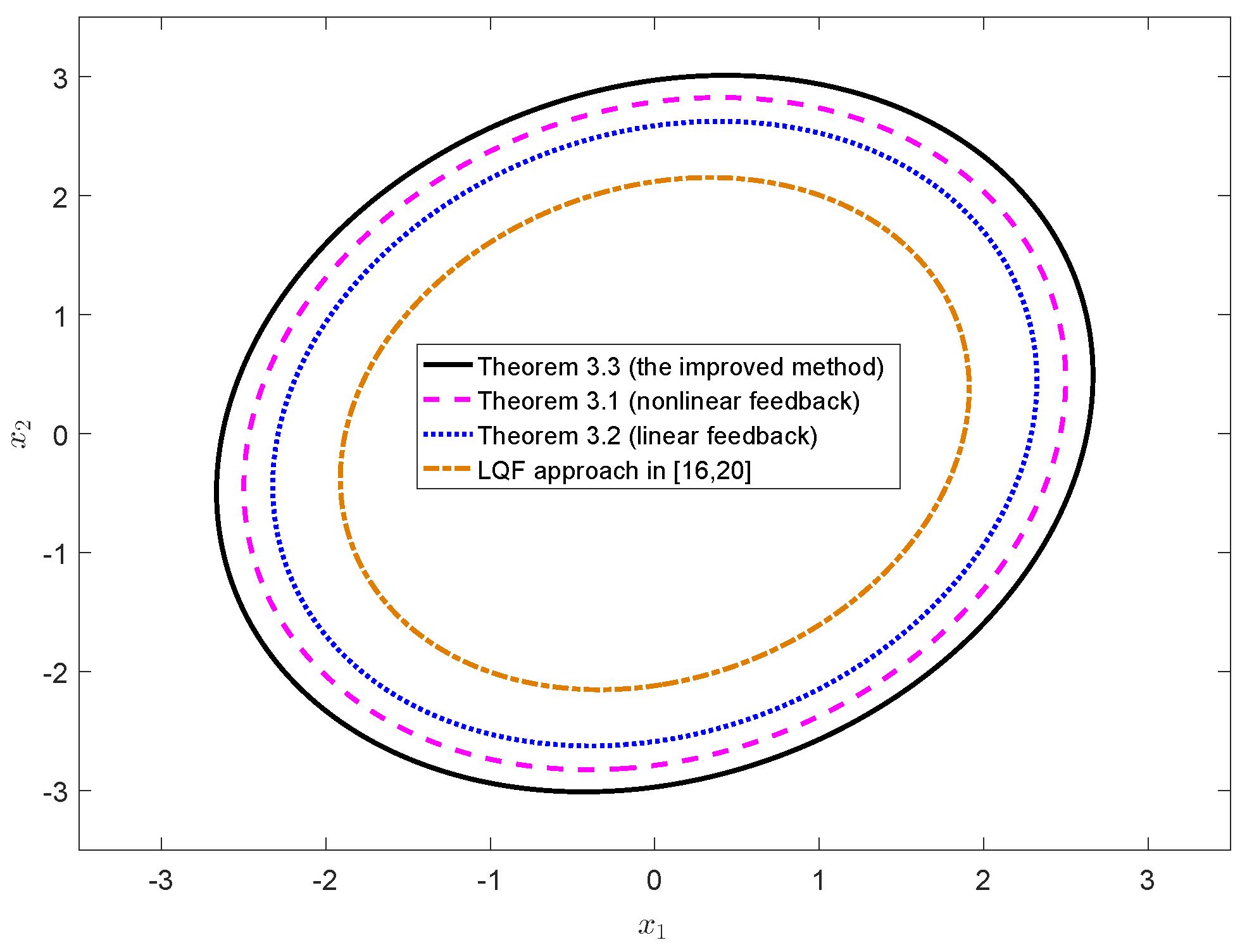
- The level set included in CLQF is established to estimate DC for saturated MASs, which larger than estimated by the LQF approach.
- An improvement of the consensus control and the estimation of DC is achieved by utilizing an alternative convex hull representation—enlarged.
2. System Description and Preparations
3. The Design of Consensus Protocol
3.1. Multiple Nonlinear Feedback for Regional Consensus
3.2. Linear Feedback for Regional Consensus
3.3. The Improved Results
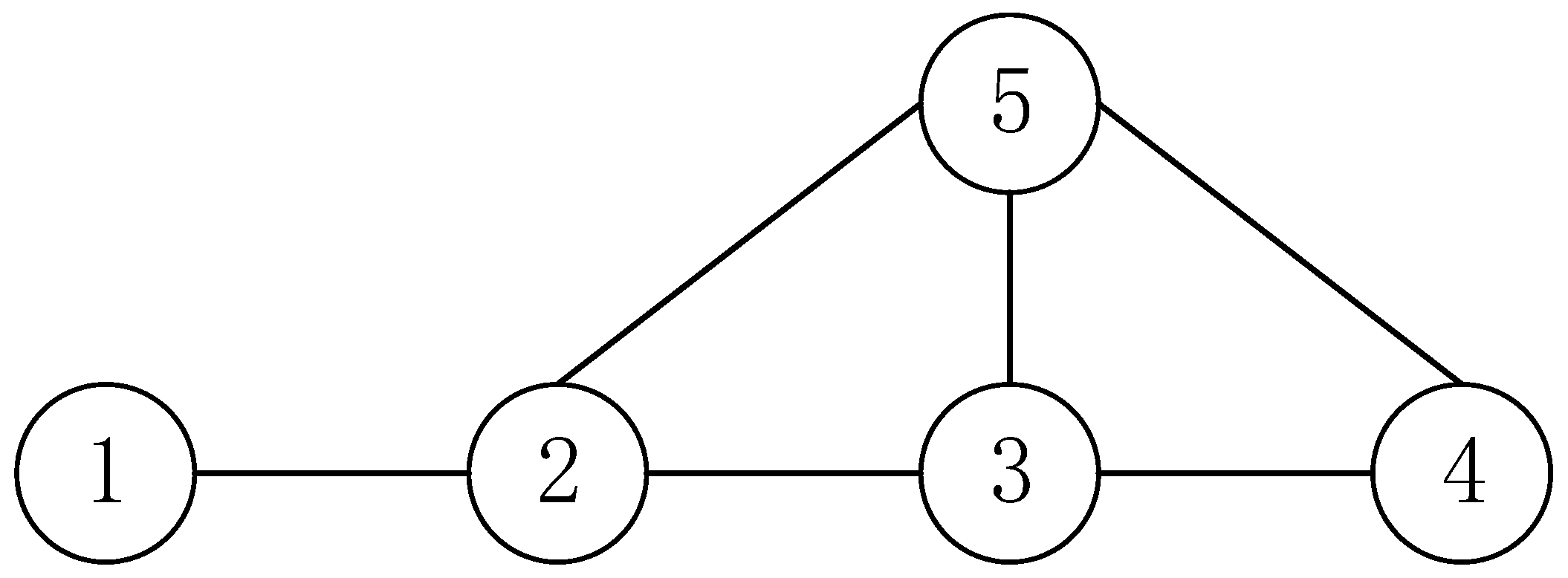
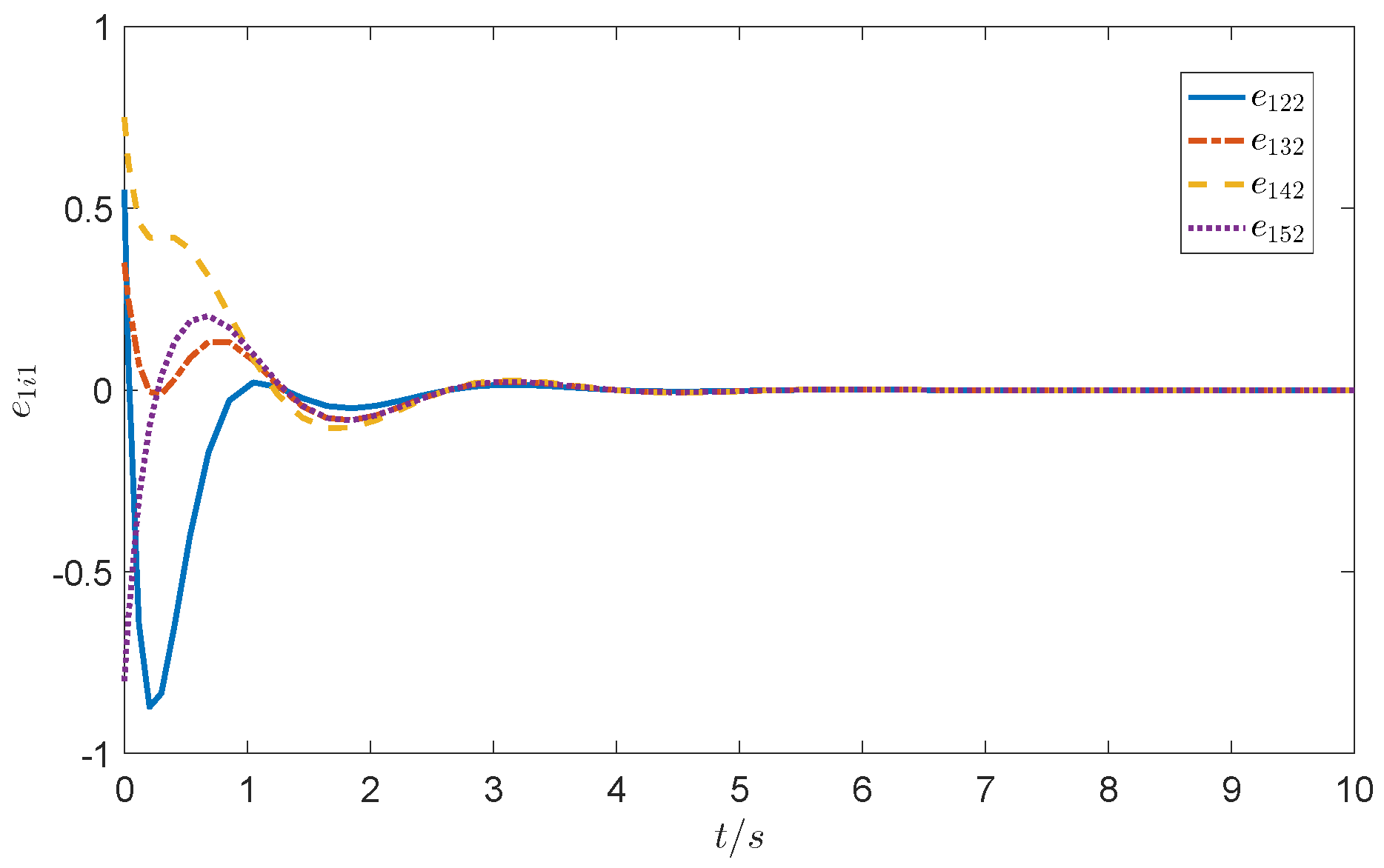
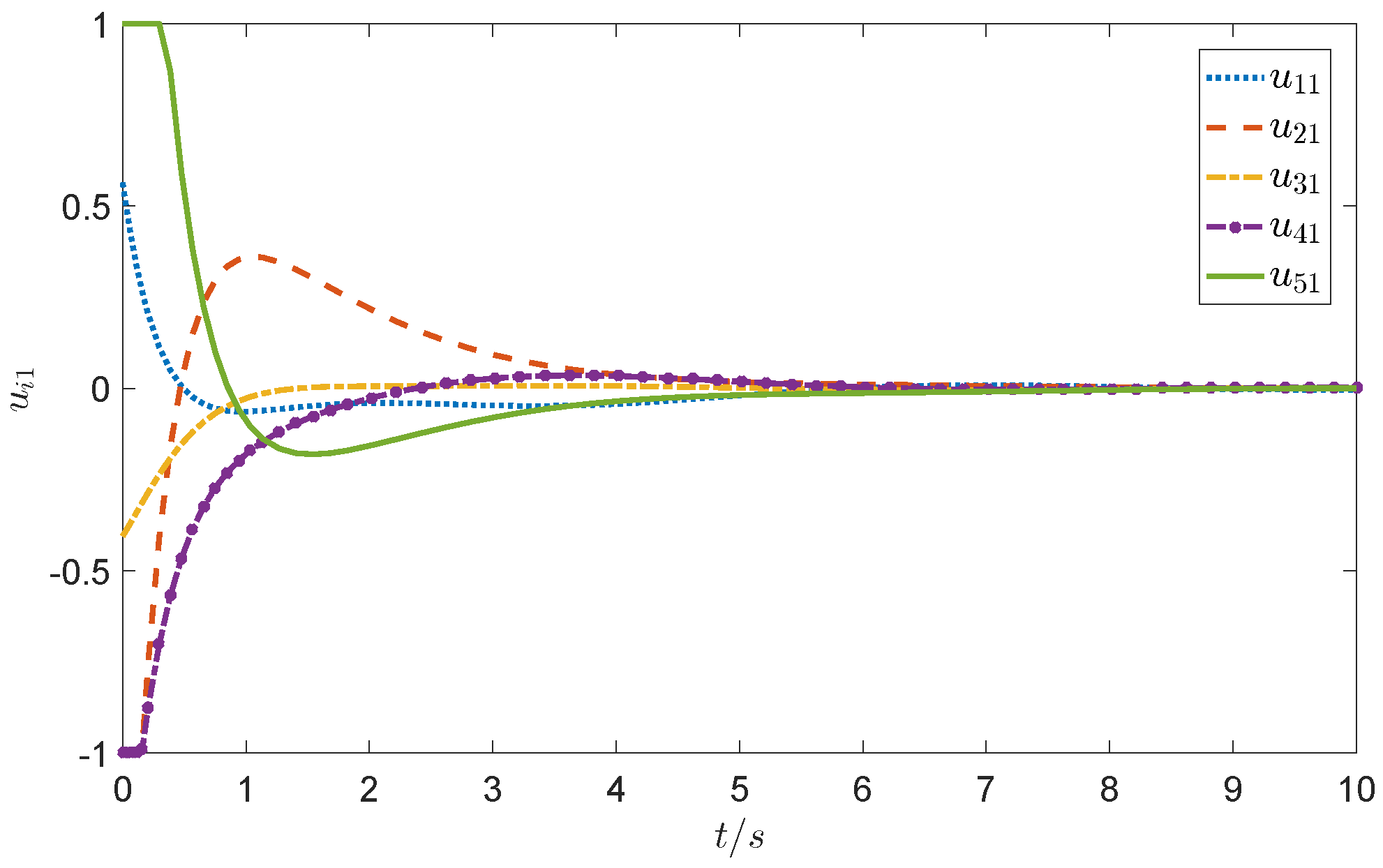
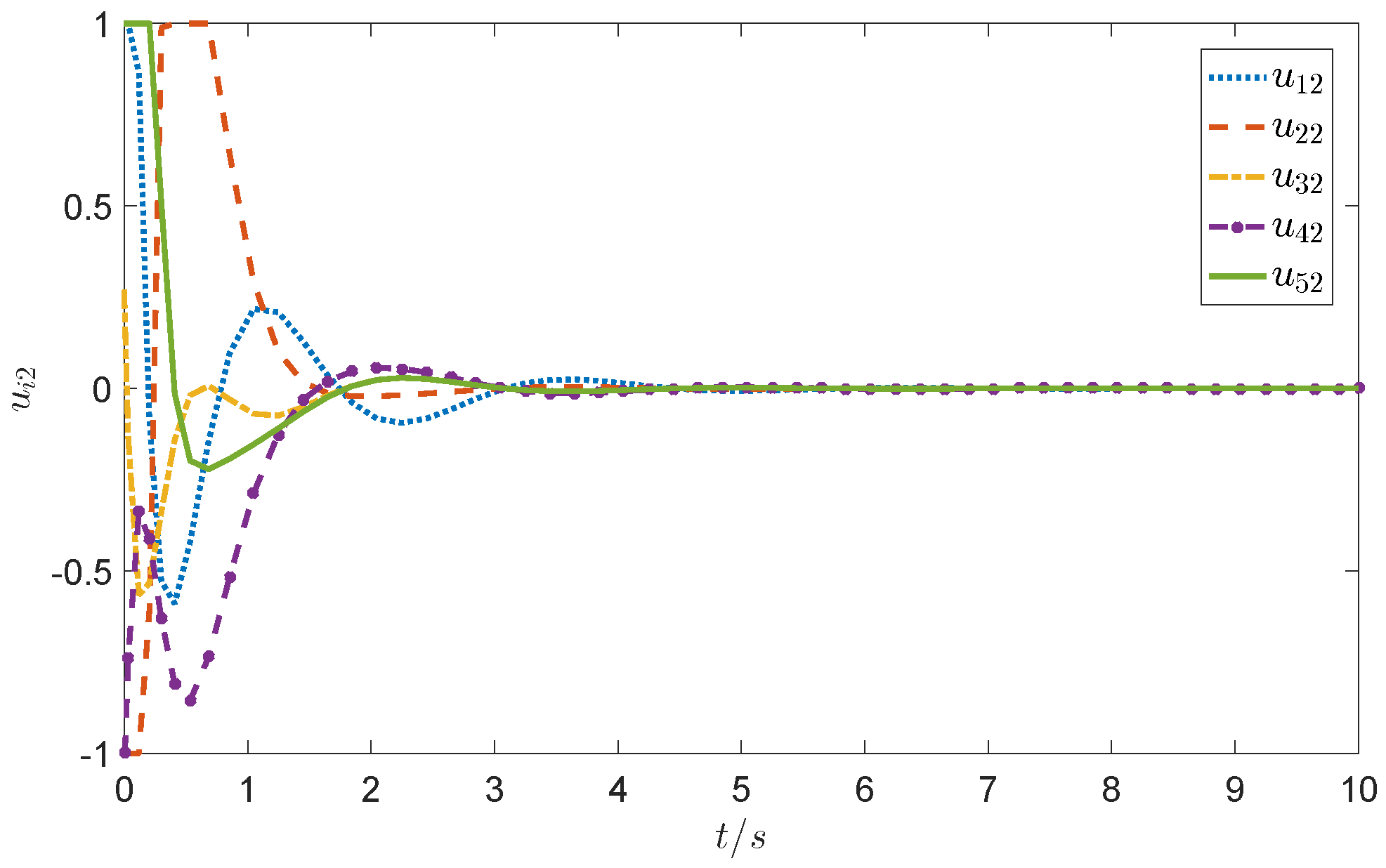
4. Case Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yamaguchi, H.; Arai, T.; Beni, G. A distributed control scheme for multiple robotic vehicles to make group formations. Robot. Auton. Syst. 2001, 36, 125–147. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 213–224. [Google Scholar]
- Ni, W.; Cheng, D. Leader-following consensus of multi-agent systems under fixed and switching topologies. Syst. Control Lett. 2010, 59, 209–217. [Google Scholar] [CrossRef]
- Xiao, W.; Cao, L.; Li, H.; Lu, R. Observer-based adaptive consensus control for nonlinear multi-agent systems with time-delay. Sci. China Inf. Sci. 2020, 63, 132202. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, H.; Ding, X.; Zhao, G. Leader–follower consensus of multiagent systems with time delays over finite fields. IEEE Trans. Cybern. 2018, 49, 3203–3208. [Google Scholar] [CrossRef]
- Yu, J.; Wang, L. Group consensus in multi-agent systems with switching topologies and communication delays. Syst. Control Lett. 2010, 59, 340–348. [Google Scholar] [CrossRef]
- Zou, W.; Shi, P.; Shi, P.; Shi, Y. Finite-time consensus of second-order switched nonlinear multi-agent systems. IEEE Trans. Neural Networks Learn. Syst. 2019, 31, 1757–1762. [Google Scholar] [CrossRef]
- Qian, Y.Y.; Liu, L.; Feng, G. Output consensus of heterogeneous linear multi-agent systems with adaptive event-triggered control. IEEE Trans. Autom. Control 2018, 64, 2606–2613. [Google Scholar] [CrossRef]
- Du, H.; Wen, G.; Wu, D.; Cheng, Y.; Lü, J. Distributed fixed-time consensus for nonlinear heterogeneous multi-agent systems. Automatica 2020, 113, 108797. [Google Scholar] [CrossRef]
- Sun, W.; Gao, H.; Kaynak, O. Vibration isolation for active suspensions with performance constraints and actuator saturation. IEEE/ASME Trans. Mechatronics 2015, 20, 675–683. [Google Scholar] [CrossRef]
- Huang, J.; Yang, L.; Trinh, H. Robust control for incremental quadratic constrained nonlinear time-delay systems subject to actuator saturation. Appl. Math. Comput. 2021, 405, 126271. [Google Scholar] [CrossRef]
- Da Silva, J.M.G.; Tarbouriech, S. Antiwindup design with guaranteed regions of stability: An LMI-based approach. IEEE Trans. Autom. Control 2005, 50, 106–111. [Google Scholar] [CrossRef]
- Yin, X.; Yue, D.; Hu, S. Adaptive periodic event-triggered consensus for multi-agent systems subject to input saturation. Int. J. Control 2016, 89, 653–667. [Google Scholar] [CrossRef]
- Ding, L.; Zheng, W.X.; Guo, G. Network-based practical set consensus of multi-agent systems subject to input saturation. Automatica 2018, 89, 316–324. [Google Scholar] [CrossRef]
- Hu, T.; Lin, Z.; Chen, B.M. Analysis and design for discrete-time linear systems subject to actuator saturation. Syst. Control. Lett. 2002, 45, 97–112. [Google Scholar] [CrossRef]
- Deng, C.; Yang, G.H. Consensus of linear multiagent systems with actuator saturation and external disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 284–288. [Google Scholar] [CrossRef]
- Sakthivel, R.; Sakthivel, R.; Kaviarasan, B.; Alzahrani, F. Leader-following exponential consensus of input saturated stochastic multi-agent systems with Markov jump parameters. Neurocomputing 2018, 287, 84–92. [Google Scholar] [CrossRef]
- Song, Q.; Song, Q.; Lin, Z. Regional consensus of linear differential inclusions subject to input saturation. Int. J. Robust Nonlinear Control 2020, 30, 2461–2474. [Google Scholar] [CrossRef]
- Lin, Z. Control design in the presence of actuator saturation: From individual systems to multi-agent systems. Sci. China Inf. Sci. 2020, 62, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Hu, T.; Lin, Z. Properties of the composite quadratic Lyapunov functions. IEEE Trans. Autom. Control 2004, 49, 1162–1167. [Google Scholar] [CrossRef]
- Chen, F.; Xiang, L.; Ren, W. Properties of composite Laplacian quadratics and their applications in consensus of linear differential inclusions. IEEE Trans. Autom. Control 2016, 61, 2269–2275. [Google Scholar] [CrossRef]
- Hu, T.; Teel, A.R.; Zaccarian, L. Stability and performance for saturated systems via quadratic and nonquadratic Lyapunov functions. IEEE Trans. Autom. Control 2006, 51, 1770–1786. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Z. Improvements to the linear differential inclusion approach to stability analysis of linear systems with saturated linear feedback. Automatica 2013, 49, 821–828. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, F.; Lan, W. Regional consensus for non-ANCBC systems with input saturation. In Proceedings of the IEEE Conference on Control Technology and Applications, Hong Kong, China, 19–21 August 2019. [Google Scholar]
- Hassibi, A.; How, J.; Boyd, S. A path-following method for solving BMI problems in control. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Qin, Y.; Huang, J.; Yang, L.; Zheng, T.; Li, Q. Regional Consensus Control for Multi-Agent Systems with Actuator Saturation. Mathematics 2023, 11, 1038. https://doi.org/10.3390/math11041038
Zhang Y, Qin Y, Huang J, Yang L, Zheng T, Li Q. Regional Consensus Control for Multi-Agent Systems with Actuator Saturation. Mathematics. 2023; 11(4):1038. https://doi.org/10.3390/math11041038
Chicago/Turabian StyleZhang, Yueyuan, Yong Qin, Jun Huang, Lin Yang, Tianjiang Zheng, and Qingyuan Li. 2023. "Regional Consensus Control for Multi-Agent Systems with Actuator Saturation" Mathematics 11, no. 4: 1038. https://doi.org/10.3390/math11041038
APA StyleZhang, Y., Qin, Y., Huang, J., Yang, L., Zheng, T., & Li, Q. (2023). Regional Consensus Control for Multi-Agent Systems with Actuator Saturation. Mathematics, 11(4), 1038. https://doi.org/10.3390/math11041038






