Anisotropy-Based Adaptive Polynomial Chaos Method for Hybrid Uncertainty Quantification and Reliability-Based Design Optimization of Structural-Acoustic System
Abstract
:1. Introduction
2. Moment-Based Arbitrary Polynomial Chaos Expansion for Hybrid Uncertainty Quantification
2.1. MAPC Approximation
2.2. Moment-Based Arbitrary Polynomial Chaos Expansion for Hybrid Analysis
3. Anisotropy-Based Adaptive Polynomial Chaos Expansion Method
3.1. Anisotropy-Based Initial Surrogate Model
3.2. Anisotropy-Based Adaptive Basis Growth
3.3. Basis Discarded Based on Variance Contribution
3.4. Adaptive Sampling Scheme
3.4.1. Initial Sampled Set
3.4.2. Sampling Technique for Sampling Point Selection
4. Adaptive Polynomial Chaos Expansion Method for Reliability-Based Optimization of Structural-Acoustic System
4.1. Structural-Acoustic Systems with Interval and Random Uncertainties
4.2. Interval and Random Analyses of an Uncertain Structural-Acoustic System
4.3. Optimization Model Based on Reliability for a Structural-Acoustic System
5. Numerical Examples
5.1. Numerical Example
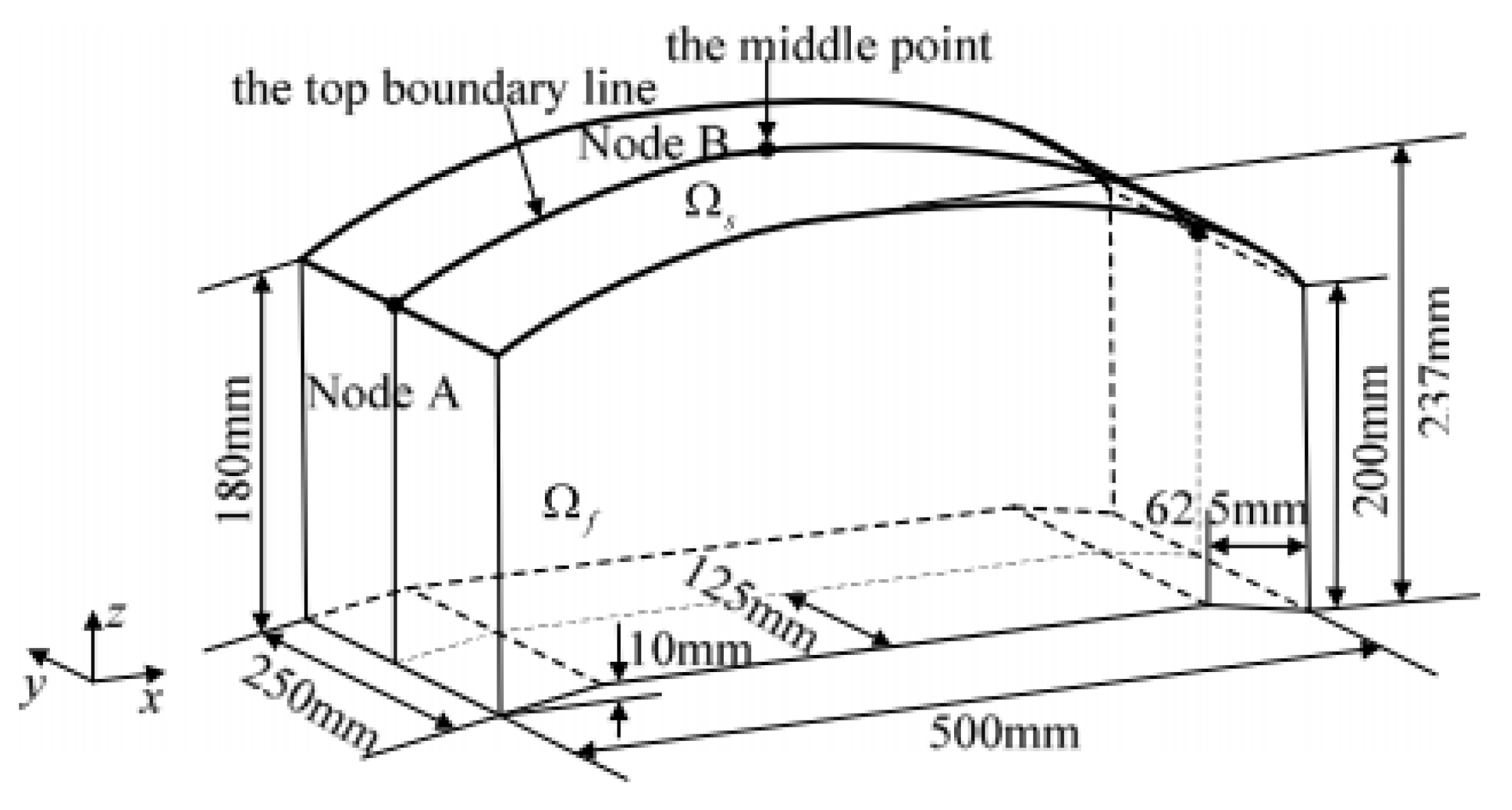
5.2. Structural-Acoustic Problem
6. Conclusions
- (1)
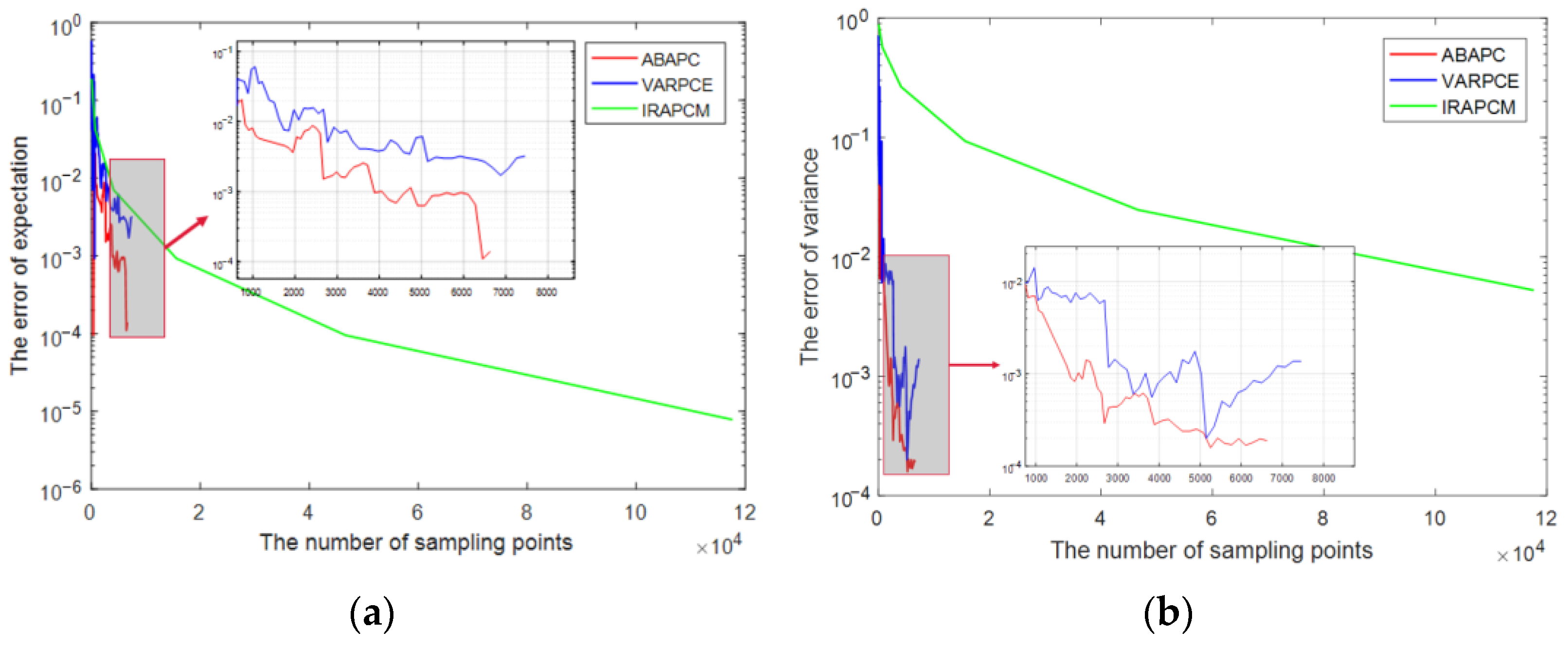
- Compared with the IRAPCM, for high-order and multi-dimensional problems, the overall computational time required by ABAPC significantly reduced when reaching the same accuracy, demonstrating a higher computational efficiency.
- (2)
- Compared with VARPCE, ABAPC could solve the problem with probability and interval parameters and improve the overall computational efficiency with the same accuracy.
- (3)
- The nested-loop RBDO problem can be transformed to an approximate single-loop problem using ABAPC to approximate the objective function and obtain component reliability. Therefore, compared with the RBDO based on IRAPCM, the RBDO based on ABAPC significantly decreased the number of polynomial basis terms and effectively improved the computational efficiency of RBDO for structural-acoustic systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, B.; Yu, D. Optimization based on reliability and confidence interval design for the structural-acoustic system with interval probabilistic variables. J. Sound Vib. 2015, 336, 1–5. [Google Scholar] [CrossRef]
- Gao, R.; Yin, S.; Xiong, F. Response analysis and reliability-based design optimization of structural-acoustic system under evidence theory. Struct. Multidiscip. Optim. 2018, 59, 959–975. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, Y.; Zhang, N. An interval uncertain optimization method for vehicle suspensions using Chebyshev metamodels. Appl. Math. Model. 2014, 38, 3706–3723. [Google Scholar] [CrossRef]
- Xia, B.; Lü, H.; Yu, D.; Jiang, C. Reliability-based design optimization of structural systems under hybrid probabilistic and interval model. Comput. Struct. 2015, 160, 126–134. [Google Scholar] [CrossRef]
- Du, X.P.; Sudjianto, A.; Huang, B.Q. Reliability-based design with the mixture of random and interval variables. J. Mech. Des. 2005, 127, 1068–1076. [Google Scholar] [CrossRef]
- Du, X.P. Reliability-based design optimization with dependent interval variables. Int. J. Numer. Methods Eng. 2012, 91, 218–228. [Google Scholar] [CrossRef]
- Kang, Z.; Luo, Y.J. Reliability-based structural optimization with probability and convex set hybrid models. Struct. Multidiscip. Optim. 2010, 42, 89–102. [Google Scholar] [CrossRef]
- Luo, Y.J.; Li, A.; Kang, Z. Reliability-based design optimization of adhesive bonded steel–concrete composite beams with probabilistic and non-probabilistic uncertainties. Eng. Struct. 2011, 33, 2110–2119. [Google Scholar] [CrossRef]
- Torii, A.J.; Lopez, R.H.; Miguel, L.F. A general RBDO decoupling approach for different reliability analysis methods. Struct. Multidisc. Optim. 2016, 54, 317–332. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.; Xu, M.; Yunglong, L. Novel reliability-based optimization method for thermal structure with hybrid random, interval and fuzzy parameters. Appl. Math. Model. 2017, 47, 573–586. [Google Scholar] [CrossRef]
- Yin, S.; Yu, D.; Luo, Z.; Xia, B. Unified polynomial expansion for interval and random response analysis of uncertain structure–acoustic system with arbitrary probability distribution. Comput. Methods Appl. Mech. Eng. 2018, 336, 260–285. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Gao, Y.; Zhang, Y.; Gao, Z. An active learning kriging model for hybrid reliability analysis with both random and interval variables. Struct. Multidiscip. Optim. 2015, 51, 1003–1016. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zheng, J.; Jiang, C. Incremental modeling of a new high-order polynomial surrogate model. Appl. Math. Modell. 2016, 40, 4681–4699. [Google Scholar] [CrossRef]
- Elishakoff, I.; Colombi, P. Combination of probabilistic and convex models of uncertainty when scarce knowledge is present on acoustic excitation parameters. Comput. Methods Appl. Mech. Eng. 1993, 104, 187–209. [Google Scholar] [CrossRef]
- Yin, S.; Yu, D.; Yin, H.; Xia, B. Interval and random analysis for structure–acoustic systems with large uncertain-but-bounded parameters. Comput. Methods Appl. Mech. Eng. 2016, 305, 910–935. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Marino, M.; Zhuang, X.; Wriggers, P.; Rabczuk, T. Sensitivity analysis for the mechanics of tendons and ligaments: Investigation on the effects of collagen structural properties via a multiscale modelling approach. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3209. [Google Scholar] [CrossRef]
- Wang, L.; Yang, G.; Li, Z. An efficient nonlinear interval uncertain optimization method using Legendre polynomial chaos expansion. Appl. Soft Comput. 2021, 108, 107454. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X.H.; Liu, X. A novel sparse polynomial expansion method for interval and random response analysis of uncertain structural-acoustic system. Shock. Vib. 2021, 2021, 1125373. [Google Scholar]
- Yin, S.; Yu, D.; Yin, H.; Xia, B. A new evidence-theory-based method for response analysis of acoustic system with epistemic uncertainty by using Jacobi expansion. Comput. Methods Appl. Mech. Eng. 2017, 322, 419–440. [Google Scholar] [CrossRef]
- Thapa, M.; Mulani, S.B.; Walters, R.W. Adaptive weighted least-squares polynomial chaos expansion with basis adaptivity and sequential adaptive sampling. Comput. Methods Appl. Mech. Eng. 2019, 360, 112759. [Google Scholar] [CrossRef]
- Li, R.; Ghanem, R.G. Adaptive PCE applied to statistics of extremes in non-linear random vibration. Probab. Eng. Mech. 1998, 13, 125–136. [Google Scholar] [CrossRef]
- Gilli, L.; Lathouwers, D.; Kloosterman, J.; van der Hagen, T.; Koning, A.; Rochman, R. Uncertainty quantification for criticality problems using non-intrusive and adaptive Polynomial Chaos techniques. Ann. Nucl. Energy 2013, 56, 71–80. [Google Scholar] [CrossRef]
- Perko, Z.; Gilli, L.; Lathouwers, D.; Kloosterman, J.L. Grid and basis adaptive polynomial chaos techniques for sensitivity and uncertainty analysis. J. Comput. Phys. 2014, 260, 54–84. [Google Scholar] [CrossRef]
- Winokur, J.; Conrad, P.; Sraj, I.; Knio, O.; Srinivasan, A.; Thacker, W.C.; Marzouk, Y.; Iskandarani, M. A priori testing of sparse adaptive polynomial chaos expansions using an ocean general circulation model database. Comput. Geosci. 2013, 17, 899–911. [Google Scholar] [CrossRef]
- Ghisu, T.; Parks, G.T.; Jarrett, J.P.; Clarkson, P.J. Adaptive polynomial chaos for gas turbine compression systems performance analysis. AIAA J. 2010, 48, 1156–1170. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probab. Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Wang, C.; Qiang, X.; Xu, M.; Wu, T. Recent Advances in Surrogate Modeling Methods for Uncertainty Quantification and Propagation. Symmetry 2022, 14, 1219. [Google Scholar] [CrossRef]
- Wang, C.; Matthies, H.G. A comparative study of two interval-random models for hybrid uncertainty propagation analysis. Mech. Syst. Signal Process. 2020, 136, 106531. [Google Scholar] [CrossRef]
- Zhu, W.; Hu, Y.; Chen, N.; Liu, J.; Beer, M. A fuzzy and random moment- based arbitrary polynomial chaos method for response analysis of composite structural–acoustic system with multi-scale uncertainties. Appl. Acoust. 2010, 177, 107913. [Google Scholar] [CrossRef]
- Ahlfeld, R.; Belkouchi, B.; Montomoli, F. SAMBA: Sparse approximation of moment-based arbitrary polynomial chaos. J. Comput. Phys. 2016, 320, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Mckay, M.D.; Beckkman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 266–294. [Google Scholar]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Zuniga, M.M.; Kucherenko, S.; Shah, N. Metamodelling with independent and dependent inputs. Comput. Phys. Commun. 2013, 184, 1570–1580. [Google Scholar] [CrossRef]
- Morris, M.D.; Mitchell, T.J. Exploratory designs for computational experiments. J. Stat. Plann. 1992, 43, 381–402. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, N.; Gao, W. A new sequential sampling method for constructing the high-order polynomial surrogate models. Eng. Comput. 2018, 35, 529–564. [Google Scholar] [CrossRef]
- Xia, B.; Yu, D. Modified sub-interval perturbation finite element method for 2D acoustic field prediction with large uncertain-but-bounded parameters. J. Sound. Vib. 2012, 331, 3774–3790. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-objective optimization of energy performance for a detached residential building with a sunspace using the NSGA-II genetic algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]


| Uncertain Parameters | Uncertain Information | |||
|---|---|---|---|---|
| 3 | ||||
| 1 | ||||
| 1 | ||||
| 1 |
| m | Method | Retained Order Vector | Number of Sampling Points | Number of Basis Terms |
|---|---|---|---|---|
| 0 | ABAPC method | {3,1,1,1} | 32 | 8 |
| IAPCE method | {3,3,3,3} | 256 | 22 | |
| 1 | ABAPC method | {4,1,1,1} | 40 | 15 |
| IAPCE method | {4,4,4,4} | 625 | 15 | |
| 2 | ABAPC method | {5,1,1,1} | 48 | 8 |
| IAPCE method | {5,5,5,5} | 1296 | 20 | |
| 3 | ABAPC method | {6,2,2,2} | 189 | 11 |
| IAPCE method | {6,6,6,6} | 2501 | 11 |
| Functions | Expression |
|---|---|
| case 1 | |
| case 2 |
| Functions | Method | Total Computational Time/s | Response Time/s | Number of Refined Basis Terms | Expansion Order | Number of Samples |
|---|---|---|---|---|---|---|
| Case 1 | ABAPC | 714.5960 | 71.5237 | 146 | [1 1 1 4 4 1] | 219 |
| VARPCE | 1558.7 | 112.1732 | 406 | [4 4 4 4 4 4] | 609 | |
| IRAPCM | 1828.6 | 1115.9 | / | [4 4 4 4 4 4] | 15625 | |
| Case 2 | ABAPC | 295.2705 | 49.0328 | 97 | [2 1 1 4 1 1] | 146 |
| VARPCE | 765.7473 | 94.1299 | 210 | [4 4 4 4 4 4] | 315 | |
| IRAPCM | 9989.00 | 3298.4 | / | [5 5 5 5 5 5] | 46,656 |
| Uncertain Parameters | Uncertainty Information |
|---|---|
| ) | 71 + 0.71 |
| Poisson’s ratio () | |
| ) | |
| ) | [1.14, 1.26] |
| Type | Design Variables | (Pa) | ||
|---|---|---|---|---|
| Initial values | 0.002 | 2700 | 0.5610 | 0.72 |
| Deterministic optimization | 0.0024 | 2160 | 0.3059 | 0.76 |
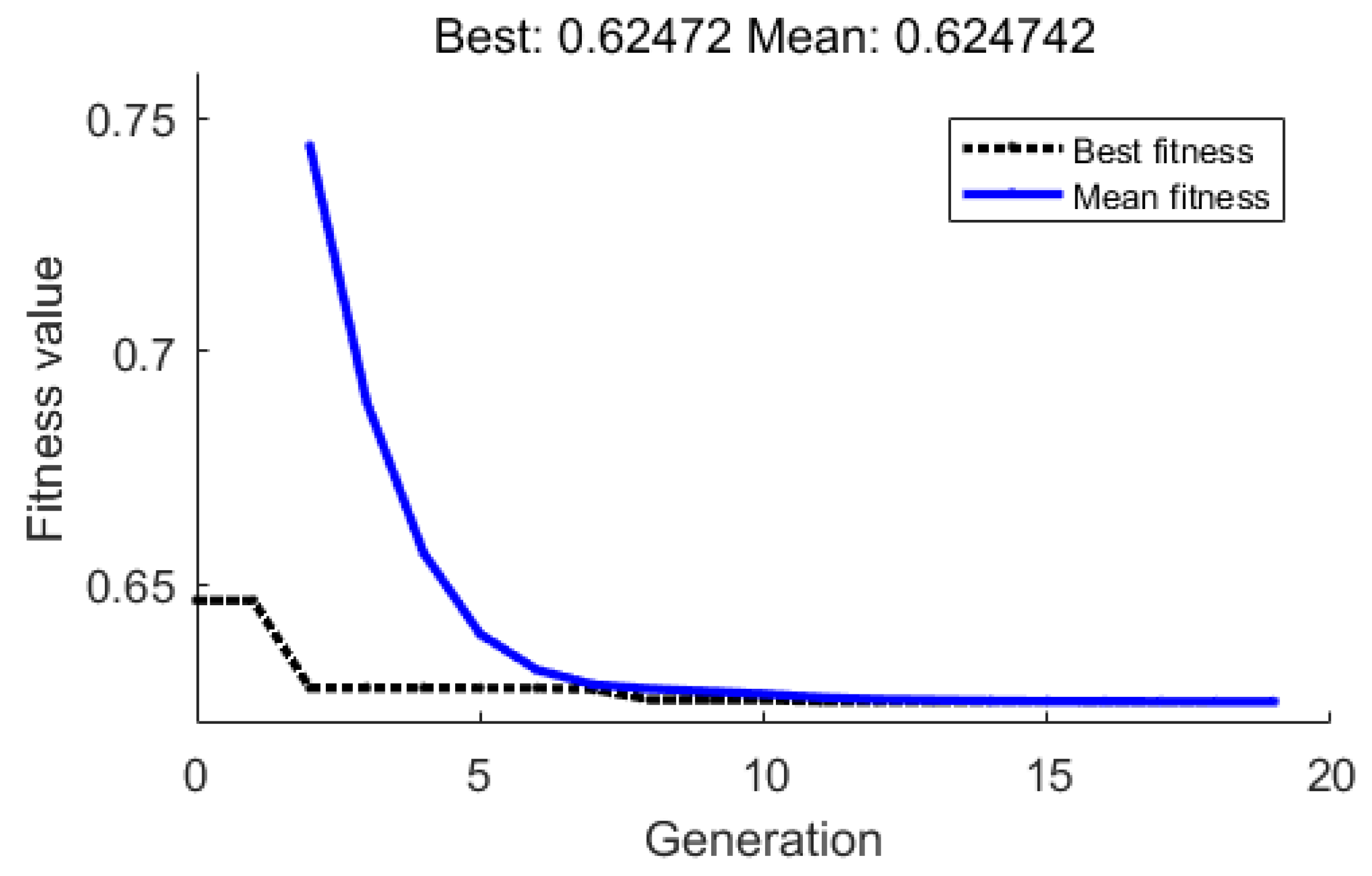
| RBDO with hybrid probabilistic and interval model | 0.0018 | 2253.9 | 0.6247 | 0.97 |
| Method | Sound Pressure (Pa) | Total Computational Time/h | Calculation Time of the Surrogate Model/s |
|---|---|---|---|
| RBDO based on ABAPC | 0.624 | 10.98 | 75.2131 |
| RBDO based on IRAPCM | 0.595 | 209.27 | 1337.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, S.; Gao, Y.; Zhu, X.; Wang, Z. Anisotropy-Based Adaptive Polynomial Chaos Method for Hybrid Uncertainty Quantification and Reliability-Based Design Optimization of Structural-Acoustic System. Mathematics 2023, 11, 836. https://doi.org/10.3390/math11040836
Yin S, Gao Y, Zhu X, Wang Z. Anisotropy-Based Adaptive Polynomial Chaos Method for Hybrid Uncertainty Quantification and Reliability-Based Design Optimization of Structural-Acoustic System. Mathematics. 2023; 11(4):836. https://doi.org/10.3390/math11040836
Chicago/Turabian StyleYin, Shengwen, Yuan Gao, Xiaohan Zhu, and Zhonggang Wang. 2023. "Anisotropy-Based Adaptive Polynomial Chaos Method for Hybrid Uncertainty Quantification and Reliability-Based Design Optimization of Structural-Acoustic System" Mathematics 11, no. 4: 836. https://doi.org/10.3390/math11040836
APA StyleYin, S., Gao, Y., Zhu, X., & Wang, Z. (2023). Anisotropy-Based Adaptive Polynomial Chaos Method for Hybrid Uncertainty Quantification and Reliability-Based Design Optimization of Structural-Acoustic System. Mathematics, 11(4), 836. https://doi.org/10.3390/math11040836





