A Comprehensive Study of the Complex mKdV Equation through the Singular Manifold Method

Abstract

In this paper, we introduce a modification of the Singular Manifold Method in order to derive the associated spectral problem for a generalization of the complex version of the modified Korteweg–de Vries equation. This modification yields the right Lax pair and allows us to implement binary Darboux transformations, which can be used to construct an iterative method to obtain exact solutions.

1. Introduction

The identification of integrable nonlinear partial differential equations (NLPDEs) can be addressed from different perspectives. This article primarily deals with two of them. One of the most accepted notions of integrability for an NLPDE lies in the existence of an associated linear problem [1], also known as a Lax pair. Nevertheless, this approach raises the issue of how to obtain the Lax pair for a given NLPDE. On the other hand, a second concept of integrability is the one derived from the Painlevé test [2]. An NLPDE is said to be integrable in the Painlevé sense when all its solutions are single-valued in a neighbourhood of the movable singularity manifolds. The main advantage of this method is that it can be straightforwardly checked whether or not a differential equation has the Painlevé Property (PP), by means of either the Ablowitz–Ramani–Segur (ARS) algorithm [3] or the Weiss–Tabor–Carnevale (WTC) algorithm [4]. Moreover, if an equation has the Painlevé Property, the Singular Manifold Method (SMM) [2] allows us to derive key properties of the NLPDE related to its integrability, such as Bäcklund transformations, Darboux transformations, $\tau$-functions, etc. Of critical importance will be the algorithmic obtention of the Lax pair by this procedure, establishing the relation among the singular manifold and the eigenfunctions of the spectral problem [5]. In this way, the SMM provides the equivalence between the integrability described by the existence of a Lax pair and the one derived from the Painlevé Property.

Nonetheless, several limitations may emerge from both the determination of the PP and the application of the SMM. The first problem is that there exist integrable differential equations that possess a Lax pair but do not pass the Painlevé test. Such is the case of the celebrated Camassa–Holm equation [6]. In a series of previous publications [7,8], it has been shown that several such equations (to which the Painlevé test is not applicable) can be transformed by reciprocal transformations [9] in equations with the PP. The spectral problem of these equations can therefore be obtained by the inverse reciprocal transformation of the Lax pair associated to the equation with the PP.

The application itself of the SMM may also present some drawbacks. This method focuses on truncations of the Painlevé series such that this process gives rise to an auto-Bäcklund transformation between solutions of the NLPDE. A major flaw emerges when the NLPDE has several branches of expansion. In this case, the SMM shall be modified to include as many singular manifolds as Painlevé branches. Such a procedure has proved to be successful for several examples [5,10]. Moreover, the SMM frequently requires setting as null every coefficient in the different powers of the singular manifold arising from the substitution of the truncated Painlevé expansion into the given NLPDE. This procedure constitutes an issue since it may retrieve trivial results for some NLPDEs. Vanishing all the coefficients for every power of the singular manifold represents a highly restrictive approach, which should be relaxed in order to obtain the desired results [11]. An example of how to perform such generalization of the SMM can be found in [12,13].

This paper aims at studying an NLPDE that presents this type of particularity. Such an equation accounts for a generalization of the complex modified Korteweg–de Vries (mKdV) equation [14,15]. The SMM, when applied to this equation in the usual way, gives rise to unsatisfactory results because it does not allow us to introduce a spectral parameter in the associated linear problem. Nevertheless, a proper generalization of the SMM leads to the complete resolution of this issue, as illustrated hereafter.

2. Generalized Complex mKdV Equation

In a recent paper [14], an integrable generalization of the complex mKdV equation [1] was introduced. This equation, referred as GcmKdV in the following, reads as

$$\begin{array}{cc}\hfill & u_t+u_{xxx}+6u^2{u}_x+3\overline{u}{\left[u·\overline{u}\right]}_x=0,\hfill \\ \hfill & {\overline{u}}_t+{\overline{u}}_{xxx}+6{\overline{u}}^2{\overline{u}}_x+3u{\left[u·\overline{u}\right]}_x=0,\hfill \end{array}$$

(1)

where $\overline{u}=\overline{u}(x,t)$ is the complex conjugate of $u=u(x,t)$.

In [14], a three-component Lax pair, Darboux transformations, soliton and breather solutions were identified for this equation. Nevertheless, no explanation of how this Lax pair was obtained ever appears in the article. This paper strives to present a comprehensive study of Equation (1) based on the Painlevé Property [4] and the SMM [2]. This procedure allows us to straightforwardly derive the Lax pair. Darboux transformation and Bäcklund transformations are also directly constructed. The $\tau$-function [16] immediately arises, and it provides an algorithmic and iterative method for the construction of solutions.

2.1. Painlevé Property

As it is well-known [2], Equation (1) has the PP if and only if all its solutions can be locally written as the Laurent series

$$\begin{array}{cc}\hfill u& =\sum _{j=0}^{\infty }{a}_j{\varphi }^{j-\alpha },\hfill \\ \hfill \overline{u}& =\sum _{j=0}^{\infty }{\overline{a}}_j{\varphi }^{j-\alpha }.\hfill \end{array}$$

(2)

with coefficients $a_j=a_j(x,t),{\overline{a}}_j={\overline{a}}_j(x,t),\alpha \in \mathbb{N},$ and where $\varphi (x,t)=0$ is the manifold of movable singularities. The index $\alpha$, as well as the leading coefficients $a_0$ and ${\overline{a}}_0$, can be obtained through a leading-order analysis. The result is

$$\alpha =1,a_0^2+{\overline{a}}_0^2+{\varphi }_x^2=0.$$

The application of the WTC test [4] is rather straightforward, and it can be conducted with the aid of Maple. There are three simple resonances at $j=0,2$ and 3 and a double resonance at $j=4$. All the resonance conditions are identically satisfied, which means that, for instance, ${\overline{a}}_0,{\overline{a}}_2,{\overline{a}}_3,a_4$ and ${\overline{a}}_4$ are arbitrary, and consequently, GcmKdV has the PP.

2.2. Truncation of the Painlevé Series: Modified SMM

Once the PP has been tested, we can proceed with the SMM. It requires the truncation of the Painlevé series (2) at constant level as

$$\begin{array}{cc}\hfill & u^{\left[1\right]}=u^{\left[0\right]}+A\frac{{\varphi }_x}{\varphi },\hfill \\ \hfill & {\overline{u}}^{\left[1\right]}={\overline{u}}^{\left[0\right]}+\overline{A}\frac{{\varphi }_x}{\varphi }.\hfill \end{array}$$

(3)

Notice that the truncation means that Equations (3) can be considered as auto-Bäcklund transformations between the seed solution $\{u^{\left[0\right]},{\overline{u}}^{\left[0\right]}\}$ and the iterated one $\{u^{\left[1\right]},{\overline{u}}^{\left[1\right]}\}$. Furthermore, $A(x,t)$ and $\overline{A}(x,t)$ are the leading terms, which we shall discuss later.

Substitution of the truncated expansion (3) in (1) yields polynomials in powers of $\varphi$ of the form

$$\begin{array}{cc}\hfill & h_4\frac{{\varphi }_x^4}{{\varphi }^4}+h_3\frac{{\varphi }_x^3}{{\varphi }^3}+h_2\frac{{\varphi }_x^2}{{\varphi }^2}+h_1\frac{{\varphi }_x}{\varphi }=0,\hfill \\ \hfill & {\overline{h}}_4\frac{{\varphi }_x^4}{{\varphi }^4}+{\overline{h}}_3\frac{{\varphi }_x^3}{{\varphi }^3}+{\overline{h}}_2\frac{{\varphi }_x^2}{{\varphi }^2}+{\overline{h}}_1\frac{{\varphi }_x}{\varphi }=0,\hfill \end{array}$$

(4)

where $h_i$ and ${\overline{h}}_i$ are complicated expressions involving $u^{\left[0\right]},{\overline{u}}^{\left[0\right]},\varphi$ and their derivatives. The SMM usually requires that all the coefficients $h_i,{\overline{h}}_i$ vanish. This procedure typically works for most parts of integrable PDEs, but sometimes this requirement is too restrictive, and it should be relaxed in order to have nontrivial results (cf. [12,13]). In our case, for GcmKdV, the usual SMM does not provide a spectral parameter when the associated linear system is obtained. In order to obtain a proper spectral problem, we shall rewrite (4) as

$$\begin{array}{ccc}& & \left(h_4+\frac{m_4\varphi }{{\varphi }_x}\right)\frac{{\varphi }_x^4}{{\varphi }^4}+\left(h_3-m_4+\frac{m_3\varphi }{{\varphi }_x}\right)\frac{{\varphi }_x^3}{{\varphi }^3}+\hfill \\ & & +\left(h_2-m_3+\frac{m_2\varphi }{{\varphi }_x}\right)\frac{{\varphi }_x^2}{{\varphi }^2}+\left(h_1-m_2\right)\frac{{\varphi }_x}{\varphi }=0,\hfill \end{array}$$

(5a)

$$\begin{array}{ccc}& & \left({\overline{h}}_4+\frac{{\overline{m}}_4\varphi }{{\varphi }_x}\right)\frac{{\varphi }_x^4}{{\varphi }^4}+\left({\overline{h}}_3-{\overline{m}}_4+\frac{{\overline{m}}_3\varphi }{{\varphi }_x}\right)\frac{{\varphi }_x^3}{{\varphi }^3}+\hfill \\ & & +\left({\overline{h}}_2-{\overline{m}}_3+\frac{{\overline{m}}_2\varphi }{{\varphi }_x}\right)\frac{{\varphi }_x^2}{{\varphi }^2}+\left({\overline{h}}_1-{\overline{m}}_2\right)\frac{{\varphi }_x}{\varphi }=0,\hfill \end{array}$$

(5b)

where—in words of the authors of ref. [11]—$\{m_i,{\overline{m}}_i\}$ are quantities which should be “judiciously chosen”. The computational complexity substantially rises when this approach is considered. For the benefit of the reader, the details are included in Appendix A, and the results are summarized thereupon:

• Leading-order terms
  The usual application of the SMM implies $h_4={\overline{h}}_4=0$, and therefore

  $$A^2+{\overline{A}}^2+1=0.$$
  Nonetheless, according to our previous discussion, this condition should be relaxed by introducing a constant $\lambda$ such that

  $$A^2+{\overline{A}}^2+1=2\lambda \frac{\varphi }{{\varphi }_x}.$$

  (6)
  This is the critical point in our modification of the SMM. As we shall see later, $\lambda$ is just the necessary spectral parameter of the Lax pair which appears as a consequence of the generalization of the SMM.
• Expression of the fields in terms of the singular manifold
  The coefficients in ${\varphi }^{-3}$ in (5) yield the following expressions for the seminal solutions in terms of the singular manifold

  $$\begin{array}{cc}\hfill u^{\left[0\right]}& =-A_x-\frac{1}{2}vA,\hfill \\ \hfill {\overline{u}}^{\left[0\right]}& =-{\overline{A}}_x-\frac{1}{2}v\overline{A},\hfill \end{array}$$

  (7)

  where v is a useful quantity related to the singular manifold defined as

  $$v=\frac{{\varphi }_{xx}}{{\varphi }_x}.$$

  (8)
• Singular manifold equations
  The truncation of the Painlevé series implies that the singular manifold $\varphi$ should satisfy a set of conditions named as singular manifold equations. These conditions can be obtained from the coefficients in ${\varphi }^{-2}$ and ${\varphi }^{-1}$ in (5) as

  $$\begin{array}{ccc}& & r=-3\left(A_x^2+{\overline{A}}_x^2\right)-v_x+\frac{v^2}{2}+3\lambda \left[-v+\left(\frac{v^2}{2}-2{\lambda }^2\right)\frac{\varphi }{{\varphi }_x}\right],\hfill \end{array}$$

  (9a)

  $$\begin{array}{ccc}& & A_t=-A_{xxx}+3A\left({\overline{A}}_x{\overline{A}}_{xx}+A_x{A}_{xx}\right)-3A_x\left(A_x^2+{\overline{A}}_x^2\right)\hfill \\ & & -\frac{3}{2}{A}_x\left(v_x-\frac{v^2}{2}\right)+\frac{3\lambda }{4}\left(2A{v}_x-A{v}^2-4v{A}_x\right)\hfill \\ & & -\frac{3v\lambda }{4}\frac{\varphi }{{\varphi }_x}\left(2A{v}_x-A{v}^2-2v{A}_x\right),\hfill \end{array}$$

  (9b)

  $$\begin{array}{ccc}& & {\overline{A}}_t=-{\overline{A}}_{xxx}+3\overline{A}\left({\overline{A}}_x{\overline{A}}_{xx}+A_x{A}_{xx}\right)-3{\overline{A}}_x\left(A_x^2+{\overline{A}}_x^2\right)\hfill \\ & & -\frac{3}{2}{\overline{A}}_x\left(v_x-\frac{v^2}{2}\right)+\frac{3\lambda }{4}\left(2\overline{A}{v}_x-\overline{A}{v}^2-4v{\overline{A}}_x\right)\hfill \\ & & -\frac{3v\lambda }{4}\frac{\varphi }{{\varphi }_x}\left(2\overline{A}{v}_x-\overline{A}{v}^2-2v{\overline{A}}_x\right),\hfill \end{array}$$

  (9c)

  where we have defined r as

  $$r=\frac{{\varphi }_t}{{\varphi }_x}.$$

  (10)
  Furthermore, the compatibility condition between (8) and (10) yields

  $$v_t={\left(r_x+rv\right)}_x.$$

  (11)

2.3. Lax Pair

As performed for several examples [5,13], Equation (7) can be linearized through the introduction of three new functions $\psi (x,t),\eta (x,t)$ and $\overline{\eta }(x,t)$ defined as

$$\begin{array}{ccc}& & {\varphi }_x={\psi }^2⟹v=2\frac{{\psi }_x}{\psi },\hfill \end{array}$$

(12a)

$$\begin{array}{ccc}& & A=\frac{\eta }{\psi },\hfill \end{array}$$

(12b)

$$\begin{array}{ccc}& & \overline{A}=\frac{\overline{\eta }}{\psi }.\hfill \end{array}$$

(12c)

The introduction of (12) in (7) yields

$$\begin{array}{ccc}& & {\psi }_x=\lambda \psi +u^{\left[0\right]}\eta +{\overline{u}}^{\left[0\right]}\overline{\eta },\hfill \end{array}$$

(13a)

$$\begin{array}{ccc}& & {\eta }_x=-u^{\left[0\right]}\psi ,\hfill \end{array}$$

(13b)

$$\begin{array}{ccc}& & {\overline{\eta }}_x=-{\overline{u}}^{\left[0\right]}\psi ,\hfill \end{array}$$

(13c)

which can be considered as the spatial part of the linear spectral problem. It can also be expressed in matrix form as

$${\overrightarrow{\Psi }}_x=B_0\left[u^{\left[0\right]}\right]\overrightarrow{\Psi }+\lambda B_1\overrightarrow{\Psi },$$

(14)

where $\overrightarrow{\Psi }={(\psi ,\eta ,\overline{\eta })}^{⊺}$ and $B_0,B_1$ are the matrices

$$B_0\left[u\right]=\left(\begin{array}{ccc}0& u& \overline{u}\\ -u& 0& 0\\ -\overline{u}& 0& 0\end{array}\right),B_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).$$

(15)

The computation of the temporal part of the Lax pair may turn out challenging. It can be derived from Equations (9)–(12) after some algebraic manipulations. The result is

$${\overrightarrow{\Psi }}_t=C_0\left[u^{\left[0\right]}\right]\overrightarrow{\Psi }+\lambda C_1\left[u^{\left[0\right]}\right]\overrightarrow{\Psi }-{\lambda }^2{B}_0\left[u^{\left[0\right]}\right]\overrightarrow{\Psi }+{\lambda }^3{C}_2\overrightarrow{\Psi },$$

(16)

where the matrices $C_0,C_1,C_2$ read

$$\begin{array}{ccc}& & C_0\left[u\right]=\left(\begin{array}{ccc}0& -2u\left(u^2+{\overline{u}}^2\right)-u_{xx}& -2\overline{u}\left(u^2+{\overline{u}}^2\right)-{\overline{u}}_{xx}\\ 2u\left(u^2+{\overline{u}}^2\right)+u_{xx}& 0& u{\overline{u}}_x-\overline{u}{u}_x\\ 2\overline{u}\left(u^2+{\overline{u}}^2\right)+{\overline{u}}_{xx}& \overline{u}{u}_x-u{\overline{u}}_x,& 0\end{array}\right),\hfill \\ & & C_1\left[u\right]=\left(\begin{array}{ccc}-\left(u^2+{\overline{u}}^2\right)& -u_x& -{\overline{u}}_x\\ -u_x& u^2& u\overline{u}\\ -{\overline{u}}_x& u\overline{u}& {\overline{u}}^2\end{array}\right),\hfill \\ & & C_2=\left(\begin{array}{ccc}-4& 0& 0\\ 0& -3& 0\\ 0& 0& -3\end{array}\right).\hfill \end{array}$$

(17)

This is essentially the Lax pair provided in [14]. Nevertheless, in this reference, the author gives no explanation about how this Lax pair is constructed. Conversely, we have proved that the SMM, through its generalization, provides the right spectral problem.

2.4. The Singular Manifold and the Eigenfunctions

An interesting consequence of the SMM is that it yields a direct relation between the eigenvector $\overrightarrow{\Psi }$ and the singular manifold $\varphi$. This relation can be deduced by combining Equations (6) and (12), resulting in

$$\varphi =\frac{1}{2\lambda }\left[{\psi }^2+{\eta }^2+{\overline{\eta }}^2\right]=\frac{\overrightarrow{\Psi }·\overrightarrow{\Psi }}{2\lambda }.$$

(18)

where $·$ denotes the usual dot product in the Euclidean space.

Notice that the parameter $\lambda$ is essential for the construction of $\varphi$. The fact that this parameter can only be introduced through the extension of the SMM provided in Equation (6) is one of the main goals of this paper.

2.5. Darboux Transformations

The SMM not only directly yields the associated linear spectral problem, it is also the basis for the construction of binary Darboux transformations [13]. It is worthwhile to remark that auto-Bäcklund and Darboux transformations arising from the Painlevé analysis and the SMM may differ from the Darboux transformations understood in the classical sense [17], as evidenced in several works [2,18]. This is due to the fact that binary Darboux transformations derived from the SMM aim to preserve not only the nonlinear PDE and its associated spectral problem, but also the relation between the singular manifold $\varphi$ and the eigenfunctions $\overrightarrow{\Psi }$, i.e., expression (18). This implies that transformations for the singular manifold must also be taken into account. Therefore, it is possible to construct truncated Painlevé series using $\varphi$ as the expansion variable (rather the eigenfunctions $\overrightarrow{\Psi }$ as in the case of classical Darboux transformations), just as prescribed by the SMM.

Let ${\overrightarrow{\Psi }}_i={\left({\psi }_i,{\eta }_i,{\overline{\eta }}_i\right)}^{⊺},i=1,2,$ be a pair of eigenvectors for the spectral problem with seed solution $\left\{u^{\left[0\right]},{\overline{u}}^{\left[0\right]}\right\}$ associated with two different values for the spectral parameter ${\lambda }_i$, respectively. Therefore, their Lax pairs read as

$$\begin{array}{ccc}& & {\left({\overrightarrow{\Psi }}_i\right)}_x=\left(B_0\left[u^{\left[0\right]}\right]+{\lambda }_i{B}_1\right){\overrightarrow{\Psi }}_i,\hfill \end{array}$$

(19a)

$$\begin{array}{ccc}& & {\left({\overrightarrow{\Psi }}_i\right)}_t=\left(C_0\left[u^{\left[0\right]}\right]+{\lambda }_i{C}_1\left[u^{\left[0\right]}\right]-{\lambda }_i^2{B}_0\left[u^{\left[0\right]}\right]+{\lambda }_i^3{C}_2\right){\overrightarrow{\Psi }}_i,\hfill \end{array}$$

(19b)

where the matrices $B_j,C_k$ have been defined in Equations (15) and (17). Singular manifolds for each value of the spectral parameter can be obtained through Equation (18) as

$${\varphi }_i=\frac{1}{2{\lambda }_i}\left[{\psi }_i^2+{\eta }_i^2+{\overline{\eta }}_i^2\right]=\frac{1}{2{\lambda }_i}{\overrightarrow{\Psi }}_i·{\overrightarrow{\Psi }}_i,i=1,2.$$

(20)

The truncation of the Painlevé series given in (3) yields iterated fields $\left\{u^{\left[1\right]},{\overline{u}}^{\left[1\right]}\right\}$ by means of the singular manifold ${\varphi }_1$ linked to the spectral parameter ${\lambda }_1$. The Lax pair for this iterated solution can be written as

$$\begin{array}{ccc}& & {\left({\overrightarrow{\Psi }}_{1,2}\right)}_x=\left(B_0\left[u^{\left[1\right]}\right]+{\lambda }_2{B}_1\right){\overrightarrow{\Psi }}_{1,2},\hfill \end{array}$$

(21a)

$$\begin{array}{ccc}& & {\left({\overrightarrow{\Psi }}_{1,2}\right)}_t=\left(C_0\left[u^{\left[1\right]}\right]+{\lambda }_2{C}_1\left[u^{\left[1\right]}\right]-{\lambda }_2^2{B}_0\left[u^{\left[1\right]}\right]+{\lambda }_2^3{C}_2\right){\overrightarrow{\Psi }}_{1,2},\hfill \end{array}$$

(21b)

where the notation ${\overrightarrow{\Psi }}_{1,2}$ refers to the eigenvector corresponding to solution $u^{\left[1\right]}$ and spectral parameter ${\lambda }_2$.

A Lax pair as (21) is frequently considered as a linear system for the eigenfunctions. Nevertheless, as we have done in several papers [5,12,13], we can also regard (21) as a nonlinear coupling between the eigenvector ${\overrightarrow{\Psi }}_{1,2}$ and the fields $\left\{u^{\left[1\right]},{\overline{u}}^{\left[1\right]}\right\}$ [19]. In this case, the Painlevé truncated expansion (3) should be completed with a similar expansion for the eigenfunctions of the form

$$\begin{array}{ccc}& & {\psi }_{1,2}={\psi }_2-{\psi }_1\frac{{\Delta }_{1,2}}{{\varphi }_1},\hfill \end{array}$$

(22a)

$$\begin{array}{ccc}& & {\eta }_{1,2}={\eta }_2-{\eta }_1\frac{{\Delta }_{1,2}}{{\varphi }_1},\hfill \end{array}$$

(22b)

$$\begin{array}{ccc}& & {\overline{\eta }}_{1,2}={\overline{\eta }}_2-{\overline{\eta }}_1\frac{{\Delta }_{1,2}}{{\varphi }_1},\hfill \end{array}$$

(22c)

where ${\Delta }_{1,2}$ is a function to be determined through the substitution of (3) and (22) in (21). This calculation may be cumbersome but straightforward, leading to

$${\Delta }_{1,2}=\frac{{\psi }_1{\psi }_2+{\eta }_1{\eta }_2+{\overline{\eta }}_1{\overline{\eta }}_2}{{\lambda }_1+{\lambda }_2}=\frac{{\overrightarrow{\Psi }}_1·{\overrightarrow{\Psi }}_2}{{\lambda }_1+{\lambda }_2}.$$

(23)

This procedure results in a binary Darboux transformation [17], i.e., the fields and eigenfunctions of the iterated Lax pair (21) can be constructed by combining two different eigenfunctions of the seed Lax pair (19), corresponding to two different values of the spectral parameter. This binary Darboux transformation can be summarized in the form

$$\begin{array}{ccc}& & u^{\left[1\right]}=u^{\left[0\right]}+\frac{{\psi }_1{\eta }_1}{{\varphi }_1},\hfill \end{array}$$

(24a)

$$\begin{array}{ccc}& & {\overline{u}}^{\left[1\right]}={\overline{u}}^{\left[0\right]}+\frac{{\psi }_1{\overline{\eta }}_1}{{\varphi }_1},\hfill \end{array}$$

(24b)

$$\begin{array}{ccc}& & {\overrightarrow{\Psi }}_{1,2}={\overrightarrow{\Psi }}_2-\frac{2{\lambda }_1}{{\lambda }_1+{\lambda }_2}\left[\frac{{\overrightarrow{\Psi }}_1·{\overrightarrow{\Psi }}_2}{{\overrightarrow{\Psi }}_1·{\overrightarrow{\Psi }}_1}\right]{\overrightarrow{\Psi }}_1.\hfill \end{array}$$

(24c)

2.6. $\tau$-Functions and Iterated Solutions

The relation between the SMM and the Hirota direct method [20] can be easily derived by also considering the iteration of Equation (20) as

$${\varphi }_{1,2}=\frac{1}{2{\lambda }_2}{\overrightarrow{\Psi }}_{1,2}·{\overrightarrow{\Psi }}_{1,2}.$$

(25)

If we look at this equation as a nonlinear relation between the iterated eigenvector ${\overrightarrow{\Psi }}_{1,2}$ and an iterated singular manifold ${\varphi }_{1,2}$, we can easily conclude that ${\varphi }_{1,2}$ could also be expanded as a truncated Painlevé series. This expansion should be

$${\varphi }_{1,2}={\varphi }_2-\frac{{\Delta }_{1,2}^2}{{\varphi }_1},$$

(26)

as it can be checked by substitution of (24) in (25). As ${\varphi }_{1,2}$ is the singular manifold for the iterated solution $\left\{u^{\left[1\right]},{\overline{u}}^{\left[1\right]}\right\}$, a second iteration can be obtained as

$$\begin{array}{ccc}& & u^{\left[2\right]}=u^{\left[1\right]}+\frac{{\psi }_{1,2}{\eta }_{1,2}}{{\varphi }_{1,2}},\hfill \end{array}$$

(27a)

$$\begin{array}{ccc}& & {\overline{u}}^{\left[2\right]}=u^{\left[1\right]}+\frac{{\psi }_{1,2}{\overline{\eta }}_{1,2}}{{\varphi }_{1,2}},\hfill \end{array}$$

(27b)

which combined with (24) and (26) yields

$$\begin{array}{ccc}& & u^{\left[2\right]}=u^{\left[0\right]}+\frac{{\varphi }_1{\psi }_2{\eta }_2+{\varphi }_2{\psi }_1{\eta }_1-{\Delta }_{1,2}\left({\psi }_1{\eta }_2+{\psi }_2{\eta }_1\right)}{{\tau }_{1,2}},\hfill \end{array}$$

(28a)

$$\begin{array}{ccc}& & {\overline{u}}^{\left[2\right]}={\overline{u}}^{\left[0\right]}+\frac{{\varphi }_1{\psi }_2{\overline{\eta }}_2+{\varphi }_2{\psi }_1{\overline{\eta }}_1-{\Delta }_{1,2}\left({\psi }_1{\overline{\eta }}_2+{\psi }_2{\overline{\eta }}_1\right)}{{\tau }_{1,2}},\hfill \end{array}$$

(28b)

where

$$\begin{array}{ccc}& & {\tau }_{1,2}={\varphi }_1{\varphi }_2-{\Delta }_{1,2}^2=det{\Delta }_{i,j},i,j=1,2,\hfill \end{array}$$

(29a)

$$\begin{array}{ccc}& & {\Delta }_{i,j}=\frac{{\overrightarrow{\Psi }}_i·{\overrightarrow{\Psi }}_j}{{\lambda }_i+{\lambda }_j},{\varphi }_i={\Delta }_{i,i}.\hfill \end{array}$$

(29b)

Expression (23) can also be iterated as

$${\Delta }_{1,2,3}=\frac{{\psi }_{1,2}{\psi }_{1,3}+{\eta }_{1,2}{\eta }_{1,3}+{\overline{\eta }}_{1,2}{\overline{\eta }}_{1,3}}{{\lambda }_2+{\lambda }_3}=\frac{{\overrightarrow{\Psi }}_{1,2}·{\overrightarrow{\Psi }}_{1,3}}{{\lambda }_2+{\lambda }_3},$$

(30)

which is satisfied when ${\Delta }_{1,2,3}$ is expanded in a truncated Painlevé series as

$$\begin{array}{ccc}& & {\Delta }_{1,2,3}={\Delta }_{2,3}-\frac{{\Delta }_{1,2}{\Delta }_{1,3}}{{\varphi }_1}.\hfill \end{array}$$

(31)

This provides a new iteration for the singular manifold in the form

$$\begin{array}{ccc}& & {\varphi }_{1,2,3}={\varphi }_{1,3}-\frac{{\left({\Delta }_{1,2,3}\right)}^2}{{\varphi }_{1,2}},\hfill \end{array}$$

(32)

which retrieves the following third iteration for the solution

$$\begin{array}{ccc}& & u^{\left[3\right]}=u^{\left[2\right]}+\frac{{\psi }_{1,2,3}{\eta }_{1,2,3}}{{\varphi }_{1,2,3}},\hfill \end{array}$$

(33a)

$$\begin{array}{ccc}& & {\overline{u}}^{\left[3\right]}={\overline{u}}^{\left[2\right]}+\frac{{\psi }_{1,2,3}{\overline{\eta }}_{1,2,3}}{{\varphi }_{1,2,3}},\hfill \end{array}$$

(33b)

where

$${\overrightarrow{\Psi }}_{1,2,3}={\overrightarrow{\Psi }}_{1,3}-\frac{{\Delta }_{1,2,3}}{{\varphi }_{1,2}}{\overrightarrow{\Psi }}_{1,2}.$$

(34)

If we define

$${\tau }_{1,2,3}={\varphi }_{1,2,3}{\varphi }_{1,2}{\varphi }_1,$$

(35)

it is easy to prove that the $\tau$-function ${\tau }_{1,2,3}$ can be rewritten in compact form as

$${\tau }_{1,2,3}=det{\Delta }_{i,j},i,j=1,2,3.$$

(36)

In general, for the nth-iteration, the $\tau$-function is

$$\begin{array}{ccc}& & {\tau }_{1,\dots ,n}=det{\Delta }_{i,j},i,j=1,\cdots ,n,\hfill \end{array}$$

(37a)

$$\begin{array}{ccc}& & {\Delta }_{i,j}=\frac{{\overrightarrow{\Psi }}_i·{\overrightarrow{\Psi }}_j}{{\lambda }_i+{\lambda }_j},\hfill \end{array}$$

(37b)

where ${\Delta }_{i,j}$ accounts for the generalization to n dimensions of the $\Delta$-matrix introduced in (29).

The key point is that the eigenfunctions of the seed Lax pair (19) are the sole ingredients we need to construct the $\tau$-function (37) in every step of the iteration procedure.

3. Solutions

The iterative procedure arising from the Darboux tansformations described in the previous section can be successfully applied in order to obtain solutions of the system (1).

3.1. Eigenfunctions for the Seed Solution

The simplest solution of the system (1) is trivially

$$u^{\left[0\right]}={\overline{u}}^{\left[0\right]}=0,$$

(38)

whilst the solutions for the Lax pair (19) are in this case

$$\begin{array}{ccc}& & {\psi }_i=H_i\left(t\right)J_i(x,t),\hfill \end{array}$$

(39a)

$$\begin{array}{ccc}& & {\eta }_i=cos\left({\theta }_i\right)H_i\left(t\right),\hfill \end{array}$$

(39b)

$$\begin{array}{ccc}& & {\overline{\eta }}_i=sin\left({\theta }_i\right)H_i\left(t\right),\hfill \end{array}$$

(39c)

where ${\theta }_i$ is an arbitrary constant, and $H_i\left(t\right),J_i(x,t)$ are the functions

$$\begin{array}{c}\hfill H_i\left(t\right)=e^{-3{\lambda }_i^{3}t},J_i(x,t)=e^{{\lambda }_i\left(x-{\lambda }_i^{2}t\right)},i=1,2.\end{array}$$

(40)

3.2. $\Delta$-Matrix

According to (29b), we have

$$\begin{array}{cc}\hfill {\varphi }_i& =\frac{H_i^2}{2{\lambda }_i}\left(J_i^2+1\right),\hfill \end{array}$$

(41a)

$$\begin{array}{cc}\hfill {\Delta }_{i,j}& =\frac{H_i{H}_j}{{\lambda }_i+{\lambda }_j}\left[J_i{J}_j+cos({\theta }_i-{\theta }_j)\right].\hfill \end{array}$$

(41b)

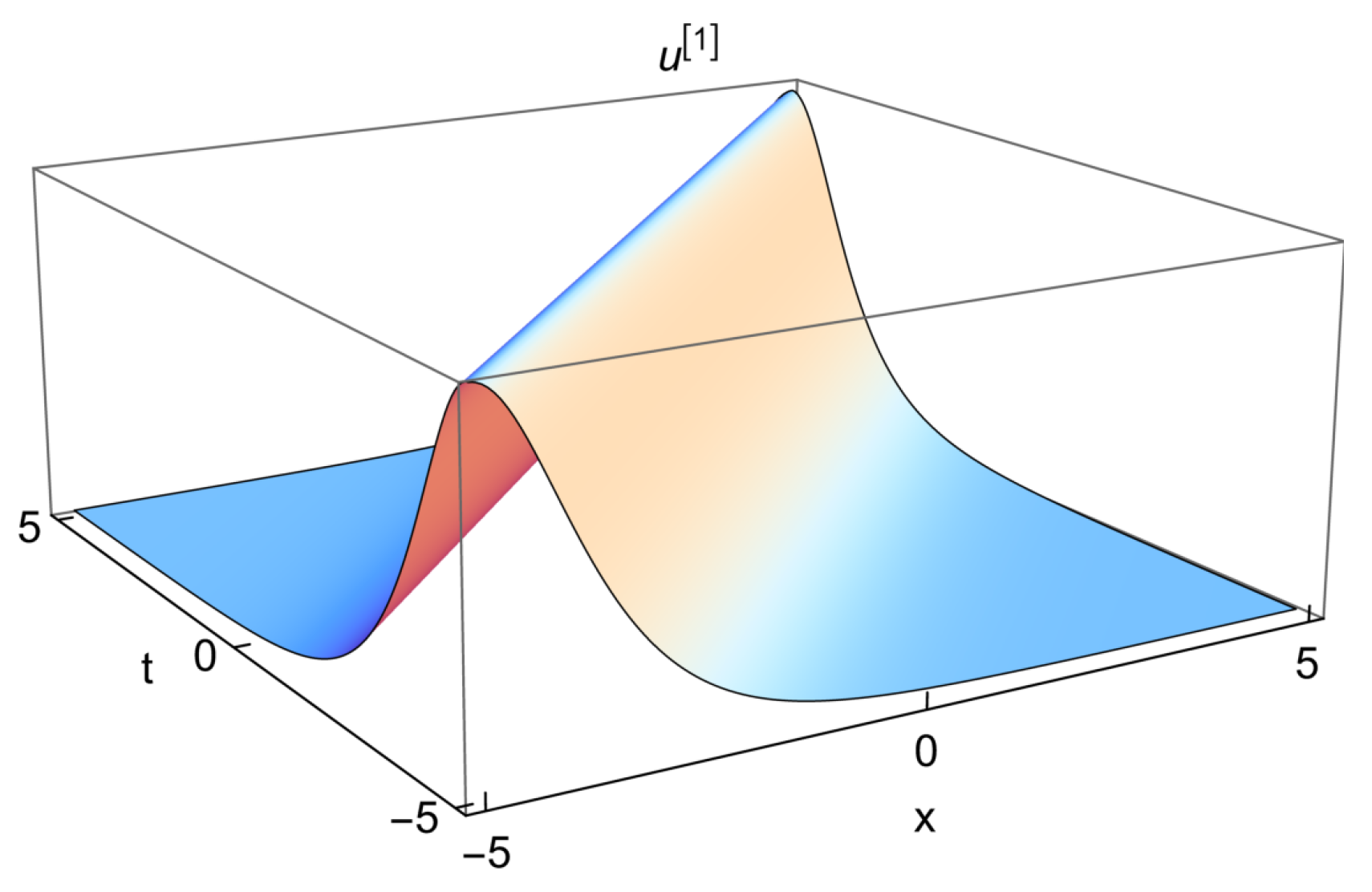
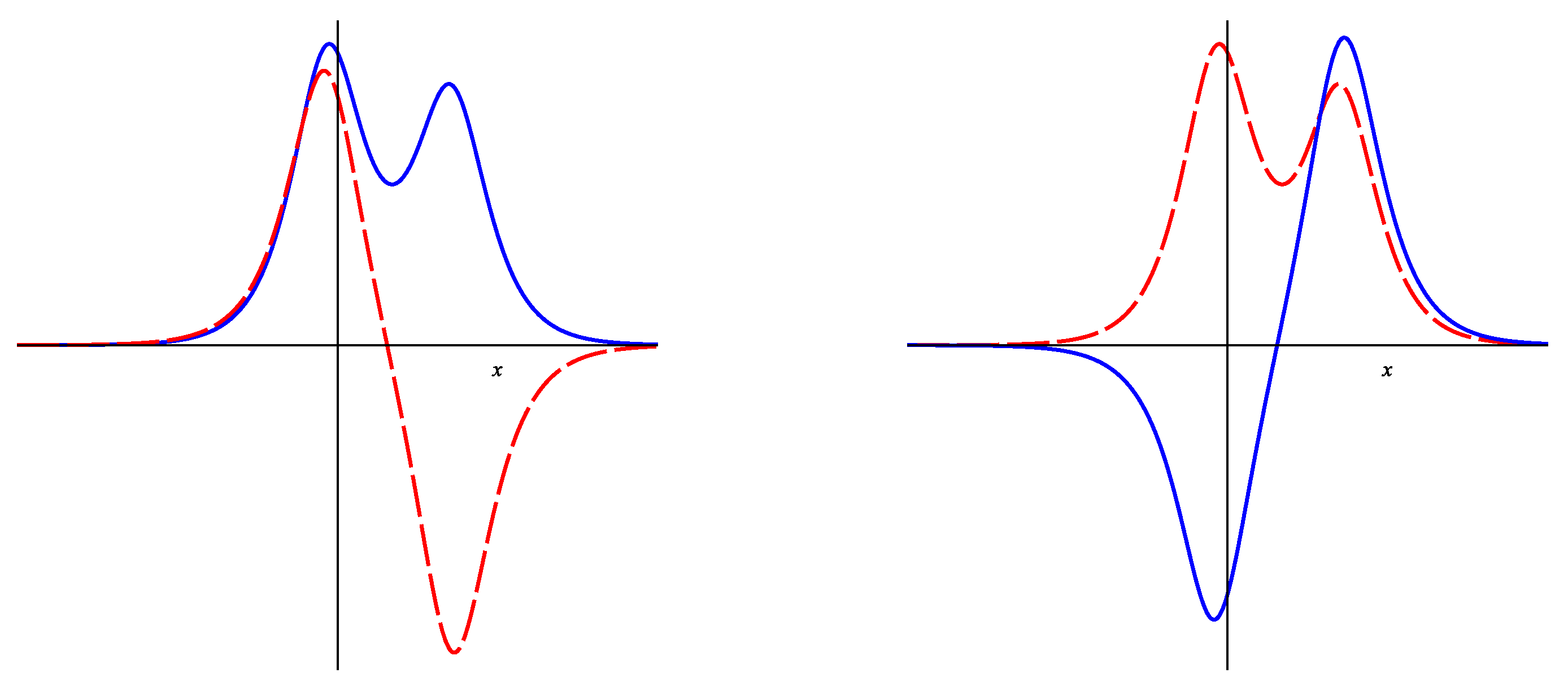
3.3. First Iterated Solution

From (24), the first iterated fields are

$$\begin{array}{cc}\hfill u^{\left[1\right]}& =\frac{{\lambda }_{1}cos\left({\theta }_1\right)}{cosh\left[{\lambda }_1\left(x-{\lambda }_1^{2}t\right)\right]},\hfill \\ \hfill {\overline{u}}^{\left[1\right]}& =\frac{{\lambda }_{1}sin\left({\theta }_1\right)}{cosh\left[{\lambda }_1\left(x-{\lambda }_1^{2}t\right)\right]}.\hfill \end{array}$$

(42)

These solutions depend on two arbitrary constants ${\lambda }_1$ and ${\theta }_1$, which can be complex. Nevertheless, these fields are free of singularities when ${\lambda }_1$ is real. The solutions display the usual profile of the travelling one-soliton solution for the mKdV equation, propagating alongside the direction $x-{\lambda }_1^{2}t$, as illustrated in Figure 1. Here, ${\lambda }_1^2$ is interpreted as the wave speed, and the angle ${\theta }_1$ establishes the orientation of the soliton, and it rescales its amplitude. For real values of the parameters, the solutions are always real and well-defined.

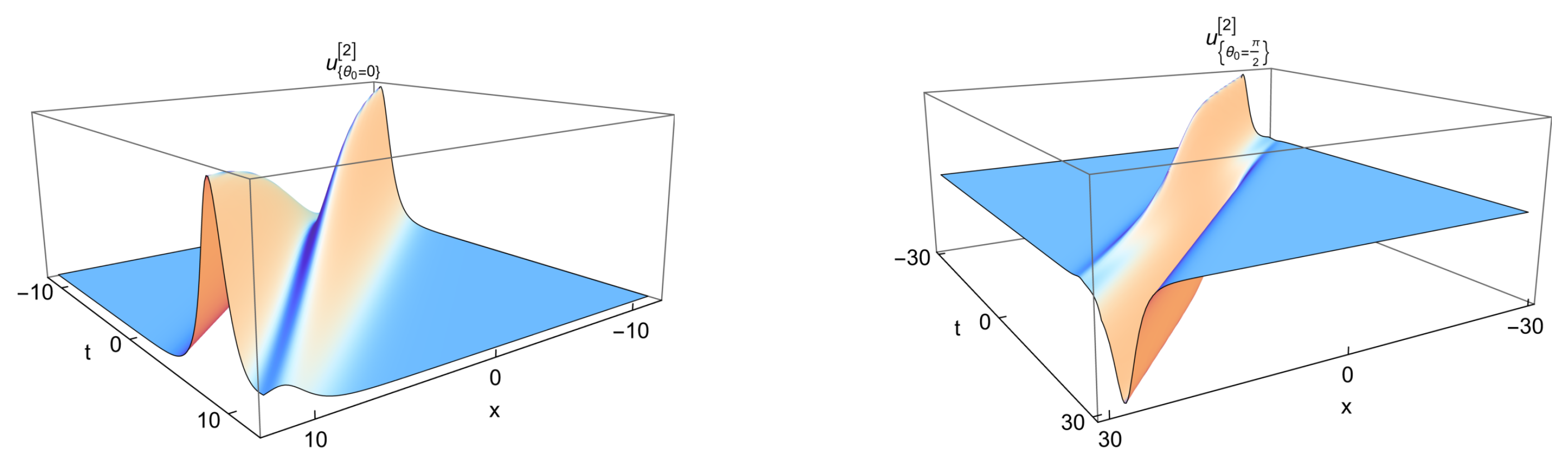
3.4. Second Iterated Solution

We select two sets of eigenfunctions of the form (39), corresponding to different eigenvalues ${\lambda }_1$ and ${\lambda }_2$. The singular manifolds and the $\Delta$-matrix (41) are

$$\begin{array}{ccc}& & {\varphi }_1=\frac{H_1^2}{2{\lambda }_1}\left(J_1^2+1\right),\hfill \end{array}$$

(43a)

$$\begin{array}{ccc}& & {\varphi }_2=\frac{H_2^2}{2{\lambda }_2}\left(J_2^2+1\right),\hfill \end{array}$$

(43b)

$$\begin{array}{ccc}& & {\Delta }_{1,2}=\frac{1}{{\lambda }_1+{\lambda }_2}{H}_1{H}_2{J}_1{J}_2,\hfill \end{array}$$

(43c)

where we have introduced the following ansatz

$${\theta }_1={\theta }_0,{\theta }_2={\theta }_0+\frac{\pi }{2},$$

(44)

and the $\tau$-function (29a) is

$$\tau =\frac{H_1^2{H}_2^2}{4{\lambda }_1{\lambda }_2}\left[1+J_1^2+J_2^2+{\left(\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2{J}_1^2{J}_2^2\right].$$

(45)

Different solutions can be derived through different choices of the spectral parameters. Notice that we are mainly interested in solutions for which the $\tau$-function (45) has no zeroes, and hence, solutions are free of singularities.

Let us introduce two arbitrary constants $k_0,{\lambda }_0$ defined as

$${\lambda }_1={\lambda }_0(1+k_0^2),{\lambda }_2={\lambda }_0(1-k_0^2).$$

(46)

Thus, Equation (45) can be written in terms of hyperbolic functions as:

$$\tau =\frac{H_1^2{H}_2^2{J}_1{J}_2}{2{\lambda }_0^2(1-k_0^4)}\left[k_0^{2}cosh(z_1+z_2)+cosh(z_1-z_2)\right],$$

(47)

where

$$\begin{array}{ccc}& & z_1={\lambda }_0(1+k_0^2)\left[x-{\lambda }_0^2{(1+k_0^2)}^{2}t\right]+ln\left(k_0\right),\hfill \end{array}$$

(48a)

$$\begin{array}{ccc}& & z_2={\lambda }_0(1-k_0^2)\left[x-{\lambda }_0^2{(1-k_0^2)}^{2}t\right]+ln\left(k_0\right),\hfill \end{array}$$

(48b)

$$\begin{array}{ccc}& & z_1+z_2=2{\lambda }_0\left[x-{\lambda }_0^2(3k_0^4+1)t\right]+2ln\left(k_0\right),\hfill \end{array}$$

(48c)

$$\begin{array}{ccc}& & z_1-z_2=2{\lambda }_0{k}_0^2\left[x-{\lambda }_0^2(k_0^4+3)t\right].\hfill \end{array}$$

(48d)

Equation (28) therefore yields the solutions

$$\begin{array}{ccc}& & u^{\left[2\right]}=\frac{2k_0{\lambda }_0\left[(1+k_0^2)cosh\left(z_2\right)cos\left({\theta }_0\right)+(1-k_0^2)sinh\left(z_1\right)sin\left({\theta }_0\right)\right]}{k_0^{2}cosh(z_1+z_2)+cosh(z_1-z_2)},\hfill \end{array}$$

(49a)

$$\begin{array}{ccc}& & {\overline{u}}^{\left[2\right]}=\frac{2k_0{\lambda }_0\left[(1+k_0^2)cosh\left(z_2\right)sin\left({\theta }_0\right)-(1-k_0^2)sinh\left(z_1\right)cos\left({\theta }_0\right)\right]}{k_0^{2}cosh(z_1+z_2)+cosh(z_1-z_2)}.\hfill \end{array}$$

(49b)

This solution depends on three arbitrary parameters $\{k_0,{\lambda }_0$ and ${\theta }_0\}$. Notice that all of these parameters can, in general, be complex. The solutions of reference [14] correspond to particular cases of this more general solution. For real values of the parameters, the behaviour of $u^{\left[2\right]}$ and ${\overline{u}}^{\left[2\right]}$ is shown in Figure 2.

It is also worthwhile to remark that solutions (49) are rotations of angle ${\theta }_0$ that linearly combine the following two independent solutions

$$\begin{array}{ccc}& & u_{\{{\theta }_0=0\}}^{\left[2\right]}=\frac{2k_0{\lambda }_0(1+k_0^2)cosh\left(z_2\right)}{k_0^{2}cosh(z_1+z_2)+cosh(z_1-z_2)},\hfill \end{array}$$

(50a)

$$\begin{array}{ccc}& & u_{\{{\theta }_0=\frac{\pi }{2}\}}^{\left[2\right]}=\frac{2k_0{\lambda }_0(1-k_0^2)sinh\left(z_1\right)}{k_0^{2}cosh(z_1+z_2)+cosh(z_1-z_2)},\hfill \end{array}$$

(50b)

whose behaviour is plotted in Figure 3.

4. Conclusions

A modification of the Singular Manifold Method has been implemented in order to derive a spectral problem for a generalized complex version of the modified Korteweg-de Vries equation. This modification yields a direct relation between the singular manifold and the three-component eigenvector of the spectral problem. The salient point is that the introduction of the spectral parameter in the Lax pair can be solely achieved when the generalization of the singular manifold is considered.

Once the spectral problem is obtained, we shall apply the truncation of the Painlevé expansion to the Lax pair itself. It allows us to derive, in an algorithmic way, many of the properties of a nonlinear integrable system such as Bäcklund and binary Darboux transformations.

We should notice that this derivation of binary Darboux transformations can be applied in the future to different systems [18] for which the truncation of the Painlevé series has been successfully applied.

The iteration of this method gives rise to the $\tau$-function and to a recursive procedure to construct solutions.

In particular, we have obtained solutions for the second iteration. These solutions depend on three arbitrary complex parameters and generalize previously known results from [14]. For real values of the parameters, the solution exhibits hyperbolic behaviour in both space and time.