MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy
Abstract
1. Introduction
- We propose the MFO-SFR algorithm, boosting the performance and enriching the diversity of the canonical MFO;
- We introduce an effective stagnation finding and replacing (SFR) strategy to boost the performance of the search process; and
- We introduce an archive to incorporate the representative and the global best flames throughout the search process in order to enrich the diversity.
2. Related Works
3. Moth-Flame Optimization (MFO) Algorithm
4. The Proposed MFO-SFR Algorithm
| Algorithm 1. The pseudocode of the archive construction process. | |
| Input: C: Number of considered flames, and κ: the maximum size of the archive Arc. | |
| Output: Returns the archive Arc. | |
| 1. | begin |
| 2. | dualPop and dualFit are created based on flame construction defined in Table 1. |
| 3. | FitBest = Ascending order of the vector dualFit and selecting the best N values. |
| 4. | PopBest = The corresponding positions of vector FitBest. |
| 5. | Computing RF using Equation (13) for C number of considered flames. |
| 6. | If the current memory size < κ−1. |
| 7. | Inserting RF and the global best flame into the Arc. |
| 8. | else |
| 9. | Replacing RF and the global best flame with two existing memory entries. |
| 10. | end if |
| 11. | end |
Complexity Analysis
| Algorithm 2. The pseudocode of the proposed MFO-SFR algorithm. | |
| Input: N: Number of moths, MaxIterations: Maximum iterations, and D: Dimension size. | |
| Output: Returns the position of the global best flame and its fitness value. | |
| 1. | Begin |
| 2. | Initiating matrix X (t) using a uniform random distribution in the D-dimensional search space. |
| 3. | Computing the fitness value of X (t) and storing them in vector OX (t). |
| 4. | Constructing the flame fitness value OF by ascending order of the vector OM (t). |
| 5. | Constructing the flame positions F based on their obtained vector OF. |
| 6. | While t ≤ MaxIterations |
| 7. | Updating F and OF by the best N moths from F and current X. |
| 8. | Computing the flame number R using Equation (2). |
| 9. | Archiving using Algorithm 1. |
| 10. | For i = 1: N |
| 11. | If i ≤ R |
| 12. | Computing the distance between flame Fi (t) and Mi (t) using Equation (9). |
| 13. | Updating the position of Xi (t) using Equation (8). |
| 14. | else |
| 15. | Computing the distance using Equation (10). |
| 16. | Updating the position of Xi (t) using Equation (8). |
| 17. | End if |
| 18. | Checking the feasibility and correcting the new position. |
| 19. | Computing the fitness value of the new position. |
| 20. | End for |
| 21. | Updating the global best flame. |
| 22. | End while |
5. Evaluation of the Proposed MFO-SFR Algorithm
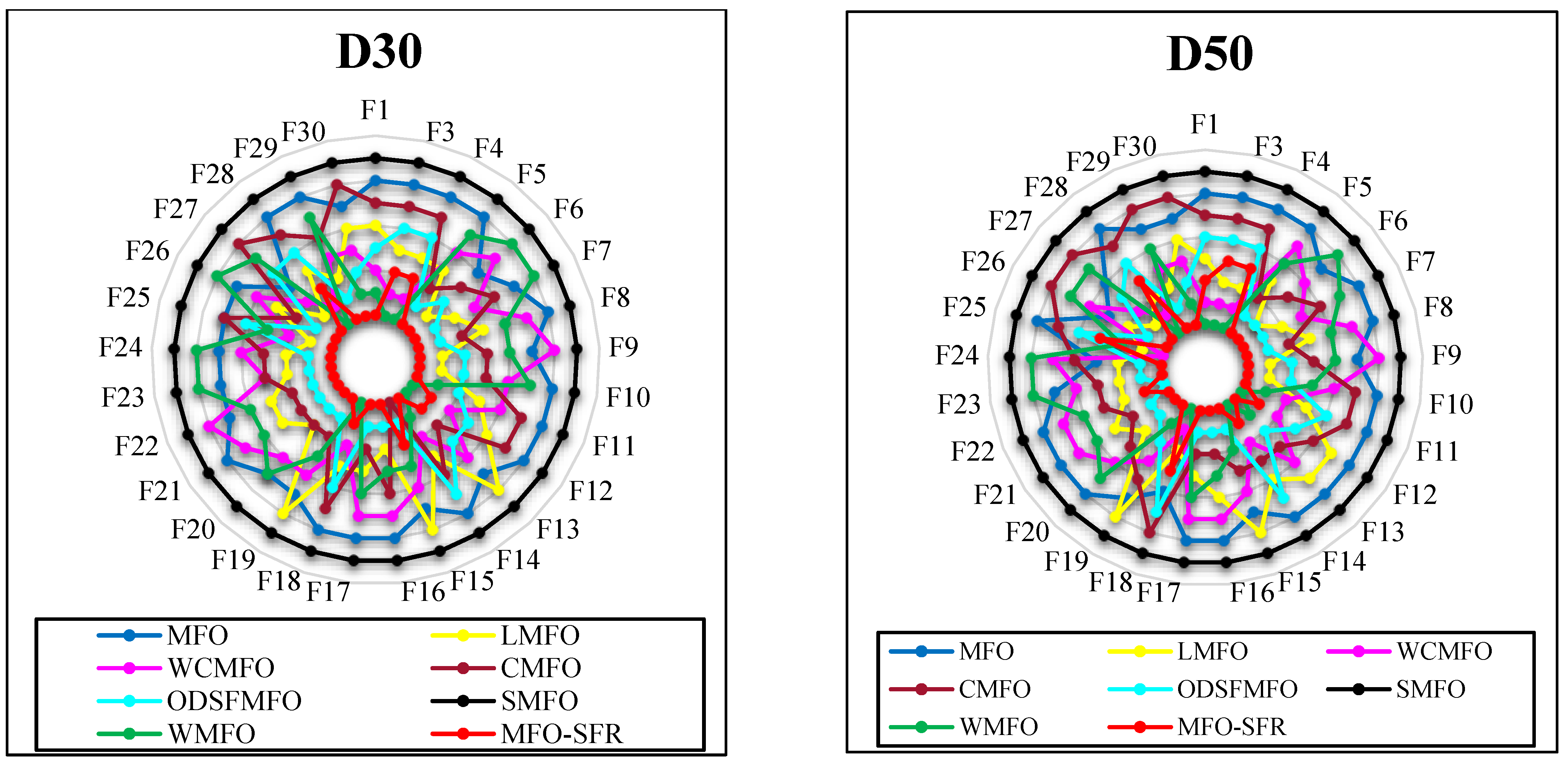
5.1. Comparing the Proposed MFO-SFR Algorithm with MFO Variants
5.2. Comparing the Proposed MFO-SFR Algorithm with Other Well-Known Optimization Algorithms
5.3. Population Diversity Analysis
5.4. The Overall Effectiveness of MFO-SFR
6. Applicability of MFO-SFR to Solving Mechanical Engineering Problems
6.1. Welded Beam Design (WBD) Problem
| Consider | (17) | ||
| Min | |||
| Subject to | |||
| Variable range | , . | ||
| where | , , in. | ||
6.2. The Four-Stage Gearbox Problem
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| #F | Max Percentage | Average Percentage | #F | Max Percentage | Average Percentage | #F | Max Percentage | Average Percentage |
|---|---|---|---|---|---|---|---|---|
| F1 | 2.03 | 0.40 | F12 | 26.05 | 3.32 | F22 | 22.13 | 3.51 |
| F3 | 0.00 | 0.00 | F13 | 1.16 | 0.16 | F23 | 0.12 | 0.01 |
| F4 | 0.90 | 0.13 | F14 | 6.85 | 0.34 | F24 | 3.41 | 0.42 |
| F5 | 0.60 | 0.16 | F15 | 2.12 | 0.21 | F25 | 0.27 | 0.03 |
| F6 | 0.00 | 0.00 | F16 | 0.10 | 0.01 | F26 | 2.53 | 0.65 |
| F7 | 4.25 | 0.34 | F17 | 0.02 | 0.00 | F27 | 3.40 | 0.28 |
| F8 | 14.97 | 0.84 | F18 | 0.37 | 0.02 | F28 | 11.15 | 0.64 |
| F9 | 0.01 | 0.00 | F19 | 2.00 | 0.13 | F29 | 28.22 | 1.46 |
| F10 | 12.05 | 1.22 | F20 | 5.24 | 0.81 | F30 | 9.30 | 0.47 |
| F11 | 1.25 | 0.31 | F21 | 0.01 | 0.00 |
References
- Zabinsky, Z.B. Stochastic methods for practical global optimization. J. Glob. Optim. 1998, 13, 433–444. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Romeijn, H.E.; Tuy, H. Recent developments and trends in global optimization. J. Comput. Appl. Math. 2000, 124, 209–228. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Masdari, M.; Rahmani, A.M.; Mohammadi, M.; Aldalwie, A.H.M.; Majeed, M.K.; Karim, S.H.T. Improved butterfly optimization algorithm for data placement and scheduling in edge computing environments. J. Grid Comput. 2021, 19, 1–27. [Google Scholar] [CrossRef]
- Hassan, B.A.; Rashid, T.A.; Mirjalili, S. Formal context reduction in deriving concept hierarchies from corpora using adaptive evolutionary clustering algorithm star. Complex Intell. Syst. 2021, 7, 2383–2398. [Google Scholar] [CrossRef]
- Hassan, B.A. CSCF: A chaotic sine cosine firefly algorithm for practical application problems. Neural Comput. Appl. 2021, 33, 7011–7030. [Google Scholar] [CrossRef]
- Yi, H.; Duan, Q.; Liao, T.W. Three improved hybrid metaheuristic algorithms for engineering design optimization. Appl. Soft Comput. 2013, 13, 2433–2444. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Asghari Varzaneh, Z.; Zamani, H.; Mirjalili, S. Binary Starling Murmuration Optimizer Algorithm to Select Effective Features from Medical Data. Appl. Sci. 2022, 13, 564. [Google Scholar] [CrossRef]
- Piri, J.; Mohapatra, P.; Acharya, B.; Gharehchopogh, F.S.; Gerogiannis, V.C.; Kanavos, A.; Manika, S. Feature Selection Using Artificial Gorilla Troop Optimization for Biomedical Data: A Case Analysis with COVID-19 Data. Mathematics 2022, 10, 2742. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S. Binary Approaches of Quantum-Based Avian Navigation Optimizer to Select Effective Features from High-Dimensional Medical Data. Mathematics 2022, 10, 2770. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Siddiqi, U.F.; Shiraishi, Y.; Dahb, M.; Sait, S.M. A memory efficient stochastic evolution based algorithm for the multi-objective shortest path problem. Appl. Soft Comput. 2014, 14, 653–662. [Google Scholar] [CrossRef]
- Kavoosi, M.; Dulebenets, M.A.; Abioye, O.; Pasha, J.; Theophilus, O.; Wang, H.; Kampmann, R.; Mikijeljević, M. Berth scheduling at marine container terminals: A universal island-based metaheuristic approach. Marit. Bus. Rev. 2019, 5, 30–66. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E. Initialisation Approaches for Population-Based Metaheuristic Algorithms: A Comprehensive Review. Appl. Sci. 2022, 12, 896. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, A. Applications of nature-inspired meta-heuristic algorithms: A survey. Int. J. Adv. Intell. Paradig. 2021, 20, 388–417. [Google Scholar] [CrossRef]
- Fister Jr, I.; Yang, X.-S.; Fister, I.; Brest, J.; Fister, D. A brief review of nature-inspired algorithms for optimization. arXiv 2013, arXiv:1307.4186. [Google Scholar]
- Dehghani, M.; Mardaneh, M.; Malik, O.P.; NouraeiPour, S.M. DTO: Donkey theorem optimization. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 1855–1859. [Google Scholar]
- Fard, E.S.; Monfaredi, K.; Nadimi, M.H. An Area-Optimized Chip of Ant Colony Algorithm Design in Hardware Platform Using the Address-Based Method. Int. J. Electr. Comput. Eng. 2014, 4, 989–998. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Schwefel, H.-P. Evolution strategies–a comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Jiao, L.; Li, Y.; Gong, M.; Zhang, X. Quantum-inspired immune clonal algorithm for global optimization. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 1234–1253. [Google Scholar] [CrossRef]
- Lu, T.-C.; Juang, J.-C. Quantum-inspired space search algorithm (QSSA) for global numerical optimization. Appl. Math. Comput. 2011, 218, 2516–2532. [Google Scholar] [CrossRef]
- Arpaia, P.; Maisto, D.; Manna, C. A Quantum-inspired Evolutionary Algorithm with a competitive variation operator for Multiple-Fault Diagnosis. Appl. Soft Comput. 2011, 11, 4655–4666. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kashan, A.H. A new metaheuristic for optimization: Optics inspired optimization (OIO). Comput. Oper. Res. 2015, 55, 99–125. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. -Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Shi, Y. Brain storm optimization algorithm. In Proceedings of the International Conference in Swarm Intelligence, Chongqing, China, 12–15 June 2011; pp. 303–309. [Google Scholar]
- Moosavian, N.; Roodsari, B.K. Soccer league competition algorithm: A novel meta-heuristic algorithm for optimal design of water distribution networks. Swarm Evol. Comput. 2014, 17, 14–24. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K. Volleyball premier league algorithm. Appl. Soft Comput. 2018, 64, 161–185. [Google Scholar] [CrossRef]
- Moosavi, S.H.S.; Bardsiri, V.K. Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Eng. Appl. Artif. Intell. 2019, 86, 165–181. [Google Scholar] [CrossRef]
- Naik, A.; Satapathy, S.C. Past present future: A new human-based algorithm for stochastic optimization. Soft Comput. 2021, 25, 12915–12976. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kar, A.K. Swarm intelligence: A review of algorithms. Nat. -Inspired Comput. Optim. 2017, 10, 475–494. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. CCSA: Conscious neighborhood-based crow search algorithm for solving global optimization problems. Appl. Soft Comput. 2019, 85, 105583. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Coelho, L.d.S. Elephant herding optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. -Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Horse herd optimization algorithm: A nature-inspired algorithm for high-dimensional optimization problems. Knowl. -Based Syst. 2021, 213, 106711. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intel. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Shayanfar, H.; Gharehchopogh, F.S. Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems. Appl. Soft Comput. 2018, 71, 728–746. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf mongoose optimization algorithm. Comput. Method Appl. M 2022, 391, 114570. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. A comparative review of approaches to prevent premature convergence in GA. Appl. Soft Comput. 2014, 24, 1047–1077. [Google Scholar] [CrossRef]
- Chaitanya, K.; Somayajulu, D.; Krishna, P.R. Memory-based approaches for eliminating premature convergence in particle swarm optimization. Appl. Intell. 2021, 51, 4575–4608. [Google Scholar] [CrossRef]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Banharnsakun, A.; Achalakul, T.; Sirinaovakul, B. The best-so-far selection in artificial bee colony algorithm. Appl. Soft Comput. 2011, 11, 2888–2901. [Google Scholar] [CrossRef]
- Xiang, W.-L.; Li, Y.-Z.; Meng, X.-L.; Zhang, C.-M.; An, M.-Q. A grey artificial bee colony algorithm. Appl. Soft Comput. 2017, 60, 1–17. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H. DMDE: Diversity-maintained multi-trial vector differential evolution algorithm for non-decomposition large-scale global optimization. Expert Syst. Appl. 2022, 198, 116895. [Google Scholar] [CrossRef]
- Wang, F.; Liao, X.; Fang, N.; Jiang, Z. Optimal Scheduling of Regional Combined Heat and Power System Based on Improved MFO Algorithm. Energies 2022, 15, 3410. [Google Scholar] [CrossRef]
- Kaur, K.; Singh, U.; Salgotra, R. An enhanced moth flame optimization. Neural Comput. Appl. 2020, 32, 2315–2349. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Y.; Zhang, S.; Song, J. Lévy-flight moth-flame algorithm for function optimization and engineering design problems. Math. Probl. Eng. 2016, 2016, 1–22. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput. 2019, 23, 1699–1722. [Google Scholar] [CrossRef]
- Hongwei, L.; Jianyong, L.; Liang, C.; Jingbo, B.; Yangyang, S.; Kai, L. Chaos-enhanced moth-flame optimization algorithm for global optimization. J. Syst. Eng. Electron. 2019, 30, 1144–1159. [Google Scholar]
- Chen, C.; Wang, X.; Yu, H.; Wang, M.; Chen, H. Dealing with multi-modality using synthesis of Moth-flame optimizer with sine cosine mechanisms. Math. Comput. Simul. 2021, 188, 291–318. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Li, Z.; Zeng, J.; Chen, Y.; Ma, G.; Liu, G. Death mechanism-based moth–flame optimization with improved flame generation mechanism for global optimization tasks. Expert Syst. Appl. 2021, 183, 115436. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Heidari, A.A.; Luo, J.; Zhang, Q.; Zhao, X.; Li, C. An efficient chaotic mutative moth-flame-inspired optimizer for global optimization tasks. Expert Syst. Appl. 2019, 129, 135–155. [Google Scholar] [CrossRef]
- Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Oliva, D. Hybridizing of Whale and Moth-Flame Optimization Algorithms to Solve Diverse Scales of Optimal Power Flow Problem. Electronics 2022, 11, 831. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Non-Linear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L. An improved moth-flame optimization algorithm with adaptation mechanism to solve numerical and mechanical engineering problems. Entropy 2021, 23, 1637. [Google Scholar] [CrossRef] [PubMed]
- Pelusi, D.; Mascella, R.; Tallini, L.; Nayak, J.; Naik, B.; Deng, Y. An Improved Moth-Flame Optimization algorithm with hybrid search phase. Knowl. -Based Syst. 2020, 191, 105277. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L.; Abd Elaziz, M. Migration-based moth-flame optimization algorithm. Processes 2021, 9, 2276. [Google Scholar] [CrossRef]
- Ma, L.; Wang, C.; Xie, N.-g.; Shi, M.; Ye, Y.; Wang, L. Moth-flame optimization algorithm based on diversity and mutation strategy. Appl. Intell. 2021, 51, 5836–5872. [Google Scholar] [CrossRef]
- Zhao, X.; Fang, Y.; Liu, L.; Li, J.; Xu, M. An improved moth-flame optimization algorithm with orthogonal opposition-based learning and modified position updating mechanism of moths for global optimization problems. Appl. Intell. 2020, 50, 4434–4458. [Google Scholar] [CrossRef]
- Sapre, S.; Mini, S. Opposition-based moth flame optimization with Cauchy mutation and evolutionary boundary constraint handling for global optimization. Soft Comput. 2019, 23, 6023–6041. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Saha, A.K.; Nama, S.; Masdari, M. An improved moth flame optimization algorithm based on modified dynamic opposite learning strategy. Artif. Intell. Rev. 2022, 1–59. [Google Scholar] [CrossRef]
- Li, C.; Niu, Z.; Song, Z.; Li, B.; Fan, J.; Liu, P.X. A double evolutionary learning moth-flame optimization for real-parameter global optimization problems. IEEE Access 2018, 6, 76700–76727. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, X.; Liu, J. An improved moth-flame optimization algorithm for engineering problems. Symmetry 2020, 12, 1234. [Google Scholar] [CrossRef]
- Shehab, M.; Alshawabkah, H.; Abualigah, L.; AL-Madi, N. Enhanced a hybrid moth-flame optimization algorithm using new selection schemes. Eng. Comput. 2021, 37, 2931–2956. [Google Scholar] [CrossRef]
- Zhang, H.; Li, R.; Cai, Z.; Gu, Z.; Heidari, A.A.; Wang, M.; Chen, H.; Chen, M. Advanced orthogonal moth flame optimization with Broyden–Fletcher–Goldfarb–Shanno algorithm: Framework and real-world problems. Expert Syst. Appl. 2020, 159, 113617. [Google Scholar] [CrossRef]
- Yu, C.; Heidari, A.A.; Chen, H. A quantum-behaved simulated annealing algorithm-based moth-flame optimization method. Appl. Math. Model. 2020, 87, 1–19. [Google Scholar] [CrossRef]
- Alzaqebah, M.; Alrefai, N.; Ahmed, E.A.; Jawarneh, S.; Alsmadi, M.K. Neighborhood search methods with moth optimization algorithm as a wrapper method for feature selection problems. Int. J. Electr. Comput. Eng. 2020, 10, 3672. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Li, K.; Beng, G.H.; Jiang, Z.; Wang, C.; Liu, N. Enhanced moth-flame optimization based on cultural learning and Gaussian mutation. J. Bionic Eng. 2018, 15, 751–763. [Google Scholar] [CrossRef]
- Helmi, A.; Alenany, A. An enhanced Moth-flame optimization algorithm for permutation-based problems. Evol. Intell. 2020, 13, 741–764. [Google Scholar] [CrossRef]
- Sayed, G.I.; Hassanien, A.E. A hybrid SA-MFO algorithm for function optimization and engineering design problems. Complex Intell. Syst. 2018, 4, 195–212. [Google Scholar] [CrossRef]
- Buch, H.; Trivedi, I.N.; Jangir, P. Moth flame optimization to solve optimal power flow with non-parametric statistical evaluation validation. Cogent Eng. 2017, 4, 1286731. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Parmar, S.A.; Jangir, N. Optimal power flow with voltage stability improvement and loss reduction in power system using Moth-Flame Optimizer. Neural Comput. Appl. 2018, 30, 1889–1904. [Google Scholar] [CrossRef]
- Jangir, P.; Jangir, N. Optimal power flow using a hybrid particle Swarm optimizer with moth flame optimizer. Glob. J. Res. Eng. 2017, 17, 15–32. [Google Scholar]
- Sahoo, S.K.; Saha, A.K. A hybrid moth flame optimization algorithm for global optimization. J. Bionic Eng. 2022, 19, 1522–1543. [Google Scholar] [CrossRef]
- Khan, B.S.; Raja, M.A.Z.; Qamar, A.; Chaudhary, N.I. Design of moth flame optimization heuristics for integrated power plant system containing stochastic wind. Appl. Soft Comput. 2021, 104, 107193. [Google Scholar] [CrossRef]
- Singh, P.; Bishnoi, S. Modified moth-Flame optimization for strategic integration of fuel cell in renewable active distribution network. Electr. Power Syst. Res. 2021, 197, 107323. [Google Scholar] [CrossRef]
- Zhang, H.; Heidari, A.A.; Wang, M.; Zhang, L.; Chen, H.; Li, C. Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 2020, 211, 112764. [Google Scholar] [CrossRef]
- Cui, Z.; Li, C.; Huang, J.; Wu, Y.; Zhang, L. An improved moth flame optimization algorithm for minimizing specific fuel consumption of variable cycle engine. IEEE Access 2020, 8, 142725–142735. [Google Scholar] [CrossRef]
- Khurma, R.A.; Aljarah, I.; Sharieh, A. A simultaneous moth flame optimizer feature selection approach based on levy flight and selection operators for medical diagnosis. Arab. J. Sci. Eng. 2021, 46, 8415–8440. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Morrison, R.W. Designing Evolutionary Algorithms for Dynamic Environments; Springer: Berlin/Heidelberg, Germany, 2004; Volume 178. [Google Scholar]
- Altabeeb, A.M.; Mohsen, A.M.; Abualigah, L.; Ghallab, A. Solving capacitated vehicle routing problem using cooperative firefly algorithm. Appl. Soft Comput. 2021, 108, 107403. [Google Scholar] [CrossRef]
- Ragsdell, K.; Phillips, D. Optimal design of a class of welded structures using geometric programming. Eng. Ind. 1976, 98, 1021–1025. [Google Scholar] [CrossRef]
- Yokota, T.; Taguchi, T.; Gen, M. A solution method for optimal weight design problem of the gear using genetic algorithms. Comput. Ind. Eng. 1998, 35, 523–526. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]





| Input: X: the positions of moths, Fit: the fitness values of moths, F: the position of the flame, and OF: the fitness values of flames. | |
| Flame construction in the first iteration when t = 1. | |
| 1. | Sort the vector Fit in ascending order and extract the sorted index in {j1, j2, …, jN}. |
| 2. | Construct the flame matrix F (t) = {F1 ← Xj1, F2 ← Xj2, …, FN ← XjN}. |
| Flame construction for the rest iteration when t > 1. | |
| 1. | Construct matrix dualPop by combining matrices F(t) and X (t − 1). |
| 2. | Construct vector dualFit by combining vectors OF(t) and Fit (t − 1). |
| 3. | Sort the vector dualFit in ascending order and extract the sorted index in {j1, j2, …, j2N}. |
| 4. | Construct the flame matrix F (t) = {F1 ← Xj1, F2 ← Xj2, …, FN ← XjN}. |
| Alg. | Parameter Settings |
|---|---|
| MFO | b = 1, a decreased linearly from −1 to −2. |
| LMFO | β = 1.5, µ and v are normal distributions, Г is the gamma function. |
| WCMFO | The number of rivers and seas = 4. |
| CMFO | b = 1, a decreased linearly from −1 to −2, chaotic map = Singer. |
| ODSFMFO | m = 6, pc = 0.5, γ = 5, α = 1, l = 10, b = 1, β = 1.5. |
| SMFO | r4 = random number between the interval (0, 1). |
| WMFO | α decreased linearly from 2 to 0, b = 1. |
| PSO | c1 = c2 = 2, vmax = 6, w = 0.9. |
| KH | Vf = 0.02, Dmax = 0.005, Nmax = 0.01, Sr = 0. |
| GWO | The parameter a decreased linearly from 2 to 0. |
| CSA | AP = 0.1, fl = 2. |
| HOA | w = 1, δD = 0.02, δI = 0.02, gδ = 1.5, hβ = 0.9, hγ = 0.5, sβ = 0.2, sγ = 0.1, iγ = 0.3, dα = 0.5, dβ = 0.2, dγ = 0.1, rδ = 0.1, rγ = 0.05 |
| MFO-SFR | b = 1, a decreased linearly from −1 to −2, κ = round (D2 × (log N)), C = N/5. |
| F. | Metrics | MFO | LMFO | WCMFO | CMFO | ODSFMFO | SMFO | WMFO | MFO-SFR |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 6.278 × 109 | 2.544 × 107 | 1.317 × 104 | 1.078 × 108 | 6.016 × 106 | 3.119 × 1010 | 3.822 × 103 | 1.791 × 103 |
| Min | 1.027 × 109 | 1.899 × 107 | 1.924 × 103 | 3.760 × 106 | 9.949 × 105 | 1.734 × 1010 | 1.013 × 102 | 1.017 × 102 | |
| F3 | Avg | 9.453 × 104 | 3.473 × 103 | 1.541 × 103 | 5.059 × 104 | 3.050 × 104 | 8.300 × 104 | 3.909 × 102 | 1.312 × 104 |
| Min | 1.203 × 104 | 1.499 × 103 | 3.111 × 102 | 2.945 × 104 | 1.631 × 104 | 7.186 × 104 | 3.007 × 102 | 7.513 × 103 | |
| F4 | Avg | 8.558 × 102 | 4.919 × 102 | 4.846 × 102 | 6.960 × 102 | 5.356 × 102 | 5.612 × 103 | 4.810 × 102 | 4.914 × 102 |
| Min | 4.991 × 102 | 4.742 × 102 | 4.009 × 102 | 5.139 × 102 | 4.985 × 102 | 2.322 × 103 | 4.249 × 102 | 4.700 × 102 | |
| F5 | Avg | 6.740 × 102 | 6.300 × 102 | 6.721 × 102 | 6.073 × 102 | 5.506 × 102 | 8.725 × 102 | 6.739 × 102 | 5.227 × 102 |
| Min | 6.114 × 102 | 5.816 × 102 | 6.126 × 102 | 5.736 × 102 | 5.270 × 102 | 8.105 × 102 | 6.234 × 102 | 5.109 × 102 | |
| F6 | Avg | 6.260 × 102 | 6.030 × 102 | 6.236 × 102 | 6.189 × 102 | 6.037 × 102 | 6.814 × 102 | 6.366 × 102 | 6.000 × 102 |
| Min | 6.113 × 102 | 6.018 × 102 | 6.137 × 102 | 6.086 × 102 | 6.010 × 102 | 6.571 × 102 | 6.143 × 102 | 6.000 × 102 | |
| F7 | Avg | 1.007 × 103 | 8.716 × 102 | 9.050 × 102 | 9.430 × 102 | 8.099 × 102 | 1.359 × 103 | 1.056 × 103 | 7.669 × 102 |
| Min | 8.538 × 102 | 8.311 × 102 | 8.045 × 102 | 8.684 × 102 | 7.824 × 102 | 1.198 × 103 | 9.248 × 102 | 7.460 × 102 | |
| F8 | Avg | 9.895 × 102 | 9.375 × 102 | 9.839 × 102 | 9.097 × 102 | 8.528 × 102 | 1.093 × 103 | 9.539 × 102 | 8.209 × 102 |
| Min | 9.126 × 102 | 8.978 × 102 | 9.344 × 102 | 8.645 × 102 | 8.343 × 102 | 1.052 × 103 | 8.547 × 102 | 8.090 × 102 | |
| F9 | Avg | 6.219 × 103 | 9.256 × 102 | 8.623 × 103 | 2.331 × 103 | 1.118 × 103 | 9.431 × 103 | 4.543 × 103 | 9.038 × 102 |
| Min | 3.323 × 103 | 9.074 × 102 | 5.118 × 103 | 1.476 × 103 | 9.647 × 102 | 7.359 × 103 | 1.675 × 103 | 9.005 × 102 | |
| F10 | Avg | 5.259 × 103 | 4.240 × 103 | 4.848 × 103 | 5.005 × 103 | 4.332 × 103 | 8.272 × 103 | 5.192 × 103 | 4.062 × 103 |
| Min | 4.231 × 103 | 3.205 × 103 | 4.003 × 103 | 4.204 × 103 | 3.570 × 103 | 7.449 × 103 | 3.759 × 103 | 2.461 × 103 | |
| F11 | Avg | 3.967 × 103 | 1.314 × 103 | 1.363 × 103 | 1.985 × 103 | 1.284 × 103 | 5.799 × 103 | 1.248 × 103 | 1.143 × 103 |
| Min | 1.370 × 103 | 1.180 × 103 | 1.252 × 103 | 1.206 × 103 | 1.204 × 103 | 2.547 × 103 | 1.170 × 103 | 1.107 × 103 | |
| F12 | Avg | 9.043 × 107 | 5.251 × 106 | 1.416 × 106 | 2.113 × 107 | 2.157 × 106 | 4.342 × 109 | 1.014 × 105 | 1.508 × 105 |
| Min | 7.305 × 104 | 1.578 × 106 | 3.718 × 104 | 7.171 × 105 | 2.328 × 105 | 2.607 × 109 | 6.932 × 103 | 2.035 × 104 | |
| F13 | Avg | 4.593 × 106 | 4.072 × 105 | 9.457 × 104 | 9.006 × 103 | 1.184 × 104 | 7.405 × 108 | 6.660 × 103 | 6.405 × 103 |
| Min | 1.003 × 104 | 1.634 × 105 | 1.150 × 104 | 2.446 × 103 | 1.596 × 103 | 1.145 × 108 | 1.400 × 103 | 1.690 × 103 | |
| F14 | Avg | 6.942 × 104 | 2.500 × 104 | 1.872 × 104 | 3.941 × 104 | 5.651 × 104 | 1.715 × 106 | 1.406 × 104 | 8.200 × 103 |
| Min | 5.450 × 103 | 2.821 × 103 | 4.075 × 103 | 6.379 × 103 | 4.686 × 103 | 7.879 × 104 | 3.027 × 103 | 2.021 × 103 | |
| F15 | Avg | 3.090 × 104 | 8.218 × 104 | 3.207 × 104 | 5.756 × 103 | 5.070 × 103 | 4.161 × 107 | 1.157 × 104 | 5.614 × 103 |
| Min | 5.117 × 103 | 4.614 × 104 | 2.547 × 103 | 1.707 × 103 | 1.703 × 103 | 1.868 × 106 | 1.609 × 103 | 1.515 × 103 | |
| F16 | Avg | 2.956 × 103 | 2.564 × 103 | 2.867 × 103 | 2.709 × 103 | 2.366 × 103 | 4.223 × 103 | 2.662 × 103 | 1.855 × 103 |
| Min | 2.398 × 103 | 2.101 × 103 | 2.267 × 103 | 2.241 × 103 | 1.965 × 103 | 3.565 × 103 | 2.068 × 103 | 1.617 × 103 | |
| F17 | Avg | 2.349 × 103 | 2.192 × 103 | 2.315 × 103 | 2.056 × 103 | 1.985 × 103 | 2.788 × 103 | 2.234 × 103 | 1.745 × 103 |
| Min | 1.975 × 103 | 1.925 × 103 | 1.942 × 103 | 1.818 × 103 | 1.764 × 103 | 2.359 × 103 | 1.958 × 103 | 1.727 × 103 | |
| F18 | Avg | 2.830 × 106 | 2.674 × 105 | 1.804 × 105 | 7.780 × 105 | 8.975 × 105 | 5.330 × 107 | 8.188 × 104 | 1.493 × 105 |
| Min | 7.725 × 104 | 3.452 × 104 | 4.774 × 104 | 7.998 × 104 | 9.364 × 104 | 2.825 × 106 | 6.883 × 103 | 4.305 × 104 | |
| F19 | Avg | 4.261 × 106 | 7.040 × 104 | 3.083 × 104 | 2.505 × 104 | 7.822 × 103 | 7.588 × 107 | 1.560 × 104 | 6.534 × 103 |
| Min | 1.293 × 104 | 3.487 × 104 | 2.168 × 103 | 3.280 × 103 | 1.968 × 103 | 5.192 × 106 | 2.310 × 103 | 1.910 × 103 | |
| F20 | Avg | 2.537 × 103 | 2.398 × 103 | 2.528 × 103 | 2.402 × 103 | 2.287 × 103 | 2.837 × 103 | 2.690 × 103 | 2.091 × 103 |
| Min | 2.215 × 103 | 2.117 × 103 | 2.103 × 103 | 2.185 × 103 | 2.053 × 103 | 2.454 × 103 | 2.294 × 103 | 2.004 × 103 | |
| F21 | Avg | 2.472 × 103 | 2.439 × 103 | 2.485 × 103 | 2.384 × 103 | 2.351 × 103 | 2.630 × 103 | 2.462 × 103 | 2.321 × 103 |
| Min | 2.420 × 103 | 2.378 × 103 | 2.430 × 103 | 2.338 × 103 | 2.331 × 103 | 2.363 × 103 | 2.389 × 103 | 2.312 × 103 | |
| F22 | Avg | 6.353 × 103 | 4.878 × 103 | 6.611 × 103 | 2.380 × 103 | 2.319 × 103 | 8.681 × 103 | 5.292 × 103 | 2.300 × 103 |
| Min | 3.223 × 103 | 2.325 × 103 | 5.330 × 103 | 2.319 × 103 | 2.305 × 103 | 5.677 × 103 | 2.300 × 103 | 2.300 × 103 | |
| F23 | Avg | 2.811 × 103 | 2.754 × 103 | 2.796 × 103 | 2.797 × 103 | 2.722 × 103 | 3.273 × 103 | 2.861 × 103 | 2.671 × 103 |
| Min | 2.740 × 103 | 2.724 × 103 | 2.749 × 103 | 2.734 × 103 | 2.697 × 103 | 3.027 × 103 | 2.763 × 103 | 2.654 × 103 | |
| F24 | Avg | 2.979 × 103 | 2.924 × 103 | 2.972 × 103 | 2.948 × 103 | 2.872 × 103 | 3.482 × 103 | 3.003 × 103 | 2.844 × 103 |
| Min | 2.926 × 103 | 2.888 × 103 | 2.927 × 103 | 2.887 × 103 | 2.848 × 103 | 3.217 × 103 | 2.912 × 103 | 2.828 × 103 | |
| F25 | Avg | 3.181 × 103 | 2.888 × 103 | 2.894 × 103 | 3.011 × 103 | 2.925 × 103 | 3.972 × 103 | 2.900 × 103 | 2.887 × 103 |
| Min | 2.895 × 103 | 2.885 × 103 | 2.884 × 103 | 2.935 × 103 | 2.890 × 103 | 3.467 × 103 | 2.884 × 103 | 2.887 × 103 | |
| F26 | Avg | 5.650 × 103 | 4.854 × 103 | 5.538 × 103 | 4.465 × 103 | 4.415 × 103 | 9.093 × 103 | 5.841 × 103 | 3.903 × 103 |
| Min | 4.921 × 103 | 4.504 × 103 | 5.074 × 103 | 3.113 × 103 | 2.876 × 103 | 5.057 × 103 | 4.741 × 103 | 3.739 × 103 | |
| F27 | Avg | 3.233 × 103 | 3.223 × 103 | 3.229 × 103 | 3.285 × 103 | 3.244 × 103 | 3.754 × 103 | 3.276 × 103 | 3.219 × 103 |
| Min | 3.206 × 103 | 3.194 × 103 | 3.204 × 103 | 3.238 × 103 | 3.218 × 103 | 3.538 × 103 | 3.220 × 103 | 3.208 × 103 | |
| F28 | Avg | 3.756 × 103 | 3.270 × 103 | 3.192 × 103 | 3.376 × 103 | 3.294 × 103 | 5.462 × 103 | 3.199 × 103 | 3.216 × 103 |
| Min | 3.263 × 103 | 3.211 × 103 | 3.100 × 103 | 3.265 × 103 | 3.271 × 103 | 4.419 × 103 | 3.122 × 103 | 3.196 × 103 | |
| F29 | Avg | 4.014 × 103 | 3.764 × 103 | 3.949 × 103 | 4.040 × 103 | 3.691 × 103 | 5.639 × 103 | 4.068 × 103 | 3.414 × 103 |
| Min | 3.499 × 103 | 3.410 × 103 | 3.574 × 103 | 3.629 × 103 | 3.475 × 103 | 4.728 × 103 | 3.545 × 103 | 3.323 × 103 | |
| F30 | Avg | 2.524 × 105 | 1.426 × 105 | 3.318 × 104 | 7.742 × 105 | 1.803 × 104 | 2.326 × 108 | 1.079 × 104 | 7.835 × 103 |
| Min | 7.219 × 103 | 6.606 × 104 | 1.642 × 104 | 5.609 × 104 | 7.769 × 103 | 2.468 × 107 | 5.674 × 103 | 6.362 × 103 | |
| Average rank | 6.06 | 3.95 | 4.51 | 4.57 | 3.28 | 7.91 | 4.18 | 1.55 | |
| Total rank | 7 | 3 | 5 | 6 | 2 | 8 | 4 | 1 | |
| F. | Metrics | MFO | LMFO | WCMFO | CMFO | ODSFMFO | SMFO | WMFO | MFO-SFR |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 3.036 × 1010 | 1.091 × 108 | 6.099 × 104 | 1.323 × 109 | 2.624 × 108 | 7.209 × 1010 | 4.264 × 103 | 3.463 × 104 |
| Min | 7.064 × 103 | 8.074 × 107 | 8.054 × 102 | 1.287 × 108 | 3.470 × 107 | 5.140 × 1010 | 1.054 × 102 | 9.385 ×3 | |
| F3 | Avg | 1.540 × 105 | 3.139 × 104 | 1.413 × 104 | 1.004 × 105 | 9.325 × 104 | 1.770 × 105 | 9.948 × 102 | 5.495 × 104 |
| Min | 1.176 × 104 | 1.960 × 104 | 2.418 × 103 | 7.381 × 104 | 6.538 × 104 | 1.457 × 105 | 3.217 × 102 | 4.223 × 104 | |
| F4 | Avg | 4.178 × 103 | 5.786 × 102 | 5.431 × 102 | 1.182 × 103 | 7.401 × 102 | 1.835 × 104 | 5.385 × 102 | 5.867 × 102 |
| Min | 1.187 × 103 | 5.296 × 102 | 4.286 × 102 | 5.419 × 102 | 6.608 × 102 | 1.005 × 104 | 4.961 × 102 | 5.196 × 102 | |
| F5 | Avg | 9.086 × 102 | 8.080 × 102 | 9.240 × 102 | 8.065 × 102 | 6.269 × 102 | 1.125 × 103 | 8.608 × 102 | 5.624 × 102 |
| Min | 7.996 × 102 | 7.226 × 102 | 7.743 × 102 | 6.742 × 102 | 5.862 × 102 | 1.032 × 103 | 7.209 × 102 | 5.318 × 102 | |
| F6 | Avg | 6.455 × 102 | 6.078 × 102 | 6.395 × 102 | 6.356 × 102 | 6.075 × 102 | 6.888 × 102 | 6.513 × 102 | 6.001 × 102 |
| Min | 6.270 × 102 | 6.035 × 102 | 6.165 × 102 | 6.239 × 102 | 6.041 × 102 | 6.780 × 102 | 6.291 × 102 | 6.000 × 102 | |
| F7 | Avg | 1.728 × 103 | 1.081 × 103 | 1.139 × 103 | 1.207 × 103 | 9.855 × 102 | 1.937 × 103 | 1.461 × 103 | 8.682 × 102 |
| Min | 1.119 × 103 | 1.011 × 103 | 1.023 × 103 | 1.031 × 103 | 8.795 × 102 | 1.769 × 103 | 1.204 × 103 | 8.099 × 102 | |
| F8 | Avg | 1.217 × 103 | 1.107 × 103 | 1.213 × 103 | 1.055 × 103 | 9.213 × 102 | 1.406 × 103 | 1.131 × 103 | 8.610 × 102 |
| Min | 1.050 × 103 | 1.021 × 103 | 1.096 × 103 | 9.983 × 102 | 8.625 × 102 | 1.315 × 103 | 1.021 × 103 | 8.318 × 102 | |
| F9 | Avg | 1.651 × 104 | 1.737 × 103 | 2.097 × 104 | 6.212 × 103 | 1.717 × 103 | 3.051 × 104 | 1.190 × 104 | 9.243 × 102 |
| Min | 8.748 × 103 | 9.529 × 102 | 1.190 × 104 | 3.607 × 103 | 1.299 × 103 | 1.925 × 104 | 5.498 × 103 | 9.066 × 102 | |
| F10 | Avg | 8.426 × 103 | 7.527 × 103 | 7.974 × 103 | 7.980 × 103 | 7.490 × 103 | 1.387 × 104 | 7.755 × 103 | 6.534 × 103 |
| Min | 6.288 × 103 | 6.340 × 103 | 6.303 × 103 | 6.040 × 103 | 5.766 × 103 | 1.198 × 104 | 6.397 × 103 | 5.135 × 103 | |
| F11 | Avg | 5.571 × 103 | 1.594 × 103 | 1.469 × 103 | 2.114 × 103 | 1.865 × 103 | 1.495 × 104 | 1.299 × 103 | 1.259 × 103 |
| Min | 1.574 × 103 | 1.439 × 103 | 1.291 × 103 | 1.417 × 103 | 1.394 × 103 | 8.985 × 103 | 1.200 × 103 | 1.146 × 103 | |
| F12 | Avg | 2.581 × 109 | 4.574 × 107 | 6.833 × 106 | 1.705 × 108 | 1.999 × 107 | 3.109 × 1010 | 5.722 × 105 | 1.873 × 106 |
| Min | 6.409 × 107 | 2.731 × 107 | 1.384 × 106 | 1.878 × 106 | 7.129 × 106 | 1.600 × 1010 | 1.341 × 105 | 1.078 × 106 | |
| F13 | Avg | 2.561 × 108 | 2.672 × 106 | 9.255 × 104 | 1.340 × 105 | 1.729 × 104 | 1.251 × 1010 | 8.898 × 103 | 5.362 × 103 |
| Min | 1.454 × 105 | 1.614 × 106 | 3.011 × 104 | 5.781 × 103 | 9.648 × 103 | 1.435 × 109 | 2.611 × 103 | 1.749 × 103 | |
| F14 | Avg | 9.567 × 105 | 1.375 × 105 | 6.855 × 104 | 1.073 × 105 | 4.132 × 105 | 2.622 × 107 | 3.670 × 104 | 4.016 × 104 |
| Min | 1.246 × 104 | 3.771 × 104 | 2.161 × 104 | 9.772 × 103 | 7.234 × 104 | 8.185 × 105 | 1.148 × 104 | 1.202 × 104 | |
| F15 | Avg | 1.078 × 107 | 5.308 × 105 | 6.616 × 104 | 8.967 × 103 | 6.016 × 103 | 1.341 × 109 | 7.075 × 103 | 2.964 × 103 |
| Min | 4.298 × 104 | 3.335 × 105 | 1.422 × 104 | 1.884 × 103 | 2.543 × 103 | 1.237 × 108 | 1.943 × 103 | 1.534 × 103 | |
| F16 | Avg | 4.104 × 103 | 3.570 × 103 | 3.769 × 103 | 3.335 × 103 | 2.915 × 103 | 6.808 × 103 | 3.575 × 103 | 2.614 × 103 |
| Min | 3.133 × 103 | 2.836 × 103 | 2.788 × 103 | 2.616 × 103 | 2.404 × 103 | 5.302 × 103 | 2.509 × 103 | 2.148 × 103 | |
| F17 | Avg | 3.846 × 103 | 3.218 × 103 | 3.787 × 103 | 3.151 × 103 | 2.690 × 103 | 4.919 × 103 | 3.478 × 103 | 2.474 × 103 |
| Min | 3.034 × 103 | 2.568 × 103 | 3.044 × 103 | 2.615 × 103 | 2.084 × 103 | 3.399 × 103 | 2.827 × 103 | 2.018 × 103 | |
| F18 | Avg | 4.168 × 106 | 1.053 × 106 | 3.688 × 105 | 2.670 × 106 | 1.816 × 106 | 5.905 × 107 | 1.937 × 105 | 1.247 × 106 |
| Min | 1.543 × 105 | 2.843 × 105 | 1.381 × 105 | 2.302 × 105 | 1.304 × 105 | 5.306 × 106 | 3.375 × 104 | 1.067 × 105 | |
| F19 | Avg | 2.346 × 106 | 2.754 × 105 | 2.368 × 104 | 6.213 × 104 | 1.682 × 104 | 9.590 × 108 | 1.541 × 104 | 1.276 × 104 |
| Min | 5.030 × 103 | 1.841 × 105 | 2.700 × 103 | 5.247 × 103 | 2.057 × 103 | 2.437 × 107 | 2.172 × 103 | 2.447 × 103 | |
| F20 | Avg | 3.529 × 103 | 2.999 × 103 | 3.311 × 103 | 3.108 × 103 | 2.830 × 103 | 3.923 × 103 | 3.317 × 103 | 2.485 × 103 |
| Min | 3.116 × 103 | 2.429 × 103 | 2.655 × 103 | 2.572 × 103 | 2.495 × 103 | 3.475 × 103 | 2.534 × 103 | 2.081 × 103 | |
| F21 | Avg | 2.682 × 103 | 2.604 × 103 | 2.720 × 103 | 2.503 × 103 | 2.408 × 103 | 3.071 × 103 | 2.635 × 103 | 2.360 × 103 |
| Min | 2.575 × 103 | 2.528 × 103 | 2.590 × 103 | 2.445 × 103 | 2.379 × 103 | 2.938 × 103 | 2.518 × 103 | 2.335 × 103 | |
| F22 | Avg | 1.028 × 104 | 9.106 × 103 | 9.780 × 103 | 7.972 × 103 | 5.227 × 103 | 1.605 × 104 | 9.538 × 103 | 8.339 × 103 |
| Min | 8.688 × 103 | 7.734 × 103 | 8.346 × 103 | 2.497 × 103 | 2.436 × 103 | 1.474 × 104 | 8.203 × 103 | 6.317 × 103 | |
| F23 | Avg | 3.133 × 103 | 3.009 × 103 | 3.095 × 103 | 3.137 × 103 | 2.888 × 103 | 3.969 × 103 | 3.183 × 103 | 2.793 × 103 |
| Min | 3.013 × 103 | 2.945 × 103 | 2.974 × 103 | 2.979 × 103 | 2.822 × 103 | 3.594 × 103 | 3.056 × 103 | 2.761 × 103 | |
| F24 | Avg | 3.197 × 103 | 3.135 × 103 | 3.224 × 103 | 3.217 × 103 | 3.030 × 103 | 4.292 × 103 | 3.274 × 103 | 2.970 × 103 |
| Min | 3.098 × 103 | 3.071 × 103 | 3.101 × 103 | 3.098 × 103 | 2.978 × 103 | 3.875 × 103 | 3.095 × 103 | 2.931 × 103 | |
| F25 | Avg | 5.123 × 103 | 3.062 × 103 | 3.048 × 103 | 3.889 × 103 | 3.242 × 103 | 1.069 × 104 | 3.061 × 103 | 3.070 × 103 |
| Min | 3.031 × 103 | 2.994 × 103 | 2.964 × 103 | 3.242 × 103 | 3.176 × 103 | 7.290 × 103 | 3.021 × 103 | 2.985 × 103 | |
| F26 | Avg | 8.137 × 103 | 6.855 × 103 | 8.205 × 103 | 8.456 × 103 | 5.513 × 103 | 1.577 × 104 | 8.342 × 103 | 4.406 × 103 |
| Min | 6.910 × 103 | 6.234 × 103 | 7.239 × 103 | 5.759 × 103 | 4.905 × 103 | 1.445 × 104 | 2.900 × 103 | 4.051 × 103 | |
| F27 | Avg | 3.538 × 103 | 3.403 × 103 | 3.489 × 103 | 4.237 × 103 | 3.525 × 103 | 5.612 × 103 | 3.759 × 103 | 3.307 × 103 |
| Min | 3.407 × 103 | 3.297 × 103 | 3.361 × 103 | 3.897 × 103 | 3.448 × 103 | 4.453 × 103 | 3.460 × 103 | 3.266 × 103 | |
| F28 | Avg | 7.554 × 103 | 3.555 × 103 | 3.296 × 103 | 4.481 × 103 | 3.749 × 103 | 9.637 × 103 | 3.300 × 103 | 3.378 × 103 |
| Min | 4.720 × 103 | 3.268 × 103 | 3.259 × 103 | 3.882 × 103 | 3.472 × 103 | 8.008 × 103 | 3.259 × 103 | 3.310 × 103 | |
| F29 | Avg | 5.133 × 103 | 4.380 × 103 | 4.681 × 103 | 5.199 × 103 | 4.191 × 103 | 1.608 × 104 | 4.870 × 103 | 3.545 × 103 |
| Min | 4.271 × 103 | 3.944 × 103 | 3.587 × 103 | 4.366 × 103 | 3.748 × 103 | 8.290 × 103 | 4.292 × 103 | 3.289 × 103 | |
| F30 | Avg | 2.924 × 107 | 5.428 × 106 | 2.810 × 106 | 2.564 × 107 | 1.768 × 106 | 2.271 × 109 | 1.204 × 106 | 1.144 × 106 |
| Min | 2.389 × 106 | 3.442 × 106 | 1.262 × 106 | 8.984 × 106 | 9.999 × 105 | 2.782 × 108 | 6.441 × 105 | 9.567 × 105 | |
| Average rank | 6.29 | 3.82 | 4.25 | 4.78 | 3.34 | 7.93 | 3.79 | 1.79 | |
| Total rank | 7 | 3 | 5 | 6 | 2 | 8 | 4 | 1 | |
| F. | Metrics | PSO | KH | GWO | CSA | HOA | MFO-SFR |
|---|---|---|---|---|---|---|---|
| F1 | Avg | 5.907 × 1010 | 1.963 × 104 | 1.145 × 109 | 3.246 × 1010 | 3.003 × 109 | 1.791 × 103 |
| Min | 3.270 × 1010 | 7.354 × 103 | 1.583 × 108 | 2.130 × 1010 | 2.203 × 109 | 1.017 × 102 | |
| F3 | Avg | 1.308 × 105 | 4.403 × 104 | 2.987 × 104 | 9.600 × 104 | 3.075 × 104 | 1.312 × 104 |
| Min | 1.039 × 105 | 2.051 × 104 | 1.476 × 104 | 5.473 × 104 | 2.032 × 104 | 7.513 × 103 | |
| F4 | Avg | 1.183 × 104 | 4.965 × 102 | 5.369 × 102 | 5.726 × 103 | 1.047 × 103 | 4.914 × 102 |
| Min | 7.302 × 103 | 4.041 × 102 | 4.933 × 102 | 3.185 × 103 | 8.889 × 102 | 4.700 × 102 | |
| F5 | Avg | 9.635 × 102 | 6.454 × 102 | 5.950 × 102 | 8.509 × 102 | 7.938 × 102 | 5.227 × 102 |
| Min | 8.845 × 102 | 6.115 × 102 | 5.511 × 102 | 8.017 × 102 | 7.612 × 102 | 5.109 × 102 | |
| F6 | Avg | 6.921 × 102 | 6.418 × 102 | 6.047 × 102 | 6.683 × 102 | 6.605 × 102 | 6.000 × 102 |
| Min | 6.828 × 102 | 6.303 × 102 | 6.009 × 102 | 6.554 × 102 | 6.496 × 102 | 6.000 × 102 | |
| F7 | Avg | 2.511 × 103 | 8.400 × 102 | 8.512 × 102 | 1.730 × 103 | 1.029 × 103 | 7.669 × 102 |
| Min | 2.201 × 103 | 7.960 × 102 | 7.932 × 102 | 1.552 × 103 | 9.979 × 102 | 7.460 × 102 | |
| F8 | Avg | 1.220 × 103 | 9.054 × 102 | 8.709 × 102 | 1.134 × 103 | 1.061 × 103 | 8.209 × 102 |
| Min | 1.163 × 103 | 8.647 × 102 | 8.450 × 102 | 1.105 × 103 | 1.041 × 103 | 8.090 × 102 | |
| F9 | Avg | 1.735 × 104 | 3.138 × 103 | 1.360 × 103 | 1.040 × 104 | 4.292 × 103 | 9.038 × 102 |
| Min | 1.271 × 104 | 2.368 × 103 | 9.830 × 102 | 7.223 × 103 | 2.668 × 103 | 9.005 × 102 | |
| F10 | Avg | 8.218 × 103 | 4.797 × 103 | 3.874 × 103 | 8.279 × 103 | 8.340 × 103 | 4.062 × 103 |
| Min | 7.661 × 103 | 3.165 × 103 | 3.030 × 103 | 7.738 × 103 | 7.745 × 103 | 2.461 × 103 | |
| F11 | Avg | 1.018 × 104 | 1.711 × 103 | 1.408 × 103 | 4.700 × 103 | 1.797 × 103 | 1.143 × 103 |
| Min | 7.488 × 103 | 1.304 × 103 | 1.236 × 103 | 3.395 × 103 | 1.699 × 103 | 1.107 × 103 | |
| F12 | Avg | 6.824 × 109 | 2.220 × 106 | 3.441 × 107 | 2.979 × 109 | 3.763 × 108 | 1.508 × 105 |
| Min | 3.870 × 109 | 7.468 × 105 | 2.122 × 106 | 1.516 × 109 | 2.821 × 108 | 2.035 × 104 | |
| F13 | Avg | 3.156 × 109 | 3.457 × 104 | 1.505 × 106 | 9.478 × 108 | 1.051 × 108 | 6.405 × 103 |
| Min | 5.760 × 108 | 1.430 × 104 | 4.674 × 104 | 5.211 × 108 | 3.296 × 107 | 1.690 × 103 | |
| F14 | Avg | 7.227 × 105 | 2.910 × 105 | 1.926 × 105 | 4.342 × 105 | 1.340 × 105 | 8.200 × 103 |
| Min | 1.041 × 105 | 1.873 × 104 | 2.446 × 104 | 1.482 × 105 | 5.216 × 104 | 2.021 × 103 | |
| F15 | Avg | 2.025 × 108 | 1.788 × 104 | 1.956 × 105 | 7.286 × 107 | 3.143 × 107 | 5.614 × 103 |
| Min | 1.064 × 107 | 9.433 × 103 | 1.435 × 104 | 2.378 × 107 | 8.141 × 106 | 1.515 × 103 | |
| F16 | Avg | 4.452 × 103 | 2.884 × 103 | 2.385 × 103 | 3.989 × 103 | 3.786 × 103 | 1.855 × 103 |
| Min | 3.827 × 103 | 2.377 × 103 | 1.949 × 103 | 3.147 × 103 | 3.419 × 103 | 1.617 × 103 | |
| F17 | Avg | 3.298 × 103 | 2.277 × 103 | 1.943 × 103 | 2.628 × 103 | 2.361 × 103 | 1.745 × 103 |
| Min | 2.755 × 103 | 1.804 × 103 | 1.778 × 103 | 2.256 × 103 | 2.102 × 103 | 1.727 × 103 | |
| F18 | Avg | 6.473 × 106 | 4.258 × 105 | 8.049 × 105 | 7.890 × 106 | 1.212 × 106 | 1.493 × 105 |
| Min | 6.593 × 105 | 4.192 × 104 | 6.880 × 104 | 2.022 × 106 | 4.281 × 105 | 4.305 × 104 | |
| F19 | Avg | 2.509 × 108 | 9.593 × 104 | 7.374 × 105 | 1.358 × 108 | 4.426 × 107 | 6.534 × 103 |
| Min | 3.341 × 107 | 1.081 × 104 | 3.279 × 103 | 6.263 × 107 | 1.774 × 107 | 1.910 × 103 | |
| F20 | Avg | 2.847 × 103 | 2.624 × 103 | 2.362 × 103 | 2.759 × 103 | 2.681 × 103 | 2.091 × 103 |
| Min | 2.574 × 103 | 2.303 × 103 | 2.146 × 103 | 2.476 × 103 | 2.487 × 103 | 2.004 × 103 | |
| F21 | Avg | 2.707 × 103 | 2.416 × 103 | 2.379 × 103 | 2.625 × 103 | 2.575 × 103 | 2.321 × 103 |
| Min | 2.615 × 103 | 2.359 × 103 | 2.351 × 103 | 2.587 × 103 | 2.539 × 103 | 2.312 × 103 | |
| F22 | Avg | 8.759 × 103 | 3.018 × 103 | 4.411 × 103 | 6.831 × 103 | 4.513 × 103 | 2.300 × 103 |
| Min | 6.900 × 103 | 2.300 × 103 | 2.406 × 103 | 5.558 × 103 | 2.705 × 103 | 2.300 × 103 | |
| F23 | Avg | 3.239 × 103 | 2.880 × 103 | 2.729 × 103 | 3.143 × 103 | 3.133 × 103 | 2.671 × 103 |
| Min | 3.101 × 103 | 2.807 × 103 | 2.678 × 103 | 3.061 × 103 | 3.059 × 103 | 2.654 × 103 | |
| F24 | Avg | 3.539 × 103 | 3.107 × 103 | 2.890 × 103 | 3.319 × 103 | 3.188 × 103 | 2.844 × 103 |
| Min | 3.253 × 103 | 2.994 × 103 | 2.849 × 103 | 3.206 × 103 | 3.122 × 103 | 2.828 × 103 | |
| F25 | Avg | 7.655 × 103 | 2.911 × 103 | 2.958 × 103 | 4.890 × 103 | 3.137 × 103 | 2.887 × 103 |
| Min | 5.843 × 103 | 2.887 × 103 | 2.916 × 103 | 4.344 × 103 | 3.069 × 103 | 2.887 × 103 | |
| F26 | Avg | 8.709 × 103 | 5.651 × 103 | 4.483 × 103 | 8.661 × 103 | 4.738 × 103 | 3.903 × 103 |
| Min | 6.500 × 103 | 2.800 × 103 | 3.473 × 103 | 7.772 × 103 | 3.736 × 103 | 3.739 × 103 | |
| F27 | Avg | 3.827 × 103 | 3.400 × 103 | 3.230 × 103 | 3.690 × 103 | 3.720 × 103 | 3.219 × 103 |
| Min | 3.591 × 103 | 3.283 × 103 | 3.212 × 103 | 3.537 × 103 | 3.616 × 103 | 3.208 × 103 | |
| F28 | Avg | 6.851 × 103 | 3.228 × 103 | 3.356 × 103 | 5.474 × 103 | 3.519 × 103 | 3.216 × 103 |
| Min | 5.611 × 103 | 3.198 × 103 | 3.283 × 103 | 4.541 × 103 | 3.468 × 103 | 3.196 × 103 | |
| F29 | Avg | 5.426 × 103 | 4.194 × 103 | 3.642 × 103 | 5.253 × 103 | 4.726 × 103 | 3.414 × 103 |
| Min | 4.907 × 103 | 3.858 × 103 | 3.439 × 103 | 4.952 × 103 | 4.454 × 103 | 3.323 × 103 | |
| F30 | Avg | 2.946 × 108 | 1.043 × 106 | 2.842 × 106 | 1.084 × 108 | 2.610 × 107 | 7.835 × 103 |
| Min | 8.913 × 107 | 8.260 × 104 | 5.249 × 105 | 4.274 × 107 | 1.221 × 107 | 6.362 × 103 | |
| Average rank | 5.84 | 2.68 | 2.45 | 5.00 | 3.93 | 1.09 | |
| Total rank | 6 | 3 | 2 | 5 | 4 | 1 | |
| F. | Metrics | PSO | KH | GWO | CSA | HOA | MFO-SFR |
|---|---|---|---|---|---|---|---|
| F1 | Avg | 1.526 × 1011 | 1.703 × 105 | 4.506 × 109 | 9.609 × 1010 | 1.149 × 1010 | 3.463 × 104 |
| Min | 8.451 × 1010 | 1.932 × 104 | 7.183 × 108 | 8.123 × 1010 | 8.346 × 109 | 9.385 × 103 | |
| F3 | Avg | 2.549 × 105 | 1.192 × 105 | 7.730 × 104 | 2.070 × 105 | 8.230 × 104 | 5.495 × 104 |
| Min | 1.957 × 105 | 7.643 × 104 | 4.662 × 104 | 1.774 × 105 | 6.990 × 104 | 4.223 × 104 | |
| F4 | Avg | 3.307 × 104 | 5.428 × 102 | 8.017 × 102 | 1.712 × 104 | 2.589 × 103 | 5.867 × 102 |
| Min | 1.811 × 104 | 4.765 × 102 | 6.224 × 102 | 1.286 × 104 | 2.058 × 103 | 5.196 × 102 | |
| F5 | Avg | 1.367 × 103 | 7.662 × 102 | 6.775 × 102 | 1.211 × 103 | 1.047 × 103 | 5.624 × 102 |
| Min | 1.256 × 103 | 7.090 × 102 | 6.316 × 102 | 1.145 × 103 | 1.011 × 103 | 5.318 × 102 | |
| F6 | Avg | 7.114 × 102 | 6.499 × 102 | 6.112 × 102 | 6.862 × 102 | 6.745 × 102 | 6.001 × 102 |
| Min | 6.991 × 102 | 6.393 × 102 | 6.075 × 102 | 6.776 × 102 | 6.645 × 102 | 6.000 × 102 | |
| F7 | Avg | 4.585 × 103 | 1.052 × 103 | 9.899 × 102 | 3.206 × 103 | 1.338 × 103 | 8.682 × 102 |
| Min | 4.142 × 103 | 9.353 × 102 | 9.057 × 102 | 2.735 × 103 | 1.289 × 103 | 8.099 × 102 | |
| F8 | Avg | 1.687 × 103 | 1.059 × 103 | 9.862 × 102 | 1.499 × 103 | 1.354 × 103 | 8.610 × 102 |
| Min | 1.575 × 103 | 1.033 × 103 | 9.423 × 102 | 1.423 × 103 | 1.283 × 103 | 8.318 × 102 | |
| F9 | Avg | 5.170 × 104 | 9.873 × 103 | 4.844 × 103 | 3.622 × 104 | 2.153 × 104 | 9.243 × 102 |
| Min | 3.909 × 104 | 7.955 × 103 | 2.552 × 103 | 3.021 × 104 | 1.416 × 104 | 9.066 × 102 | |
| F10 | Avg | 1.441 × 104 | 7.948 × 103 | 5.919 × 103 | 1.429 × 104 | 1.412 × 104 | 6.534 × 103 |
| Min | 1.356 × 104 | 6.701 × 103 | 4.473 × 103 | 1.342 × 104 | 1.324 × 104 | 5.135 × 103 | |
| F11 | Avg | 2.610 × 104 | 4.813 × 103 | 2.766 × 103 | 1.573 × 104 | 3.782 × 103 | 1.259 × 103 |
| Min | 1.947 × 104 | 3.034 × 103 | 1.652 × 103 | 1.157 × 104 | 3.239 × 103 | 1.146 × 103 | |
| F12 | Avg | 4.300 × 1010 | 1.287 × 107 | 3.406 × 108 | 2.210 × 1010 | 2.417 × 109 | 1.873 × 106 |
| Min | 2.464 × 1010 | 4.289 × 106 | 3.715 × 107 | 1.421 × 1010 | 1.705 × 109 | 1.078 × 106 | |
| F13 | Avg | 1.683 × 1010 | 5.864 × 104 | 1.026 × 108 | 6.132 × 109 | 5.696 × 108 | 5.362 × 103 |
| Min | 5.672 × 109 | 2.099 × 104 | 8.150 × 104 | 3.709 × 109 | 4.310 × 108 | 1.749 × 103 | |
| F14 | Avg | 6.142 × 106 | 5.701 × 105 | 3.453 × 105 | 4.140 × 106 | 8.316 × 105 | 4.016 × 104 |
| Min | 1.659 × 106 | 1.615 × 105 | 2.928 × 104 | 1.829 × 106 | 2.222 × 105 | 1.202 × 104 | |
| F15 | Avg | 5.029 × 109 | 1.956 × 104 | 4.078 × 106 | 1.190 × 109 | 2.294 × 108 | 2.964 × 103 |
| Min | 2.307 × 109 | 9.499 × 103 | 2.722 × 104 | 4.163 × 108 | 9.908 × 107 | 1.534 × 103 | |
| F16 | Avg | 7.306 × 103 | 3.250 × 103 | 2.896 × 103 | 6.252 × 103 | 5.184 × 103 | 2.614 × 103 |
| Min | 6.699 × 103 | 2.463 × 103 | 2.326 × 103 | 5.731 × 103 | 4.749 × 103 | 2.148 × 103 | |
| F17 | Avg | 1.334 × 104 | 3.359 × 103 | 2.661 × 103 | 5.190 × 103 | 3.888 × 103 | 2.474 × 103 |
| Min | 5.938 × 103 | 2.849 × 103 | 2.264 × 103 | 4.547 × 103 | 3.183 × 103 | 2.018 × 103 | |
| F18 | Avg | 3.800 × 107 | 2.330 × 106 | 3.051 × 106 | 3.471 × 107 | 8.478 × 106 | 1.247 × 106 |
| Min | 1.430 × 107 | 1.131 × 106 | 3.848 × 105 | 1.224 × 107 | 4.500 × 106 | 1.067 × 105 | |
| F19 | Avg | 2.060 × 109 | 1.719 × 105 | 1.231 × 106 | 5.231 × 108 | 7.924 × 107 | 1.276 × 104 |
| Min | 6.897 × 108 | 2.586 × 104 | 9.261 × 103 | 2.060 × 108 | 2.979 × 107 | 2.447 × 103 | |
| F20 | Avg | 4.010 × 103 | 3.276 × 103 | 2.743 × 103 | 3.903 × 103 | 3.675 × 103 | 2.485 × 103 |
| Min | 3.712 × 103 | 2.764 × 103 | 2.380 × 103 | 3.680 × 103 | 3.261 × 103 | 2.081 × 103 | |
| F21 | Avg | 3.164 × 103 | 2.556 × 103 | 2.473 × 103 | 2.994 × 103 | 2.850 × 103 | 2.360 × 103 |
| Min | 3.046 × 103 | 2.455 × 103 | 2.422 × 103 | 2.896 × 103 | 2.767 × 103 | 2.335 × 103 | |
| F22 | Avg | 1.609 × 104 | 1.049 × 104 | 8.211 × 103 | 1.603 × 104 | 1.527 × 104 | 8.339 × 103 |
| Min | 1.492 × 104 | 9.115 × 103 | 6.990 × 103 | 1.493 × 104 | 4.474 × 103 | 6.317 × 103 | |
| F23 | Avg | 4.077 × 103 | 3.379 × 103 | 2.916 × 103 | 3.777 × 103 | 3.749 × 103 | 2.793 × 103 |
| Min | 3.763 × 103 | 3.052 × 103 | 2.826 × 103 | 3.595 × 103 | 3.533 × 103 | 2.761 × 103 | |
| F24 | Avg | 4.174 × 103 | 3.643 × 103 | 3.109 × 103 | 3.983 × 103 | 3.744 × 103 | 2.970 × 103 |
| Min | 3.943 × 103 | 3.406 × 103 | 2.991 × 103 | 3.738 × 103 | 3.597 × 103 | 2.931 × 103 | |
| F25 | Avg | 2.556 × 104 | 3.092 × 103 | 3.355 × 103 | 1.580 × 104 | 4.331 × 103 | 3.070 × 103 |
| Min | 1.693 × 104 | 3.052 × 103 | 3.146 × 103 | 1.384 × 104 | 3.997 × 103 | 2.985 × 103 | |
| F26 | Avg | 1.697 × 104 | 9.335 × 103 | 5.804 × 103 | 1.506 × 104 | 5.800 × 103 | 4.406 × 103 |
| Min | 1.280 × 104 | 3.159 × 103 | 4.993 × 103 | 1.326 × 104 | 5.170 × 103 | 4.051 × 103 | |
| F27 | Avg | 5.456 × 103 | 4.354 × 103 | 3.516 × 103 | 5.185 × 103 | 5.049 × 103 | 3.307 × 103 |
| Min | 4.582 × 103 | 3.985 × 103 | 3.402 × 103 | 4.636 × 103 | 4.657 × 103 | 3.266 × 103 | |
| F28 | Avg | 1.242 × 104 | 3.346 × 103 | 3.927 × 103 | 1.039 × 104 | 4.740 × 103 | 3.378 × 103 |
| Min | 9.606 × 103 | 3.311 × 103 | 3.545 × 103 | 8.991 × 103 | 4.469 × 103 | 3.310 × 103 | |
| F29 | Avg | 1.018 × 104 | 5.360 × 103 | 4.202 × 103 | 8.981 × 103 | 6.514 × 103 | 3.545 × 103 |
| Min | 8.653 × 103 | 4.196 × 103 | 3.826 × 103 | 7.451 × 103 | 6.113 × 103 | 3.289 × 103 | |
| F30 | Avg | 2.508 × 109 | 4.241 × 107 | 7.032 × 107 | 1.287 × 109 | 3.337 × 108 | 1.144 × 106 |
| Min | 1.281 × 109 | 1.429 × 107 | 3.629 × 107 | 6.453 × 108 | 2.374 × 108 | 9.567 × 105 | |
| Average rank | 5.93 | 2.70 | 2.29 | 4.98 | 3.92 | 1.18 | |
| Total rank | 6 | 3 | 2 | 5 | 4 | 1 | |
| Algorithms | 30 (W|T|L) | 50 (W|T|L) | Total (W|T|L) | OE |
|---|---|---|---|---|
| MFO | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| LMFO | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| WCMFO | 1|0|28 | 2|0|27 | 3|0|55 | 5.17% |
| CMFO | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| ODSFMFO | 1|0|28 | 1|0|28 | 2|0|56 | 3.45% |
| SMFO | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| WMFO | 4|0|25 | 6|0|23 | 10|0|48 | 17.24% |
| MFO-SFR | 23|0|6 | 20|0|9 | 43|0|15 | 74.14% |
| Algorithms | 30 (W|T|L) | 50 (W|T|L) | Total (W|T|L) | OE |
|---|---|---|---|---|
| PSO | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| KH | 0|0|29 | 2|0|27 | 2|0|56 | 3.45% |
| GWO | 1|0|28 | 2|0|27 | 3|0|55 | 5.17% |
| CSA | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| HOA | 0|0|29 | 0|0|29 | 0|0|58 | 0% |
| MFO-SFR | 28|0|1 | 25|0|4 | 53|0|5 | 91.38% |
| Algorithms | Optimal Values for Variables | Optimum Cost | |||
|---|---|---|---|---|---|
| h | l | t | b | ||
| MFO | 0.20576 | 3.47017 | 9.03582 | 0.20577 | 1.72499 |
| LMFO | 0.20739 | 3.43588 | 9.25131 | 0.20807 | 1.77799 |
| WCMFO | 0.20573 | 3.47035 | 9.03670 | 0.20573 | 1.72489 |
| CMFO | 0.18276 | 4.49027 | 8.98308 | 0.20819 | 1.82934 |
| ODSFMFO | 0.20569 | 3.47128 | 9.03662 | 0.20573 | 1.72490 |
| SMFO | 0.20836 | 3.46324 | 8.99144 | 0.20853 | 1.74135 |
| WMFO | 0.20722 | 3.45341 | 8.99834 | 0.20748 | 1.73151 |
| MFO-SFR | 0.20573 | 3.47056 | 9.03662 | 0.20573 | 1.72486 |
| Variables | MFO | LMFO | WCMFO | CMFO | ODSFMFO | SMFO | WMFO | MFO-SFR |
|---|---|---|---|---|---|---|---|---|
| x1 | 21.9311 | 26.0390 | 13.2709 | 14.4470 | 19.9522 | 7.4896 | 11.6081 | 19.7537 |
| x2 | 56.2686 | 59.6014 | 38.0428 | 35.9087 | 42.7879 | 36.8603 | 36.5289 | 51.3053 |
| x3 | 6.5100 | 23.4280 | 47.0038 | 13.7051 | 16.7363 | 9.6905 | 32.5497 | 17.3633 |
| x4 | 21.2349 | 62.1487 | 64.7345 | 27.4891 | 34.3685 | 35.0066 | 48.2554 | 35.7343 |
| x5 | 17.8415 | 41.7704 | 6.9925 | 19.5000 | 15.1662 | 15.4976 | 18.6551 | 17.4063 |
| x6 | 37.9201 | 50.8023 | 16.3730 | 32.6744 | 27.1178 | 36.7195 | 35.1674 | 30.5308 |
| x7 | 23.1300 | 18.5328 | 16.3790 | 13.5190 | 22.4386 | 37.1973 | 15.6177 | 21.5071 |
| x8 | 27.5979 | 49.6525 | 33.9110 | 31.5029 | 56.4417 | 15.5455 | 38.4569 | 44.0394 |
| x9 | 0.5100 | 0.9809 | 0.7443 | 1.3021 | 0.9727 | 2.0702 | 1.4277 | 0.8917 |
| x10 | 3.3914 | 0.5964 | 0.8894 | 2.4919 | 0.8552 | 0.7589 | 1.3920 | 1.2137 |
| x11 | 0.5100 | 0.7173 | 4.2285 | 1.4999 | 1.2069 | 0.8063 | 0.9781 | 0.6197 |
| x12 | 0.5100 | 0.5100 | 1.2452 | 1.4996 | 0.9356 | 1.3444 | 1.0893 | 1.1821 |
| x13 | 7.8792 | 5.4735 | 6.3799 | 3.4649 | 2.3679 | 0.9250 | 1.6757 | 4.1070 |
| x14 | 5.9533 | 4.8956 | 5.5138 | 6.4560 | 5.1076 | 4.7899 | 5.7668 | 6.8698 |
| x15 | 5.3993 | 4.9521 | 5.8834 | 5.1835 | 5.0748 | 0.5867 | 5.6259 | 2.6797 |
| x16 | 6.9070 | 4.8722 | 2.7391 | 5.1577 | 4.1023 | 4.6470 | 5.0989 | 2.2119 |
| x17 | 6.7122 | 4.6078 | 5.4174 | 6.4936 | 5.1441 | 4.0477 | 4.6631 | 4.2234 |
| x18 | 7.5214 | 7.5663 | 8.3727 | 6.4751 | 5.1403 | 3.3638 | 3.5762 | 1.5645 |
| x19 | 4.7338 | 3.7869 | 3.5741 | 4.4972 | 3.9364 | 3.6366 | 3.7593 | 3.7526 |
| x20 | 5.3254 | 4.3966 | 3.3184 | 3.4597 | 4.8508 | 4.6303 | 3.5222 | 5.4510 |
| x21 | 4.8923 | 3.3528 | 5.7764 | 4.4278 | 2.8171 | 2.9203 | 2.6439 | 4.0416 |
| x22 | 5.6086 | 4.0724 | 4.8985 | 4.4763 | 2.7781 | 3.9267 | 5.6805 | 5.2131 |
| Optimum Weight | 7.2632 × 101 | 6.6228 × 101 | 2.1631 × 1012 | 5.2157 × 101 | 3.6565 × 101 | 3.4380 × 1017 | 2.6870 × 1014 | 3.6555 × 101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadimi-Shahraki, M.H.; Zamani, H.; Fatahi, A.; Mirjalili, S. MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy. Mathematics 2023, 11, 862. https://doi.org/10.3390/math11040862
Nadimi-Shahraki MH, Zamani H, Fatahi A, Mirjalili S. MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy. Mathematics. 2023; 11(4):862. https://doi.org/10.3390/math11040862
Chicago/Turabian StyleNadimi-Shahraki, Mohammad H., Hoda Zamani, Ali Fatahi, and Seyedali Mirjalili. 2023. "MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy" Mathematics 11, no. 4: 862. https://doi.org/10.3390/math11040862
APA StyleNadimi-Shahraki, M. H., Zamani, H., Fatahi, A., & Mirjalili, S. (2023). MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy. Mathematics, 11(4), 862. https://doi.org/10.3390/math11040862









