Significance of Darcy–Forchheimer Law, Activation Energy, and Brownian Motion of Tiny Particles on the Dynamics of Rotating MHD Micropolar Nanofluid

Abstract

The time-independent performance of a micropolar nanofluid under the influence of magneto hydrodynamics and the existence of a porous medium on a stretching sheet has been investigated. Nano-sized particles were incorporated in the base fluid because of their properties such as their extraordinary heat-enhancing ability, which plays a very important role in modern nanotechnology, cooling electronic devices, various types of heat exchangers, etc. The effects of Brownian motion and thermophoresis are accounted for in this comprehensive study. Using similarity conversion, the leading equations based on conservation principles are non-dimensionalized with various parameters yielding a set of ODEs. The numerical approach boundary value problem fourth-order method (bvp4c) was implemented as listed in the MATLAB computational tool. The purpose of this examination was to study and analyze the influence of different parameters on velocity, micro-rotation, concentration, and temperature profiles. The primary and secondary velocities reduced against the higher inputs of boundary concentration, rotation, porosity, and magnetic parameters, however, the base fluid temperature distribution grows with the increasing values of these parameters. The micro-rotation distribution increased against the rising strength of the Lorentz force and a decline is reported against the growing values of the micropolar material and rotational parameters.

1. Introduction

Fluids with micro-structures are referred to as micropolar fluids. Physically, these fluids are constituted of randomly orientated particles suspended in viscous media. The model of this type of fluid can be utilized to illustrate the liquid crystals movement, suspension solutions, animal blood, colloidal liquids, etc. Micropolar theory has acquired a lot of attention in recent decades due to its numerous implementations in various industrial processes such as nuclear power plants, lubricant liquids in biological structures, less concentration suspension flux, polymer solution flows, turbulent shear, etc. [1,2]. The theory of micropolar fluids was first raised by Eringen [3]. In recent decades, studies performing excellent analyses of the applications and relevance of this sort of fluid have been conducted [4,5,6,7,8]. Ramya and Doh [9] studied the hydrodynamic impact of radiation on the dynamics of micropolar fluid subjects to gyrostatic microorganisms. They used gyrostatic microorganisms to prevent the possible sedimentation of tiny particles to enhance the effective heat transfer rate. Bilal et al. [10] investigated the micropolar nanofluid flow to observe the behavior of Brownian motion and thermophoresis on the dynamics of a base fluid. They found that the base fluid temperature enhanced due to the higher strength of the Brownian motion and thermophoresis.

Magneto hydradynamics (MHD) is described as the analysis of the magnetic attributes of conducting fluids. Due to their outstanding work on MHD in 1970, Hannes Alfven was bestowed the Nobel Prize. Various characteristics of these phenomena have aided their implementations in several fields including the physiological field, petroleum industry, mechanical engineering, and chemical engineering. These considerations are advantageous for magnetic resonance imaging, blood pumping, treating cancer tumors, metallurgical procedures, nuclear reactors, magnetic electro-catalysis, cooling thermal protection, etc. In their study, Jang et al. [11] performed the theoretical and experimental analysis of the magneto-hydradynamics micropump. Alsaedi et al. [12] numerically investigated the flow of the MHD hybrid nanofluid between two coaxial cylinders. The finite element analysis of the MHD rotational flux of Carreau Casson nanofluid with activation energy was performed by Ali et al. [13]. Nazeer et al. [14] investigated the electric osmotical flow of fluid of 3rd grade in a micro channel by magneto hydradynamics.

The phenomenon of mass and heat transport on surfaces that are embedded in a permeable medium has recently fascinated investigators and engineers, generating significant attention due to its many industrial and engineering applications including in underground water systems, electronic cooling, drying technology, catalytic reactors, geothermal systems, and insulation processes. Ahmad et al. [15] analyzed the mass and heat transport characteristics of aluminum oxide–copper hybrid nanoparticles flux by a permeable medium. Badruddin et al. [16] examined the conjugate thermal and mass transport in a vertically permeable cylinder. The convective heat transmission flux of nanoliquids in a porous medium was described by Hassan et al. [17]. Banerjee et al. [18] reported the permeable medium combustion applications and developments. Waini et al. [19] discussed the symmetrical solution of a hybrid nanoliquid flux using permeable medium.

In current research, the analysis of fluid in a rotating frame has become a charming matter. It has momentous applications in the fields of crystal development, gas turbine rotors, biomechanics, cosmic fluid dynamics, turbomechanics, crystal development, the food industry, and filtration processes. Wang [20] made the most significant contribution in this regard. Rajeswari et al. [21] delineated the time-dependent flux in the rotating fluid above the stretching surface. Rotating the micropolar fluid on the extending surface in the case of quadratic and linear convection significance in thermal management was investigated by Ali et al. [22]. Nadeem et al. [23] studied the numerical analysis of the CNTs’ water-based flux of micropolar fluid by a rotational frame. Kumar et al. [24] investigated the rotating frame analysis of ferro–nanoliquid reaction and radiation considering viscous dissipation and Joule heating. AI-Kouz et al. [25] examined the numerical analysis of Casson nanofluid 3D flux above the rotatory frame subject to a prescribed heated flow during viscous heating.

All the aforementioned studies limited their analysis to investigating the mass and heat transfer of the Newtonian fluid flow model subject to an extending surface, and showing that non-Newtonian nanofluids have wide-ranging applications in heat exchangers, plastic films, polymer extrusion, and many others industries. To the best of the authors’ knowledge, no studies have been communicated that have analyzed the micropolar rotational nanofluid flow above the stretching sheet horizontally subject to the Darcy–Forchheimer law and activation energy. The basic goal of this examination was to enhance the heat transportation with micropolar nanofluid. The novelties of this analysis were:

(i)

The non-Newtonian (micropolar) nanofluid with a water base fluid was analyzed;

(ii)

The MHD effect and micro-rotation of nanoparticles were assimilated.

(iii)

The Buongiorno model of nanofluid was implemented.

(iv)

The activation energy and porous medium were incorporated.

The authors observed that the elaborated problem has not been contemplated by the above-cited reports, whose analyses were instead motivated by the various applications of non-Newtonian micropolar nanofluids in modern technologies. The bvp4c technique was graphically applied to obtain the results. The results for the micro-rotation, velocity, Nusselt number, concentration of nanoparticles, temperature, and Sherwood number were presented via graphs.

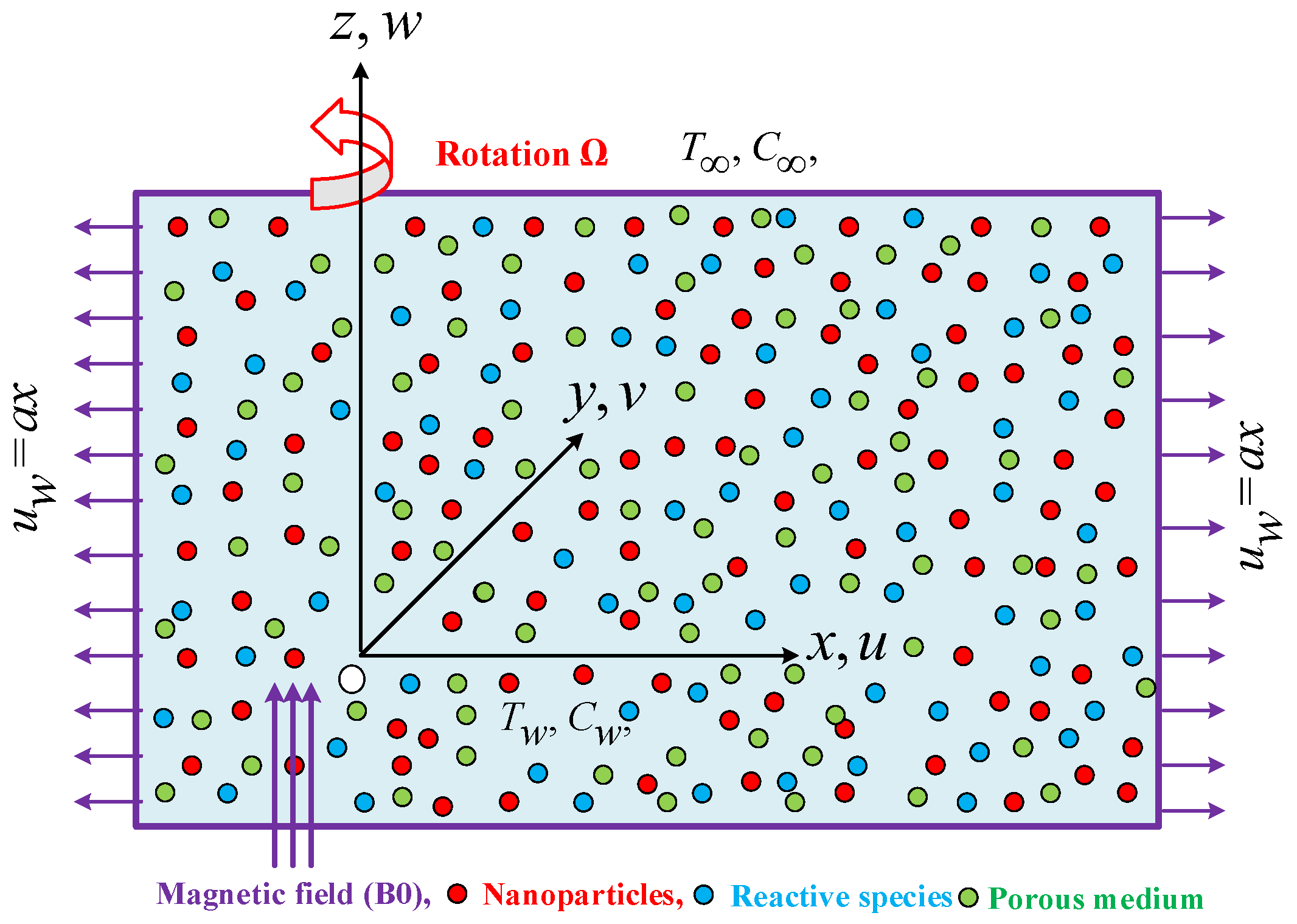
2. Mathematical Formulation

The time-independent three-dimensional incompressible magnetohydrodynamics water-based micropolar nanofluid flow on a stretchable sheet with a rotational frame was assumed. Both forces went in opposite directions from one another and acted identically in the x direction to stretch the sheet at a speed of U(x). The magnetic field, denoted by $B_o$, acted uniformly in the z direction. The ambient temperature and surface temperature were also considered and are represented by $T_{\infty }$ and $T_w$, while $C_{\infty }$ and $C_w$ denote the ambient concentration and concentration of particles at the surface, respectively. The elaborated fluid problem was assumed to be stable and the particle agglomeration was ignored due to the stable fluid. The induced magnetic field was ignored because the magnetic Reynolds number is was excessively small and the strength of the magnetic field was not excessively strong; as such, the Ohmic dissipation and Hall’s current were also ignored [26]. The geometry of the problem is shown in Figure 1.

We subjected the water-based nanofluid to nano-sized particles to improve the thermal conductivity of the base fluid.Under the above assumptions, the leading equations are as follows [27,28,29]:

$$\begin{array}{c}\frac{\partial \breve{v_1}}{\partial \breve{x}}+\frac{\partial \breve{v_2}}{\partial \breve{y}}+\frac{\partial \breve{v_3}}{\partial \breve{z}}=0\end{array}$$

(1)

$$\begin{array}{c}\breve{v_1}\frac{\partial \breve{v_1}}{\partial \breve{x}}+\breve{v_2}\frac{\partial \breve{v_1}}{\partial \breve{y}}+\breve{v_3}\frac{\partial \breve{v_1}}{\partial \breve{z}}-2\Omega \breve{v_2}=\left(\nu +\frac{k}{\rho }\right)\frac{{\partial }^2\breve{v_1}}{\partial \breve{z^2}}+\frac{k}{\rho }\frac{\partial N}{\partial \breve{z}}-\frac{\nu }{k}\breve{v_1}-F{\breve{v_1}}^2-\frac{{\sigma }_{nf}}{{\rho }_{nf}}{B}_o^2\breve{v_1}\end{array}$$

(2)

$$\begin{array}{c}\breve{v_1}\frac{\partial \breve{v_2}}{\partial \breve{x}}+\breve{v_2}\frac{\partial \breve{v_2}}{\partial \breve{y}}+\breve{v_3}\frac{\partial \breve{v_2}}{\partial \breve{z}}+2\Omega \breve{v_1}=\left(\nu +\frac{k}{\rho }\right)\frac{{\partial }^2\breve{v_2}}{\partial {\breve{z}}^2}-\frac{\nu }{k}\breve{v_2}-F{\breve{v_2}}^2-\frac{{\sigma }_{nf}}{{\rho }_{nf}}{B}_o^2\breve{v_2}\end{array}$$

(3)

$$\begin{array}{c}\breve{v_1}\frac{\partial N}{\partial \breve{x}}+\breve{v_2}\frac{\partial N}{\partial \breve{y}}+\breve{v_3}\frac{\partial N}{\partial \breve{z}}=\frac{\gamma }{\rho j}\frac{{\partial }^{2}N}{\partial {\breve{z}}^2}-\frac{k}{\rho j}\left(2N+\frac{\partial \breve{v_1}}{\partial \breve{z}}\right)\end{array}$$

(4)

$$\begin{array}{c}\breve{v_1}\frac{\partial T}{\partial \breve{x}}+\breve{v_3}\frac{\partial T}{\partial \breve{z}}+\breve{v_2}\frac{\partial T}{\partial \breve{y}}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial {\breve{z}}^2}+{\tau }^{\mathrm{*}}\left[D_B\frac{\partial C}{\partial \breve{z}}\frac{\partial T}{\partial \breve{z}}+\frac{D_T}{\partial T_{\infty }}{\left(\frac{\partial T}{\partial \breve{z}}\right)}^2\right]\end{array}$$

(5)

$$\begin{array}{c}\breve{v_1}\frac{\partial C}{\partial \breve{x}}+\breve{v_2}\frac{\partial C}{\partial \breve{y}}+\breve{v_3}\frac{\partial C}{\partial \breve{z}}=D_B\frac{{\partial }^{2}C}{\partial {\breve{z}}^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial {\breve{z}}^2}-k_r^2{\left(\frac{T}{T_{\infty }}\right)}^m{e}^{\frac{-Ea}{kT}}\left(C-C_{\infty }\right)\end{array}$$

(6)

Here, $\breve{v_1}$, $\breve{v_2}$ and $\breve{v_3}$ are the velocity components acting in the x, y, and z directions, respectively. C and T denote the nanoparticle concentration and nanoliquid temperature. N, $\nu$, ${\sigma }_{nf}$, ${\rho }_{nf}$, D, ${\alpha }_{nf}$ represent the micro-rotation, kinematic viscosity, electric conductivity, density, solute diffusibility, and diffusion of heat, respectively, and the per unit mass inertia are j, k, $\gamma$. The relevant boundary conditions are:

$$\begin{array}{c}\left.\begin{array}{c}\hfill v_1=ax,v_2=0,v_3=0,N=-\beta \frac{\partial v_1}{\partial z},T=T_w,C=C_w\mathbf{at}z=0\\ \hfill u⟶0,vs.⟶0,N⟶0,T⟶T_{\infty },C⟶C_{\infty }\mathbf{when}z⟶\infty \end{array}\right\}\end{array}$$

(7)

The following similarity transformation was used to begin the examination [29,30]:

$$\begin{array}{c}\eta =\sqrt{\frac{a}{v}}z,v_1=ax{F}_1^{\prime }\left(\eta \right),v_3=-{\left(a\nu \right)}^{\frac{1}{2}}{F}_1\left(\eta \right),v_2=ax{F}_2\left(\eta \right),\end{array}$$

(8)

$$\begin{array}{c}N=ax\sqrt{\frac{a}{\nu }}H\left(\eta \right),\mathrm{\Phi }\left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}.\end{array}$$

(9)

By the use of the similarity transformation, Equation (1) is identically satisfied. In view of Equations (8) and (9), Equations (2)–(7) are converted into the following nonlinear ODEs:

$$\begin{array}{c}(1+\nabla )F_1^{‴}+F_1{F}_1^{″}+2\Gamma F_2+\nabla H^{\prime }-k_P{F}_1^{\prime }-F_1^{\prime 2}(1+Fr)-M{F}_1^{\prime }=0\end{array}$$

(10)

$$\begin{array}{c}(1+\nabla )F_2^{″}-F_1^{\prime }{F}_2+F_1{F}_2^{\prime }-2\Gamma F_1^{\prime }-k_p{F}_2-Fr{F}_2^2-M{F}_2=0\end{array}$$

(11)

$$\begin{array}{c}(1+\frac{\nabla }{2})H^{″}+F_1{H}^{\prime }-F_1^{\prime }H-(2H+F_1^{″})=0\end{array}$$

(12)

$$\begin{array}{c}{\theta }^{″}+Prf{\theta }^{\prime }+NbPr\theta \mathrm{\Phi }+NtPr{\theta }^{\prime 2}=0\end{array}$$

(13)

$$\begin{array}{c}{\mathrm{\Phi }}^{″}+Scf{\mathrm{\Phi }}^{\prime }+\frac{Nt}{Nb}{\mathrm{\Phi }}^{″}-Sc\sigma {(\theta \delta +1)}^m.exp\left(\frac{-E_e}{\theta \delta +1}\right)\mathrm{\Phi }=0\end{array}$$

(14)

with the boundary conditions

$$\left.\begin{array}{c}\hfill F_1(\eta =0)=0,F_1^{\prime }(\eta =0)=1,F_2(\eta =0)=0,H=-\beta F_1^{″},\theta (\eta =0)=1,\mathrm{\Phi }(\eta =0)=1,\\ \hfill F_1^{\prime }(\infty )⟶0,F_2(\infty )⟶0,H=0,\theta (\infty )⟶0,\mathrm{\Phi }(\infty )⟶0when\eta ⟶\infty .\end{array}\right\}$$

(15)

where—in Equations (10)–(15)—∇ is a dimensionless micropolar material parameter [31]; the rotatory and porosity parameters are represented by $\Gamma$; $k_p$, M, $F_r$, $Pr$, $Sc$, $\sigma$, $Nt$, and $Nb$ denote the magnetic parameter, Forchheimer number, Prandtl number, Schmidt number, reaction rate, thermophoresis parameter, and Brownian motion, respectively, which are defined as:

$$\begin{array}{c}\hfill \nabla =\frac{k}{\mu },\Gamma =\frac{\Omega }{a},k_p=\frac{\nu }{Ka},M=\frac{{\sigma }_{nf}{B}_o^2}{{\rho }_{nf}a},F_r=\frac{C_b}{k^{\frac{1}{2}}},Sc=\frac{\nu }{D},\sigma =\frac{K_r^2}{a}\\ \hfill Pr=\frac{{\left(\mu C_p\right)}_f}{k_f}F=\frac{C_b}{x{k}^{\frac{1}{2}}},Nt=\frac{{\tau }^{\mathrm{*}}{D}_T(T_w-T_{\infty })}{\nu T_{\infty }},Nb=\frac{{\tau }^{\mathrm{*}}{D}_B(C_w-C_{\infty })}{\nu }\end{array}$$

The skin friction coefficient expressions along x axis and y axis, the local Nusselt number, and Sherwood number are, respectively, defined as:

$$\begin{array}{c}\left.\begin{array}{c}\hfill C{f}_x=\frac{{\tau }_w^x}{\rho {\left(ax\right)}^2},\\ \hfill C{f}_y=\frac{{\tau }_w^y}{\rho {\left(ax\right)}^2},\\ \hfill Nu=\frac{x{q}_w}{k_f(T-T_{\infty })},\\ \hfill S{h}_x=\frac{x{j}_w}{D(C_w-C_{\infty })},\end{array}\right\}\end{array}$$

(16)

where the skin friction tensor at the wall is ${\tau }_w^x=(\mu +\kappa ){(\partial \breve{v_1}\partial z+\kappa N)}_{z=0}$ (x direction) and ${\tau }_w^y=(\mu +\kappa ){(\partial \breve{v_2}\partial z+\kappa N)}_{z=0}$ (y direction), the wall heat transfer is $q_w=-\kappa {\left(\partial T\partial z\right)}_{z=0}$, and the mass flux from the sheet is $q_m=-{\tilde{D}}_B{\left(\partial \tilde{C}\partial z\right)}_{z=0}$. Thanks to the similarity transformation Equations (8) and (9), we obtain:

$$\begin{array}{c}{q}_w=-k\frac{\partial T}{\partial z}{{|}_{z=0}...,j_w=-D\frac{\partial C}{\partial z}|}_{z=0}\end{array}$$

(17)

Finally, we have

$$\begin{array}{c}\left.\begin{array}{c}\hfill R{e}_x^{0.5}C{f}_x=((1-\beta )\nabla +1)F_1^{″}\left(0\right),\\ \hfill R{e}_x^{0.5}C{f}_y=((1-\beta )\nabla +1)F_2^{\prime }\left(0\right),\\ \hfill R{e}_x^{-0.5}Nu=-{\theta }^{\prime }\left(0\right),\\ \hfill R{e}_x^{-0.5}S{h}_x=-{\mathrm{\Phi }}^{\prime }\left(0\right),\end{array}\right\}\end{array}$$

(18)

where $R{e}_x$ is the local Reynolds number that is defined as $\frac{a{x}^2}{\nu }$.

3. Results and Discussion

The solution for the developed ODEs (10)–(15) related to constraints is required to show the physical analysis of this problem and the bvp4c method is used to graphically solve the problem. A detailed computational process is used to check the influence of different parameters on primary and secondary velocity ($F_1^{\prime }\left(\eta \right)$, $F_2\left(\eta \right)$), micro-rotation distribution $H\left(\eta \right)$, temperature $\theta \left(\eta \right)$ and concentration $\left(\mathrm{\Phi }\right)$. Furthermore, the $Nu$ (Nusselt number) and $C{f}_x$, $C{f}_y$ (skin friction coefficients) and $Sh{r}_x$ (Sherwood number) are graphically detected. A comparison of outcomes was carried out in order to certify the use of the technique as shown in

Table 1. The comparison of $F_1^{″}\left(0\right)$ and $F_2^{\prime }\left(0\right)$ against rotating parameter $\Gamma$ when others involved parameters values are zero.

$\mathbf{\Gamma }$	Nazar et al. [32]			Current Results
	$-F_1^{″}\left(0\right)$	$-F_2^{\prime }\left(0\right)$		$-F_1^{″}\left(0\right)$	$-F_2^{\prime }\left(0\right)$
1	1.3250	0.8371		1.32503	0.837104
2	1.6523	1.2873		1.652325	1.287249
3	1.6523	1.2870		1.92894	1.624741

and

Table 2. The comparison of ${\theta }^{\prime }\left(0\right)$ against rotating $\Gamma$ and Prandtl number $\left(Pr\right)$ parameters when others involved parameters values are zero.

$\mathbf{\Gamma }$	Ali et al. [33]			Current Results
	$Pr=2.0$	$Pr=7.0$		$Pr=2.0$	$Pr=7.0$
0.5	0.8525	1.8500		0.85243	1.851168
1	0.7703	1.7877		0.77033	1.787704
2	0.6381	1.6642		0.63822	1.664314

. An excellent relation between already existing outcomes is observed. The recent analysis’s estimation was performed using the following values of the involved parameters: $\Gamma =0.5$, $Pr=6.2$, $\sigma =0.4$, $Sc=2$, $\delta =0.4$, $m=0.4$, $kp=0.3$, $M=1$, $Fr=1.0$, $E_e=0.3$, $\nabla =0.5$, $\beta =0.5$, $Nb=0.2$, $Nt=0.2$.

Figure 2a,b represents the impact of the rotating parameter $\Gamma$ and the material parameter ∇ on the primary velocity $F_1^{\prime }$ and the secondary velocity $F_2$. This indicates that $F_1^{\prime }$ and $F_2$ are abated near the sheet and later on experience a variation when $\Gamma$ is increased. The primary velocity $F_1^{\prime }$ obtains a maximum value when $\Gamma =0$. It is worth noting that, along the x axis, extending the sheet causes the momentum to rise in this direction, whereas momentum in the y direction is unsupported. As such, Figure 2a,b exhibit that $F_1^{\prime }$ is marginally influenced and $F_2$ is particularly influenced. While the primary velocity is boosted with the escalating values of the material parameter, the magnitude of the secondary velocity is decreased. Figure 3a,b depicts the effects of magnetic parameter M and the micropolar boundary parameter on the velocity profile. It is noted that the growing value of M causes the decline in $F_1^{\prime }$ and $F_2$. This is correlated with the thickness of the boundary layer. This confirms the magnetic effect’s general behavior. Physically, increasing the value of the magnetic parameter means enhancing the drag force, i.e., the resistive force. As such, $F_1^{\prime }$ and $F_2$ are decreased. Furthermore, $F_1^{\prime }$ and $F_2$ are also decreased with amplified values of $\beta$.

Figure 4a,b reveals the variation in $F_1^{\prime }$ and $F_2$ due to the Forchheimer number ($Fr$) and porosity factor ($kp$). $F_1^{\prime }$ and $F_2$ decreased with higher contributions from both parameters. Physically, the fluid becomes more viscous with the association of the porous medium and resistive force is created which slows down the primary and secondary velocities. The impacts of the material parameter, rotational parameter, magnetic parameter, and boundary concentration parameter on the micro-rotation distribution profile are shown in Figure 5a,b. With the effect of rising values of $\Gamma$ and ∇, the micro-rotation profile decreased, but with growing values of M and $\beta$, $H\left(\eta \right)$ increased. Figure 6 portrayed the effect of the $Fr$ (Forchheimer number) and $kp$ (porosity factor) on the temperature profile. With an increasing value of both parameters, the temperature increases. Physically, the resistive forces are generates because of a permeable space due to which the fluid is dragged into a zone of the boundary layer, resulting in heat dissipation generating more heat in this zone. Therefore, $\theta \left(\eta \right)$ is on rise with $Fr$ and $kp$. Figure 6b presented the implication of the parameters of Buongiorno’s model (Brownian motion and thermophoresis) on $\theta \left(\eta \right)$. Nanoparticles move from the hot zone to the cold zone due to the thermophoretic force and as a result, more heat transmission occurs in the region of the boundary layer. Similarly, a faster random movement of species particles in nanoliquids prompted the Brownian forces to enhance the thermal transportation. As such, the increment in temperature is reported in Figure 6b.

The impact of the rotational parameter and material parameter on the temperature of the nanofluid is sketched in Figure 7a. It increased with increasing values of the rotational parameter. The development in heat is satisfied on the basis of the higher diffusion processes because of increased rotation. It is noted that incremental values of ∇ cause a decrease in temperature. The effect of M and $\beta$ on $\theta \left(\eta \right)$ is represented in Figure 7b. The temperature field is increased with amplified values of M and $\beta$. With growing values of M, the fluid flux is stopped and dissipation appends to the thermal energy of the fluid. Figure 8a displayed the effect of ∇ and $\Gamma$ on $\mathrm{\Phi }\left(\eta \right)$. The concentration field decreased with increasing values of the material parameter, but rises on with incremented values of the rotational parameter. Variation in the concentration of the fluid due to $Nt$ and $Nb$ is illustrated by Figure 8b. It is clearly analyzed that a larger $Nb$ parameter discloses a decay in $\mathrm{\Phi }\left(\eta \right)$. However, with incremental values of $Nt$, the concentration profile is increased. Physically, the Brownian motion aggravates the particles far off from the field zone and also warms the liquid in the boundary layer. As such, a reduction is observed in the concentration. With the increasing value of $Nt$, the intense diffusion of particles in the host fluid results the expansion of the boundary layers of concentration. Thus, $\mathrm{\Phi }\left(\eta \right)$ becomes magnified. Figure 9a demonstrates the outcome of the activation energy ($E_e$) and reaction rate constant ($\sigma$). The concentration distribution is increasingly activating the energy. Because $E_e$ aggrandizes, the modified Arrhenius function decays. This stimulates the generative chemical process, which raises the concentration of nanoparticles. While there is an opposite behavior for $\sigma$. By incremented values of $\sigma$, $\mathrm{\Phi }\left(\eta \right)$ decreased. Figure 9b was organized to express the extent of the impact of the fitted rate constant $\left(m\right)$ and $\delta$ on the concentration of fluid. By increasing the values of both parameters, the concentration of the liquid reduced. Physically, the growing values of the fitted rate constantly increased the mathematical relation factor $\sigma {(\theta \delta +1)}^m.exp\left(\frac{-E_e}{\theta \delta +1}\right)$. The rise in this factor ultimately helps the disastrous chemical reaction which enhances the volume fraction profile of the nanoparticles.

Figure 10a,b are drawn to present the fluctuation in $C{f}_x{\left(Re\right)}^{0.5}$ and $C{f}_y{\left(Re\right)}^{0.5}$, which is subject to the parameters M, $\Gamma$, and ∇, which were given different values. The skin friction coefficient ($C{f}_{x}R{e}^{0.5}$) undergoes a notable decrease with the incremental values of M, $\Gamma$, and ∇, while $C{f}_y{\left(Re\right)}^{0.5}$ increased against M and ∇ but decreased against $\Gamma$. The Nusselt numbers are sketched in Figure 11a,b. Figure 11a depicts that the magnitude of $NuR{e}^{0.5}$ reduced with higher values of the magnetic parameter and the rotational parameter, but increased with larger values of the material parameter. With the rising strength of the Lorentz force, we also noticed the expected escalation in $NuR{e}^{0.5}$, since, by heating the nanofluid subject and thus giving it a very strong magnetic strength, there will be a heat transfer loss at the surface of the stretch sheet that will manifest in a decline in $NuR{e}^{0.5}$. The magnitude of Nusselt numbers lessened with larger inputs of the Forchheimer number, Brownian motion, and thermophoresis, as plotted in Figure 11b. Physically, we observed that, due to the greater resistance and viscosity between the nanoparticles which produce more heat, the magnitude of the Nusselt numbers declined. The influences of different parameters on $S{h}_{x}R{e}^{0.5}$ are presented in Figure 12a,b. The magnitude of the Sherwood number is boosted with elevated values of $Nb$ but decreased against the activation energy and $\Gamma$, as revealed in Figure 12a. Figure 12b discloses that the magnitude of $S{h}_x{\left(Re\right)}^{0.5}$ reduced against $Nt$, $\Gamma$, and $E_e$.

4. Conclusions

In this article, 3D rotating water-based micropolar nanofluid flow above a linearly stretching surface was investigated and the bvp4c method was applied to analyze the enhancement of the heat transportation in the presence of the MHD rotating non-Newtonian nanofluid using a porous medium. The graphical outcomes for the velocity components, micro-rotation distribution, temperature, skin friction coefficient, particle concentration, Nusselt numbers, and Sherwood number were obtained. Some of the significant consequences are as follows:

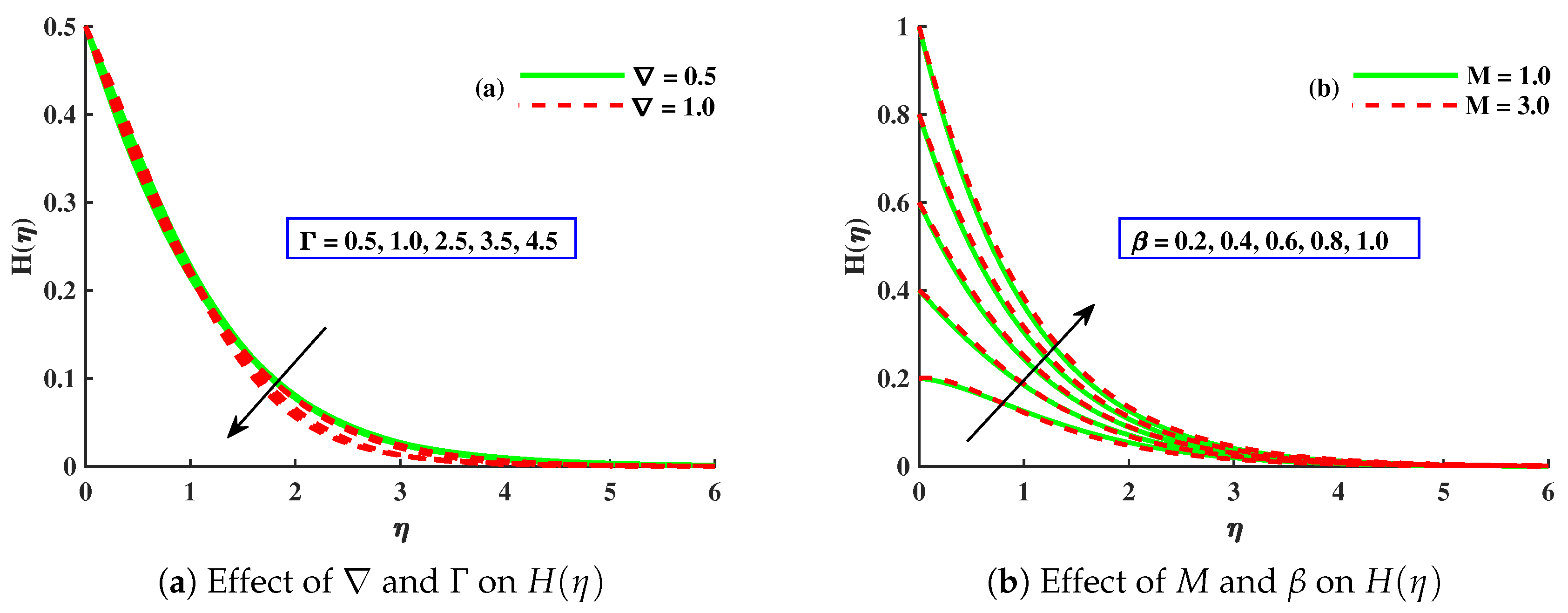
• $F_1^{\prime }\left(\eta \right)$ and $F_2\left(\eta \right)$ decreased significantly with higher values of $F_r$, $\beta$, $kp$, M, and $\Gamma$. However, $F_1^{\prime }$ displayed an increasing behavior for ∇ and a magnitude of $F_2$ with a decreasing behavior for ∇.
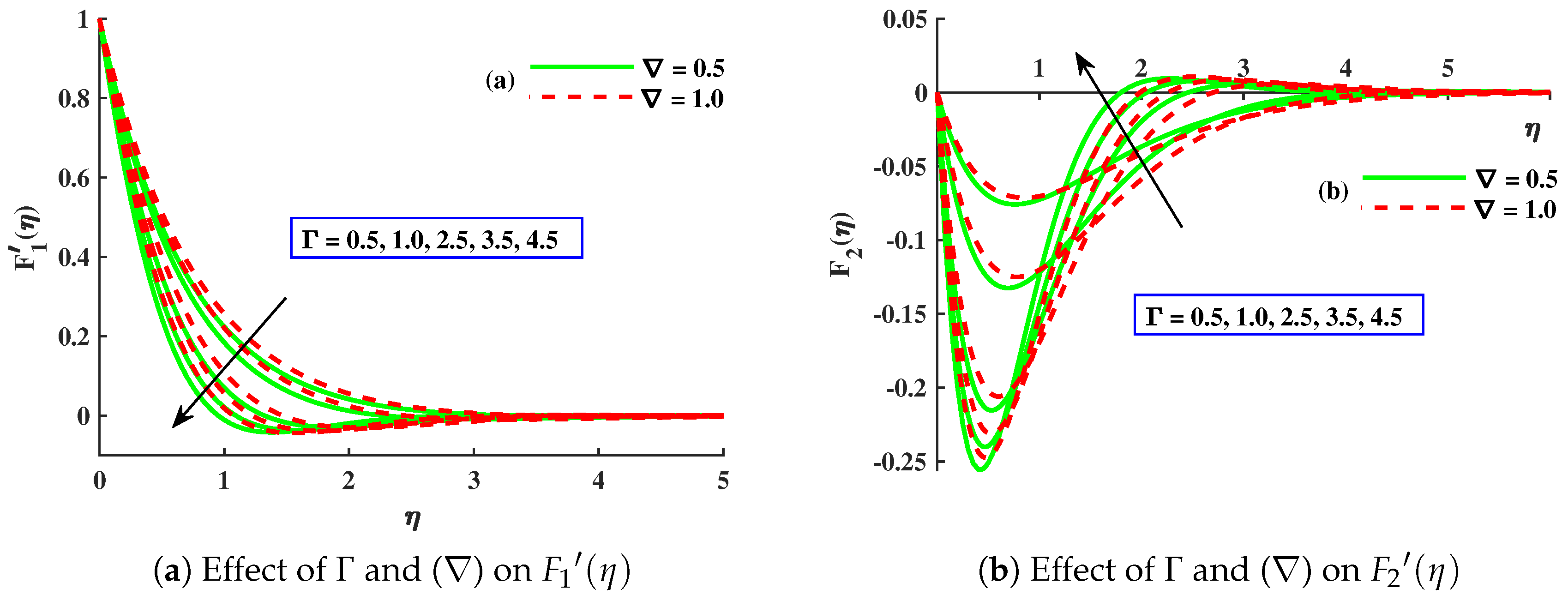
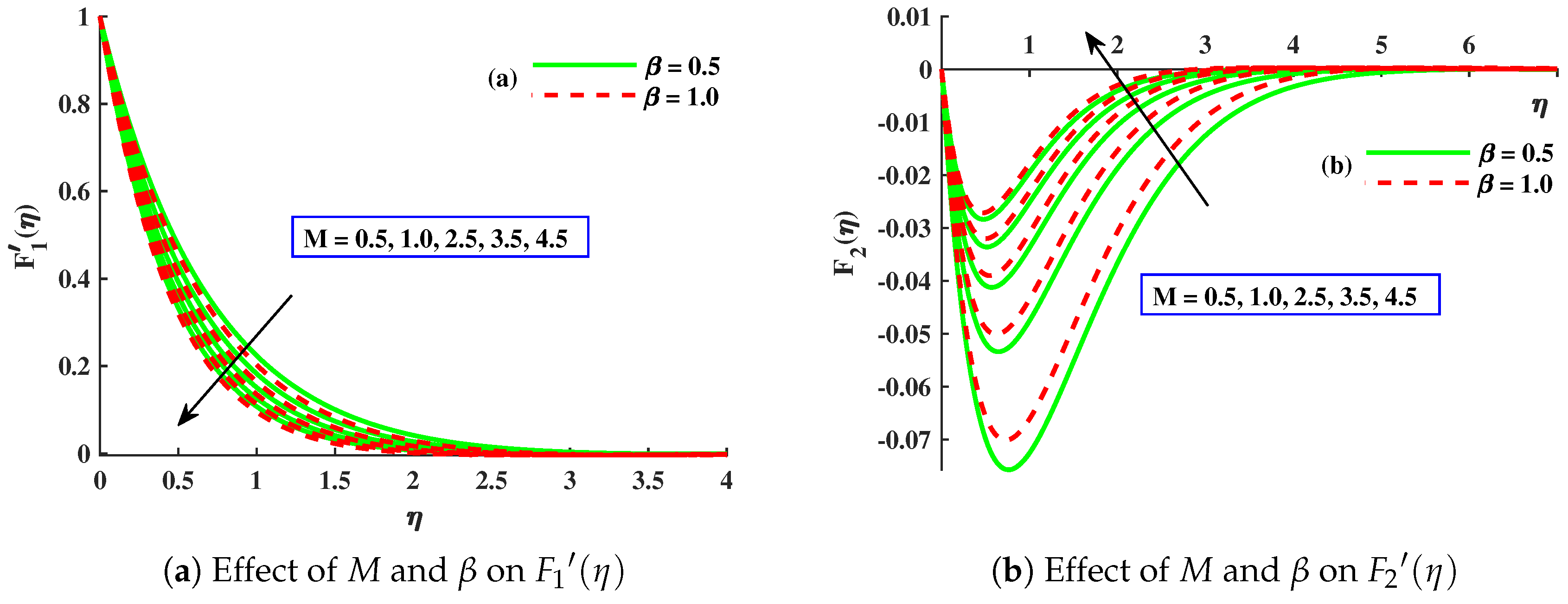
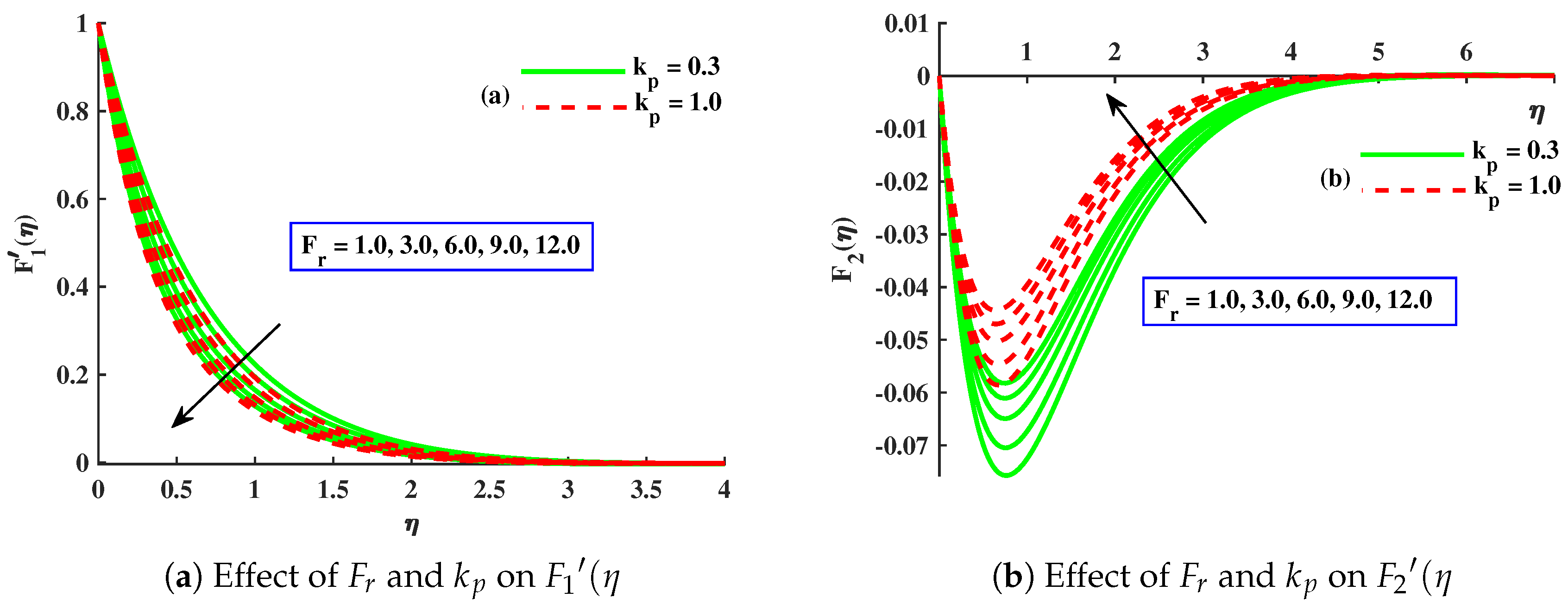
• The amplified values of concentration boundary parameter and Lorentz force enhanced the micro-rotation distribution, but displayed an opposite behavior against the growing values of material parameter.
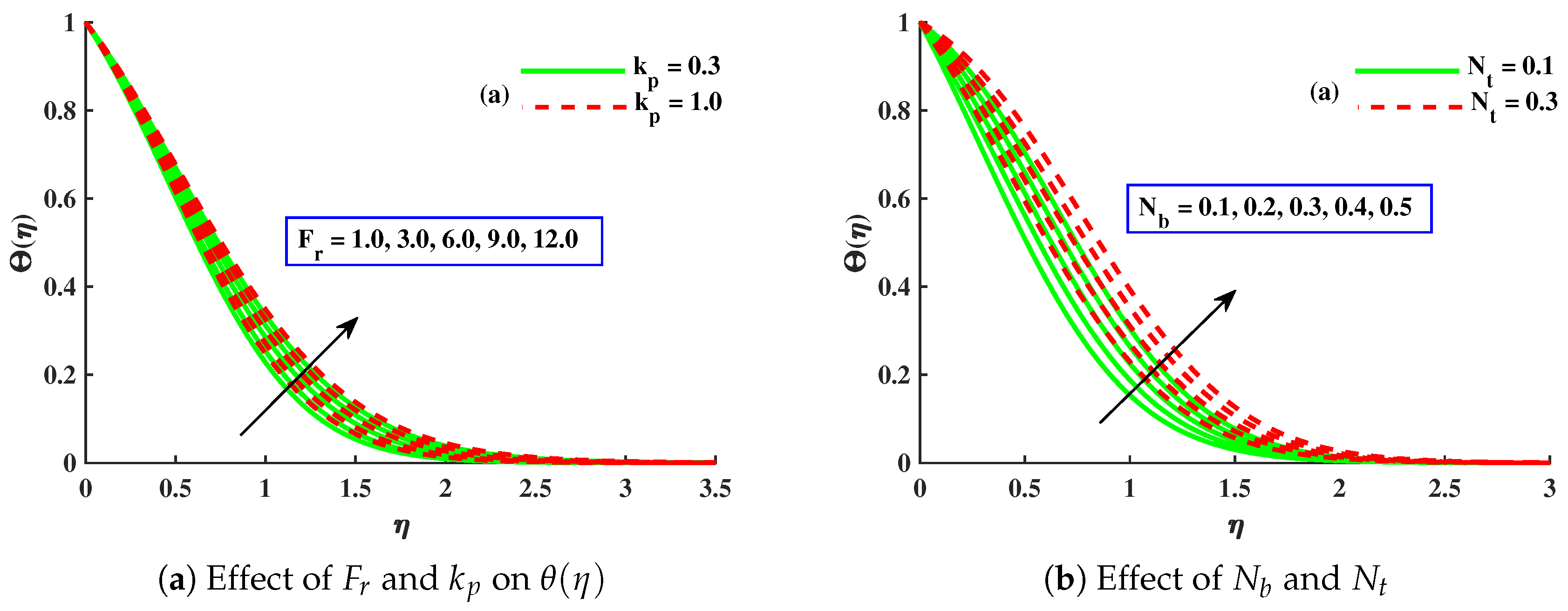
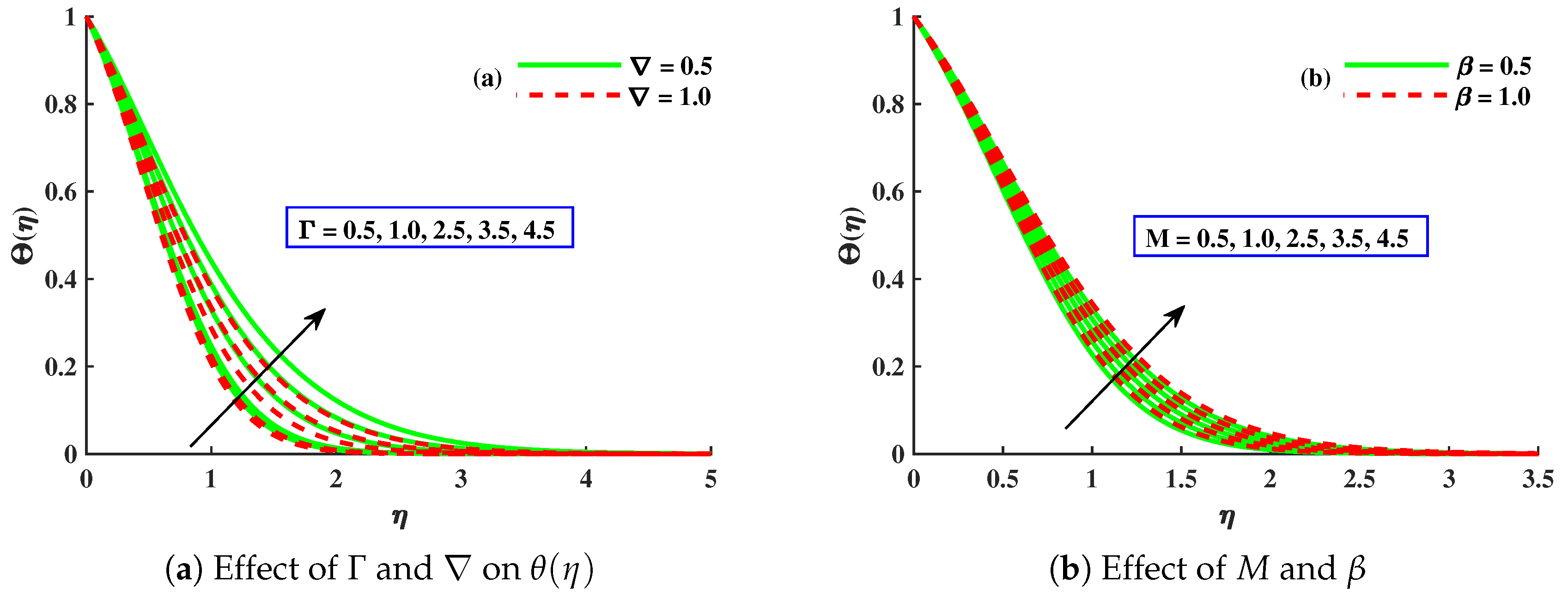
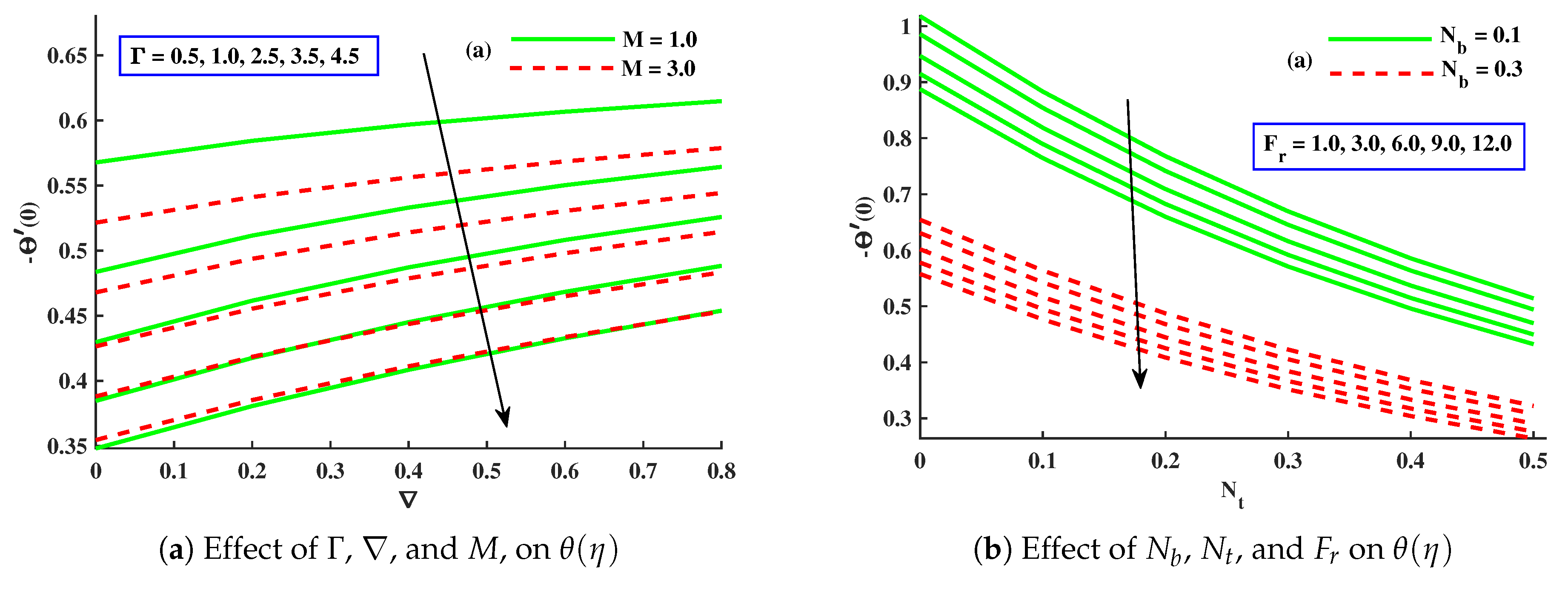
• The thermal performance of the host fluid was enhanced against the growing strength of the Brownian motion, thermophoresis, and porous medium parameters, but the opposite trend was noticed against the dimensionless micropolar material parameter.
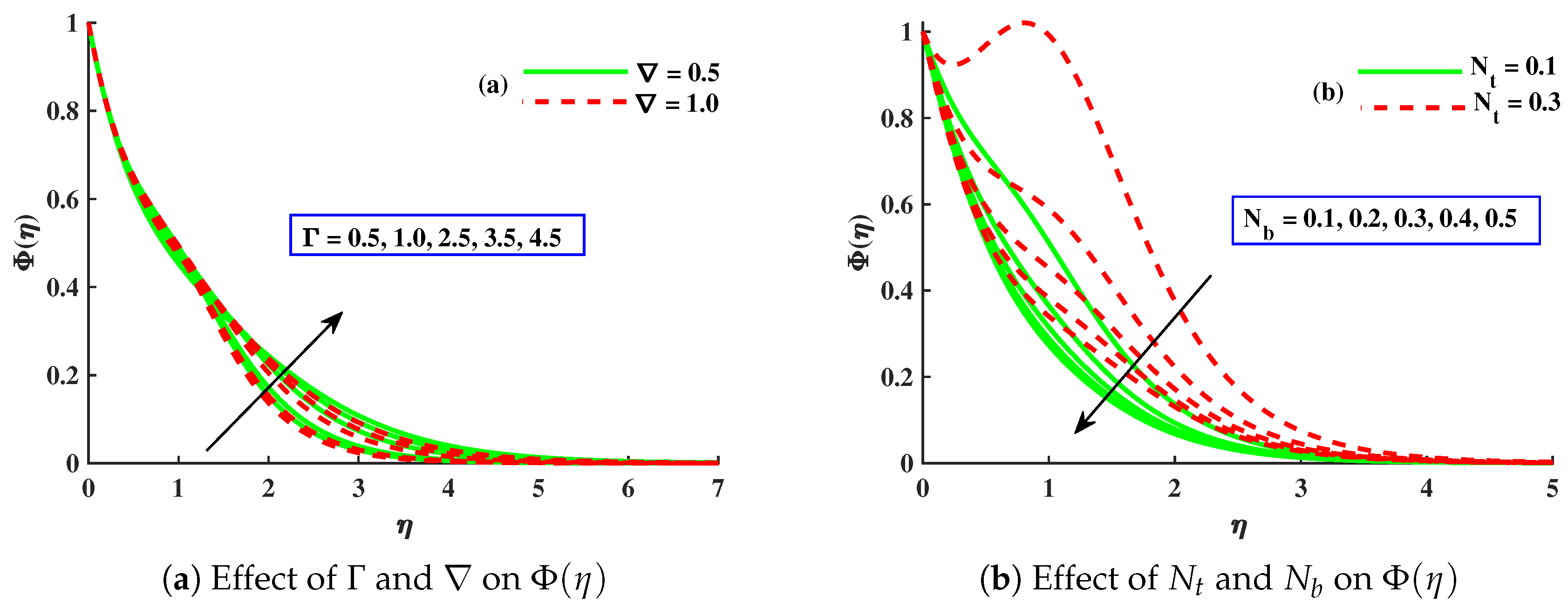
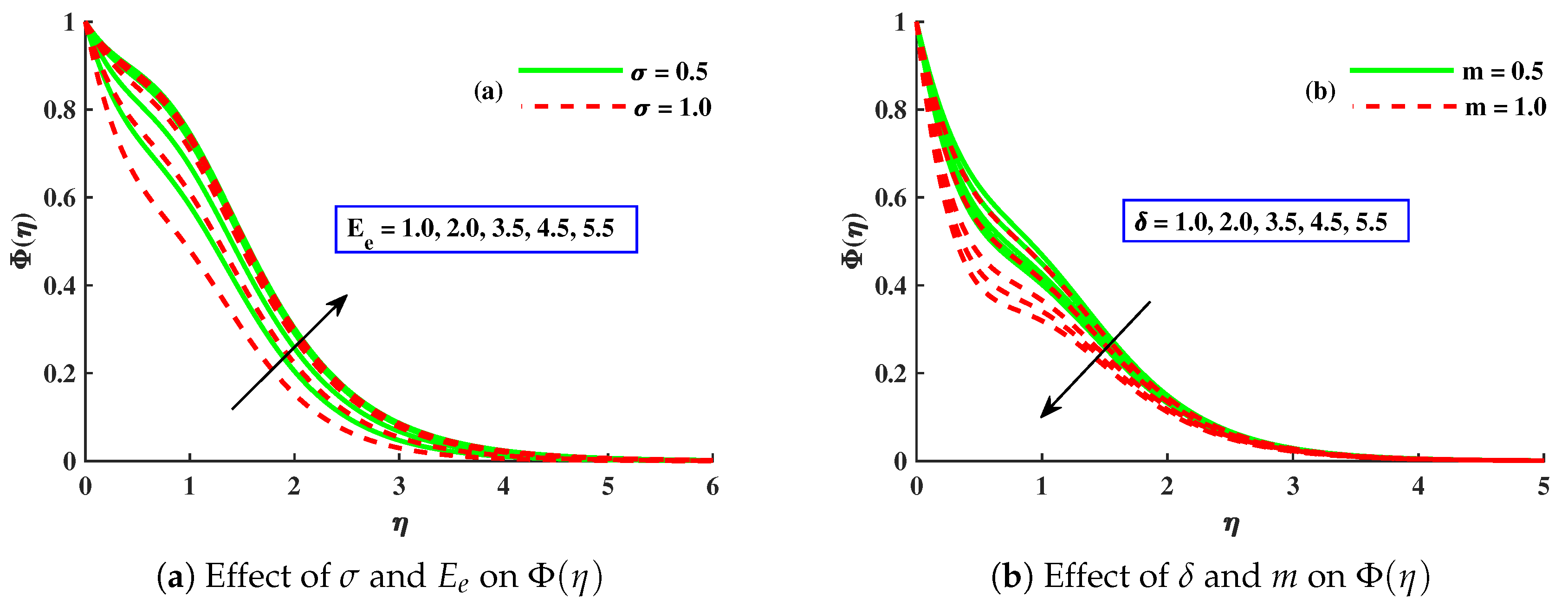
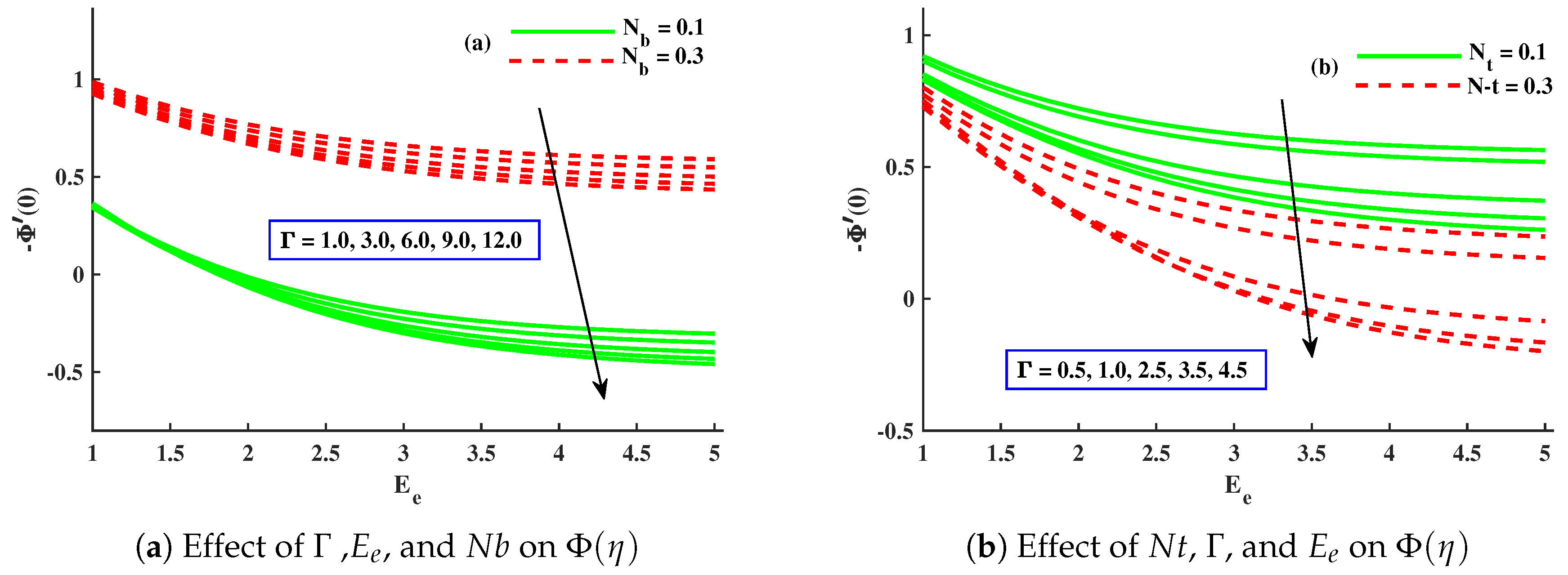
• With amplified values of $\Gamma$, $Nt$, and $E_e$, the concentration profile was enhanced, while it was decreased against ∇, $\sigma$, $\delta$, m, and $Nb$.
• The magnitude of the Sherwood number displayed an increasing behavior against $Nb$, but showed a decreasing behavior for $Nt$, $\Gamma$, and $E_e$.
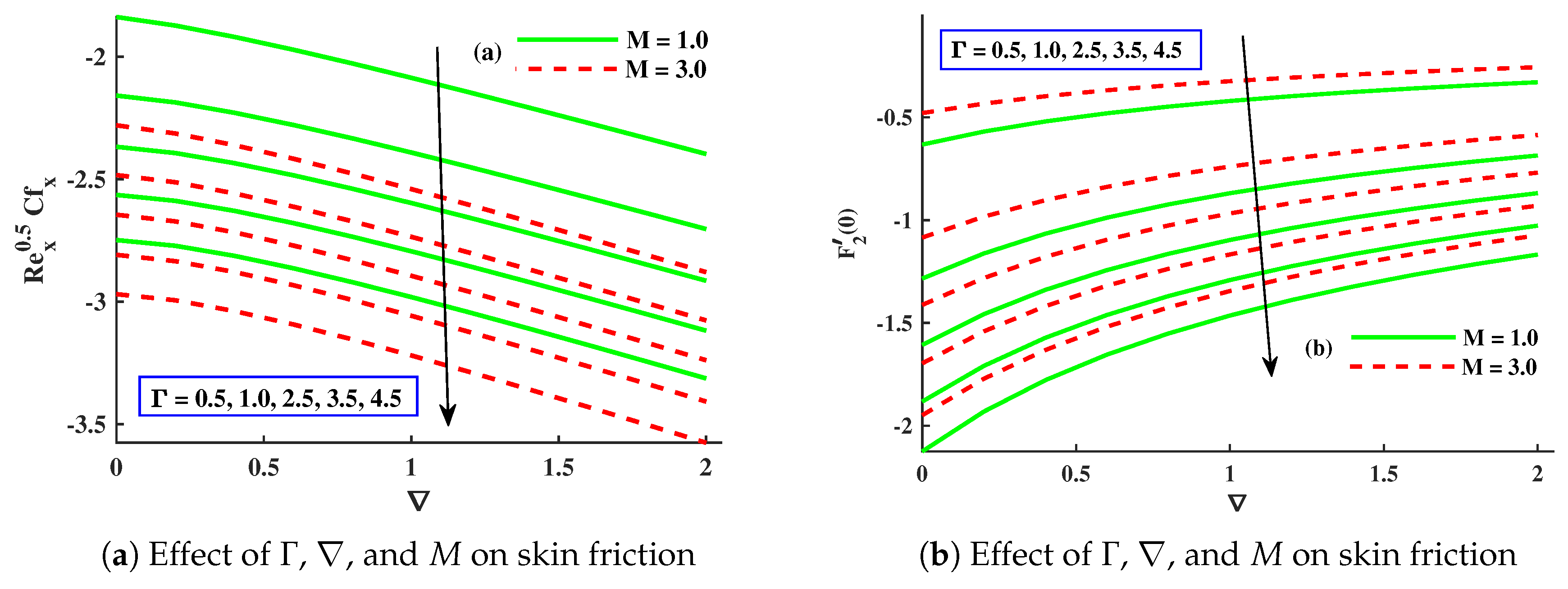
• The skin friction coefficient in the x direction decreased with a larger value of M, $\Gamma$, and ∇, whilst the skin friction coefficient in the y direction increased due to enhancements in M and ∇ but decreased for $\Gamma$.
• The magnitude of the Nusselt numbers was decreased with increasing contributions of $Nt$, $Nb$, $\Gamma$, $Fr$, and M, but increased against ∇.

Through this computational effort, we successfully elucidated the parametric impacts on the dynamics of micropolar nanofluid. In a future study, this study may be extended for various types of non-Newtonian fluid flow models. This study will be applicable in modern nanotechnology, the cooling of electronic devices, paper production, and with momentous applications in the industry and engineering fields.