Significance of Darcy–Forchheimer Law, Activation Energy, and Brownian Motion of Tiny Particles on the Dynamics of Rotating MHD Micropolar Nanofluid
Abstract
:1. Introduction
- (i)
- The non-Newtonian (micropolar) nanofluid with a water base fluid was analyzed;
- (ii)
- The MHD effect and micro-rotation of nanoparticles were assimilated.
- (iii)
- The Buongiorno model of nanofluid was implemented.
- (iv)
- The activation energy and porous medium were incorporated.
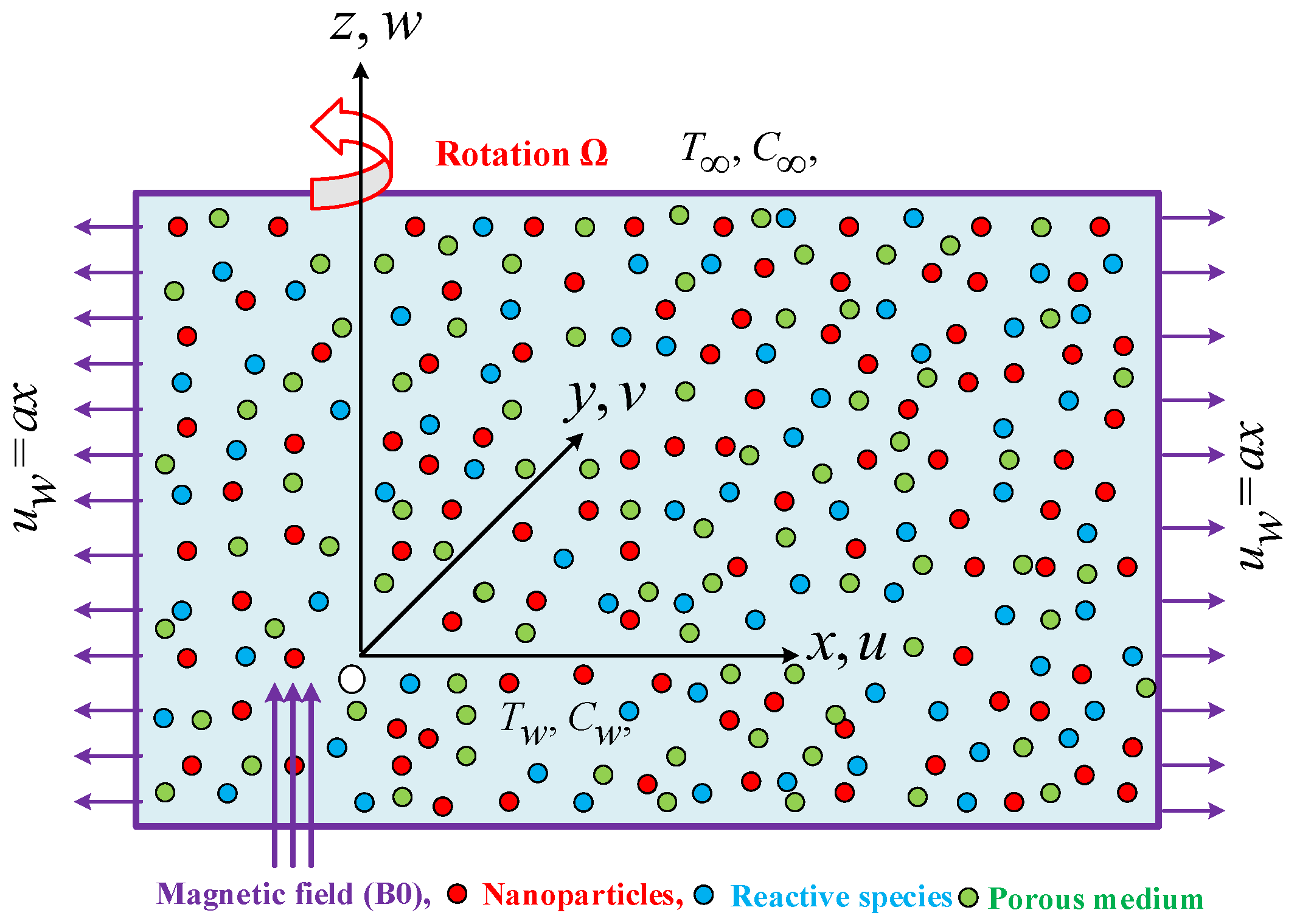
2. Mathematical Formulation
3. Results and Discussion
4. Conclusions
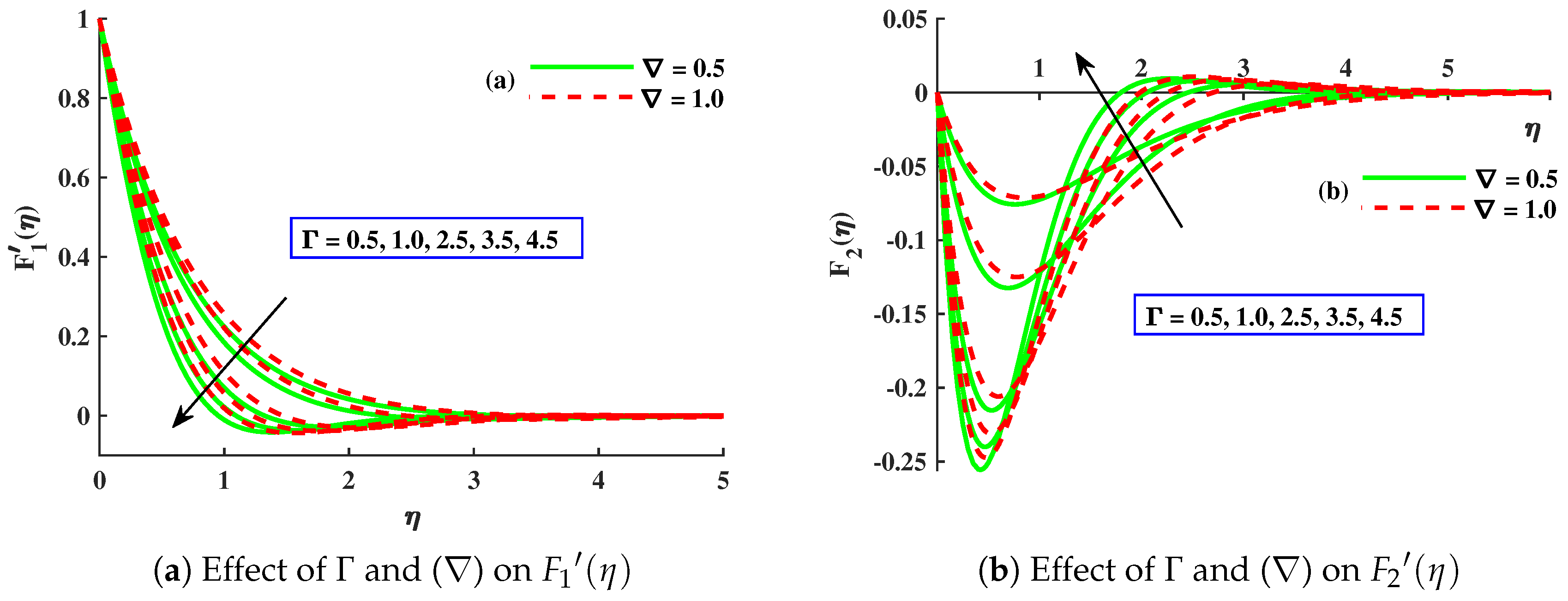
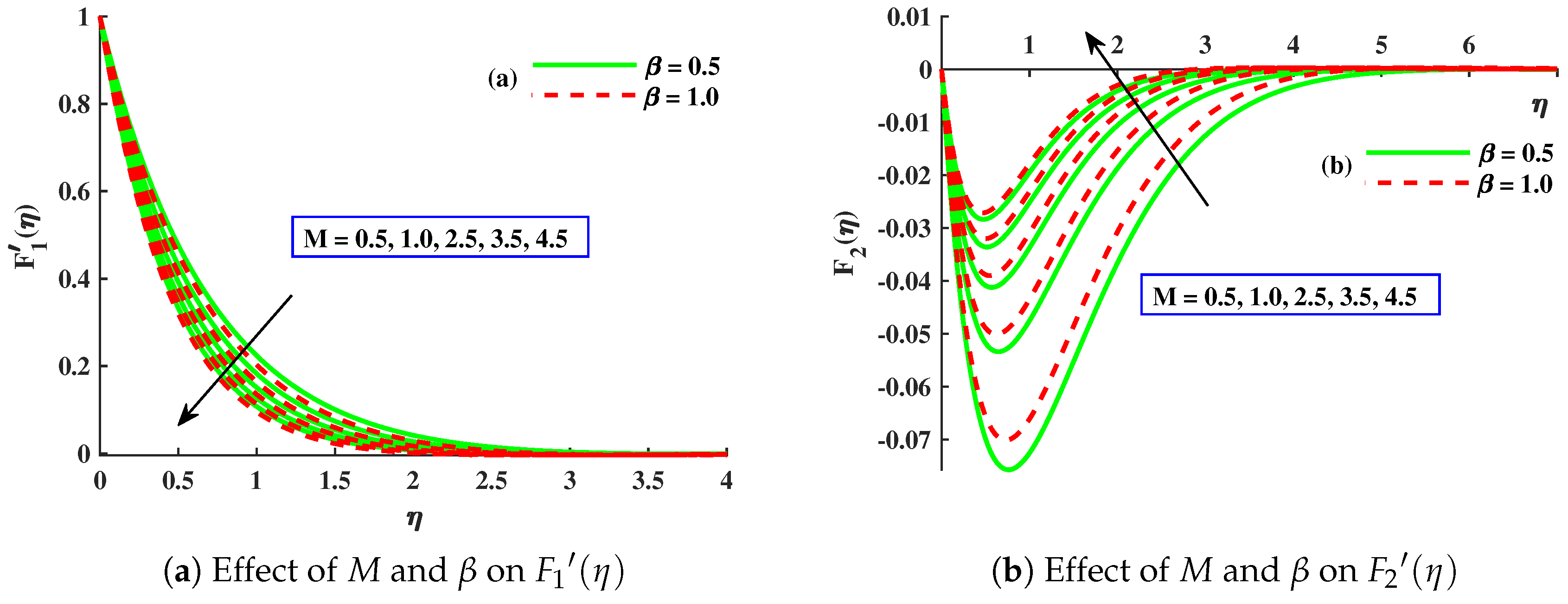
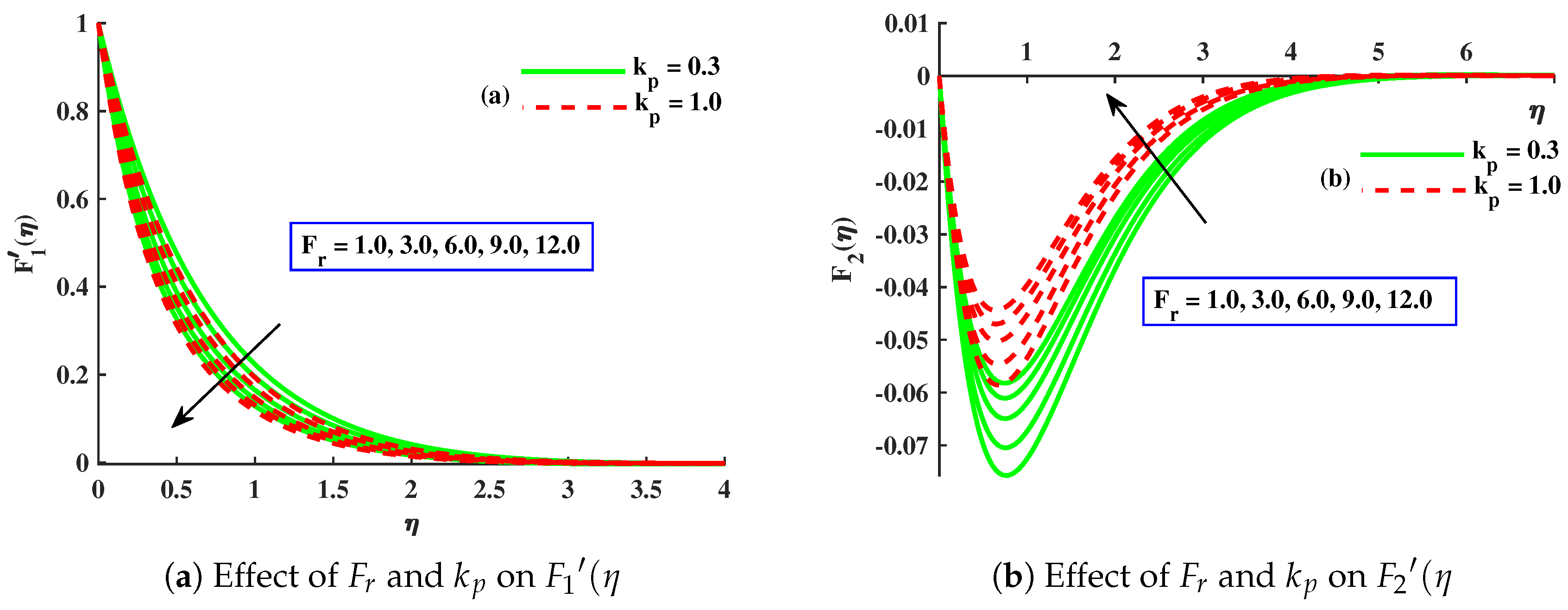
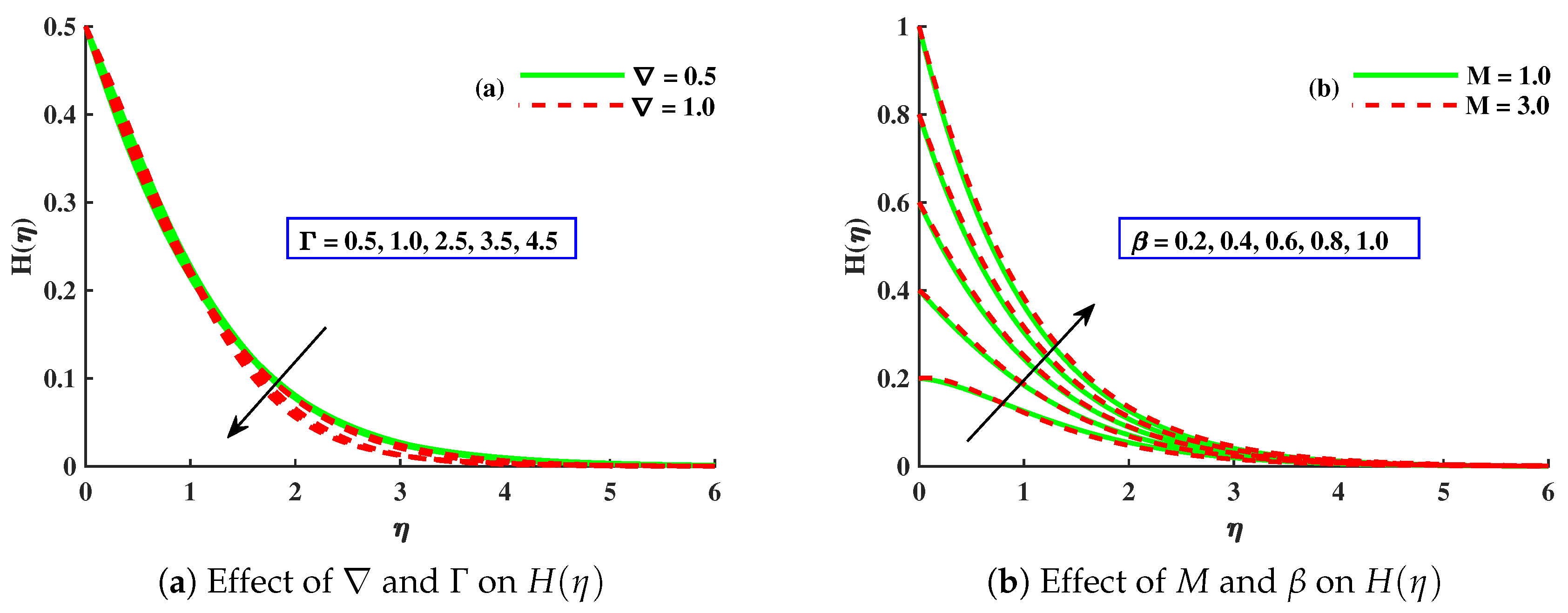
- and decreased significantly with higher values of , , , M, and . However, displayed an increasing behavior for ∇ and a magnitude of with a decreasing behavior for ∇.
- The amplified values of concentration boundary parameter and Lorentz force enhanced the micro-rotation distribution, but displayed an opposite behavior against the growing values of material parameter.
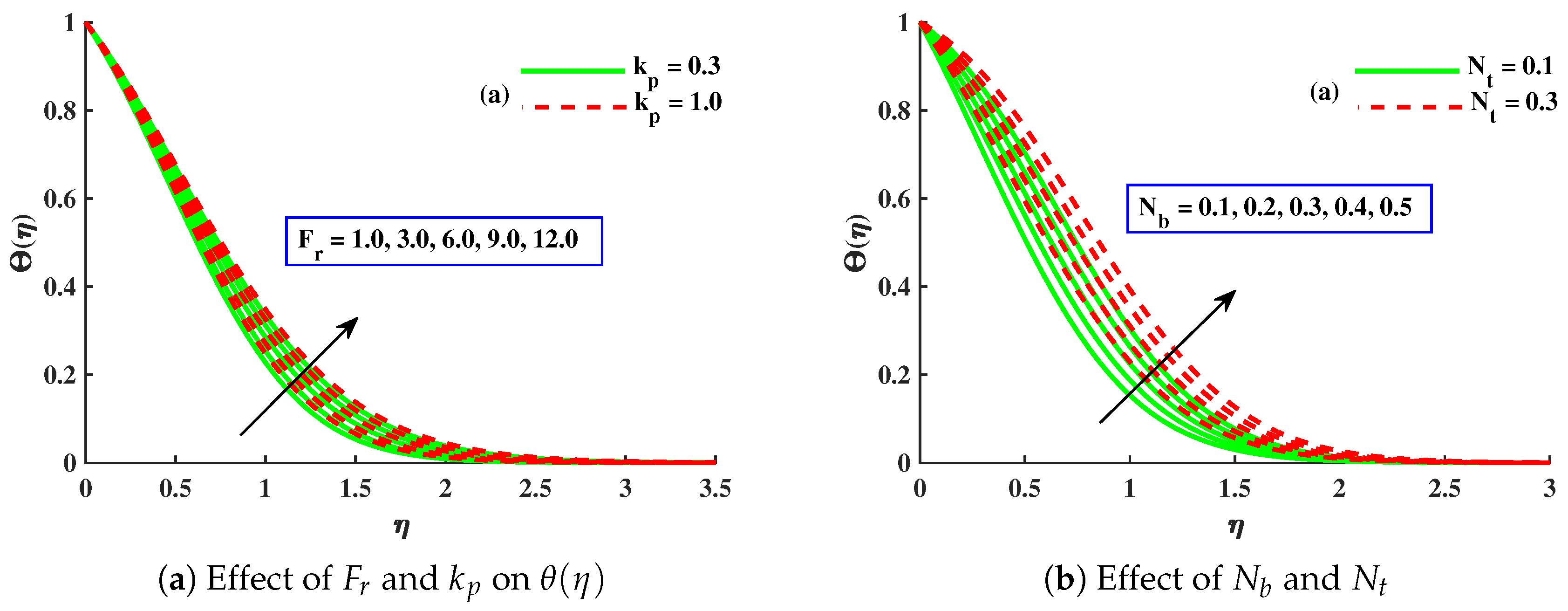
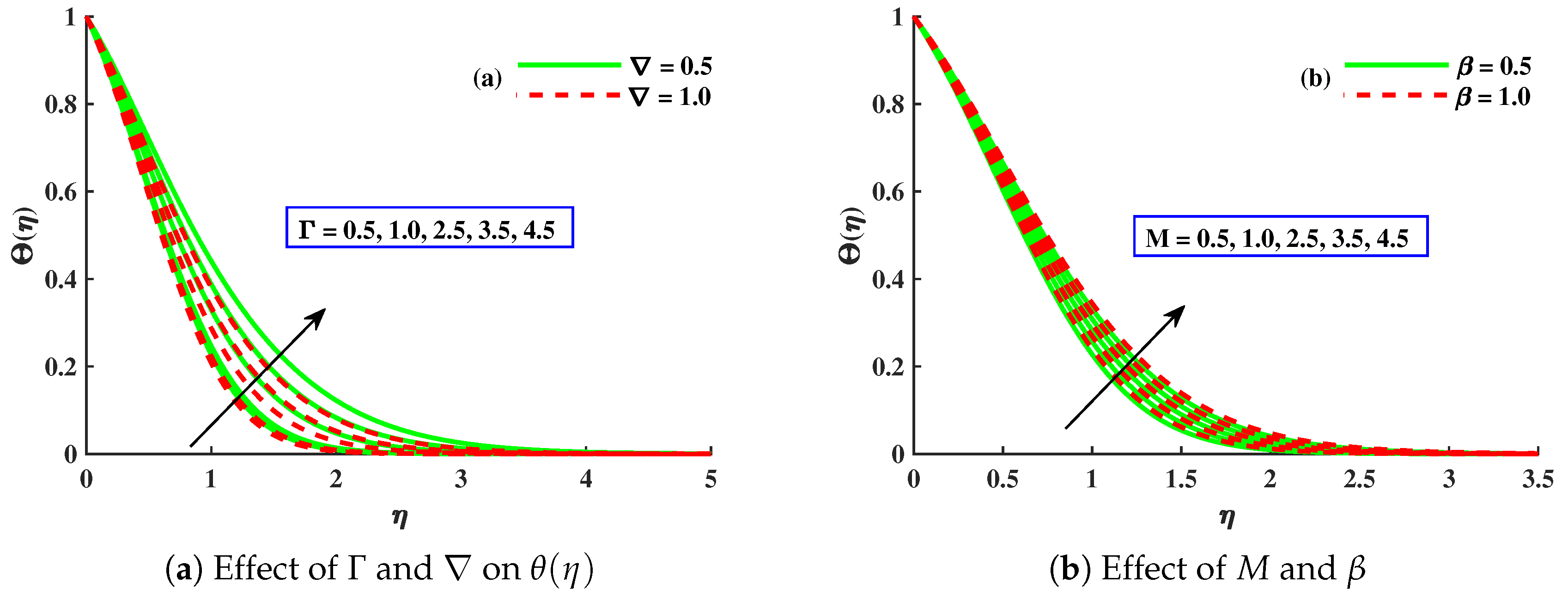
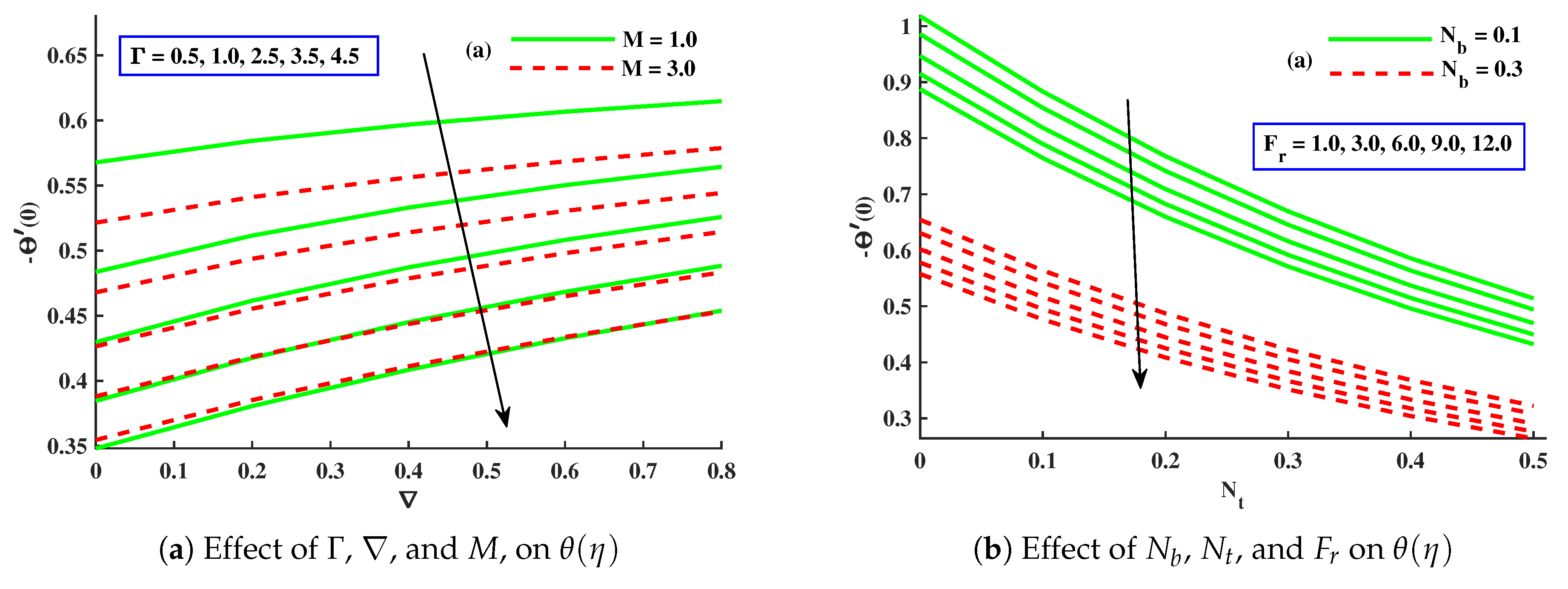
- The thermal performance of the host fluid was enhanced against the growing strength of the Brownian motion, thermophoresis, and porous medium parameters, but the opposite trend was noticed against the dimensionless micropolar material parameter.
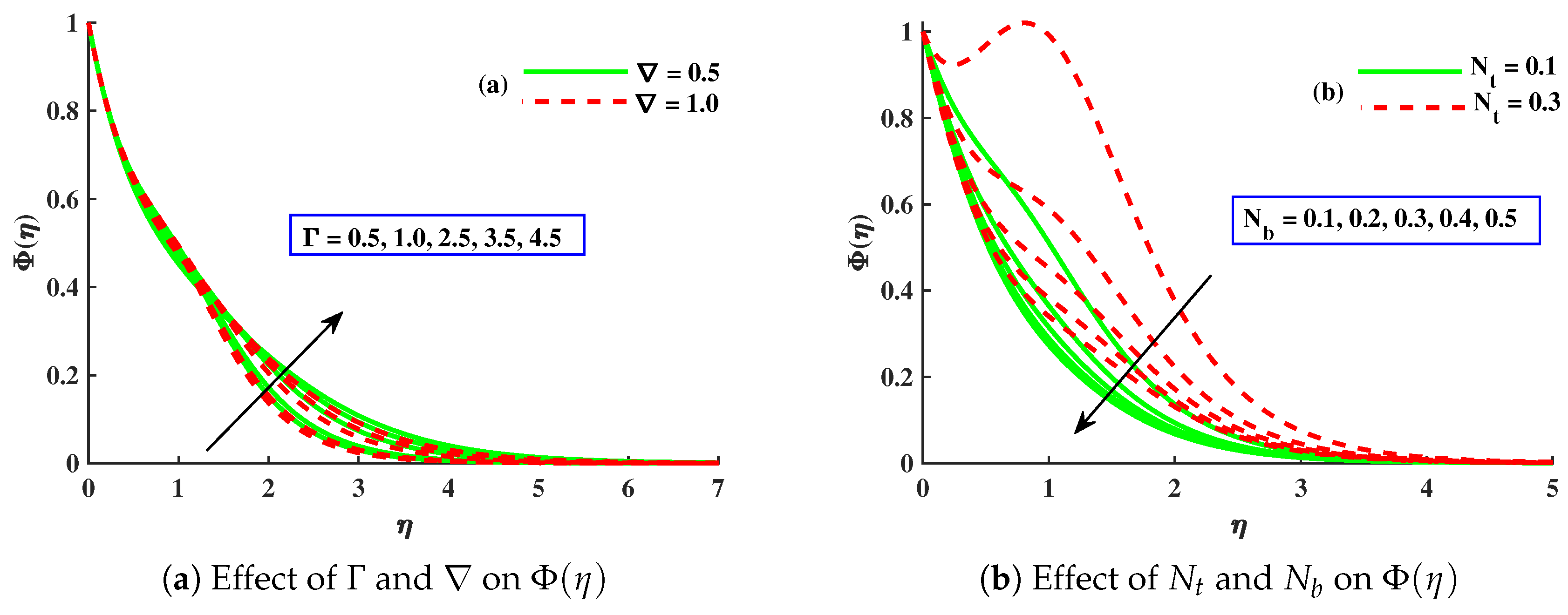
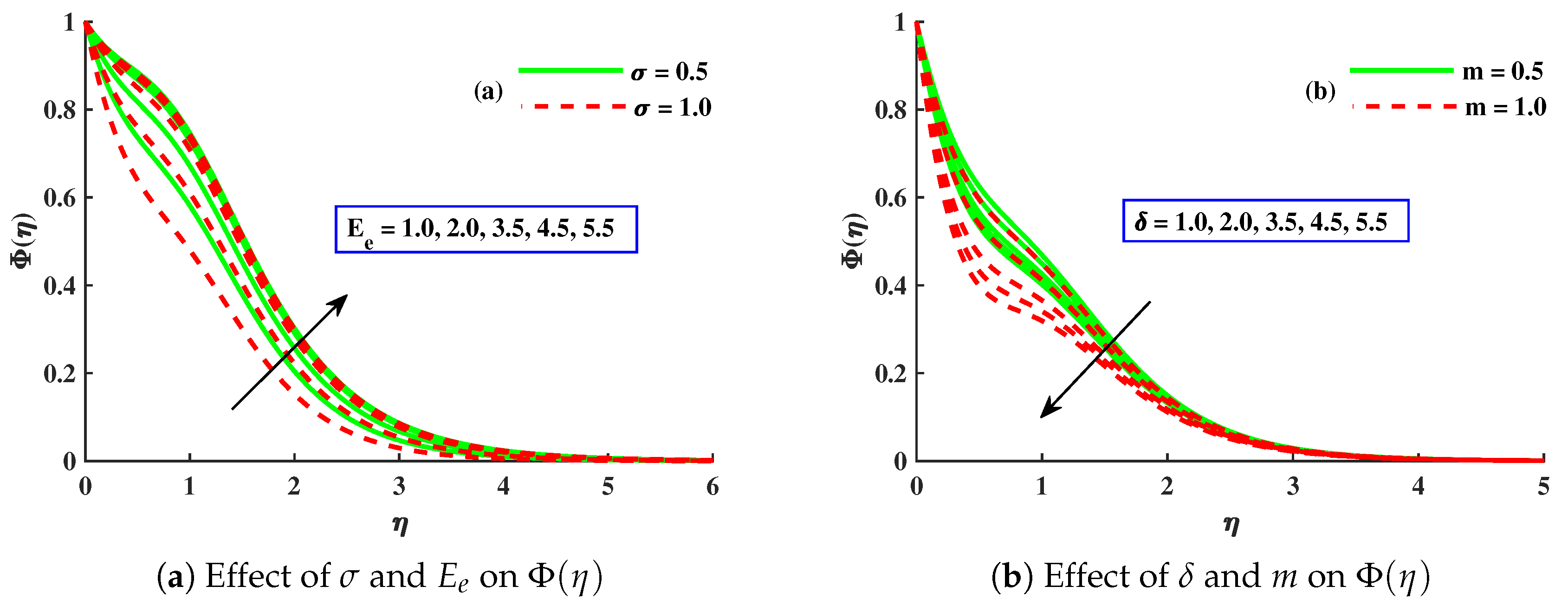
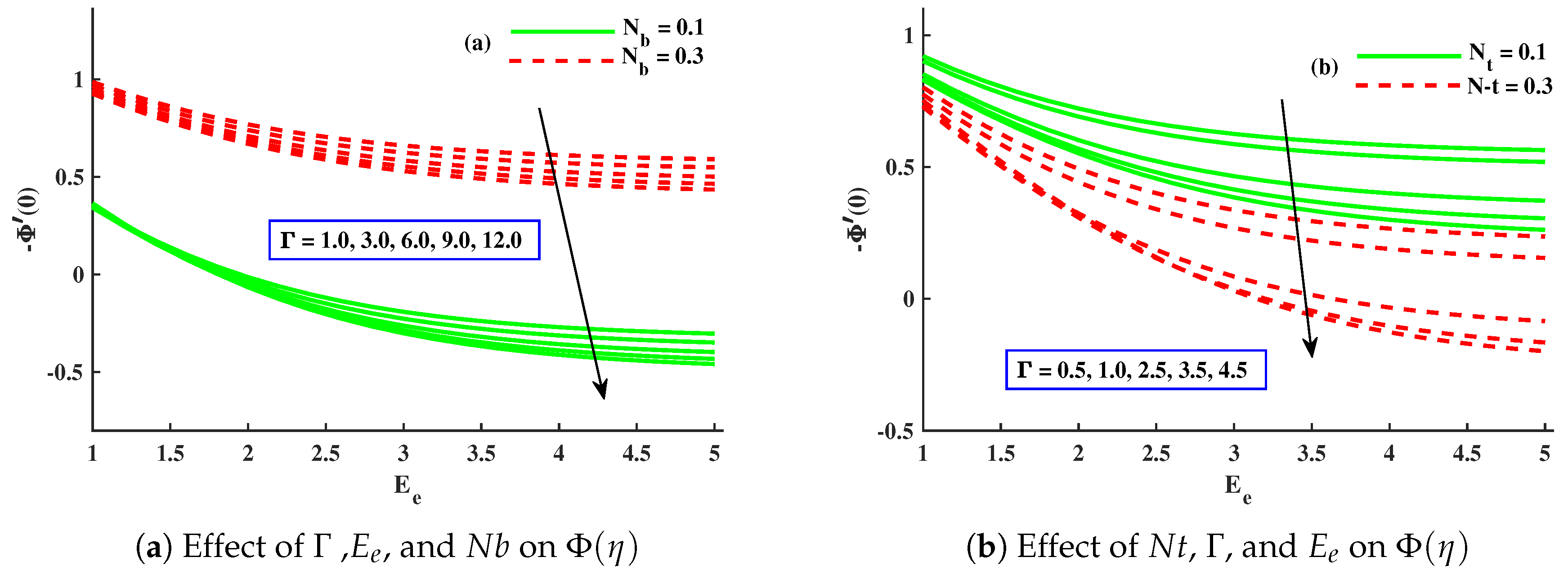
- With amplified values of , , and , the concentration profile was enhanced, while it was decreased against ∇, , , m, and .
- The magnitude of the Sherwood number displayed an increasing behavior against , but showed a decreasing behavior for , , and .
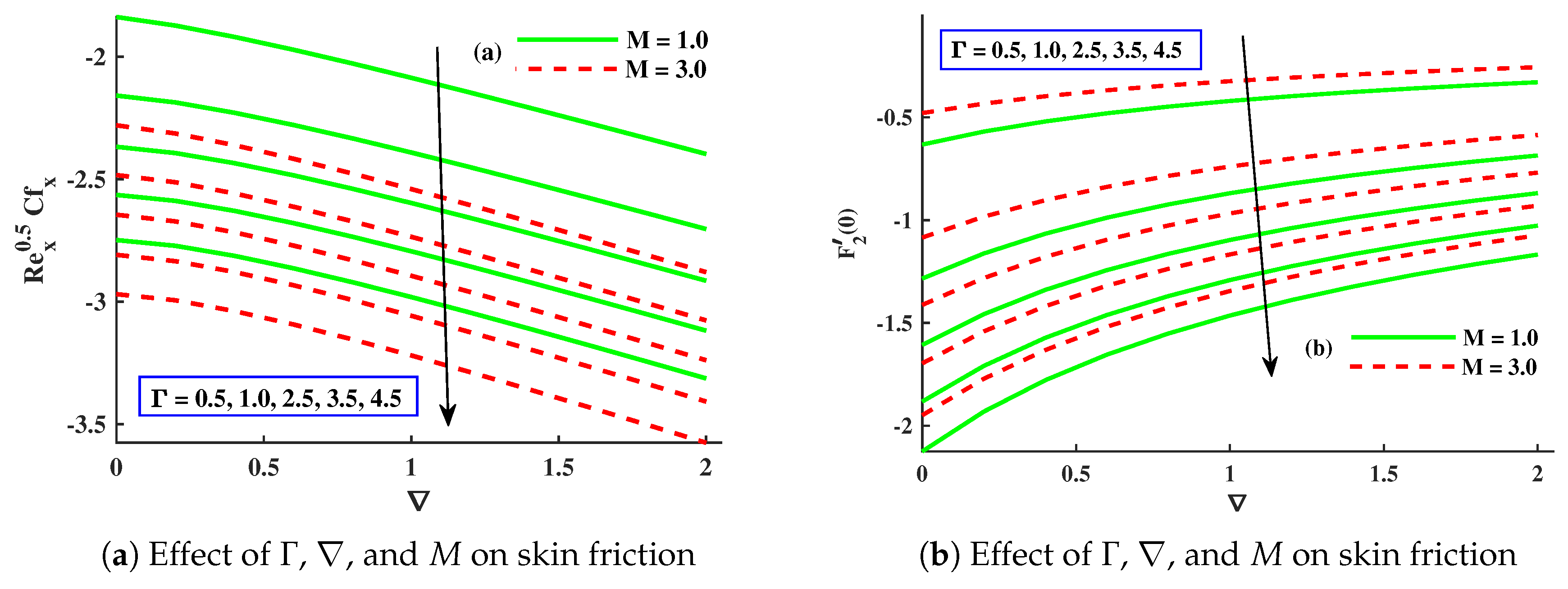
- The skin friction coefficient in the x direction decreased with a larger value of M, , and ∇, whilst the skin friction coefficient in the y direction increased due to enhancements in M and ∇ but decreased for .
- The magnitude of the Nusselt numbers was decreased with increasing contributions of , , , , and M, but increased against ∇.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, U.; Irfan, M.; Rehman, K.U.; Alqahtani, A.S.; Malik, M.; Shatanawi, W. On the Cattaneo–Christov heat flux theory for mixed convection flow due to the rotating disk with slip effects. Waves Random Complex Media 2022, 10, 1–15. [Google Scholar] [CrossRef]
- Pattnaik, P.; Bhatti, M.; Mishra, S.; Abbas, M.A.; Bég, O.A. Mixed convective-radiative dissipative magnetized micropolar nanofluid flow over a stretching surface in porous media with double stratification and chemical reaction effects: ADM-Padé computation. J. Math. 2022, 2022, 9888379. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Galdi, G.P.; Rionero, S. A note on the existence and uniqueness of solutions of the micropolar fluid equations. Int. J. Eng. Sci. 1977, 15, 105–108. [Google Scholar] [CrossRef]
- Bilal, M.; Saeed, A.; Gul, T.; Kumam, W.; Mukhtar, S.; Kumam, P. Parametric simulation of micropolar fluid with thermal radiation across a porous stretching surface. Sci. Rep. 2022, 12, 2542. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Khan, I.; Masood, B.; Hussain, S. Magnetic dipole and thermal radiation effects on hybrid base micropolar CNTs flow over a stretching sheet: Finite element method approach. Results Phys. 2021, 25, 104145. [Google Scholar] [CrossRef]
- Pasha, P.; Mirzaei, S.; Zarinfar, M. Application of numerical methods in micropolar fluid flow and heat transfer in permeable plates. Alex. Eng. J. 2022, 61, 2663–2672. [Google Scholar] [CrossRef]
- Mohanty, B.; Mohanty, S.; Mishra, S.; Pattnaik, P. Analysis of entropy on the peristaltic transport of micropolar nanofluid: A simulation obtained using approximate analytical technique. Eur. Phys. J. Plus 2021, 136, 1–19. [Google Scholar] [CrossRef]
- Ramya, E.; Muthtamilselvan, M.; Doh, D.H. Absorbing/emitting radiation and slanted hydromagnetic effects on micropolar liquid containing gyrostatic microorganisms. Appl. Math. Comput. 2018, 324, 69–81. [Google Scholar] [CrossRef]
- Bilal, M.; Hussain, S.; Sagheer, M. Boundary layer flow of magneto-micropolar nanofluid flow with Hall and ion-slip effects using variable thermal diffusivity. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.; Lee, S.S. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sens. Actuators Phys. 2000, 80, 84–89. [Google Scholar] [CrossRef]
- Alsaedi, A.; Muhammad, K.; Hayat, T. Numerical study of MHD hybrid nanofluid flow between two coaxial cylinders. Alex. Eng. J. 2022, 61, 8355–8362. [Google Scholar] [CrossRef]
- Ali, B.; Rasool, G.; Hussain, S.; Baleanu, D.; Bano, S. Finite Element Study of Magnetohydrodynamics (MHD) and Activation Energy in Darcy–Forchheimer Rotating Flow of Casson Carreau Nanofluid. Processes 2020, 8, 1185. [Google Scholar] [CrossRef]
- Nazeer, M.; Hussain, F.; Khan, M.I.; El-Zahar, E.R.; Chu, Y.M.; Malik, M. Theoretical study of MHD electro-osmotically flow of third-grade fluid in micro channel. Appl. Math. Comput. 2022, 420, 126868. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Rizwan, M.; Ashraf, M. Heat and mass transfer attributes of copper–aluminum oxide hybrid nanoparticles flow through a porous medium. Case Stud. Therm. Eng. 2021, 25, 100932. [Google Scholar] [CrossRef]
- Badruddin, I.A.; Salman Ahmed, N.; Anqi, A.E.; Kamangar, S. Conjugate heat and mass transfer in a vertical porous cylinder. J. Thermophys. Heat Transf. 2019, 33, 548–558. [Google Scholar] [CrossRef]
- Hassan, M.; Marin, M.; Alsharif, A.; Ellahi, R. Convective heat transfer flow of nanofluid in a porous medium over wavy surface. Phys. Lett. A 2018, 382, 2749–2753. [Google Scholar] [CrossRef]
- Banerjee, A.; Paul, D. Developments and applications of porous medium combustion: A recent review. Energy 2021, 221, 119868. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Symmetrical solutions of hybrid nanofluid stagnation-point flow in a porous medium. Int. Commun. Heat Mass Transf. 2022, 130, 105804. [Google Scholar] [CrossRef]
- Wang, C. Stretching a surface in a rotating fluid. Zeitschrift für Angewandte Mathematik und Physik ZAMP 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Rajeswari, V.; Nath, G. Unsteady flow over a stretching surface in a rotating fluid. Int. J. Eng. Sci. 1992, 30, 747–756. [Google Scholar] [CrossRef]
- Ali, B.; Ahammad, N.A.; Awan, A.U.; Guedri, K.; Tag-ElDin, E.M.; Majeed, S. Dynamics of Rotating Micropolar Fluid over a Stretch Surface: The Case of Linear and Quadratic Convection Significance in Thermal Management. Nanomaterials 2022, 12, 3100. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Elmasry, Y.; Malik, M. Numerical analysis of water based CNTs flow of micropolar fluid through rotating frame. Comput. Methods Programs Biomed. 2020, 186, 105194. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, R.; Shehzad, S.A.; Sheikholeslami, M. Rotating frame analysis of radiating and reacting ferro-nanofluid considering Joule heating and viscous dissipation. Int. J. Heat Mass Transf. 2018, 120, 540–551. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Owhaib, W. Numerical analysis of Casson nanofluid three-dimensional flow over a rotating frame exposed to a prescribed heat flux with viscous heating. Sci. Rep. 2022, 12, 4256. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Hussain, S.; Habib, D.; Abdal, S. Insight into the dynamics of fluid conveying tiny particles over a rotating surface subject to Cattaneo–Christov heat transfer, Coriolis force, and Arrhenius activation energy. Comput. Math. Appl. 2021, 93, 130–143. [Google Scholar] [CrossRef]
- Awan, A.U.; Ahammad, N.A.; Majeed, S.; Gamaoun, F.; Ali, B. Significance of hybrid nanoparticles, Lorentz and Coriolis forces on the dynamics of water based flow. Int. Commun. Heat Mass Transf. 2022, 135, 106084. [Google Scholar] [CrossRef]
- Ali, B.; Pattnaik, P.; Naqvi, R.A.; Waqas, H.; Hussain, S. Brownian motion and thermophoresis effects on bioconvection of rotating Maxwell nanofluid over a Riga plate with Arrhenius activation energy and Cattaneo-Christov heat flux theory. Therm. Sci. Eng. Prog. 2021, 23, 100863. [Google Scholar] [CrossRef]
- Javed, T.; Ahmad, I.; Abbas, Z.; Hayat, T. Rotating flow of a micropolar fluid induced by a stretching surface. Zeitschrift für Naturforschung A 2010, 65, 829–843. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Mustafa, M.; Alsaedi, A. An optimal study for three-dimensional flow of Maxwell nanofluid subject to rotating frame. J. Mol. Liq. 2017, 229, 541–547. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Jaradat, M.; Pop, I. Three-dimensional micropolar flow due to a stretching flat surface. Int. J. Fluid Mech. Res. 2003, 30, 357–366. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady magneto-hydrodynamic transport of rotating Maxwell nanofluid flow on a stretching sheet with Cattaneo–Christov double diffusion and activation energy. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Hussain, S.; Manan, A.; Sadiq, M.T. TUnsteady boundary layer flow due to a stretching surface in a rotating fluid. Therm. Sci. Eng. Prog. 2020, 20, 100720. [Google Scholar] [CrossRef]
| Nazar et al. [32] | Current Results | ||||
|---|---|---|---|---|---|
| 1 | 1.3250 | 0.8371 | 1.32503 | 0.837104 | |
| 2 | 1.6523 | 1.2873 | 1.652325 | 1.287249 | |
| 3 | 1.6523 | 1.2870 | 1.92894 | 1.624741 | |
| Ali et al. [33] | Current Results | ||||
|---|---|---|---|---|---|
| 0.5 | 0.8525 | 1.8500 | 0.85243 | 1.851168 | |
| 1 | 0.7703 | 1.7877 | 0.77033 | 1.787704 | |
| 2 | 0.6381 | 1.6642 | 0.63822 | 1.664314 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, M.M.; Hendi, A.A.; Ali, B.; Majeed, S.; Hussein, A.K.; Shah, N.A. Significance of Darcy–Forchheimer Law, Activation Energy, and Brownian Motion of Tiny Particles on the Dynamics of Rotating MHD Micropolar Nanofluid. Mathematics 2023, 11, 866. https://doi.org/10.3390/math11040866
Alanazi MM, Hendi AA, Ali B, Majeed S, Hussein AK, Shah NA. Significance of Darcy–Forchheimer Law, Activation Energy, and Brownian Motion of Tiny Particles on the Dynamics of Rotating MHD Micropolar Nanofluid. Mathematics. 2023; 11(4):866. https://doi.org/10.3390/math11040866
Chicago/Turabian StyleAlanazi, Meznah M., Awatif A. Hendi, Bagh Ali, Sonia Majeed, Ahmed Kadhim Hussein, and Nehad Ali Shah. 2023. "Significance of Darcy–Forchheimer Law, Activation Energy, and Brownian Motion of Tiny Particles on the Dynamics of Rotating MHD Micropolar Nanofluid" Mathematics 11, no. 4: 866. https://doi.org/10.3390/math11040866
APA StyleAlanazi, M. M., Hendi, A. A., Ali, B., Majeed, S., Hussein, A. K., & Shah, N. A. (2023). Significance of Darcy–Forchheimer Law, Activation Energy, and Brownian Motion of Tiny Particles on the Dynamics of Rotating MHD Micropolar Nanofluid. Mathematics, 11(4), 866. https://doi.org/10.3390/math11040866







