Mixed-Delay-Dependent Augmented Functional for Synchronization of Uncertain Neutral-Type Neural Networks with Sampled-Data Control
Abstract
:1. Introduction
- (i)
- A sampled-data controller is designed considering the communication delay . Such a method is easier to calculate and implement than the event-triggered communication scheme proposed in [20]. While guaranteeing system stability, this method can reduce network congestion and improve control efficiency.
- (ii)
- A mixed-delay-dependent augmented LKF is constructed. The interconnected relationship between transmission delay and communication delay is taken into account, and the interaction between transmission delay and neutral delay is considered simultaneously. This interconnected relationship is utilized by introducing some integral and double integral terms associated with the mixed delay. Thus, the connection between those states is strengthened.
- (iii)
- In order to reduce the conservatism of the synchronization criteria, a two-sided looped LKF is proposed, which utilizes the information of intervals . This functional can obtain better results for sampled-data synchronization problems in NTNNs. Two less conservative synchronization criteria are derived based on the LKF and a free-matrix-based integral inequality.
2. Preliminaries
3. Main Results
| Algorithm 1 Find the maximum sampling period and the controller gain matrix K. |
|
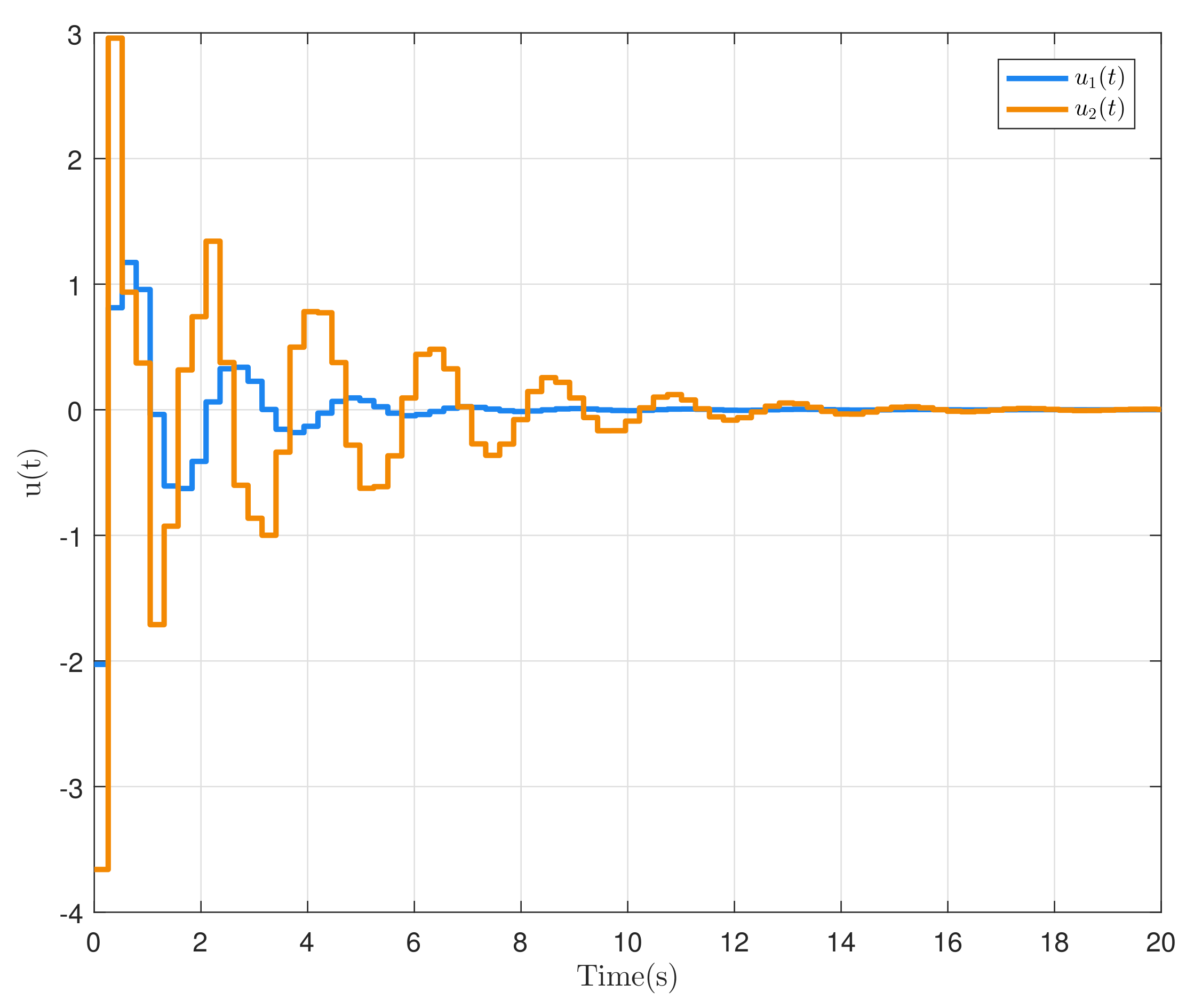
4. Illustrative Examples
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
References
- Egmont-Petersen, M.; de Ridder, D.; Handels, H. Image processing with neural networks—A review. Pattern Recognit. 2002, 35, 2279–2301. [Google Scholar] [CrossRef]
- Kothari, S.; Oh, H. Neural Networks for Pattern Recognition. Adv. Comput. 1993, 37, 119–166. [Google Scholar]
- Mestari, M.; Benzirar, M.; Saber, N.; Khouil, M. Solving Nonlinear Equality Constrained Multiobjective Optimization Problems Using Neural Networks. IEEE Trans. Neural Netw. Learn Syst. 2015, 26, 2500–2520. [Google Scholar] [CrossRef]
- Chen, Y.H.; Fang, S.C. Neurocomputing with time delay analysis for solving convex quadratic programming problems. IEEE Trans. Neural Netw. Learn Syst. 2000, 11, 230–240. [Google Scholar] [CrossRef]
- Zhang, J. Globally exponential stability of neural networks with variable delays. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 288–290. [Google Scholar] [CrossRef]
- Lv, Y.; Lv, W.; Sun, J. Convergence dynamics of stochastic reaction-diffusion recurrent neural networks with continuously distributed delays. Nonlinear Anal. Real World Appl. 2008, 9, 1590–1606. [Google Scholar] [CrossRef]
- Shi, K.; Zhu, H.; Zhong, S.; Zeng, Y.; Zhang, Y. New stability analysis for neutral type neural networks with discrete and distributed delays using a multiple integral approach. J. Frankl. Inst. 2015, 352, 155–176. [Google Scholar] [CrossRef]
- Kolmanovskii, V.B.; Nosov, V.R. Stability of Functional Differential Equations; Academic: London, UK, 1986. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic: Boston, MA, USA, 1993. [Google Scholar]
- Cai, X.; Shi, K.; She, K.; Zhong, S.; Tang, Y. Quantized Sampled-Data Control Tactic for T-S Fuzzy NCS Under Stochastic Cyber-Attacks and Its Application to Truck-Trailer System. IEEE Trans. Veh. Technol. 2022, 71, 7023–7032. [Google Scholar] [CrossRef]
- Cai, X.; Shi, K.; She, K.; Zhong, S.; Soh, Y.; Yu, Y. Performance Error Estimation and Elastic Integral Event Triggering Mechanism Design for T-S Fuzzy Networked Control System Under DoS Attacks. IEEE Trans. Fuzzy Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Fridman, E.; Seuret, A.; Richard, J.P. Robust sampled-data stabilization of linear systems: An input delay approach. Automatica 2004, 40, 1441–1446. [Google Scholar] [CrossRef]
- Fujioka, H. A Discrete-Time Approach to Stability Analysis of Systems With Aperiodic Sample-and-Hold Devices. IEEE Trans. Autom. Control 2009, 54, 2440–2445. [Google Scholar] [CrossRef] [Green Version]
- Naghshtabrizi, P.; Hespanha, J.P.; Teel, A.R. Exponential stability of impulsive systems with application to uncertain sampled-data systems. Syst. Control Lett. 2008, 57, 378–385. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.; He, Y. A new looped-functional for stability analysis of sampled-data systems. Automatica 2017, 82, 328–331. [Google Scholar] [CrossRef]
- Zeng, H.B.; Zhai, Z.L.; He, Y.; Teo, K.L.; Wang, W. New insights on stability of sampled-data systems with time-delay. Appl. Math. Comput. 2020, 374, 125041. [Google Scholar] [CrossRef]
- Zeng, H.B.; Zhai, Z.L.; Yan, H.; Wang, W. A New Looped Functional to Synchronize Neural Networks With Sampled-Data Control. IEEE Trans. Neural Netw. Learn Syst. 2022, 33, 406–415. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Long, F.; Zhang, C.K. Mixed-Delay-Based Augmented Functional for Sampled-Data Synchronization of Delayed Neural Networks With Communication Delay. IEEE Trans. Neural Netw. Learn Syst. 2022, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Wang, T.; Li, T.; Fei, S. Multiple integral Lyapunov approach to mixed-delay-dependent stability of neutral neural networks. Neurocomputing 2018, 275, 1782–1792. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Q.; Lu, J.; Chu, Y.; Li, Y. Synchronization control of neutral-type neural networks with sampled-data via adaptive event-triggered communication scheme. J. Frankl. Inst. 2021, 358, 1999–2014. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; She, J. New results on stability analysis for systems with discrete distributed delay. Automatica 2015, 60, 189–192. [Google Scholar] [CrossRef]
- Li, T.; Guo Song, A.; Min Fei, S. Robust stability of stochastic Cohen–Grossberg neural networks with mixed time-varying delays. Neurocomputing 2009, 73, 542–551. [Google Scholar] [CrossRef]
- Seuret, A. A novel stability analysis of linear systems under asynchronous samplings. Automatica 2012, 48, 177–182. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.L. Further improvement on delay-dependent robust stability criteria for neutral-type recurrent neural networks with time-varying delays. ISA Trans. 2015, 55, 92–99. [Google Scholar] [CrossRef]
- Yin, C.; Cheng, Y.; Huang, X.; ming Zhong, S.; Li, Y.; Shi, K. Delay-partitioning approach design for stochastic stability analysis of uncertain neutral-type neural networks with Markovian jumping parameters. Neurocomputing 2016, 207, 437–449. [Google Scholar] [CrossRef]
- Wei, W.; Zeng, H.B.; Teo, K.L. Free-matrix-based time-dependent discontinuous Lyapunov functional for synchronization of delayed neural networks with sampled-data control. Chin. Phys. B 2017, 26, 127–134. [Google Scholar]
- Xiao, S.P.; Lian, H.H.; Teo, K.L.; Zeng, H.B.; Zhang, X.H. A new Lyapunov functional approach to sampled-data synchronization control for delayed neural networks. J. Frankl. Inst. 2018, 355, 8857–8873. [Google Scholar] [CrossRef]
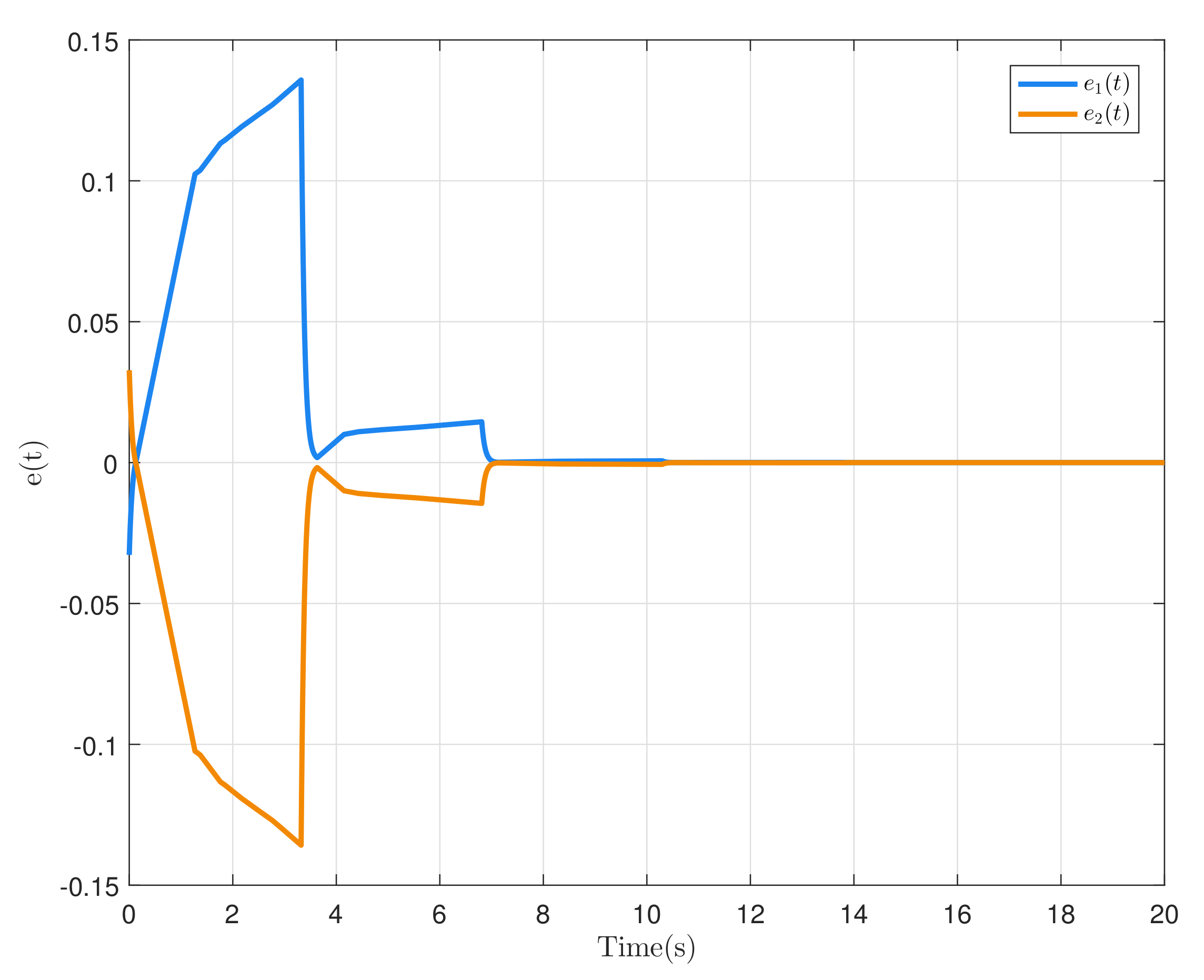
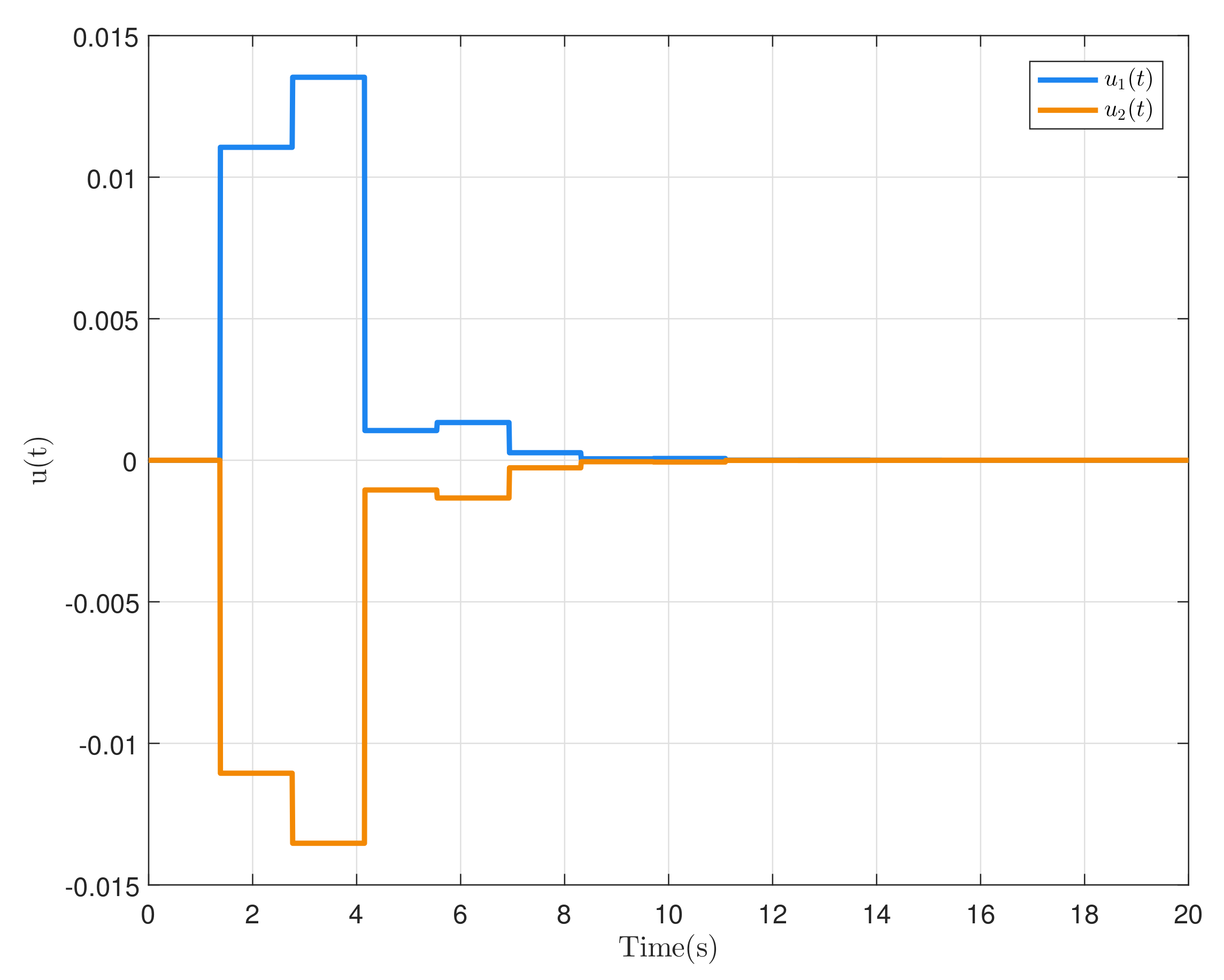
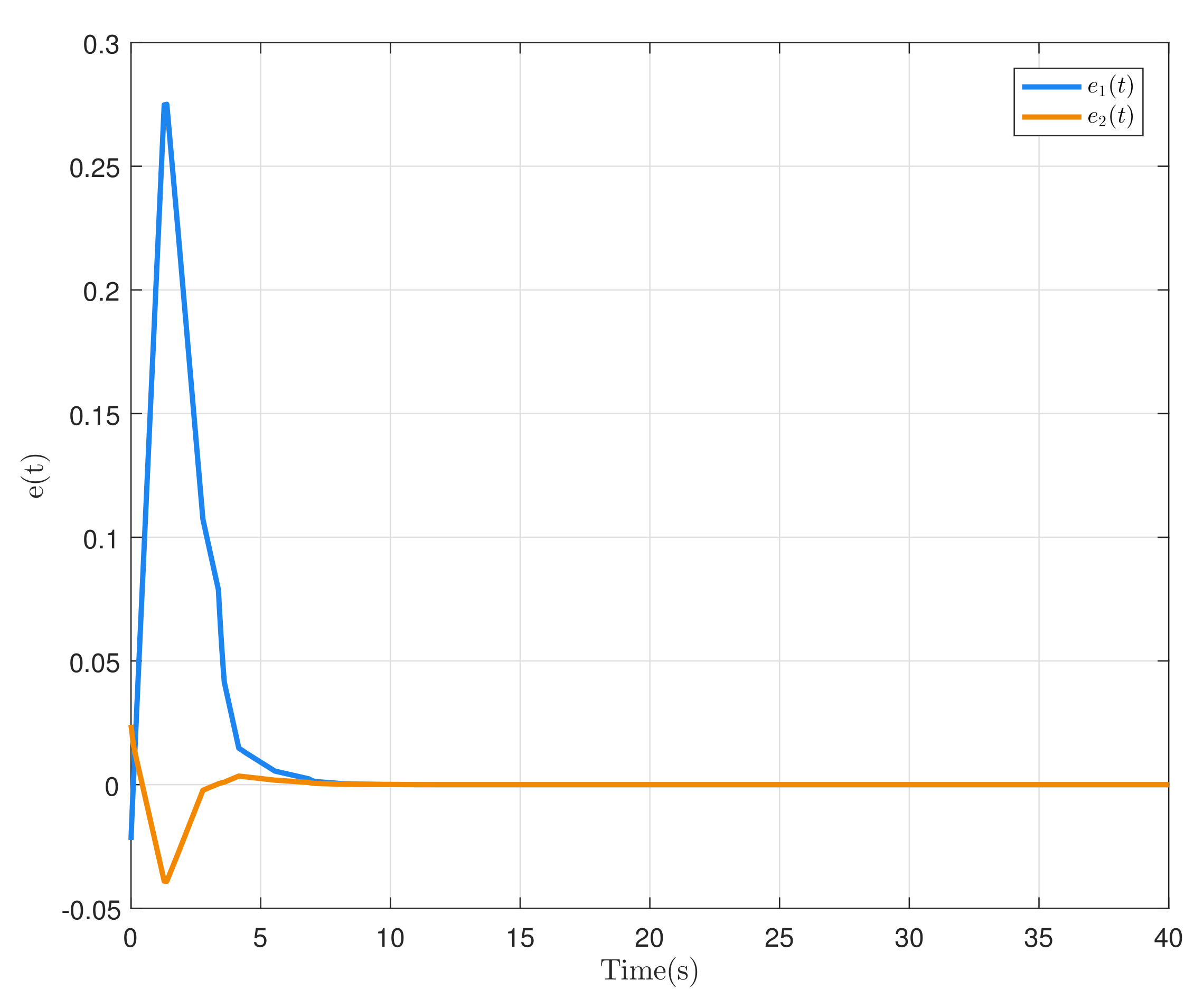
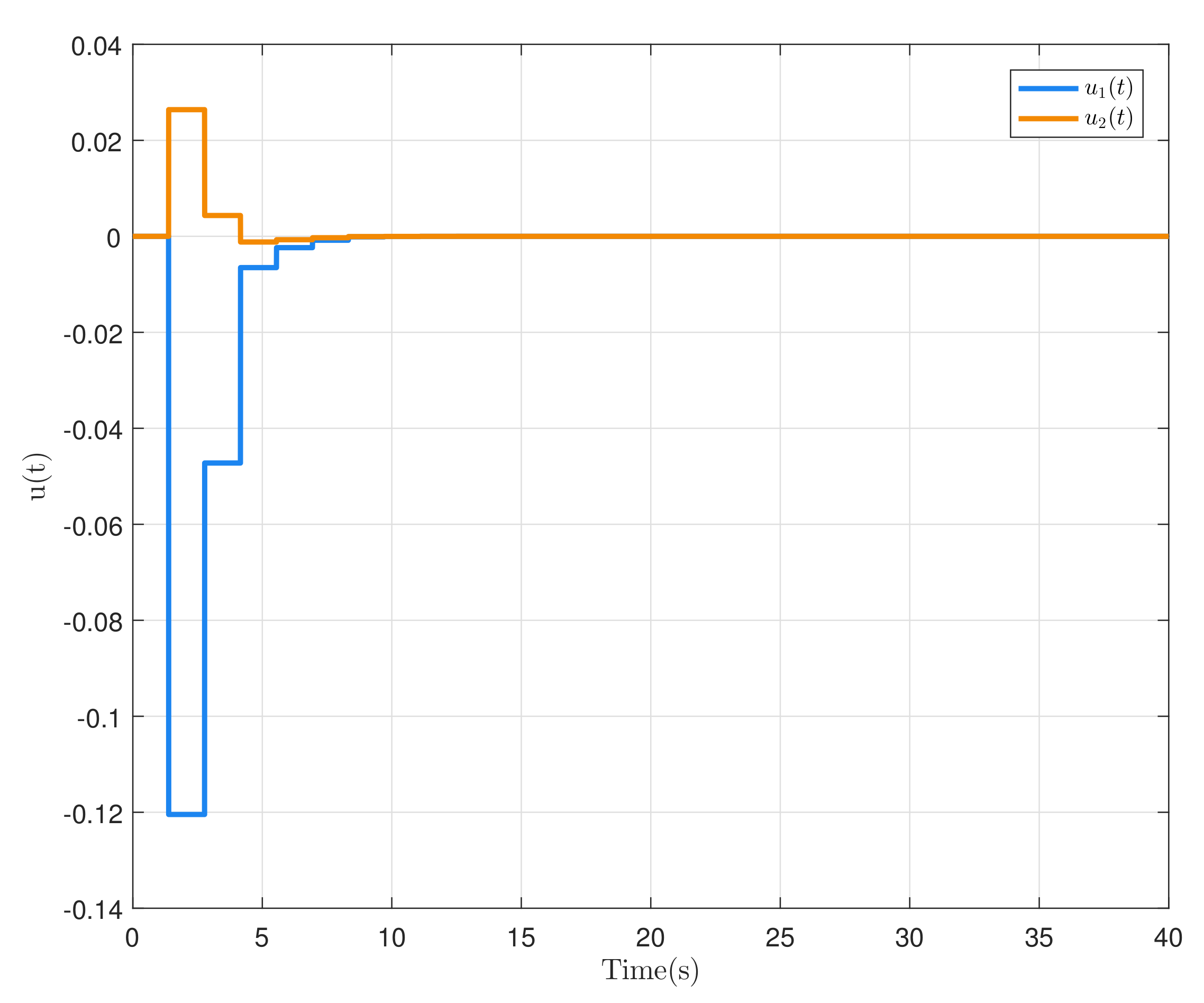

| 0.01 | 0.03 | 0.05 | 0.07 | 0.09 | |
|---|---|---|---|---|---|
| Corollary 1 | 1.3766 | 1.3499 | 1.3296 | 1.3134 | 1.2996 |
| Theorem 1 | 1.3881 | 1.3865 | 1.3820 | 1.3777 | 1.3738 |
| Improvement | 0.835% | 4.9406% | 3.9411% | 4.8957% | 5.7094% |
| 0.01 | 0.03 | 0.05 | 0.07 | 0.09 | |
|---|---|---|---|---|---|
| Corollary 2 | 25.9631 | 24.1682 | 22.6097 | 21.2437 | 20.0398 |
| Theorem 2 | 26.2134 | 25.2686 | 24.3970 | 23.4741 | 22.5952 |
| Improvement | 0.964% | 4.5530% | 7.9050% | 10.4991% | 12.7516% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Shi, K. Mixed-Delay-Dependent Augmented Functional for Synchronization of Uncertain Neutral-Type Neural Networks with Sampled-Data Control. Mathematics 2023, 11, 872. https://doi.org/10.3390/math11040872
Wang S, Shi K. Mixed-Delay-Dependent Augmented Functional for Synchronization of Uncertain Neutral-Type Neural Networks with Sampled-Data Control. Mathematics. 2023; 11(4):872. https://doi.org/10.3390/math11040872
Chicago/Turabian StyleWang, Shuoting, and Kaibo Shi. 2023. "Mixed-Delay-Dependent Augmented Functional for Synchronization of Uncertain Neutral-Type Neural Networks with Sampled-Data Control" Mathematics 11, no. 4: 872. https://doi.org/10.3390/math11040872
APA StyleWang, S., & Shi, K. (2023). Mixed-Delay-Dependent Augmented Functional for Synchronization of Uncertain Neutral-Type Neural Networks with Sampled-Data Control. Mathematics, 11(4), 872. https://doi.org/10.3390/math11040872







