Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation
Abstract
:1. Introduction
- Firstly, the differential/integral operators of the baseline controller are retrofitted with pre-calibrated real-numbered fractional-order operators to develop an FO-LQIR.
- The FO-LQIR is systematically extended to a CFO-LQIR to robustify the control law’s performance. This is achieved by replacing the real-numbered fractional order of each operator in the control law with pre-configured complex-order operators. The new parameters introduced in each control law are empirically tuned by iteratively minimising a quadratic objective function that considers the position regulation errors and control input energy.
- The efficacies and benefits of the proposed CFO-LQIR are benchmarked against the integer-order LQIR and FO-LQIR by conducting credible real-time hardware experiments on the Quanser single-link rotary pendulum setup [25].
2. System Description
3. Linear–Quadratic–Integral Regulator (LQIR)
3.1. LQIR Formulation
3.2. Parameter Tuning Procedure
4. Fractional-Order LQIR
4.1. Fractional Calculus
4.2. Fractional-Order Control Law Formulation
5. Complex Fractional-Order LQIR
6. Experimental Evaluation and Discussions
6.1. Experimental Setup
- Rod displacement limit: .
- Arm displacement limit: .
- Control input limit: .
6.2. Tests and Results
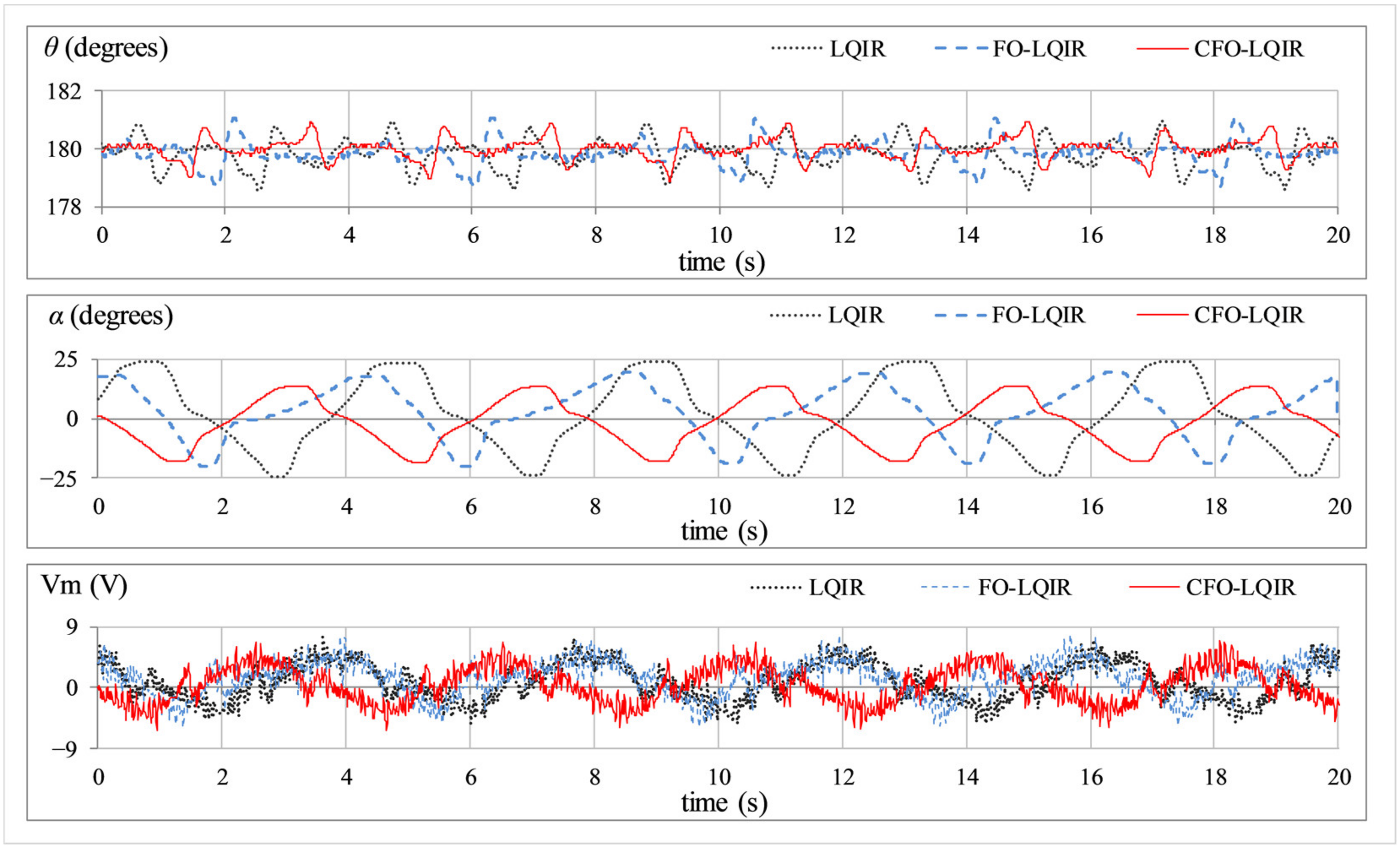
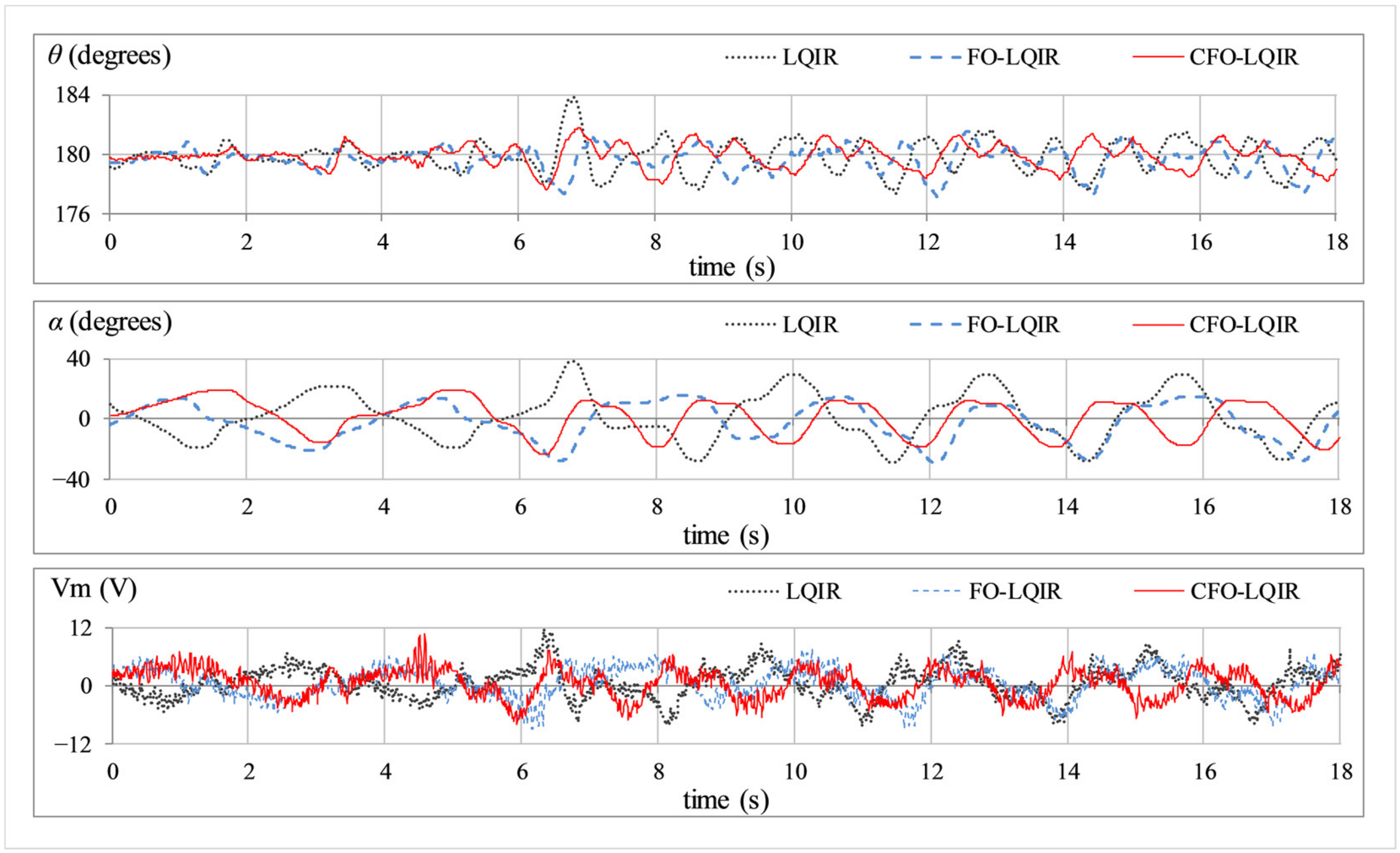
- Position regulation and station keeping: This experiment serves to analyse the vertical position regulation of the apparatus rod and the station-keeping capability of the arm in the absence of exogenous disturbances. The responses of ,, and are depicted in Figure 4.
- Impulsive disturbance rejection: The second experiment aims to investigate the controller’s robustness against the impulsive disturbances that are typically caused by the application of sudden yet short-term parametric variations and random forces. The test is performed by artificially applying a −5.0 V pulse with a duration of 100 ms in the control input profile at regular intervals. The responses of ,, and are shown in Figure 5.
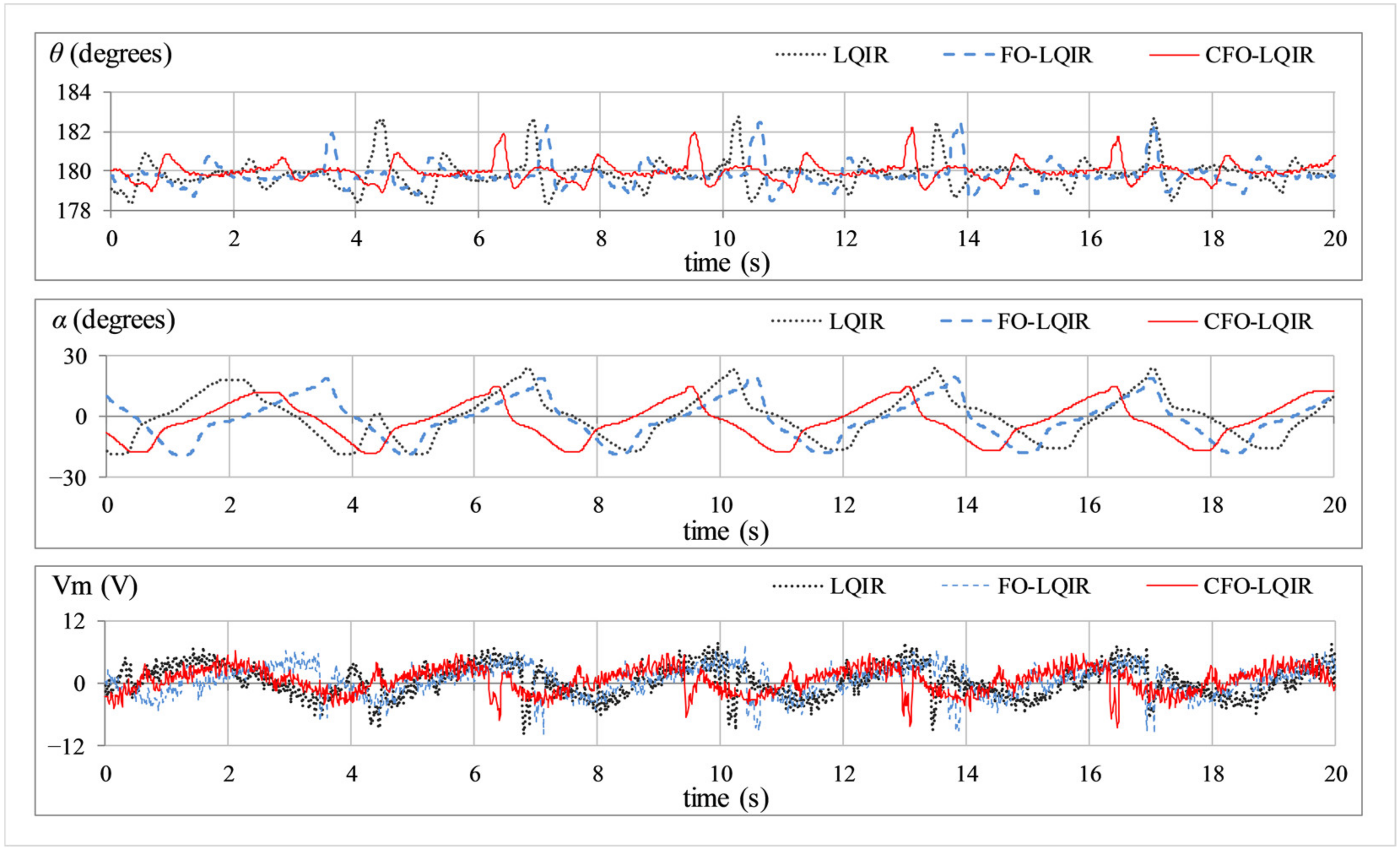
- Step disturbance rejection: This experiment characterises the controller’s ability to reject sudden yet permanent load variations caused by constant exogenous forces. The pendulum is perturbed by artificially injecting a −5.0 V step signal in the control signal at t ≈ 6.0 s. The responses of ,, and are shown in Figure 6.
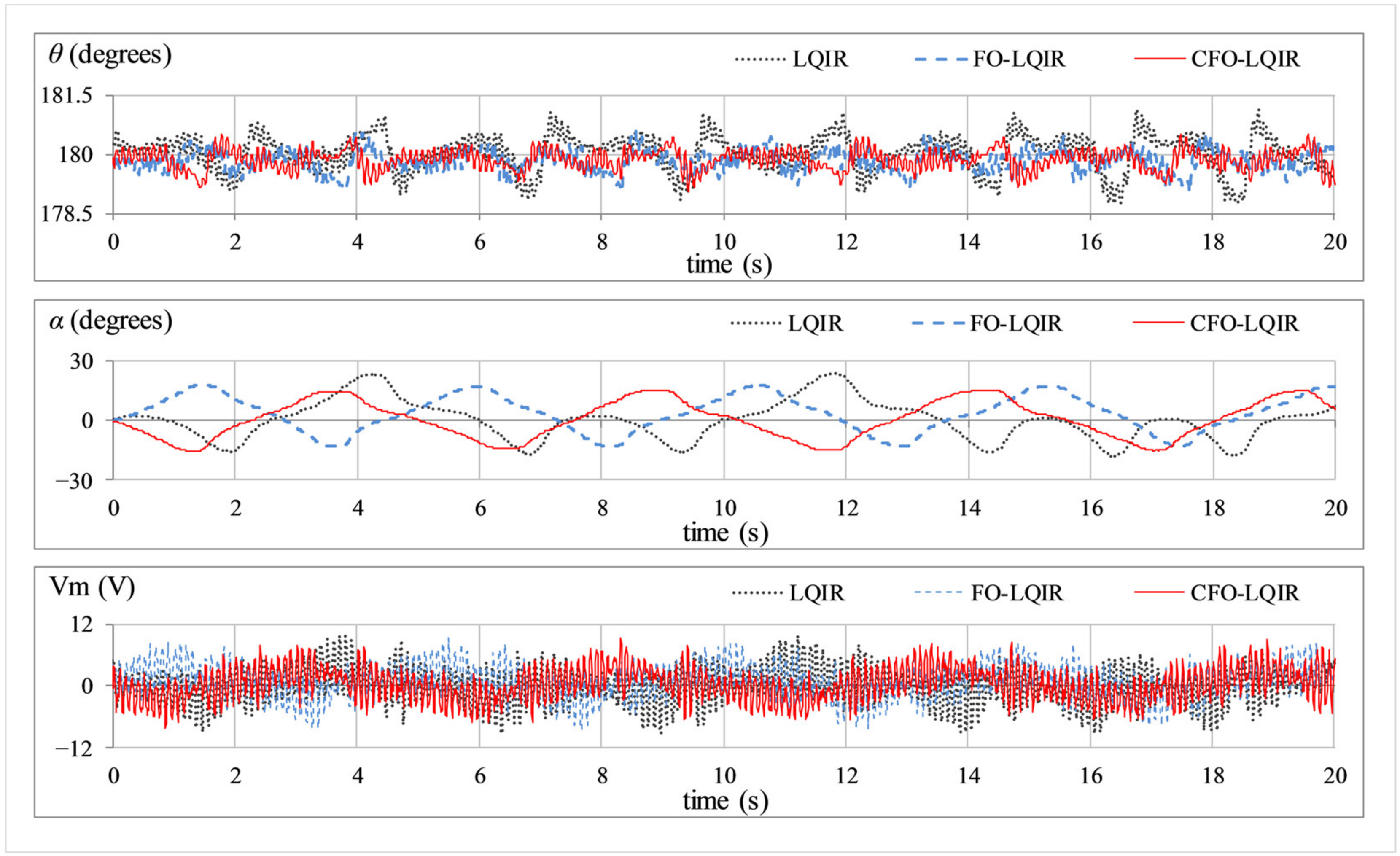
- Sinusoidal noise attenuation: This experiment analyses the controller’s ability to attenuate the lumped disturbances caused by mechanical vibrations, measurement noise, and the chattering caused by the hysteresis in parasitic impedances. The test is performed by artificially injecting a sinusoidal signal of the form in the control signal. The responses of , , and are shown in Figure 7.
- Modeling error compensation: The final experiment investigates the controller’s ability to compensate for the unprecedented modeling errors that are typically caused by inaccurate model identification or permanent model changes during the trials. The test is performed by attaching a 0.10 kg mass beneath the pendulum rod arm joint at t ≈ 6.0 s, as shown in Figure 4. This arrangement abruptly changes the actual system’s physical dynamics as compared to the reference model, which inevitably induces fluctuations in the state response(s). The responses of ,, and are shown in Figure 8.
6.3. Discussion
- ex_RMS: The root-mean-square value of error ( or ), .
- ex_ITAE: The integral time-weighted absolute value of error ( or ), .
- ts,θ: The time taken by the pendulum’s apparatus rod to recover from a transient disturbance.
- |Mp,x|: The magnitude of peak overshoot (or undershoot) contributed by the transient disturbances.
- αoff: The offset in the arm’s position contributed by the step disturbance.
- αp-p: The peak-to-peak amplitude of post-disturbance oscillations in the arm.
- MSVm: The mean-square value of DC motor voltage.
- Vp: The peak value of DC motor voltage under transient disturbances.
6.4. A Special Comparison Case
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Yang, C.; Fan, L. Advanced Control of Wheeled Inverted Pendulum Systems; Springer: London, UK, 2013. [Google Scholar]
- Johnson, T.; Zhou, S.; Cheah, W.; Mansell, W.; Young, R.; Watson, S. Implementation of a Perceptual Controller for an Inverted Pendulum Robot. J. Intell. Robot. Syst. 2020, 99, 683–692. [Google Scholar] [CrossRef]
- Krafes, S.; Chalh, Z.; Saka, A. A Review on the Control of Second Order Underactuated Mechanical Systems. Complexity 2018, 2018, 9573514. [Google Scholar] [CrossRef]
- Ilyas, M.; Khaqan, A.; Iqbal, J.; Riaz, R.A. Regulation of hypnosis in Propofol anesthesia administration based on non-linear control strategy. Braz. J. Anesthesiol. 2017, 67, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Koryakovskiy, I.; Kudruss, M.; Babuška, R.; Caarls, W.; Vallery, H. Benchmarking model-free and model-based optimal control. Robot. Auton Syst 2017, 92, 81–90. [Google Scholar] [CrossRef]
- Sirisha, V.; Junghare, A.S. A Comparative study of controllers for stabilizing a Rotary Inverted Pendulum. Int. J. Chaos Control Model. Simul. 2014, 3, 1–13. [Google Scholar] [CrossRef]
- Huang, A.-C.; Kai, C.-Y.; Chen, Y.-F. Adaptive Control of Underactuated Mechanical Systems; World Scientific: Singapore, 2015. [Google Scholar]
- Gritli, H.; Belghit, S. Robust feedback control of the underactuated Inertia Wheel Inverted Pendulum under parametric uncertainties and subject to external disturbances: LMI formulation. J. Franklin Inst. 2018, 355, 9150–9191. [Google Scholar] [CrossRef]
- Lee, H.; Gil, J.; You, S.; Gui, Y.; Kim, W. Arm Angle Tracking Control with Pole Balancing Using Equivalent Input Disturbance Rejection for a Rotational Inverted Pendulum. Mathematics 2021, 9, 2745. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Iqbal, J. Modern control laws for an articulated robotic arm: Modelling and simulation. Eng. Technol. Appl. Sci. Res. 2019, 9, 4057–4061. [Google Scholar] [CrossRef]
- Wang, J.J. Simulation studies of inverted pendulum based on PID controllers. Simul. Model. Pract. Theory 2011, 19, 440–449. [Google Scholar] [CrossRef]
- Iqbal, J.; Heikkila, S.; Halme, A. Tether tracking and control of ROSA robotic rover. In Proceedings of the 10th IEEE International Conference on Control, Automation, Robotics and Vision, Vietnam, Hanoi, Vietnam, 17–20 December 2008; pp. 689–693. [Google Scholar]
- Khan, O.; Pervaiz, M.; Ahmad, E.; Iqbal, J. On the derivation of novel model and sophisticated control of flexible joint manipulator. Revue Roumaine des Sciences Techniques-Serie Electrotechnique et Energetique 2017, 62, 103–108. [Google Scholar]
- Balamurugan, S.; Venkatesh, P.; Varatharajan, M. Fuzzy sliding-mode control with low pass filter to reduce chattering effect: An experimental validation on Quanser SRIP. Sadhana 2017, 42, 1693–1703. [Google Scholar] [CrossRef]
- Anjum, M.; Khan, Q.; Ullah, S.; Hafeez, G.; Fida, A.; Iqbal, J.; Albogamy, F.R. Maximum power extraction from a standalone photo voltaic system via neuro-adaptive arbitrary order sliding mode control strategy with high gain differentiation. Appl. Sci. 2022, 12, 2773. [Google Scholar] [CrossRef]
- Bhatti, O.S.; Tariq, O.B.; Manzar, A.; Khan, O.A. Adaptive intelligent cascade control of a ball-riding robot for optimal balancing and station-keeping. Adv. Robot. 2018, 32, 63–76. [Google Scholar] [CrossRef]
- Wang, X.; Abtahi, S.M.; Chahari, M.; Zhao, T. An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System. Mathematics 2022, 10, 976. [Google Scholar] [CrossRef]
- Sukontanakarn, V.; Parnichkun, M. Real-Time Optimal Control for Rotary Inverted Pendulum. Am. J. Appl. Sci. 2009, 6, 1106–1115. [Google Scholar]
- Prasad, L.B.; Tyagi, B.; Gupta, H.A. Optimal Control of Nonlinear Inverted Pendulum System Using PID Controller and LQR: Performance Analysis Without and With Disturbance Input. Int. J. Autom. Comput. 2014, 11, 661–670. [Google Scholar] [CrossRef]
- Faisal, R.F.; Abdulwahhab, O.W. Design of an Adaptive Linear Quadratic Regulator for a Twin Rotor Aerodynamic System. J. Control Autom. Electr. Syst. 2021, 32, 404–415. [Google Scholar] [CrossRef]
- Dwivedi, P.; Pandey, S.; Junghare, A.S. Stabilization of Unstable Equilibrium Point of Rotary Inverted Pendulum using Fractional Controller. J. Frankl. Inst. 2017, 354, 7732–7766. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Dehgan, S.; Chen, Y.Q.; Xue, D. A review and evaluation of numerical tools for fractional calculus and fractional order controls. Int. J. Control 2017, 90, 1165–1181. [Google Scholar] [CrossRef]
- Kumar, N.; Alotaibi, M.A.; Singh, A.; Malik, H.; Nassar, M.E. Application of Fractional Order-PID Control Scheme in Automatic Generation Control of a Deregulated Power System in the Presence of SMES Unit. Mathematics 2022, 10, 521. [Google Scholar] [CrossRef]
- Saleem, O.; Mahmood-ul-Hasan, K. Robust stabilisation of rotary inverted pendulum using intelligently optimised nonlinear self-adaptive dual fractional order PD controllers. Int. J. Syst. Sci. 2019, 50, 1399–1414. [Google Scholar] [CrossRef]
- Dwivedi, P.; Pandey, S.; Junghare, A.S. Robust and novel two degree of freedom fractional controller based on two-loop topology for inverted pendulum. ISA Trans 2018, 75, 189–206. [Google Scholar] [CrossRef] [PubMed]
- Abdulwahhab, O.W.; Abbas, N.H. A New Method to Tune a Fractional-Order PID Controller for a Twin Rotor Aerodynamic System. Arab. J. Sci. Eng. 2017, 42, 5179–5189. [Google Scholar] [CrossRef]
- Shahiri, M.; Ranjbar, A.; Karami, M.; Ghaderi, R. Robust control of nonlinear PEMFC against uncertainty using fractional complex order control. Nonlinear Dyn. 2015, 80, 1785–1800. [Google Scholar] [CrossRef]
- Guefrachi, A.; Najar, A.; Amairi, M.; Aoun, M. Tuning of fractional complex order PID controller. IFAC−PapersOnLine 2017, 50, 14563–14568. [Google Scholar]
- Abdulwahhab, O.W. Design of a complex fractional order PID controller for a first order plus time delay system. ISA Trans 2020, 99, 154–158. [Google Scholar] [CrossRef]
- Shah, P.; Sekhar, R.; Iswanto, I.; Shah, M. Complex Order PIa+jbDc+jd Controller Design for a Fractional Order DC Motor System. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 541–551. [Google Scholar] [CrossRef]
- Tare, A.; Jacob, J.; Vyawahare, V.; Pande, V. Design of novel optimal complex-order controllers for systems with fractional-order dynamics. Int. J. Dyn. Control 2019, 7, 355–367. [Google Scholar] [CrossRef]
- Irfan, A.; Mehmood, A.; Razzaq, M.T.; Iqbal, J. Advanced sliding mode control techniques for inverted pendulum: Modelling and simulation. Eng. Sci. Technol. Int. J. 2018, 21, 753–759. [Google Scholar] [CrossRef]
- Jian, Z.; Yongpeng, Z. Optimal Linear Modeling and its Applications on Swing-up and Stabilization Control for Rotary Inverted Pendulum. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 493–500. [Google Scholar]
- Astom, K.J.; Apkarian, J.; Karam, P.; Levis, M.; Falcon, J. Student Workbook: QNET Rotary Inverted Pendulum Trainer for NI ELVIS; Quanser Inc.: Markham, ON, Canada, 2011. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Valencia-Rivera, G.H.; Merchan-Villalba, L.R.; Tapia-Tinoco, G.; Lozano-Garcia, J.M.; Ibarra-Manzano, M.A.; Avina-Cervantes, J.G. Hybrid LQR-PI Control for Microgrids under Unbalanced Linear and Nonlinear Loads. Mathematics 2020, 8, 1096. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M.; Mahmood-ul-Hasan, K. Self-tuning state-feedback control of a rotary pendulum system using adjustable degree-of-stability design. Automatika 2021, 62, 84–97. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Halder, K.; Das, S.; Gupta, A. Optimum weight selection based LQR formulation for the design of fractional order PIλDμ controllers to handle a class of fractional order systems. In Proceedings of the 2013 International Conference on Computer Communication and Informatics, Coimbatore, India, 4–6 January 2013; pp. 1–6. [Google Scholar]
- Micev, M.; Ćalasan, M.; Oliva, D. Fractional Order PID Controller Design for an AVR System Using Chaotic Yellow Saddle Goatfish Algorithm. Mathematics 2020, 8, 1182. [Google Scholar] [CrossRef]
- Mishra, S.K.; Chandra, D. Stabilization and Tracking Control of Inverted Pendulum Using Fractional Order PID Controllers. J. Eng. 2014, 2014, 752918. [Google Scholar] [CrossRef]
- Saleem, O.; Awan, F.G.; Mahmood-ul-Hasan, K.; Ahmad, M. Self-adaptive fractional-order LQ-PID voltage controller for robust disturbance compensation in DC-DC buck converters. Int. J. Numer. Model. 2020, 33, e2718. [Google Scholar] [CrossRef]
- Monje, C.; Chen, Y.; Vinagre, B.; Xue, D.; Feliu, V. Fractional Order Systems and Control—Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Shahiri, M.; Ranjbar, A.; Karami, M.R.; Ghaderi, R. New tuning design schemes of fractional complex-order PI controller. Nonlinear Dyn. 2016, 84, 1813–1835. [Google Scholar] [CrossRef]
- Sekhar, R.; Singh, T.P.; Shah, P. Complex Order PIα+jβDγ+jθ Design for Surface Roughness Control in Machining CNT Al-Mg Hybrid Composites. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 299–306. [Google Scholar] [CrossRef]
- Astrom, K.J.; Apkarian, J.; Karam, P.; Levis, M.; Falcon, J. Instructor Workbook: QNET Rotary Invrted Pendulum Trainer for NI ELVIS; Quanser: Markham, ON, Canada, 2011; pp. 24–26. [Google Scholar]
- Saleem, O.; Mahmood-ul-Hasan, K.; Rizwan, M. An Experimental Comparison of Different Hierarchical Self-Tuning Regulatory Control Procedures for Under-Actuated Mechatronic Systems. PLoS ONE 2021, 16, e0256750. [Google Scholar] [CrossRef]
- Hfaiedh, A.; Chemori, A.; Abdelkrim, A. Stabilization of the Inertia Wheel Inverted Pendulum by Advanced IDA-PBC Based Controllers: Comparative Study and Real-Time Experiments. In Proceedings of the SSD 2022 17th International Multi-Conference on Systems, Signals & Devices, Monastir, Tunisia, 20–23 July 2020; pp. 753–760. [Google Scholar]
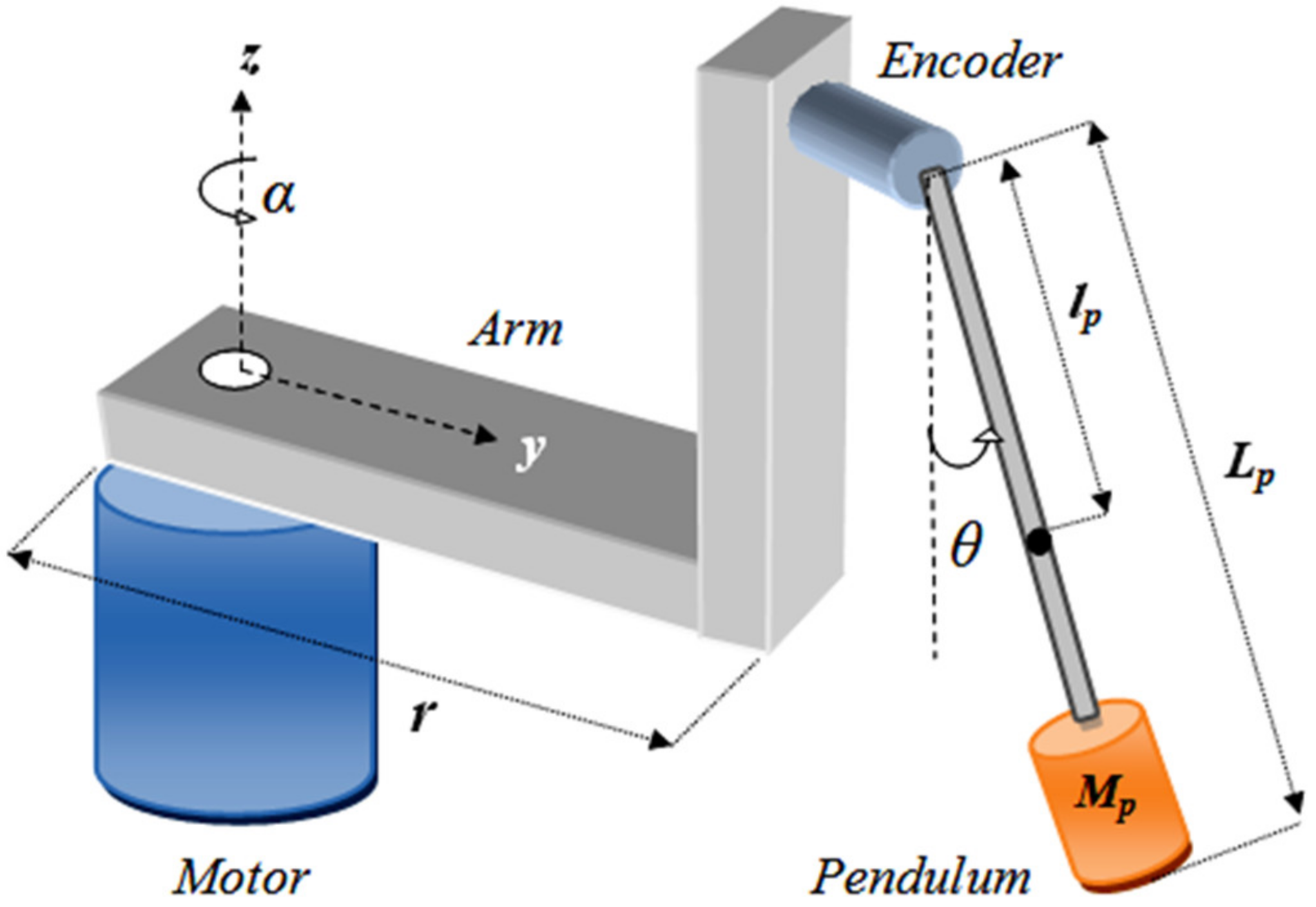




| Parameters | Description | Value | Units |
|---|---|---|---|
| Mp | Mass of pendulum | 0.027 | kg |
| lp | Pendulum center of mass | 0.153 | m |
| Lp | Length of pendulum rod | 0.191 | M |
| r | Length of horizontal arm | 0.083 | M |
| Marm | Mass of arm | 0.028 | Kg |
| g | Gravitational acceleration | 9.810 | m/s2 |
| Je | Moment about motor shaft | 1.23 × 10−4 | kgm2 |
| Jp | Moment about pendulum | 1.10 × 10−4 | kgm2 |
| Rm | Motor armature resistance | 3.30 | Ω |
| Lm | Motor armature inductance | 47.0 | mH |
| Kt | Motor torque constant | 0.028 | Nm |
| Km | Back e.m.f. constant | 0.028 | V/(rad/s) |
| Tm | Maximum torque | 0.14 | Nm |
| Experiment | KPI | Control Scheme | |||
|---|---|---|---|---|---|
| Symbol | Unit | LQIR | FO-LQIR | CFO-LQIR | |
| A | eθ_RMS | degrees | 0.53 | 0.43 | 0.36 |
| eθ_ITAE | s.degrees | 7.84 | 6.15 | 5.35 | |
| eα_RMS | degrees | 15.69 | 11.85 | 10.08 | |
| eα_ITAE | s.degrees | 263.50 | 196.18 | 167.61 | |
| MSVm | V2 | 8.47 | 8.20 | 7.18 | |
| B | eθ_RMS | degrees | 0.71 | 0.64 | 0.47 |
| eθ_ITAE | s.degrees | 9.64 | 9.30 | 6.44 | |
| |Mp,θ| | degrees | 2.77 | 2.48 | 2.23 | |
| ts,θ | s | 0.72 | 0.58 | 0.51 | |
| eα_RMS | degrees | 11.51 | 10.34 | 9.68 | |
| eα_ITAE | s.degrees | 189.14 | 168.30 | 161.69 | |
| MSVm | V2 | 9.61 | 8.22 | 6.39 | |
| Vp | V | −9.85 | −9.63 | −8.47 | |
| C | eθ_RMS | degrees | 1.12 | 0.56 | 0.42 |
| eθ_ITAE | s.degrees | 18.27 | 8.32 | 7.52 | |
| eα_RMS | degrees | 32.47 | 28.10 | 22.06 | |
| eα_ITAE | s.degrees | 524.41 | 458.96 | 380.65 | |
| αoff | degrees | −38.46 | −33.02 | −23.72 | |
| αp-p | degrees | −28.74 | −30.75 | −21.61 | |
| MSVm | V2 | 27.93 | 28.68 | 25.35 | |
| Vp | V | −11.73 | −10.52 | −10.34 | |
| D | eθ_RMS | degrees | 0.46 | 0.32 | 0.29 |
| eθ_ITAE | s.degrees | 7.24 | 5.13 | 4.50 | |
| eα_RMS | degrees | 10.14 | 9.85 | 9.53 | |
| eα_ITAE | s.degrees | 160.08 | 165.78 | 160.63 | |
| MSVm | V2 | 12.62 | 11.73 | 10.50 | |
| E | eθ_RMS | degrees | 1.06 | 0.90 | 0.78 |
| eθ_ITAE | s.degrees | 15.83 | 12.82 | 11.88 | |
| eα_RMS | degrees | 16.01 | 12.97 | 11.78 | |
| eα_ITAE | s.degrees | 281.17 | 223.89 | 201.48 | |
| MSVm | V2 | 11.44 | 10.63 | 9.48 | |
| KPI | Control Scheme | ||
|---|---|---|---|
| Symbol | Unit | CFO-LQIR | MCFO-LQIR |
| eθ_RMS | degrees | 0.36 | 0.40 |
| eθ_ITAE | s.degrees | 5.35 | 6.32 |
| eα_RMS | degrees | 10.08 | 7.34 |
| eα_ITAE | s.degrees | 167.61 | 121.65 |
| MSVm | V2 | 7.18 | 13.50 |
| Vp | V | 7.05 | −14.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, O.; Abbas, F.; Iqbal, J. Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation. Mathematics 2023, 11, 913. https://doi.org/10.3390/math11040913
Saleem O, Abbas F, Iqbal J. Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation. Mathematics. 2023; 11(4):913. https://doi.org/10.3390/math11040913
Chicago/Turabian StyleSaleem, Omer, Faisal Abbas, and Jamshed Iqbal. 2023. "Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation" Mathematics 11, no. 4: 913. https://doi.org/10.3390/math11040913
APA StyleSaleem, O., Abbas, F., & Iqbal, J. (2023). Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation. Mathematics, 11(4), 913. https://doi.org/10.3390/math11040913







