Reliability Prediction of Tunnel Roof with a Nonlinear Failure Criterion
Abstract
:1. Introduction
2. Methodology
2.1. Reliability Analysis Methods
2.1.1. FORM
2.1.2. RSM
- (a)
- Sampling points are chosen around the mean value . Usually, mean value points with are selected to evaluate the performance function , in which is the sampling range factor.
- (b)
- Altogether coefficients of Equation (5) can be obtained by solving the set of linear equations. Thus, a tentative response surface is generated.
- (c)
- Calculating the reliability index and corresponding design points by FORM and Equation (1). In this computation, is subject to the constraint that .
- (d)
- Repeating steps (a)–(c) until or converges. Besides the first trial, new sampling points may be selected around the tentative design points concerning the interpolation method.
2.1.3. MCS
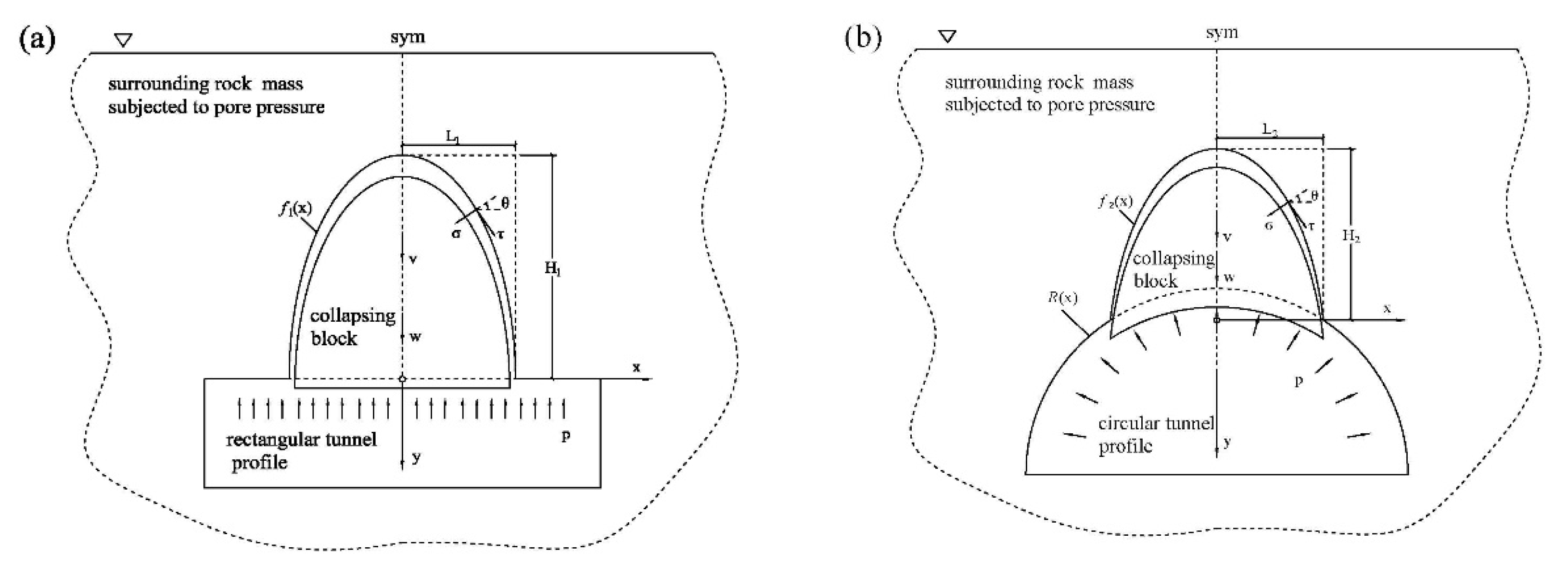
2.2. Kinematic Analysis of Tunnels Roofs with Hoek-Brown Criterion
2.3. Performance Functions of Roof Collapse
3. Results and Discussion
3.1. Reliability Analysis of Rectangular Tunnels
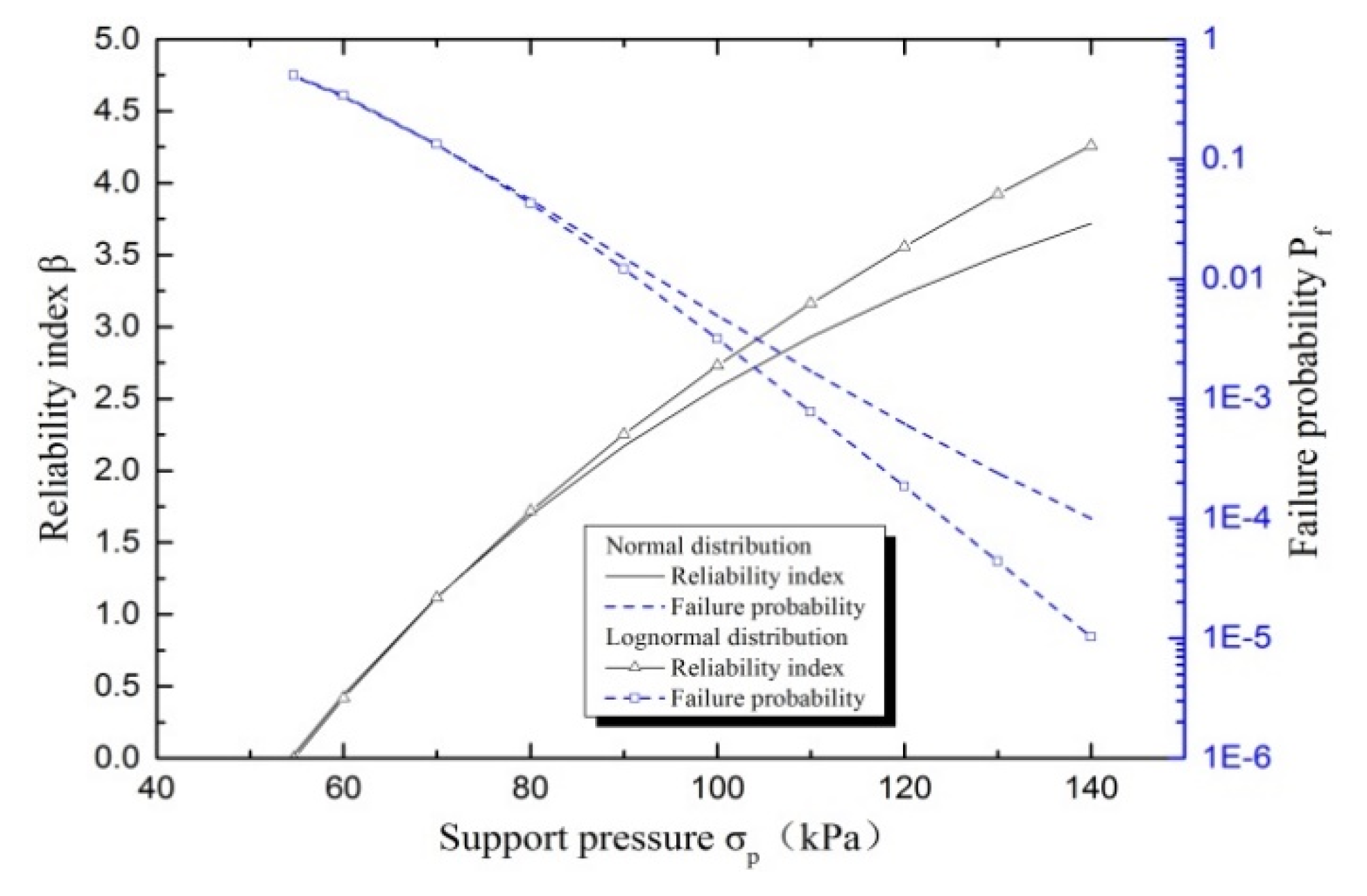
3.1.1. Reliability Index and Failure Probability
3.1.2. Sensitivity Analysis
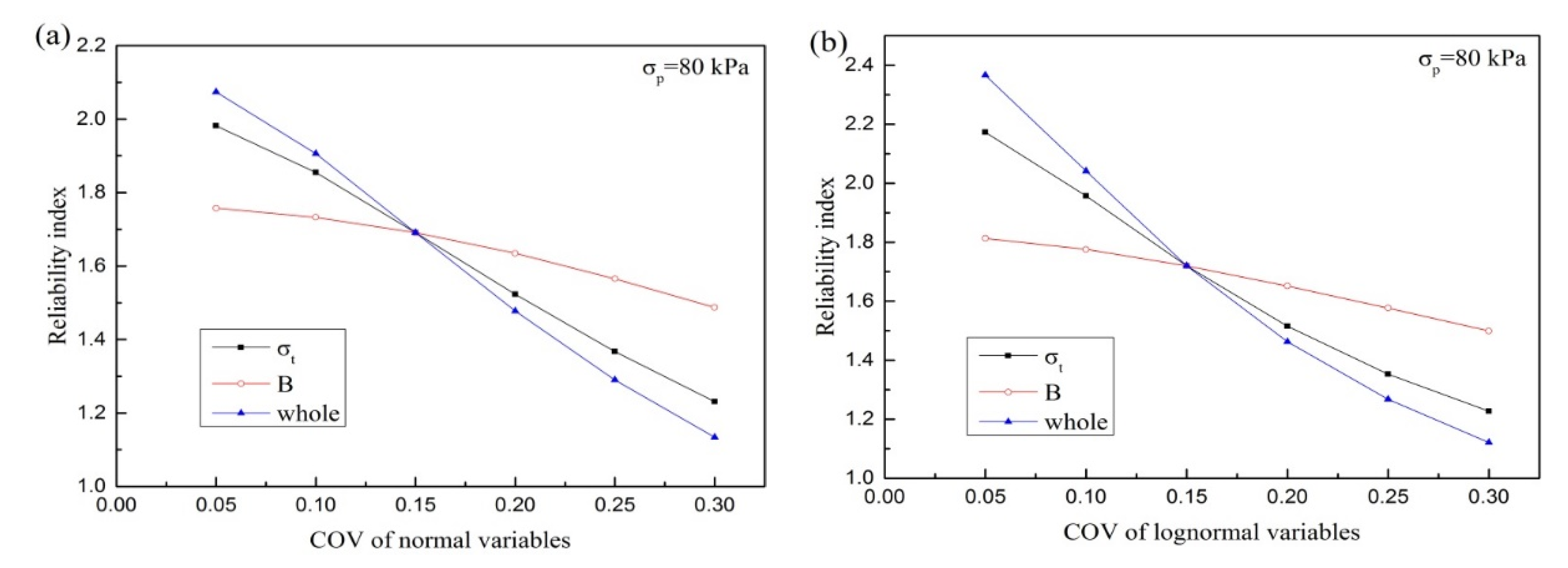
3.1.3. Influence of Coefficient of Variation
3.2. Reliability Analysis of Circular Tunnels
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Nomenclature
| coefficients in response surface method | |
| material constant | |
| coefficients in response surface method | |
| material constant | |
| covariance matrix | |
| energy dissipation density of the internal forces | |
| sampling range factor. | |
| failure region | |
| collapsing curve | |
| first derivative of | |
| original probability density function ordinate at | |
| original non-normal CDF evaluated at | |
| performance function | |
| performance function of a rectangular tunnel | |
| performance function of a circular tunnel | |
| weight of failure block | |
| height of the collapsing block | |
| half width of the collapsing block | |
| unit vector | |
| number of samples | |
| total energy dissipation at the impending collapse | |
| work rate done by weight | |
| work rate of the pore pressure | |
| work rate of supporting force | |
| failure probability | |
| support pressure | |
| pore water coefficient |
References
- Hou, C.; Zhong, J.; Yang, X. Three-dimensional stability assessments of a non-circular tunnel face reinforced by bolts under seepage flow conditions. Tunn. Undergr. Space Technol. 2023, 131, 104831. [Google Scholar] [CrossRef]
- Zhong, J.; Hou, C.; Yang, X. Three-dimensional face stability analysis of rock tunnels excavated in Hoek-Brown media with a novel multi-cone mechanism. Comp. Geotech. 2023, 154, 105158. [Google Scholar] [CrossRef]
- Chen, B.; Gong, B.; Wang, S.; Tang, C. Research on Zonal Disintegration Characteristics and Failure Mechanisms of Deep Tunnel in Jointed Rock Mass with Strength Reduction Method. Mathematics 2022, 10, 922. [Google Scholar] [CrossRef]
- Lee, Y.-L.; Zhu, M.-L.; Ma, C.-H.; Chen, C.-S.; Lee, C.-M. Effect of Overburden Depth and Stress Anisotropy on a Ground Reaction Caused by Advancing Excavation of a Circular Tunnel. Mathematics 2023, 11, 243. [Google Scholar] [CrossRef]
- Qiu, J.; Feng, F. Effect of Different Tunnel Distribution on Dynamic Behavior and Damage Characteristics of Non-Adjacent Tunnel Triggered by Blasting Disturbance. Mathematics 2022, 10, 3705. [Google Scholar] [CrossRef]
- Berisavljević, Z.; Bajić, D.; Jovičić, V. Development and application of methodology for quantification of overbreaks in hard rock tunnel construction. Appl. Sci. 2023, 13, 1379. [Google Scholar] [CrossRef]
- Su, Y.H.; Li, X.; Xie, Z.Y. Probabilistic evaluation for the implicit limit-state function of stability of a highway tunnel in China. Tunn. Undergr. Space Technol. 2011, 26, 422–434. [Google Scholar] [CrossRef]
- Lü, Q.; Low, B.K. Probabilistic analysis of underground rock excavations using response surface method and SORM. Comp. Geotech. 2011, 38, 1008–1021. [Google Scholar] [CrossRef]
- Hussaine, S.M.; Mu, L. Intelligent Prediction of Maximum Ground Settlement Induced by EPB Shield Tunneling Using Automated Machine Learning Techniques. Mathematics 2022, 10, 4637. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, W. Reliability assessment of stability of underground rock caverns. Int. J. Rock Mech. Min. Sci. 2012, 55, 157–163. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C. Reliability assessment on ultimate and serviceability limit states and determination of critical factor of safety for underground rock caverns. Tunn. Undergr. Space Technol. 2012, 32, 221–230. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Probabilistic analysis of circular tunnels in homogeneous soil using response surface methodology. J. Geotech. Geoenviron. Eng. 2009, 135, 1314–1325. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Probabilistic analysis of pressurized tunnels against face stability using collocation-based stochastic response surface method. J. Geotech. Geoenviron. Eng. 2010, 137, 385–397. [Google Scholar] [CrossRef]
- Zeng, P.; Senent, S.; Jimenez, R. Reliability analysis of circular tunnel face stability obeying Hoek–Brown failure criterion considering different distribution types and correlation structures. J. Comput. Civ. Eng. 2014, 30, 04014126. [Google Scholar] [CrossRef]
- Pan, Q.J.; Dias, D. Probabilistic analysis of a rock tunnel face using polynomial chaos expansion method. Int. J. Geomech. 2018, 18. [Google Scholar] [CrossRef]
- Fraldi, M.; Cavuoto, R.; Cutolo, A.; Guarracino, F. Stability of tunnels according to depth and variability of rock mass parameters. Int. J. Rock Mech. Min. Sci. 2019, 119, 222–229. [Google Scholar] [CrossRef]
- Fraldi, M.; Guarracino, F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections. Int. J. Solids Struct. 2010, 47, 216–223. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Yang, X.L.; Wang, J.M. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second-moment code format. Am. Soc. Civ. Eng. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Chan, C.L.; Low, B.K. Practical second-order reliability analysis applied to foundation engineering. Int. J. Numer. Anal. Meth. Geomech. 2012, 36, 1387–1409. [Google Scholar] [CrossRef]
- Rackwitz, R.; Flessler, B. Structural reliability under combined random load sequences. Comp. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Tandjiria, V.; Teh, C.I.; Low, B.K. Reliability analysis of laterally loaded piles using response surface methods. Struct. Saf. 2000, 22, 335–355. [Google Scholar] [CrossRef]
- Theodorou, D.N. Progress and outlook in Monte Carlo simulations. Ind. Eng. Chem. Res. 2010, 49, 3047–3058. [Google Scholar] [CrossRef]
- Dias, D.; Kastner, R. Movements caused by the excavation of tunnels using face pressurized shields analysis of monitoring and numerical modeling results. Eng. Geol. 2013, 152, 17–25. [Google Scholar] [CrossRef]
- Zou, J.F.; Xia, M.Y. A new approach for the cylindrical cavity expansion problem incorporating deformation dependent of intermediate principal stress. Geomech. Eng. 2017, 12, 347–360. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Three-dimensional roof collapse analysis in circular tunnels in rock. Int. J. Rock Mech. Min. Sci. 2020, 128, 104275. [Google Scholar] [CrossRef]
- Qin, C.B.; Li, Y.Y.; Yu, J.; Chian, S.C.; Liu, H.L. Closed-form solutions for collapse mechanisms of tunnel crown in saturated non-uniform rock surrounds. Tunn. Undergr. Space Technol. 2022, 126, 104529. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Active earth pressure for soils with tension cracks under steady unsaturated flow conditions. Can. Geotech. J. 2018, 55, 1850–1859. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhu, J.Q.; Yang, X.L. Three-dimensional active earth pressures for unsaturated backfills with cracks considering steady seepage. Int. J. Geomech. 2023, 23, 04022270. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L.; Li, T.Z. Static and seismic stability assessment of 3D slopes with cracks. Eng. Geol. 2020, 265, 105450. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Pseudodynamic analysis of three-dimensional fissured slopes reinforced with piles. Int. J. Geomech. 2022, 23, 04022315. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity; Elsevier Science: Amsterdam, The Netherlands, 1975. [Google Scholar] [CrossRef]
- Fang, X.; Du, E.; Zheng, K.; Yang, J.; Chen, Q. Locational pricing of uncertainty based on robust optimization. CSEE J. Power Energy Syst. 2020, 7, 1345–1356. [Google Scholar] [CrossRef]
- Xiao, D.; Qiao, W. Hybrid scenario generation method for stochastic virtual bidding in electricity market. CSEE J. Power Energy Syst. 2021, 7, 1312–1321. [Google Scholar] [CrossRef]
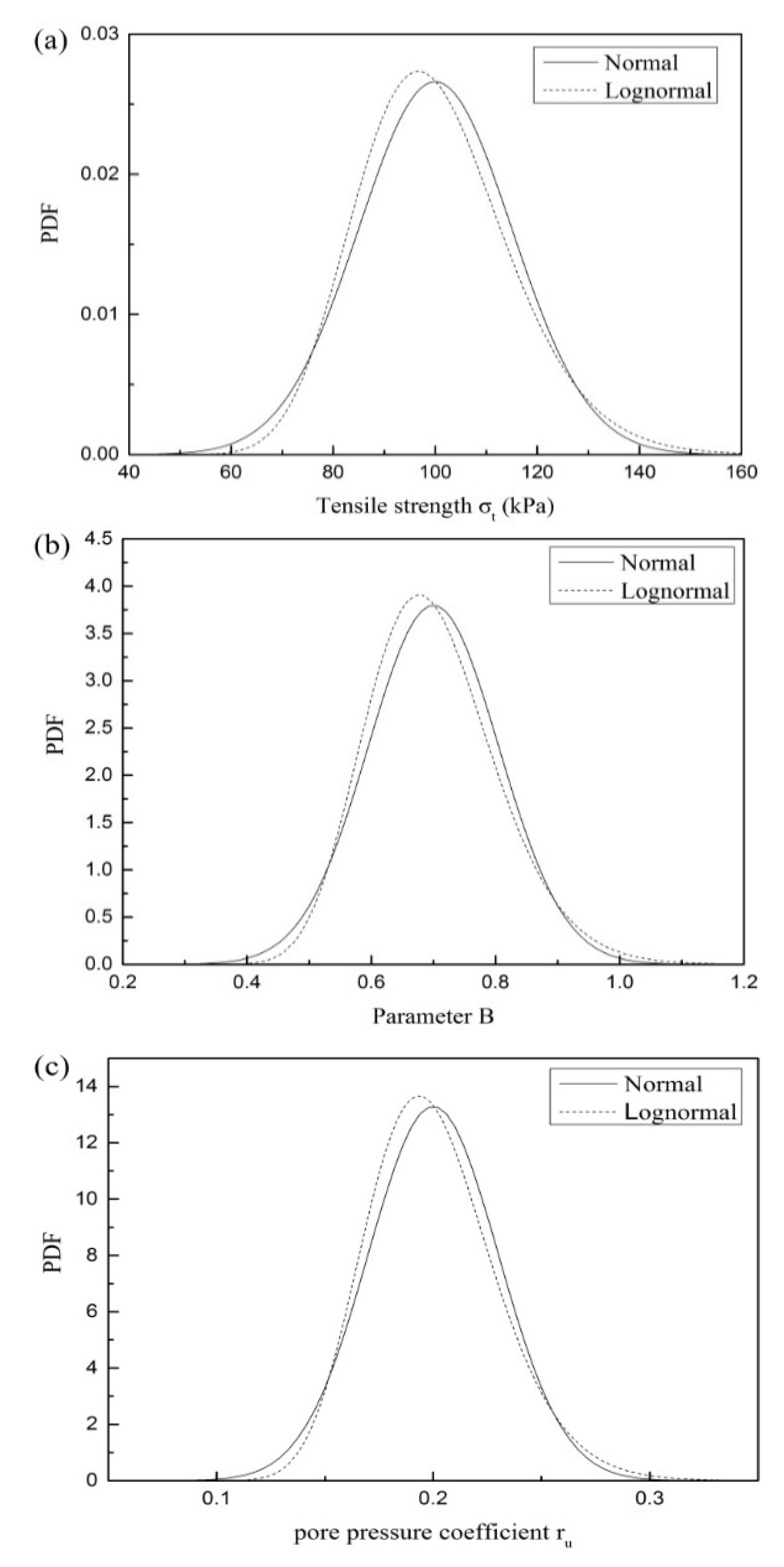

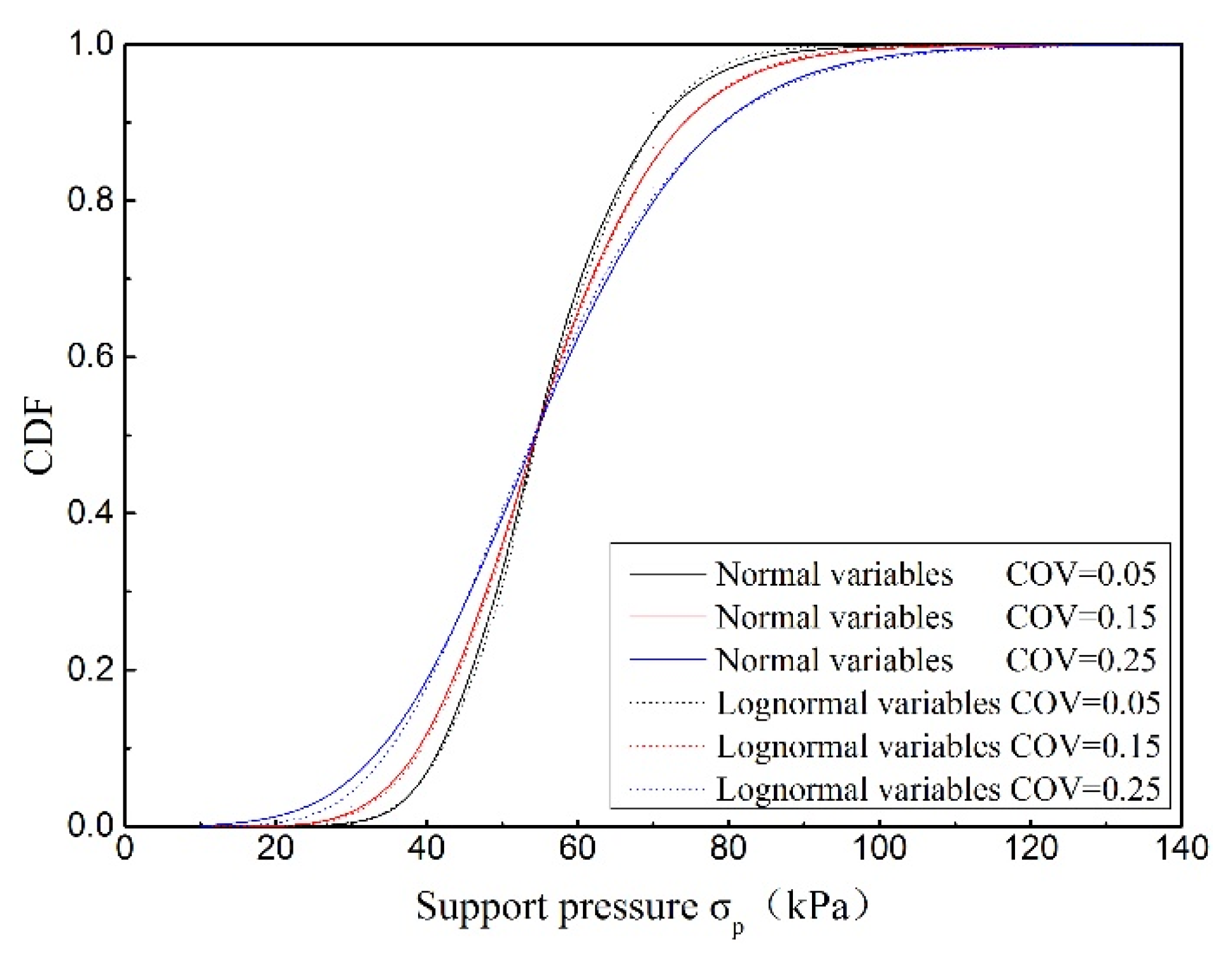
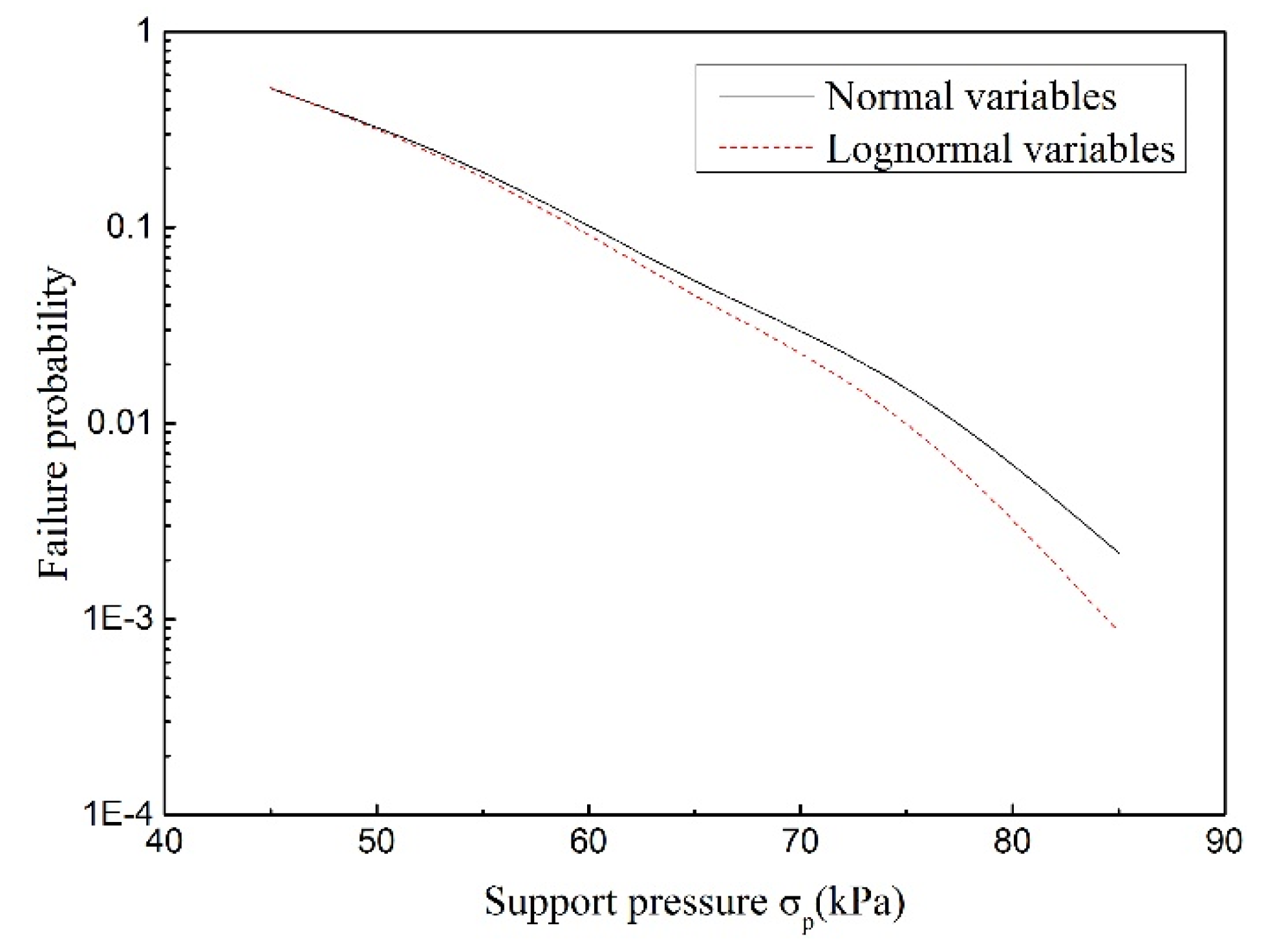
| Random Variable | Mean Value | Distribution Type | |
|---|---|---|---|
| Case 1 | 100 | normal | |
| B | 0.7 | normal | |
| 0.2 | normal | ||
| normal | |||
| Case 2 | 100 | lognormal | |
| B | 0.7 | lognormal | |
| 0.2 | lognormal | ||
| lognormal |
| Case 1 | Case 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Design Point | Reliability Index | Design Point | Reliability Index | |||||||||
| FORM | RSM | MCS | FORM | RSM | MCS | |||||||
| 60 | 104.255 | 0.686 | 0.199 | 0.442 | 0.442 | 0.433 | 103.150 | 0.679 | 0.197 | 0.420 | 0.420 | 0.433 |
| 70 | 109.965 | 0.664 | 0.198 | 1.122 | 1.122 | 1.107 | 110.640 | 0.659 | 0.196 | 1.116 | 1.116 | 1.130 |
| 80 | 113.933 | 0.648 | 0.198 | 1.691 | 1.691 | 1.673 | 117.598 | 0.642 | 0.195 | 1.720 | 1.720 | 1.738 |
| 90 | 116.649 | 0.635 | 0.197 | 2.171 | 2.171 | 2.154 | 124.120 | 0.628 | 0.195 | 2.253 | 2.253 | 2.269 |
| 100 | 118.462 | 0.627 | 0.197 | 2.579 | 2.579 | 2.566 | 130.280 | 0.616 | 0.194 | 2.731 | 2.731 | 2.770 |
| 110 | 119.618 | 0.621 | 0.197 | 2.929 | 2.929 | 2.919 | 136.130 | 0.605 | 0.194 | 3.164 | 3.164 | 3.160 |
| 120 | 120.296 | 0.618 | 0.197 | 3.230 | 3.230 | 3.226 | 141.713 | 0.596 | 0.193 | 3.559 | 3.559 | 3.633 |
| 130 | 120.628 | 0.616 | 0.196 | 3.491 | 3.491 | 3.486 | 147.061 | 0.588 | 0.193 | 3.923 | 3.923 | 3.911 |
| 140 | 120.710 | 0.616 | 0.196 | 3.719 | 3.719 | 3.707 | 152.203 | 0.580 | 0.192 | 4.260 | 4.260 | 4.244 |
| 60 | 0.641 | −0.308 | −0.050 |
| 70 | 0.592 | −0.304 | −0.048 |
| 80 | 0.549 | −0.296 | −0.046 |
| 90 | 0.511 | −0.284 | −0.043 |
| 100 | 0.477 | −0.271 | −0.041 |
| 110 | 0.447 | −0.257 | −0.038 |
| 120 | 0.419 | −0.243 | −0.036 |
| Mean value | 0.520 | −0.280 | −0.043 |
| Random Variables | Normal/Lognormal Distribution | |
|---|---|---|
| Mean Value | Coefficient of Variation | |
| (MPa) | 0.1 | 0.15 |
| (MPa) | 10 | 0.15 |
| 0.5 | 0.15 | |
| 0.7 | 0.15 | |
| (kN/m3) | 25 | 0.15 |
| 0.2 | 0.15 | |
| 0.15 | ||
| Support Pressure (kPa) | Sample Size | COV of Failure Probability | |
|---|---|---|---|
| Normal Distribution | Lognormal Distribution | ||
| 45 | 0.0098 | 0.0097 | |
| 55 | 0.0087 | 0.0090 | |
| 65 | 0.0113 | 0.0122 | |
| 75 | 0.0117 | 0.0140 | |
| 85 | 0.0214 | 0.0340 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Long, J. Reliability Prediction of Tunnel Roof with a Nonlinear Failure Criterion. Mathematics 2023, 11, 937. https://doi.org/10.3390/math11040937
Yang X, Long J. Reliability Prediction of Tunnel Roof with a Nonlinear Failure Criterion. Mathematics. 2023; 11(4):937. https://doi.org/10.3390/math11040937
Chicago/Turabian StyleYang, Xin, and Jiangping Long. 2023. "Reliability Prediction of Tunnel Roof with a Nonlinear Failure Criterion" Mathematics 11, no. 4: 937. https://doi.org/10.3390/math11040937
APA StyleYang, X., & Long, J. (2023). Reliability Prediction of Tunnel Roof with a Nonlinear Failure Criterion. Mathematics, 11(4), 937. https://doi.org/10.3390/math11040937






