Optimization of MHD Flow of Radiative Micropolar Nanofluid in a Channel by RSM: Sensitivity Analysis
Abstract
:1. Background
1.1. Literature Review
1.2. Motivations
- The problem of viscoelastic fluid in a confined space (channel) with extending walls was discussed by Misra et al. [24]. According to the study, reverse flow occurs close to the region’s (channel’s) centre and can be managed by applying an external magnetic field.
- Ashraf et al. [25] looked into the issue of micropolar fluid flow with heat transmission in a channel with stretching walls. Equations of fourth order coupled nonlinear ordinary differential type were solved using the quasi-linearization approach. The study exposed the fact that shear, coupled stresses and heat transfer rate at the walls are increased by stretching the channel walls. They also quantified that their investigation may be valuable for the flow and thermal control of polymeric processing.
1.3. Contributions
- It proposes the single-phase nanofluid model of micropolar copper–blood nanoparticles in a channel with stretching and shrinking walls.
- Thermal radiations are also present in the channel to make the problem more appealing for heat transfer.
- To control the reversibility of the flow due to the stretching walls, we impose a transverse magnetic field.
- This research also investigates sensitivity analysis using response surface methodology (RSM).
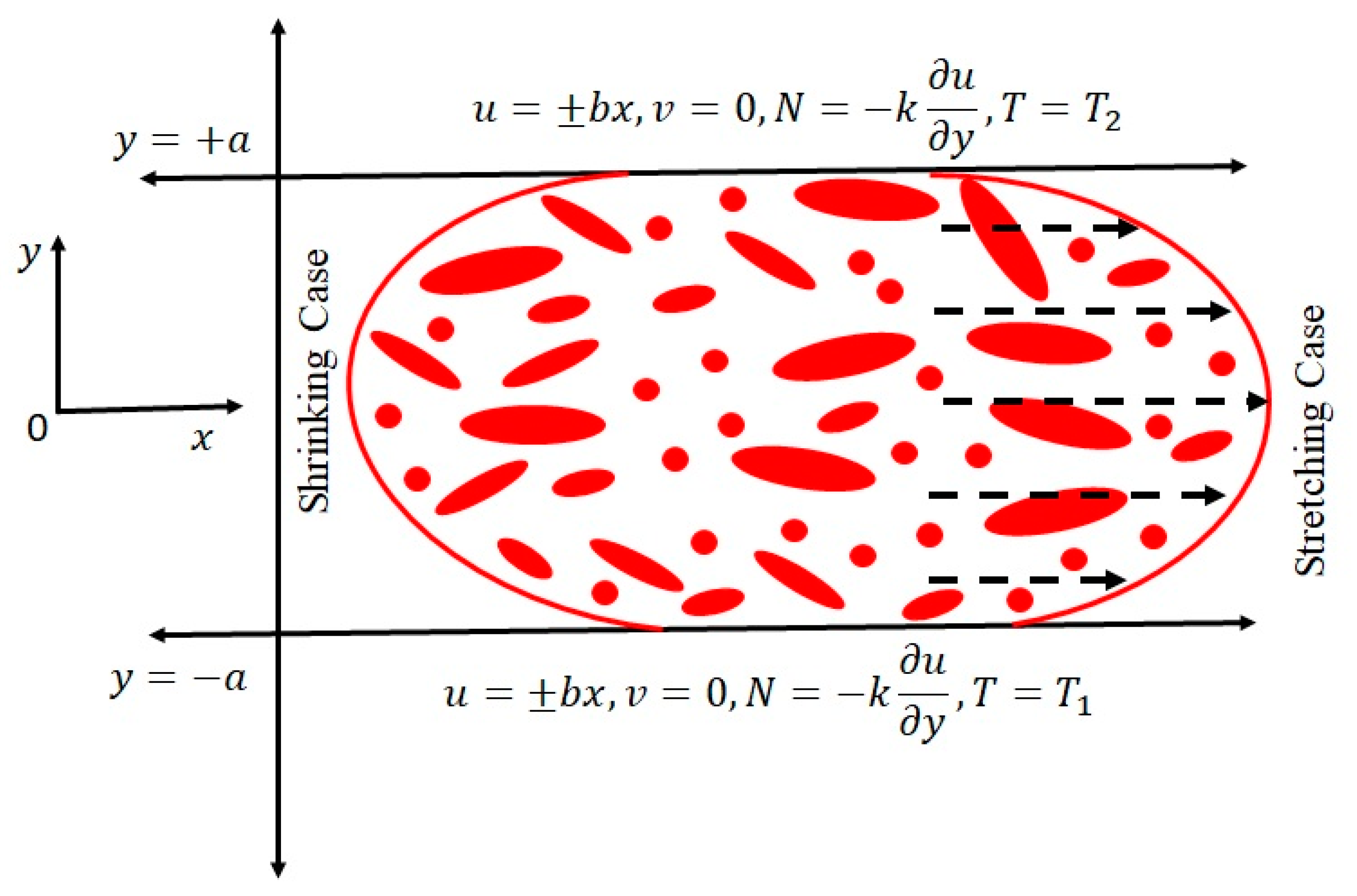
2. Proposed Model
2.1. Governing Equations
2.2. Similarity Solution
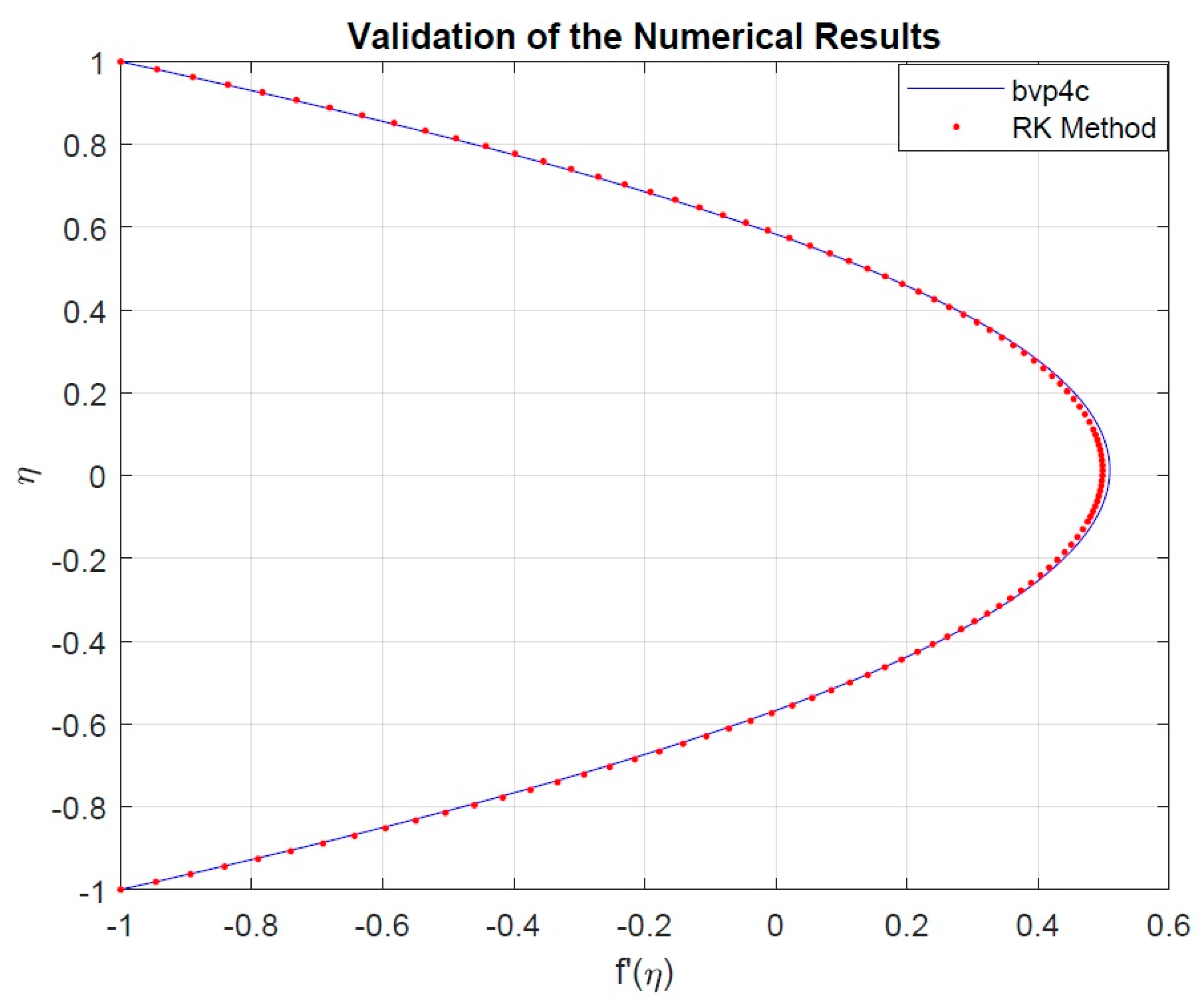
3. Results and Discussion
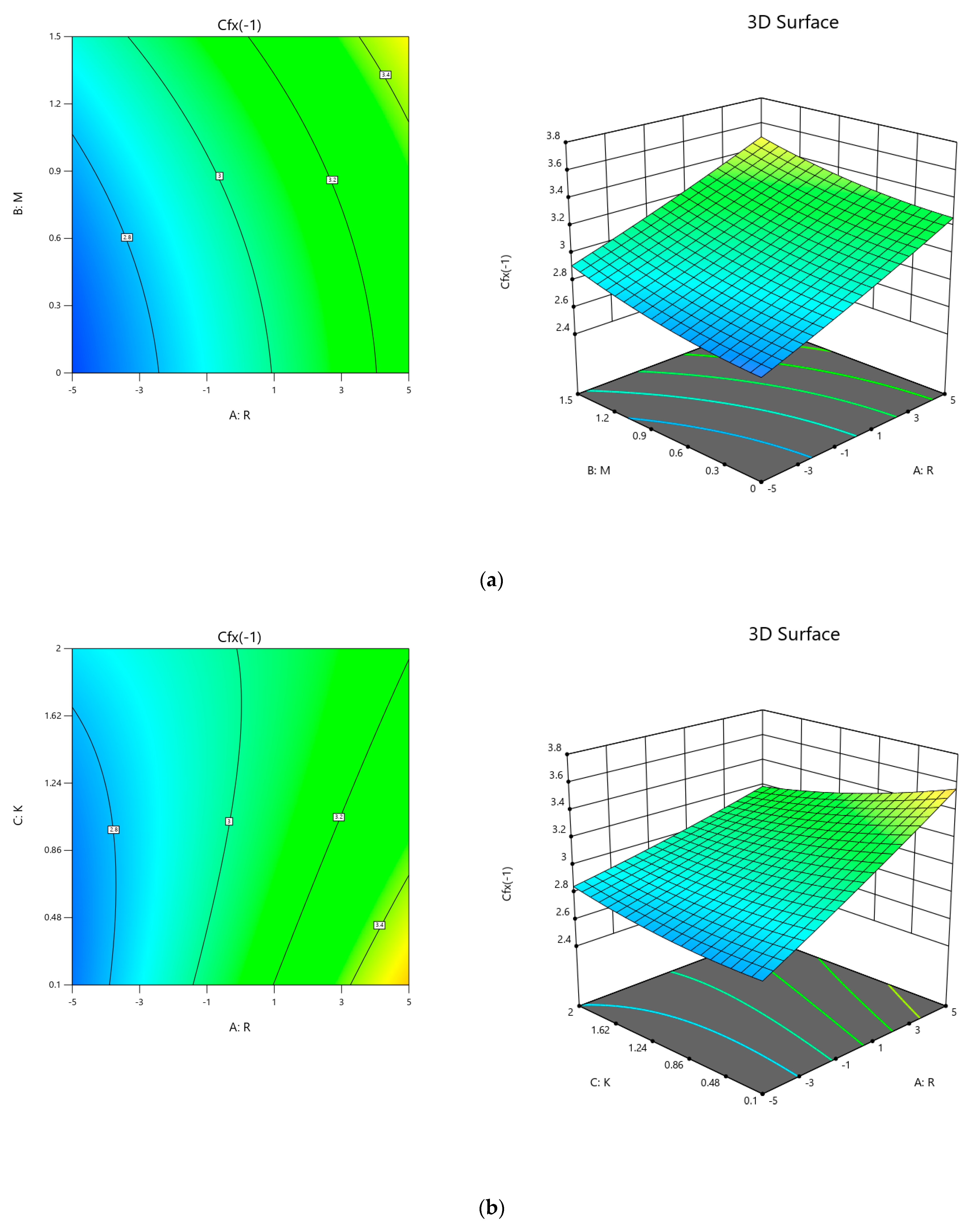
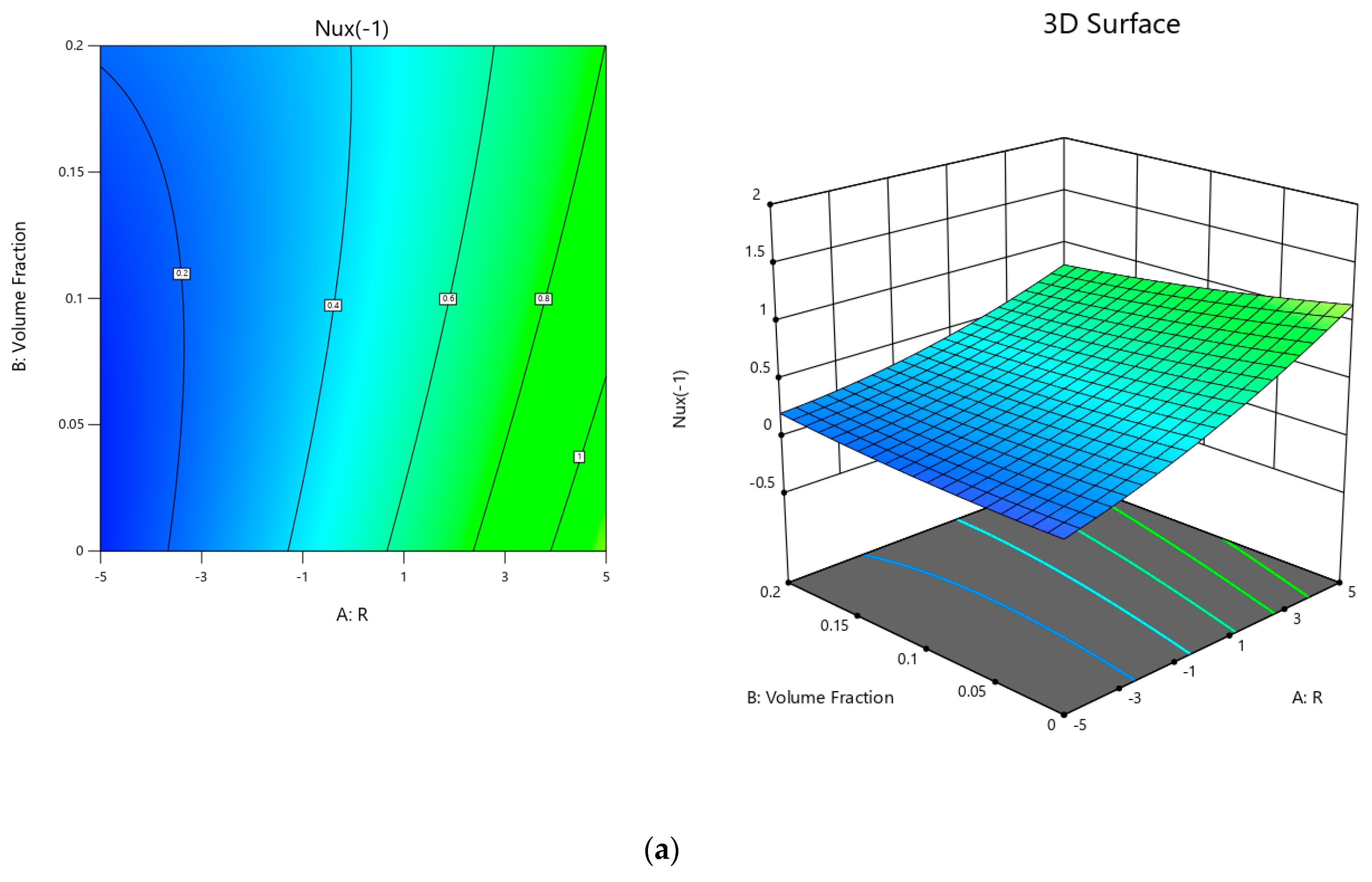
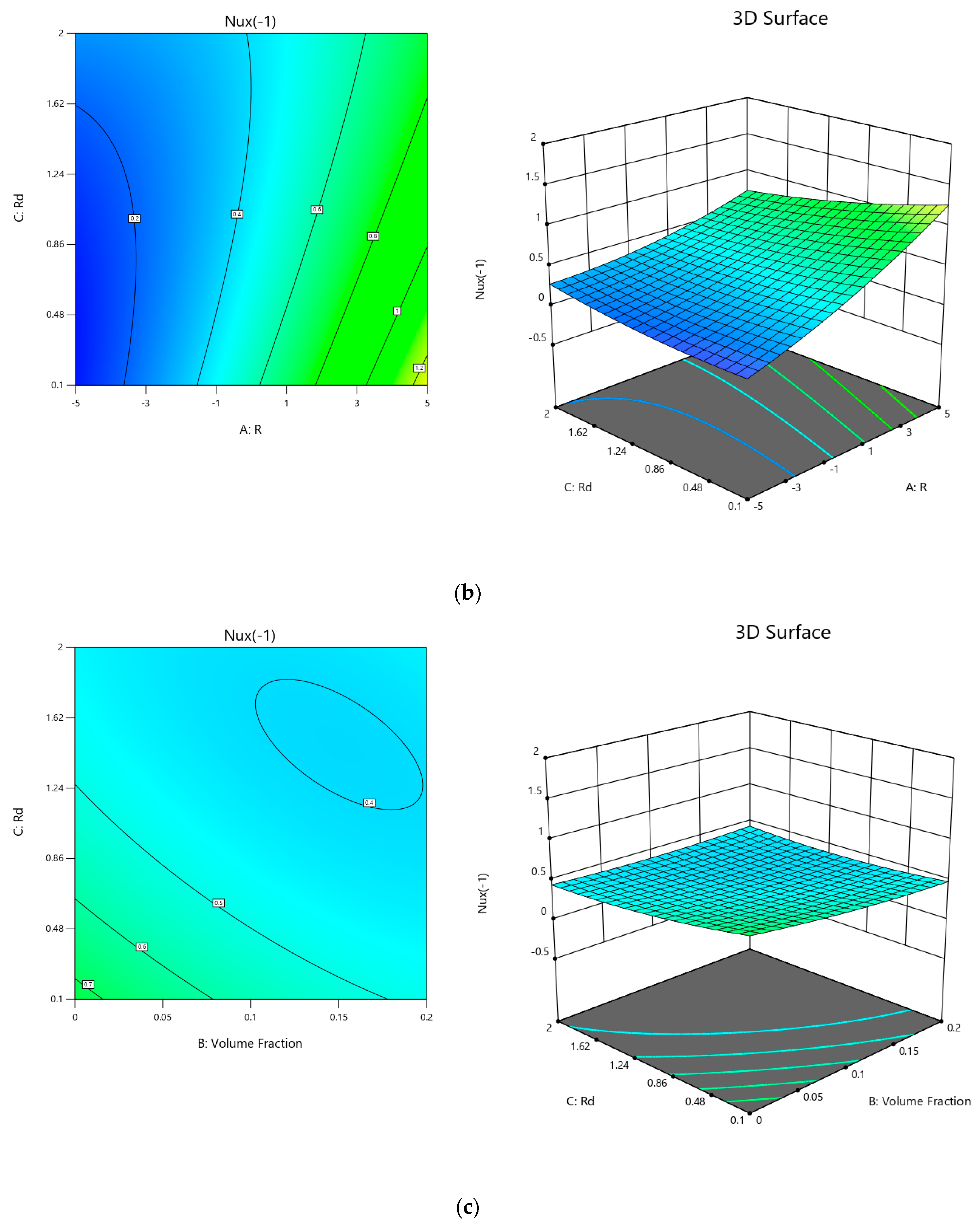
3.1. Application of Response Surface Methodology (RSM)
3.1.1. Optimization Process
- To reach the suitable and believable requirements for the intended response, we planned and investigated the data values.
- We outlined the most appropriate mathematical models for the response surface.
- We described the mathematical models for the response surface that are most suited.
- We used an analysis of the variance to examine the parametric direct and interaction impacts (ANOVA).
3.1.2. Optimization Analysis by RSM
4. Conclusions
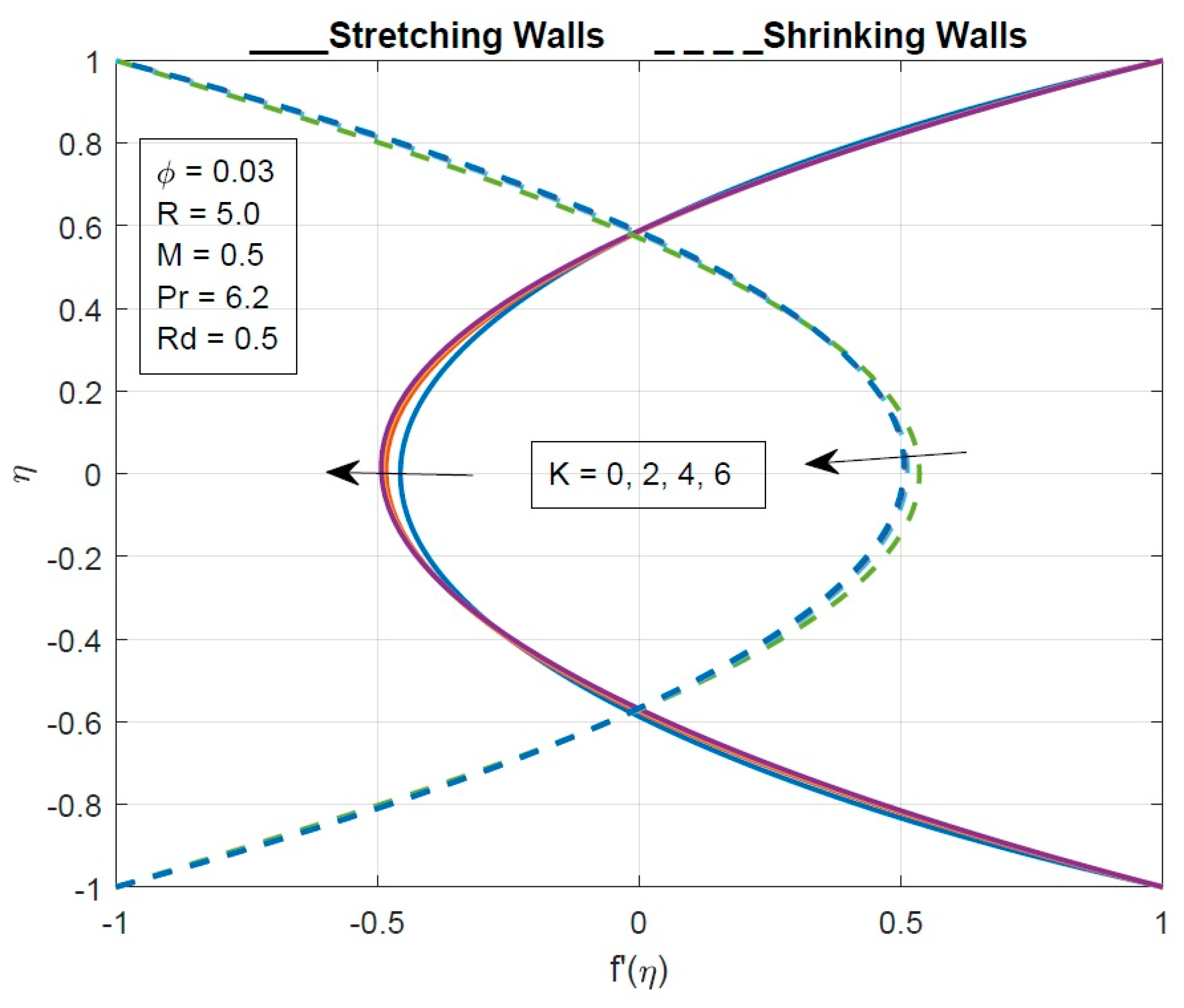
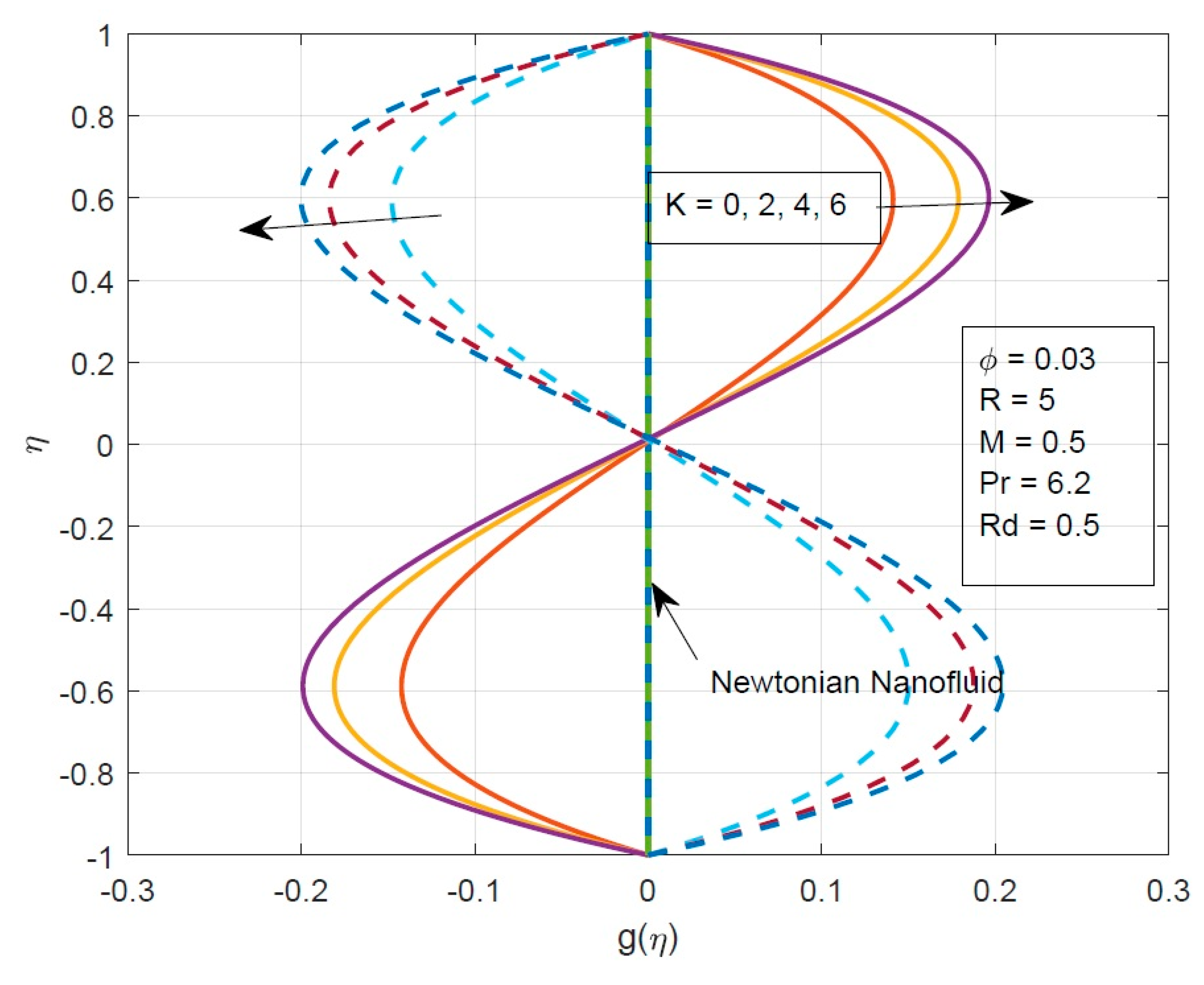
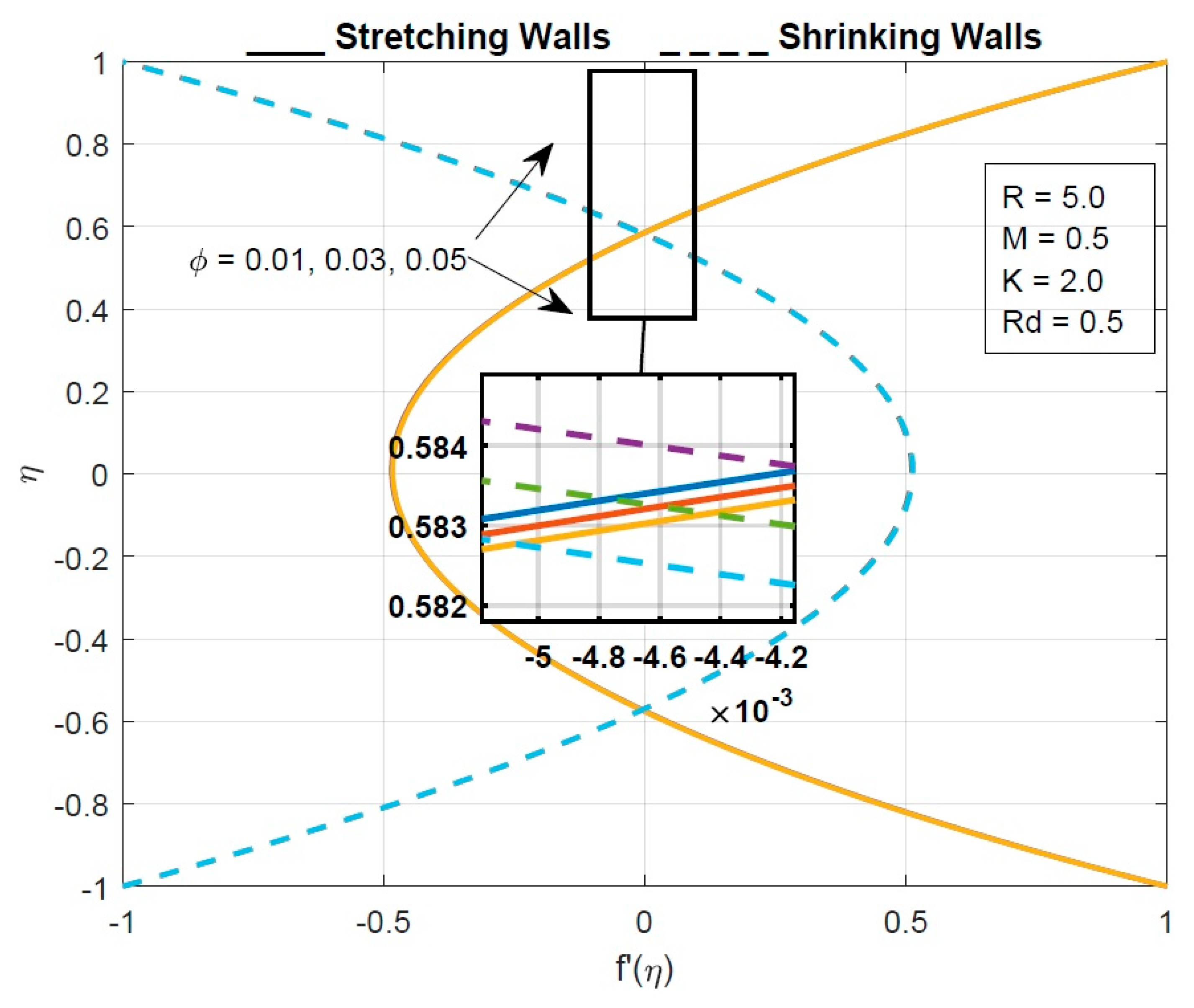
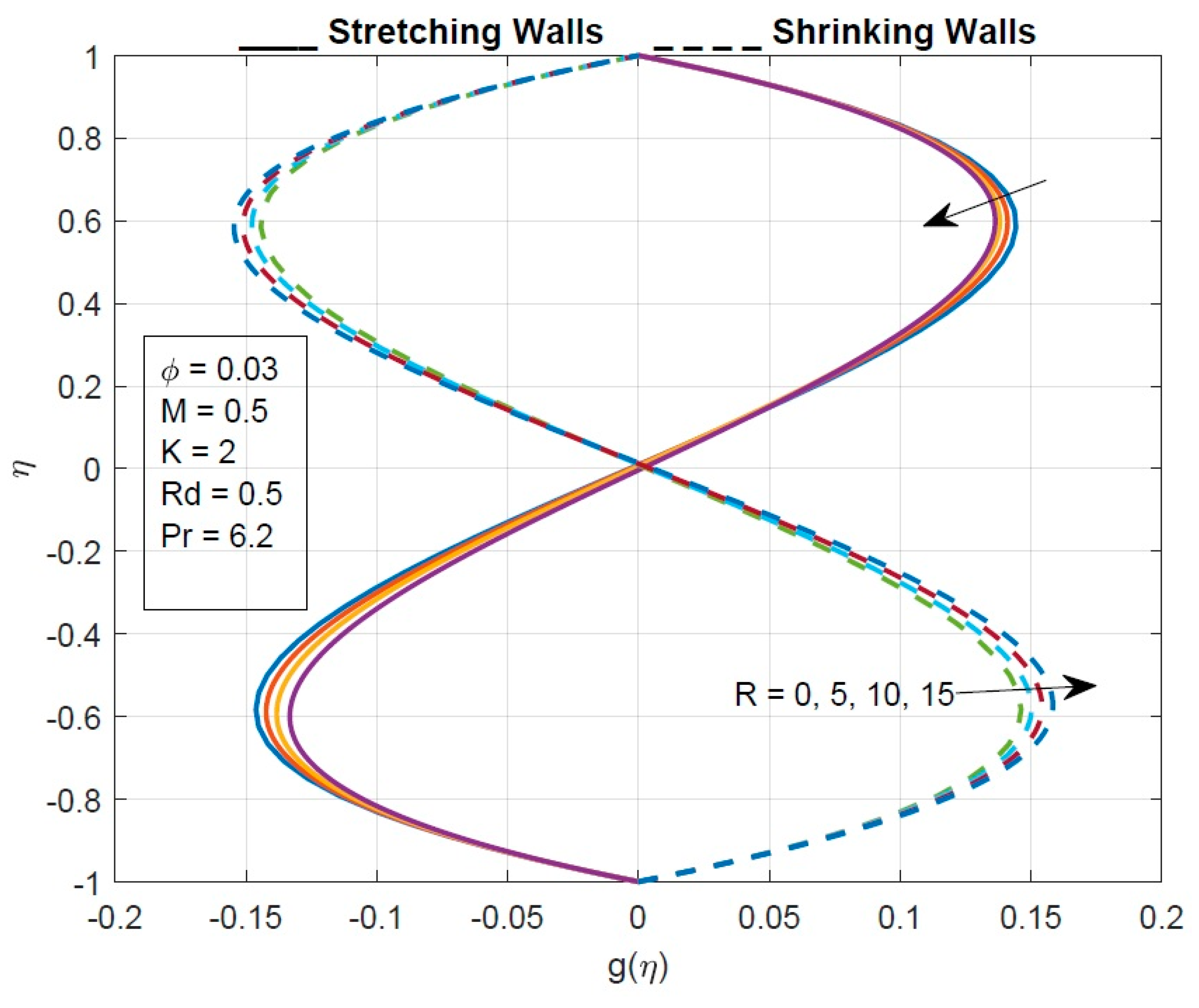
- The velocity of the fluid particles decreases by increasing the values of the micropolar parameter.
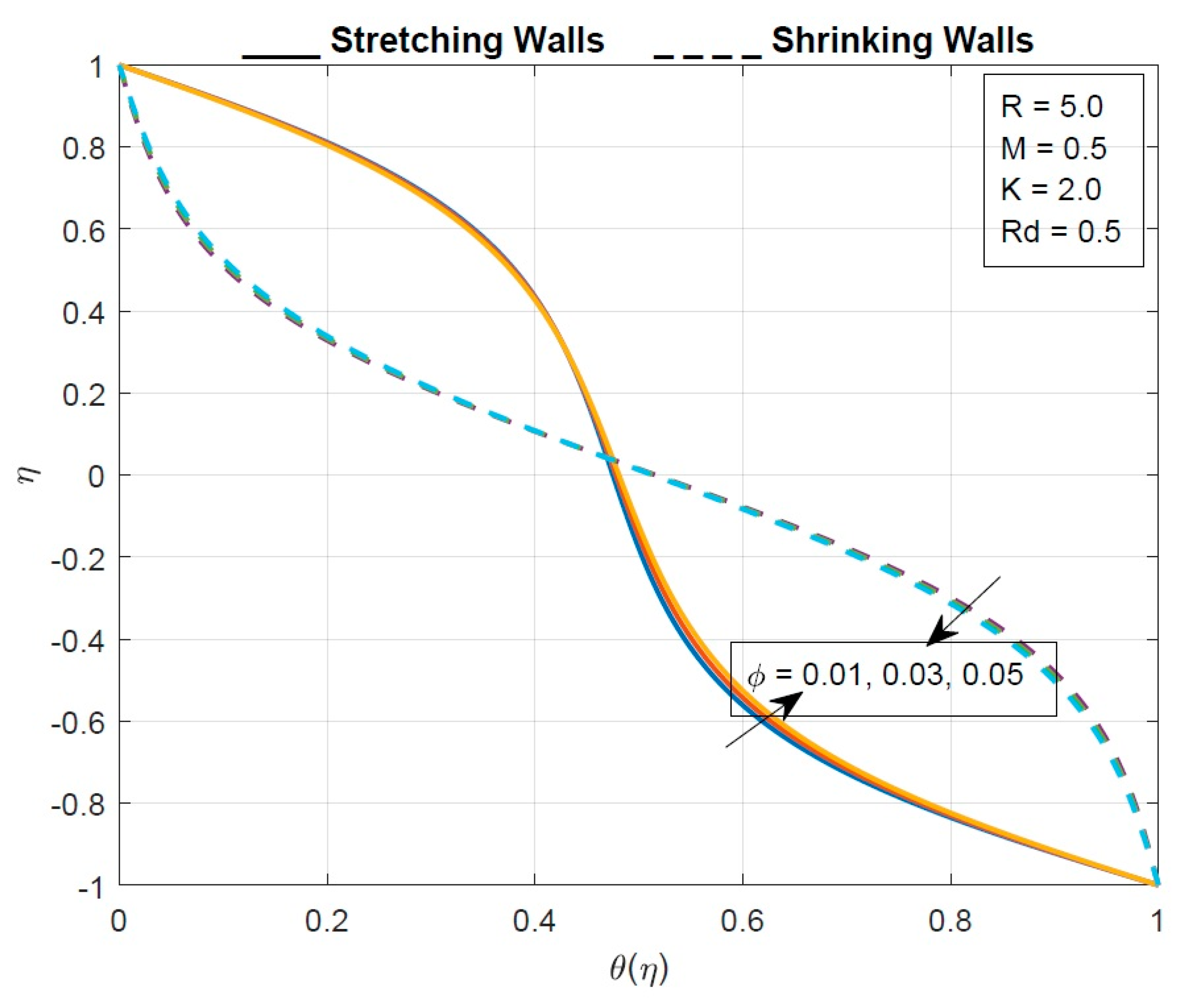
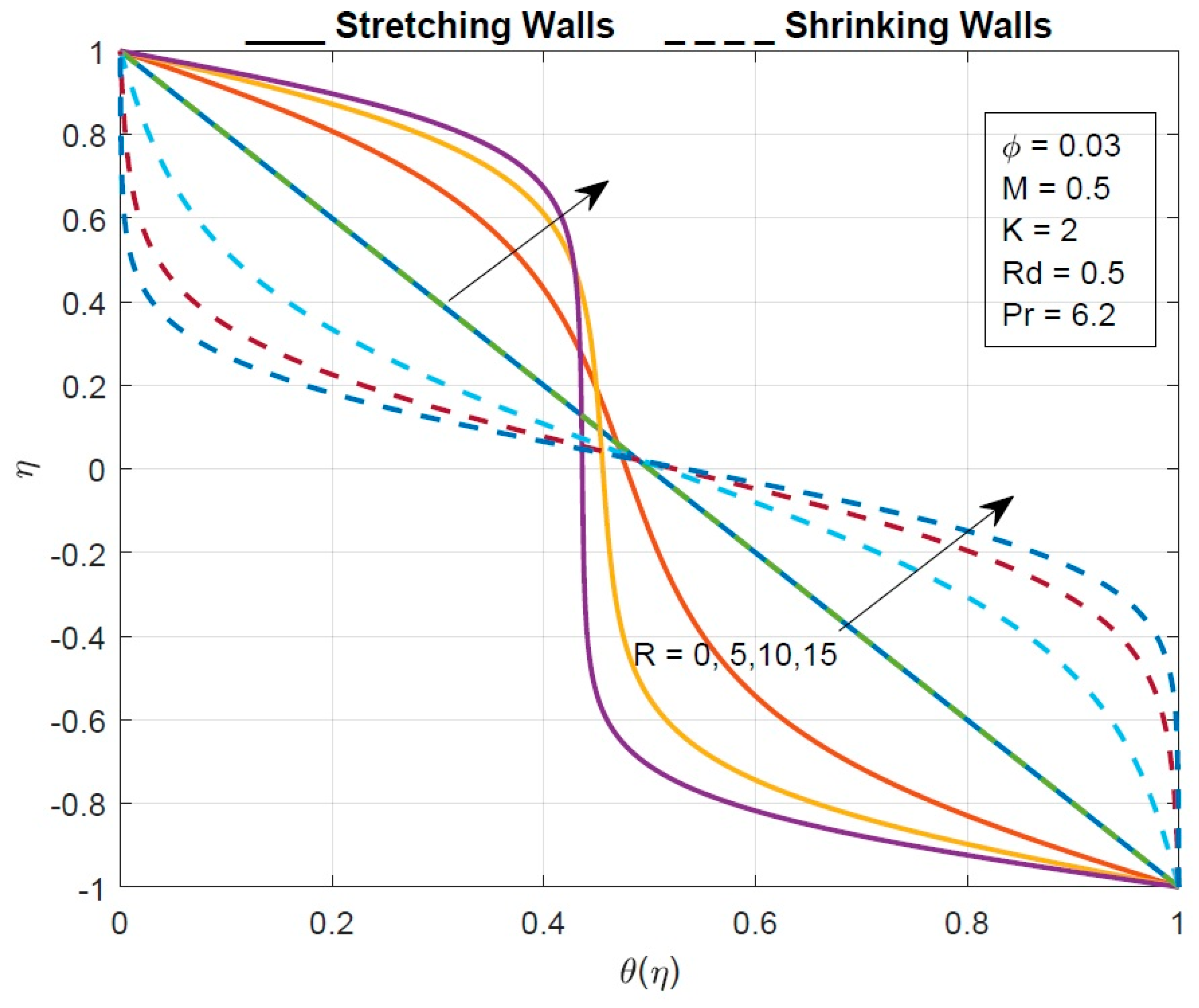
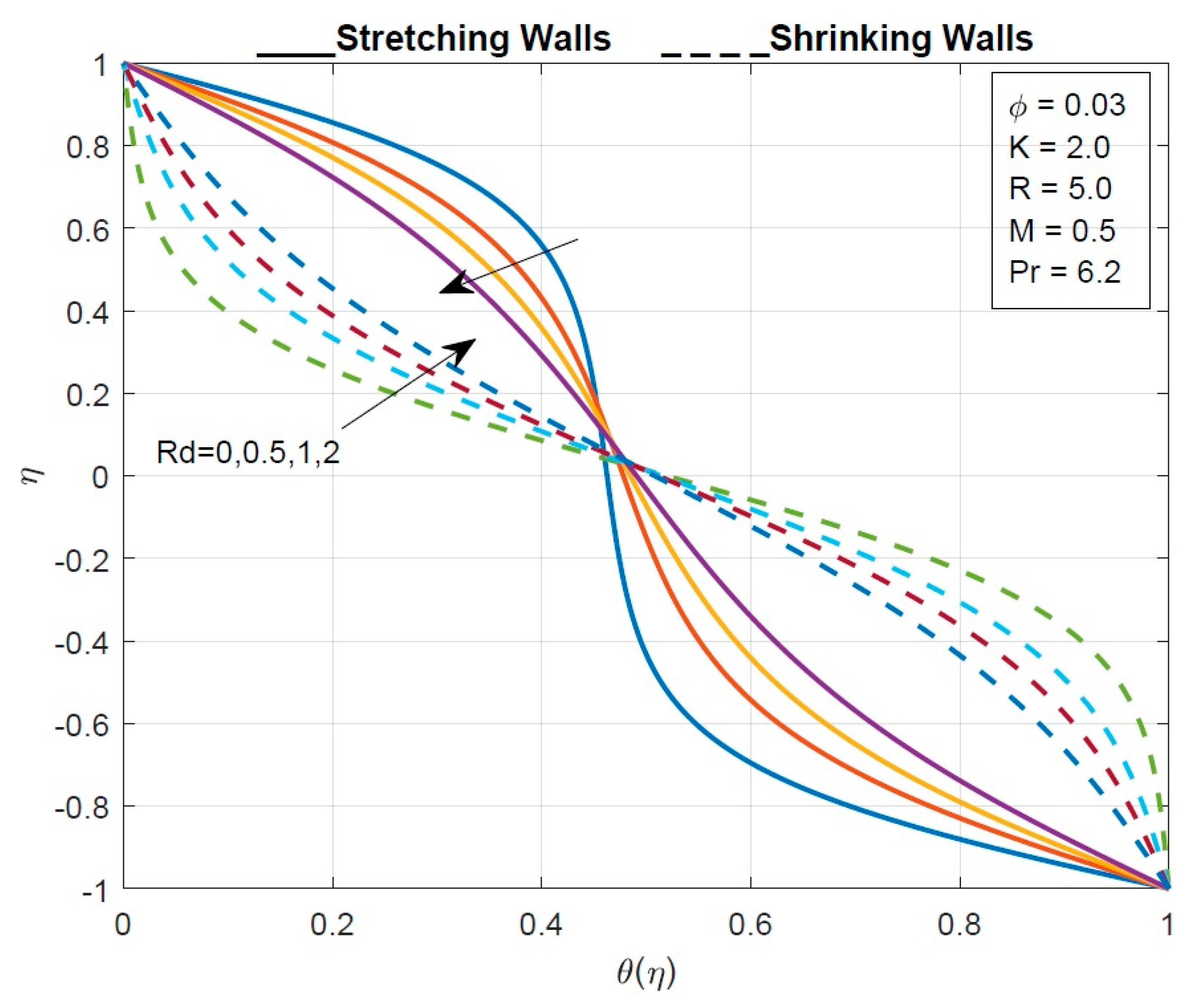
- As the radiation parameter increases, the temperature profile decreases from the lower wall to the middle and increases from the centre to the upper wall of the tube.
- The velocity profile declines as a solid volume fraction enhances for the stretching walls and increases for the shrinking walls.
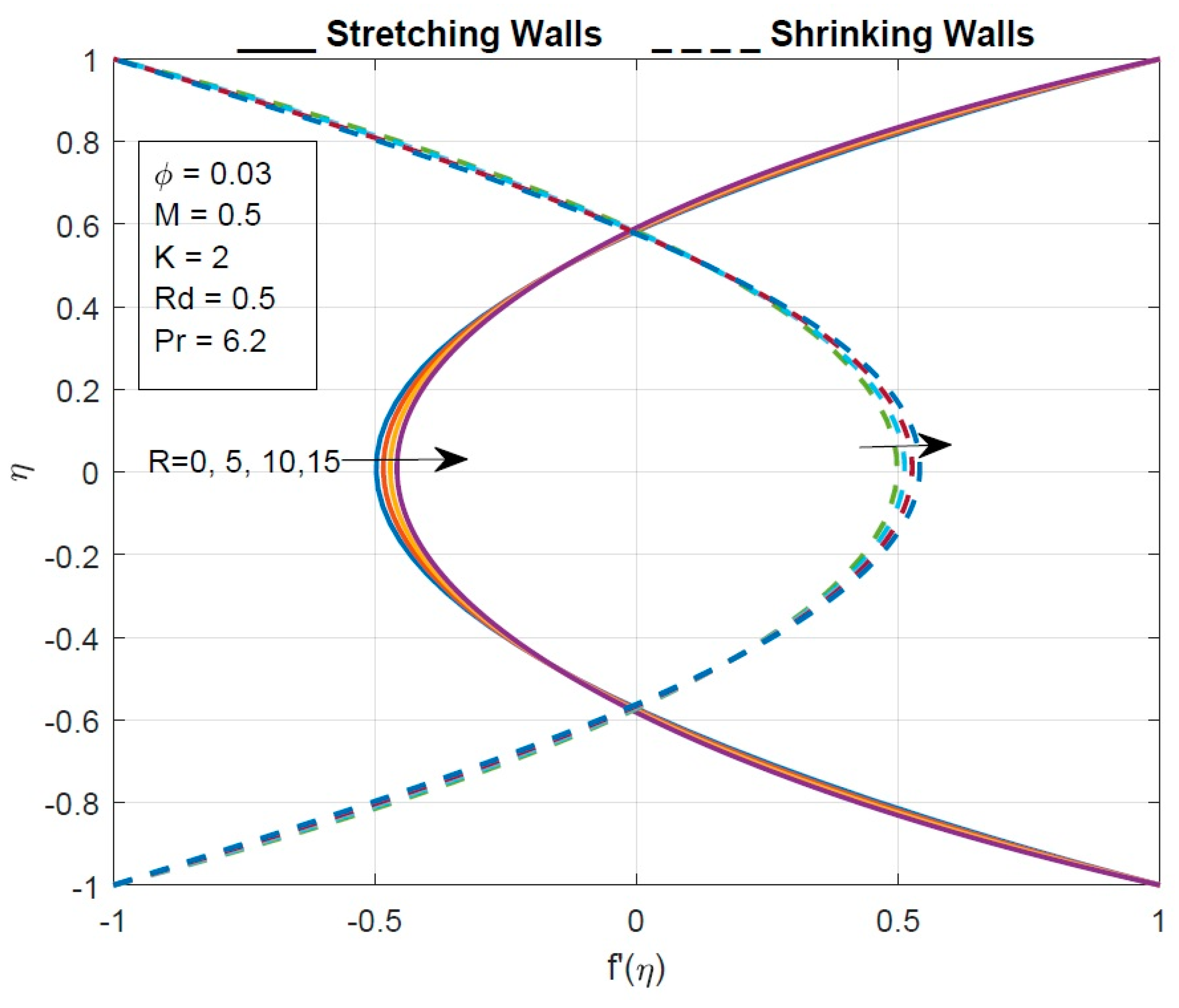
- The skin friction coefficient increases as the magnetic and Reynolds number are increased.
- The Nusselt number is increased when the solid volume fraction is lower.
- The sensitivity of to the Reynolds number and magnetic parameter is positive and negative for the micropolar parameter.
- is optimized by taking higher values of the Reynolds number and lower values of the radiation parameter.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar elasticity. In Microcontinuum Field Theories; Springer: New York, NY, USA, 1999; pp. 101–248. [Google Scholar]
- Mohammadein, A.A.; Gorla, R.S.R. Effects of transverse magnetic field on mixed convection in a micropolar fluid on a horizontal plate with vectored mass transfer. Acta Mech. 1996, 118, 1–12. [Google Scholar] [CrossRef]
- Peddieson, J. Boundary Layer Theory for a Micropolar Fluid. 1970. Available online: web (accessed on 1 January 2023).
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Gupta, A.S. Hydromagnetic flow and heat transfer over a stretching sheet. Q. Appl. Math. 1979, 37, 73–78. [Google Scholar] [CrossRef]
- Incropera, F.P.; Bergman, T.L.; Lavine, A.S.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Springer: New York, NY, USA, 2011. [Google Scholar]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 8th ed.; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Cengel, Y.A. Heat Transfer: A Practical Approach, 2nd ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Zhao, N.; Li, S.; Yang, J. A review on nanofluids: Data-driven modeling of thermalphysical properties and the application in automotive radiator. Renew Sustain. Energy Rev. 2016, 66, 596–616. [Google Scholar] [CrossRef]
- Krishna, V.M.; Kumar, M.S. Numerical analysis of forced convective heat transfer of nanofluids in microchannel for cooling electronic equipment. Mater. Today Proc. 2019, 17, 295–302. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Okwose, C.F.; Abid, M.; Ratlamwala, T.A.H. Second-law analysis and exergoeconomics optimization of a solar tower—Driven combined-cycle power plant using supercritical CO2. J. Energy Eng. ASCE 2018, 144, 04018021. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Abid, M.; Ratlamwala, T.A.H. Numerical analysis of heat transfer enhancement in a parabolic trough collector based on geometry modifications and working fluid usage. J. Sol. Energy Eng. 2018, 140, 0510091. [Google Scholar] [CrossRef]
- Meseguer, J.; Pérez-Grande, I.; Sanz-Andrés, A. Spacecraft Thermal Control, 1st ed.; Elsevier: London, UK, 2012. [Google Scholar]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Patel, H.E. Heat transfer in nanofluids—A review heat transfer in nanofluids. Heat Transf. Eng. 2007, 27, 37–41. [Google Scholar]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Liu, L.H.; Métivier, R.; Wang, S.; Wang, H. Advanced nanohybrid materials: Surface modification and applications. J. Nanomater. 2012, 2012, 536405. [Google Scholar] [CrossRef]
- Rashid, I.; Haq, R.U.; Al-Mdallal, Q.M. Aligned magnetic field effects on water based metallic nanoparticles over a stretching sheet with PST and thermal radiation effects. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 89, 33–42. [Google Scholar] [CrossRef]
- ul Haq, R.; Aman, S. Water functionalized CuO nanoparticles filled in a partially heated trapezoidal cavity with inner heated obstacle: FEM approach. Int. J. Heat Mass Transf. 2019, 128, 401–417. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Melting heat transfer in the MHD flow of Cu–water nanofluid with viscous dissipation and Joule heating. Adv. Powder Technol. 2016, 27, 1301–1308. [Google Scholar] [CrossRef]
- Sandeep, N.; Sharma, R.P.; Ferdows, M. Enhanced heat transfer in unsteady magnetohydrodynamic nanofluid flow embedded with aluminum alloy nanoparticles. J. Mol. Liq. 2017, 234, 437–443. [Google Scholar] [CrossRef]
- Shah, F.; Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A.; Khan, W.A. Theoretical and mathematical analysis of entropy generation in fluid flow subject to aluminum and ethylene glycol nanoparticles. Comput. Methods Programs Biomed. 2019, 182, 105057. [Google Scholar] [CrossRef] [PubMed]
- Misra, J.C.; Shit, G.C.; Rath, H.J. Flow and heat transfer of a MHD viscoelastic fluid in a channel with stretching walls: Some applications to haemodynamics. Comput. Fluids 2008, 37, 1–11. [Google Scholar] [CrossRef]
- Ashraf, M.; Jameel, N.; Ali, K. MHD non-Newtonian micropolar fluid flow and heat transfer in channel with stretching walls. Appl. Math. Mech. 2013, 34, 1263–1276. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. MHD flow and heat transfer of Cu–water nanofluid in a semi porous channel with stretching walls. Int. J. Heat Mass Transf. 2016, 103, 336–340. [Google Scholar] [CrossRef]
- Reza, J.; Mebarek-Oudina, F.; Makinde, O.D. MHD slip flow of Cu-Kerosene nanofluid in a channel with stretching walls using 3-stage Lobatto IIIA formula. In Defect and Diffusion Forum; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2018; Volume 387, pp. 51–62. [Google Scholar]
- Raza, J.; Rohni, A.M.; Omar, Z. Numerical investigation of copper-water (Cu-water) nanofluid with different shapes of nanoparticles in a channel with stretching wall: Slip effects. Math. Comput. Appl. 2016, 21, 43. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Raza, J.; Khan, I. Magnetohydrodynamic flow of Cu–Fe 3 O 4/H 2 O hybrid nanofluid with effect of viscous dissipation: Dual similarity solutions. J. Therm. Anal. Calorim. 2021, 143, 915–927. [Google Scholar] [CrossRef]
- Chan, S.Q.; Aman, F.; Mansur, S. Sensitivity analysis on thermal conductivity characteristics of a water-based bionanofluid flow past a wedge surface. Math. Probl. Eng. 2018, 2018, 9410167. [Google Scholar] [CrossRef]
- Vahedi, S.M.; Pordanjani, A.H.; Raisi, A.; Chamkha, A.J. Sensitivity analysis and optimization of MHD forced convection of a Cu-water nanofluid flow past a wedge. Eur. Phys. J. Plus 2019, 134, 124. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci. Rep. 2020, 10, 19792. [Google Scholar] [CrossRef]
- Thriveni, K.; Mahanthesh, B. Significance of variable fluid properties on hybrid nanoliquid flow in a micro-annulus with quadratic convection and quadratic thermal radiation: Response surface methodology. Int. Commun. Heat Mass Transf. 2021, 124, 105264. [Google Scholar] [CrossRef]



| Properties | Blood | Copper |
|---|---|---|
| 1150 | 8933 | |
| 0.53 | 401 | |
| 3617 | 385 |
| Parameters | Symbols | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| A | −5 | 2 | 5 | |
| B | 0 | 1 | 1.5 | |
| C | 0.1 | 1 | 2 | |
| Parameters | Symbols | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| A | −5 | 2 | 5 | |
| B | 0 | 0.05 | 0.2 | |
| C | 0.1 | 1 | 2 | |
| Runs | Coded Values | ||||
|---|---|---|---|---|---|
| A | B | C | |||
| 1 | −1 | −1 | −1 | 2.569977654 | 0.039218876 |
| 2 | 1 | −1 | −1 | 3.4412049 | 1.706219612 |
| 3 | −1 | 1 | −1 | 2.931369225 | 0.182650354 |
| 4 | 1 | 1 | −1 | 3.797708428 | 0.975161305 |
| 5 | −1 | −1 | 1 | 2.808665994 | 0.256515544 |
| 6 | 1 | −1 | 1 | 3.173524221 | 0.828662877 |
| 7 | −1 | 1 | 1 | 2.954689881 | 0.315102036 |
| 8 | 1 | 1 | 1 | 3.315963627 | 0.717271607 |
| 9 | −1 | 0 | 0 | 2.832551727 | 0.185583893 |
| 10 | 1 | 0 | 0 | 3.347006534 | 0.981815599 |
| 11 | 0 | −1 | 0 | 3.092057592 | 0.701100814 |
| 12 | 0 | 1 | 0 | 3.302840544 | 0.617231054 |
| 13 | 0 | 0 | −1 | 3.340485946 | 0.860674809 |
| 14 | 0 | 0 | 1 | 3.124384046 | 0.614658362 |
| 15 | 0 | 0 | 0 | 3.187362637 | 0.679561304 |
| 16 | 0 | 0 | 0 | 3.187362637 | 0.679561304 |
| 17 | 0 | 0 | 0 | 3.187362637 | 0.679561304 |
| 18 | 0 | 0 | 0 | 3.187362637 | 0.679561304 |
| 19 | 0 | 0 | 0 | 3.187362637 | 0.679561304 |
| 20 | 0 | 0 | 0 | 3.187362637 | 0.679561304 |
| Source | DF | Adjusted Sum of Square | Adjusted Mean Square | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|
| Model | 9 | 1.27499 | 0.141666 | 211.26 | 0.000 | Significant |
| Linear | 3 | 1.05111 | 0.350369 | 522.48 | 0.000 | Significant |
| R | 1 | 0.87703 | 0.877027 | 1307.85 | 0.000 | Significant |
| M | 1 | 0.14695 | 0.146950 | 219.14 | 0.000 | Significant |
| K | 1 | 0.03201 | 0.032010 | 47.73 | 0.000 | Significant |
| Square | 3 | 0.03435 | 0.011451 | 17.08 | 0.000 | Significant |
| R.R | 1 | 0.00055 | 0.000546 | 0.81 | 0.388 | Not Significant |
| M.M | 1 | 0.00474 | 0.004738 | 7.07 | 0.024 | Significant |
| K.K | 1 | 0.00509 | 0.005093 | 7.59 | 0.020 | Significant |
| 2-Way Interaction | 3 | 0.15276 | 0.050919 | 75.93 | 0.000 | Significant |
| R.M | 1 | 0.00036 | 0.000362 | 0.54 | 0.480 | Not Significant |
| R.K | 1 | 0.12739 | 0.127394 | 189.97 | 0.000 | Significant |
| M.K | 1 | 0.02220 | 0.022204 | 33.11 | 0.000 | Significant |
| Error | 10 | 0.00671 | 0.000671 | |||
| Lack-of-Fit | 5 | 0.00671 | 0.001341 | * | * | |
| Pure Error | 5 | 0.00000 | 0.000000 | |||
| Total | 19 | 1.28170 | ||||
| 99.48% | 99.01% | |||||
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|
| Model | 9 | 2.39452 | 0.26606 | 26.11 | 0.000 | Significant |
| Linear | 3 | 1.76127 | 0.58709 | 57.62 | 0.000 | Significant |
| R | 1 | 1.65970 | 1.65970 | 162.90 | 0.000 | Significant |
| Phi | 1 | 0.03905 | 0.03905 | 3.83 | 0.079 | Not Significant |
| Rd | 1 | 0.06770 | 0.06770 | 6.64 | 0.028 | Significant |
| Square | 3 | 0.09999 | 0.03333 | 3.27 | 0.067 | Not Significant |
| R.R | 1 | 0.01970 | 0.01970 | 1.93 | 0.194 | Not Significant |
| Phi.Phi | 1 | 0.00191 | 0.00191 | 0.19 | 0.674 | Not Significant |
| Rd.Rd | 1 | 0.00982 | 0.00982 | 0.96 | 0.349 | Not Significant |
| 2-Way Interaction | 3 | 0.41288 | 0.13763 | 13.51 | 0.001 | Significant |
| R.Phi | 1 | 0.11203 | 0.11203 | 11.00 | 0.008 | Not Significant |
| R.Rd | 1 | 0.26292 | 0.26292 | 25.81 | 0.000 | Significant |
| Phi.Rd | 1 | 0.02855 | 0.02855 | 2.80 | 0.125 | Not Significant |
| Error | 10 | 0.10188 | 0.01019 | |||
| Lack-of-Fit | 5 | 0.10188 | 0.02038 | * | * | |
| Pure Error | 5 | 0.00000 | 0.00000 | |||
| Total | 19 | 2.49640 | ||||
| 95.92% | 92.25% | |||||
| A | B | C | Sensitivity to A | Sensitivity to B | Sensitivity to C |
|---|---|---|---|---|---|
| 0 | −1 | −1 | 0.11431 | 0.0171 | −0.1283 |
| 0 | −1 | 0 | 0.08816 | −0.056 | −0.0325 |
| 0 | −1 | 1 | 0.06201 | −0.1291 | 0.0633 |
| 0 | 0 | −1 | 0.11431 | 0.1857 | −0.2014 |
| 0 | 0 | 0 | 0.08816 | 0.1126 | −0.1056 |
| 0 | 0 | 1 | 0.06201 | 0.0395 | −0.0098 |
| 0 | 1 | −1 | 0.11431 | 0.3543 | −0.2745 |
| 0 | 1 | 0 | 0.08816 | 0.2812 | −0.1787 |
| 0 | 1 | 1 | 0.06201 | 0.2081 | −0.0829 |
| A | B | C | Sensitivity to A | Sensitivity to B | Sensitivity to C |
|---|---|---|---|---|---|
| −1 | 0 | −1 | 0.18169 | 0 | −0.25041 |
| −1 | 0 | 0 | 0.1441 | 0 | −0.25041 |
| −1 | 0 | 1 | 0.10651 | 0 | −0.25041 |
| 0 | 0 | −1 | 0.18169 | 0 | −0.288 |
| 0 | 0 | 0 | 0.1441 | 0 | −0.288 |
| 0 | 0 | 1 | 0.10651 | 0 | −0.288 |
| 1 | 0 | −1 | 0.18169 | 0 | −0.32559 |
| 1 | 0 | 0 | 0.1441 | 0 | −0.32559 |
| 1 | 0 | 1 | 0.10651 | 0 | −0.32559 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alahmadi, R.A.; Raza, J.; Mushtaq, T.; Abdelmohsen, S.A.M.; R. Gorji, M.; Hassan, A.M. Optimization of MHD Flow of Radiative Micropolar Nanofluid in a Channel by RSM: Sensitivity Analysis. Mathematics 2023, 11, 939. https://doi.org/10.3390/math11040939
Alahmadi RA, Raza J, Mushtaq T, Abdelmohsen SAM, R. Gorji M, Hassan AM. Optimization of MHD Flow of Radiative Micropolar Nanofluid in a Channel by RSM: Sensitivity Analysis. Mathematics. 2023; 11(4):939. https://doi.org/10.3390/math11040939
Chicago/Turabian StyleAlahmadi, Reham A., Jawad Raza, Tahir Mushtaq, Shaimaa A. M. Abdelmohsen, Mohammad R. Gorji, and Ahmed M. Hassan. 2023. "Optimization of MHD Flow of Radiative Micropolar Nanofluid in a Channel by RSM: Sensitivity Analysis" Mathematics 11, no. 4: 939. https://doi.org/10.3390/math11040939
APA StyleAlahmadi, R. A., Raza, J., Mushtaq, T., Abdelmohsen, S. A. M., R. Gorji, M., & Hassan, A. M. (2023). Optimization of MHD Flow of Radiative Micropolar Nanofluid in a Channel by RSM: Sensitivity Analysis. Mathematics, 11(4), 939. https://doi.org/10.3390/math11040939






