Abstract
The delay differential equations are of great importance in real-life phenomena. A special type of these equations is the Pantograph delay differential equation. Generally, solving a delay differential equation is a challenge, especially when the complexity of the delay terms increases. In this paper, the homotopy perturbation method is proposed to solve the Pantograph delay differential equation via two different canonical forms; thus, two types of closed-form solutions are determined. The first gives the standard power series solution while the second introduces the exponential function solution. It is declared that the current solution agrees with the corresponding ones in the literature in special cases. In addition, the properties of the solution are provided. Furthermore, the results are numerically validated through performing several comparisons with the available exact solutions. Moreover, the calculated residuals tend to zero, even in a huge domain, which reflects the high accuracy of the current analysis. The obtained results reveal the effectiveness and efficiency of the current analysis which can be further extended to other types of delay equations.
Keywords:
pantograph equation; delay equation; homotopy perturbation method; series solution; exact solution MSC:
34k06
1. Introduction
The pantograph is a particular device which collects the current in electric trains. The pantograph problem has been extensively studied in the literature. Andrews [1] calculated the behavior of an overhead catenary system for railway electrification. Abbott [2] introduced a numerical method for calculating the dynamic behavior of a trolley wire overhead contact system for electric railways. The Pantograph motion on a nearly uniform railway overhead line and system has been discussed in [3,4,5], respectively. The Pantograph’s model has been investigated by Kato and McLeod [6], Iserles [7], Derfel and Iserles [8], Patade and Bhalekar [9], Fox et al. [10], and recently by Alenazy et al. [11]. However, this problem still has undiscovered properties as will be declared in this paper. Although a considerable amount of real-world problems were modeled by means of ordinary differential equations (ODEs), it is observed that such ODEs cannot model the actual behavior of natural systems. This is because the ordinary derivative is a local operator which cannot be used to model the memory/hereditary properties in real-life phenomena. Hence, physical phenomena can be accurately modeled by incorporating nonlocal components such as delays. Obtaining an exact/approximate solution of an ODE is regularly easier in contrast with a delay differential equation (DDE). As simple examples, it is easy to find the exact solution of the ODE by any of the standard methods while finding solutions for the very simple DDEs , , is not an easy task. Actually, there are no standard methods for solving DDEs and, accordingly, the DDEs are difficult to solve when compared with ODEs. Despite the excellency of the obtained results in the literature for the pantograph delay differential equation (PDDE) [6]:
the authors believe that the PDDE (1) still needs an effort to determine its exact solution for all possible real values of parameters , and . As a special case, Equation (1) reduces to the standard Ambartsumian delay differential equation (ADDE) when and () which has been used for describing the theory of surface brightness in the Milky Way [12]. The ADDE has been investigated in the literature using different methodologies such as the Taylor series [13] and the exponential function solution [14,15,16]. It was also generalized using different approaches by Khaled et al. [17] and Kumar et al. [18]. Moreover, Ebaid and Al-Jeaid [19] obtained the exact periodic solution for Equation (1) for the special case such that . In addition, they determined the exact solution when and . The purpose of this paper is to obtain the closed-form solution of the PDDE for arbitrary values of the proportional delay parameter c.
In order to contribute to an improved series solution of the PDDE (1), it may be reasonable to implement the Adomian decomposition method (ADM) [20] which was effectively applied on BVPs [21], Fisher’s equation [22], delay-type equation [23], nonlinear equations [24,25] with the bibliography [26], and Kepler’s equation [27]. However, the ADM needs to calculate what is called the Adomian’s polynomials.
On the other hand, the homotopy perturbation method (HPM) is a relatively recent method, see [28,29,30,31,32,33,34]. It will be shown that the HPM is an effective tool to deal with the current PDDE through utilizing two different canonical forms. The first provides the standard power series solution (PSS) while the second gives the exponential function solution (EFS). In addition, it will be declared that the current PSS agrees with the corresponding PSS in [10] when and also agrees with the EFS in [15,16] when , () for the ADDE. Furthermore, the properties of the EFS, in terms of exponential functions, will be provided. Moreover, several comparisons between the EFS and the available exact ones in the literature are to be performed and, accordingly, the advantages of the present analysis over those in previously published papers will be demonstrated.
The paper has the following structure. In Section 2, the PSS is derived, where the existing results in the literature are obtained for particular cases. Section 3 focuses on evaluating the EFS while its characteristics are discussed in Section 4. Section 5 applies the quantum calculus notations on a general-component formula. Section 6 is devoted to analyze and discuss the results which are concluded in Section 7.
2. The first Canonical Form: PSS
In order to apply the HPM on the PDDE (1), we first rewrite Equation (1) in the following canonical form:
where is an embedding parameter which is used to construct the homotopy series solution:
On substituting Equation (3) into Equation (2), we have
or
i.e.,
Equation (6) leads to the following systems of initial value problems (IVPs):
and
The solution of Equation (7) is given by
From Equation (8), the -order component can be obtained as
Since , then
Utilizing Equation (11), we obtain
The HPM gives the solution as by
At , the solution (17) becomes
which is the same closed-form series solution obtained by Fox et al. [10]. In addition, if and , then the PDDE (1) becomes the ADDE:
Substituting and into Equation (17) gives
i.e.,
which is the same solution obtained in [15,16].
3. The Second Canonical Form: EPS
In this section, we start with transforming Equation (1) into the following equivalent integral equation:
The canonical form of the HPM, in this case, is of the form:
Inserting Equation (3) into Equation (23) yields
or
which gives the recurrence scheme:
For , we obtain
where . Evaluating the last integral gives
Similarly, at and , we can get
and
From above, the calculation of the first few components of the homotopy series is indicated, however, the components of higher-order can be easily derived via any software. It will be shown later in a subsequent section that it is possible to derive a unified formula for the -component , . To do so, at first, we have to list the main characteristics of the preceding components , , and . These characteristics are investigated in the next section and, hence, a unified formula for will be possible.
4. Characteristics of the Components and a Unified Formula for
4.1. Characteristics of the Components
From the expressions for the components , , and , it can be noticed that
- involves two terms and can be written aswhere
- consists of three terms in the form:where
- contains four terms and we can writewhere
- Similarly, can be evaluated from (26) and is given bywhere
- In view of (31), (34), (38), and (44), takes the form . Moreover, the initial component where . Based on the above characteristics, unified formulas for the coefficients and, hence, the -order component will be determined. This is the issue of the next section.
4.2. Unified Formula for
Theorem 1.
The general component of the homotopy series is given by
where
Proof.
From the previous section, the coefficients , , , and can be written as
It is noticed from (51) and (52) that the numerators and denominators of these coefficients follow the rules and , respectively, . It can also be checked that the other higher-order coefficients () follow the same patterns. Hence, a unified formula for may be given as
Similarly, the coefficients , , , and can be written as
and, thus,
For , we observe that satisfies
and, accordingly, we have
At , Formula (60) reduces to Formula (53). In addition, when , Formula (60) gives Formula (56). In addition, for , we have from (60) that which leads to the initial component (from Equation (49)). This means that (60) is valid as a unified formula for the coefficients , which completes the proof. □
5. Closed-Form Solution via Quantum Calculus
The objective of this section is to obtain a closed- form solution by means of some properties in the quantum calculus [35]. We start with the product:
where denotes the Pochhammer symbol. For , we have
Using the above property, we are able to construct the closed-form solution of Equation (1) by means of quantum calculus notations as addressed in the theorem below.
Theorem 2.
The solution of the PDDE (1) is given by
Proof.
Let us start the proof by rewriting the general component , from Theorem 1, in the form:
The products in the denominator of (64) can be written in view of quantum calculus notations as
Substituting (65) into (64) and simplifying, then
The homotopy series solution is given in terms of the auxiliary parameter p as
and, hence, the solution can be obtained by letting . Thus,
From (66) and (68), we obtain
i.e.,
which completes the proofs. □
6. Discussion
In previous sections, two types of closed-form solutions were established. In this discussion, the behaviors of the two types of solutions, mainly the PSS and the EFS, are explored. Before launching, it is better to mention that the PSS in Equation (17) reduces to several forms of exact solutions at , as pointed out in [19]. In this case, the PDDE (1) becomes
For , the exact solution of Equation (71) reads [20]
For , the periodic solution of Equation (71) was obtained in the form [19]:
The r-term approximation of the EFS solution is given from Equation (70) as
At the special case , the approximations can be obtained by taking the limit of Equation (74) as :
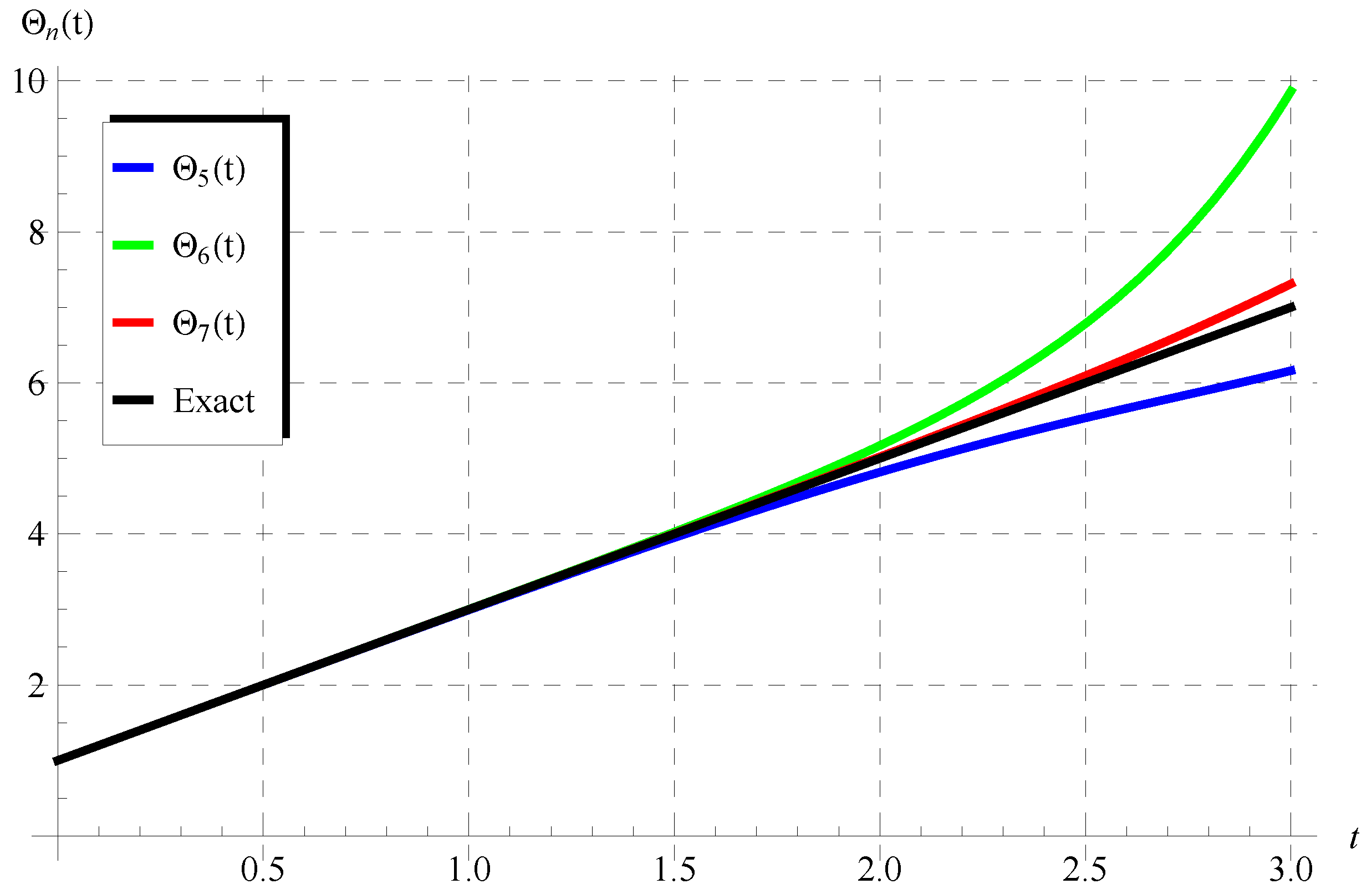
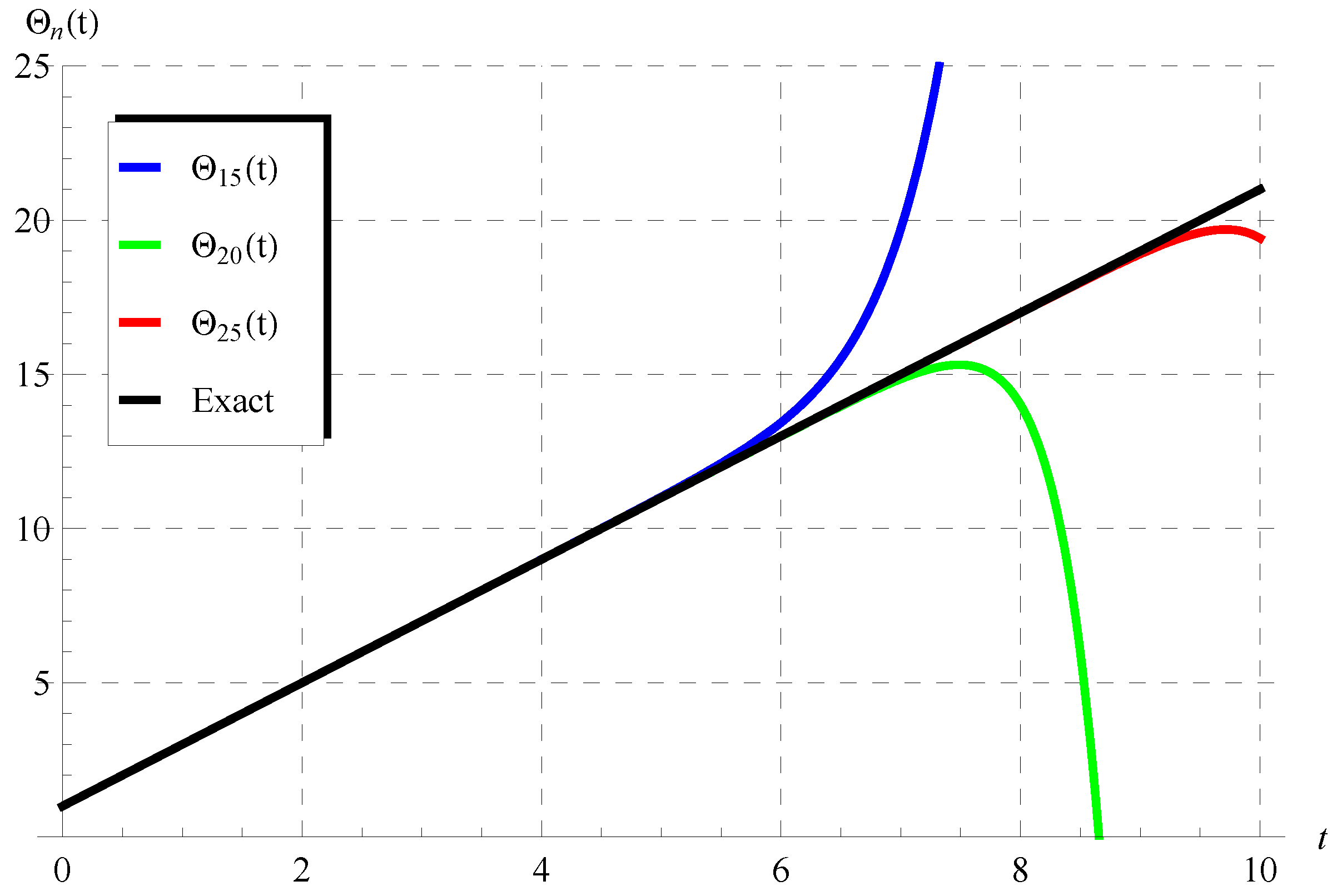
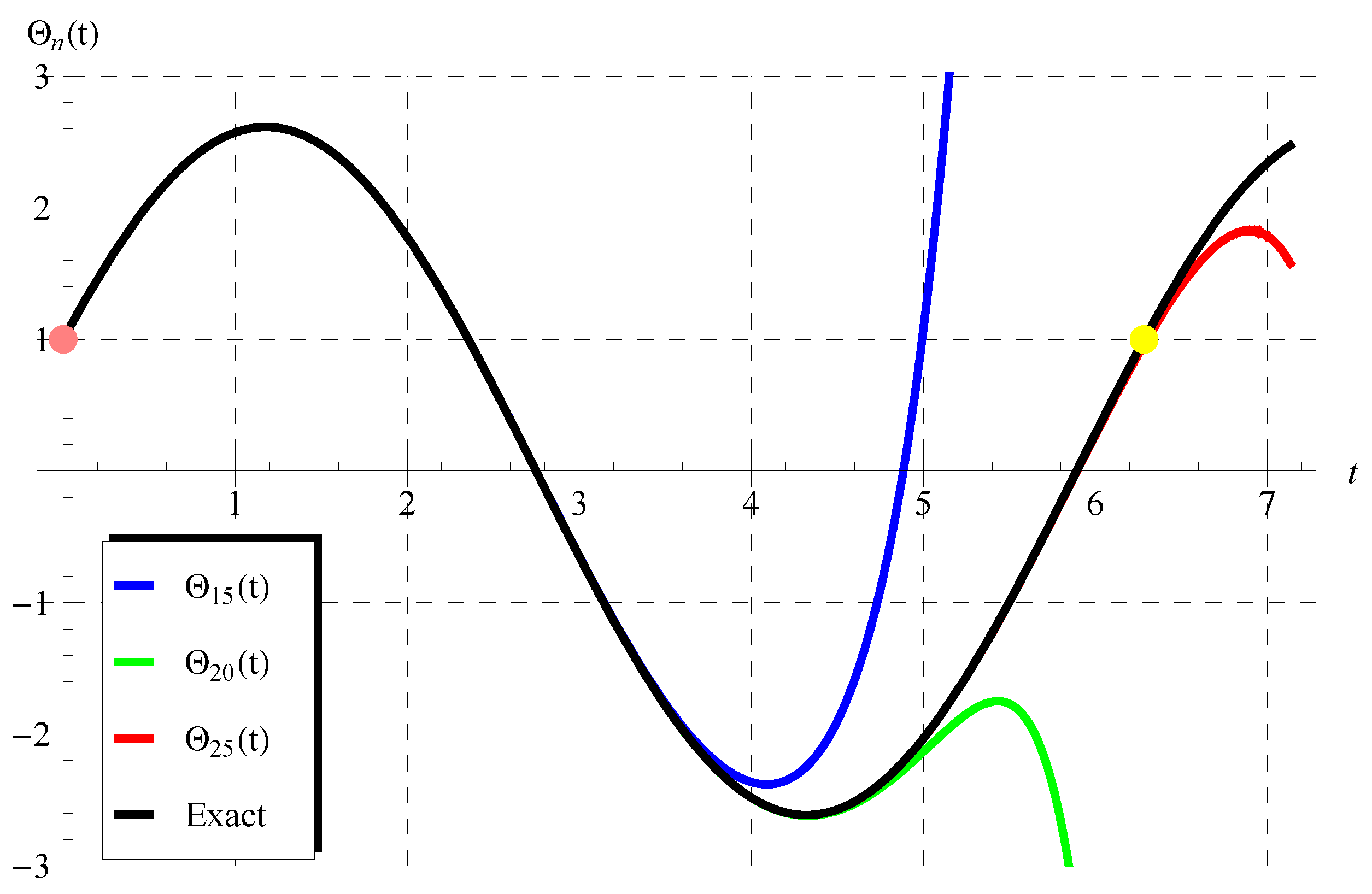
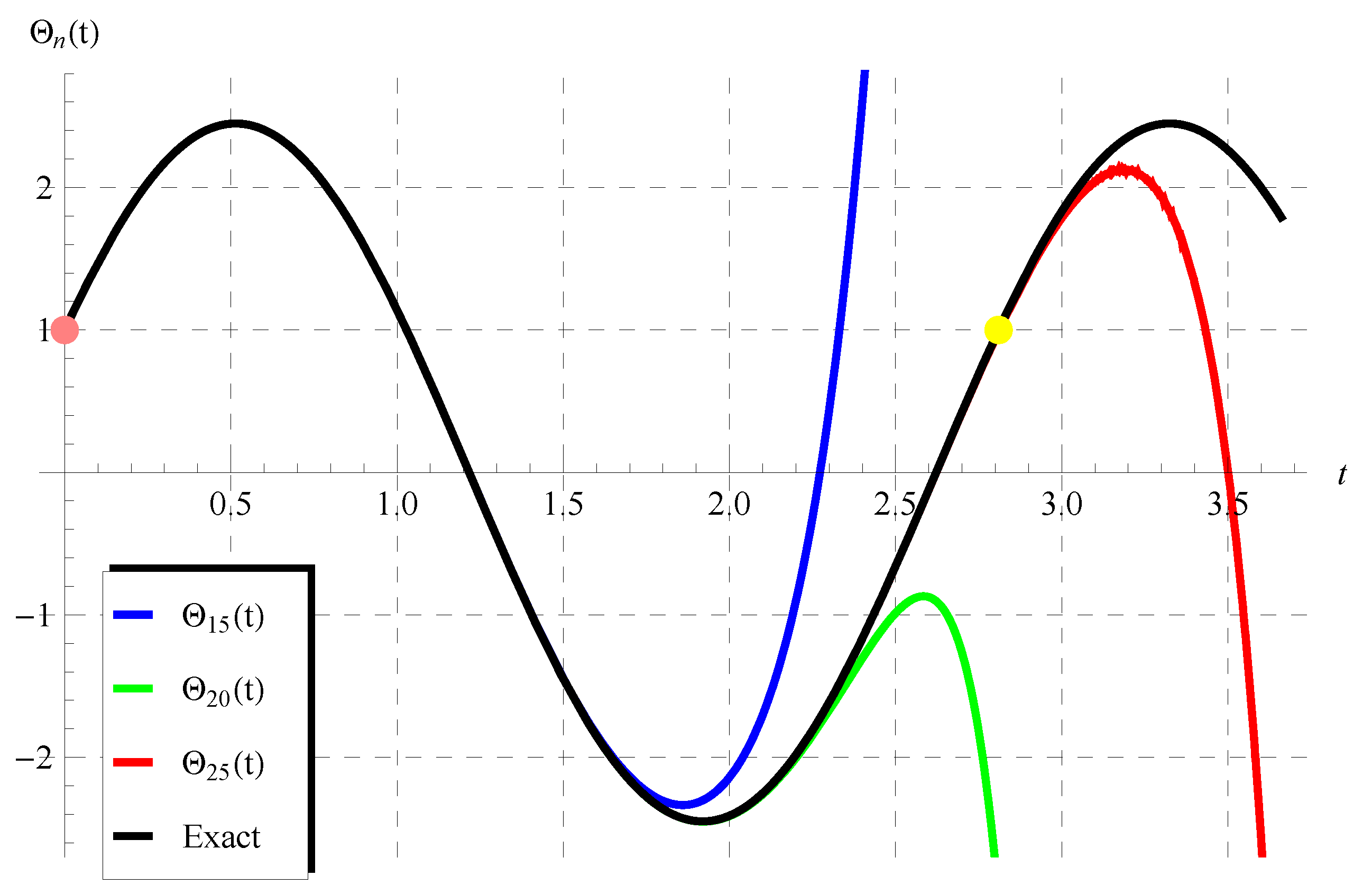
So, we focus in the first part of this discussion on performing comparisons between the approximations in Equation (75) and the exact solutions given by Equation (72) () and Equation (73) (). Figure 1 and Figure 2 show the comparisons between the approximations , , (Figure 1) and the approximations , , (Figure 2) with the exact solution (72) when , . It is seen from these figures that the domain of coincidence between the approximations and the exact solution increases as the number of terms r increases. Additional comparisons are depicted in Figure 3 and Figure 4 between the approximations , , and the periodic solution (73) when , , (Figure 3) and , , (Figure 4). It is also observed from these figures that is in full agreement with the exact periodic solution (73) for a complete period indicated by the points in pink and yellow. For , the accuracy of the approximations is validated through calculating the residuals defined by
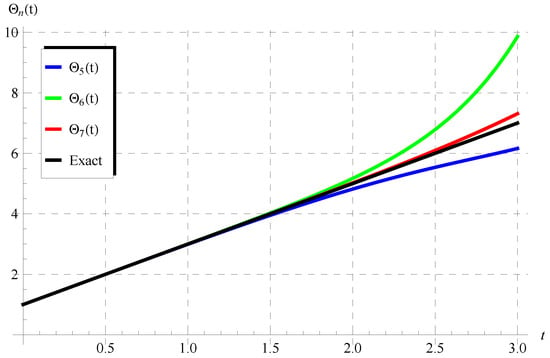
Figure 1.
Comparisons between the approximate solutions in Equation (75) and the exact solution (72) at , ().
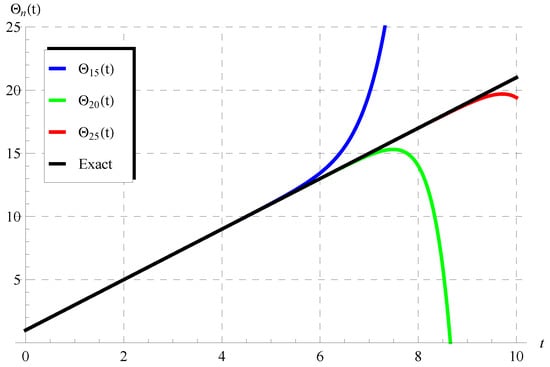
Figure 2.
Comparisons between the approximate solutions in Equation (75) and the exact solution (72) at , ().
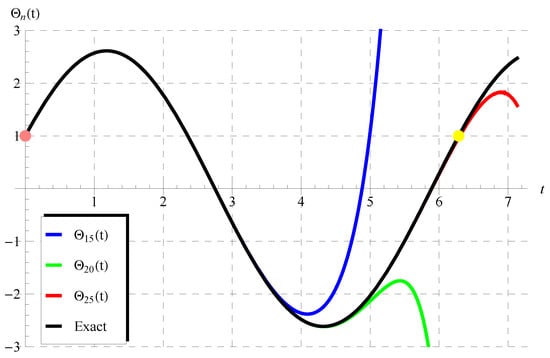
Figure 3.
Comparisons between the approximate solutions in Equation (75) and the exact periodic solution (73) at , , ().
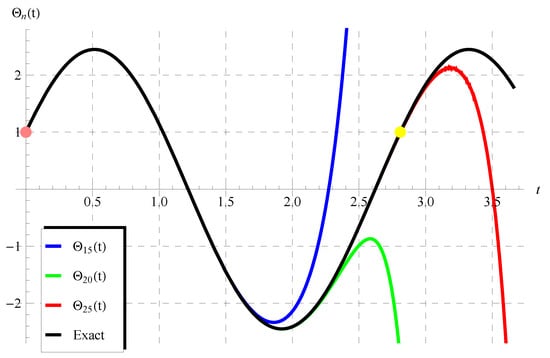
Figure 4.
Comparisons between the approximate solutions in Equation (75) and the exact periodic solution (73) at , , ().
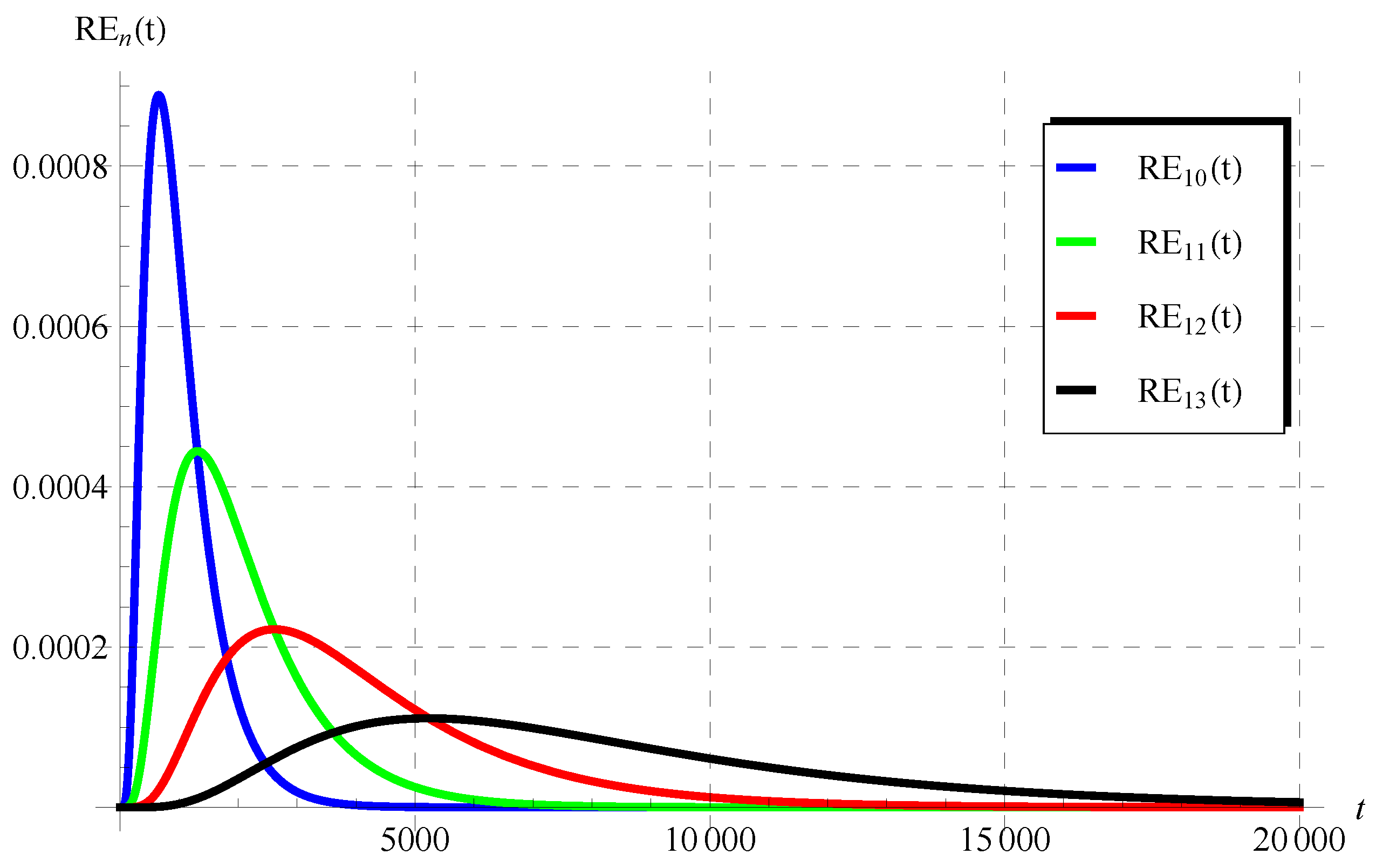
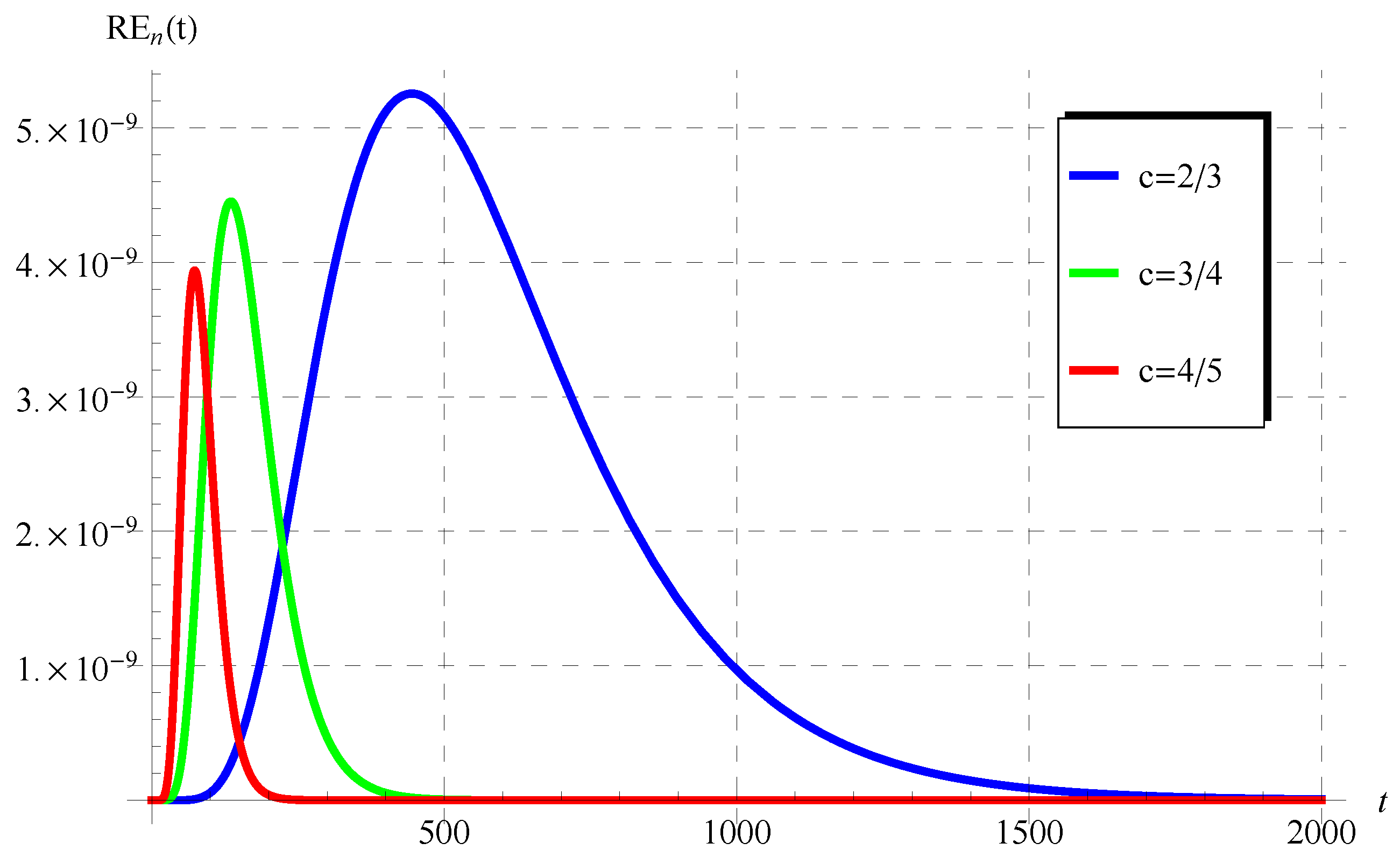
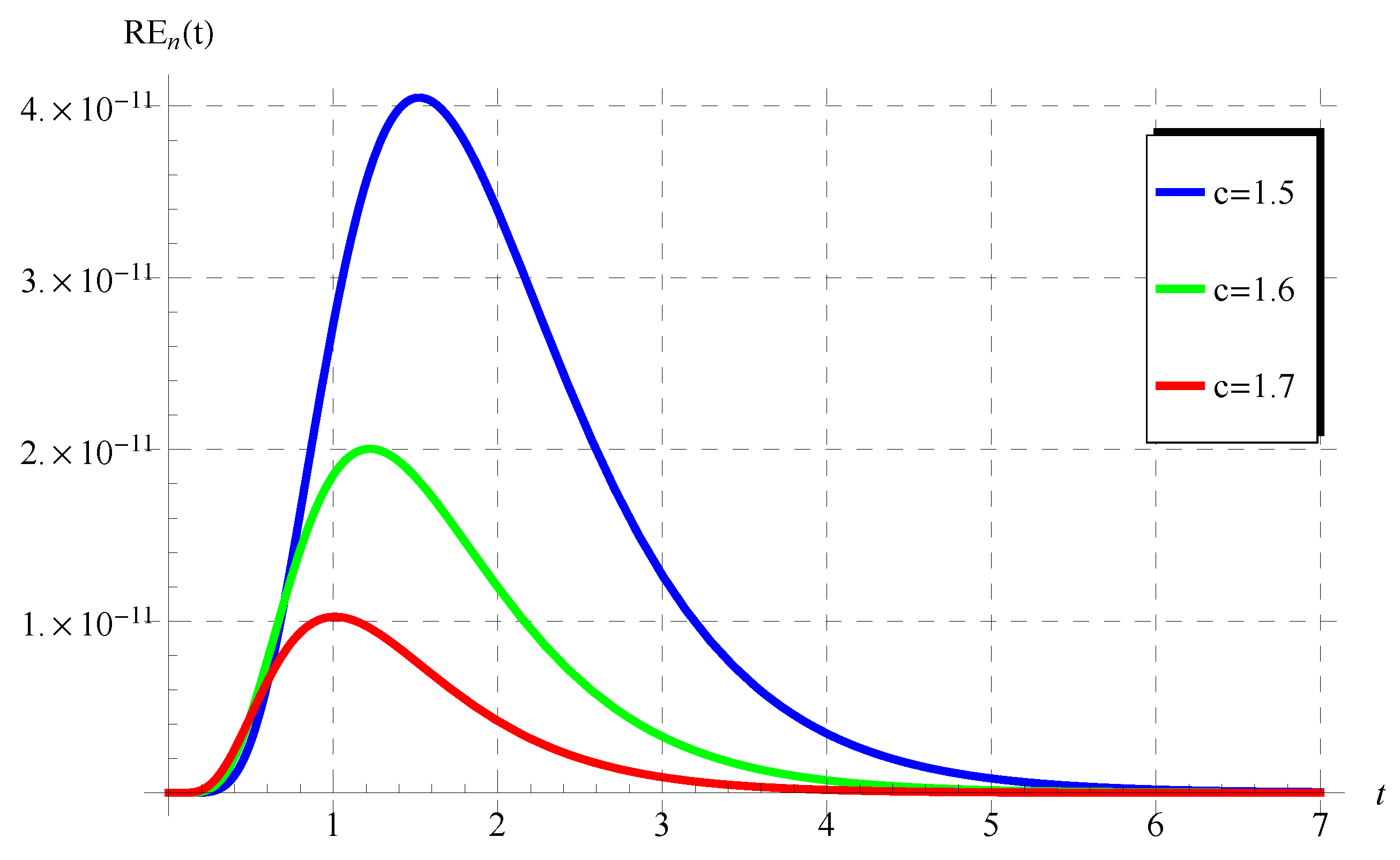
The numerical results in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 for the obtained residuals reveal the high accuracy of the present analysis, even in a huge domain.
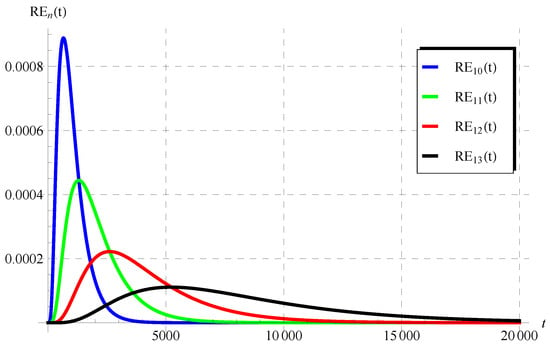
Figure 5.
The residuals in Equation (76) at , , , and .
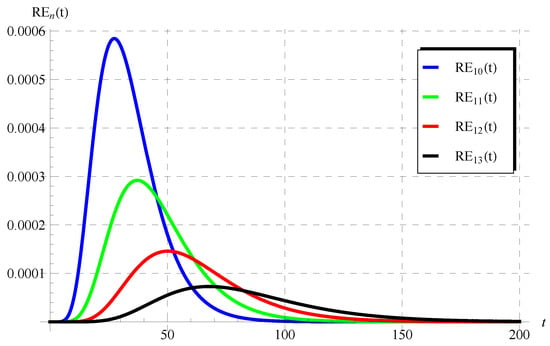
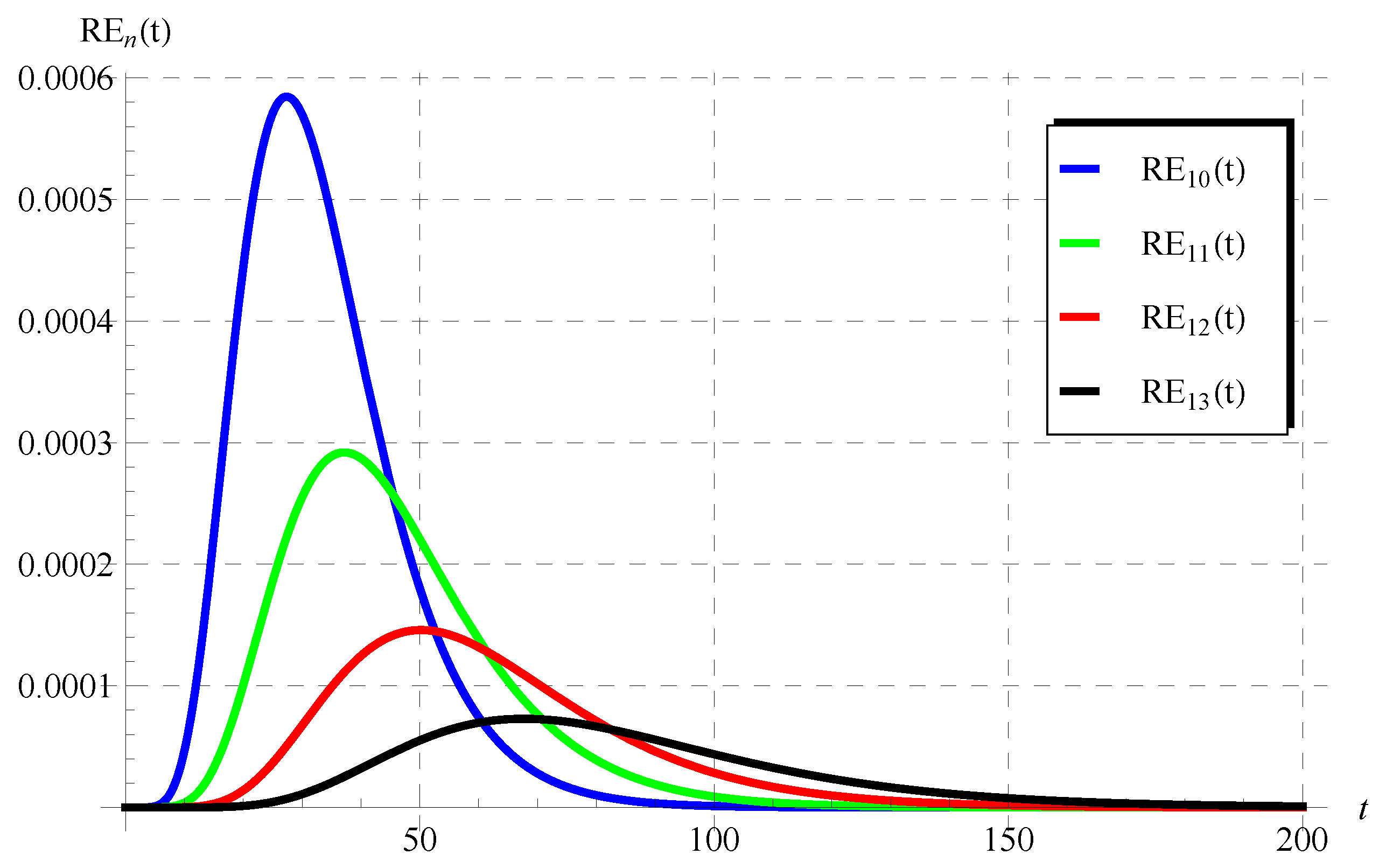
Figure 6.
The residuals in Equation (76) at , , , and .
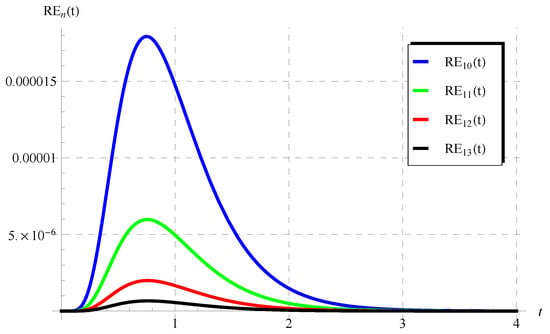
Figure 7.
The residuals in Equation (76) at , , , and .
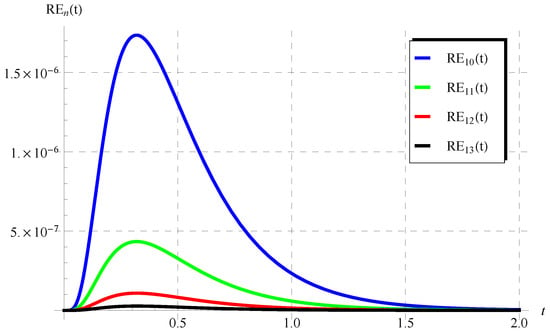
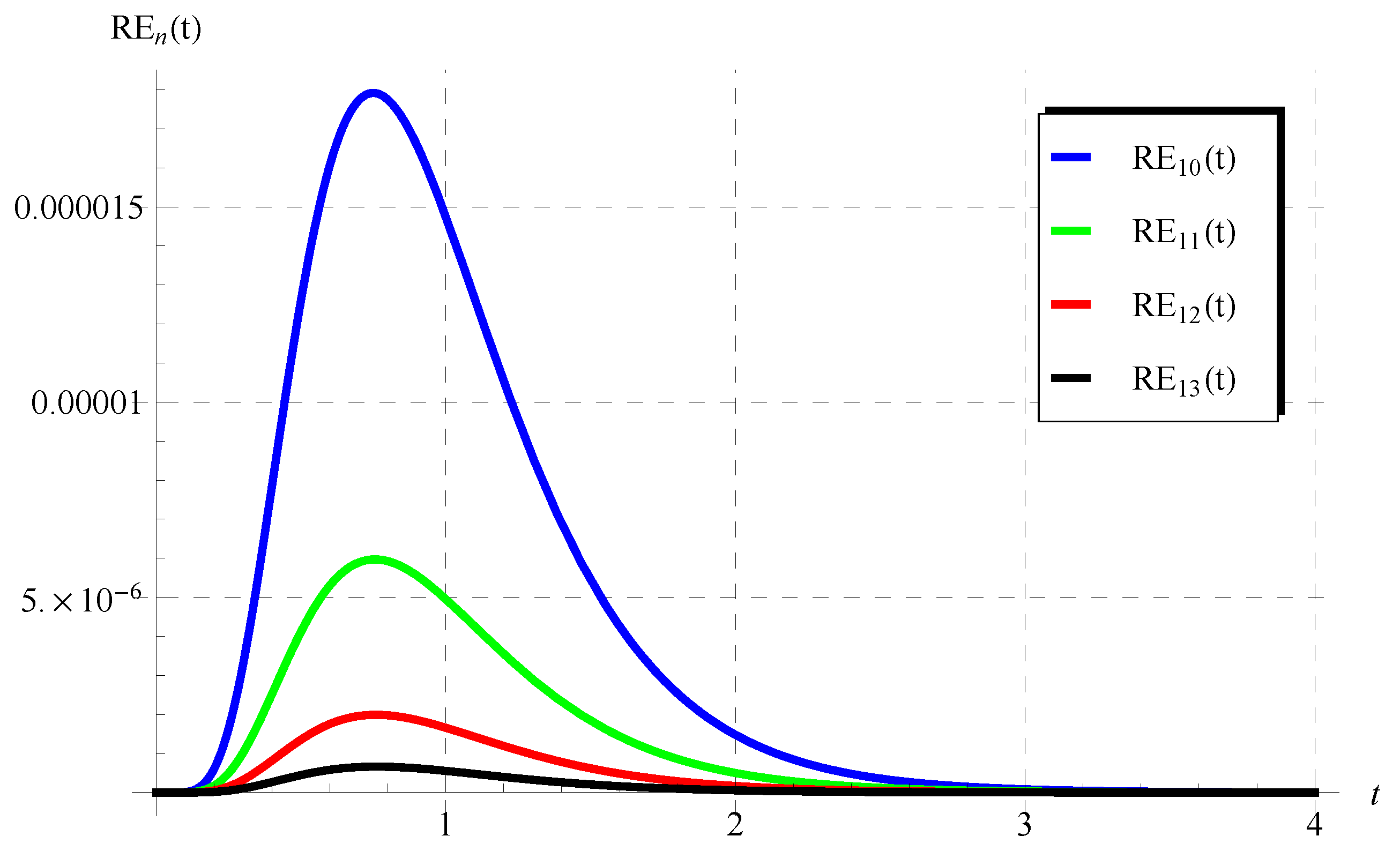
Figure 8.
The residuals in Equation (76) at , , , and .
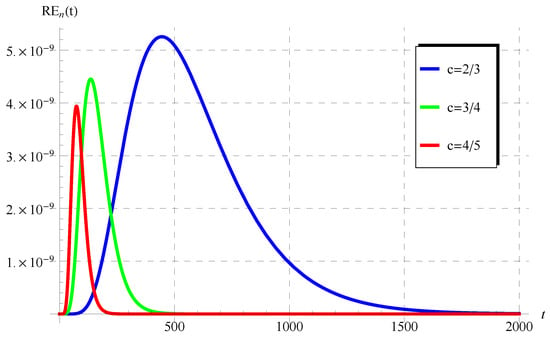
Figure 9.
The residuals in Equation (76) at various values of c () when , , and .
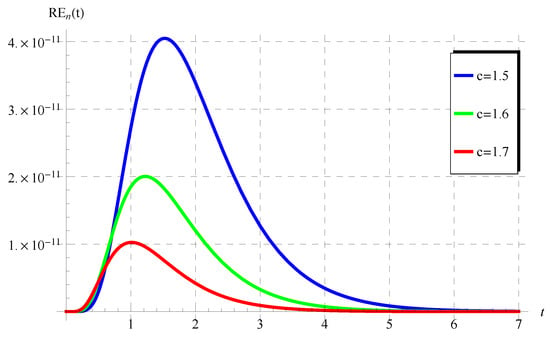
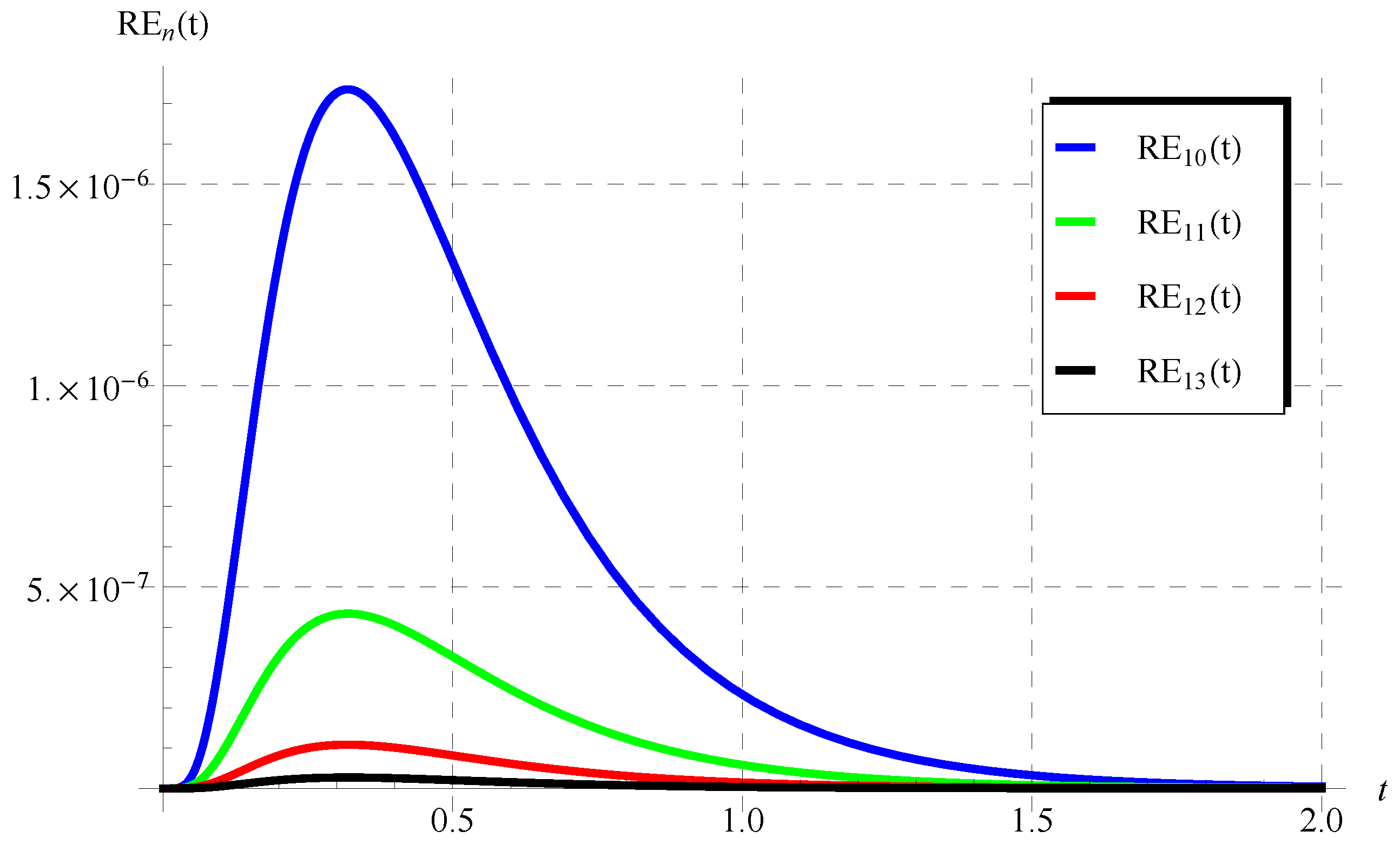
Figure 10.
The residuals in Equation (76) at various values of c () when , , and .
7. Conclusions
In this paper, the HPM is applied to solve the PDDE using two different canonical forms. Accordingly, two types of closed-form solutions, the PSS and EFS, were obtained. It was shown that the present PSS reduces to the corresponding ones in the literature [12,15] for the ADDE in special cases. A unified formula for the homotopy components was successfully obtained for the EFS. The results were numerically validated through several comparisons with the available exact solutions. The calculated residuals reflect the high accuracy of the current analysis, especially, residuals were close to zero even in a huge domain of the studied PDDE. The obtained results reveal that the current approach is effective and straightforward and can be further applied to include other DDEs of higher orders [36,37,38,39].
Author Contributions
Conceptualization, A.B.A., A.E. and H.K.A.-J.; methodology, A.B.A., N.E.K., A.E. and H.K.A.-J.; software, A.E.; validation, A.B.A., N.E.K., A.E. and H.K.A.-J.; formal analysis, A.B.A., N.E.K., A.E. and H.K.A.-J.; investigation, A.B.A., N.E.K., A.E. and H.K.A.-J.; data curation, A.E.; writing—original draft preparation, N.E.K.; writing—review and editing, N.E.K., A.E. and H.K.A.-J.; visualization, A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andrews, H.I. Third paper: Calculating the behaviour of an overhead catenary system for railway electrification. Proc. Inst. Mech. Eng. 1964, 179, 809–846. [Google Scholar] [CrossRef]
- Abbott, M.R. Numerical method for calculating the dynamic behaviour of a trolley wire overhead contact system for electric railways. Comput. J. 1970, 13, 363–368. [Google Scholar] [CrossRef]
- Gilbert, G.; Davtcs, H.E.H. Pantograph motion on a nearly uniform railway overhead line. Proc. Inst. Electr. Eng. 1966, 113, 485–492. [Google Scholar] [CrossRef]
- Caine, P.M.; Scott, P.R. Single-wire railway overhead system. Proc. Inst. Electr. Eng. 1969, 116, 1217–1221. [Google Scholar] [CrossRef]
- Ockendon, J.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1971, 322, 447–468. [Google Scholar]
- Kato, T.; McLeod, J.B. The functional-differential equation y′(x) = ay(λx) + by(x). Bull. Am. Math. Soc. 1971, 77, 891–935. [Google Scholar]
- Iserles, A. On the generalized pantograph functional-differential equation. Eur. J. Appl. Math. 1993, 4, 1–38. [Google Scholar] [CrossRef]
- Derfel, G.; Iserles, A. The pantograph equation in the complex plane. J. Math. Anal. Appl. 1997, 213, 117–132. [Google Scholar] [CrossRef]
- Patade, J.; Bhalekar, S. Analytical Solution of Pantograph Equation with Incommensurate Delay. Phys. Sci. Rev. 2017, 2. [Google Scholar] [CrossRef]
- Fox, L.; Mayers, D.; Ockendon, J.R.; Tayler, A.B. On a functional differential equation. IMA J. Appl. Math. 1971, 8, 271–307. [Google Scholar] [CrossRef]
- Alenazy, A.H.S.; Ebaid, A.; Algehyne, E.A.; Al-Jeaid, H.K. Advanced Study on the Delay Differential Equation y′(t) = ay(t) + by(ct). Mathematics 2022, 10, 4302. [Google Scholar] [CrossRef]
- Ambartsumian, V.A. On the fluctuation of the brightness of the milky way. Dokl. Akad Nauk. USSR 1994, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On Analytical Solution of Ambartsumian Equation. Natl. Acad. Sci. Lett. 2017, 40, 291–293. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Ebaid, A. New Analytic Solution for Ambartsumian Equation. J. Math. Syst. Sci. 2018, 8, 182–186. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Enazi, A.; Albalawi, B.Z.; Aljoufi, M.D. Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method. Math. Comput. Appl. 2019, 24, 7. [Google Scholar] [CrossRef]
- Khaled, S.M.; El-Zahar, E.R.; Ebaid, A. Solution of Ambartsumian delay differential equation with conformable derivative. Mathematics 2019, 7, 425. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 2018, 133, 133–259. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. On the exact solution of the functional differential equation y′(t) = ay(t) + by(−t). Adv. Differ. Equ. Control Process. 2022, 26, 39–49. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Bhalekar, S.; Patade, J. An analytical solution of fishers equation using decomposition Method. Am. J. Comput. Appl. Math. 2016, 6, 123–127. [Google Scholar]
- Diblík, J.; Kúdelcíková, M. Two classes of positive solutions of first order functional differential equations of delayed type. Nonlinear Anal. 2012, 75, 4807–4820. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to nonlinear equations. Math. Comput. Model. 1994, 20, 69–73. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G. Decomposition Methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Rach, R. A bibliography of the theory and applications of the Adomian decomposition method, 1961–2011. Kybernetes 2012, 41, 1087–1148. [Google Scholar] [CrossRef]
- Alshaery, A.; Ebaid, A. Accurate analytical periodic solution of the elliptical Kepler equation using the Adomian decomposition method. Acta Astronaut. 2017, 140, 27–33. [Google Scholar] [CrossRef]
- Ebaid, A. Remarks on the homotopy perturbation method for the peristaltic flow of Jeffrey fluid with nano-particles in an asymmetric channel. Comput. Math. Appl. 2014, 68, 77–85. [Google Scholar] [CrossRef]
- Ayati, Z.; Biazar, J. On the convergence of Homotopy perturbation method. J. Egypt. Math. Soc. 2015, 23, 424–428. [Google Scholar] [CrossRef]
- Pasha, S.A.; Nawaz, Y.; Arif, M.S. The modified homotopy perturbation method with an auxiliary term for the nonlinear oscillator with discontinuity. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1363–1373. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Bayat, M. Approximate analytical solution of nonlinear systems using homotopy perturbation method. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2016, 230, 10–17. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; De la Sen, M. A novel homotopy perturbation method with applications to nonlinear fractional order KdV and Burger equation with exponential-decay kernel. J. Funct. Spaces 2021, 2021, 8770488. [Google Scholar] [CrossRef]
- He, J.-H.; El-Dib, Y.O.; Mady, A.A. Homotopy perturbation method for the fractal Toda oscillator. Fractal Fract. 2021, 5, 93. [Google Scholar] [CrossRef]
- Obeya, P.O.; Akinlabi, G.O. Application of the regular perturbation method for the solution of first-order initial value problems. J. Phys. Conf. Ser. 2021, 1734, 012021. [Google Scholar] [CrossRef]
- Kac, V.G.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Sezer, M.; Akyuz-Dascıoglu, A. A Taylor method for the numerical solution of generalized pantograph equations with linear functional argument. J. Comput. Appl. Math. 2007, 200, 217–225. [Google Scholar] [CrossRef]
- Yüzbası, S.; Sezer, M. An exponential approximation for solutions of generalized pantograph-delay differential equations. Appl. Math. Model. 2013, 37, 9160–9173. [Google Scholar] [CrossRef]
- Rihan, F.A.; Rihan, A.F. An Analysis of the Theta-Method for Pantograph Type Delay Differential Equations. Complexity 2022, 2022, 8961352. [Google Scholar] [CrossRef]
- Rihan, F.A. Delay Differential Equations and Applications to Biology (Forum for Interdisciplinary Mathematics), 1st ed.; 2021 Edition; Springer: New York, NY, USA, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).