The Study on Mathematical Simulation and Analysis of the Molecular Discrete System of the Sulfurated Eucommia Ulmoides Gum
(This article belongs to the Section E2: Control Theory and Mechanics)
Abstract
:1. Introduction
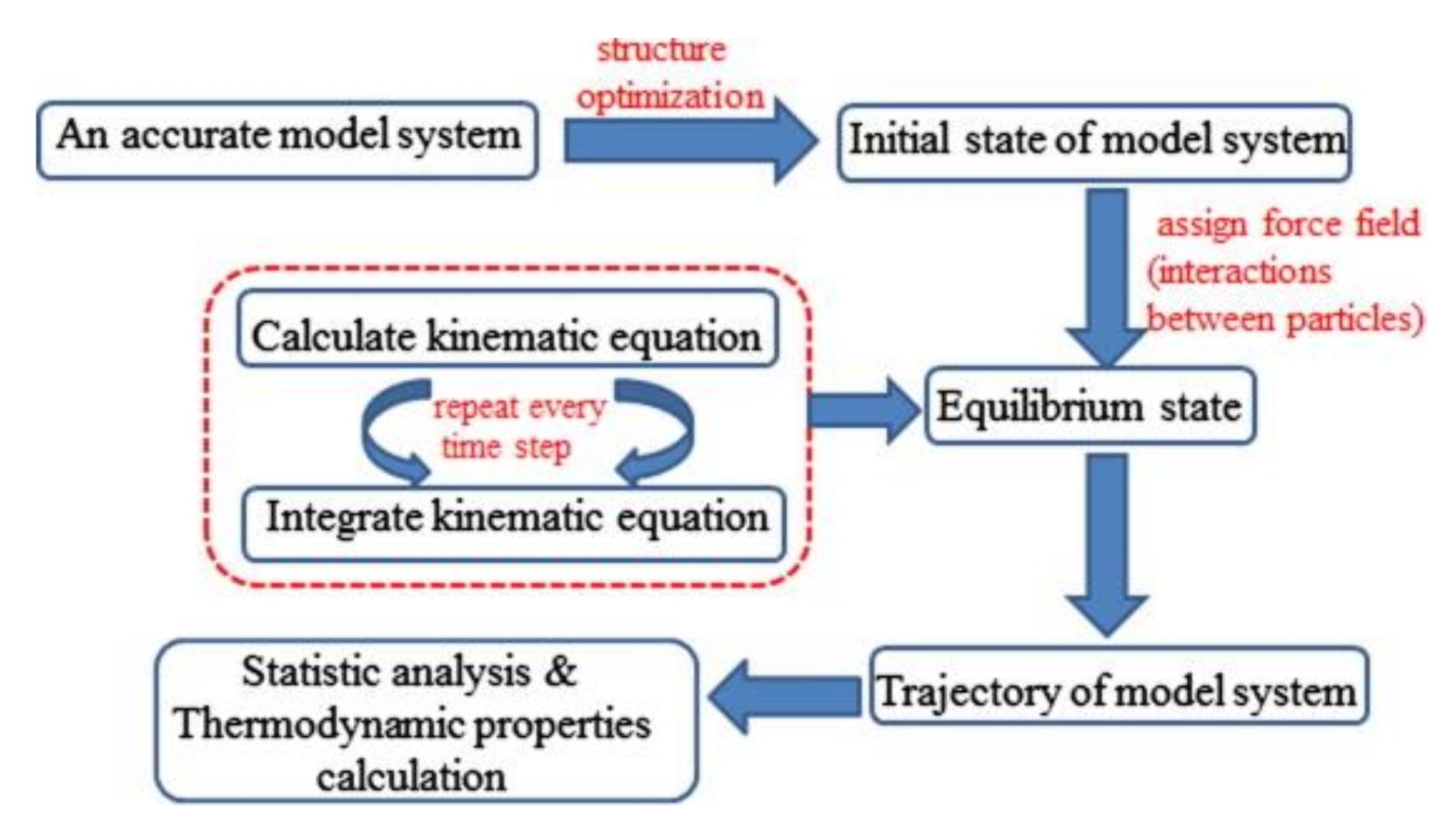
2. Theoretical Basis
2.1. Basic Principles
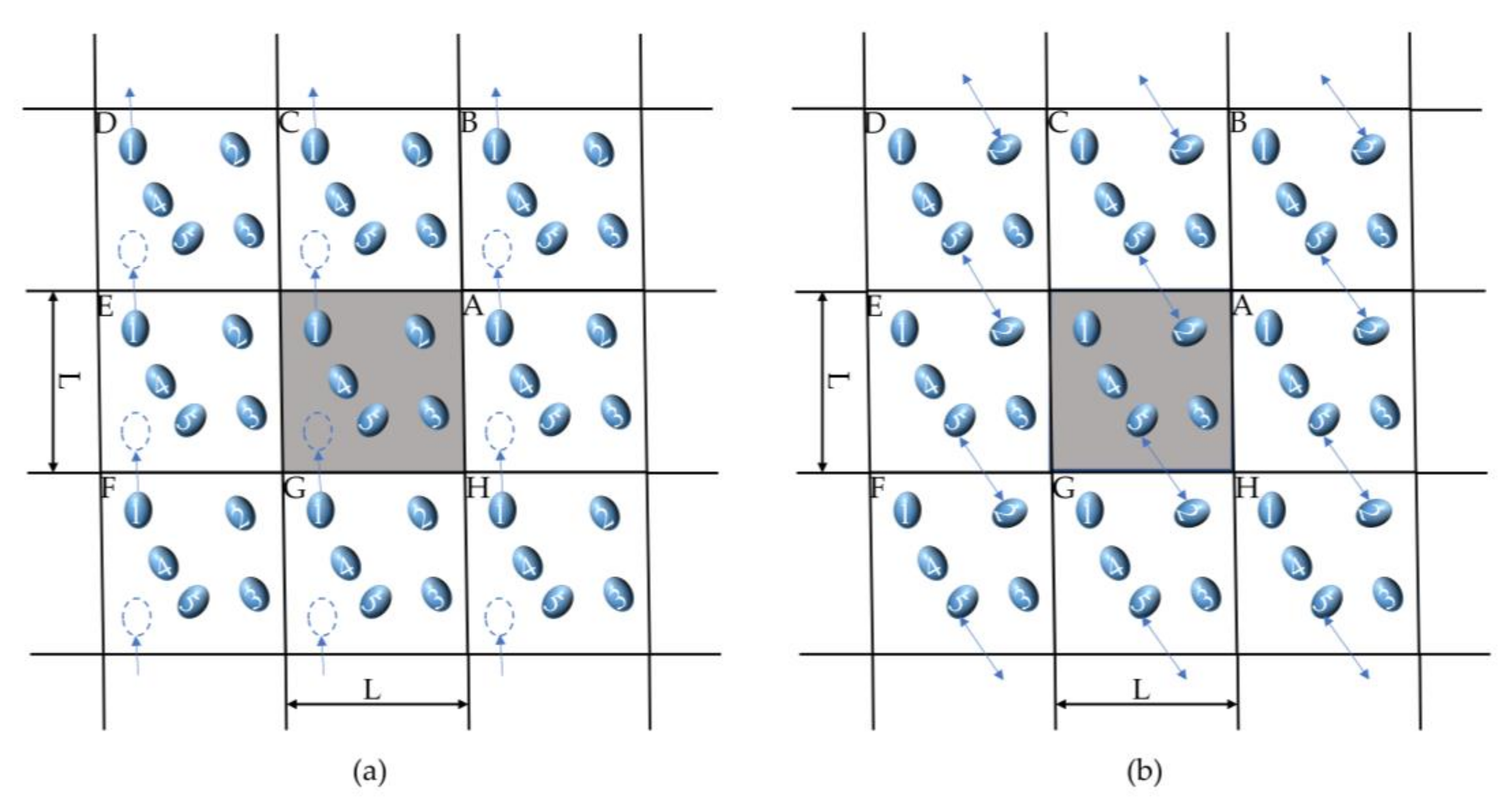
2.1.1. Equations of Motion
2.1.2. Boundary Conditions
2.1.3. Basic Solution of Motion Equation
- (1)
- Verlet’s algorithm: Using the positions of the first two moments of the particle, Taylor’s formula calculates the position of the following moment. Although this method decreases the complexity of the calculations, the results are inaccurate. In Equation (3), the specific expressions are given [16]:where ri(t), t denotes the position and time of particle i, respectively.
- (2)
- The Velocity Verlet algorithm, which is based on the Verlet algorithm with appropriate improvements to give the position, velocity, and acceleration rate of the particles, while also having the advantages of a greater computational accuracy and a moderate computational volume is now more widely used, and its expression is given by Equations (4) and (5) [17,18].
2.2. Force Field
2.3. Ensemble
- (1)
- In the canonical ensemble (NVT), the total momentum and the number of particles are kept constant. This is analogous to placing an isolated isoenergetic system in a virtual constant temperature, maintaining both the system and the heat source at a constant temperature, and calibrating the system’s kinetic energy using the particle rate.
- (2)
- Isothermal–isobaric ensemble (NPT): The number of particles N, the pressure P, and the temperature T are kept constant in this system. However, fluctuations in its system energy E and system volume V are possible.
2.4. Simulation Programs
3. Construction of MS Model of EUG
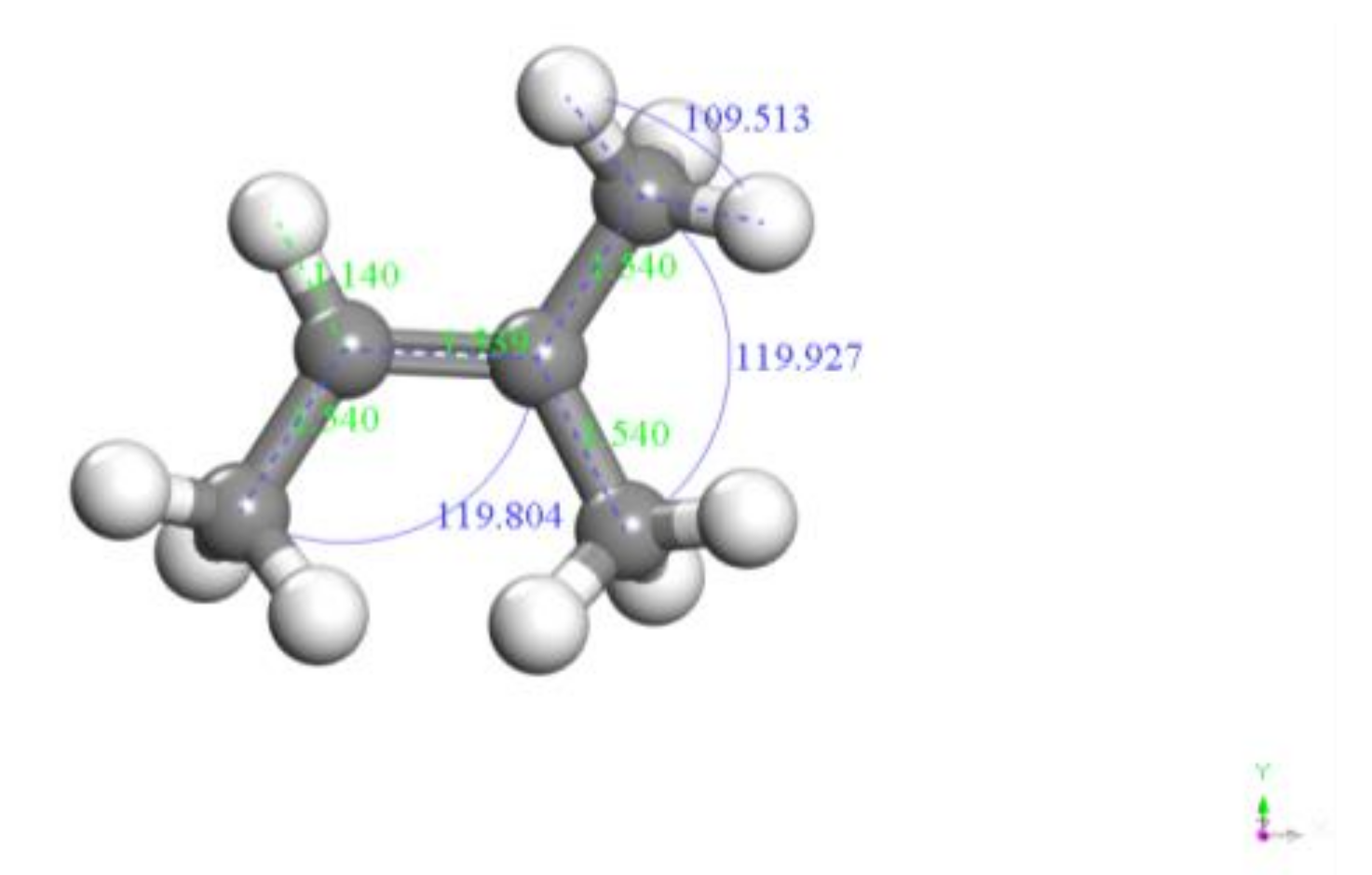
3.1. Composition and Structure of EUG
3.2. EUG Model Construction and Reliability Verification
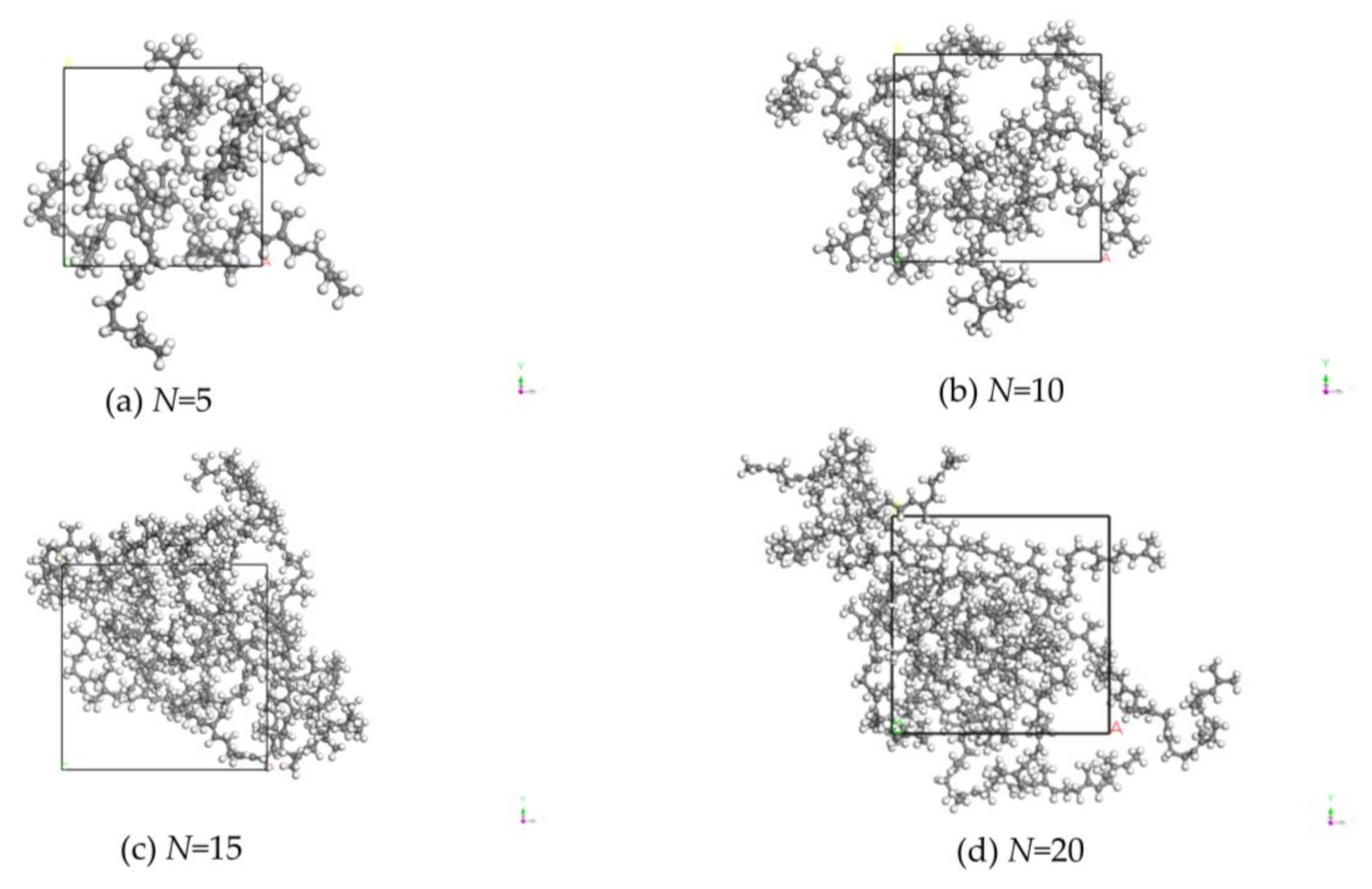
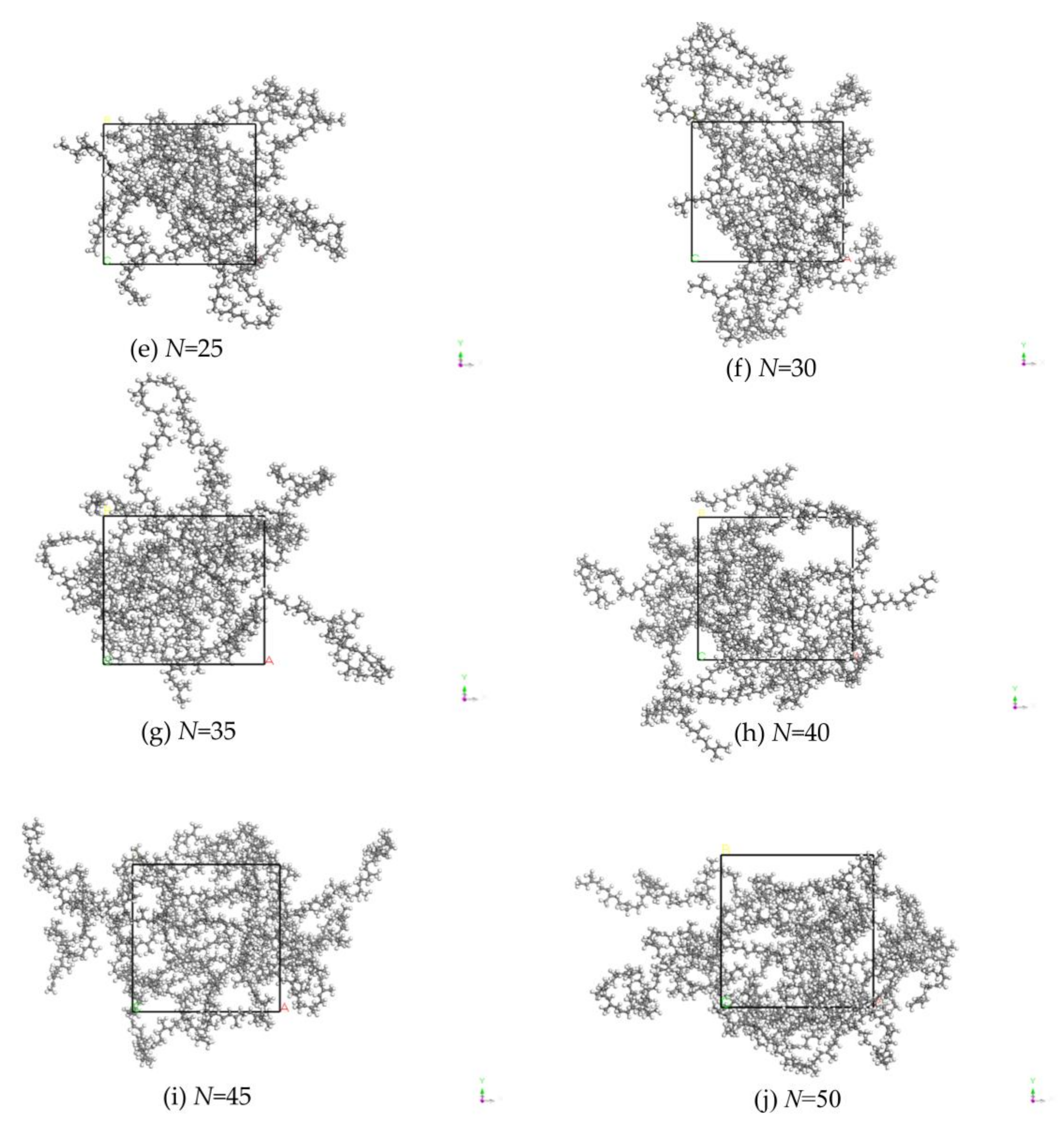
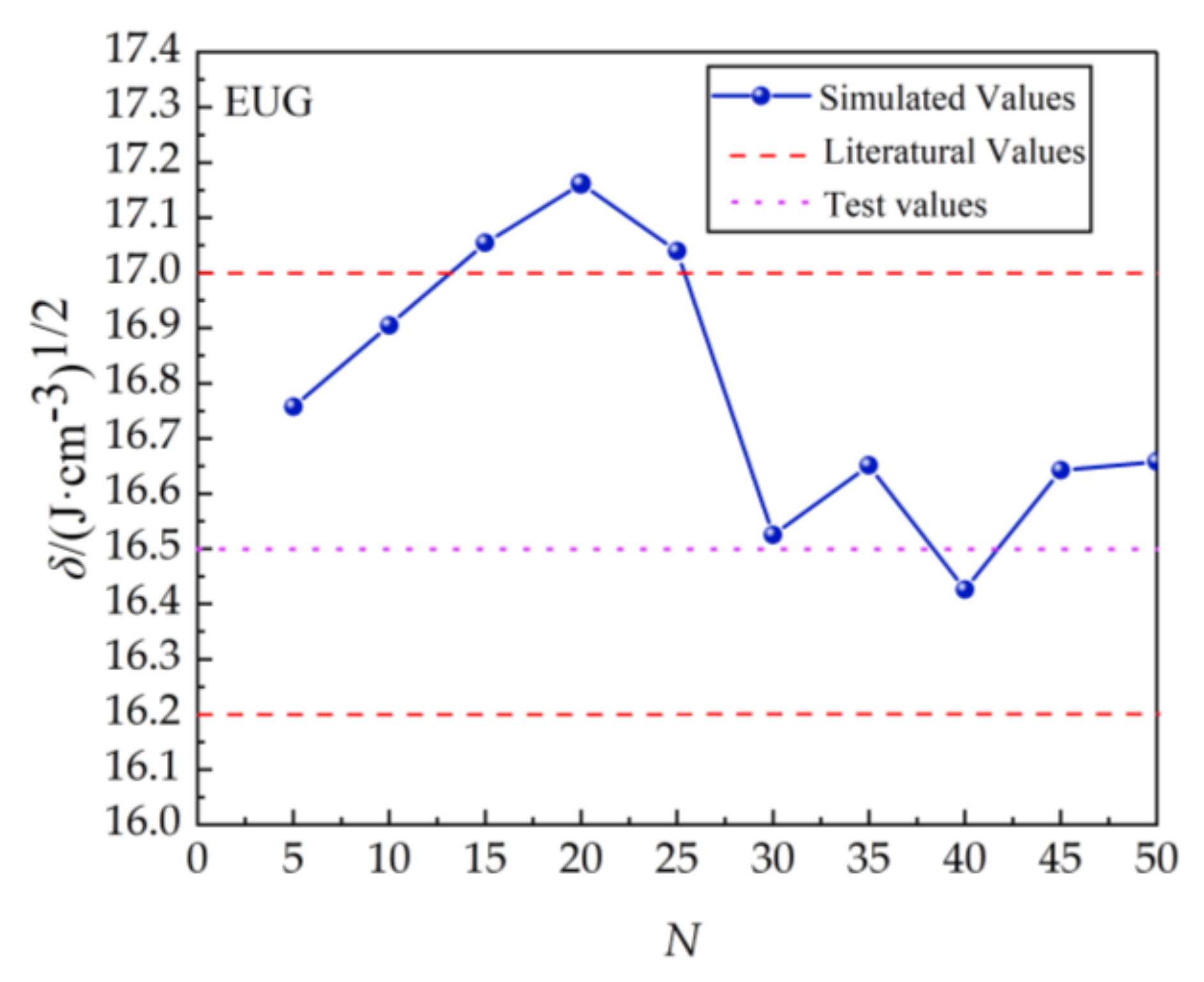
- Since EUG polymers can reflect the real EUG, it is necessary to determine the minimum degree of polymerization that can reflect the real EUG, utilizing the Materials Visualizer module in MS (Materials Studio 2004) software to construct molecular chain polymerization degrees of 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50, respectively, for EUG molecular models [25,26], with the goal of calculating the solubility parameter (δ) for the polymers of different lengths by varying the length of the polymer. Then, using Forcite, geometry and energy optimization were performed sequentially to find the configuration with the lowest molecular potential energy and to eliminate any local unreasonable structures, such as molecular overlap and offset, that may exist during the modelling process to ensure that subsequent kinetic calculations proceed smoothly [27]. Figure 7 depicts the constructed EUG models with eleven distinct polymerization degrees.
- On this basis, the lowest energy conformation was selected for annealing in the temperature range of 200–600K with a temperature gradient of 50 K for five cycles at 50 ps.
- The molecular dynamics of the annealed EUG model were optimized by (1) running molecular dynamics simulations at 50 ps in the NVT ensemble to further relax the EUG chains and (2) running molecular dynamics simulations at 50 ps in the NPT ensemble to achieve kinetic equilibrium.
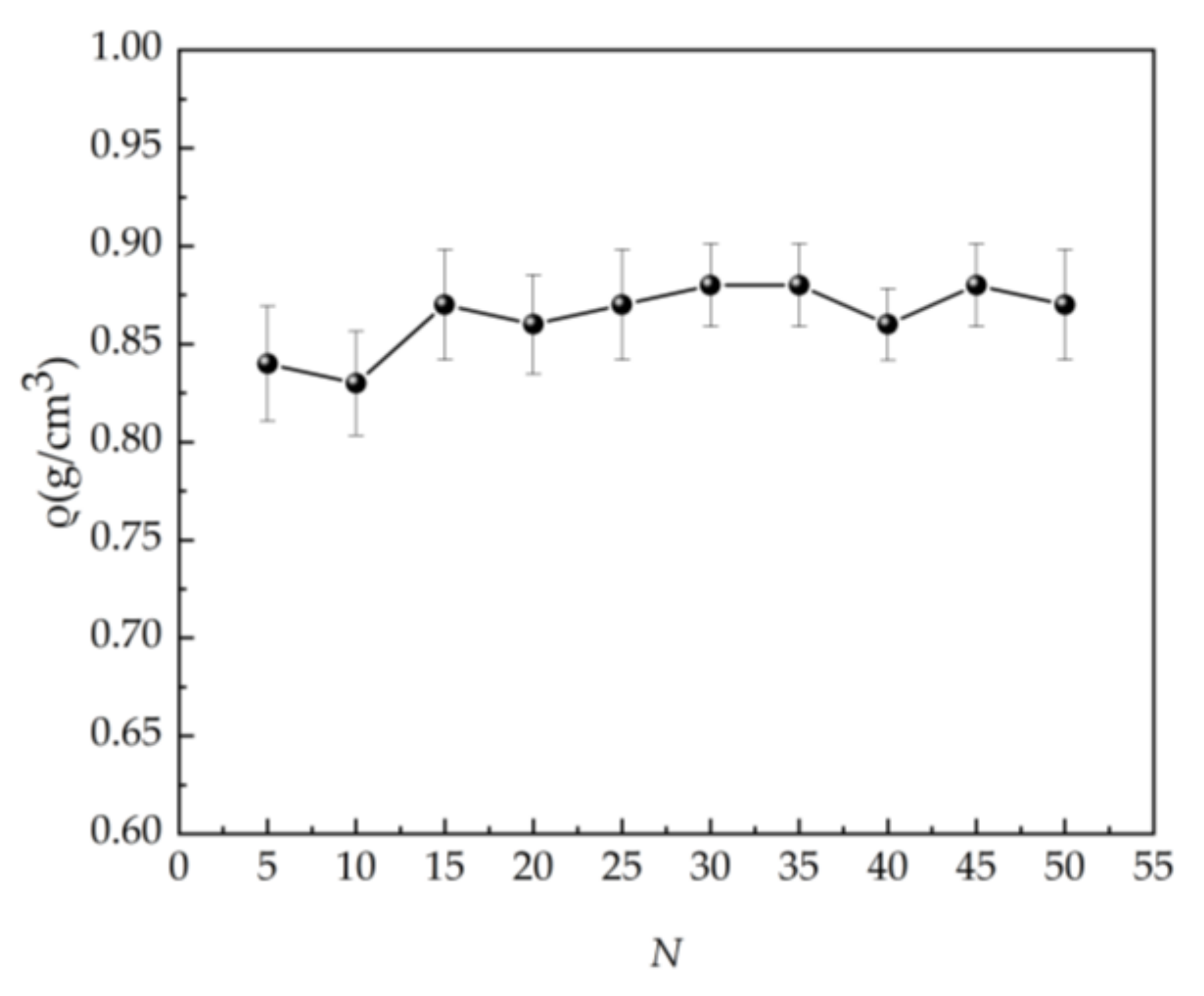
3.3. Determination of the Minimum Aggregation Degree of the EUG Model
4. Construction of SEUG MD Model
4.1. Construction of SEUG Models
- The Materials Visualizer module was applied to SEUG single chain models [29] with varying degrees of cross-linking, utilizing sulphur bridges (C-S-S-C) as cross-linking bonds, as illustrated in Figure 10, where the degree of cross-linking is calculated by using Equation (6). Since Packmol [29] has the advantage of a fast computational speed for large system molecules in the packing process, we decided to randomly combine the resulting pdb. files in Packmol into a 100-monomer SEUG model and export it as a pdb. file. The generated SEUG molecular configuration with a 20% cross-linking degree was conformed, as shown in Figure 11.
- Using the geometry optimization module and energy minimization in the Forcite module, the configuration of SEUG molecules with the lowest molecular potential energy was found.
- For molecular dynamics optimization, an annealing treatment with a 50 K temperature gradient for 10 cycles and 50 ps in the temperature range of 100 K–600 K was used until a global energy minimum SEUG molecular conformation was found.
- Using the generated models, molecular dynamics simulations were performed: (1) molecular dynamics simulations at 100 ps in the NVT system further relaxed the EUG molecular chains; (2) molecular dynamics simulations at 100 ps in the NPT system achieved kinetic equilibrium and obtained a stable SEUG molecular structure.
4.2. Reliability Verification of SEUG Model
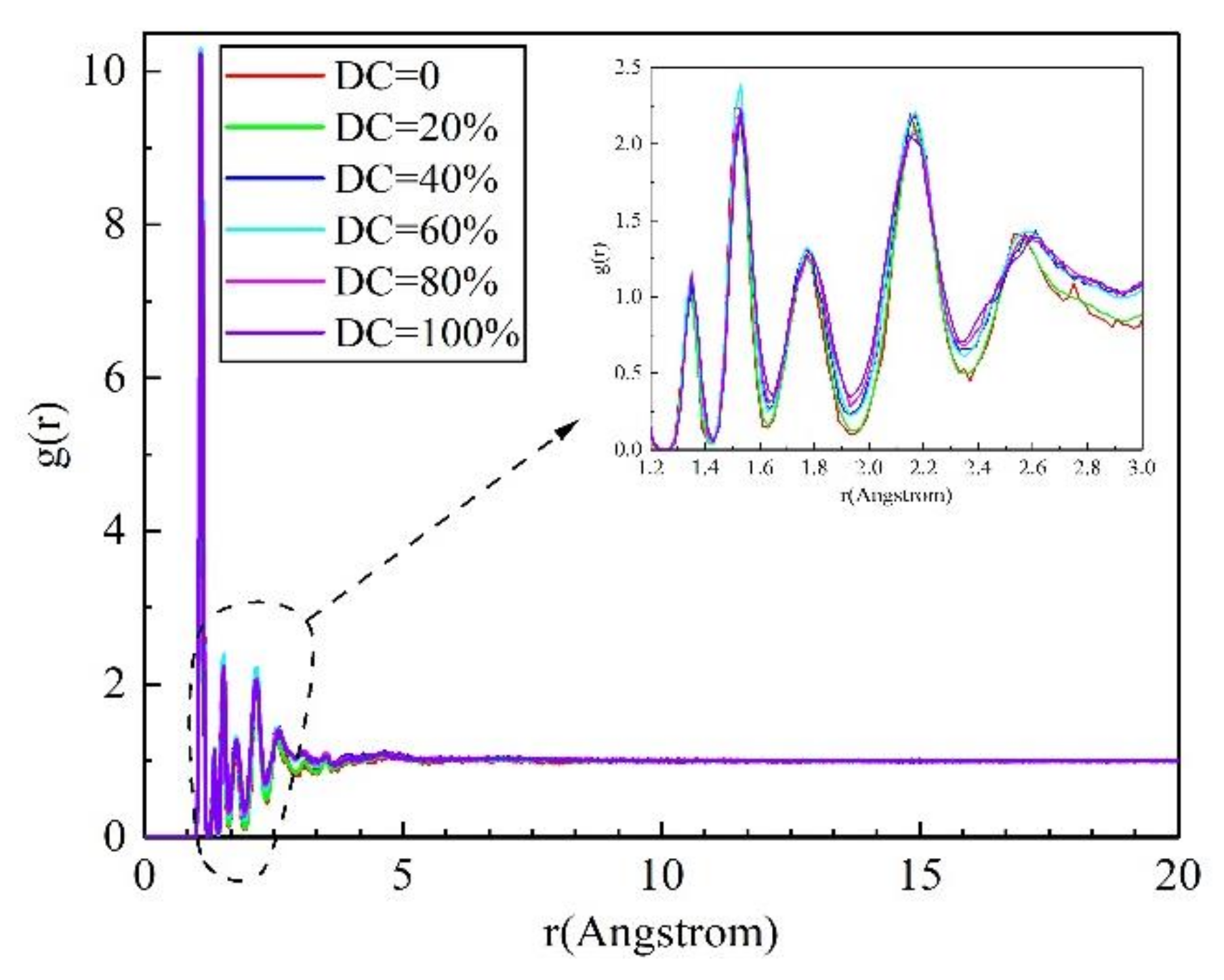
4.3. Radial Distribution Function of SEUG Model
- Intramolecular C-C radial distribution function of SEUG.
- 2.
- Intermolecular C-C radial distribution function of SEUG.
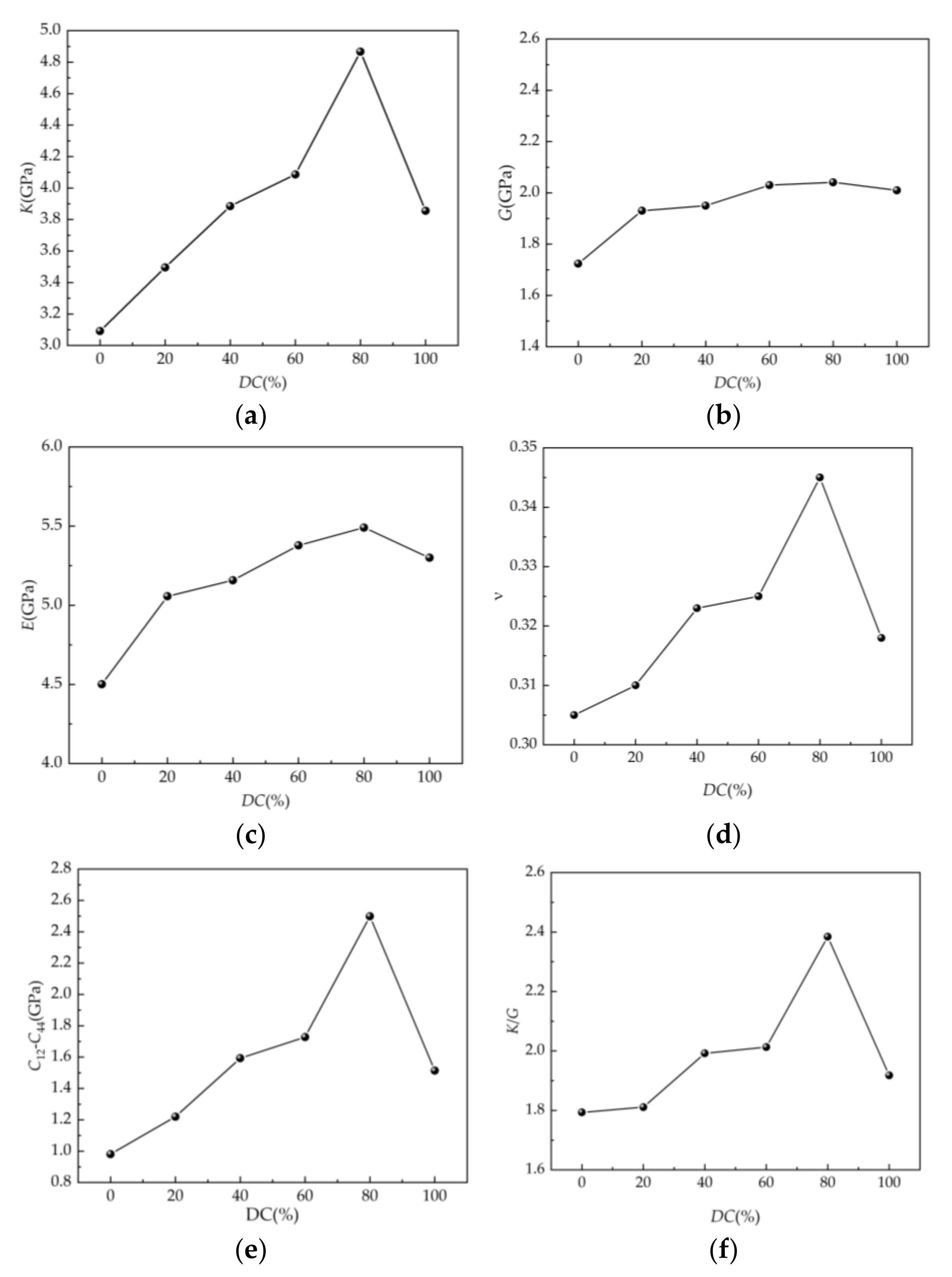
4.4. Mechanical Property Parameters of SEUG Model
5. Test
5.1. Materials and Recipes
5.2. Synthesis Process of SEUG
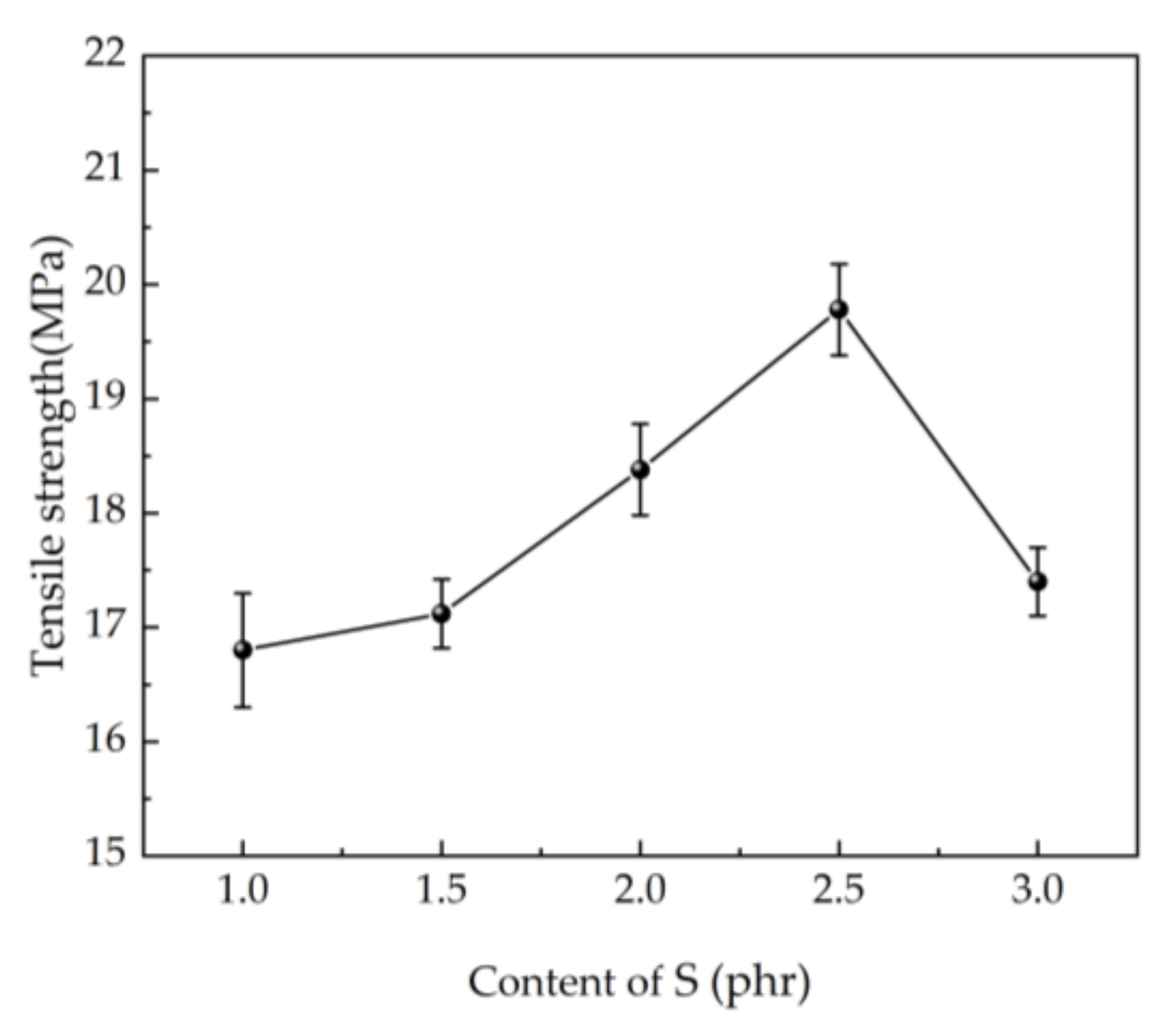
5.3. Test of Tensile Strength
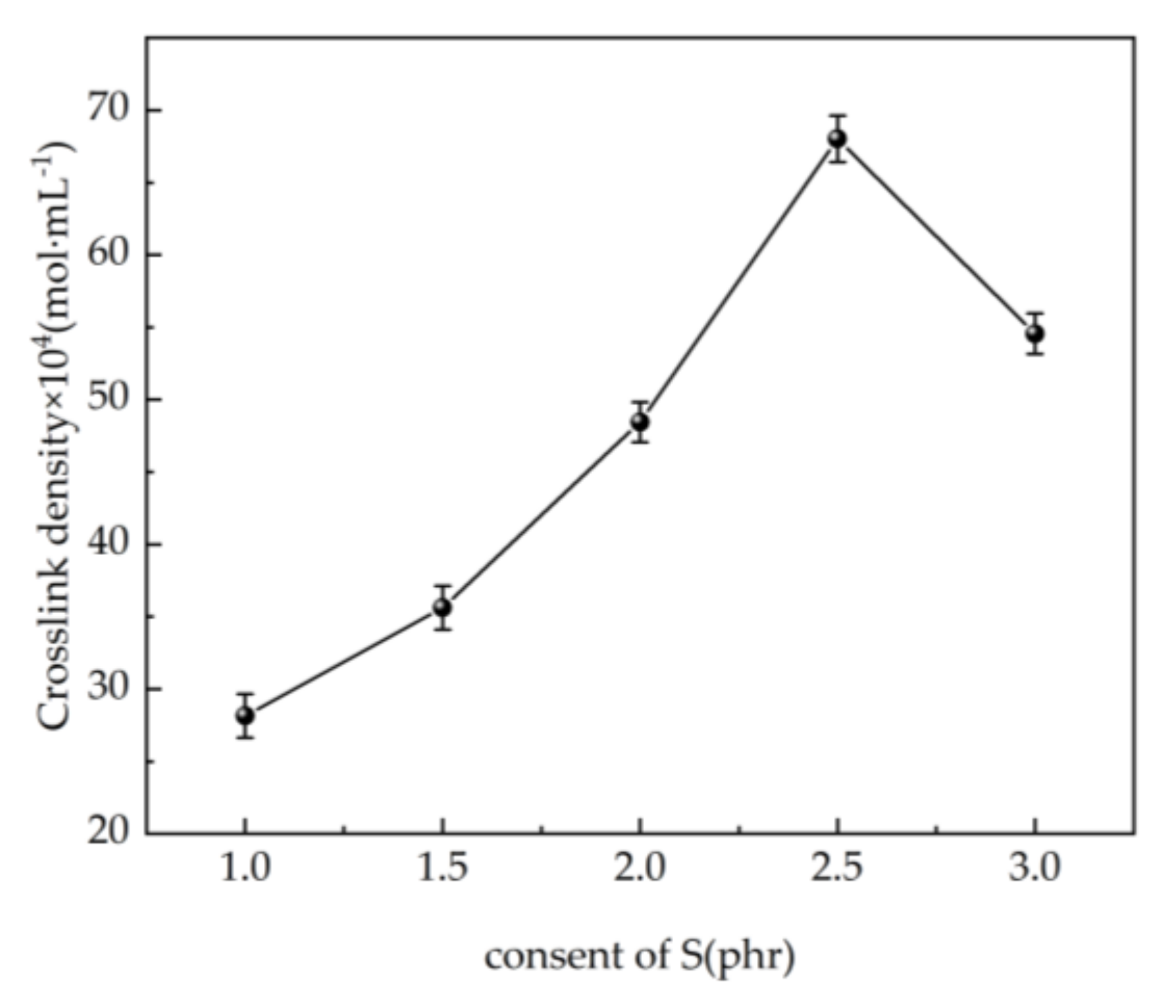
5.4. Cross-Link Density Test
5.5. Test Results and Discussion
5.5.1. Tensile Strength
5.5.2. Cross-link Density Test
6. Conclusions
- MD models of EUG with polymerization degrees from 5 to 50 were constructed, and the reliability of the EUG models was verified by calculating the density and solubility parameters of the EUG models with different polymerization degrees. The solubility parameter of 16.50, which is more consistent with the experimental test results and empirical values, was obtained, and furthermore, the minimum polymerization of 30 was determined, which can reflect the real situation of EUG.
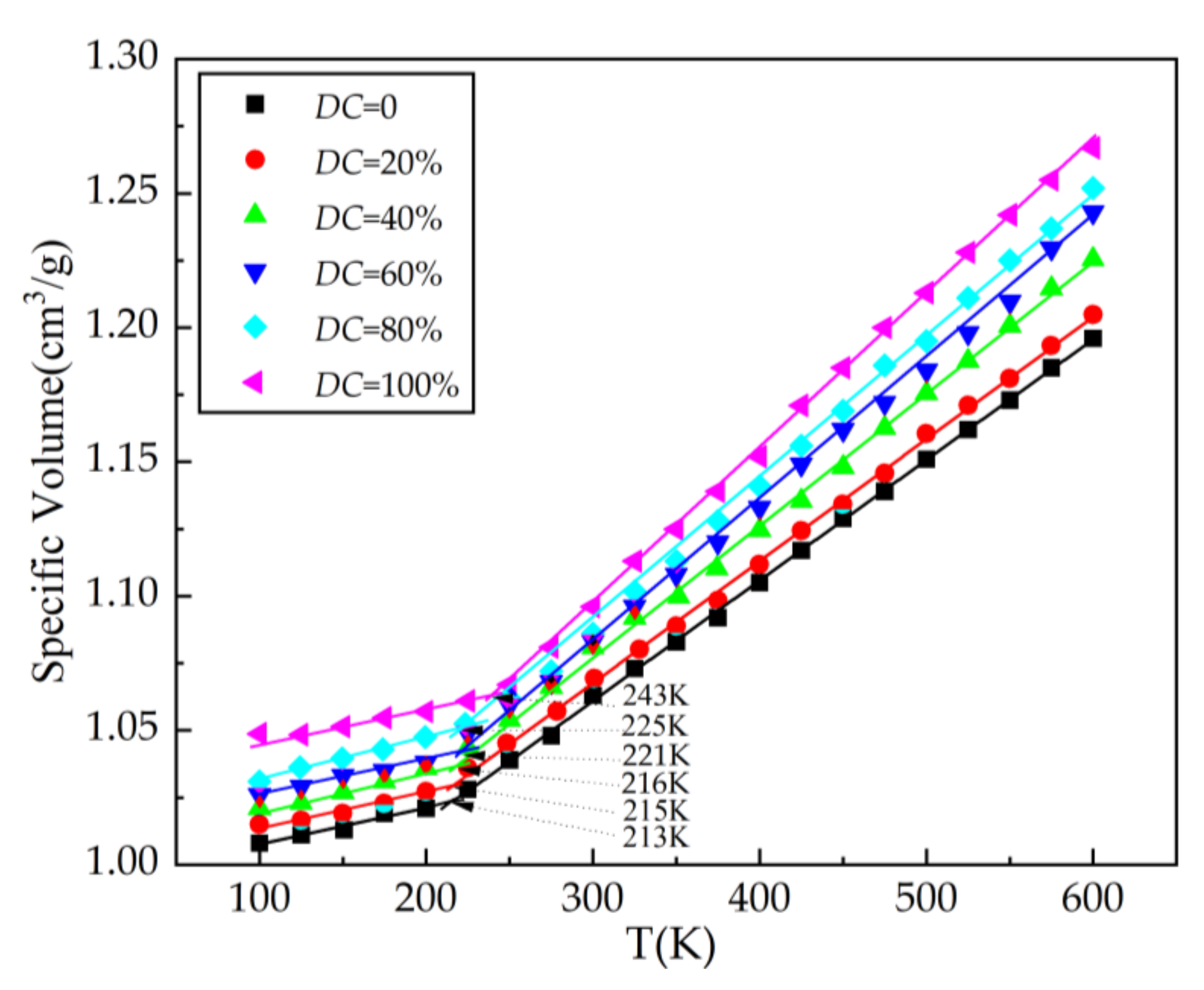
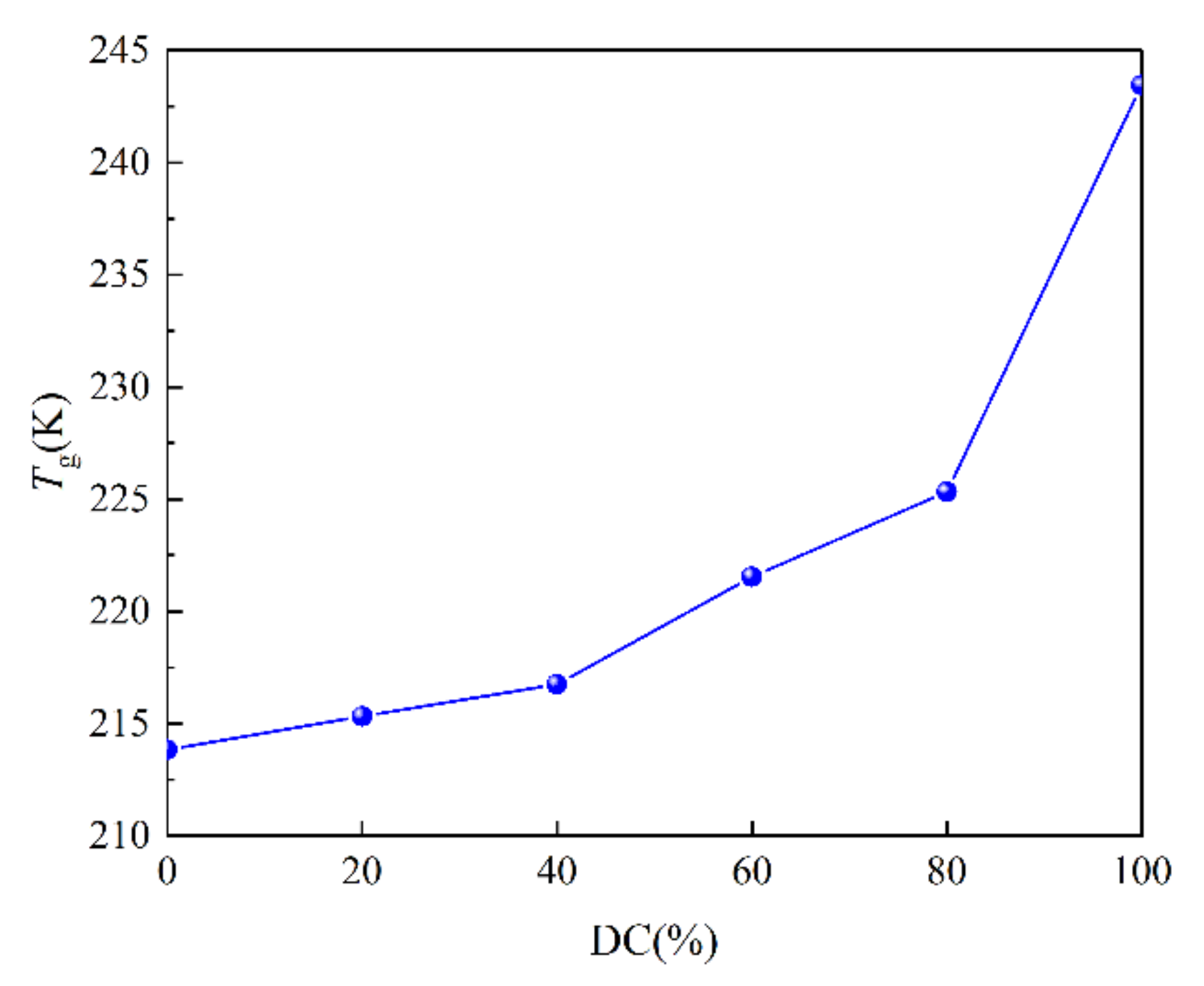
- SEUGs with cross-linking degrees of 20%, 40%, 60%, 80%, and 100% were constructed to test the effects of different cross-linking degrees on the SEUG performance from a microscopic perspective, and Tg increases with increasing cross-linking degree. When DC is 40%, SEUG is in mild cross-linking, which greatly improves its viscosity. When DC = 40–60%, SEUG is in moderate cross-linking; the Tg of the curve further increases, and the rate of the increase is obviously faster. When DC = 100%, the intrinsic crystals in EUG are all destroyed, SEUG is in the elastic cross-linking stage, and SEUG completely becomes an elastomer, which is consistent with the research conclusion of Professor Yan Ruifang [2]. Therefore, it can be proven that the MD model of SEUG is reliable.
- The intra- and intermolecular radial distribution function curves of SEUG models with varying degrees of cross-linking were analyzed, and it was determined that sulfidation had a relatively large effect on the intra-molecular radial distribution of SEUG, and that as sulfidation increased, the C-C bond was replaced by the C-S-S-C bond, and the molecular distribution became more dense. The effect on the intermolecular radial distribution was not so apparent because it was mixed with other substances, and this is consistent with the objective evidence.
- By calculating and analyzing the mechanical property parameters of SEUG with varying degrees of cross-linking, it is demonstrated that from the perspective of the mathematical simulation method, the suitable cross-linking degree of SEUG should be controlled to be between 40% and 80% when SEUG has rubber–plastic duality and the most ideal mechanical properties, which can serve as a reference for the ratio of EUG and cross-linking agent in the vulcanization process of EUG.
- The variation pattern of vulcanization tensile strength and cross-linking density of SEUG by different degrees of cross-linking with the dosage of S is consistent with the molecular dynamics simulation, which shows that increasing the dosage of S within a certain degree is beneficial to the cross-linking of eucalyptus gum beyond a certain limit, and then it has the opposite effect. It also shows that the simulation of the molecular dynamics of SEUG is effective.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, S.Q.; Zhang, J.C.; Zhang, L.Q. Research Progress in Biorubber. Polym. Bull. 2013, 4, 42–50. [Google Scholar]
- Yan, R.F. The gutta-percha material engineering-the theoretical basis for commercial development. Chem. Technol. Mark. 1999, 7, 3–4. [Google Scholar]
- Zhao, J.L.; Li, Z.G. Optimized Design and Research on Performance of Asphalt Modified by Eucommia Ulmoides Gum. Highway 2013, 10, 189–193. [Google Scholar]
- Li, Z.G.; Deng, X.Y.; Shen, J.X. Test and Research on Effect of Eucommia Ulmoides Gum Blending with SBS Modified Asphalt. Highway 2008, 8, 217–220. [Google Scholar]
- Chen, Z.Q.; Li, Z.G. Study on the vulcanization cross-linking degree of eucommia gum for asphalt modification. Highway 2013, 8, 267–270. [Google Scholar]
- Deng, X.Y.; Li, Z.G.; Huang, Y.X.; Luan, Y. Improving mechanism and effect analysis of sulfurated and grafted Eucommia Ulmoides Gum modified rubber asphalt. Constr. Build. Mater. 2017, 148, 715–722. [Google Scholar] [CrossRef]
- Li, N. Study on Preparation, Property Characterization and Modification Mechanism of Vulcanized Eucommia Ulmoides Gum Modified Asphalt. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 2021. [Google Scholar]
- Zheng, M.Y.; Ni, F.A.; Gu, X.Y. Study of vulcanized dulcimer for asphalt modification. Mod. Transp. Technol. 2009, 6, 14–17. [Google Scholar]
- Gang, M.J.; Guo, Y.Z.; Shi, X.T.; Zhang, J.B. Effect of sulfur dosage on the performance of bio-based dulcimer. Chem. Enterp. Manag. 2019, 17, 25–26. [Google Scholar]
- Yi, B. Study on Rubber Modified Asphalt Based on Molecular Simulation Technology. Master’s Thesis, Xinjiang University, Xinjiang, China, 2020. [Google Scholar]
- Habasaki, J.; Casalini, R.; Ngai, K.L. Molecular Dynamics Study of Thermodynamic Scaling of the Glass-Transition Dynamics in Ionic Liquids over Wide Temperature and Pressure Ranges. Phys. Chem. B 2010, 114, 3902–3911. [Google Scholar] [CrossRef]
- De Arenaza, I.M.; Meaurio, E.; Coto, B.; Sarasua, J.R. Molecular dynamics modelling for the analysis and prediction of miscibility in polylactide/polyvinilphenol blends. Polymer 2010, 51, 4431–4438. [Google Scholar] [CrossRef]
- Dai, X.R.; Zhao, J.J.; Xun, X.X.; Liu, Y.; Qiao, X.S. Advances in Molecular Dynamics Simulation of Glass Structures and Properties Calculation. J. Chin. Ceram. Soc. 2021, 49, 2691–2709. [Google Scholar]
- Alipour, P.; Toghraie, D.; Karimipour, A.; Hajian, M. Molecular dynamics simulation of fluid flow passing through a nanochannel: Effects of geometric shape of roughnesses. J. Mol. Liq. 2019, 275, 192–203. [Google Scholar] [CrossRef]
- Shao, J. Asymptotic Behavior and Ergodicity for the Time Inhomogeneous Diffusion Process. Nanjing University of Aeronautics and Astronautics. Master’s Thesis, Nanjing University, Nanjing, China, 2019. [Google Scholar]
- Yan, S.R.; Shirani, N.; Zarringhalam, M.; Toghraie, D.; Nguyen, Q.; Karimipour, A. Prediction of boiling flow characteristics in rough and smooth microchannels using molecular dynamics simulation: Investigation the effects of boundary wall temperatures. J. Mol. Liq. 2020, 306, 112937. [Google Scholar] [CrossRef]
- Alipour, P.; Toghraie, D.; Karimipour, A.; Hajian, M. Modeling different structures in perturbed Poiseuille flow in ananochannel by using of molecular dynamics simulation: Study the equilibrium. Phys. A Stat. Mech. Its Appl. 2019, 515, 13–30. [Google Scholar] [CrossRef]
- Jolfaei, N.A.; Jolfaei, N.A.; Hekmatifar, M.; Piranfar, A.; Toghraie, D.; Sabetvand, R.; Rostami, S. Investigation of thermal properties of DNA structure with precise atomic arrangement via equilibrium and non-equilibrium molecular dynamics approaches. Comput. Methods Programs Biomed. 2020, 185, 105–169. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applicationss Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model. 2016, 22, 47. [Google Scholar] [CrossRef]
- Wen, Y.H.; Zhu, R.Z.; Zhou, F.X. An overview on molecular dynamics simulation. Adv. Mech. 2003, 33, 65–73. [Google Scholar]
- Zhao, S.; Li, J.F.; Zhou, Y.H. Molecular Dynamics Simulation and Its Application in the Materials Science. Mater. Rev. 2007, 21, 5–8. [Google Scholar]
- Yang, J.; Guo, N.S.; Guo, X.Y.; Wang, Z.; Fang, C.; Chu, Z. Adhesion of Foamed Asphalt-Aggregate Interface Based on Molecular Dynamics. Mater. Rep. 2021, 35 (z2), 138–144. [Google Scholar]
- Akten, E.D.; Mattice, W.L. Monte Carlo Simulation of Head-to-Head, Tail-to-Tail Polypropylene and Its Mixing with Polyethylene in the Melt. Macromolecules 2001, 34, 3389–3395. [Google Scholar] [CrossRef]
- Liu, Q.; Yue, H.; Jiang, H.; Chen, C. Molecular Dynamics and Dissipative Particle Dynamics Simulation of TPI/NR Blends. Mater. Rep. 2012, 26, 141–145. [Google Scholar]
- Zhuang, C.Q.; Yue, H.; Zhang, H.J.; Liu, Q. Molecular Simulation of the Glass Transition Temperature for Guatta-Percha. J. Funct. Polym. 2010, 23, 409–412. [Google Scholar]
- Li, T.R. Molecular Dynamics Simulation Study of the Structure and Mechanical Properties of the Main Components of Cement. Master’s Thesis, Shenzhen University, Shenzhen, China, 2019. [Google Scholar]
- Xin, X. Preparation and Characterization of New Trans-polyisoprene Latex. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2018. [Google Scholar]
- Aleksandr, V.; Tommy, L.; Cornelia, B. Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations. Polymers 2021, 13, 315. [Google Scholar]
- Fu, Y.Z.; Liu, Y.Q.; Zhang, L.Y. Molecular simulation of the glass transition of different configuration of polypropylene. J. Mol. Sci. 2009, 25, 1–4. [Google Scholar]
- Yang, J. Adhesion of Foamed Asphalt—Aggregate Interface Based on Molecular Dynamics Simulation. Master’s Thesis, Dalian Maritime University, Dalian, China, 2022. [Google Scholar]
- Zhao, Z.Y.; Zhao, X. Electronic, optical, and mechanical properties of Cu2ZnSnS4 with four crystal structures. J. Semicond. 2015, 36, 52–64. [Google Scholar] [CrossRef]
- Li, F.Z. Study on Compatible Mechanism and Properties of Blend Systems from Eucommia Ulmoides Gum and Common rubber. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2019. [Google Scholar]
- Tang, C.; Zhang, S.; Zhang, F.Z.; Li, X.; Zhou, Q. Simulation and Experimental about the Thermal Aging Performance Improvement of Cellulose Insulation Paper. Trans. China Electrotech. Soc. 2016, 31, 68–76. [Google Scholar]
- Leng, Z.J.; Yue, P.P.; Chen, J.; Hao, X.; Peng, F. Research Progress on Modification and Application of Natural Eucommia ulmoides Gum. Biomass Chem. Eng. 2021, 55, 49–58. [Google Scholar]
- Yan, R.F.; Xue, Z.H. The High Elastic Vulcanizate of Gutta-Percha And Its Vulcanizing-Elasticity Mechanisium. China Elastomerics 1991, 3, 12–15. [Google Scholar]
- Xu, S.L.; Zhang, Y.Y.; Wang, M. Comparative study of cross-link density determination methods for silicone rubber. China Rubber Ind. 2017, 64, 624–626. [Google Scholar]
- Wang, Z.L.; Zhang, Z.Y. Rubber test methods (53). Rubber Plast. Resour. Util. 2015, 3, 32–42. [Google Scholar]
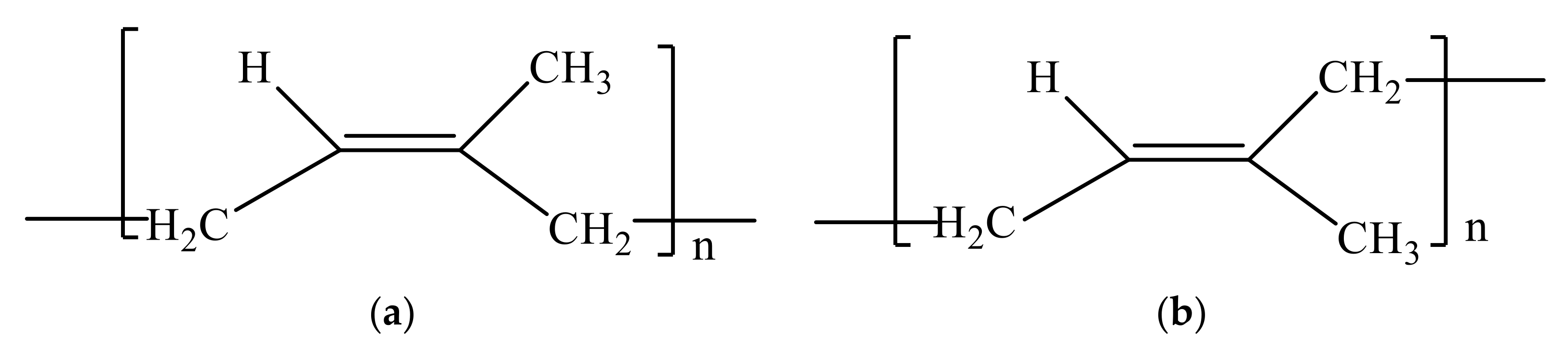




| Polymer | Degrees of Polymerization | NetMass | δMD (J/cm3)1/2 | δLit. (J/cm3)1/2 | δtest (J/cm3)1/2 |
|---|---|---|---|---|---|
| EUG | 30 | 2045.59 | 16.525 | 16.20~17.0 | 16.50 |
| DC Content (%) | C12 (GPa) | C44 (GPa) | C12-C44 (GPa) | K (GPa) | G (GPa) | E (GPa) | ν | K/G |
|---|---|---|---|---|---|---|---|---|
| 0 | 2.705 | 1.724 | 0.981 | 3.092 | 1.724 | 4.501 | 0.305 | 1.793 |
| 20 | 3.150 | 1.930 | 1.220 | 3.495 | 1.930 | 5.057 | 0.310 | 1.811 |
| 40 | 3.543 | 1.950 | 1.593 | 3.885 | 1.950 | 5.158 | 0.323 | 1.992 |
| 60 | 3.758 | 2.030 | 1.728 | 4.086 | 2.030 | 5.378 | 0.325 | 2.013 |
| 80 | 4.540 | 2.041 | 2.499 | 4.867 | 2.041 | 5.491 | 0.345 | 2.384 |
| 100 | 3.524 | 2.010 | 1.514 | 3.855 | 2.010 | 5.300 | 0.318 | 1.918 |
| EUG | S | Zinc Oxide | Stearic Acid (ZA) | Accelerator CZ | Nano-Silica | Naphthenic Oil | Gummaron Resin |
|---|---|---|---|---|---|---|---|
| 100 | Variants | 4.5 | 1.5 | 1 | 20 | 4.5 | 4.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, S.; Guo, N.; Jin, X.; Chu, Z.; Yan, S. The Study on Mathematical Simulation and Analysis of the Molecular Discrete System of the Sulfurated Eucommia Ulmoides Gum. Mathematics 2023, 11, 964. https://doi.org/10.3390/math11040964
Yan S, Guo N, Jin X, Chu Z, Yan S. The Study on Mathematical Simulation and Analysis of the Molecular Discrete System of the Sulfurated Eucommia Ulmoides Gum. Mathematics. 2023; 11(4):964. https://doi.org/10.3390/math11040964
Chicago/Turabian StyleYan, Simeng, Naisheng Guo, Xin Jin, Zhaoyang Chu, and Sitong Yan. 2023. "The Study on Mathematical Simulation and Analysis of the Molecular Discrete System of the Sulfurated Eucommia Ulmoides Gum" Mathematics 11, no. 4: 964. https://doi.org/10.3390/math11040964
APA StyleYan, S., Guo, N., Jin, X., Chu, Z., & Yan, S. (2023). The Study on Mathematical Simulation and Analysis of the Molecular Discrete System of the Sulfurated Eucommia Ulmoides Gum. Mathematics, 11(4), 964. https://doi.org/10.3390/math11040964







