Fusion and Allocation Network for Light Field Image Super-Resolution
Abstract
:1. Introduction
- We propose two operators (AFO and SFO), which can equally extract and fuse spatial and angular features. The AFO models the correlations among all views in angular subspace, and the SFO models the spatial information of each view in space subspace. Note that the designed AFO and SFO can be regarded as generic modules to use in other LF works (e.g., LF depth estimation and LF segmentation), which are effective at extracting angular and spatial information.
- We propose a fusion and allocation strategy to aggregate and distribute the fusion features. Based on this strategy, our method can effectively exploit spatial and angular information from all LF views. Meanwhile, this strategy can provide more informative features for the next AFO and SFO. Our strategy can not only generate high-quality reconstruction results but also preserve LF structural consistency.
- Our LF-FANet is an end-to-end network for LF image SR, which has significantly improved compared with the state-of-the-art methods developed in recent years.
2. Related Work
2.1. Single Image SR
2.2. LF Image SR
2.2.1. Explicit-Based Methods
2.2.2. Implicit-Based Methods
3. Architecture and Methods
3.1. Problem Formulation
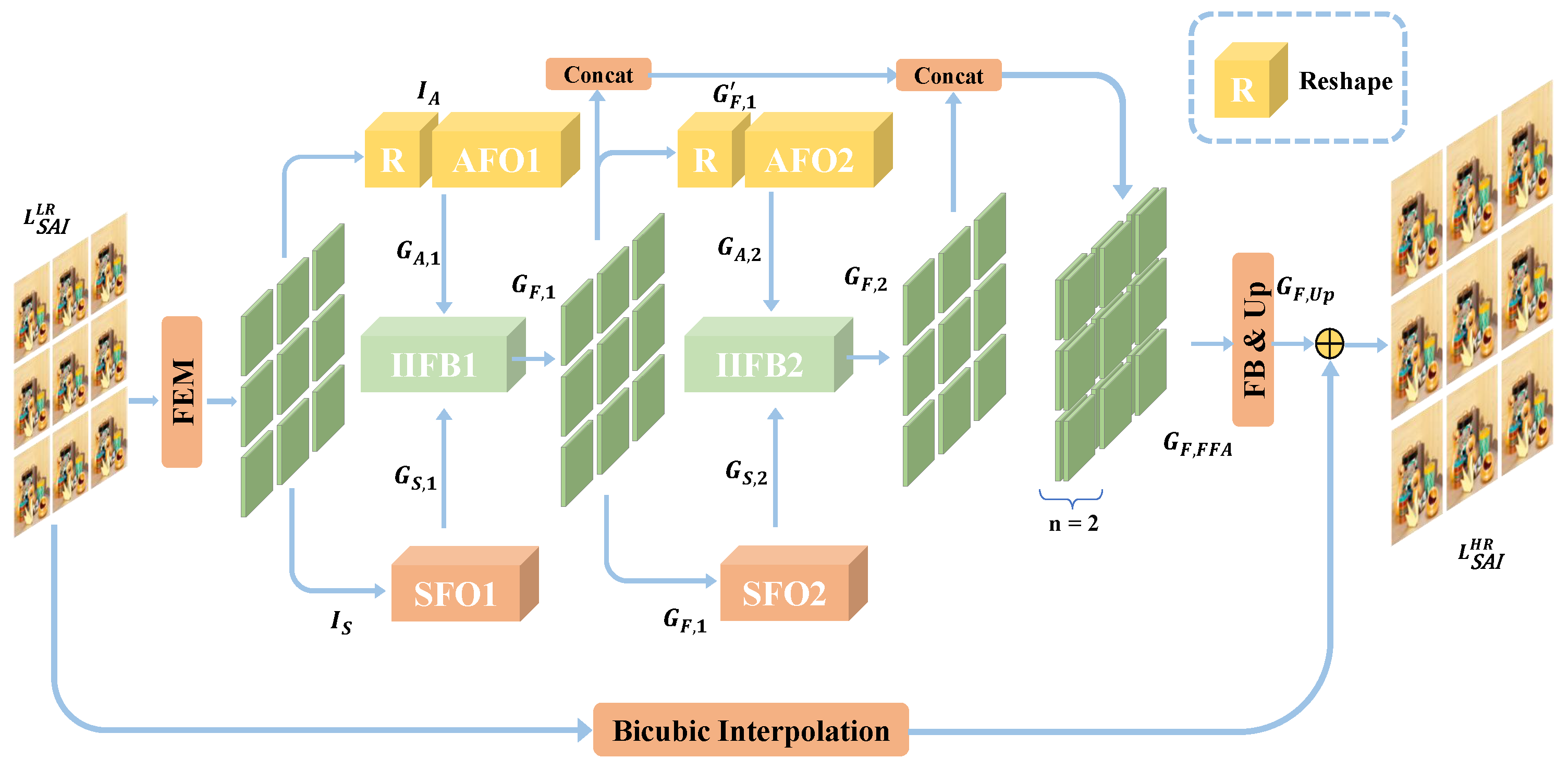
3.2. Network Architecture
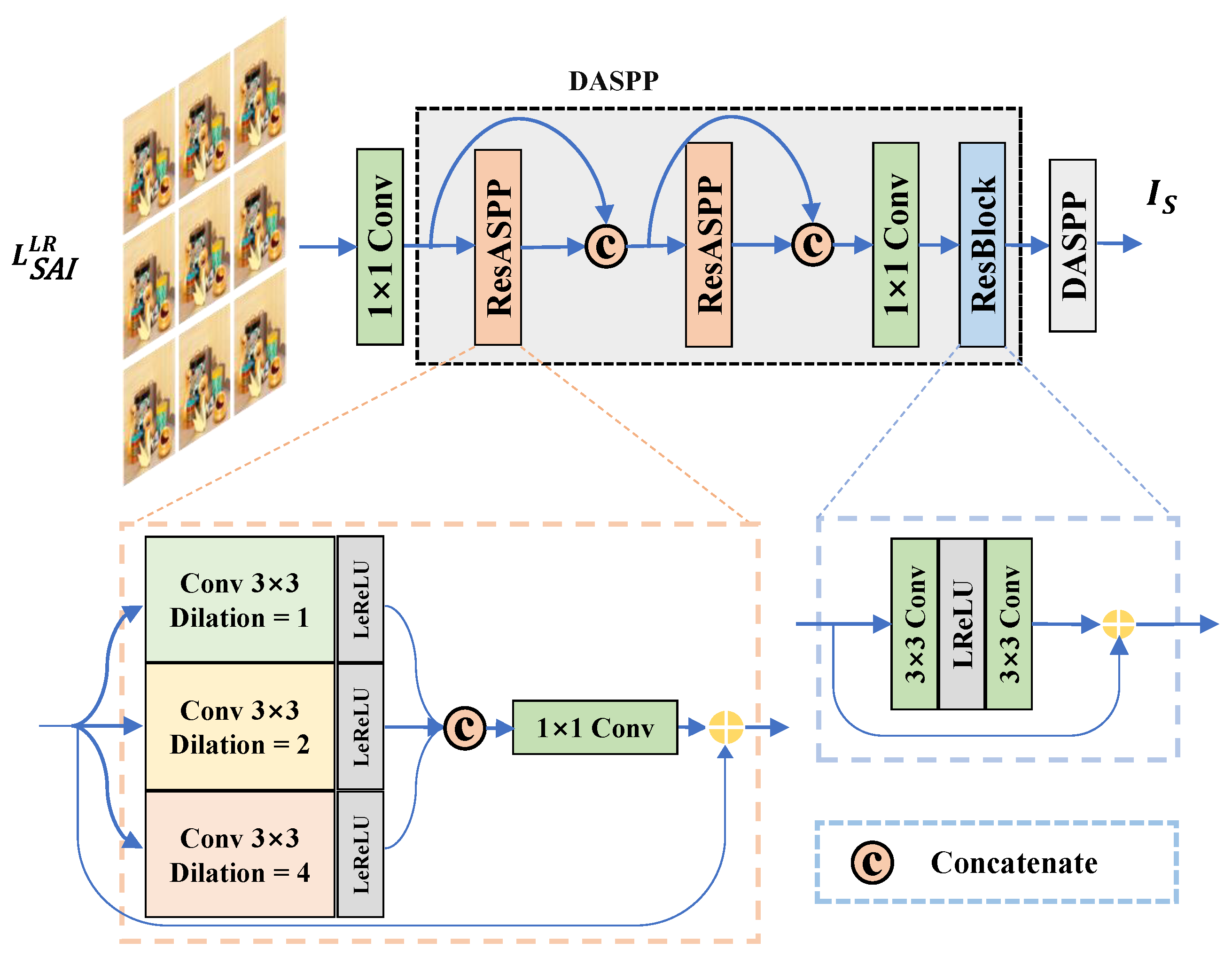
3.2.1. Feature Extraction Module (FEM)
3.2.2. Feature Fusion and Allocation Module (FFAM)
3.2.3. Angular Fusion Operator (AFO)
3.2.4. Spatial Fusion Operator (SFO)
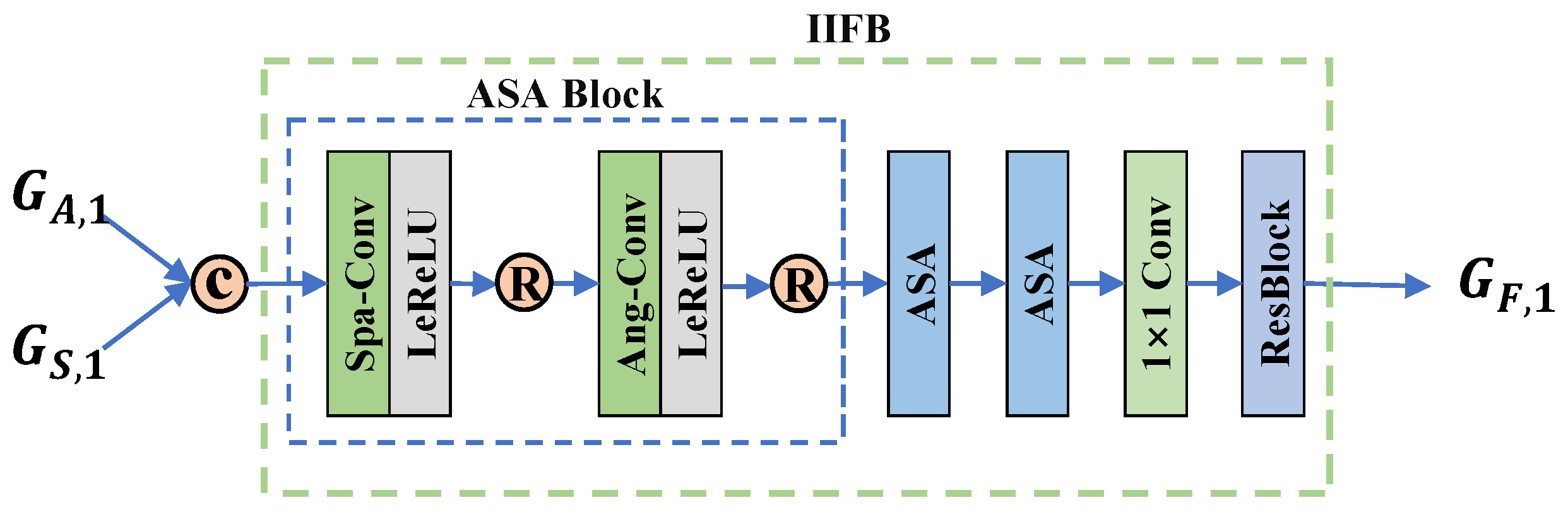
3.2.5. Interaction Information Fusion Block (IIFB)
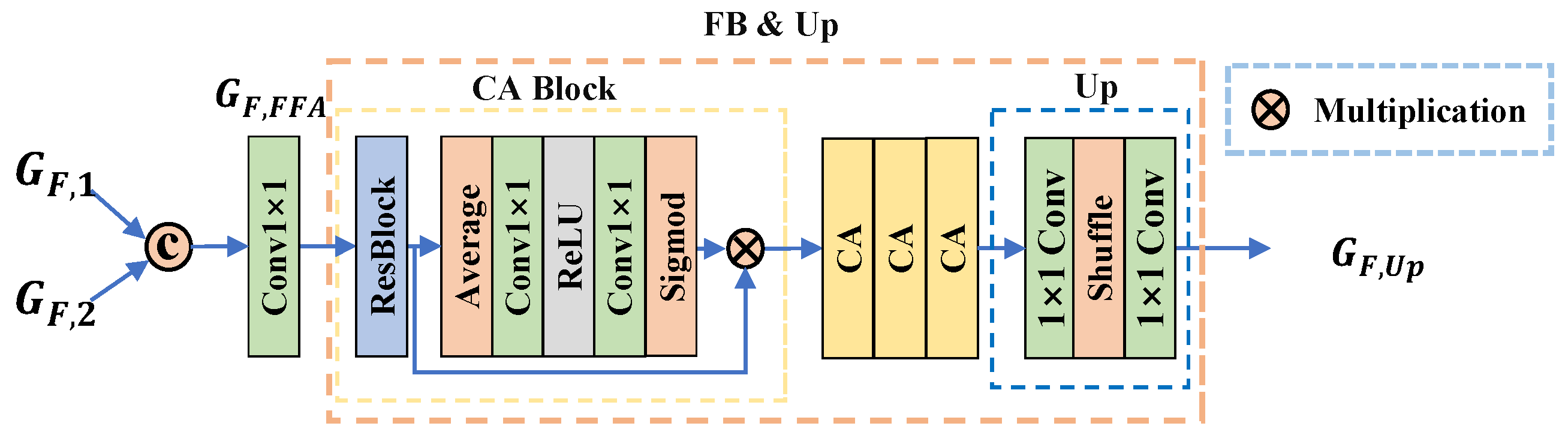
3.2.6. Feature Blending and Upsampling Module (FB & UP)
3.3. Loss Function
4. Experiments
4.1. Datasets and Evaluation Metrics
4.2. Settings and Implementation Details
4.3. Comparisons with State-of-the-Art Methods
4.3.1. Quantitative Results
4.3.2. Qualitative Results
4.3.3. Parameters and FLOP
4.3.4. Performance on Real-World LF Images
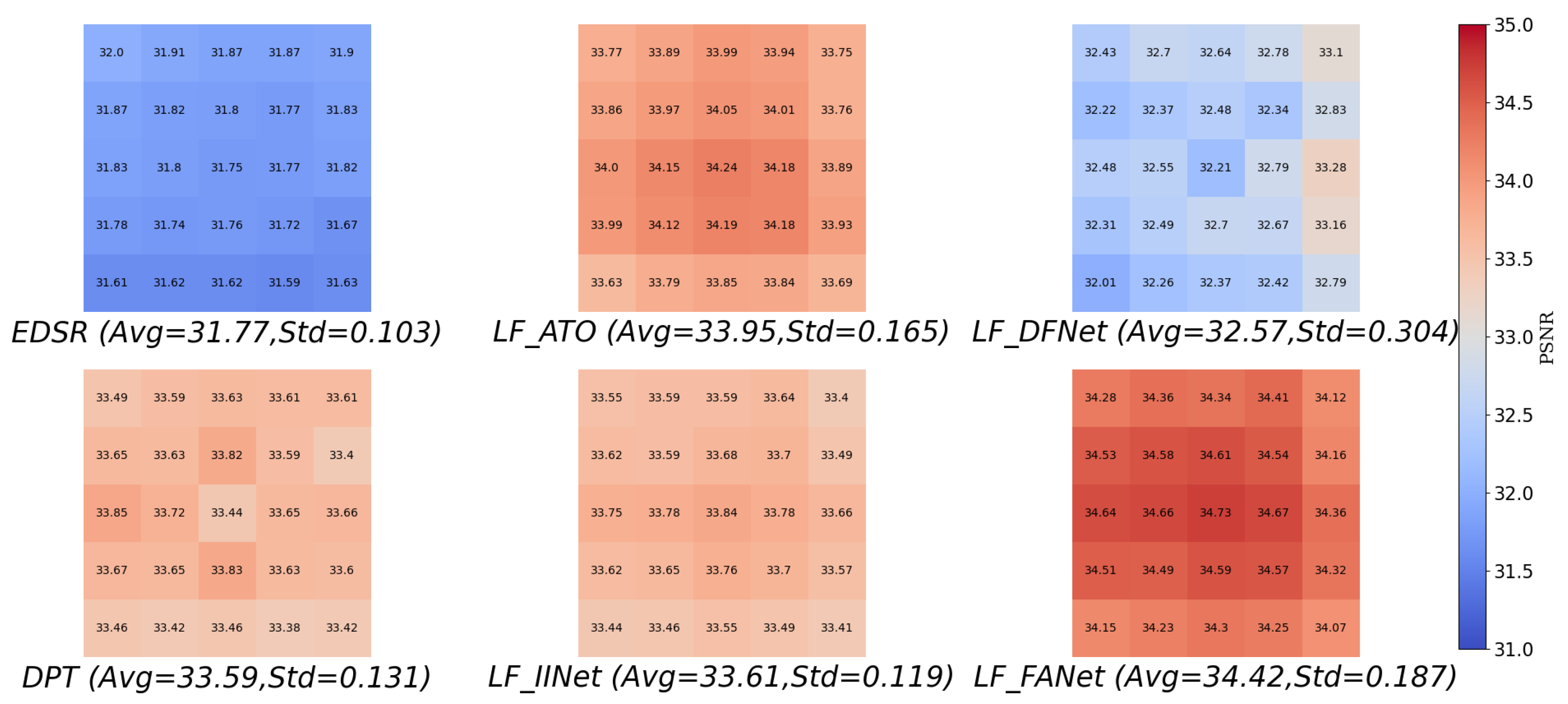
4.3.5. Performance of Different Perspectives
4.4. Ablation Study for Different Components of LF-FANet
4.4.1. LF-FANet w/o DASPP
4.4.2. LF-FANet w/o AFO
4.4.3. LF-FANet w/o SFO
4.4.4. LF-FANet w/o IIFB
4.4.5. LF-FANet w/o FB
4.4.6. LF-FANet w/o dual_branch
4.4.7. Number of Fusion and Allocation Mechanisms
4.4.8. Performance of Different Angular Resolutions
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Perwa, C.; Wietzke, L. Raytrix: Light Filed Technology; Raytrix GmbH: Kiel, Germany, 2018. [Google Scholar]
- Zhu, H.; Wang, Q.; Yu, J. Occlusion-model guided antiocclusion depth estimation in light field. IEEE J. Sel. Top. Signal Process. 2017, 11, 965–978. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Li, J.; Wei, J.; Piao, Y.; Lu, H.; Wallach, H.; Larochelle, H.; Beygelzimer, A.; d’Alche Buc, F.; Fox, E. Memory-oriented Decoder for Light Field Salient Object Detection. In Proceedings of the NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; pp. 896–906. [Google Scholar]
- Bishop, T.E.; Favaro, P. The light field camera: Extended depth of field, aliasing, and superresolution. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 972–986. [Google Scholar] [CrossRef] [PubMed]
- Wanner, S.; Goldluecke, B. Spatial and angular variational super-resolution of 4D light fields. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 608–621. [Google Scholar]
- Wanner, S.; Goldluecke, B. Variational light field analysis for disparity estimation and super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 606–619. [Google Scholar] [CrossRef] [PubMed]
- Mitra, K.; Veeraraghavan, A. Light field denoising, light field superresolution and stereo camera based refocussing using a GMM light field patch prior. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 22–28. [Google Scholar]
- Rossi, M.; Frossard, P. Geometry-consistent light field super-resolution via graph-based regularization. IEEE Trans. Image Process. 2018, 27, 4207–4218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Wang, Y.; Liu, F.; Zhang, K.; Hou, G.; Sun, Z.; Tan, T. LFNet: A novel bidirectional recurrent convolutional neural network for light-field image super-resolution. IEEE Trans. Image Process. 2018, 27, 4274–4286. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Lin, Y.; Sheng, H. Residual networks for light field image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 11046–11055. [Google Scholar]
- Jin, J.; Hou, J.; Chen, J.; Kwong, S. Light field spatial super-resolution via deep combinatorial geometry embedding and structural consistency regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2260–2269. [Google Scholar]
- Wang, Y.; Wang, L.; Yang, J.; An, W.; Yu, J.; Guo, Y. Spatial-angular interaction for light field image super-resolution. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 290–308. [Google Scholar]
- Wang, Y.; Yang, J.; Wang, L.; Ying, X.; Wu, T.; An, W.; Guo, Y. Light field image super-resolution using deformable convolution. IEEE Trans. Image Process. 2020, 30, 1057–1071. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Chang, S.; Lin, Y. End-to-end light field spatial super-resolution network using multiple epipolar geometry. IEEE Trans. Image Process. 2021, 30, 5956–5968. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ke, W.; Sheng, H.; Xiong, Z. Progressive Multi-Scale Fusion Network for Light Field Super-Resolution. Appl. Sci. 2022, 12, 7135. [Google Scholar] [CrossRef]
- Zhang, W.; Ke, W.; Yang, D.; Sheng, H.; Xiong, Z. Light field super-resolution using complementary-view feature attention. Comput. Vis. Media 2023. [Google Scholar] [CrossRef]
- Liu, G.; Yue, H.; Wu, J.; Yang, J. Intra-Inter View Interaction Network for Light Field Image Super-Resolution. IEEE Trans. Multimed. 2021, 25, 256–266. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Mao, X.J.; Shen, C.; Yang, Y.B. Image restoration using convolutional auto-encoders with symmetric skip connections. arXiv 2016, arXiv:1606.08921. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4799–4807. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11065–11074. [Google Scholar]
- Yoon, Y.; Jeon, H.G.; Yoo, D.; Lee, J.Y.; So Kweon, I. Learning a deep convolutional network for light-field image super-resolution. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Santiago, Chile, 7–13 December 2015; pp. 24–32. [Google Scholar]
- Cheng, Z.; Xiong, Z.; Liu, D. Light field super-resolution by jointly exploiting internal and external similarities. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 2604–2616. [Google Scholar] [CrossRef]
- Meng, N.; Wu, X.; Liu, J.; Lam, E. High-order residual network for light field super-resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11757–11764. [Google Scholar]
- Mo, Y.; Wang, Y.; Xiao, C.; Yang, J.; An, W. Dense Dual-Attention Network for Light Field Image Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 4431–4443. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, T.; Lu, Y.; Di, H. Detail preserving transformer for light field image super-resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022. [Google Scholar]
- Wang, Y.; Wang, L.; Wu, G.; Yang, J.; An, W.; Yu, J.; Guo, Y. Disentangling light fields for super-resolution and disparity estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 425–443. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeung, H.W.F.; Hou, J.; Chen, X.; Chen, J.; Chen, Z.; Chung, Y.Y. Light field spatial super-resolution using deep efficient spatial-angular separable convolution. IEEE Trans. Image Process. 2018, 28, 2319–2330. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Honauer, K.; Johannsen, O.; Kondermann, D.; Goldluecke, B. A dataset and evaluation methodology for depth estimation on 4d light fields. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 19–34. [Google Scholar]
- Wanner, S.; Meister, S.; Goldluecke, B. Datasets and benchmarks for densely sampled 4D light fields. In Proceedings of the VMV, Lugano, Switzerland, 11–13 September 2013; Volume 13, pp. 225–226. [Google Scholar]
- Rerabek, M.; Ebrahimi, T. New light field image dataset. In Proceedings of the 8th International Conference on Quality of Multimedia Experience (QoMEX), Lisbon, Portugal, 6–8 June 2016. [Google Scholar]
- Le Pendu, M.; Jiang, X.; Guillemot, C. Light field inpainting propagation via low rank matrix completion. IEEE Trans. Image Process. 2018, 27, 1981–1993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaish, V.; Adams, A. The (New) Stanford Light Field Archive; Computer Graphics Laboratory, Stanford University: Stanford, CA, USA, 2008; Volume 6. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]









| Datasets | Training | Test | LF Disparity | Type |
|---|---|---|---|---|
| HCInew [35] | 20 | 4 | [−4, 4] | Synthetic |
| HCIold [36] | 10 | 2 | [−3, 3] | Synthetic |
| EPFL [37] | 70 | 10 | [−1, 1] | Real-world |
| INRIA [38] | 35 | 5 | [−1, 1] | Real-world |
| STFgantry [39] | 9 | 2 | [−7, 7] | Real-world |
| Total | 144 | 23 |
| Methods | Scale | Datasets | Average | ||||
|---|---|---|---|---|---|---|---|
| EPFL | HCInew | HCIold | INRIA | STFgantry | |||
| Bicubic | 29.50/0.935/0.198 | 31.69/0.934/0.222 | 37.46/0.978/0.115 | 31.10/0.956/0.200 | 30.82/0.947/0.156 | 32.11/0.950/0.178 | |
| VDSR [10] | 32.64/0.960/0.092 | 34.45/0.957/0.122 | 40.75/0.987/0.050 | 34.56/0.975/0.093 | 35.59/0.979/0.034 | 35.60/0.972/0.078 | |
| EDSR [11] | 33.05/0.963/0.077 | 34.83/0.959/0.111 | 41.00/0.987/0.047 | 34.88/0.976/0.080 | 36.26/0.982/0.022 | 36.00/0.973/0.067 | |
| LFSSR [33] | 32.84/0.969/0.050 | 35.58/0.968/0.069 | 42.05/0.991/0.027 | 34.68/0.980/0.066 | 35.86/0.984/0.032 | 36.20/0.978/0.049 | |
| resLF [13] | 33.46/0.970/0.044 | 36.40/0.972/0.039 | 43.09/0.993/0.018 | 35.25/0.980/0.057 | 37.83/0.989/0.017 | 37.21/0.981/0.035 | |
| LF-ATO [14] | 34.22/0.975/0.041 | 37.13/0.976/0.040 | 44.03/0.994/0.017 | 36.16/0.984/0.056 | 39.20/0.992/0.011 | 38.15/0.984/0.033 | |
| LF-InterNet [15] | 34.14/0.975/0.040 | 37.28/0.977/0.043 | 44.45/0.995/0.015 | 35.80/0.985/0.054 | 38.72/0.991/0.035 | 38.08/0.985/0.037 | |
| LF-DFNet [16] | 34.44/0.976/0.045 | 37.44/0.979/0.048 | 44.23/0.994/0.020 | 36.36/0.984/0.058 | 39.61/0.994/0.015 | 38.42/0.985/0.037 | |
| MEG-Net [17] | 34.30/0.977/0.048 | 37.42/0.978/0.063 | 44.08/0.994/0.023 | 36.09/0.985/0.061 | 38.77/0.991/0.028 | 38.13/0.985/0.044 | |
| DPT [30] | 34.48/0.976/0.045 | 37.35/0.977/0.046 | 44.31/0.994/0.019 | 36.40/0.984/0.059 | 39.52/0.993/0.015 | 38.41/0.985/0.037 | |
| LF-IINet [20] | 34.68/0.977/0.038 | 37.74/0.978/0.033 | 44.84/0.995/0.014 | 36.57/0.985/0.053 | 39.86/0.993/0.010 | 38.74/0.986/0.030 | |
| DistgSSR [31] | 34.78/0.978/0.035 | 37.95/0.980/0.030 | 44.92/0.995/0.014 | 36.58/0.986/0.051 | 40.27/0.994/0.009 | 38.90/0.987/0.028 | |
| Ours | 34.81/0.979/0.034 | 37.93/0.979/0.030 | 44.90/0.995/0.014 | 36.59/0.986/0.050 | 40.30/0.994/0.008 | 38.91/0.987/0.027 | |
| Bicubic | 25.26/0.832/0.435 | 27.71/0.852/0.464 | 32.58/0.934/0.339 | 26.95/0.887/0.412 | 26.09/0.845/0.432 | 27.72/0.870/0.416 | |
| VDSR [10] | 27.22/0.876/0.287 | 29.24/0.881/0.325 | 34.72/0.951/0.204 | 29.14/0.920/0.278 | 28.40/0.898/0.198 | 29.74/0.905/0.258 | |
| EDSR [11] | 27.85/0.885/0.270 | 29.54/0.886/0.313 | 35.09/0.953/0.197 | 29.72/0.926/0.268 | 28.70/0.906/0.175 | 30.18/0.911/0.245 | |
| LFSSR [33] | 28.13/0.904/0.246 | 30.38/0.908/0.281 | 36.26/0.967/0.148 | 30.15/0.942/0.245 | 29.64/0.931/0.180 | 30.91/0.931/0.220 | |
| resLF [13] | 28.17/0.902/0.236 | 30.61/0.909/0.261 | 36.59/0.968/0.136 | 30.25/0.940/0.233 | 30.05/0.936/0.141 | 31.13/0.931/0.202 | |
| LF-ATO [14] | 28.74/0.913/0.222 | 30.97/0.915/0.256 | 37.01/0.970/0.135 | 30.88/0.949/0.220 | 30.85/0.945/0.116 | 31.69/0.938/0.190 | |
| LF-InterNet [15] | 28.58/0.913/0.227 | 30.89/0.915/0.258 | 36.95/0.971/0.131 | 30.58/0.948/0.227 | 30.32/0.940/0.133 | 31.47/0.937/0.195 | |
| LF-DFNet [16] | 28.53/0.906/0.225 | 30.66/0.900/0.269 | 36.58/0.965/0.134 | 30.55/0.941/0.226 | 29.87/0.927/0.159 | 31.32/0.928/0.203 | |
| MEG-Net [17] | 28.75/0.902/0.239 | 31.10/0.907/0.278 | 37.29/0.9663.144 | 30.67/0.940/0.239 | 30.77/0.930/0.179 | 31.72/0.929/0.216 | |
| DPT [30] | 28.93/0.917/0.241 | 31.19/0.919/0.273 | 37.39/0.972/0.145 | 30.96/0.950/0.236 | 31.14/0.949/0.157 | 31.92/0.941/0.210 | |
| LF-IINet [20] | 29.04/0.919/0.215 | 31.36/0.921/0.245 | 37.44/0.973/0.123 | 31.03/0.952/0.216 | 31.21/0.950/0.125 | 32.02/0.943/0.185 | |
| DistgSSR [31] | 28.98/0.919/0.231 | 31.38/0.922/0.244 | 37.38/0.971/0.134 | 30.99/0.952/0.227 | 31.63/0.954/0.118 | 32.07/0.944/0.191 | |
| Ours | 29.14/0.920/0.213 | 31.41/0.923/0.235 | 37.50/0.973/0.112 | 31.04/0.952/0.213 | 31.68/0.954/0.109 | 32.15/0.944/0.176 | |
| Ang | Scale | Params. (M) | FLOPs (G) | Avg. PSNR/SSIM |
|---|---|---|---|---|
| EDSR [11] | 38.89 | 1016.59 | 30.18/0.911 | |
| LFSSR [33] | 1.77 | 113.76 | 31.23/0.935 | |
| LF-ATO [14] | 1.36 | 597.66 | 31.69/0.938 | |
| LF-DFNet [16] | 3.94 | 57.22 | 31.32/0.928 | |
| DPT [30] | 3.78 | 58.64 | 31.92/0.941 | |
| LF-FANet (Ours) | 3.38 | 257.38 | 32.15/0.944 |
| Models | Params. | Datasets | Average | ||||
|---|---|---|---|---|---|---|---|
| EPFL | HCInew | HCIold | INRIA | STFgantry | |||
| Bicubic | – | 25.14/0.831 | 27.61/0.851 | 32.42/0.934 | 26.82/0.886 | 25.93/0.943 | 27.58/0.869 |
| LF-FANet w/o DASPP | 2.86 M | 28.80/0.916 | 31.19/0.919 | 37.37/0.972 | 30.78/0.950 | 31.12/0.949 | 31.85/0.941 |
| LF-FANet w/o AFO_only | 2.69 M | 28.13/0.894 | 30.11/0.899 | 35.83/0.961 | 30.12/0.935 | 29.41/0.922 | 30.70/0.922 |
| LF-FANet w/o AFO_rm | 3.10 M | 28.59/0.912 | 31.00/0.916 | 37.01/0.970 | 30.75/0.948 | 30.87/0.946 | 31.65/0.938 |
| LF-FANet w/o SFO_only | 2.82 M | 27.76/0.885 | 29.57/0.886 | 35.12/0.954 | 29.70/0.926 | 28.87/0.909 | 30.20/0.912 |
| LF-FANet w/o SFO_rm | 3.07 M | 28.43/0.910 | 30.86/0.913 | 36.90/0.970 | 30.56/0.947 | 30.49/0.941 | 31.45/0.936 |
| LF-FANet w/o IIFB_only | 2.57 M | 28.46/0.910 | 30.82/0.913 | 36.88/0.969 | 30.56/0.946 | 30.47/0.941 | 31.44/0.936 |
| LF-FANet w/o IIFB_rm | 2.49 M | 28.27/0.897 | 30.26/0.902 | 36.05/0.963 | 30.37/0.938 | 29.67/0.927 | 30.92/0.925 |
| LF-FANet w/o FB | 2.34 M | 28.64/0.912 | 30.95/0.916 | 36.95/0.970 | 30.72/0.948 | 30.69/0.944 | 31.59/0.938 |
| LF-FANet w/o dual_branch | 3.64 M | 28.82/0.915 | 31.16/0.919 | 37.28/0.972 | 30.89/0.950 | 31.06/0.948 | 31.84/0.941 |
| LF-FANet | 3.38 M | 29.14/0.920 | 31.41/0.923 | 37.50/0.973 | 31.04/0.952 | 31.68/0.954 | 32.15/0.944 |
| Ang | Num | Scale | Params. (M) | Ave. PSNR | Ave. SSIM |
|---|---|---|---|---|---|
| 1 | 2.79 | 31.51 | 0.936 | ||
| 2 | 3.38 | 32.15 | 0.944 | ||
| 3 | 3.97 | 32.19 | 0.945 | ||
| 4 | 4.77 | 32.20 | 0.945 | ||
| 5 | 5.16 | 32.20 | 0.945 |
| Method | Dataset | Scale | Params. | PSNR | SSIM | Scale | Params. | PSNR | SSIM |
|---|---|---|---|---|---|---|---|---|---|
| LF-FANet_3x3 | EPFL | 2.85 M | 33.73 | 0.972 | 3.17 M | 28.52 | 0.907 | ||
| HCInew | 37.04 | 0.975 | 30.92 | 0.914 | |||||
| HCIold | 43.88 | 0.994 | 36.93 | 0.970 | |||||
| INRIA | 35.56 | 0.982 | 30.80 | 0.946 | |||||
| STFgantry | 38.96 | 0.992 | 30.75 | 0.944 | |||||
| LF-FANet_5x5 | EPFL | 3.00 M | 34.81 | 0.979 | 3.38 M | 29.14 | 0.920 | ||
| HCInew | 37.93 | 0.979 | 31.41 | 0.923 | |||||
| HCIold | 44.90 | 0.995 | 37.50 | 0.973 | |||||
| INRIA | 36.59 | 0.986 | 31.04 | 0.952 | |||||
| STFgantry | 40.30 | 0.994 | 31.68 | 0.954 | |||||
| LF-FANet_7x7 | EPFL | 3.50 M | 34.88 | 0.981 | 4.09 M | 29.20 | 0.921 | ||
| HCInew | 38.13 | 0.980 | 31.43 | 0.923 | |||||
| HCIold | 45.39 | 0.997 | 37.68 | 0.974 | |||||
| INRIA | 36.80 | 0.986 | 31.10 | 0.953 | |||||
| STFgantry | 40.56 | 0.995 | 31.80 | 0.955 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Ke, W.; Wu, Z.; Zhang, Z.; Sheng, H.; Xiong, Z. Fusion and Allocation Network for Light Field Image Super-Resolution. Mathematics 2023, 11, 1088. https://doi.org/10.3390/math11051088
Zhang W, Ke W, Wu Z, Zhang Z, Sheng H, Xiong Z. Fusion and Allocation Network for Light Field Image Super-Resolution. Mathematics. 2023; 11(5):1088. https://doi.org/10.3390/math11051088
Chicago/Turabian StyleZhang, Wei, Wei Ke, Zewei Wu, Zeyu Zhang, Hao Sheng, and Zhang Xiong. 2023. "Fusion and Allocation Network for Light Field Image Super-Resolution" Mathematics 11, no. 5: 1088. https://doi.org/10.3390/math11051088
APA StyleZhang, W., Ke, W., Wu, Z., Zhang, Z., Sheng, H., & Xiong, Z. (2023). Fusion and Allocation Network for Light Field Image Super-Resolution. Mathematics, 11(5), 1088. https://doi.org/10.3390/math11051088






