Transformer-Based Seq2Seq Model for Chord Progression Generation

Abstract

Machine learning is widely used in various practical applications with deep learning models demonstrating advantages in handling huge data. Treating music as a special language and using deep learning models to accomplish melody recognition, music generation, and music analysis has proven feasible. In certain music-related deep learning research, recurrent neural networks have been replaced with transformers. This has achieved significant results. In traditional approaches with recurrent neural networks, input sequences are limited in length. This paper proposes a method to generate chord progressions for melodies using a transformer-based sequence-to-sequence model, which is divided into a pre-trained encoder and decoder. A pre-trained encoder extracts contextual information from melodies, whereas a decoder uses this information to produce chords asynchronously and finally outputs chord progressions. The proposed method addresses length limitation issues while considering the harmony between chord progressions and melodies. Chord progressions can be generated for melodies in practical music composition applications. Evaluation experiments are conducted using the proposed method and three baseline models. The baseline models included the bidirectional long short-term memory (BLSTM), bidirectional encoder representation from transformers (BERT), and generative pre-trained transformer (GPT2). The proposed method outperformed the baseline models in Hits@k (k = 1) by 25.89, 1.54, and 2.13 %, respectively.

1. Introduction

Machine learning has started making inroads in daily life; its use in various practical applications, particularly deep learning with its advantages of handling huge data, is significant. Due to the excellent performance of deep learning in natural language processing tasks, it has also been applied to other research fields where data are in the form of sequences [1]. Digital music data has increased significantly, as the Internet has become more widely used and streaming services have become more popular. Treating music as a special language and using deep learning models to accomplish melody recognition [2,3], music generation [4,5], and music analysis [6,7] has proven feasible. Music-related research has primarily focused on melody thus far. Additionally, chord progression is an essential element in music and equally significant as melody. Chord progression refers to a sequence of chords that create various emotional effects and is the foundation of harmony in western music theory.

In early computer composition, researchers attempted to design a set of rules based on music theory to guide computers in creating chord progressions. One approach [8] suggests that a trance is the section of a song that contains highlights and usually repeats a chord in a 16-measure loop. A statistical model was designed to generate chord loops that could be trained on a chord corpus. Another approach [9] suggests a system, namely, the artificial immune system (AIS), which uses a penalty function for encoding musical rules. The penalty function was minimized during the training process of the AIS for generating chords in chord progressions. The trained AIS provides multiple suitable chords in parallel to produce chord progressions.

Unlike the acquisition of knowledge through encoding music theory, a few researchers produced chord progressions based on reinforcement learning. An automatic chord progression generator [10] based on reinforcement learning was introduced, which uses music theory to define rewards and Q-learning algorithms to train an agent. A trained agent can serve as an alternative tool for generating chord progressions and producing suitable chord progressions that composers can use in their compositions. Although the utilization of music theory can assist in the generation of harmonically sound chord progressions by the model, the modeling of music theory or the definition of rewards based on it is challenging. Additionally, this reliance on music theory may cause limitations in model generalization and diversity of generated chord progressions. Therefore, researchers have attempted to view music data as a special type of language by applying language modeling techniques.

Given that grammar is not required in natural language modeling, music theory may not be required in music modeling. In the early days of machine learning, when deep learning technology was not mature, the hidden Markov model (HMM) was used in language modeling to generate chord progressions. One such system, MySong [11], uses the HMM model to automatically select chords to accompany vocal melodies. Results indicate that chord progressions assigned to melodies using MySong received subjective scores similar to those assigned manually by musicians. Recurrent neural networks (RNNs), including long short-term memory (LSTM) and gate recurrent unit (GRU), show improved performance in the processing of discrete temporal sequence data. An LSTM-based dynamic chord progression generation system [12] is designed to handle polyphonic guitar music. Chord progression generation is formulated as a prediction process. Therefore, an LSTM-based network architecture incorporating neural attention is proposed, which can learn the mapping between previous symbolic representations of chords and future chord candidates. Additionally, a bidirectional long short-term memory (BLSTM)-based chord-progression generation approach [13] was introduced to generate chord progressions from symbolic melodies. Furthermore, BLSTM networks are trained on a lead sheet database, where a group of feature vectors composed of 12 semitones is extracted from the notes in each measure of the monophonic melodies. To ensure that the notes share a uniform key and duration, the key and time signatures of the vectors are normalized. Subsequently, BLSTM learn temporal dependencies from the music corpus to generate chord progressions. However, the length of the sequence representing the melody is a limitation of a chord progression generator based on RNNs. Because of back-propagation through time (BPTT), RNNs cannot handle long-distance dependencies well. A common approach to resolving this issue is to shorten the length of the sequences to the extent possible, enabling only a few measures of melodies as input and only generating a single chord for each measure.

This paper proposes a method for generating chord progressions for melodies using a transformer-based sequence-to-sequence (Seq2Seq) model. The model consists of two parts: a pre-trained encoder and decoder. The pre-trained encoder takes melodies as input and analyzes them from both directions to extract contextual information. Subsequently, the contextual information is passed to the decoder. The decoder receives the same melodies as the input, however, in an asynchronous manner. The decoder generates chords step-by-step by considering contextual information and input melodies and finally outputs chord progressions.

The proposed method has several advantages. First, it relies entirely on a music corpus and does not require music theory. Second, it addresses the issue of long-distance dependencies, which RNNs cannot handle well. Finally, the pretrained encoder ensures that chord progressions generated are suitable for melodies by pulling contextual information from them.

The proposed method makes the following contributions: (1) compared to the chord progression generation approaches based on music theory, the Seq2Seq model of the proposed method trained on a music corpus has higher adjustability and generalizability; (2) it overcomes the limitations of traditional RNN-based approaches in chord progression generation, which are unable to handle long-distance dependencies and makes the transitions in chord progression smoother rather than being limited to only one chord per measure; and (3) by considering melody compatibility, the proposed method can generate suitable chord progressions for melodies and serve as an alternative tool for composition.

The remainder of this paper is organized as follows. Section 2 reviews studies on transformer-based music generation. Section 3 describes the proposed method for the generation of chord progressions. Section 4 presents the experimental results and discussions of the results. Section 5 presents the concluding remarks.

2. Related Work

The transformer has replaced RNNs and achieved notable results in temporal sequence processing. The use of transformers has also become a trend in the field of music generation. The most widely used approaches are reviewed briefly in this section.

2.1. Transformer (-XL) Based Approaches

One of the current state-of-the-art transformer-based music generation approaches [14] is trained with a single sequence of notes. LakhNES [15] focused on generating multi-instrumental music scores using a transformer architecture. A transformer is a complex, high-dimensional language model that can capture long-term structures in sequence data. LakhNES uses the NES-MDB dataset of four-instrument scores rather than a single note sequence from an early video game sound synthesis chip and Lakh MIDI dataset for pre-training to improve the performance of the model.

To enable the transformer to handle longer music, Museformer [16] improves the full attention of the original transformer by using fine- and coarse-grained attention, which processes sequences that are three times longer than the original transformer.

Another framework based on transformer-XL [17] has been suggested, which includes two novel approaches [18]: building time-valued note sequences and the separation of four sequences for individual use for the joint training of four transformer-XL networks.

2.2. Transformer-GANs-Based Approaches

Generative adversarial networks (GANs) are composed of generators and discriminators. They are widely used to generate new samples through unsupervised learning on datasets. The combination of transformers and GANs to generate music is a creative task. A transformer-XL generator and pre-trained bidirectional encoder representation from transformers (BERT) model as the discriminator were used to design transformer-GANs [19], which helps to stabilize the training. The Gumbel-Softmax trick was used to obtain a differentiable approximation of the sampling process, making discrete sequences easy to optimize.

Another transformer-GAN-based research suggests a learning adversarial transformer [20], which computes the reward for each generated step (REGS) for a long sequence rather than adopting the time-consuming Monte Carlo (MC) search method commonly used in sequence generative models. The discriminator is trained to optimize the elaborately designed global and local loss objective functions simultaneously, enabling it to provide reliable REGS for the generator.

2.3. Conditional Transformer-Based Approaches

By adding conditional vectors to the transformer, user-specified music was generated. Among them, the theme-conditioned transformer [21] explicitly trains the transformer to treat the conditioning sequence as thematic material that must manifest itself multiple times in its generation result. Additionally, a controllable music transformer [22] receives images as conditional input and combines user-defined features to generate background music for videos.

2.4. Differences between the Proposed Method and Previous Works

The proposed method uses the transformer-based Seq2Seq model to produce chord progressions for melodies. This differs from previous works in the following ways. (1) The proposed method focuses on generating chord progressions based on a given melody, which is a more purposeful generation task. (2) To achieve this goal, the proposed method uses a parallel model based on the attention mechanism, which is adept at handling such tasks to fully understand the given melodies and generate chord progressions based on them. (3) Pre-training techniques are used in the proposed method to make the pre-trained encoder in the Seq2Seq model more effective in extracting contextual information.

3. Transformer-Based Seq2Seq Model for Chord Progression Generation

In this paper, a method is proposed to generate chord progressions for melodies using a transformer-based Seq2Seq model. First, the representations of melodies and chord progressions are demonstrated. Then, the process of pre-training the encoder is introduced. Finally, the process of generating chord progressions for melodies based on the Seq2Seq model is explained.

3.1. Symbolic Data Representation

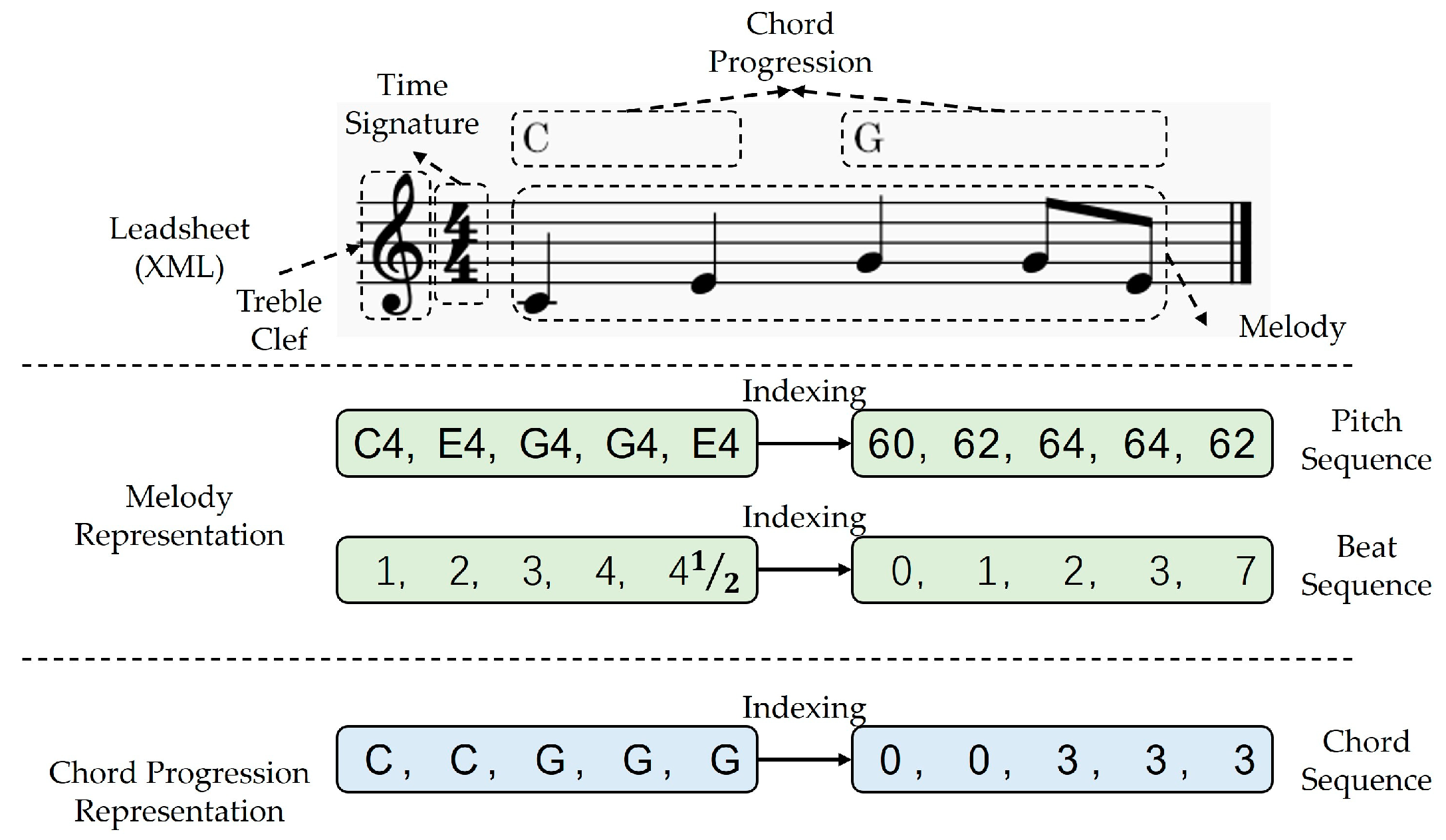
Figure 1 shows that the required melodies and chord progressions for training are obtained from lead sheets in XML format, which are sourced from the OpenEWLD music corpus. The Python library music21 is utilized to extract relevant events for notes and chords, which include information on time signature, pitch, beat, and chord types. The time signature specifies how many beats are contained in each measure, and which note value is equivalent to a beat. For example, in a 4/4 time signature, each measure consists of four quarter notes, and each quarter note lasts for one beat. In order for computers to understand melody and chord progression, they must be converted into a kind of indexed sequence.

Melody is represented as pitch and beat sequences, where each element in pitch sequence consists of two parts: pitch name and octave. The pitch names consist of 12 different types, which are C, C#(=Db), D, D#(=Eb), E, F, F#(=Gb), G, G#(=Ab), A, A#(=Bb), and B. The octaves are represented by integers, and adjacent octaves differ by 12 semitones. In treble clef, the note represented by a ledger line below the staff is C4. To index the pitch sequence, the Musical Instrument Digital Interface (MIDI) is used as a reference. MIDI is the most widely used music standard format in the music composition industry and can represent a range of 128 pitches from C-1 (index = 0) to G9 (index = 127). In addition, the index of <PAD> is defined as 128 to ensure a same input length during model training.

The elements in the beat sequence and pitch sequence correspond one-to-one. Each beat of a measure starts at 1, and the interval between adjacent integer beats is the length of a quarter note. The music in the corpus is all monophonic, meaning that only one note is played at a time. Beats are used to indicate the starting position of notes, and they last until the beginning of the next note. As shown in Figure 1, the beat sequence of a measure is “1, 2, 3, 4, 4$\frac{1}{2}$,” meaning that the notes in this measure start at beats 1, 2, 3, 4, and 4$\frac{1}{2}$. The note on the first beat represents a note that starts at the beat 1 and lasts for one quarter note. The note on the last beat represents a note that starts at the beat 4$\frac{1}{2}$ and lasts for a half quarter note (because the length of a measure with 4/4 time signature is 4 quarter notes). A total of 46 kinds of beat in different kinds of time signature are extracted from the music corpus, and each beat is assigned an index from 0 to 45. The index of <PAD> is set to 46, and the index of <UNK> is set to 47. The reason for adding <UNK> is to prevent the model from failing to run due to uncommon beats during testing or actual application.

The chord progressions are represented by sequences of chords, which includes triads, seventh, ninth chords, and so on. Additionally, chords can also be further classified into major, minor, augmented, and diminished chords. In the music corpus, a total of 428 chords were extracted and assigned an index from 0 to 429, where 0 represents <PAD> and 401 represents <UNK>. As shown in Figure 1, the chord sequence corresponding to the pitch and beat sequences is generated. “C” represents the C major triad converted to index 1, and “G” represents the G major triad converted to index 2. Each chord influences the pitch of the current and subsequent pitches in the melody until a new chord is appeared. For example, C major triad affects the pitches of C4 and E4, while G major triad affects the pitches of G4, B4, and D5.

3.2. Pre-Training of Encoder

During the pre-training of the encoder, five noise patterns are designed to encourage the encoder to understand the melodies, as shown in Figure 2. The noise patterns include Start Note Permutation, End Note Permutation, Random Notes Changing, Random Notes Masking, and Neighbor Notes Rotation. Start Note Permutation is designed to swap the starting note of a melody with a random note from the melody. This enables the encoder to learn the relationship between the starting note and remaining melody as well as potential effects of changing the starting note on the overall structure of the melody. End Note Permutation is similar to Start Note Permutation, which involves swapping the position of the last note with the other notes in the melody. Random Notes Changing and Random Notes Masking are designed to randomly replace notes in a melody with notes from the melody, or with the special masking symbol “_”. The two patterns refer to masked language modeling [23]. This helps the encoder learn to detect incorrect notes and fill in missing notes, thereby deepening the understanding of melodies. Neighbor Notes Rotation is designed to randomly swap the positions of two adjacent notes in a melody. Because melodies have a certain trend, such as rising or falling, the encoder can strengthen its understanding of the melody by rotating the notes. During pre-training, a melody can have all five noise patterns applied to them simultaneously.

As shown in Figure 3, the pitch ($p_1,p_2,p_3,\dots ,p_n$) and beat sequences ($b_1,b_2,b_3,\dots ,b_n$) of a melody are paired and then noised (an example utilized two noise patterns, Start Note Permutation and Random Notes Masking) to obtain ($p_3,\_,p_1,\dots ,p_n$) and ($b_3,\_,b_1,\dots ,b_n$), which are then embedded in the encoder. The encoder is composed of multiple layers of transformers. The encoder uses transformers to capture long-distance dependencies in both directions, which is crucial for understanding and restoring a melody to obtain ($p_1^{\prime }, p_2^{\prime }, p_3^{\prime }$) and ($b_1^{\prime }, b_2^{\prime }, b_3^{\prime }$). This enables the encoder to accurately identify and repair errors or inconsistencies in the melody. After pretraining, the pitch and beat prediction layers were discarded.

3.3. Generating Chord Progressions by Seq2Seq Model

In this paper, a transformer-based Seq2Seq model is proposed to generate chord progressions for melodies. The Seq2Seq model consists of a pre-trained encoder and decoder. As shown in Figure 4, the Seq2Seq model generates chord progressions based on melodies. First, pitch ($p_1, p_2,p_3, \dots , p_n$) and beat sequences ($b_1, b_2,b_3, \dots , b_n$) were passed through the note and beat embedding layers, respectively. These embedded features were then concatenated and fed into the pre-trained encoder. The transformers within the pre-trained encoder were fully connected, enabling full consideration of the input melodies from both directions and extraction of contextual information to ensure that the future generated chord progressions were suitable for the input melodies.

Additionally, the decoder input is divided into two types. One is the concatenated embedding feature obtained from the embedding layers and the other is the contextual information $h_n$ extracted from the pre-trained encoder. This contextual information is input as the key and the value through cross-attention in each transformer in the decoder, whereas the query uses the concatenated embedding features of the pitch and beat sequences. In the decoder, the connections between transformers are unidirectional. This implies that when predicting the current chord, only the current and previous pitches and beats can be considered. In this manner, chord sequences are generated asynchronously by the chord prediction layer, which is a linear layer with Softmax. The chord prediction layer output is a probability distribution that predicts the chord corresponding to both the pitch and beat. To obtain the chord sequence ($c_1, c_2,c_3, \dots , c_n$), the argmax function is used to identify the indexes with the highest values. To present the result, the chord sequences are first reverse indexed to get chord progressions. Then, the chord progressions are re-encoded using the Python library music21 to output music in MIDI format.

It should be noted that compared to traditional Seq2Seq models that use RNNs, transformer-based Seq2Seq models have greater advantages. Firstly, the parallel mechanism of the transformer does not require sequential calculation like RNNs. Therefore, even if the number of layers and dimensions of the transformer increases, it can still be trained and inferred more quickly. Secondly, the transformer-based decoder can asynchronously receive input to obtain information for the current time step. Compared to traditional Seq2Seq models that only rely on last hidden states of encoder, transformer-based Seq2Seq models consider both contextual and asynchronous features simultaneously.

4. Experiments

The proposed method and three types of baseline models were trained and evaluated using the OpenEWLD [24] dataset. In this section, details of the dataset, the structure of the baseline models, training hypermeters, and evaluation results are introduced.

4.1. Dataset

Enhanced Wikifonia Leadsheet Dataset (EWLD) is a music lead sheet corpus in MusicXML format. OpenEWLD [24] is a subset of EWLD that contains only lead sheets in the public domain, and it is used as the experimental dataset in this paper. This subset includes 502 lead sheet music formats, from which 502 pairs of pitch, beat sequences from melodies, and chord sequences from chord progressions were extracted. Additionally, 328 types of chords were extracted from the dataset. Figure 5 shows the chords for the top-30 frequency. Among them, the C major triad had the highest frequency, accounting for approximately 8.1% of all chord occurrences.

4.2. Baseline Models

In this paper, three baseline models were designed. As shown in Figure 6A, this is a BLSTM-based chord progression generation model composed of two LSTM layers in the forward and backward directions. The model is an improved version of the BLSTM model of Lim et al. [13], in which the embedding layer is replaced with the same embedding layer as in the proposed method. The model in Figure 6B is designed according to BERT [23], which is a bidirectional model that can consider contextual features. The last layer of the model was fully connected to a linear layer using Softmax to generate chord progressions. The model shown in Figure 6C is designed to refer to a generative pre-trained transformer (GPT2) [25], which is asynchronous and only considers information from the current time step and previous steps. The final layer is fully connected directly to a linear layer with Softmax.

4.3. Experimental Environment

The experiment was conducted on the model of the proposed method as well as on three other baseline models.

Table 1. Hyperparameters of the model of proposed method and baseline models.

Hyperparameters	Proposed Method	BLSTM [13]	BERT [23]	GPT2 [25]
Number of Layers	24 1	32	32	32
Hidden size	1024	1024	1024	1024
FFN inner hidden size	4096	-	4096	4096
Attention heads	16	-	16	16
Attention head size	8 $\times$ 8	-	8 $\times$ 8	8 $\times$ 8
Dropout	0.1	0.1	0.1	0.1
Max Sequence Length	512	512	512	512
Max Epochs	100	100	100	100
Warmup Epochs	10	10	10	10
Batch Size	8	8	8	8
Learning Rate Decay	Line	Line	Line	Line
Weight Decay	0.01	0.01	0.01	0.01
Adam $ϵ$	$1\times {10}^6$	$1\times {10}^6$	$1\times {10}^6$	$1\times {10}^6$
Adam ${\beta }_1$	0.9	0.9	0.9	0.9
Adam ${\beta }_2$	0.98	0.98	0.98	0.98
Number of Trainable Parameters	408 M	397 M	382 M	476 M

¹ The model of proposed method was composed of a total of 24 transformer layers, with the pre-trained encoder and decoder each consisting of 12 transformer layers.

lists the hyperparameters used in the training of each model. When setting the hyperparameters, the values were set as similar as possible in four models. In this case, Max Sequence Length, Max Epochs, Warmup Epochs, Batch Size, and optimizer-related hyperparameters such as Learning Rate Decay, Weight Decay, Adam $ϵ$, Adam ${\beta }_1$, and Adam ${\beta }_2$ were set to the same in all models. Since the length of music can be diverse, the Max Sequence Length of the input sequences has been set to 512, which is also the maximum sequence length that the transformer can handle. Based on the proposed data representation method, all music in the dataset is no longer than this length, and any shorter sequences were padded with <PAD>. Because the output chord sequence corresponds to the pitch and beat sequences, its maximum sequence length was also set to 512. Additionally, in the three models using transformers, transformer-related parameters such as Hidden size, FFN inner hidden size, Attention heads, Attention head size, and Dropout were set to the same value. Additionally, the model using BLSTM has its Hidden size set to 1024 and Dropout set to 0.1. Finally, to balance the number of trainable parameters in a comparable range, the number of layers in the four models was set to 24, 32, 32, and 32, respectively.

Table 2. Hardware, software, and machine learning based libraries used in experiments.

Item	Description	Number
CPU	Intel Xeon Silver 4310	2
GPU	NVIDIA RTX3090 24GB	4
RAM	Samsung 32GB DDR4	4
SSD	Seagate FireCuda 530 2TB	1
OS	Ubuntu 20.04.1 LTS (GNU/Linux 5.4.0)	-
Programming Language	Python 3.8.10	-
Python IDE	PyCharm 2021.1.1	-
Machine Learning Library	PyTorch 1.13.0 Numpy 1.23.4 Transformers 4.24.0 Accelerate 0.15.0	-

shows the hardware, software, and machine learning based libraries used in experiments. The experiments were carried out on an Ubuntu 20.04.1 LTS (GNU/Linux 5.4.0) operating system with the source code written in Python 3.8.10 using PyCharm 2021.1.1. PyTorch 1.13.0, NumPy 1.23.4, Transformers 4.24.0, and Accelerate 0.15.0 machine learning libraries were used. PyTorch and Transformers were used for model building, NumPy was used for data preprocessing and representation, and Accelerate was used to optimize the training process to speed up training. The hardware environment used for the experiments is detailed in the table, and included CPU, GPU, RAM, and SSD.

4.4. Experimental Results and Discussion

Figure 7 shows the change in the average loss per epoch for the four models during the training process, where the loss calculation used the cross-entropy function. The BLSTM model had a more evident downward trend than other models at the beginning of training. However, the loss did not continuously decrease. The loss-decreasing trend of the three models using the transformer was approximately the same. The losses of BERT and GPT2 approached equality after 60 epochs and converged after 80 epochs. In the first 20 epochs, the convergence speed of the proposed method was not the fastest. However, after 40 epochs, the decline in loss exceeded that of the other models, and even after 80 epochs, a slight downward trend was observed in the loss.

The experimental results show that BLSTM cannot overcome the long-distance dependencies issue. In comparison, the transformer-based model demonstrated significant advantages in handling long sequences. Additionally, the proposed method using the Seq2Seq model outperformed BERT and GPT2 in terms of loss convergence.

Hits@k [22] was utilized as the metric to evaluate the generated chord progressions for calculating the ratio of the reference chord (from chord progressions assigned by human composers) presence among the top k candidate chords, where k = 1, 3, 5, 10, and 20. Hits@k is a widely used metric for evaluating recommendation models and is also employed in music generation to assess the quality of generated results [26]. Hits@k was calculated as shown in Formula 1, where n represents the number of samples; $\mathbb{I}\left(·\right)$ is an indicator function that returns 1 if the rank of the target is less than k, and 0 otherwise.

$$Hits@k=\frac{1}{n} {{\displaystyle \sum }}_{i=1}^n\mathbb{I}\left(ran{k}_i\le k\right)$$

(1)

Table 3. Hits@k scores of the proposed method and baseline models.

Model	HITS@1 (%)	HITS@3 (%)	HITS@5 (%)	HITS@10 (%)	HITS@20 (%)
Proposed Method	36.29	53.23	64.24	76.75	86.28
BERT [13]	34.75	51.56	62.46	75.93	85.76
GPT2 [23]	34.16	45.52	55.07	69.36	80.70
BLSTM [25]	10.40	24.30	36.70	53.53	71.63

shows the Hits@k scores of the proposed method and baseline models. The experimental results based on Hits@k indicated that BLSTM was not effective in completing the chord progression generation. However, the model of the proposed method outperformed the other models when evaluated using various k values. This implies that in the proposed method, the contextual information provided by the pre-trained encoder and asynchronous generation of the decoder collaborates effectively and is considered sufficient for melody compatibility.

Figure 8 shows the confusion matrices of the model of the proposed and other baseline models on chords with the top-30 frequency. The horizontal axis represents the generated chords, and the vertical axis represents the target chords. Furthermore, BLSTM only generated the C major triad chord, which appeared with the highest probability in the training dataset, indicating that it was unable to discover the relationship between melodies and chord progressions. A diagonal line was observed in the confusion matrices of the three transformer-based models, which indicates that the chords generated by these models align with those of human composers. In the part marked by the red box, the performance of the proposed method was significantly better than that of the other two transformer-based models.

This paper proposes a method that utilizes a transformer-based Seq2Seq model to generate chord progressions for melodies. The proposed method outperformed other baseline models, as observed in the Hits@k and confusion matrix.

In Table 3, the asynchronous GPT2 model performs approximately the same as BERT that considers contextual information only when k = 1 but is lower than BERT by about 5% to 6% in other k values. This indicated that considering contextual information can lead to more suitable chord progressions generated for a given melody. Furthermore, the proposed method, which considers both contextual information and asynchronous features, outperforms BERT by approximately 1% to 2% in all k values. This also suggested that emphasizing the input from the current and previous time steps is helpful for generating appropriate chords. However, generating chord progressions was distinct from classification; as in music, the relationship between melody and chord progression was not one-to-one. For instance, as shown in Figure 8, the three transformer-based models mostly predict the E minor triad as the G major triad. However, by analyzing the composition of the chords, it could be seen that the E minor triad is composed of E, G, and B, and G major triad is composed of G, B, and D. Both G and B appeared in both G major and E minor triads, which suggested that the appearance of the G major triad was not an error. However, the G major triad could serve as an alternative to the E minor triad under certain conditions.

The goal of chord progression generation is to generate chord progressions that comply with music theory and that possess diversity and uniqueness. However, collecting high-quality symbolic music data with chord progressions is challenging, therefore achieving breakthroughs in diversity and uniqueness is challenging. As shown in Figure 4, the distribution of chords in the OpenEWLD music corpus is unbalanced. Thus, the bright regions in Figure 8 tend to concentrate on the left part of the confusion matrix. When the model was uncertain, it tended to select chords with a higher frequency in the dataset.

5. Conclusions

This paper proposes a method for generating chord progressions using a transformer-based Seq2Seq model. The model was divided into two parts: a pre-trained encoder and decoder. The pre-trained encoder uses transformers to understand melodies from both the forward and reverse directions, extracting context information to pass on to the decoder. Additionally, the decoder takes the melodies as input and generates chord progressions asynchronously, considering the contextual information obtained from the pre-trained encoder. Based on the experimental results, the proposed method outperformed the three baseline models based on BLSTM, BERT, and GPT2 by 25.89, 1.54, and 2.13%, respectively, in terms of the Hits@k (k = 1) quantitative evaluation. Furthermore, BLSTM was unable to generate effective chord progressions due to the difficulty in handling long-term dependencies.

This transformer-based Seq2Seq model can be used in fields such as automatic music composition, chord recommendation, and automatic music accompaniment. For example, in music composition, the model can assist composers in creating more beautiful melodies and harmonies by generating chord progressions. In terms of chord recommendation, the model can automatically generate corresponding chord progressions based on the input melodies, thus providing users with a richer and more diverse selection of chords. In terms of automatic music accompaniment, the model can generate corresponding chord progressions based on the input melodies and use them as a basis for automatic accompaniment. In future research, to increase the diversity and uniqueness of generated chord progressions, melody and chords recognition and data balancing should be studied while continuously exploring the relationship between melodies and chord progressions.