Measuring and Modelling the Concentration of Vehicle-Related PM2.5 and PM10 Emissions Based on Neural Networks
Abstract
:1. Introduction
Literature Review
2. Materials and Methods
2.1. A Methodology for Calculating the Amount of Finely Dispersed Pollutant Emissions from Traffic Flows
- I—passenger vehicles;
- II—vehicles with a load capacity up to 3.5 tons;
- III—heavy-duty vehicles (over 3.5 tons).
2.2. Method Used to Calculate the Concentration of Finely Dispersed Pollutant Emissions from Traffic Flows
3. Experiment and Verification
3.1. Implementation of the Algorithm to Calculate the Amount and Concentration of Emissions from Mobile Emission Sources
- A = 160 for Chelyabinsk;
- F = 1 (gaseous pollutants and fine aerosols with a diameter of no more than 10µm);
- η = 1 (terrain features and urban development are not taken into account);
- H = 2 m (minimum source height);
- TGAM = 100 °C;
- D is the distance traveled by the vehicle;
- ω0 = 0.01 m/s (since the vehicle exhaust pipe is directed horizontally, we used the minimum vertical speed of the air–water mixture).
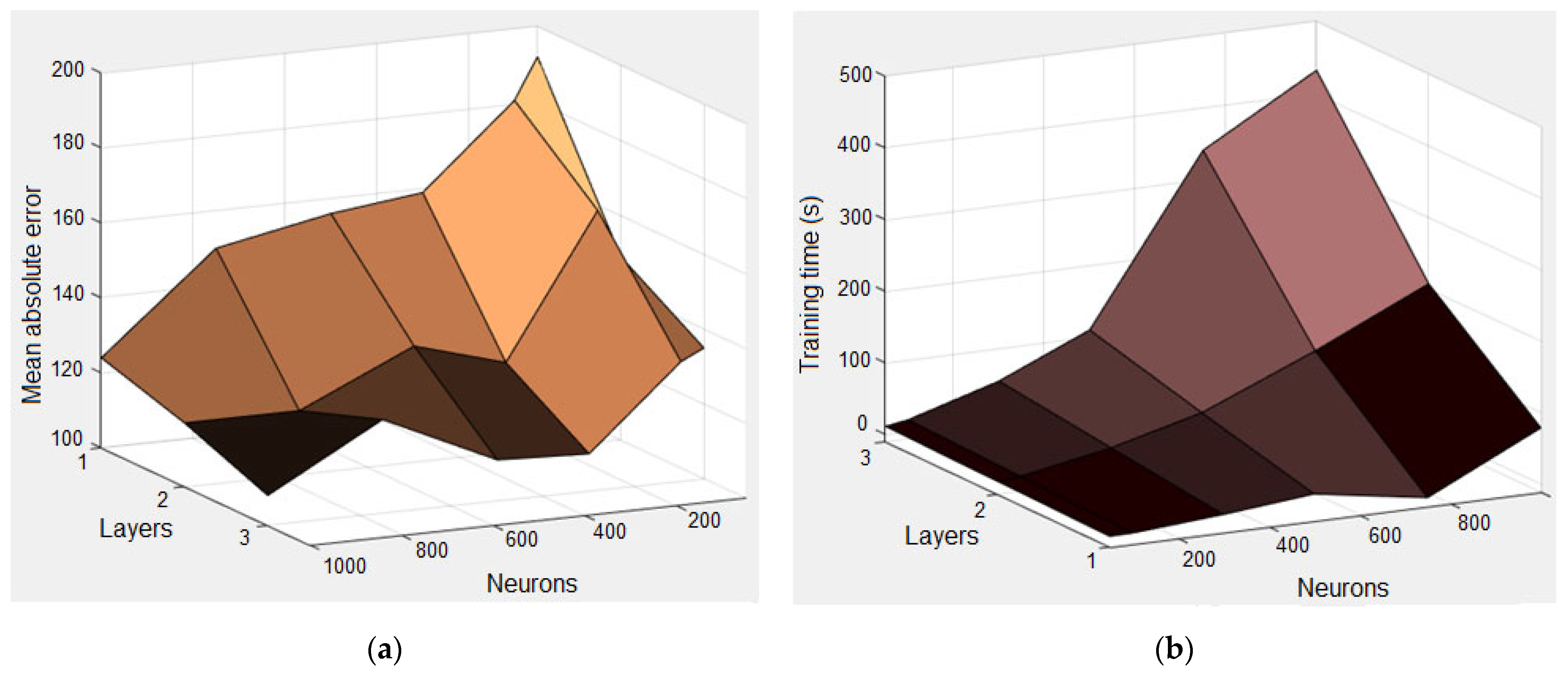
3.2. Forecasting the Number of Vehicles
- LSTM (a recurrent layer);
- Dropout with rate = 0.2 (a layer that prevents retraining by ignoring randomly selected neurons during training);
- Dense (an output layer that changes the shape of the data into the desired form).
- Number of LSTM layers: 1, 2, 3;
- Number of neurons in each of the LSTM layers: 50, 100, 300, 500, 750, 1000.
- The number of learning epochs was 500.
3.3. Forecasting the Amount of Emissions
- LSTM (a recurrent layer);
- Dropout with rate = 0.2 (a layer that prevents retraining by ignoring randomly selected neurons during training). This layer follows each LSTM layer;
- Dense (an output layer that changes the shape of the data into the desired form).
- Number of LSTM layers: 1, 2, 3, 4;
- Number of neurons in each of the LSTM layers: 50, 100, 250, 400, 600, 800, 1000, and 1200.
4. Discussion and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, S.; Younis, M.; Murali, A.; Lee, M. Dynamic local vehicular flow optimization using real-time traffic conditions at multiple road intersections. IEEE Access 2019, 7, 28137–28157. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, S.; Qiu, Y.; Zhang, Y.; Ying, J.; Du, Y. Traffic signal optimization under connected-vehicle environment: An overview. J. Adv. Transp. 2021, 2021, 3584569. [Google Scholar] [CrossRef]
- Yau, K.-L.A.; Qadir, J.; Khoo, H.L.; Ling, M.H.; Komisarczuk, P. A survey on Reinforcement learning models and algorithms for traffic signal control. ACM Comput. Surv. 2017, 50, 1–38. [Google Scholar] [CrossRef]
- Fusco, G.; Gentile, G.; Meschini, P. Urban traffic signal optimization. In Intelligent Transport Systems (ITS): Past, Present and Future Directions; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2017. [Google Scholar]
- Toan, D.T.; Lam, H.S.; Meng, M.; Wong, D.Y. Travel demand management policies: A case study of Singapore and transferability potentials for Hanoi. Case Stud. Transp. Policy 2023, 11, 100934. [Google Scholar] [CrossRef]
- Giuliano, G. Transportation Demand Management: Promise or Panacea? J. Am. Plan. Assoc. 1992, 58, 327–335. [Google Scholar] [CrossRef]
- Habibian, M.; Kermanshah, M. Coping with congestion: Understanding the role of simultaneous transportation demand management policies on commuters. Transp. Policy 2013, 30, 229–237. [Google Scholar] [CrossRef]
- Li, H.; Andrews, G.E.; Savvidis, D.; Daham, B.; Ropkins, K.; Bell, M.; Tate, J. Impact of driving cycles on greenhouse gas (GHG) emissions, global warming potential (GWP) and fuel economy for SI car real world urban driving. SAE Int. J. Fuels Lubr. 2009, 1, 1320–1333. [Google Scholar] [CrossRef]
- Boubaker, S.; Rehimi, F.; Kalboussi, A. Impact of intersection type and a vehicular fleet’s hybridization level on energy consumption and emissions. J. Traffic Transp. Eng. 2016, 3, 253–261. [Google Scholar] [CrossRef] [Green Version]
- Gu, Z.-Y.; Chen, C.; Zheng, J.-J.; Sun, D.-H. Traffic flow prediction based on STG-CRNN. Kongzhi Yu Juece/Control Decis. 2022, 37, 645–653. [Google Scholar] [CrossRef]
- Adams, M.D.; Kanaroglou, P.S. Mapping real-time air pollution health risk for environmental management: Combining mobile and stationary air pollution monitoring with neural network models. J. Environ. Manag. 2016, 168, 133–141. [Google Scholar] [CrossRef]
- Brazil, N. Environmental inequality in the neighborhood networks of urban mobility in US cities. Proc. Natl. Acad. Sci. USA 2022, 119, e2117776119. [Google Scholar] [CrossRef] [PubMed]
- Colmer, J.; Hardman, I.; Shimshack, J.; Voorheis, J. Disparities in PM 2.5 air pollution in the United States. Science 2020, 369, 575–578. [Google Scholar] [CrossRef] [PubMed]
- Bell, M.L.; Ebisu, K. Environmental Inequality in Exposures to Airborne Particulate Matter Components in the United States. Environ. Health Perspect. 2012, 120, 1699–1704. [Google Scholar] [CrossRef] [Green Version]
- Balsa-Barreiro, J.; Morales, A.J.; Lois-González, R.C. Mapping Population Dynamics at Local Scales Using Spatial Networks. Complex 2021, 2021, 8632086. [Google Scholar] [CrossRef]
- Fernandes, P.; Salamati, K.; Rouphail, N.M.; Coelho, M.C. Identification of emission hotspots in roundabouts corridors. Transp. Res. Part D Transp. Environ. 2015, 37, 48–64. [Google Scholar] [CrossRef]
- Coelho, M.C.; Farias, T.L.; Rouphail, N.M. Effect of roundabout operations on pollutant emissions. Transp. Res. Part D Transp. Environ. 2006, 11, 333–343. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, Y. Exploration of correlation between environmental factors and mobility at signalized intersections. Transp. Res. Part D Transp. Environ. 2014, 32, 24–34. [Google Scholar] [CrossRef]
- Pathivada, B.K.; Perumal, V. Modeling Driver Behavior in Dilemma Zone under Mixed Traffic Conditions. Transp. Res. Procedia 2017, 27, 961–968. [Google Scholar] [CrossRef]
- Najmi, A.; Choupani, A.; Aghayan, I. Characterizing driver behavior in dilemma zones at signalized roundabouts. Transp. Res. Part F Traffic Psychol. Behav. 2019, 63, 204–215. [Google Scholar] [CrossRef]
- Calvi, A.; Petrella, C. An evaluation of the effectiveness of countermeasures for improving the safety of dilemma zones: A driving simulator study. Transp. Res. Part F Traffic Psychol. Behav. 2022, 87, 295–312. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, Z.; Yu, C.W. Large eddy simulation of vehicle induced turbulence in an urban street canyon with a new dynamically vehicle-tracking scheme. Aerosol Air Qual. Res. 2017, 17, 865–874. [Google Scholar] [CrossRef] [Green Version]
- Voordeckers, D.; Meysman, F.J.R.; Billen, P.; Tytgat, T.; Van Acker, M. The impact of street canyon morphology and traffic volume on NO2 values in the street canyons of Antwerp. Build. Environ. 2021, 197, 107825. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, J. CFD simulations of wind flow and pollutant dispersion in a street canyon with traffic flow: Comparison between RANS and LES. Sustain. Cities Soc. 2021, 75, 103307. [Google Scholar] [CrossRef]
- Hermosilla, T.; Palomar-Vázquez, J.; Balaguer-Beser, Á.; Balsa-Barreiro, J.; Ruiz, L.A. Using street based metrics to characterize urban typologies. Computers. Environ. Urban Syst. 2014, 44, 68–79. [Google Scholar] [CrossRef] [Green Version]
- Kaur, S.; Nieuwenhuijsen, M.J.; Colvile, R.N. Fine particulate matter and carbon monoxide exposure concentrations in urban street transport microenvironments. Atmos. Environ. 2007, 41, 4781–4810. [Google Scholar] [CrossRef]
- Berkowicz, R.; Winther, M.; Ketzel, M. Traffic pollution modelling and emission data. Environ. Model. Softw. 2006, 21, 454–460. [Google Scholar] [CrossRef]
- Mensink, C.; Cosemans, G. From traffic flow simulations to pollutant concentrations in street canyons and backyards. Environ. Model. Softw. 2008, 23, 288–295. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, Y.; Lv, Z.; He, T.; Zhao, J.; Wang, Y.; Liu, H. Impacts of vehicle emission on air quality and human health in china. Sci. Total Environ. 2022, 813, 152655. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Wu, J.; Zhang, H.; Zhang, W.; Dai, Q.; Gong, P. Contributions of vehicle emissions to PM2.5 in roadside microenvironments. Zhongguo Huanjing Kexue/China Environ. Sci. 2021, 41, 5086–5093. [Google Scholar]
- Song, N.; Xu, H.; Bi, X.; Wu, J.; Zhang, Y.; Yang, H.; Feng, Y. Source Apportionment of PM2.5 and PM10 in Haikou. Res. Environ. Sci. 2015, 28, 1501–1509. [Google Scholar] [CrossRef]
- Teng, H.; Liu, Y.; Liu, A.; Xiong, N.N.; Cai, Z.; Wang, T.; Liu, X. A novel code data dissemination scheme for Internet of Things through mobile vehicle of smart cities. Future Gener. Comput. Syst. 2019, 94, 351–367. [Google Scholar] [CrossRef]
- Shahrour, I.; Xie, X. Role of internet of things (IoT) and crowdsourcing in smart city projects. Smart Cities 2021, 4, 1276–1292. [Google Scholar] [CrossRef]
- Hu, C.; Fan, W.; Zeng, E.; Hang, Z.; Wang, F.; Qi, L.; Bhuiyan, M.Z.A. Digital twin-assisted real-time traffic data prediction method for 5G-Enabled Internet of Vehicles. IEEE Trans. Ind. Inform. 2022, 18, 2811–2819. [Google Scholar] [CrossRef]
- Yu, S.; Chang, C.T.; Ma, C.M. Simulation and measurement of air quality in the traffic congestion area. Sustain. Environ. Res. 2021, 31, 26. [Google Scholar] [CrossRef]
- Air Quality Modeling. Available online: https://www.epa.gov/air-research/air-quality-modeling (accessed on 9 February 2023).
- Baghestani, A.; Tayarani, M.; Allahviranloo, M.; Gao, H.O. Cordon Pricing, Daily Activity Pattern, and Exposure to Traffic-Related Air Pollution: A Case Study of New York City. Atmosphere 2021, 12, 1458. [Google Scholar] [CrossRef]
- Liu, H.; Xu, X.; Rodgers, M.O.; Xu, Y.; Guensler, R.L. MOVES-Matrix and distributed computing for microscale line source dispersion analysis. J. Air Waste Manag. Assoc. 2017, 67, 763–775. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Liu, H.; Rodgers, M.O.; Guensler, R. Development of roadway link screening model for regional-level near-road air quality analysis: A case study for particulate matter. Atmos. Environ. 2020, 237, 117677. [Google Scholar] [CrossRef]
- Teng, M.; Li, S.; Xing, J.; Song, G.; Yang, J.; Dong, J.; Zeng, X.; Qin, Y. 24-Hour prediction of PM2.5 concentrations by combining empirical mode decomposition and bidirectional long short-term memory neural network. Sci. Total Environ. 2022, 821, 153276. [Google Scholar] [CrossRef]
- Shuai, C.; Wang, W.; Xu, G.; He, M.; Lee, J. Short-Term traffic flow prediction of expressway considering spatial influences. J. Transp. Eng. Part A Syst. 2022, 148, 04022026. [Google Scholar] [CrossRef]
- Shang, P.; Liu, X.; Yu, C.; Yan, G.; Xiang, Q.; Mi, X. A new ensemble deep graph reinforcement learning network for spatio-temporal traffic volume forecasting in a freeway network. Digit. Signal Process. A Rev. J. 2022, 123, 103419. [Google Scholar] [CrossRef]
- Nasser, A.; Simon, V. Wavelet-attention-based traffic prediction for smart cities. IET Smart Cities 2022, 4, 3–16. [Google Scholar] [CrossRef]
- Bai, Y.; Li, Y.; Wang, X.; Xie, J.; Li, C. Air pollutants concentrations forecasting using back propagation neural network based on wavelet decomposition with meteorological conditions. Atmos. Pollut. Res. 2016, 7, 557–566. [Google Scholar] [CrossRef]
- Baskar, P.K.; Kaluvan, H. Long short-term memory (LSTM) recurrent neural network (RNN) based traffic forecasting for intelligent transportation. AIP Conf. Proc. 2022, 2435, 020039. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, J.; Wei, X.; Xing, W.; Lu, W. Adaptive spatial-temporal graph attention networks for traffic flow forecasting. Appl. Intell. 2022, 52, 4300–4316. [Google Scholar] [CrossRef]
- Hembeck, L.; Dickerson, R.R.; Canty, T.P.; Allen, D.J.; Salawitch, R.J. Investigation of the Community Multiscale air quality (CMAQ) model representation of the Climate Penalty Factor (CPF). Atmos. Environ. 2022, 283, 119157. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Y.; Fung, J.C.H.; Lin, C.; Lau, A.K.H. A novel hybrid clustering model of region segmentation to fuse CMAQ simulations with observations. Atmos. Environ. 2022, 278, 119062. [Google Scholar] [CrossRef]
- Du, W.; Chen, L.; Wang, H.; Shan, Z.; Zhou, Z.; Li, W.; Wang, Y. Deciphering urban traffic impacts on air quality by deep learning and emission inventory. J. Environ. Sci. 2023, 124, 745–757. [Google Scholar] [CrossRef] [PubMed]
- Glushkov, A.; Shepelev, V. Development of reliable models of signal-controlled intersections. Transp. Telecommun. 2021, 22, 417–424. [Google Scholar] [CrossRef]
- Qin, D.; Gao, C. Control measures for automobile exhaust emissions in PM2.5 governance. Discret. Dyn. Nat. Soc. 2022, 2022, 8461406. [Google Scholar] [CrossRef]
- Shepelev, V.; Kostyrchenko, V. Modeling the Operation of Signal-Controlled Intersections with Different Lane Occupancy. Mathematics 2022, 10, 4829. [Google Scholar] [CrossRef]
- Hoque, J.M.; Erhardt, G.D.; Schmitt, D.; Chen, M.; Chaudhary, A.; Wachs, M.; Souleyrette, R.R. The changing accuracy of traffic forecasts. Transportation 2022, 49, 445–466. [Google Scholar] [CrossRef]
- Shepelev, V.; Glushkov, A.; Fadina, O.; Gritsenko, A. Comparative Evaluation of Road Vehicle Emissions at Urban Intersections with Detailed Traffic Dynamics. Mathematics 2022, 10, 1887. [Google Scholar] [CrossRef]
- Shepelev, V.; Aliukov, S.; Glushkov, A.; Shabiev, S. Identification of distinguishing characteristics of intersections based on statistical analysis and data from video cameras. J. Big Data 2020, 7, 46. [Google Scholar] [CrossRef]
- Shepelev, V.; Zhankaziev, S.; Aliukov, S.; Varkentin, V.; Marusin, A.; Marusin, A.; Gritsenko, A. Forecasting the passage time of the queue of highly automated vehicles based on neural networks in the services of cooperative intelligent transport systems. Mathematics 2022, 10, 282. [Google Scholar] [CrossRef]
- Shepelev, V.; Glushkov, A.; Bedych, T.; Gluchshenko, T.; Almetova, Z. Predicting the traffic capacity of an intersection using fuzzy logic and computer vision. Mathematics 2021, 9, 2631. [Google Scholar] [CrossRef]
- Order of the Ministry of Natural Resources and Ecology of the Russian Federation No. 804 Dated November 27, 2019 “On Approval of the Methodology for Determining Emissions of Pollutants into the Atmospheric air from Mobile Sources for Conducting Summary Calculations of Atmospheric Air Pollution”. Available online: https://www.garant.ru/products/ipo/prime/doc/73240708/ (accessed on 7 November 2022).
- Order of the Ministry of Natural Resources and Ecology of the Russian Federation No 273 Dated June 6, 2017 “On Approval of Methods for Calculating the Dispersion of Emissions of Harmful (Polluting) Substances in the Atmospheric Air”. Available online: https://docs.cntd.ru/document/456074826 (accessed on 7 November 2022).
- Ntziachristos, L.; Gkatzoflias, D.; Kouridis, C.; Samaras, Z. COPERT: A European road transport emission inventory model. In Proceedings of the 4th International ICSC Symposium, Thessaloniki, Greece, 28–29 May 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 491–504. [Google Scholar] [CrossRef]
- Ntziachristos, L.; Samaras, Z. COPERT III: Computer Programme to Calculate Emissions from Road Transport-Methodology and Emission Factors. European Topic Centre on Air Emissions; EEA: Copenhagen, Denmark, 2000. [Google Scholar]
- Weather Forecasts, Newscasts and History in a Fast and Elegant Way. Available online: https://openweathermap.org/ (accessed on 30 August 2022).
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. Part C Emerg. Technol. 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, J.; Jin, N.; Jin, X.; Du, Y. Air quality forecasting with hybrid LSTM and extended stationary wavelet transform. Build. Environ. 2022, 213, 108822. [Google Scholar] [CrossRef]
- DustTrak™ DRX Aerosol Monitor 8533. Available online: https://tsi.com/products/aerosol-and-dust-monitors/aerosol-and-dust-monitors/dusttrak%E2%84%A2-drx-aerosol-monitor-8533/ (accessed on 17 August 2022).















| Models | Types of Models | Studies and Year | Input Data |
|---|---|---|---|
| Traffic management models | Adaptive control of traffic light signals | Lee et al. [1] Wang et al. [2] Fusco et al. [4] |
|
| Modeling Driver Behavior | Pathivada and Perumal [19] Najmi et al. [20] Calvi et al. [21] |
| |
| Air quality models | Operational Street Pollution Model | Berkowicz et al. [27] Mensink and Cosemans [28] |
|
| Comprehensive Air-quality Model | Luo et al. [21] |
| |
| Chemical mass balance | Gao et al. [30] Song et al. [31] |
| |
| Dispersion models for predicting air pollutant concentrations | CALINE4 | Yu et al. [35] Air Quality Modeling [36] |
|
| AERMOD | Baghestani et al. [37] Liu et al. [38] Kim et al. [39] |
| |
| CMAQ | Hembeck et al. [47] Wang et al. [48] |
|
| Vehicle Group Name | Group Number | Emissions (g/min) | |
|---|---|---|---|
| CO | PM2.5 | ||
| Cars | I | 0.17 | 0.011 |
| Vans and minibuses weighing up to 3.5 tons | II | 1.00 | 0.033 |
| Trucks weighing 3.5 to 12 tons | III | 1.00 | 0.220 |
| Trucks weighing over 12 tons | IV | 2.00 | 0.450 |
| Buses weighing over 3.5 tons | V | 0.90 | 0.120 |
| Vehicle Group Name | Group Number | Emissions (g/min) | |
|---|---|---|---|
| CO | PM2.5 | ||
| Cars | I | 0.90 | 0.55 × 10−2 |
| Vans and minibuses weighing up to 3.5 tons | II | 4.60 | 3.70 × 10−2 |
| Trucks weighing 3.5 to 12 tons | III | 5.30 | 0.37 |
| Trucks weighing over 12 tons | IV | 5.60 | 0.44 |
| Buses weighing over 3.5 tons | V | 3.90 | 0.15 |
| Vehicle Type | Vehicle Type, per COPERT | PM2.5 (g/min) | PM10 (g/min) | ||||
|---|---|---|---|---|---|---|---|
| Brake Pad Wear | Tire Wear | Road Surface Wear | Brake Pad Wear | Tire Wear | Road Surface Wear | ||
| I | I | 0.00293 | 0.00449 | 0.00405 | 0.00735 | 0.00642 | 0.00750 |
| II | II | 0.00456 | 0.00710 | 0.00405 | 0.01147 | 0.01014 | 0.00750 |
| III | III | 0.01277 | 0.01887 | 0.02052 | 0.03209 | 0.02696 | 0.03800 |
| IV | III | 0.01277 | 0.01887 | 0.02052 | 0.03209 | 0.02696 | 0.03800 |
| V | III | 0.01277 | 0.01887 | 0.02052 | 0.03209 | 0.02696 | 0.03800 |
| # | Region | Coefficient A |
|---|---|---|
| 1 | Republic of Buryatia and Trans-Baikal Territory | 250 |
| 2 | Regions of the European part of the Russian Federation south of 50 °N, other regions of the Lower Volga territory, Asian part of the Russian Federation, except for those indicated in Items 1 and 3 of this Table | 200 |
| 3 | European part of the Russian Federation and the Urals from 50 °N to 52 °N inclusive, except for the areas falling into this zone, listed in Items 1 and 2 of this Table, as well as for the areas of the Asian part of the Russian Federation located north of the Arctic Circle and west of the meridian 108 °e. | 180 |
| 4 | European part of the Russian Federation and the Urals north of 52 °N (except for the center of the European part of the Russian Federation) | 160 |
| 5 | Vladimir, Ivanovo, Kaluga, Moscow, Ryazan, and Tula regions | 140 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shepelev, V.; Glushkov, A.; Slobodin, I.; Cherkassov, Y. Measuring and Modelling the Concentration of Vehicle-Related PM2.5 and PM10 Emissions Based on Neural Networks. Mathematics 2023, 11, 1144. https://doi.org/10.3390/math11051144
Shepelev V, Glushkov A, Slobodin I, Cherkassov Y. Measuring and Modelling the Concentration of Vehicle-Related PM2.5 and PM10 Emissions Based on Neural Networks. Mathematics. 2023; 11(5):1144. https://doi.org/10.3390/math11051144
Chicago/Turabian StyleShepelev, Vladimir, Aleksandr Glushkov, Ivan Slobodin, and Yuri Cherkassov. 2023. "Measuring and Modelling the Concentration of Vehicle-Related PM2.5 and PM10 Emissions Based on Neural Networks" Mathematics 11, no. 5: 1144. https://doi.org/10.3390/math11051144
APA StyleShepelev, V., Glushkov, A., Slobodin, I., & Cherkassov, Y. (2023). Measuring and Modelling the Concentration of Vehicle-Related PM2.5 and PM10 Emissions Based on Neural Networks. Mathematics, 11(5), 1144. https://doi.org/10.3390/math11051144







