Toward Zero-Determinant Strategies for Optimal Decision Making in Crowdsourcing Systems
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Problem Formulation
1.3. Solution and Contributions
- A crowdsourcing scenario is modeled, where workers have incomplete information, as an iterative game. In this model, the requester allocates the reward according to the “winner-takes-all” rule, for which solutions provided by different workers are independent, and selfish workers compete for the reward also with incomplete information.
- A theoretic method with ZD strategies is proposed to analyze the optimal decision-making problem in crowdsourcing systems. Moreover, the conditions to reach the maximum payoff of the focused worker who uses ZD strategies are obtained.
- Our analysis helps understand what solutions selfish workers will submit under the condition of having incomplete information. Furthermore, we provide a new optimization method, by which the optimal decision is reached in a bottom–up manner subject to incomplete information.
2. Literature Review
3. Method and System Model
3.1. Crowdsourcing System
3.2. Modeling Crowdsourcing System as an Iterated Game
3.3. ZD Strategies for Multiple-Player Iterated Games
3.4. Game Analysis with ZD Strategies
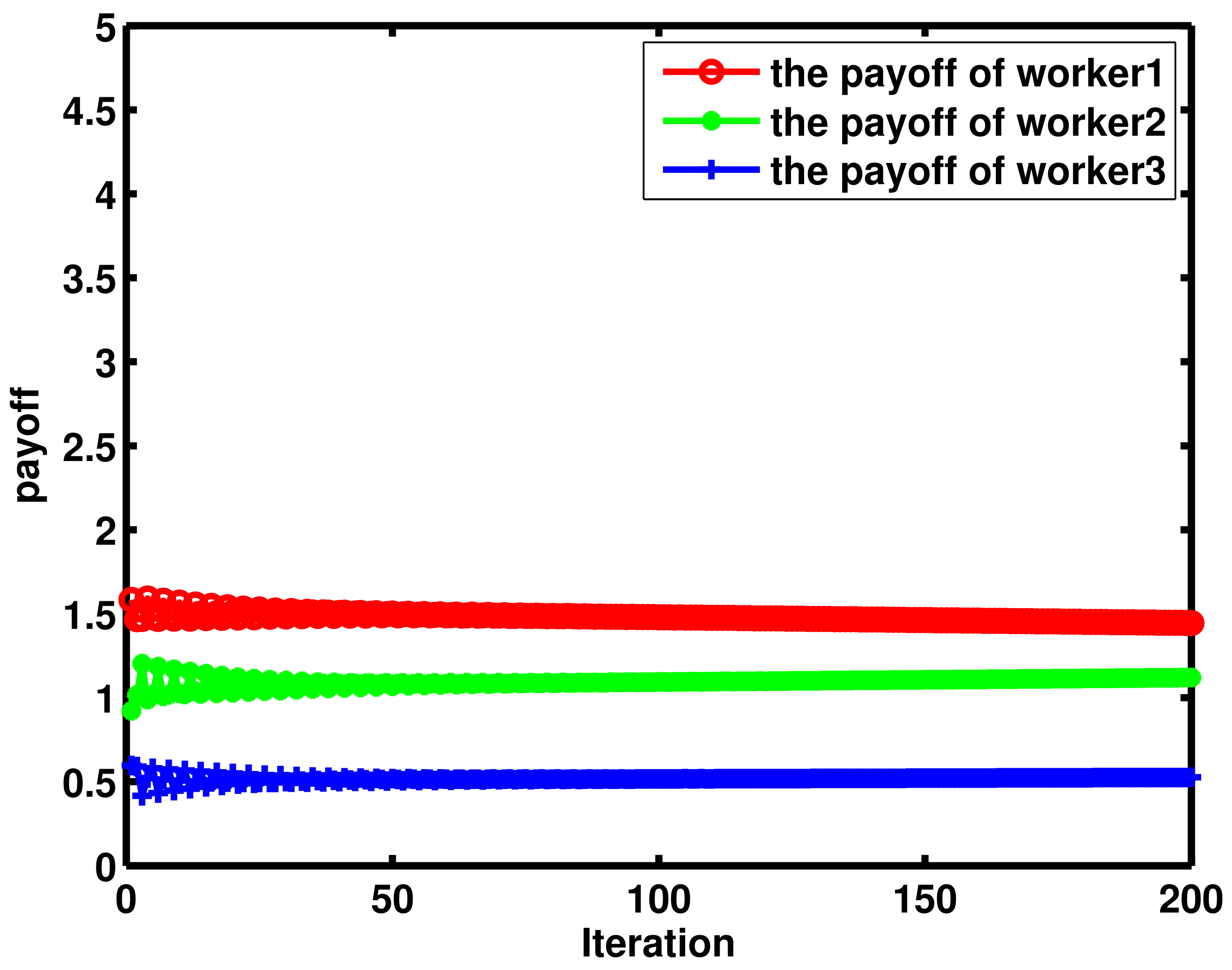
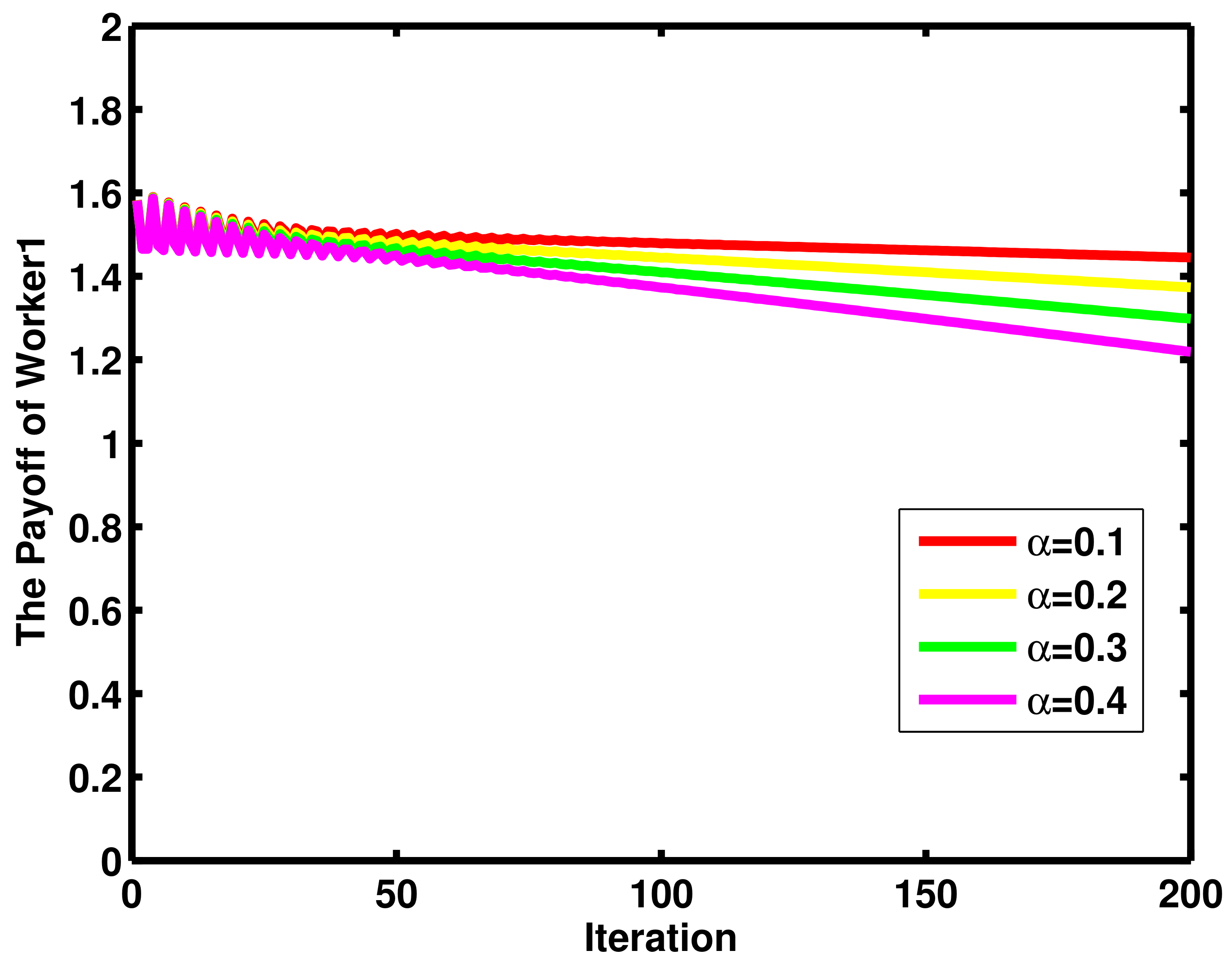
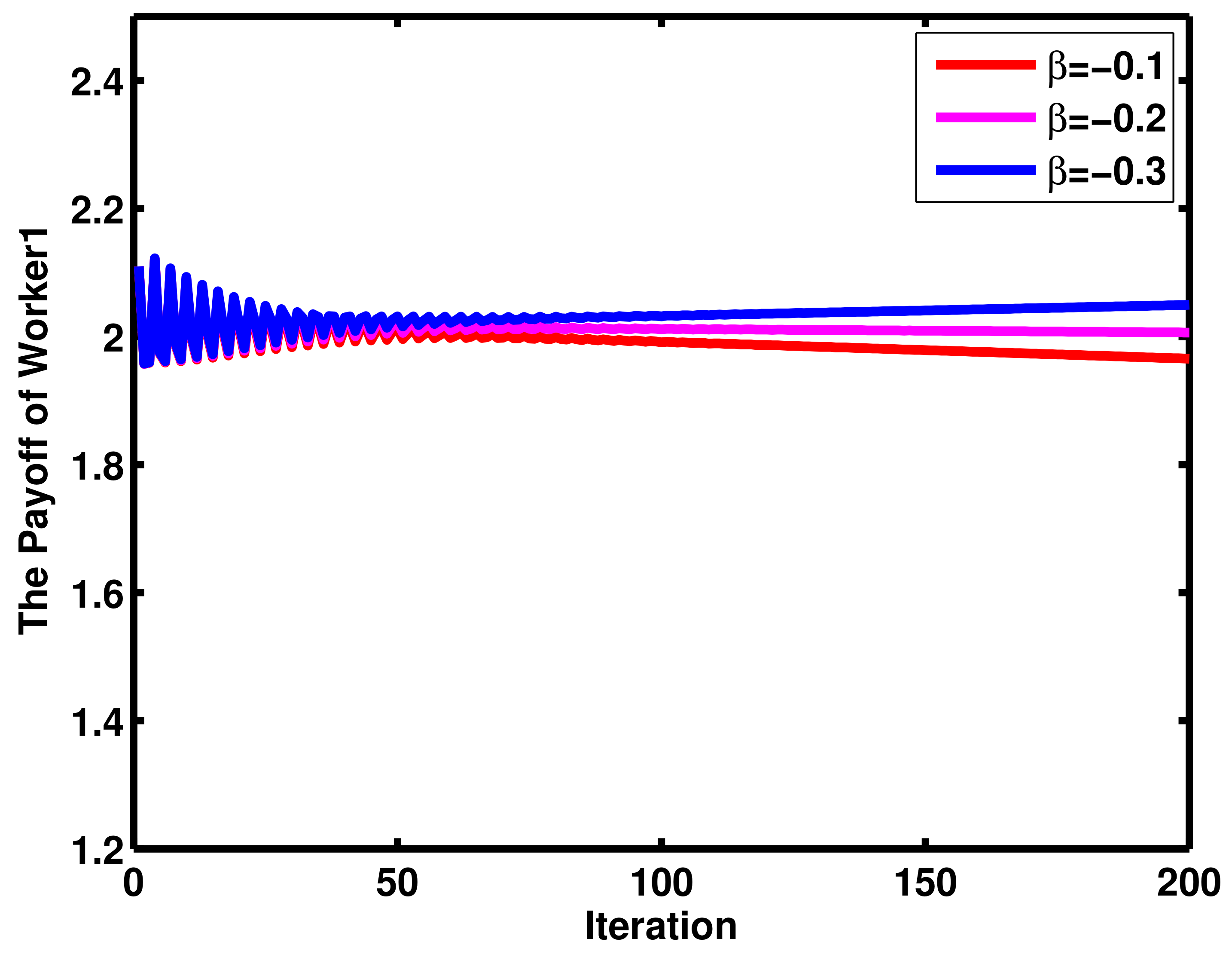
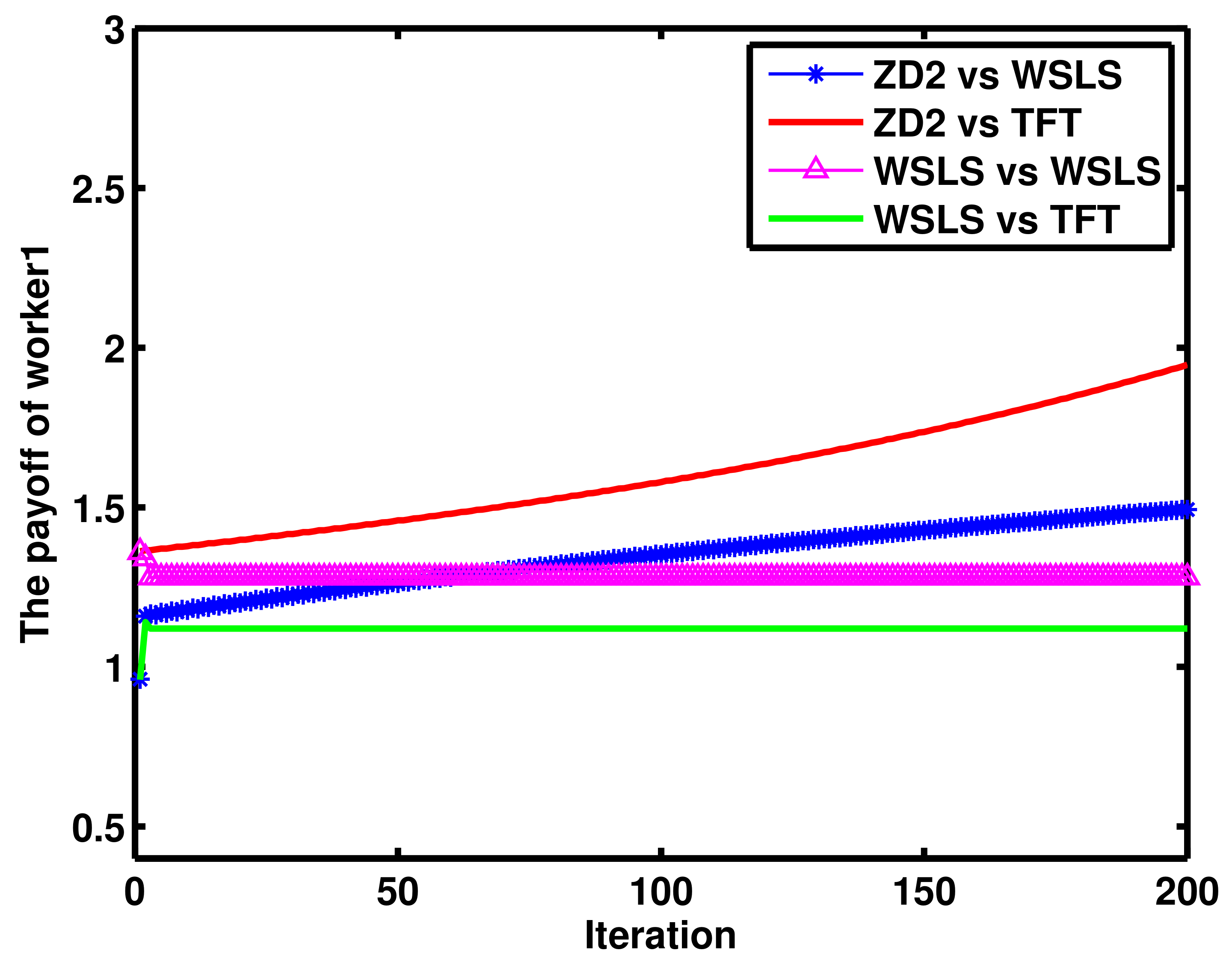
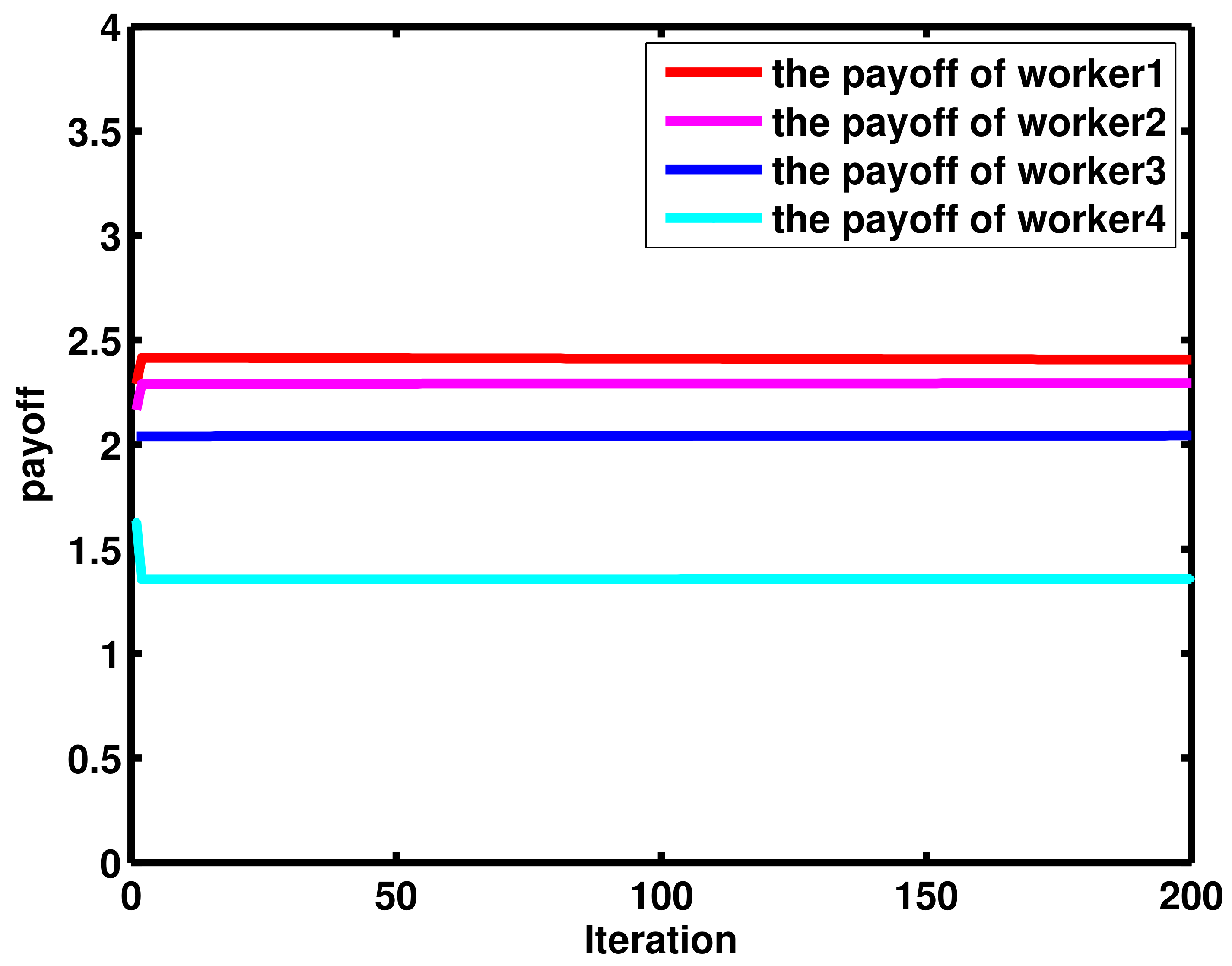
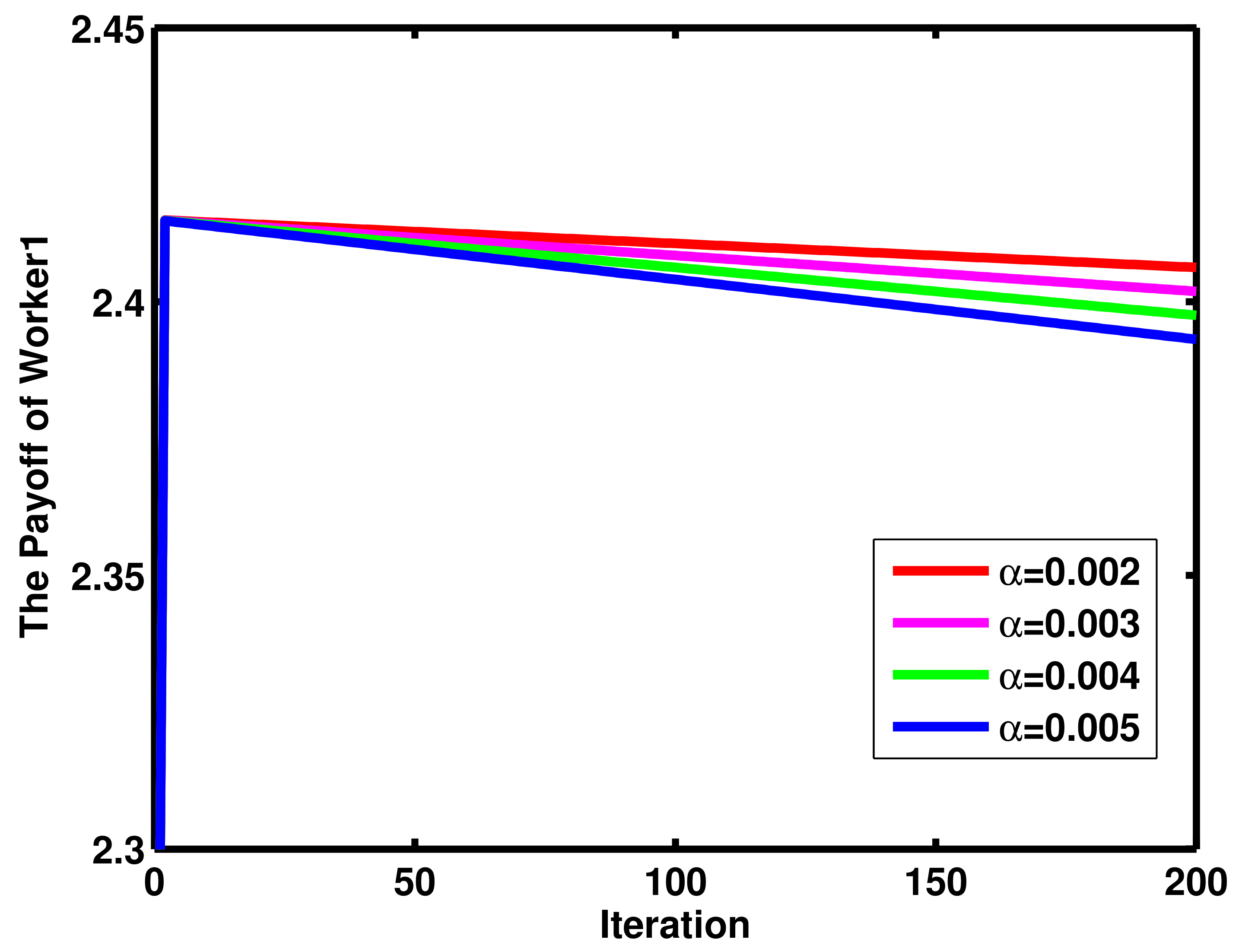
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Slivkins, A.; Vaughan, J.W. Online decision making in crowdsourcing markets: Theoretical challenges. ACM SIGecom Exch. 2014, 12, 4–23. [Google Scholar] [CrossRef]
- Wang, N.; Wu, J. Cost-efficient heterogeneous worker recruitment under coverage requirement in spatial crowdsourcing. IEEE Trans. Big Data 2021, 7, 407–420. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.; Gao, L.; Liu, Y.F.; Huang, J. Incentivizing Wi-Fi network crowdsourcing: A contract theoretic approach. IEEE ACM Trans. Netw. 2018, 26, 1035–1048. [Google Scholar] [CrossRef]
- Tang, C.; Li, X.; Cao, M.; Zhang, Z.; Yu, X. Incentive mechanism for macrotasking crowdsourcing: A zero-determinant strategy approach. IEEE Internet Things J. 2019, 6, 8589–8601. [Google Scholar] [CrossRef]
- Giglio, C.; Maio, A.D. A structural equation model for analysing the determinants of crowdshipping adoption in the last-mile delivery within university cities. Int. J. Appl. Decis. Sci. 2022, 15, 117–142. [Google Scholar] [CrossRef]
- Dortheimer, J. Collective Intelligence in Design Crowdsourcing. Mathematics 2022, 10, 539. [Google Scholar] [CrossRef]
- Elance. Available online: https://www.elance.com/ (accessed on 1 October 2022).
- Fiverr. Available online: https://www.fiverr.com/ (accessed on 1 October 2022).
- Lu, W.; Hu, S.; Liu, X.; He, C.; Gong, Y. Incentive mechanism based cooperative spectrum sharing for OFDM cognitive IoT network. IEEE Trans. Netw. Sci. Eng. 2019, 7, 662–672. [Google Scholar] [CrossRef]
- Zha, W.; Chen, J.; Peng, Z. Dynamic multi-team antagonistic games model with incomplete information and its application to multi-UAV. IEEE/CAA J. Autom. Sin. 2015, 2, 74–84. [Google Scholar]
- Ghosh, A.; McAfee, P. Incentivizing high-quality user-generated content. In Proceedings of the 20th International Conference on World Wide Web, Hyderabad, India, 28 March–1 April 2011; pp. 137–146. [Google Scholar]
- Shen, D. Iterative learning control with incomplete information: A survey. IEEE/CAA J. Autom. Sin. 2018, 5, 885–901. [Google Scholar] [CrossRef]
- Xie, H.; Lui, J.C. Incentive mechanism and rating system design for crowdsourcing systems: Analysis, tradeoffs and inference. IEEE Trans. Serv. Comput. 2016, 11, 90–102. [Google Scholar] [CrossRef]
- Wang, J.; Tang, C.; Liu, Y.; Zhang, Z. Zero-Determinant Strategies in Winner Takes All Game. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 892–897. [Google Scholar]
- Jin, L.; Liang, S.; Luo, X.; Zhou, M. Distributed and Time-Delayed k-Winner-Take-All Network for Competitive Coordination of Multiple Robots. IEEE Trans. Cybern. 2022, 53, 641–652. [Google Scholar] [CrossRef]
- Press, W.H.; Dyson, F.J. Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl. Acad. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; An, B.; Jiang, Y.; Lin, D. Context-aware reliable crowdsourcing in social networks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 50, 617–632. [Google Scholar] [CrossRef]
- He, S.; Shin, D.H.; Zhang, J.; Chen, J.; Lin, P. An exchange market approach to mobile crowdsensing: Pricing, task allocation, and walrasian equilibrium. IEEE J. Sel. Areas Commun. 2017, 35, 921–934. [Google Scholar] [CrossRef]
- Zhang, J. Knowledge Learning With Crowdsourcing: A Brief Review and Systematic Perspective. IEEE/CAA J. Autom. Sin. 2022, 9, 749–762. [Google Scholar] [CrossRef]
- Mason, W.; Suri, S. Conducting behavioral research on Amazon’s Mechanical Turk. Behav. Res. Methods 2012, 44, 1–23. [Google Scholar] [CrossRef]
- Hu, Q.; Wang, S.; Ma, P.; Cheng, X.; Lv, W.; Bie, R. Quality control in crowdsourcing using sequential zero-determinant strategies. IEEE Trans. Knowl. Data Eng. 2019, 32, 998–1009. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.; Zhou, X.; Zhu, N.; Gao, Y.; Li, K. Multi-stage complex task assignment in spatial crowdsourcing. Inf. Sci. 2022, 586, 119–139. [Google Scholar] [CrossRef]
- Hyman, P. Software aims to ensure fairness in crowdsourcing projects. Commun. ACM 2013, 56, 19–21. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Y.; Tong, X.; Mu, C.; Chen, Y.; Li, Y. Data-driven many-objective crowd worker selection for mobile crowdsourcing in industrial IoT. IEEE Trans. Industr. Inform. 2021, 19, 531–540. [Google Scholar] [CrossRef]
- Wang, S.; Taha, A.F.; Wang, J.; Kvaternik, K.; Hahn, A. Energy crowdsourcing and peer-to-peer energy trading in blockchain-enabled smart grids. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1612–1623. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.N.; Yang, F.C.; Vo, N.T.; Nguyen, V.T.T. Wireless communications for data security: Efficiency assessment of cybersecurity industry—A promising application for UAVs. Drones 2022, 6, 363. [Google Scholar] [CrossRef]
- Binas, J.; Rutishauser, U.; Indiveri, G.; Pfeiffer, M. Learning and stabilization of winner-take-all dynamics through interacting excitatory and inhibitory plasticity. Front. Comput. Neurosci. 2014, 8, 68. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhou, M.; Luo, X.; You, Z.H. Distributed winner-take-all in dynamic networks. IEEE Trans. Autom. Control 2016, 62, 577–589. [Google Scholar] [CrossRef]
- Qi, Y.; Jin, L.; Luo, X.; Shi, Y.; Liu, M. Robust k-WTA network generation, analysis, and applications to multiagent coordination. IEEE Trans. Cybern. 2021, 52, 8515–8527. [Google Scholar] [CrossRef]
- Dlugosz, R.; Talaska, T.; Pedrycz, W.; Wojtyna, R. Realization of the conscience mechanism in CMOS implementation of winner-takes-all self-organizing neural networks. IEEE Trans. Neural Netw. 2010, 21, 961–971. [Google Scholar] [CrossRef]
- Zuo, Y.; Guo, J.; Zhang, Y.; Hu, Y.; Lei, B.; Qiu, X.; Ding, C. Winner Takes All: A Superpixel Aided Voting Algorithm for Training Unsupervised PolSAR CNN Classifiers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Singh, V.K.; Jain, R.; Kankanhalli, M.S. Motivating contributors in social media networks. In Proceedings of the First SIGMM Workshop on Social Media, Beijing, China, 23 October 2009; pp. 11–18. [Google Scholar]
- Fei, L.; Dong, X.; Yu, J.; Hua, Y.; Li, Q.; Ren, Z. Distributed Nash equilibrium seeking of N-coalition non-cooperative games with application to UAV swarms. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2392–2405. [Google Scholar]
- Ichinose, G.; Masuda, N. Zero-determinant strategies in finitely repeated games. J. Theor. Biol. 2018, 438, 61–77. [Google Scholar] [CrossRef]
- Taha, M.A.; Ghoneim, A. Zero-determinant strategies in repeated asymmetric games. Appl. Math. Comput. 2020, 369, 124862. [Google Scholar] [CrossRef]
- Govaert, A.; Cao, M. Zero-determinant strategies in repeated multiplayer social dilemmas with discounted payoffs. IEEE Trans. Autom. Control 2020, 66, 4575–4588. [Google Scholar] [CrossRef]
- Zhang, H.; Niyato, D.; Song, L.; Jiang, T.; Han, Z. Zero-determinant strategy for resource sharing in wireless cooperations. IEEE Trans. Wirel. Commun. 2015, 15, 2179–2192. [Google Scholar] [CrossRef]
- Miao, Y.; Tang, C.; Lu, J.; Li, X. Zero-determinant strategy for cooperation enforcement in crowdsourcing. In Proceedings of the 2017 IEEE Second International Conference on Data Science in Cyberspace (DSC), Shenzhen, China, 26–29 June 2017; pp. 1–6. [Google Scholar]
- Tang, C.; Li, C.; Yu, X.; Zheng, Z.; Chen, Z. Cooperative mining in blockchain networks with zero-determinant strategies. IEEE Trans. Cybern. 2019, 50, 4544–4549. [Google Scholar] [CrossRef]
- He, X.; Dai, H.; Ning, P.; Dutta, R. Zero-determinant strategies for multi-player multi-action iterated games. IEEE Signal Process. Lett. 2016, 23, 311–315. [Google Scholar] [CrossRef]





| Notations | Meaning of Expression |
|---|---|
| N | Total number of players |
| r | The reward provided by requester |
| The cost of worker with the s-th level of the solution | |
| The reward of worker k | |
| k | The index of worker |
| j | The index of focused worker |
| The strategy of worker k | |
| The threshold value of strategy | |
| i | The i-th result of each round |
| n | The number of workers with high-quality solutions except the focused worker |
| Worker k’s mixed strategy vector | |
| The focused worker j takes a ZD strategy | |
| The conditional probability of worker k with outcome i | |
| The payoff vector of worker k | |
| The payoff of worker k of i-th outcome | |
| Conditional probability of worker k in the case that he uses X. Meanwhile, his opponents had n workers using H in the previous round | |
| The payoff of worker k in the case that he uses X. Meanwhile, his opponents had n workers using H in the previous round | |
| The expected payoff of worker k | |
| The transition probabilistic matrix | |
| Parameter of the system | |
| , | The weight factors of payoff function |
| Number of H | N − 1 | … | … | 1 | 0 | |
|---|---|---|---|---|---|---|
| Payoff of H | … | … | ||||
| Payoff of L | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Tang, C.; Lu, J.; Chen, G. Toward Zero-Determinant Strategies for Optimal Decision Making in Crowdsourcing Systems. Mathematics 2023, 11, 1153. https://doi.org/10.3390/math11051153
Wang J, Tang C, Lu J, Chen G. Toward Zero-Determinant Strategies for Optimal Decision Making in Crowdsourcing Systems. Mathematics. 2023; 11(5):1153. https://doi.org/10.3390/math11051153
Chicago/Turabian StyleWang, Jiali, Changbing Tang, Jianquan Lu, and Guanrong Chen. 2023. "Toward Zero-Determinant Strategies for Optimal Decision Making in Crowdsourcing Systems" Mathematics 11, no. 5: 1153. https://doi.org/10.3390/math11051153
APA StyleWang, J., Tang, C., Lu, J., & Chen, G. (2023). Toward Zero-Determinant Strategies for Optimal Decision Making in Crowdsourcing Systems. Mathematics, 11(5), 1153. https://doi.org/10.3390/math11051153







