A Novel Monte Carlo Method to Calculate the Thermal Conductivity in Nanoscale Thermoelectric Phononic Crystals Based on Universal Effective Medium Theory

Abstract

Thermal reduction by enhancing heat-generation phonon scattering can improve thermoelectric performance. In this paper, the phonon transport subjected to internal heat generation in two-dimensional nanoscale thermoelectric phononic crystals is investigated by a novel Monte Carlo method based on the universal effective medium theory, called the MCBU method. The present approach is validated. Compared with the universal effective medium theory method, the MCBU method is easier to implement. More importantly, the deviation of the computation time between the two methods can be ignored. With almost the same time cost, the present method can accurately calculate the effective thermal conductivity of complex geometric structures that cannot be calculated by the effective medium theory. The influences of porosity, temperature, pore shape and material parameters on thermal conductivity are discussed in detail. This study offers useful methods and suggestions for fabricating these materials with heat isolation and reduction.

1. Introduction

In the past decades, nanotechnology has been used more and more widely in thermoelectric devices, which makes the study of heat conduction theory extremely important. Generally, the phonon Boltzmann transport equation (BTE) can characterize thermal transport well in nanostructures. In order to solve the BTE, researchers have made a lot of progress [1,2,3,4,5,6,7,8]. The Gray model is commonly used [2]; however, solving the BTE in this way sometimes leads to inaccurate solutions that cannot be ignored. The different lattice Boltzmann methods have also been developed by the methods mentioned in references [3,4,5,6]. However, the lattice Boltzmann methods still have some shortcomings. For example, they are used for non-physical prediction in the ballistic state [5,6]. There is another method that can directly solve the BTE by using the finite difference method, namely the discrete ordinate method [7]. However, in addition to requiring a large amount of memory to solve the equation, this method also shows a slow convergence near the diffusion limit. Moreover, the discrete unified gas dynamics scheme [8] has been proven to be effective and deliver high-precision for low-dimensional thermal phonon transport, but it has not been used to solve the BTE in three-dimensional geometry. The state-space strategies are the basis of the novel theory of control and its advantage is the characterization of approaches of importance through the BTE in favoring transport functions. However, for this method, in the previous duration the processes were sufficient for them with only one differential equation for a reasonably low order [9]. The main step of the finite element method for solving the BTE is obtaining the equations of motion for the finite elements [10]. However, this method is very time consuming and it cannot handle the infinite domain problems well. So far, the Monte Carlo (MC) simulation has been proved to be an efficient method for solving the BTE. Two typical MC methods are used, of which the ensemble MC method is employed to calculate the effective thermal conductivity in many kinds of nanostructures, for example, silicon structures [11,12] and even composites [13,14]. The other method, the phonon tracing MC method, simulates the trajectories of phonons independently which reduces the computation time greatly [15,16]. Therefore, both the ensemble MC and the phonon tracing MC are suitable methods used for phonon transport in many kinds of nanostructures with a larger size, and they can also solve the BTE with high accuracy and minimum calculation time [1].

Recently, Yu-Chao Hua and Bing-Yang Cao proposed an efficient two-step Monte Carlo method for heat conduction in nanostructures [1]. However, it is difficult to calculate the effective thermal conductivity of complex structures with different pore shapes. Effective medium theory (EMT) is a widely used analytical method to study the optical responses of subwavelength periodic structures [17,18,19] and it can achieve similar functions of the whole system by defining the average value of materials with effective parameters [20]. The Maxwell-Garnett theory and the Bruggeman EMT are based on the material characteristics of each component in the mixture, which play an important role in effective medium methods. The composition of dielectric materials usually shows different structural properties. To calculate the thermal conductivity of these materials, EMT should be a favored method; for a given material and geometric structure, the EMT method can calculate the thermal conductivity by achieving the functions of the given system [21]. Due to these characteristics of EMT, it has many applications in electrical conductivity and related issues [22,23,24,25,26].

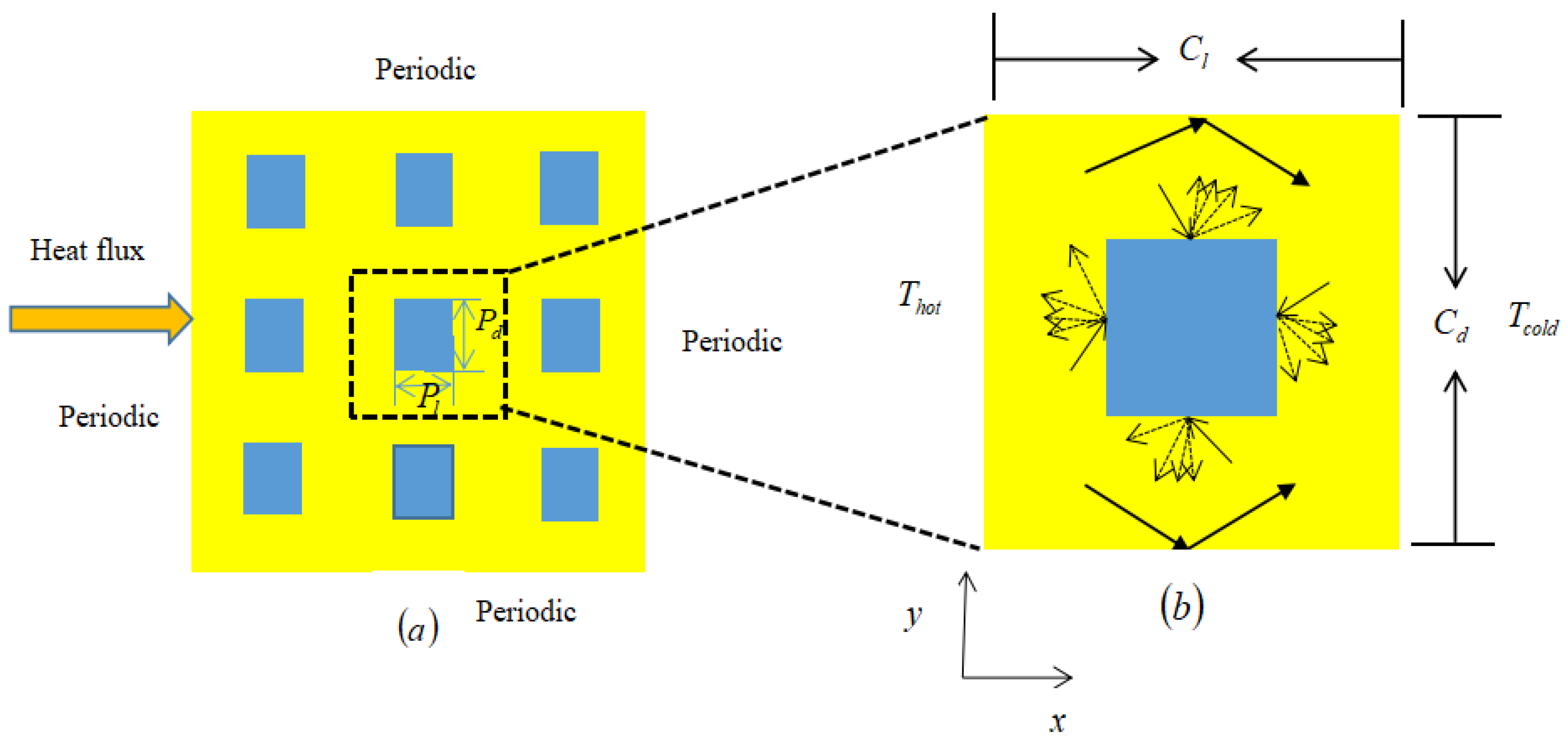
At nanoscale, the size characteristics of phononic crystals are very close to or even smaller than the mean free path (MFP) of phonons, and the heat conduction no longer obeys the Fourier law. Therefore, in order to deeply understand phonon transport in thermoelectric phononic crystals, the correct models and methods are required to simulate the phonon transport. The EMT method can effectively calculate the effective thermal conductivity, and the value of the effective thermal conductivity only depends on the porosity. However, the EMT method is not the best method to calculate the effective thermal conductivity of complex geometry. The MC method mainly calculates the effective thermal conductivity through the MC model, which can reduce the calculation time without damaging the accuracy. However, this method still has problems in calculating the effective thermal conductivity of complex pore shapes. The general effective medium theory can calculate the effective thermal conductivity of different pore shapes by implementing the suppression function. Therefore, we combine the MC method with the general effective medium theory method to develop a novel method for calculating the effective thermal conductivity of complex pore shapes as effectively as these two methods. In this paper, a novel Monte Carlo method based on the universal effective medium theory is developed to calculate the thermal conductivity in nanoscale thermoelectric phononic crystals with complex geometries, which is the creativity point in this paper. The outline of this paper is as follows. In Section 2, the method description is introduced. In addition, the numerical experiments are conducted to numerically illustrate some properties of the present method in Section 3, followed by a summary in Section 4. In this paper, the MCBU method is compared with the EMT method and it is found that the MCBU method can effectively and accurately calculate the effective thermal conductivity of different geometric shapes, while the EMT method cannot deal with it well, which is the main focus of this paper.

2. Method Description

2.1. Geometric Model

In this paper, a nanoporous phononic crystal is considered. First, a schematic diagram of phononic crystals is shown in Figure 1. In order to reduce calculation resources, the whole phononic crystal is divided into several unit cells, in which the pore shape of each unit cell is rectangular. The heat flux is parallel to the plane of the crystal for transmission. The two-dimensional (2D) view of the geometry is also shown in Figure 1b. The model illustrates phonon activities during the transport process where a temperature difference is applied between two boundaries along the x-direction. Phonons are emitted from the hot temperature boundaries, diffusive reflection occurs when the phonon meets the inner surface of the unit cell hole, and specular reflection occurs when it encounters the boundary of the unit cell, as shown in Figure 1b. In the present work, when calculating the effective thermal conductivity of a nanostructure with different pore shapes, such as circle pores, rhombus pores and triangle pores, we can replace the rectangle pores of the schematic diagram of phononic crystals shown in Figure 1 can be replaced with the above shapes.

2.2. Boltzmann Transport Equation

The BTE can be used to model phonon behavior in phononic crystals. In a lattice, without external force, the BTE equation is expressed as

$$\frac{\partial f(t,r,k)}{\partial t}+v\cdot \nabla f(t,r,k)={(\frac{\partial f(t,r,k)}{\partial t})}_{scatter}$$

(1)

Equation (1) in ref. [25] is related to the variation of distribution function f(t, r, k), and f(t, r, k) is a function which is dependent on time t, phonon position r and phonon wave k. The phonon group velocity v is v = ∇_kω. The left side of Equation (1) represents the drift term of phonons in the phononic crystals. The right side of the equation describes the scattering term of phonons and phonons, impurities and boundaries.

2.3. Thermal Conductivity in Phononic Crystals Based on Universal Effective Medium Theory

In this section, in order to calculate the effective thermal conductivity in phononic crystals with complex geometric parameters, the effective thermal conductivity in nanoscale thermoelectric phononic crystals will be calculated by using the MCBU method.

First, we can develop the phonon BTE into anisotropic-MFP-BTE [27,28,29,30,31,32,33,34,35]:

$$F_{ml}\cdot \nabla \Delta T_{ml}^{(n)}+\Delta T_{ml}^{(n)}={\sum }_{m\prime l\prime }{\alpha }_{m\prime l\prime }\Delta T_{m\prime l\prime }^{(n-1)}$$

(2)

where $F_{ml}={\mathsf{\Lambda }}_m{\widehat{S}}_l$ and ${\widehat{S}}_l=\sin ({\varphi }_l) \widehat{\mathrm{x}}+\cos ({\varphi }_l)\widehat{\mathrm{y}}$.

Then the effective thermal conductivity is given as follows:

$${\mathrm{k}}_{eff}=-\frac{L}{\Delta TA}\int J\cdot \widehat{n}d\mathrm{S}$$

(3)

where A is the surface area, L is the periodicity, $\widehat{n}=\widehat{x}$, ΔT is the pseudo-temperature, J is the heat flux and it can be described by

$$\begin{array}{l}J=\frac{C_v\mathsf{\Lambda }{v}_j}{4\pi }\frac{dT}{dx}A{\int }_0^{2\pi }{\int }_{-1}^1(\exp (-\frac{L_{rp}}{\mathsf{\Lambda }\sqrt{1-{\mu }^2}})-1){\mu }^{2}d\mu d\phi \\ =\frac{C_v\mathsf{\Lambda }{v}_j}{3}\frac{dT}{dx}{A}^2\frac{3}{4\pi A}{\int }_0^{2\pi }{\int }_{-1}^1(\exp (-\frac{L_{rp}}{\mathsf{\Lambda }\sqrt{1-{\mu }^2}})-1){\mu }^{2}d\mu d\phi \\ =-\frac{C_v\mathsf{\Lambda }{v}_j}{3}\frac{dT}{dx}{A}^{2}S({\overline{\mathsf{\Lambda }}}_{bulk,j}).\end{array}$$

(4)

where C_v is the heat capacity, v_j is the velocity, L_rp is the length from the point r to the point p at pore boundaries, Λ is the intrinsic MFP, $S({\overline{\mathsf{\Lambda }}}_{bulk,j})$ is the suppression function. Then we can obtain the effective thermal conductivity by substituting Equation (4) into Equation (3) as follows:

$$\begin{array}{l}{k}_{eff}=-\frac{L}{\Delta TA}\int -\frac{C_v\mathsf{\Lambda }{v}_j}{3}\frac{dT}{dx}{A}^{2}S({\overline{\mathsf{\Lambda }}}_{bulk,j})\cdot \widehat{n}d\mathrm{S}\\ \hspace{1em} =\int L\frac{C_v\mathsf{\Lambda }{v}_j}{3}AS({\overline{\mathsf{\Lambda }}}_{bulk,j})\cdot \widehat{n}d\mathrm{S}\\ \hspace{1em} =\int k_{bulk}(\mathsf{\Lambda })S({\overline{\mathsf{\Lambda }}}_{bulk,j},L)d\mathsf{\Lambda }\end{array}$$

(5)

where $S({\overline{\mathsf{\Lambda }}}_{bulk,j},L)$ is the suppression function which can describe the degree of reduction of heat transport with respect to the bulk for a given intrinsic MFP.

Integrating $\int k_{bulk}(\mathsf{\Lambda })S({\overline{\mathsf{\Lambda }}}_{bulk,j},L)d\mathsf{\Lambda }$ by parts and substituting it into Equation (5), we can obtain the following formula:

$$k_{eff}=k_{bulk}[S(\infty )-{\int }_0^{\infty }\frac{1}{1+\frac{{\mathsf{\Lambda }}_0}{\mathsf{\Lambda }}}\frac{\partial S(\mathsf{\Lambda })}{\partial \mathsf{\Lambda }}d\mathsf{\Lambda }]$$

(6)

To obtain the final equation, we take $S(\infty )=S(0)+{\int }_0^{\infty }\frac{\partial S(\mathsf{\Lambda })}{\partial \mathsf{\Lambda }}d\mathsf{\Lambda }$ and $\mathrm{S}(\mathsf{\Lambda })=\frac{S(\mathsf{\Lambda }\to 0)}{1+\frac{\mathsf{\Lambda }}{L_c}}$ into Equation (6):

$$\begin{array}{c}\frac{k_{eff}}{k_{bulk}}=S(0)+{\int }_0^{\infty }(1-\frac{1}{1+\frac{{\mathsf{\Lambda }}_0}{\mathsf{\Lambda }}})\frac{\partial S(\mathsf{\Lambda })}{\partial \mathsf{\Lambda }}d\mathsf{\Lambda } \\ \hspace{1em}\hspace{1em}=S(0)-S(0){\int }_0^{\infty }\frac{{\mathsf{\Lambda }}_0}{\mathsf{\Lambda }+{\mathsf{\Lambda }}_0}\frac{L_c}{{(L_c+\mathsf{\Lambda })}^2}d\mathsf{\Lambda }\\ \hspace{1em}=S(0)[1-{\int }_0^{\infty }\frac{{\mathsf{\Lambda }}_0}{\mathsf{\Lambda }+{\mathsf{\Lambda }}_0}\frac{L_c}{{(L_c+\mathsf{\Lambda })}^2}d\mathsf{\Lambda }]\\ =S(0)[1-{\mathrm{\Lambda }}_0{L}_c\frac{1}{L_c{}^2+{\mathrm{\Lambda }}_0({\mathrm{\Lambda }}_0-2L_c)}(-\ln \left(\frac{{\mathrm{\Lambda }}_0}{L_c}\right)+({\mathrm{\Lambda }}_0-2L_c)/L_c+1)]\end{array}$$

(7)

Then Equation (7) is the final equation of the effective thermal conductivity.

Where Λ₀ is the medium MFP of the thermal conductivity distribution, L_c is the mean light-of-sight between phonon scattering events with the nanostructure. Then we obtain the effective thermal conductivity in terms of the Monte Carlo method combined with the universal effective medium theory.

The graphic below describes the sequence of processing steps and the parameters used:

3. Results and Discussions

In this section, the accuracy of the MCBU method is checked and the results are compared with those of the two-step MC method and the MC model in Reference [1]. The two-step MC method calculates the thermal conductivity through the formula $\frac{{\mathrm{k}}_{eff\_\lim it}}{k_{bulk}}=\frac{3\Delta L}{4l_0}\frac{p_0}{1-p_i}$, where ΔL is the length of simulation unit, l₀ is the average MFP and p₀ is the initial phonon transmittance, p_i is the internal phonon transmittance. The MC model calculates the thermal conductivity through the formula $\frac{k_{eff,po}}{k_{bulk}}=1-\frac{3}{\pi R_p{}^2({\epsilon }^{-1}-1)}{\int }_{R_p}^{\raisebox{1ex}{$R_p$}\!\left/ \!\raisebox{-1ex}{$\sqrt{\epsilon }$}\right.}rdr{\int }_0^{2\pi }{\int }_0^1\exp (-\frac{L_{rp}}{l_0\sqrt{1-{\mu }^2}}){\mu }^{2}d\mu d\phi$, where R_p is the pore radius and ε is the porosity.

The deviation between p₀ and p_i can be ignored. Therefore, when calculating the effective thermal conductivity by the two-step MC method, p_i can be replaced by p₀. Figure 2 illustrates the effective thermal conductivity varying with L_c. It is found that the effective thermal conductivity increases with increasing L_c, and the results obtained by the MCBU method agree well with those predicted by the two-step MC method; the deviation between them decreases with increasing L_c. In addition, the results obtained by the two methods are both slightly less than those obtained by the MC model, and approach the value predicted by the MC model.

In the following, numerical experiments are conducted to show the effectiveness of the MCBU method, and the comparison between the MCBU method and effective medium theory (EMT) method is discussed in detail. First, the results are illustrated in

Table 1. The effective thermal conductivity in material made of AlN, at 300 k, with the comparison of the EMT method and the MCBU method.

Φ	ks	km	$\left|\frac{k_m-k_s}{k_m}\right|$ (%)	$\left|t_s-t_m\right|$ (s)
0.05	0.8170	0.9048	9.7%	3.35 × 10−3
0.10	0.7241	0.8182	11.5%	3.19 × 10−3
0.15	0.6707	0.7391	9.3%	3.30 × 10−3
0.20	0.5962	0.6667	10.6%	3.31 × 10−3
0.25	0.5486	0.6000	8.6%	3.21 × 10−3
0.30	0.5093	0.5385	5.4%	3.19 × 10−3
0.35	0.4675	0.4815	2.9%	3.29 × 10−3
0.40	0.4403	0.4286	2.7%	3.33 × 10−3

and Figure 3. In Table 1, k_s is denoted as the thermal conductivity of rectangle pores in the MCBU method, k_m as the thermal conductivity of the EMT method; and t_s is denoted as the computation time of the MCBU method, and t_m as the computation time of the EMT method. From Table 1, we can see that the MCBU method is consistent with the EMT method with a deviation of less than 12%. In the AlN with rectangular pore shape, when the porosity is 0.35 and 0.4, the MCBU method is consistent with the EMT method, with a deviation of about 3%. In addition, the deviation of the computation time between the two methods can be ignored. Figure 3 shows that the effective thermal conductivity decreases with the increase of porosity, and the deviation between the MCBU method and EMT method in rectangular and circular holes decreases sharply with the increase of porosity. For triangular and rhombic pores, the deviation between the two methods decreases with the decrease of porosity. With the change of pore shapes, the same value is obtained by using the EMT method, which indicates that the EMT method may have some problems in calculating the effective thermal conductivity of complex geometric pore shapes. Therefore, when calculating the effective thermal conductivity of pores with complex geometry, the MCBU method is a more suitable and quicker method.

Next, based on other influencing factors, we compare the results between the MCBU method and the EMT method in detail. From

Table 2. The effective thermal conductivity of rectangle pores compared with the EMT method.

Λ0 (μm)	ks	km	$\frac{k_m-k_s}{k_m}$ (%)	Deviation of the Computation Time (s)
0.1	0.5782	0.6000	3.6%	3.31 × 10−3
0.15	0.5531	0.6000	7.8%	3.21 × 10−3
0.20	0.5324	0.6000	11.3%	3.29 × 10−3
0.25	0.5148	0.6000	14.2%	3.31 × 10−3
0.30	0.4994	0.6000	16.8%	3.30 × 10−3
0.35	0.4856	0.6000	19.1%	3.32 × 10−3

, we can conclude that when the characteristic MFP Λ₀ is equal to 0.1 till 0.35, the effective thermal conductivity of rectangular pores is consistent with the EMT method, with a deviation of less than 20%, or even less than 5%. In addition, we find that the calculation time deviation between the two methods can be ignored, which shows the superiority of our method. In other words, it can accurately calculate more complex geometry than the effective medium theory in almost the same time. Figure 4 illustrates that the effective thermal conductivity calculated by the EMT method does not change with the changing of pore shapes and Λ₀. Moreover, from Figure 4, we can conclude that at the porosity of 0.25, the effective thermal conductivity in four kinds of shapes decreases with the increase of the characteristic MFP, and the deviation between the MCBU method and the EMT method decreases when the characteristic MFP decreases. In this figure, the effective thermal conductivity of rectangle pores is the closest to the EMT method.

Then, we analyze the influence of S(0) on the effective thermal conductivity in AlN, at 300 k, and compare the results between MCBU method and the EMT method. From

Table 3. The effective thermal conductivity in circle pores compared with the effective medium theory method.

S(0)	kc	km	$\frac{k_m-k_c}{k_m}$ (%)	Deviation of the Computation Time (s)
0.3	0.2321	0.2987	22.3%	3.21 × 10−3
0.4	0.3227	0.3986	19.0%	3.22 × 10−3
0.5	0.4150	0.5038	17.6%	3.19 × 10−3
0.6	0.5084	0.6000	15.3%	3.30 × 10−3
0.7	0.6027	0.7007	13.9%	3.33 × 10−3
0.8	0.6976	0.8018	12.8%	3.31 × 10−3
0.9	0.7930	0.9000	11.9%	3.30 × 10−3

, we can conclude that the MCBU method is consistent with the effective medium theory method. With the increase of S(0), the deviation will be less than 15%. In addition, we can see that the difference in calculation time between the two methods can be ignored, which again shows the superiority of our method. Figure 5 illustrates that the effective thermal conductivity in four kinds of pore shapes calculated by the MCBU method, and the effective thermal conductivity calculated by the EMT method increases with the increase of S(0) and the deviation between the MCBU method and the EMT method decreases with the increase of S(0).

In the following, we analyze the influence of L_c/L on the effective thermal conductivity in AlN, at 300k, with four kinds of pore shapes and compare the results of the MCBU method and the EMT method. As shown in

Table 4. The effective thermal conductivity in circle pores compared with the EMT method.

Lc/L	kc	km	$\frac{k_m-k_c}{k_m}$ (%)	Deviation of the Computation Time (s)
1.5	0.3691	0.4493	17.8%	3.21 × 10−3
1.6	0.3969	0.4815	17.6%	3.22 × 10−3
1.7	0.4331	0.5152	15.9%	3.17 × 10−3
1.8	0.4611	0.5504	16.2%	3.39 × 10−3
1.9	0.4892	0.5748	15.0%	3.22 × 10−3
2.0	0.5174	0.6129	15.6%	3.10 × 10−3

, the MCBU method agrees with the EMT method with a deviation between them of less than 20%. Except for the cases where L_c/L equals to 1.8 and 2.0, the deviation between the two methods decreases with the increase of L_c/L, and when L_c/L ≥ 1.7, the deviation between the two methods is less than 16.2%. From Figure 6, we can see that the two curves increase with the increase of L_c/L.

Then we calculate the effective thermal conductivity in rectangle pores and compare it with the EMT method. From

Table 5. The effective thermal conductivity in rectangle pores compared with the EMT method.

Lc/L	ks	km	$\frac{k_m-k_s}{k_m}$ (%)	Deviation of the Computation Time (s)
1.5	0.5496	0.6667	17.6%	3.21 × 10−3
1.6	0.5953	0.7241	17.8%	3.26 × 10−3
1.7	0.6330	0.7544	16.1%	3.37 × 10−3
1.8	0.6791	0.8182	17.0%	3.19 × 10−3
1.9	0.7170	0.8519	15.8%	3.14 × 10−3
2.0	0.7549	0.8868	14.9%	3.19 × 10−3

, we can conclude that the MCBU method agrees with the EMT method with the deviation between them being less than 18%, and except for the cases where L_c/L equals to 1.6 and 1.7, the deviation between the two methods decreases with the increase of L_c/L and when 1.9 ≤ L_c/L ≤ 2.0, the deviation between the two methods is less than 16%. Compared with Table 4, we can conclude that k_s is larger than k_c for all the values of L_c/L. From Figure 7, we can conclude that the two curves increase with the increase of L_c/L.

Next, we calculate the effective thermal conductivity in triangle pores and compare it with the EMT and we denote k_t as the thermal conductivity of the MCBU method and k_m as the thermal conductivity of the EMT method. From

Table 6. The effective thermal conductivity in triangle pores compared with the EMT method.

Lc/L	kt	km	$\frac{k_m-k_t}{k_m}$ (%)	Deviation of the Computation Time (s)
1.5	0.4511	0.5504	18.0%	3.22 × 10−3
1.6	0.4878	0.5873	16.9%	3.16 × 10−3
1.7	0.5164	0.6260	17.6%	3.30 × 10−3
1.8	0.5533	0.6667	17.0%	3.11 × 10−3
1.9	0.5904	0.6949	15.0%	3.09 × 10−3
2.0	0.6192	0.7241	14.5%	3.19 × 10−3

and Figure 8, we can conclude that the effective thermal conductivity increases with the increase of L_c/L. From Table 6, we can conclude that MCBU method agrees with the EMT method with the deviation between them less than 18% and except for the cases where L_c/L equals to 1.6, the deviation between the two methods decreases with the increase of L_c/L and when 1.9 ≤ L_c/L ≤ 2.0, the deviation between the two method is less than 15%. Compared with Table 4, Table 5 and Table 6, we have k_c < k_t < k_s for all the values of L_c/L.

Last, we calculate the effective thermal conductivity in rhombus pores and compare it with the EMT and we denote k_r as the thermal conductivity of the MCBU method and k_m as the thermal conductivity of the EMT method. From

Table 7. The effective thermal conductivity in rhombus pores compared with the EMT method.

Lc/L	kr	km	$\frac{k_m-k_r}{k_m}$ (%)	Deviation of the Computation Time (s)
1.5	0.4183	0.5152	18.8%	3.32 × 10−3
1.6	0.4548	0.5504	17.4%	3.26 × 10−3
1.7	0.4831	0.5748	16.0%	3.27 × 10−3
1.8	0.5114	0.6129	16.6%	3.31 × 10−3
1.9	0.5483	0.6529	16.0%	3.39 × 10−3
2.0	0.5768	0.6807	15.3%	3.30 × 10−3

and Figure 9, we can see that the effective thermal conductivity increases with the increase of L_c/L, and from Table 7, we can conclude that the MCBU method agrees with the EMT method with the deviation between them less than 19% and except for this, cases where L_c/L equals to 1.7, the deviation between the two methods decreases with the increase of L_c/L and when 1.7 ≤ L_c/L ≤ 2.0, the deviation between the two method is less than 16.6%. Compared with Table 4, Table 5 and Table 6, we can conclude that k_c < k_r < k_t < k_s for all the values of L_c/L.

Finally, a detailed analysis of influences of geometric parameters is conducted and discussed. In previous studies, the influences of porosity on thermal conductivity have been studied. However, little work has been done on the effects of different porosities on periodic nanoscale structures. In this paper, the effects of porosities on periodic nanostructures in different pore shapes are studied and shown in Figure 10. The black line denotes the circle pores, the blue line denotes the rectangle pores, the green line denotes the triangle pores and the red line denotes the rhombus pores. From Figure 10, it can be observed that the effective thermal conductivity decreases when the porosity increases and this is because the greater the porosity, the more loss of the heat flux passthrough to the material. The effective thermal conductivity of the triangle pore shapes is the most affected and it decreases most rapidly with the increase of the porosity. The thermal conductivity of the rectangle pore shapes is the least affected. With the increase of the porosity, the effective thermal conductivity of the rectangle pores decreases the slowest, followed by the circle pores and the rhombus pores. Let k_c, k_s, k_t, k_r be the effective thermal conductivity of circle pores, rectangle pores, triangle pores, and rhombus pores, respectively. It is clear that under the same porosity and the same temperature, we always have k_s > k_c > k_r > k_t as shown in Figure 10.

To evaluate the influence of the temperature, we calculate the effective thermal conductivity in different temperatures. When the temperature increases, no matter what the shape of the pore and the porosity, the effective thermal conductivity increases too. Without the loss of generality, we calculated the effective thermal conductivity with square shapes in at 200 k, 300 k, 400 k and 500 k, respectively, as shown in Figure 11. From this figure, we can conclude that at the same temperature, the trend of the effective thermal conductivity is dropping while the porosity is increasing and under the same porosity, the trend of conductivity is increasing while the temperature increasing. That is because when the temperature increases, the heat flux increases too and that causes the effective thermal conductivity increase.

To study the influence of the materials, we calculate the effective thermal conductivity with different pore shapes in four materials: AlAs, AlN, GaAs and Si. Without the loss of generality, we calculate the effective thermal conductivity in rectangle shapes in at 300 k. As shown in Figure 12, we can see that under the same porosity and the same temperature, the effective thermal conductivity in material made of AlN is the highest while, at the same time, the effective thermal conductivity in material made of Si is the lowest; the effective thermal conductivity in material made of GaAs is higher than that made of AlAs. Moreover, the thermal conductivity in material made of AlN and GaAs differs slightly but the conductivity in materials made of Si is significantly lower than the former, and this conclusion will not change with the change of the pore shapes. From this result, we can say that in materials made of AlN, there will be less loss of heat flux while in materials made of Si, there will be more loss of heat flux.

In order to evaluate the influence of the location of pore shapes, we calculate the effective thermal conductivity in material made of AlAs for two kinds of rectangles. For one kind of rectangle, we set the parameter as P_l = 2P_d which means the aspect ratio of the rectangle is 2 and for the other kind of the rectangle, we set the parameter as P_d = 2P_l which means the aspect ratio of the rectangle is 0.5, as shown in Figure 13. From this figure, it can be clearly seen that the effective thermal conductivity of the rectangle with P_l = 2P_d structure is always higher than the rectangle with P_d = 2P_l structure and the gap between the two line widens with the growth of the porosity. From this result, we can see that the locations of the pores block the heat flux through the materials, changing the direction of the heat flux and affecting the effective thermal conductivity.

4. Conclusions

The EMT is a widely used method to predict the thermal conductivity in nanostructures. However, the thermal conductivity of different pore shapes cannot be described well. In the present work, a novel MC method is developed to overcome this deficiency. Several numerical experiments have been conducted to verify the present MCBU method. The MUBU method estimates the results well. The following conclusions can be obtained:

• Λ₀, S(0), L_c are the main parameters which can influence the effective thermal conductivity which is calculated by the MCBU method. The effective thermal conductivity decreases with the increases of Λ₀ and the effective thermal conductivity increases with the increases of the S(0), L_c, respectively.
• Pore shapes and porosity can influence the effective thermal conductivity. For the same porosity, the effective thermal conductivity in rectangle pores is always higher than circle pores, triangle pores and rhombus pores. At the same time, the effective thermal conductivity in triangle pores is the lowest compared to other pores. For the same pore shape, the effective thermal conductivity decreases with the increases of porosity.
• The MCBU method can agree well with the EMT method with the same time requirements and the MCBU can calculate the effective thermal conductivity in complex pore shapes more accurately.

The MCBU method can efficiently calculate the thermal conductivity of different pore shapes. Although it can calculate the thermal conductivity of regular pore shapes, such as circle, rectangle, triangle and rhombus, it still has some limitations. To date, little work has been done on irregular pore shapes. The future research direction is to develop a method to calculate the effective thermal conductivity with irregular pore shapes, or try to cut irregular pore shapes into relatively regular shapes. In this way, a new method can be obtained to calculate the effective thermal conductivity with irregular and arbitrary pore shapes.