Studying the Effect of Introducing Chaotic Search on Improving the Performance of the Sine Cosine Algorithm to Solve Optimization Problems and Nonlinear System of Equations
Abstract
1. Introduction
- (1)
- Introducing the chaotic search sine cosine algorithm (CSSCA), a novel method that combines chaotic search and SCA to resolve NSEs.
- (2)
- Utilizing chaotic search to enhance the SCA-obtained solution.
- (3)
- Numerous well-known functions and many NSEs are used to test CSSCA.
- (4)
- Demonstrate the outstanding performance of the proposed method with numerical results and prove it statistically.
- (5)
- Examining the introduction of the chaotic search on SCA and its effect on enhancing the outcomes by altering the chaotic search’s parameters and attaining improved results.
2. Methods and Materials
2.1. Nonlinear System of Equations (NSEs)
2.2. Traditional SCA
- Updating Phase
- B.
- Balancing Phase
2.3. Chaos Theory
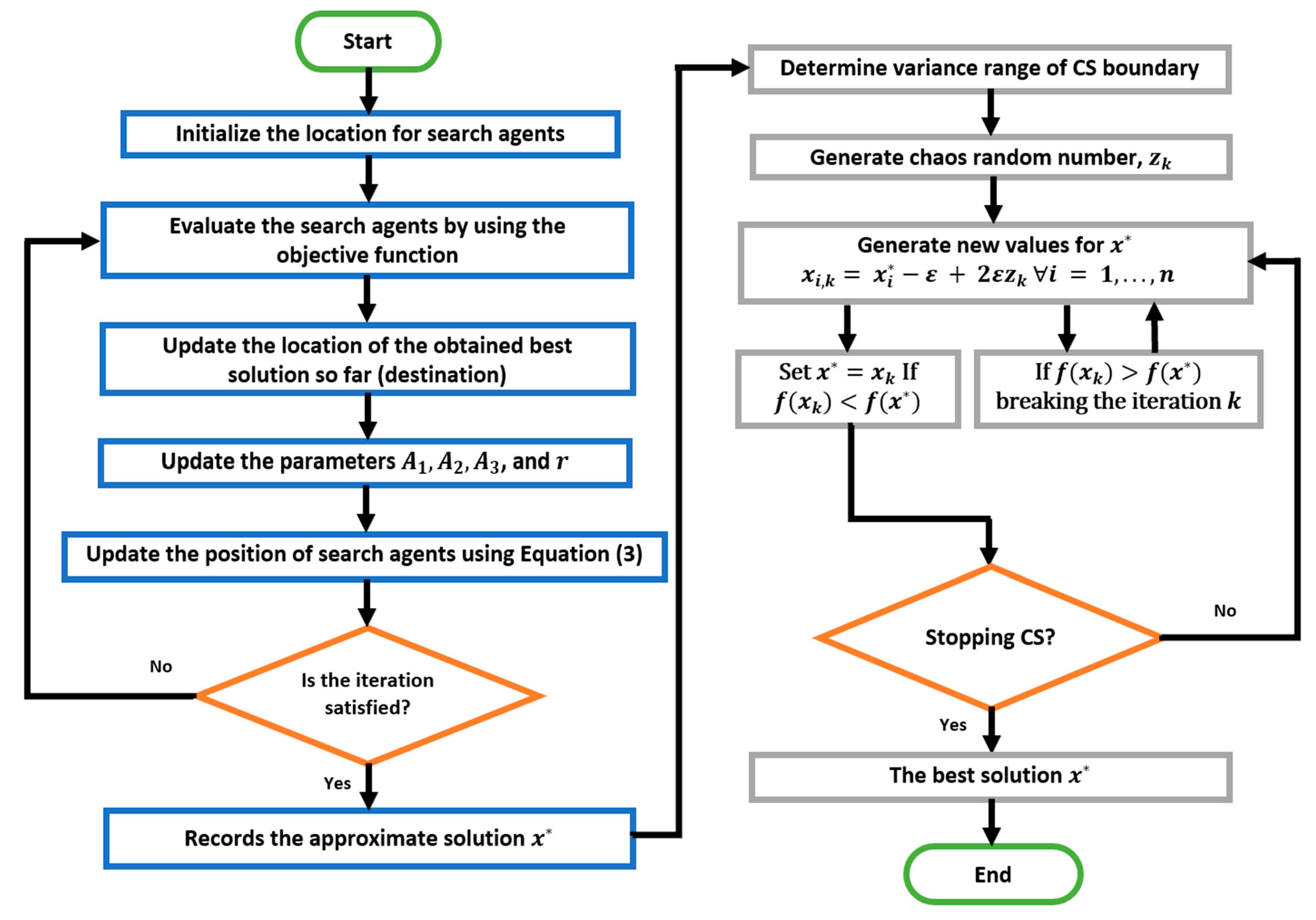
3. The Proposed Methodology
4. Numerical Results
4.1. Results for 19 Test Functions
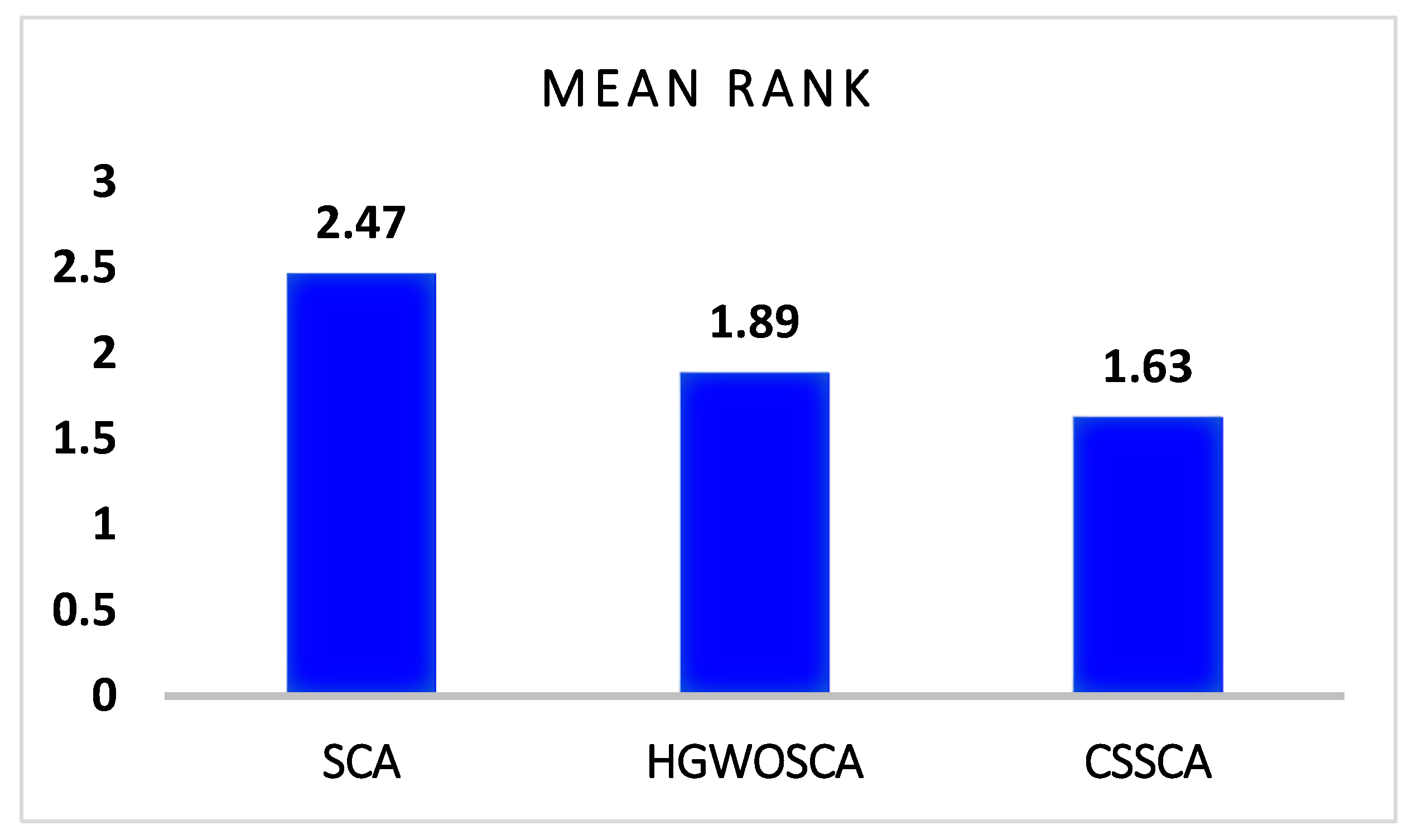
4.1.1. Friedman Test
4.1.2. Wilcoxon Signed-Rank Test
4.2. Case Study: Solving NSEs
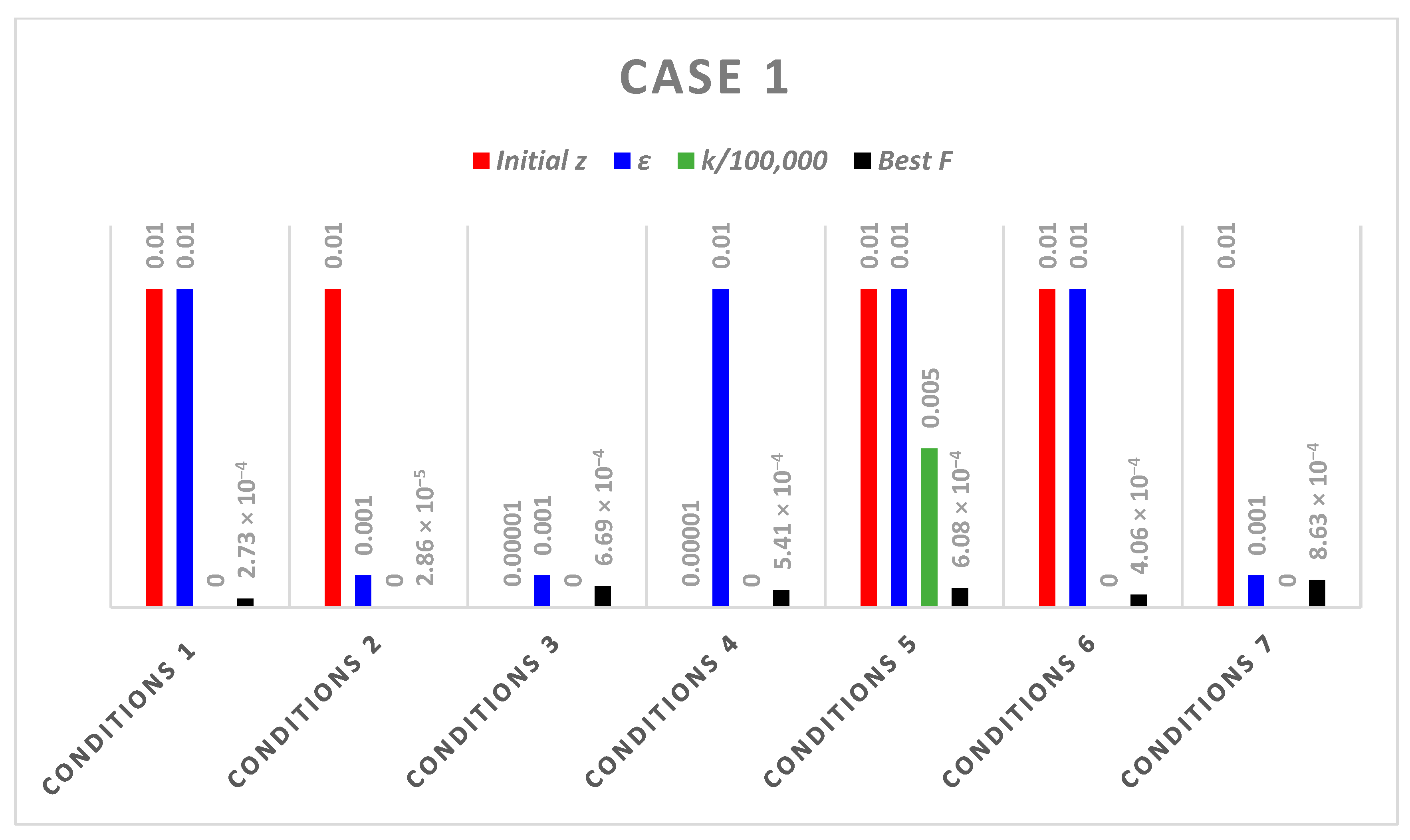
- Case 1: It contains the following two nonlinear algebraic equations.
- Case 2: It contains the following three nonlinear equations:
- Case 3: It contains non-differentiable system of non-linear equations as follows:
- Case 4: It contains the following two nonlinear equations:
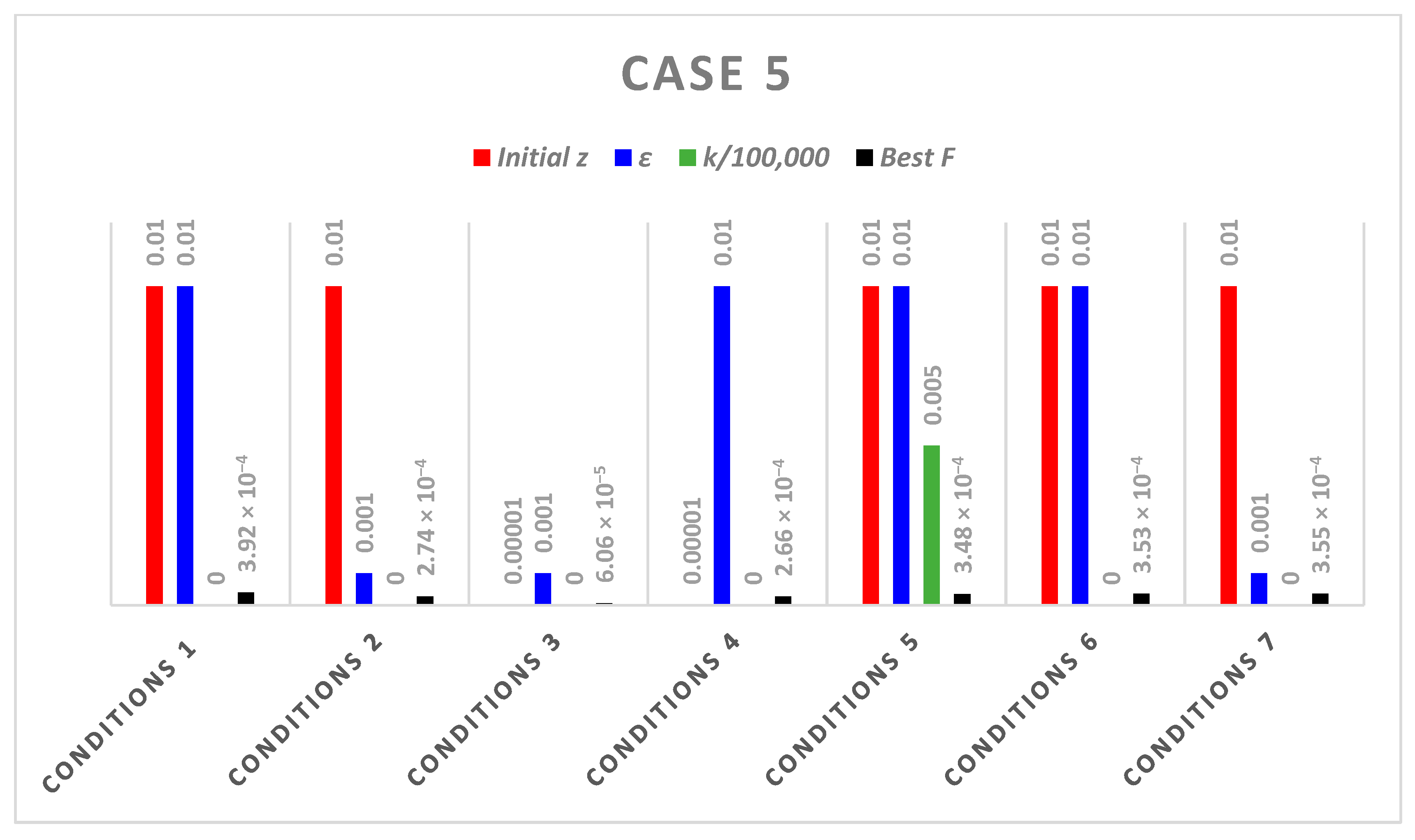
- Case 5: It is a combustion problem with a complex set of nonlinear equations, as shown below:
- Case 6: It is a neurophysiology problem with a complex set of nonlinear equations, as illustrated below:
- Case 7: It is an arithmetic application that has a complex set of nonlinear equations, as illustrated below:
Results for Nonlinear Systems of Equations
4.3. Computational Complexity of the CSSCA
5. Discussion and Conclusions
- (1)
- According to the results that were obtained in Table 1, we see those results of CSSCA are better than those obtained by the original SCA and the other SCA-based algorithm (HGWOSCA).
- (2)
- The results obtained in Table 1, by the percentage decrease equation (Equation (9)), shows that adding CS to SCA improves the original SCA results by 12.71%. So, we can therefore infer that CS instructs SCA to get rid of the local minimum and optimize the search results for a better solution.
- (3)
- Friedman and Wilcoxon’s tests were used for the statistical analysis, and the findings are shown in Table 2 and Table 3. Based on the results, it can be shown that the CSSCA and the other two algorithms that were also tested have significant differences, with a p-value of less than 0.05 (α = 0.022). In addition, Figure 4 demonstrates that the CSSCA surpasses other algorithms by obtaining the first rank. Furthermore, Table 3 shows that CSSCA performs better than the other two algorithms since its R+ values are larger than its than its R− values. This indicates that CSSCA performs better according to achieve lower objective function values for most testing functions.
- (4)
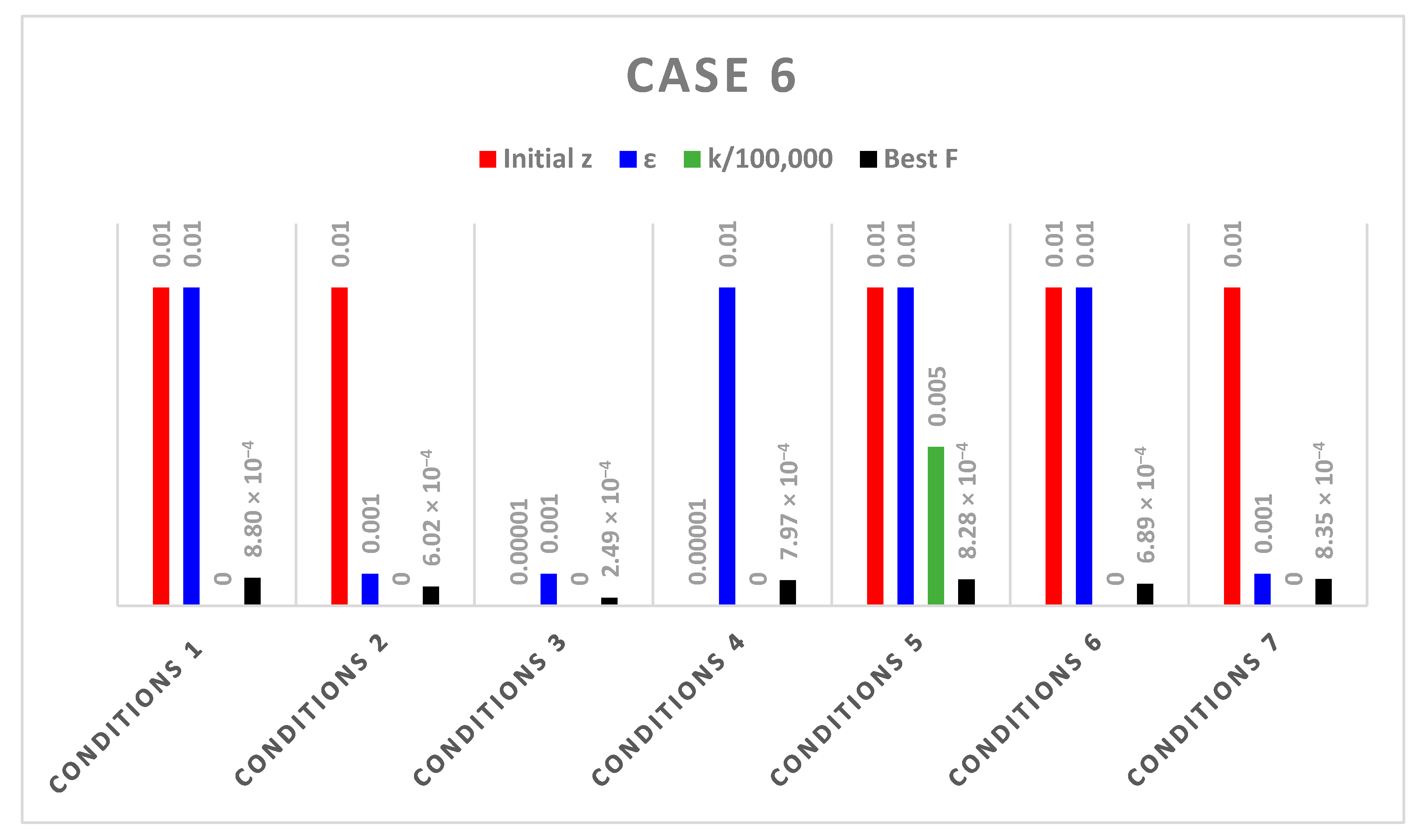
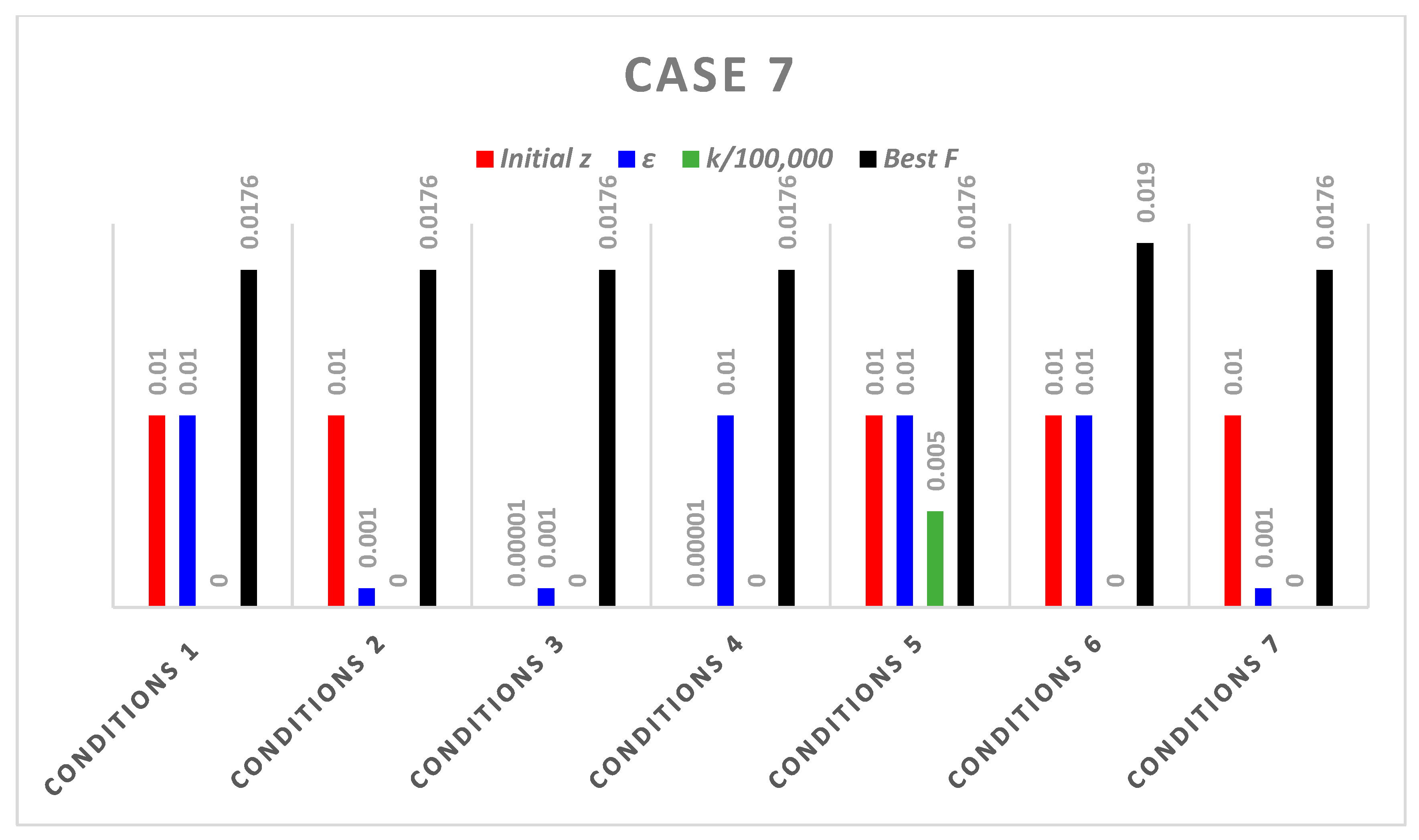
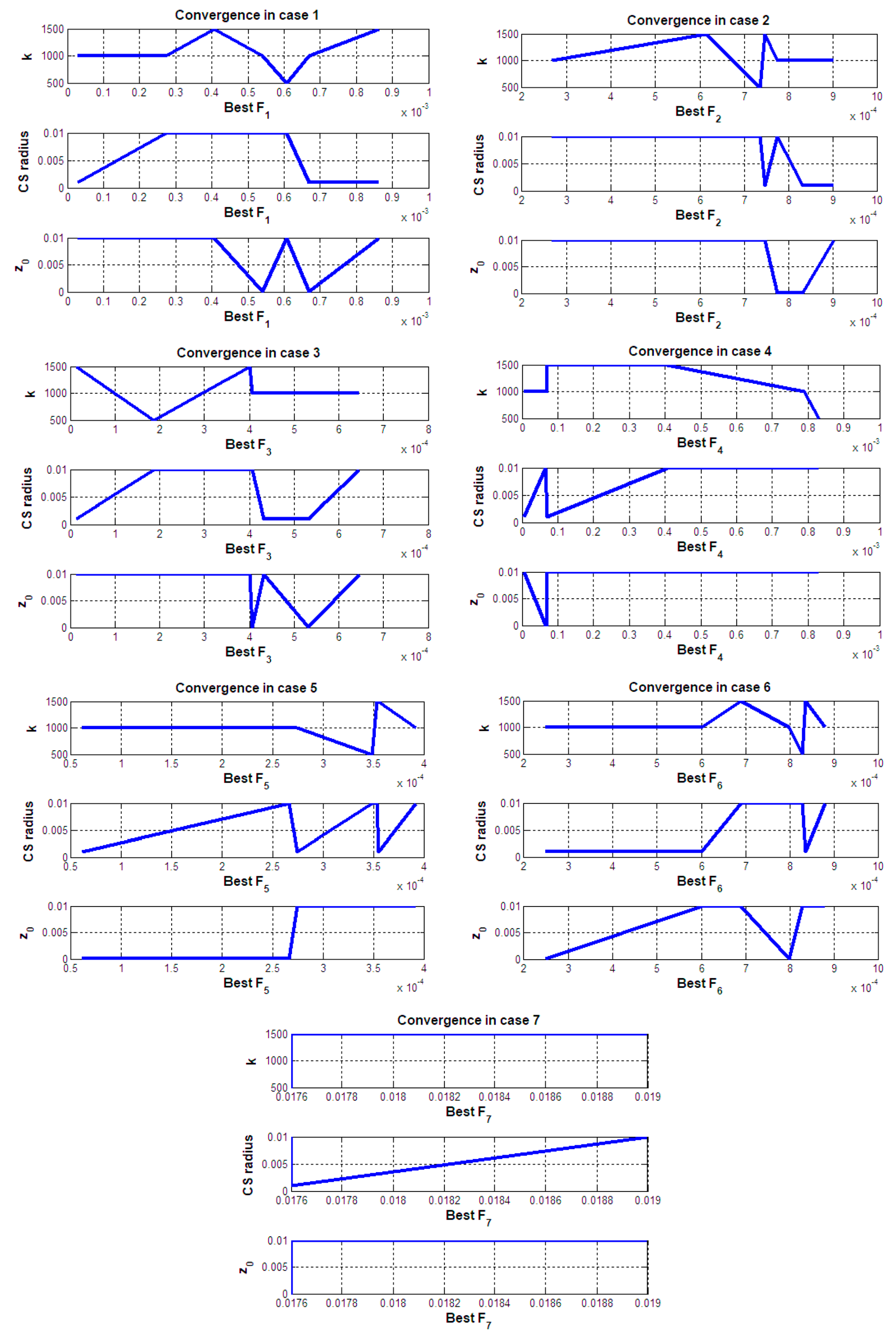
- The results of NSEs in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 and Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show that the introduction of CS on the SCA affects its performance as it was found that changing the CS parameters has an impact on the quality of the solution and obtaining better results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Chaotic Maps [73]
- –
- Sinusoidal map: The equation that produces the sine wave in Sinusoidal map iswhere
- –
- Chebyshev map: The Chebyshev map is shown as
- –
- Singer map: The formulation of the one-dimensional chaotic Singer map is as follows:where
- –
- Tent map: The following iterative equation defines the tent map:
- –
- Sine map: As an example, consider the sine map:where
- –
- Circle map: According to the following typical equation, a circle map is:where and
- –
- Piecewise map: The formulation of the piecewise map is as follows:where and
- –
- Gauss map: A nonlinear iterated map of the reals into a real interval determined by the Gaussian function is called the Gauss map, often referred to as the Gaussian map or mouse map:where α and β are real parameters.
- –
- Logistic map: Without the need for any random sequence, the logistic map illustrates how complicated behavior can develop from a straightforward deterministic system. Its foundation is a straightforward polynomial equation that captures the dynamics of a biological population.where and when The logistic map creates a chaotic sequence.
- –
- Intermittency map: Two iterative equations are used to create the intermittency map, which is shown as:where and is very close to zero.
- –
- Liebovitch map: According to the proposed chaotic map,where and
- –
- Iterative map: The definition of the iterative chaotic map with infinite collapses is as follows:where
Appendix B. Test Functions [31]
| Function | Dim | Range | Shift Position | |
|---|---|---|---|---|
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 |
| Function | Dim | Range | Shift Position | |
|---|---|---|---|---|
| 20 | ||||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 | |||
| 20 | 0 |
| Function | Dim | Range | |
|---|---|---|---|
| 10 | 0 | ||
| 10 | 0 | ||
| 10 | 0 | ||
| 10 | 0 | ||
| 10 | 0 | ||
| 10 | 0 |
References
- Jeeves, T.A. Secant modification of Newton’s method. Commun. ACM 1958, 1, 9–10. [Google Scholar] [CrossRef]
- Moré, J.J.; Cosnard, M.Y. Numerical solution of nonlinear equations. ACM Trans. Math. Softw. (TOMS) 1979, 5, 64–85. [Google Scholar] [CrossRef]
- Azure, I.; Aloliga, G.; Doabil, L. Comparative study of numerical methods for solving non-linear equations using manual computation. Math. Lett. 2019, 5, 41. [Google Scholar] [CrossRef]
- Dennis, J.E., Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Society for Industrial and Applied Mathematics: University City, PA, USA, 1996. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P. A globally convergent augmented Lagrangian algorithm for optimization with general constraints and simple bounds. SIAM J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Frankel, S. Numerical Methods for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Beheshti, Z.; Shamsuddin, S.M. A review of population-based meta-heuristic algorithms. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–35. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Ayoub, A.Y.; El-Shorbagy, M.A.; El-Desoky, I.M.; Mousa, A.A. Cell blood image segmentation based on genetic algorithm. In The International Conference on Artificial Intelligence and Computer Vision; Springer: Cham, Switzerland, 2020; pp. 564–573. [Google Scholar]
- Hansen, N. The CMA evolution strategy: A comparing review. In Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Price, K.V. Differential evolution. In Handbook of Optimization: From Classical to Modern Approach; Springer: Berlin/Heidelberg, Germany, 2013; pp. 187–214. [Google Scholar]
- Zhou, X.; Ma, H.; Gu, J.; Chen, H.; Deng, W. Parameter adaptation-based ant colony optimization with dynamic hybrid mechanism. Eng. Appl. Artif. Intell. 2022, 114, 105139. [Google Scholar] [CrossRef]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Hendawy, Z.M.; El-Shorbagy, M.A. Combined Trust Region with Particle swarm for Multi-objective Optimisation. In Proceedings of International Academic Conferences, no. 2703860; International Institute of Social and Economic Sciences: London, UK, 2015. [Google Scholar]
- A El-Shorbagy, M.; El-Refaey, A.M. A hybrid genetic–firefly algorithm for engineering design problems. J. Comput. Des. Eng. 2022, 9, 706–730. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A. Chaotic Fruit Fly Algorithm for Solving Engineering Design Problems. Complexity 2022, 2022, 6627409. [Google Scholar] [CrossRef]
- Kaya, E.; Gorkemli, B.; Akay, B.; Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Eng. Appl. Artif. Intell. 2022, 115, 105311. [Google Scholar] [CrossRef]
- Yang, X.-S.; Suash, D. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Zhou, Y.; Xin, C.; Guo, Z. An improved monkey algorithm for a 0-1 knapsack problem. Appl. Soft Comput. 2016, 38, 817–830. [Google Scholar] [CrossRef]
- Ma, C.; Huang, H.; Fan, Q.; Wei, J.; Du, Y.; Gao, W. Gray wolf optimizer based on aquila exploration method. Expert Syst. Appl. 2022, 205, 117629. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Omar, H.A.; Fetouh, T. Hybridization of Manta-Ray Foraging Optimization Algorithm with Pseudo Parameter-Based Genetic Algorithm for Dealing Optimization Problems and Unit Commitment Problem. Mathematics 2022, 10, 2179. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Eldesoky, I.M.; Basyouni, M.M.; Nassar, I.; El-Refaey, A.M. Chaotic Search-Based Salp Swarm Algorithm for Dealing with System of Nonlinear Equations and Power System Applications. Mathematics 2022, 10, 1368. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Feng, Y.; Deb, S.; Wang, G.-G.; Alavi, A.H. Monarch butterfly optimization: A comprehensive review. Expert Syst. Appl. 2021, 168, 114418. [Google Scholar] [CrossRef]
- Mirjalili, S.; Andrew, L. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Liu, Y.; Heidari, A.A.; Cai, Z.; Liang, G.; Chen, H.; Pan, Z.; Alsufyani, A.; Bourouis, S. Simulated annealing-based dynamic step shuffled frog leaping algorithm: Optimal performance design and feature selection. Neurocomputing 2022, 503, 325–362. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V. Colliding bodies optimization: A novel meta-heuristic method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Erol, O.K.; Ibrahim, E. A new optimization method: Big bang–Big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization. Prog Electromagn. Res. 2007, 77, 425–491. [Google Scholar] [CrossRef]
- Hosseini, H.S. Principal components analysis by the galaxy-based search algorithm: A novel metaheuristic for continuous optimisation. Int. J. Comput. Sci. Eng. 2011, 6, 132. [Google Scholar] [CrossRef]
- Moghaddam, F.F.; Moghaddam, R.F.; Cheriet, M. Curved space optimization: A random search based on general relativity theory. arXiv 2012, arXiv:1208.2214. [Google Scholar]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2018, 163, 283–304. [Google Scholar] [CrossRef]
- Kashan, A.H. League championship algorithm: A new algorithm for numerical function optimization. In Proceedings of the 2009 International Conference of Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Rahoual, M.; Saad, R. Solving Timetabling problems by hybridizing genetic algorithms and taboo search. In Proceedings of the 6th International Conference on the Practice and Theory of Automated Timetabling (PATAT 2006), Brno, Czech Republic, 30 August–1 September 2006. [Google Scholar]
- Yong, L. An Improved Harmony Search Based on Teaching-Learning Strategy for Unconstrained Binary Quadratic Programming. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021. [Google Scholar]
- He, S.; Wu, Q.H.; Saunders, J.R. Group search optimizer: An optimization algorithm inspired by animal searching behavior. IEEE Trans. Evol. Comput. 2009, 13, 973–990. [Google Scholar] [CrossRef]
- Moosavian, N.; Roodsari, B.K. Soccer league competition algorithm: A novel meta-heuristic algorithm for optimal design of water distribution networks. Swarm Evol. Comput. 2014, 17, 14–24. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar]
- Dai, C.; Chen, W.; Zhu, Y.; Zhang, X. Seeker optimization algorithm for optimal reactive power dispatch. IEEE Trans. Power Syst. 2009, 24, 1218–1231. [Google Scholar]
- Ghorbani, N.; Ebrahim, B. Exchange market algorithm. Appl. Soft Comput. 2014, 19, 177–187. [Google Scholar] [CrossRef]
- Hofmeyr, S.A.; Forrest, S. Architecture for an artificial immune system. Evol. Comput. 2000, 8, 443–473. [Google Scholar] [CrossRef]
- Abdullahi, M.; Ngadi, A.; Abdulhamid, S.M. Symbiotic organism search optimization based task scheduling in cloud computing environment. Future Gener. Comput. Syst. 2016, 56, 640–650. [Google Scholar] [CrossRef]
- Jahangiri, M.; Hadianfard, M.A.; Najafgholipour, M.A.; Jahangiri, M.; Gerami, M.R. Interactive autodidactic school: A new metaheuristic optimization algorithm for solving mathematical and structural design optimization problems. Comput. Struct. 2020, 235, 106268. [Google Scholar] [CrossRef]
- Randolph, H.E.; Barreiro, L.B. Herd immunity: Understanding COVID-19. Immunity 2020, 52, 737–741. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Das, S.; Arijit, B.; Sambarta, D.; Ajith, A. Bacterial foraging optimization algorithm: Theoretical foundations, analysis, and applications. In Foundations of Computational Intelligence Volume 3: Global Optimization; Springer: Berlin/Heidelberg, Germany, 2009; pp. 23–55. [Google Scholar]
- Halim, A.H.; Ismail, I.; Das, S. Performance assessment of the metaheuristic optimization algorithms: An exhaustive review. Artif. Intell. Rev. 2020, 54, 2323–2409. [Google Scholar] [CrossRef]
- Algelany, A.M.; El-Shorbagy, M.A. Chaotic Enhanced Genetic Algorithm for Solving the Nonlinear System of Equations. Comput. Intell. Neurosci. 2022, 2022, 1376479. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Liu, H.; Wang, Q. Conjugate direction particle swarm optimization solving systems of nonlinear equations. Comput. Math. Appl. 2009, 57, 1877–1882. [Google Scholar] [CrossRef]
- Jia, R.; He, D. Hybrid artificial bee colony algorithm for solving nonlinear system of equations. In Proceedings of the 2012 Eighth International Conference on Computational Intelligence and Security, Guangzhou, China, 17–18 November 2012; pp. 56–60. [Google Scholar]
- Zhou, R.H.; Li, Y.G. An improve cuckoo search algorithm for solving nonlinear equation group. Appl. Mech. Mater. 2014, 651–653, 2121–2124. [Google Scholar] [CrossRef]
- Ariyaratne, M.; Fernando, T.; Weerakoon, S. Solving systems of nonlinear equations using a modified firefly algorithm (MODFA). Swarm Evol. Comput. 2019, 48, 72–92. [Google Scholar] [CrossRef]
- Omar, H.A.; El-Shorbagy, M.A. Modified grasshopper optimization algorithm-based genetic algorithm for global optimization problems: The system of nonlinear equations case study. Soft Comput. 2022, 26, 9229–9245. [Google Scholar] [CrossRef]
- Mousa, A.A.; El-Shorbagy, M.A.; Mustafa, I.; Alotaibi, H. Chaotic search based equilibrium optimizer for dealing with nonlinear programming and petrochemical application. Processes 2021, 9, 200. [Google Scholar] [CrossRef]
- Cuyt, A.A.M.; Rall, L.B. Computational implementation of the multivariate Halley method for solving nonlinear systems of equations. ACM Trans. Math. Softw. (TOMS) 1985, 11, 20–36. [Google Scholar] [CrossRef]
- Nie, P.-Y. A null space method for solving system of equations. Appl. Math. Comput. 2004, 149, 215–226. [Google Scholar] [CrossRef]
- Nie, P.-Y. An SQP approach with line search for a system of nonlinear equations. Math. Comput. Model. 2006, 43, 368–373. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Sterkenburg, T.F.; Grünwald, P.D. The no-free-lunch theorems of supervised learning. Synthese 2021, 199, 9979–10015. [Google Scholar] [CrossRef]
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Lorenz, E. The Essence of Chaos; University of Washington Press: Washington, DA, USA, 1996. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Aguirre, L.A.; Christophe, L. Modeling nonlinear dynamics and chaos: A review. Math. Probl. Eng. 2009, 2009, 238960. [Google Scholar] [CrossRef]
- Yang, D.; Li, G.; Cheng, G. On the efficiency of chaos optimization algorithms for global optimization. Chaos Solitons Fractals 2007, 34, 1366–1375. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Nasr, S.M.; Mousa, A.A. A Chaos Based Approach for Nonlinear Optimization Problems; LAP (Lambert Academic Publishing): Saarbrücken, Germany, 2016. [Google Scholar]
- El-Shorbagy, M.; Mousa, A.; Nasr, S. A chaos-based evolutionary algorithm for general nonlinear programming problems. Chaos Solitons Fractals 2016, 85, 8–21. [Google Scholar] [CrossRef]
- Grosan, C.; Abraham, A. A new approach for solving nonlinear equations systems. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2008, 38, 698–714. [Google Scholar] [CrossRef]
- Ren, H.; Wu, L.; Bi, W.; Argyros, I.K. Solving nonlinear equations system via an efficient genetic algorithm with symmetric and harmonious individuals. Appl. Math. Comput. 2013, 219, 10967–10973. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Ebrahimi, R.; Mirzaei, M.; Shams, M. Applying genetic algorithms for solving nonlinear algebraic equations. Appl. Math. Comput. 2013, 219, 11483–11494. [Google Scholar] [CrossRef]
- Wasserman, L. All of Nonparametric Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021, 38, 3025–3056. [Google Scholar] [CrossRef]





| PD% between the Original SCA and CSSCA | CSSCA Result | HGWOSCA | SCA Result | PD% between the Original SCA and CSSCA |
|---|---|---|---|---|
| F1 | 0.083239 | 0.0053 | 0.0535 | 35.72724324 |
| F2 | 2.7645 × 10−19 | 0.0319 | 2.7645 × 10−19 | 0 |
| F3 | 4.8556 × 10−8 | 1.06612 × 10−4 | 4.4013 × 10−8 | 9.356207266 |
| F4 | 1.3407 × 10−10 | 0.7785 | 1.3407 × 10−10 | 0 |
| F5 | 7.3038 | 26.5837 | 7.0772 | 3.102494592 |
| F6 | 0.80834 | 0.0031 | 0.6747 | 16.53264715 |
| F7 | 4.6115 × 10−4 | 0.0024 | 3.5722 × 10−4 | 22.53713542 |
| F8 | −2049.352 | −5553.8 | −4272.3 | 108.4707752 |
| F9 | 6.1611 | 0 | 5.8554 | 4.961776306 |
| F10 | 8.8818 × 10−16 | 0.0026 | 8.8818 × 10−16 | 0 |
| F11 | 0.23479 | 0 | 0.2061 | 12.21943013 |
| F12 | 0.084886 | 0.0025 | 0.0729 | 14.12011404 |
| F13 | 0.21134 | 0.0011 | 0.2009 | 4.939907258 |
| F14 | 1.0128 | 0.9980 | 0.9980 | 1.461295419 |
| F15 | 0.00070061 | 0.0012 | 6.4760 × 10−4 | 7.566263685 |
| F16 | −1.0316 | −1.0315 | −1.0316 | 0 |
| F17 | 0.40039 | 0.3979 | 0.3984 | 0.49701541 |
| F18 | 3.0001 | 3 | 3.0000 | 0.003333222 |
| F19 | −3.8598 | −3.8625 | −3.8600 | 0.005181616 |
| Test Statistics | Rank | ||
|---|---|---|---|
| N | 19 | Algorithm | Mean Rank |
| Chi-Square | 7.657 | SCA | 2.47 |
| df | 2 | HGWOSCA | 1.89 |
| Asymp. Sig. | 0.022 | CSSCA | 1.63 |
| Test Statistics a a. Wilcoxon Signed-Ranks Test | Ranks | |||||
|---|---|---|---|---|---|---|
| Sum | N | Mean Rank | Sum of Ranks | < Or > Or = | ||
| SCA—CSSCA | R− | 0 a | 0.00 | 0.00 | a. SCA < CSSCA | |
| Z | −3.408 b | R+ | 15 b | 8.00 | 120.00 | b. SCA > CSSCA |
| Asymp. Sig. (2-tailed) | 0.001 | Ties | 4 c | c. SCA = CSSCA | ||
| b. Based on negative ranks. | Total | 19 | ||||
| HGWOSCA—CSSCA | R− | 9 d | 10.67 | 96.00 | d. HGWOSCA < CSSCA | |
| Z | −0.923 c | R+ | 8 e | 7.13 | 57.00 | e. HGWOSCA > CSSCA |
| Asymp. Sig. (2-tailed) | 0.356 | Ties | 2 f | f. HGWOSCA = CSSCA | ||
| c. Based on negative ranks. | Total | 19 | ||||
| Conditions | k | Best Position () | Best F1 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | 2.0002, 0.9999 | 2.7336 × 10−4 |
| Conditions 2 | 0.01 | 0.001 | 1000 | 1.0000, 2.0000 | 2.8633 × 10−5 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | 1.9996, 1.0007 | 6.6914 × 10−4 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | 2.0004, 0.9995 | 5.4087 × 10−4 |
| Conditions 5 | 0.01 | 0.01 | 500 | 1.0006, 1.9996 | 6.0820 × 10−4 |
| Conditions 6 | 0.01 | 0.01 | 1500 | 1.0001,2.0000 | 4.0604 × 10−4 |
| Conditions 7 | 0.01 | 0.001 | 1500 | 2.0006, 0.9991 | 8.6317 × 10−4 |
| Conditions | k | Best Position () | Best F2 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | −0.0329, 1.2648, 1.4006 | 2.6693 × 10−4 |
| Conditions 2 | 0.01 | 0.001 | 1000 | −0.0230, 1.2645, 1.4009 | 9.0229 × 10−4 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | −0.0333, 1.2627, 1.4056 | 8.3069 × 10−4 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | −0.0339, 1.2649, 1.3999 | 7.7486 × 10−4 |
| Conditions 5 | 0.01 | 0.01 | 500 | −0.0338, 1.2650, 1.4002 | 7.3606 × 10−4 |
| Conditions 6 | 0.01 | 0.01 | 1500 | −0.0338, 1.2648, 1.4001 | 6.1370 × 10−4 |
| Conditions 7 | 0.01 | 0.001 | 1500 | −0.0336, 1.2650, 1.3998 | 7.4714 × 10−4 |
| Conditions | k | Best Position () | Best F3 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | −1.3659, 3.1273 | 6.4579 × 10−4 |
| Conditions 2 | 0.01 | 0.001 | 1000 | −1.3657, 3.1273 | 4.3137 × 10−4 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | 1.4419, 3.1273 | 5.3103 × 10−4 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | −1.3657, 3.1273 | 4.0623 × 10−4 |
| Conditions 5 | 0.01 | 0.01 | 500 | 1.4417, 3.1273 | 1.8692 × 10−4 |
| Conditions 6 | 0.01 | 0.01 | 1500 | 1.4419, 3.1273 | 4.0073 × 10−4 |
| Conditions 7 | 0.01 | 0.001 | 1500 | 1.4416, 3.1273 | 1.4685 × 10−5 |
| Conditions | k | Best Position () | Best F4 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | 0.1570, 0.4935 | 7.8956 × 10−4 |
| Conditions 2 | 0.01 | 0.001 | 1000 | 0.1565, 0.4934 | 4.7106 × 10−6 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | 0.1566, 0.4934 | 7.0050 × 10−5 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | −2.9851, −2.6482 | 6.6633 × 10−5 |
| Conditions 5 | 0.01 | 0.01 | 500 | 6.4402, 6.7768 | 8.2988 × 10−4 |
| Conditions 6 | 0.01 | 0.01 | 1500 | 0.1568, 0.4935 | 4.0707 × 10−4 |
| Conditions 7 | 0.01 | 0.001 | 1500 | 0.1570, 0.4936 | 7.1143 × 10−5 |
| Conditions | k | Best Pos () | Best F5 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | −5.0135 × 10−6, 2.8680 × 10−5, −10, 0.0037, 6.0578 × 10−12, 10, −0.0018, 10, −3.4240 × 10−6, −10 | 3.9154 × 10−4 |
| Conditions 2 | 0.01 | 0.001 | 1000 | 0.0038, −0.0054, −0.0104, −0.0044, 2.1600 × 10−11, 0.0095, 0.0019, 0.0145, −0.0307, 0.0082 | 2.7376 × 10−4 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | −1.1033 × 10−8, −3.1127 × 10−6, −10, −5.5679 × 10−4, −1.8332 × 10−12, 10, 2.8015 × 10−4, 10, 2.1671 × 10−5, −10 | 6.0646 × 10−5 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | −0.0104, −1.7648 × 10−4, −0.0222, 3.1607 × 10−4, 1.2687 × 10−10, −0.0152, −5.5569 × 10−5, 0.0251, −0.0671, 0.0487 | 2.6557 × 10−4 |
| Conditions 5 | 0.01 | 0.01 | 500 | 1.3712 × 10−7, −2.1896 × 10−4, −9.9991, −7.0970 × 10−7, −1.1578 × 10−13, 10, −1.4509 × 10−5, 10, −2.5461 × 10−4, −10 | 3.4767 × 10−4 |
| Conditions 6 | 0.01 | 0.01 | 1500 | 1.5492 × 10−7, −2.7488 × 10−4, −10, −4.9143 × 10−6, −2.9417 × 10−12, 10, 3.0756 × 10−6, 10, 2.9057 × 10−4, −10 | 3.5273 × 10−4 |
| Conditions 7 | 0.01 | 0.001 | 1500 | 1.2119 × 10−6, −3.0283 × 10−4, 10, 3.6210 × 10−5, 2.3696 × 10−12, −10, −1.1715 × 10−5, −10, 3.0054 × 10−4, 10 | 3.5469 × 10−4 |
| Conditions | K | Best Pos () | Best F6 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | 0.1933, −0.9973, −0.9804, 0.0730, −5.0824 × 10−4, 0.0031 | 8.7958 × 10−4 |
| Conditions 2 | 0.01 | 0.001 | 1000 | 0.1431, 0.9524, −0.9896, 0.3050, 7.5318 × 10−4, −0.0023 | 6.0153 × 10−4 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | −1.0000, 0.9687, 0.0030, −0.2495, −0.0017, −0.0013 | 2.4897 × 10−4 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | 1.7130 × 10−5, −0.9636, 1.0019, 0.2684, 3.3332 × 10−4, 4.3633 × 10−5 | 7.9744 × 10−4 |
| Conditions 5 | 0.01 | 0.01 | 500 | 0.7161, 1.0010, −0.6963, −0.0190, −1.5278 × 10−4, 4.4880 × 10−6 | 8.2790 × 10−4 |
| Conditions 6 | 0.01 | 0.01 | 1500 | 0.1862, 0.6602, −0.9835, 0.7511, 0.0015, 8.7707 × 10−4 | 6.8913 × 10−4 |
| Conditions 7 | 0.01 | 0.001 | 1500 | 0.0092, 0.0114, 1.0000, 1.0013, −9.9631 × 10−4, −0.0012 | 8.3455 × 10−4 |
| Conditions | k | Best Pos () | Best F7 | ||
|---|---|---|---|---|---|
| Conditions 1 | 0.01 | 0.01 | 1000 | 0.2317, 0.3962, 0.2888, 0.2005, 0.4093, 0.1540, 0.4427, 0.0634, 0.2999, 0.4428 | 0.0176 |
| Conditions 2 | 0.01 | 0.001 | 1000 | 0.2317, 0.3962, 0.2888, 0.2005, 0.4093, 0.1540, 0.4427, 0.0634, 0.2999, 0.4428 | 0.0176 |
| Conditions 3 | 0.00001 | 0.001 | 1000 | 0.2317, 0.3962, 0.2888, 0.2005, 0.4093, 0.1540, 0.4427, 0.0634, 0.2999, 0.4428 | 0.0176 |
| Conditions 4 | 0.00001 | 0.01 | 1000 | 0.2317, 0.3962, 0.2888, 0.2005, 0.4093, 0.1540, 0.4427, 0.0634, 0.2999, 0.4428 | 0.0176 |
| Conditions 5 | 0.01 | 0.01 | 500 | 0.2317, 0.3962, 0.2888, 0.2005, 0.4093, 0.1540, 0.4427, 0.0634, 0.2999, 0.4428 | 0.0176 |
| Conditions 6 | 0.01 | 0.01 | 1500 | 0.2066, 0.4182, 0.2583, 0.1698, 0.4791, 0.1494, 0.4275, 0.0728, 0.3549, 0.4234 | 0.0190 |
| Conditions 7 | 0.01 | 0.001 | 1500 | 0.2317, 0.3962, 0.2888, 0.2005, 0.4093, 0.1540, 0.4427, 0.0634, 0.2999, 0.4428 | 0.0176 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Shorbagy, M.A.; Al-Drees, F.M. Studying the Effect of Introducing Chaotic Search on Improving the Performance of the Sine Cosine Algorithm to Solve Optimization Problems and Nonlinear System of Equations. Mathematics 2023, 11, 1231. https://doi.org/10.3390/math11051231
El-Shorbagy MA, Al-Drees FM. Studying the Effect of Introducing Chaotic Search on Improving the Performance of the Sine Cosine Algorithm to Solve Optimization Problems and Nonlinear System of Equations. Mathematics. 2023; 11(5):1231. https://doi.org/10.3390/math11051231
Chicago/Turabian StyleEl-Shorbagy, Mohammed A., and Fatma M. Al-Drees. 2023. "Studying the Effect of Introducing Chaotic Search on Improving the Performance of the Sine Cosine Algorithm to Solve Optimization Problems and Nonlinear System of Equations" Mathematics 11, no. 5: 1231. https://doi.org/10.3390/math11051231
APA StyleEl-Shorbagy, M. A., & Al-Drees, F. M. (2023). Studying the Effect of Introducing Chaotic Search on Improving the Performance of the Sine Cosine Algorithm to Solve Optimization Problems and Nonlinear System of Equations. Mathematics, 11(5), 1231. https://doi.org/10.3390/math11051231







