A Novel Model for Quantitative Risk Assessment under Claim-Size Data with Bimodal and Symmetric Data Modeling
Abstract
:1. Introduction
2. The New Model
- (1)
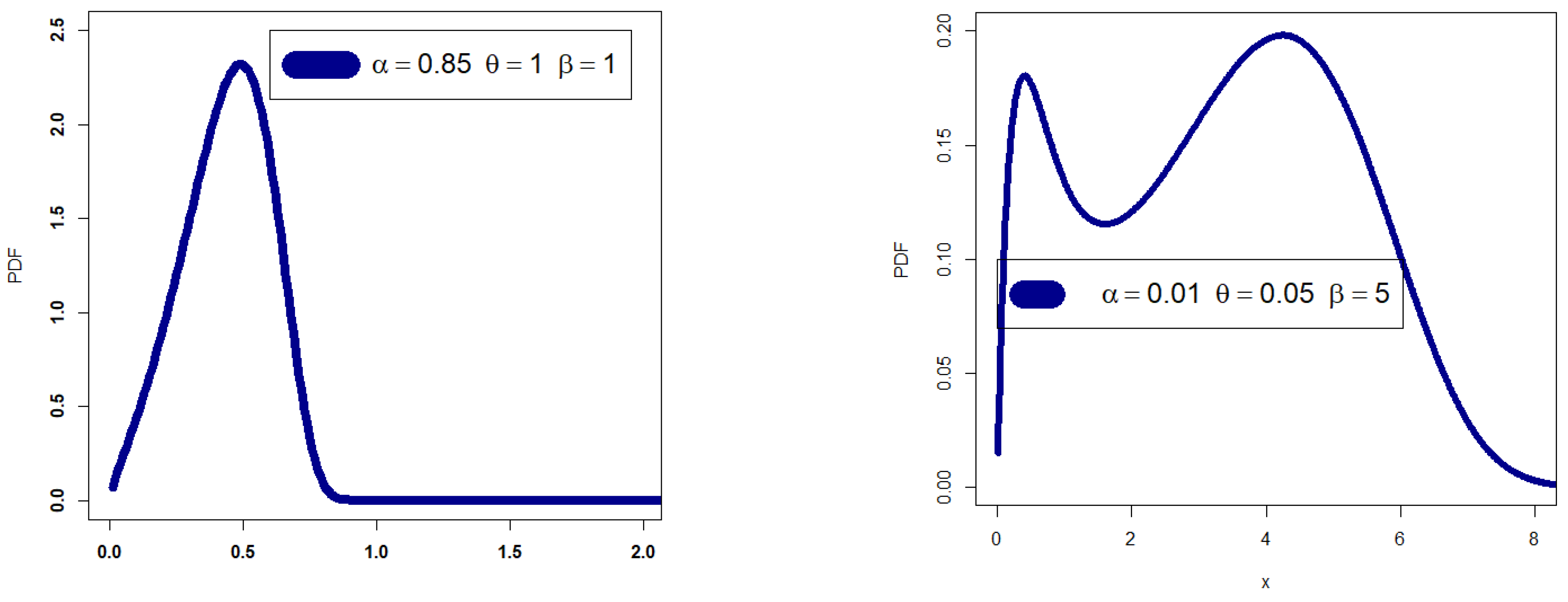
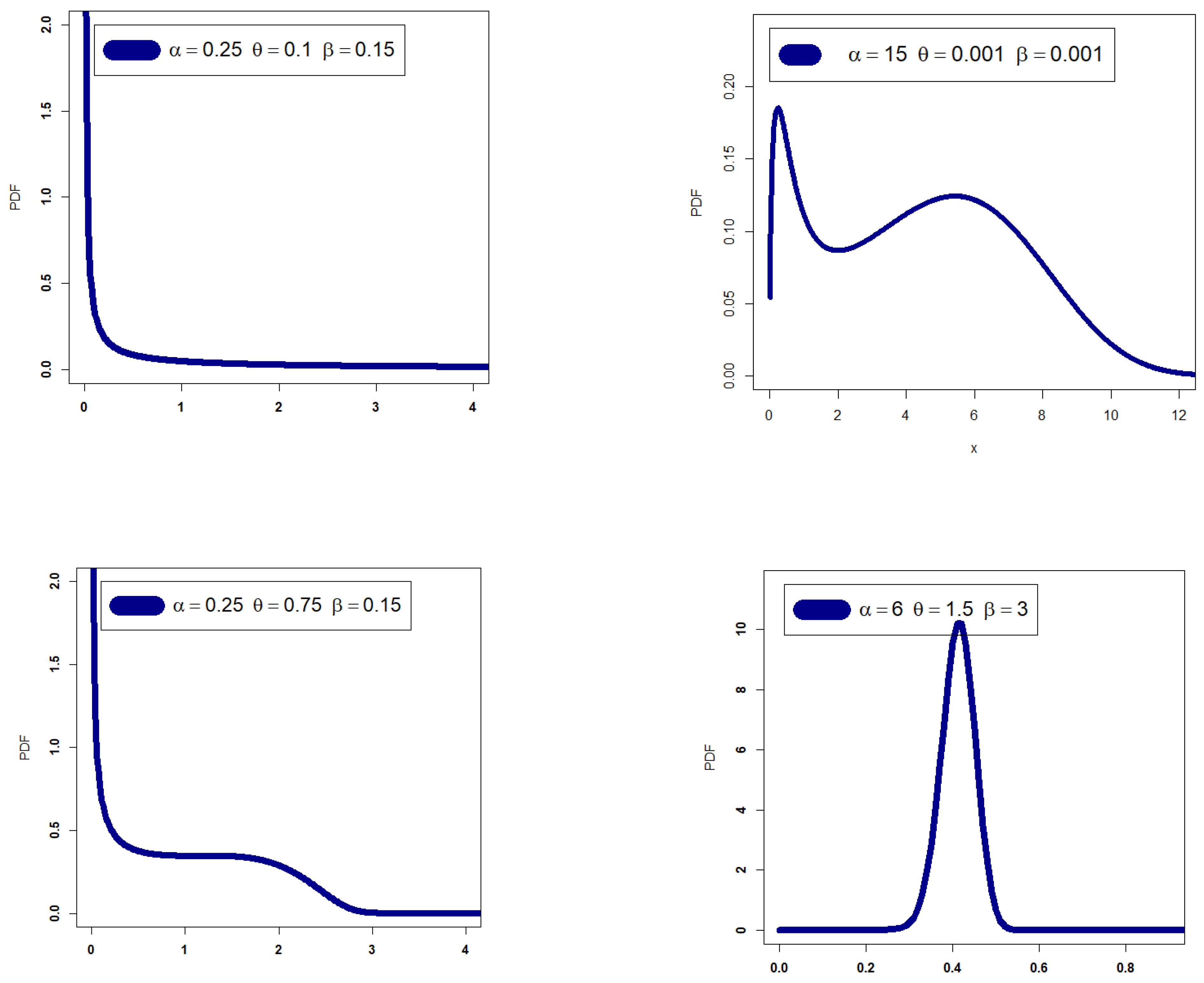
- The new PDF in (4) can be “symmetric density”, “unimodal with right skewed shape”, “bimodal with right skewed shape”, and “left skewed density with no peaks” (see Figure 1).
- (2)
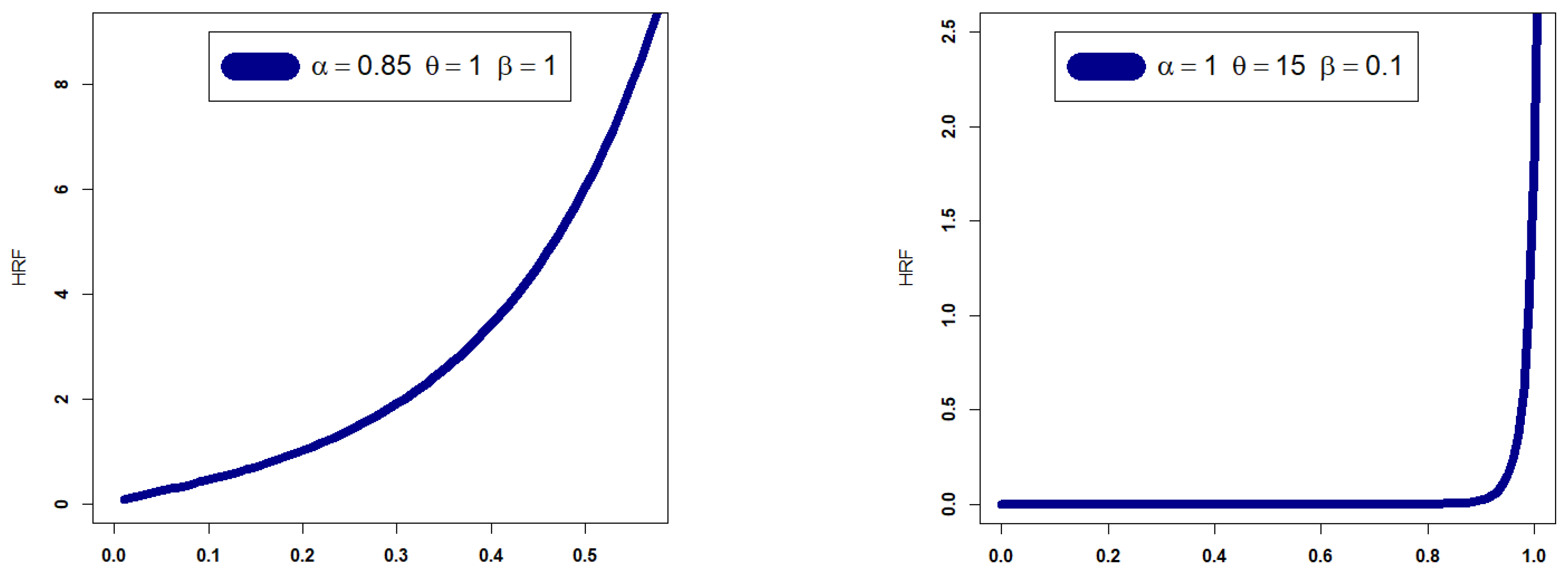
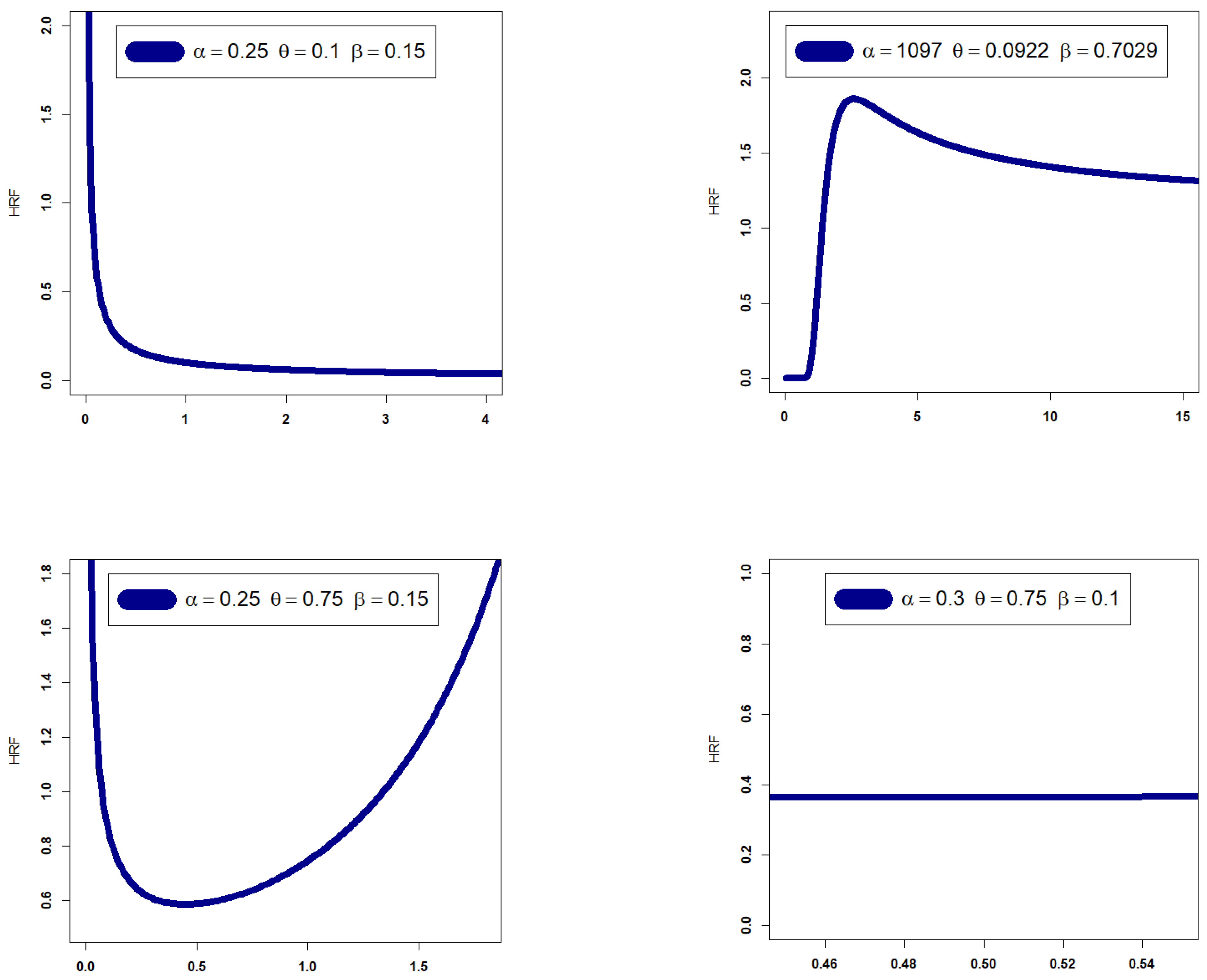
- The HRF of the GRC model can be “monotonically increasing”, “J-HRF” and “upside down”, “decreasing–constant–increasing (bathtub)”, “monotonically decreasing”, and “constant-HRF “ (see Figure 2).
- (3)
- The GRC model may be selected as the optimum probabilistic model for reliability analysis, particularly when modelling the right heavy tail bimodal asymmetric and left heavy tail bimodal asymmetric real data.
3. Properties
3.1. Linear Representation
3.2. Moments
3.3. The Conditional Moments
3.4. Rényi Entropy
4. Actuarial Risk Indictors
4.1. VAR Indicator
4.2. TVAR Risk Indicator
4.3. TV Risk Indicator
4.4. TMV Risk Indicator
5. Applications for Asymmetrical Bimodal Data
6. Risk Analysis
6.1. Risk Analysis under Artificial Experiments
- The (), and increase when q increases for all estimation methods.
- The and decrease when q increases for all estimation methods.
- The results of the four tables allow us to confirm that all methods work properly and that it is impossible to clearly advocate one strategy over another. We are required to create an application based on real data considering this basic discovery in the hopes that it will help us choose one approach over another and identify the best and most relevant ways. In other words, while the four approaches gave us comparable findings in risk assessment, the simulation research did not assist us in deciding how to weight the methodologies. These convergent findings reassure us that all techniques perform well and within acceptable limits when modelling actuarial data and assessing risk. More specifically, some main results can be highlighted due to Table A1, Table A2, Table A3, Table A4 and Table A5.
6.2. Risk Analysis for Insurance Claims Data
6.3. Quantitative Risk Analysis Based on the Quantiles
7. Conclusions and Discussions
- In the field of insurance and actuarial sciences, we can use the GRC distribution to examine the insurance claims payment. The standard exponential distribution, the standard Chen distribution, the Rayleigh Chen distribution, the exponential Chen distribution, the Marshall–Olkin generalized Chen distribution, the reduced Burr-X Chen distribution, the Weibull Chen distribution, the Lomax Chen distribution, the standard exponentiated distribution, and the Burr-X exponentiated Chen distribution are just a few of the competing distributions in the field of statistical modelling in insurance and actuarial sciences data. With minimum values of the Akaike Information Criteria, Bayesian Information Criteria, Cramer–Von Mises test, Anderson–Darling test, Kolmogorov–Smirnov test, and its corresponding p-value, the GRC distribution demonstrated its superiority in statistically modelling the planning and management of the use of water resources data.
- The new density accommodates the “symmetric shape”, “unimodal with right skewed shape”, “bimodal with right skewed shape”, and “left skewed density with no peaks”. The new hazard function can be “monotonically increasing”, “J-HRF”, “decreasing–constant–increasing (bathtub)”, “monotonically decreasing”, “upside down”, and “ constant”. Under the proposed distribution, five risk indicators are considered and examined in reference to the insurance claims payments data. The GRC distribution has an advantage over the standard exponentiated distribution, the Burr-X exponentiated Chen distribution, the Burr-XII Chen distribution, the reduced Burr-X Chen distribution, the Weibull Chen distribution, the Lomax Chen distribution, and the Marshall–Olkin generalized Chen distribution as a result of the variety of the HRFs.
- For all risk assessment methodsand
- Under the GRC model and the MLE method, the VAR() is a monotonically increasing indicator starting with 2995.433059 and ending with 8156.146208. The TVAR() in a monotonically increasing indicator starts with 4275.474776 and ends with 4275.474776.
- Under the GRC model and the LS method, the VAR() is a monotonically increasing indicator starting with 2995.79625 and ending with 11,699.26883. The TVAR() in a monotonically increasing indicator starts with 4823.79565 and ends with 12740.63136. However, the TV(), the TMV(), and the MEL() are monotonically decreasing.
- Under the GRC model and the WLSE method, the VAR() is a monotonically increasing indicator starting with 2993.45166 and ending with 8505.4338. The TVAR() in a monotonically increasing indicator starts with 4368.83178 and ends with 9010.49496. However, the TV(), the TMV(), and the MEL() are monotonically decreasing.
- Under the GRC model and the CVM method, the VAR() is a monotonically increasing indicator starting with 2975.27503 and ending with 10,984.15414. The TVAR() in a monotonically increasing indicator starts with 4684.45314 and ends with 11,922.07451. However, the TV(), the TMV(), and the MEL() are monotonically decreasing.
- Under the GRC model and the ADE method, the VAR() is a monotonically increasing indicator starting with 2977.72629 and ending with 9548.8129. The TVAR() in a monotonically increasing indicator starts with 4499.40165 and ends with 10227.62167.
- Under the GRC model and the moment method, the VAR() is a monotonically increasing indicator starting with 2938.57331 and ending with 8197.24619. The TVAR() in a monotonically increasing indicator starts with 4201.12314 and ends with 8712.92223.
- For the GRC model, the OLSE approach is recommended since it offers the most acceptable risk exposure analysis, followed by the CVME method and finally the ADE method. The other three techniques work well, though.
- The GRC model performs better than the Chen model for all q values and for all risk methodologies. The new distribution performs the best when modelling insurance claims reimbursement data and determining actuarial risk, despite the fact that the probability distributions have the same number of parameters. In upcoming actuarial and applied research, we anticipate that actuaries and practitioners will be very interested in the new distribution.
- The proposed GRC estimator has smaller bias and MSE values in the estimation of the parameter θ than the Chen estimator. On the other hand, in the case of the estimation of the parameter β, the Chen estimator is better. It can be observed that the estimation of β and θ from the GRC distribution offers the lowest bias and MSE in all cases. In addition, the estimators of the two distributions, GRC and Chen, show empirical consistency as the MSE decreases with increasing sample size. The GRC provides competitive estimators of the two parameters of the Chen distribution. It is universally the best for samples generated from the GRC distribution and shows lesser bias and MSE even for samples generated from the Chen distribution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALRV | Aggregate-loss RV |
| AIC | Akaike information criterion |
| ADE | Anderson–Darling estimation |
| BIC | Bayesian information criterion |
| BC | Beta-Chen |
| CTE | Conditional tail expectation |
| CAIC | Consistent Akaike information criterion |
| CVME | Cramér–von Mises estimation |
| CDF | Cumulative distribution function |
| E-HRF | Estimated hazard rate function |
| E-PDF | Estimated probability density function |
| GC | Gamma-Chen |
| GRC | Generalized Rayleigh Chen |
| HQIC | Hannan–Quinn information criterion |
| HRF | Hazard rate function |
| K.S | Kolmogorov–Smirnov |
| KUMC | Kumaraswamy Chen |
| MOC | Marshall–Olkin Chen |
| MLE | Maximum likelihood estimation |
| MEL | Mean excess loss |
| MSE | Mean square error |
| NKDE | Nonparametric kernel density estimation |
| OLSE | Ordinary least squares estimation |
| p-v | p-value |
| P–P | Probability–probability |
| Q–Q | Quantile–quantile. |
| RV | Random variable |
| RIs | Risk indicators |
| SEs | Standard errors |
| SF | Survival function |
| TVAR | Tailed-value-at-risk |
| TTT | Total time in test |
| TC | Transmuted Chen |
| VAR | Value-at-risk |
| WLSE | Weighted least squares estimation |
Appendix A
| MLE | 0.575558 | 0.717965 | 0.012018 | 0.723974 | 0.142407 | |
| 0.630413 | 0.75645 | 0.010016 | 0.761458 | 0.126037 | ||
| 0.694374 | 0.804036 | 0.008061 | 0.808067 | 0.109662 | ||
| 0.782051 | 0.873112 | 0.00595 | 0.876087 | 0.091061 | ||
| 0.853078 | 0.931657 | 0.004631 | 0.933972 | 0.078578 | ||
| 0.981683 | 1.04207 | 0.002912 | 1.043527 | 0.060387 | ||
| 1.116905 | 1.162705 | 0.001734 | 1.163573 | 0.0458 | ||
| LS | 0.57494 | 0.718544 | 0.012192 | 0.72464 | 0.143604 | |
| 0.630321 | 0.757342 | 0.01015 | 0.762417 | 0.12702 | ||
| 0.694848 | 0.80528 | 0.016736 | 0.813648 | 0.110432 | ||
| 0.783204 | 0.874802 | 0.006009 | 0.877807 | 0.091598 | ||
| 0.854695 | 0.933664 | 0.00467 | 0.935999 | 0.078969 | ||
| 0.983946 | 1.044539 | 0.002929 | 1.046004 | 0.060594 | ||
| 1.119606 | 1.165499 | 0.00174 | 1.166369 | 0.045893 | ||
| WLS | 0.58276 | 0.72621 | 0.01211 | 0.73227 | 0.14345 | |
| 0.63821 | 0.76494 | 0.01006 | 0.76997 | 0.12673 | ||
| 0.70271 | 0.81274 | 0.00807 | 0.81677 | 0.11003 | ||
| 0.79084 | 0.88194 | 0.00593 | 0.8849 | 0.0911 | ||
| 0.86201 | 0.94044 | 0.0046 | 0.94274 | 0.07843 | ||
| 0.99038 | 1.05042 | 0.00287 | 1.05186 | 0.06004 | ||
| 1.12476 | 1.17013 | 0.00169 | 1.17098 | 0.04537 | ||
| CVM | 0.57329 | 0.71613 | 0.01207 | 0.72217 | 0.14284 | |
| 0.62835 | 0.75473 | 0.01006 | 0.75975 | 0.12637 | ||
| 0.69252 | 0.80243 | 0.00809 | 0.80647 | 0.1099 | ||
| 0.78043 | 0.87163 | 0.00596 | 0.87461 | 0.0912 | ||
| 0.85159 | 0.93025 | 0.00464 | 0.93256 | 0.07865 | ||
| 0.98032 | 1.04071 | 0.00291 | 1.04217 | 0.06039 | ||
| 1.11553 | 1.16129 | 0.00173 | 1.16216 | 0.04576 | ||
| ADE | 0.57539 | 0.71919 | 0.01222 | 0.7253 | 0.1438 | |
| 0.63085 | 0.75804 | 0.01017 | 0.76313 | 0.12719 | ||
| 0.69547 | 0.80604 | 0.00818 | 0.81013 | 0.11057 | ||
| 0.78394 | 0.87564 | 0.00602 | 0.87865 | 0.0917 | ||
| 0.85552 | 0.93457 | 0.00468 | 0.93691 | 0.07905 | ||
| 0.9849 | 1.04555 | 0.00293 | 1.04702 | 0.06065 | ||
| 1.12069 | 1.16661 | 0.00174 | 1.16749 | 0.04593 | ||
| Moment | 0.628173 | 0.763601 | 0.011684 | 0.769442 | 0.135428 | |
| 0.660538 | 0.787498 | 0.010577 | 0.792786 | 0.12696 | ||
| 0.696556 | 0.81483 | 0.009459 | 0.819559 | 0.118274 | ||
| 0.738432 | 0.847483 | 0.008298 | 0.851632 | 0.109051 | ||
| 0.790834 | 0.88951 | 0.007035 | 0.893028 | 0.098676 | ||
| 0.867614 | 0.953064 | 0.005508 | 0.955819 | 0.085451 | ||
| 1.007441 | 1.073498 | 0.0035 | 1.075248 | 0.066057 |
| MLE | 0.578158 | 0.722400 | 0.012275 | 0.728538 | 0.144242 | |
| 0.633844 | 0.761359 | 0.01021 | 0.766464 | 0.127515 | ||
| 0.698678 | 0.809469 | 0.008197 | 0.813567 | 0.11079 | ||
| 0.787371 | 0.879185 | 0.006029 | 0.882199 | 0.091813 | ||
| 0.859065 | 0.938165 | 0.00468 | 0.940505 | 0.0791 | ||
| 0.988534 | 1.049155 | 0.002929 | 1.05062 | 0.060622 | ||
| 1.124239 | 1.170102 | 0.001733 | 1.170969 | 0.045864 | ||
| LS | 0.57787 | 0.72244 | 0.01232 | 0.72861 | 0.14458 | |
| 0.63371 | 0.76149 | 0.01024 | 0.76661 | 0.12778 | ||
| 0.69871 | 0.80969 | 0.00822 | 0.8138 | 0.11099 | ||
| 0.78758 | 0.87952 | 0.00604 | 0.88254 | 0.09193 | ||
| 0.85939 | 0.93856 | 0.00469 | 0.94091 | 0.07917 | ||
| 0.98898 | 1.04962 | 0.00293 | 1.05109 | 0.06064 | ||
| 1.12472 | 1.17057 | 0.00173 | 1.17144 | 0.04585 | ||
| WLS | 0.57791 | 0.72267 | 0.01234 | 0.72884 | 0.14476 | |
| 0.63386 | 0.76176 | 0.01025 | 0.76689 | 0.1279 | ||
| 0.69896 | 0.81 | 0.00822 | 0.81411 | 0.11104 | ||
| 0.78791 | 0.87983 | 0.00603 | 0.88285 | 0.09193 | ||
| 0.85973 | 0.93886 | 0.00468 | 0.9412 | 0.07913 | ||
| 0.98925 | 1.04981 | 0.00292 | 1.05127 | 0.06056 | ||
| 1.1248 | 1.17055 | 0.00173 | 1.17142 | 0.04576 | ||
| CVM | 0.57823 | 0.72227 | 0.01224 | 0.72839 | 0.14404 | |
| 0.63384 | 0.76117 | 0.01018 | 0.76626 | 0.12733 | ||
| 0.69859 | 0.80921 | 0.00817 | 0.81329 | 0.11062 | ||
| 0.78715 | 0.87881 | 0.00601 | 0.88182 | 0.09167 | ||
| 0.85873 | 0.9377 | 0.00466 | 0.94003 | 0.07897 | ||
| 0.98798 | 1.0485 | 0.00292 | 1.04996 | 0.06051 | ||
| 1.12345 | 1.16922 | 0.00173 | 1.17009 | 0.04578 | ||
| ADE | 0.57913 | 0.72364 | 0.01231 | 0.72979 | 0.1445 | |
| 0.63494 | 0.76266 | 0.01023 | 0.76778 | 0.12772 | ||
| 0.6999 | 0.81084 | 0.00821 | 0.81495 | 0.11094 | ||
| 0.78873 | 0.88063 | 0.00604 | 0.88365 | 0.0919 | ||
| 0.86051 | 0.93966 | 0.00468 | 0.942 | 0.07915 | ||
| 0.99006 | 1.05069 | 0.00293 | 1.05216 | 0.06063 | ||
| 1.12578 | 1.17163 | 0.00173 | 1.17249 | 0.04585 | ||
| Moment | 0.63385 | 0.76648 | 0.01112 | 0.77204 | 0.13263 | |
| 0.66569 | 0.78987 | 0.01005 | 0.79489 | 0.12418 | ||
| 0.70107 | 0.81658 | 0.00896 | 0.82107 | 0.11552 | ||
| 0.74211 | 0.84845 | 0.00784 | 0.85237 | 0.10634 | ||
| 0.79336 | 0.88939 | 0.00663 | 0.89271 | 0.09604 | ||
| 0.86822 | 0.95116 | 0.00517 | 0.95375 | 0.08294 | ||
| 1.00396 | 1.06779 | 0.00326 | 1.06941 | 0.06382 |
| MLE | 0.577686 | 0.72254 | 0.012356 | 0.728717 | 0.144854 | |
| 0.633662 | 0.761654 | 0.010268 | 0.766788 | 0.127992 | ||
| 0.698793 | 0.809929 | 0.008235 | 0.814046 | 0.111136 | ||
| 0.787813 | 0.879831 | 0.006048 | 0.882854 | 0.092018 | ||
| 0.859702 | 0.93892 | 0.004689 | 0.941265 | 0.079219 | ||
| 0.98937 | 1.050009 | 0.002929 | 1.051473 | 0.060639 | ||
| 1.125096 | 1.170922 | 0.001731 | 1.171787 | 0.045826 | ||
| LS | 0.57931 | 0.72407 | 0.01234 | 0.73024 | 0.14476 | |
| 0.63525 | 0.76316 | 0.01026 | 0.76828 | 0.12791 | ||
| 0.70033 | 0.8114 | 0.00823 | 0.81551 | 0.11107 | ||
| 0.78929 | 0.88126 | 0.00604 | 0.88428 | 0.09197 | ||
| 0.86114 | 0.94032 | 0.00468 | 0.94266 | 0.07918 | ||
| 0.99074 | 1.05136 | 0.00293 | 1.05282 | 0.06062 | ||
| 1.12642 | 1.17223 | 0.00173 | 1.1731 | 0.04581 | ||
| WLS | 0.58012 | 0.72476 | 0.01231 | 0.73091 | 0.14464 | |
| 0.63605 | 0.76381 | 0.01022 | 0.76892 | 0.12777 | ||
| 0.70109 | 0.81199 | 0.00819 | 0.81609 | 0.1109 | ||
| 0.78995 | 0.88173 | 0.00601 | 0.88474 | 0.09178 | ||
| 0.86167 | 0.94066 | 0.00466 | 0.94299 | 0.07899 | ||
| 0.99097 | 1.0514 | 0.00291 | 1.05285 | 0.06043 | ||
| 1.12622 | 1.17187 | 0.00172 | 1.17273 | 0.04565 | ||
| CVM | 0.57811 | 0.72292 | 0.01235 | 0.7291 | 0.14482 | |
| 0.63407 | 0.76203 | 0.01026 | 0.76716 | 0.12796 | ||
| 0.69918 | 0.81029 | 0.00823 | 0.8144 | 0.11111 | ||
| 0.78818 | 0.88017 | 0.00604 | 0.88319 | 0.09199 | ||
| 0.86005 | 0.93925 | 0.00469 | 0.94159 | 0.0792 | ||
| 0.98968 | 1.05031 | 0.00293 | 1.05177 | 0.06062 | ||
| 1.12537 | 1.17119 | 0.00173 | 1.17205 | 0.04582 | ||
| ADE | 0.57831 | 0.72327 | 0.01237 | 0.72946 | 0.14496 | |
| 0.63434 | 0.76242 | 0.01028 | 0.76756 | 0.12808 | ||
| 0.69952 | 0.81072 | 0.00824 | 0.81484 | 0.1112 | ||
| 0.7886 | 0.88066 | 0.00605 | 0.88369 | 0.09206 | ||
| 0.86053 | 0.93978 | 0.00469 | 0.94213 | 0.07925 | ||
| 0.99025 | 1.05091 | 0.00293 | 1.05238 | 0.06066 | ||
| 1.12602 | 1.17185 | 0.00173 | 1.17272 | 0.04583 | ||
| Moment | 0.63382 | 0.76479 | 0.01079 | 0.77018 | 0.13097 | |
| 0.66536 | 0.78787 | 0.00973 | 0.79274 | 0.12252 | ||
| 0.70035 | 0.81422 | 0.00867 | 0.81855 | 0.11387 | ||
| 0.7409 | 0.84561 | 0.00757 | 0.8494 | 0.10471 | ||
| 0.79146 | 0.8859 | 0.00639 | 0.88909 | 0.09444 | ||
| 0.86518 | 0.94658 | 0.00498 | 0.94907 | 0.0814 | ||
| 0.99842 | 1.06087 | 0.00311 | 1.06242 | 0.06245 |
| MLE | 0.578834 | 0.723928 | 0.012394 | 0.730125 | 0.145094 | |
| 0.634911 | 0.763106 | 0.010298 | 0.768255 | 0.128196 | ||
| 0.700153 | 0.811455 | 0.008258 | 0.815584 | 0.111303 | ||
| 0.789313 | 0.881458 | 0.006063 | 0.88449 | 0.092145 | ||
| 0.861306 | 0.940627 | 0.0047 | 0.942977 | 0.079321 | ||
| 0.991142 | 1.05185 | 0.002935 | 1.053317 | 0.060708 | ||
| 1.127019 | 1.172891 | 0.001734 | 1.173758 | 0.045872 | ||
| LS | 0.578709 | 0.723708 | 0.012376 | 0.729896 | 0.144999 | |
| 0.634752 | 0.76286 | 0.010283 | 0.768001 | 0.128108 | ||
| 0.699953 | 0.811175 | 0.008245 | 0.815298 | 0.111223 | ||
| 0.789051 | 0.881126 | 0.006054 | 0.884153 | 0.092075 | ||
| 0.860991 | 0.940249 | 0.004692 | 0.942595 | 0.079258 | ||
| 0.990724 | 1.051381 | 0.00293 | 1.052846 | 0.060657 | ||
| 1.126486 | 1.172317 | 0.001731 | 1.173182 | 0.045831 | ||
| WLS | 0.58055 | 0.72519 | 0.0123 | 0.73134 | 0.14463 | |
| 0.63648 | 0.76423 | 0.01022 | 0.76934 | 0.12775 | ||
| 0.70152 | 0.81241 | 0.00819 | 0.8165 | 0.11089 | ||
| 0.79037 | 0.88214 | 0.00601 | 0.88514 | 0.09177 | ||
| 0.86208 | 0.94105 | 0.00466 | 0.94338 | 0.07897 | ||
| 0.99135 | 1.05176 | 0.00291 | 1.05321 | 0.06041 | ||
| 1.12656 | 1.17219 | 0.00171 | 1.17304 | 0.04563 | ||
| CVM | 0.57826 | 0.72333 | 0.01239 | 0.72953 | 0.14508 | |
| 0.63433 | 0.76251 | 0.01029 | 0.76765 | 0.12818 | ||
| 0.69957 | 0.81085 | 0.00825 | 0.81497 | 0.11128 | ||
| 0.78872 | 0.88083 | 0.00606 | 0.88386 | 0.09211 | ||
| 0.86069 | 0.93998 | 0.0047 | 0.94233 | 0.07929 | ||
| 0.99047 | 1.05115 | 0.00293 | 1.05261 | 0.06067 | ||
| 1.12627 | 1.17211 | 0.00173 | 1.17298 | 0.04584 | ||
| ADE | 0.57847 | 0.72362 | 0.0124 | 0.72982 | 0.14515 | |
| 0.63457 | 0.76281 | 0.0103 | 0.76796 | 0.12823 | ||
| 0.69984 | 0.81117 | 0.00826 | 0.8153 | 0.11132 | ||
| 0.78903 | 0.88118 | 0.00606 | 0.88421 | 0.09215 | ||
| 0.86103 | 0.94035 | 0.0047 | 0.9427 | 0.07932 | ||
| 0.99086 | 1.05156 | 0.00293 | 1.05302 | 0.06069 | ||
| 1.12671 | 1.17256 | 0.00173 | 1.17343 | 0.04585 | ||
| Moment | 0.63452 | 0.76457 | 0.01061 | 0.76988 | 0.13005 | |
| 0.66587 | 0.78749 | 0.00958 | 0.79228 | 0.12162 | ||
| 0.70064 | 0.81364 | 0.00853 | 0.8179 | 0.113 | ||
| 0.74091 | 0.84479 | 0.00744 | 0.84851 | 0.10388 | ||
| 0.7911 | 0.88475 | 0.00627 | 0.88788 | 0.09365 | ||
| 0.86423 | 0.94491 | 0.00487 | 0.94734 | 0.08068 | ||
| 0.99628 | 1.0581 | 0.00305 | 1.05963 | 0.06183 |
| MLE | 0.578635 | 0.723537 | 0.012361 | 0.729718 | 0.144903 | |
| 0.634639 | 0.762663 | 0.01027 | 0.767798 | 0.128025 | ||
| 0.699795 | 0.810948 | 0.008236 | 0.815065 | 0.111153 | ||
| 0.788836 | 0.880856 | 0.006047 | 0.883879 | 0.09202 | ||
| 0.860731 | 0.939945 | 0.004687 | 0.942288 | 0.079214 | ||
| 0.990391 | 1.051016 | 0.002927 | 1.05248 | 0.060625 | ||
| 1.126083 | 1.171892 | 0.001729 | 1.172756 | 0.045809 | ||
| LS | 0.578565 | 0.723659 | 0.01239 | 0.729854 | 0.145094 | |
| 0.63465 | 0.762835 | 0.010294 | 0.767982 | 0.128186 | ||
| 0.699895 | 0.811178 | 0.008253 | 0.815305 | 0.111283 | ||
| 0.789048 | 0.881164 | 0.006058 | 0.884193 | 0.092117 | ||
| 0.861023 | 0.940312 | 0.004695 | 0.942659 | 0.079288 | ||
| 0.990806 | 1.051478 | 0.002931 | 1.052943 | 0.060672 | ||
| 1.1266 | 1.172436 | 0.001731 | 1.173302 | 0.045837 | ||
| WLS | 0.58097 | 0.72551 | 0.01229 | 0.73165 | 0.14454 | |
| 0.63687 | 0.76453 | 0.0102 | 0.76963 | 0.12766 | ||
| 0.70187 | 0.81267 | 0.00818 | 0.81676 | 0.1108 | ||
| 0.79065 | 0.88234 | 0.006 | 0.88534 | 0.09169 | ||
| 0.86231 | 0.94121 | 0.00465 | 0.94354 | 0.07891 | ||
| 0.99146 | 1.05182 | 0.0029 | 1.05327 | 0.06036 | ||
| 1.12655 | 1.17213 | 0.00171 | 1.17299 | 0.04558 | ||
| CVM | 0.57891 | 0.72388 | 0.01237 | 0.73007 | 0.14498 | |
| 0.63494 | 0.76303 | 0.01028 | 0.76817 | 0.12809 | ||
| 0.70013 | 0.81133 | 0.00824 | 0.81545 | 0.1112 | ||
| 0.78921 | 0.88127 | 0.00605 | 0.8843 | 0.09206 | ||
| 0.86114 | 0.94038 | 0.00469 | 0.94273 | 0.07924 | ||
| 0.99085 | 1.05149 | 0.00293 | 1.05296 | 0.06064 | ||
| 1.12658 | 1.1724 | 0.00173 | 1.17327 | 0.04582 | ||
| ADE | 0.57897 | 0.72398 | 0.01238 | 0.73017 | 0.14501 | |
| 0.63502 | 0.76313 | 0.01028 | 0.76828 | 0.12812 | ||
| 0.70023 | 0.81145 | 0.00825 | 0.81558 | 0.11123 | ||
| 0.78933 | 0.88141 | 0.00605 | 0.88443 | 0.09208 | ||
| 0.86127 | 0.94053 | 0.00469 | 0.94287 | 0.07926 | ||
| 0.991 | 1.05165 | 0.00293 | 1.05312 | 0.06065 | ||
| 1.12675 | 1.17258 | 0.00173 | 1.17344 | 0.04583 | ||
| Moment | 0.634903 | 0.76443 | 0.010529 | 0.769694 | 0.129527 | |
| 0.666138 | 0.787257 | 0.009492 | 0.792003 | 0.121119 | ||
| 0.700776 | 0.813294 | 0.00845 | 0.817519 | 0.112519 | ||
| 0.740894 | 0.844309 | 0.007374 | 0.847996 | 0.103416 | ||
| 0.790872 | 0.884086 | 0.006211 | 0.887192 | 0.093214 | ||
| 0.863675 | 0.943957 | 0.004819 | 0.946367 | 0.080282 | ||
| 0.995081 | 1.056576 | 0.003013 | 1.058083 | 0.061495 |
References
- Chen, Z. A new two-parameter lifetime distribution with bathtub shape or increasing failure rate function. Stat. Probab. Lett. 2000, 49, 155–161. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M.M. Modeling actuarial data with a composite lognormal-Pareto model. Scand. Actuar. J. 2005, 2005, 321–334. [Google Scholar] [CrossRef]
- Shrahili, M.; Elbatal, I.; Yousof, H.M. Asymmetric Density for Risk Claim-Size Data: Prediction and Bimodal Data Applications. Symmetry 2021, 13, 2357. [Google Scholar] [CrossRef]
- Mohamed, H.S.; Cordeiro, G.M.; Minkah, R.; Yousof, H.M.; Ibrahim, M. A size-of-loss model for the negatively skewed insurance claims data: Applications, risk analysis using different methods and statistical forecasting. J. Appl. Stat. Forthcom. 2022. [Google Scholar] [CrossRef]
- Klugman, S.A.; Panjer, H.H.; Willmot, G.E. Loss Models: From Data to Decisions; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 715. [Google Scholar]
- Wirch, J.L. Raising value at risk. N. Am. Actuar. J. 1999, 3, 106–115. [Google Scholar] [CrossRef]
- Tasche, D. Expected Shortfall and Beyond. J. Bank. Financ. 2002, 26, 1519–1533. [Google Scholar] [CrossRef] [Green Version]
- Acerbi, C.; Tasche, D. On the coherence of expected shortfall. J. Bank. Financ. 2002, 26, 1487–1503. [Google Scholar] [CrossRef] [Green Version]
- Furman, E.; Landsman, Z. Tail Variance premium with applications for elliptical portfolio of risks. ASTIN Bull. J. IAA 2006, 36, 433–462. [Google Scholar] [CrossRef] [Green Version]
- Landsman, Z. On the tail mean–Variance optimal portfolio selection. Insur. Math. Econ. 2010, 46, 547–553. [Google Scholar] [CrossRef]
- Artzner, P. Application of coherent risk measures to capital requirements in insurance. N. Am. Actuar. J. 1999, 3, 11–25. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Hamedani, G.G.; Aryal, G. The Burr X generator of distributions for lifetime data. J. Stat. Theory Appl. 2017, 16, 288–305. [Google Scholar] [CrossRef] [Green Version]
- Cordeiro, G.M.; Afify, A.Z.; Yousof, H.M.; Pescim, R.R.; Aryal, G.R. The exponentiated Weibull-H family of distributions: Theory and Applications. Mediterr. J. Math. 2017, 14, 155. [Google Scholar] [CrossRef]
- Dey, S.; Kumar, D.; Ramos, P.L.; Louzada, F. Exponentiated Chen distribution: Properties and estimation. Commun. Stat. Simul. Comput. 2017, 46, 8118–8139. [Google Scholar] [CrossRef]
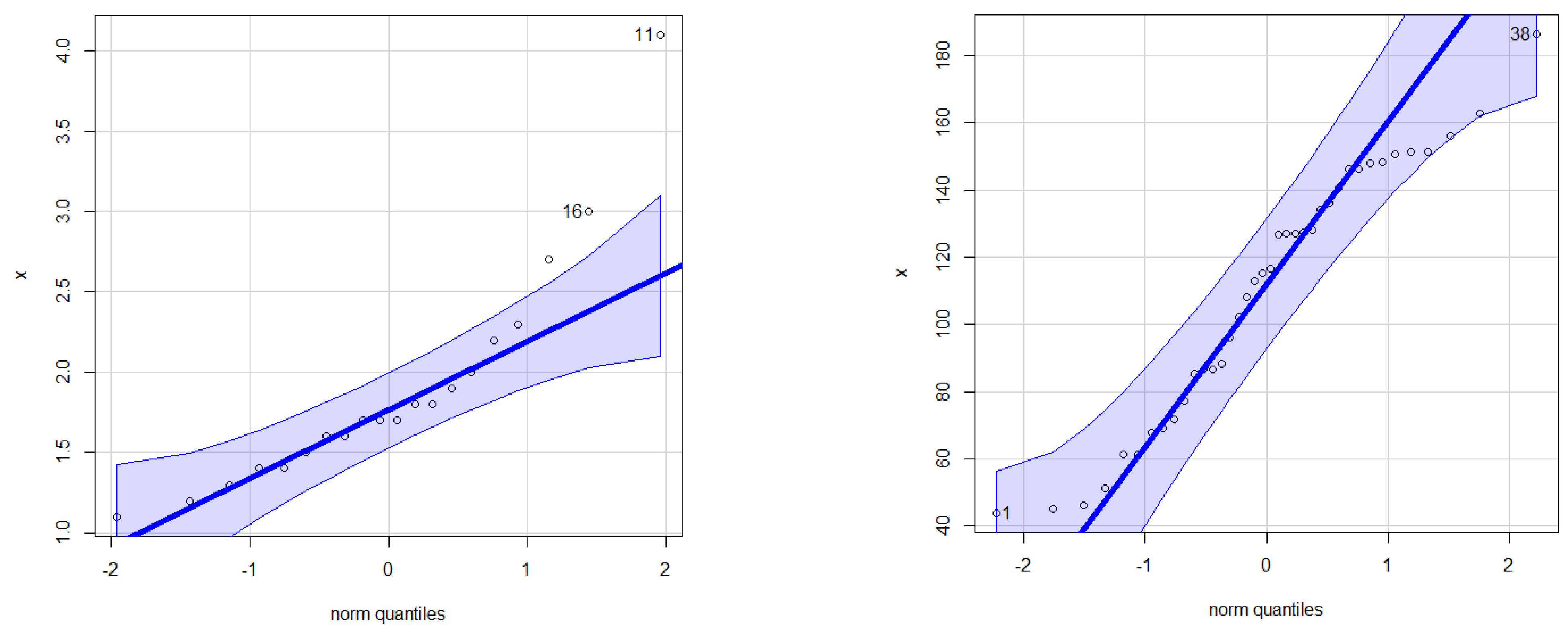



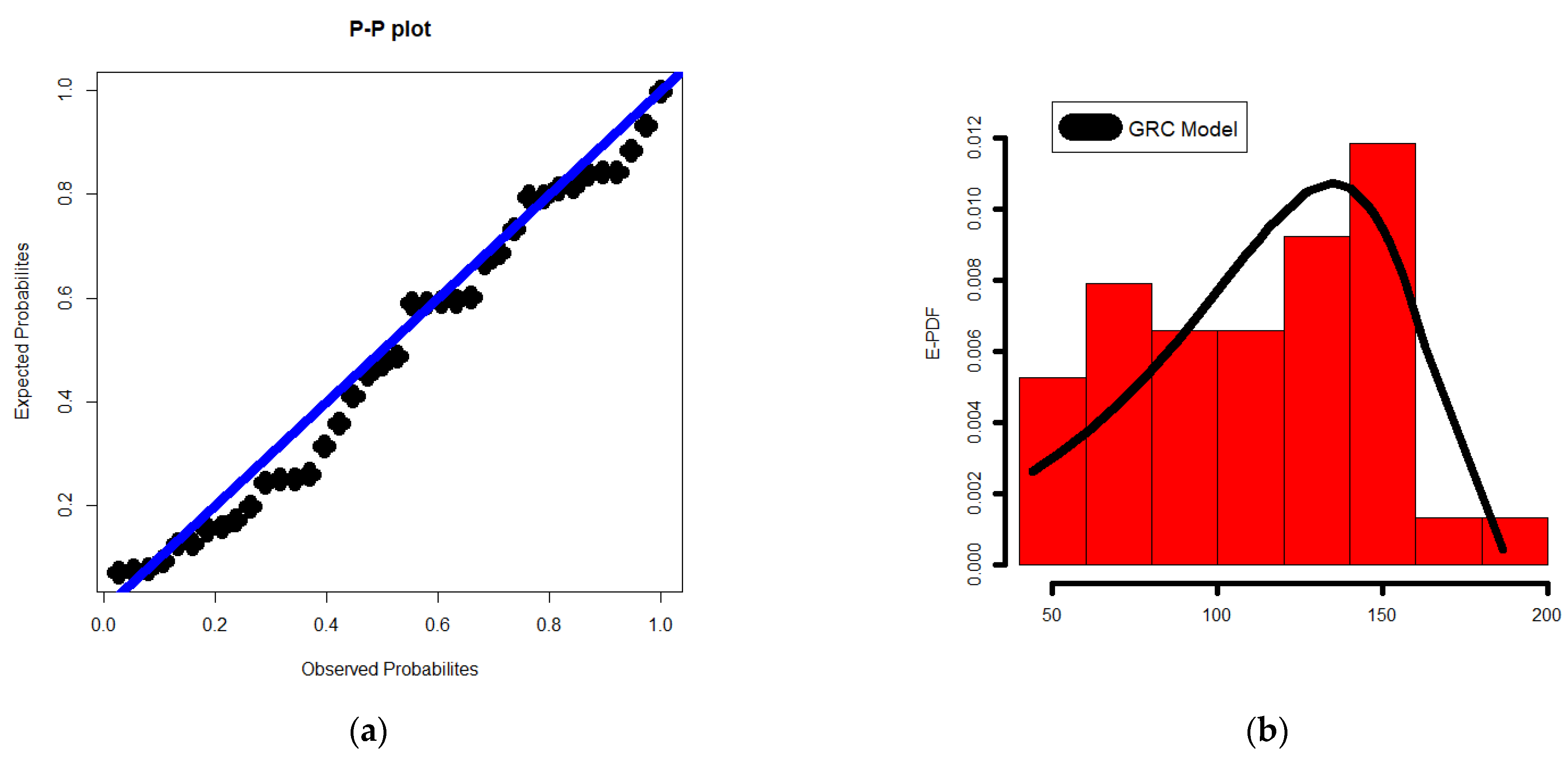

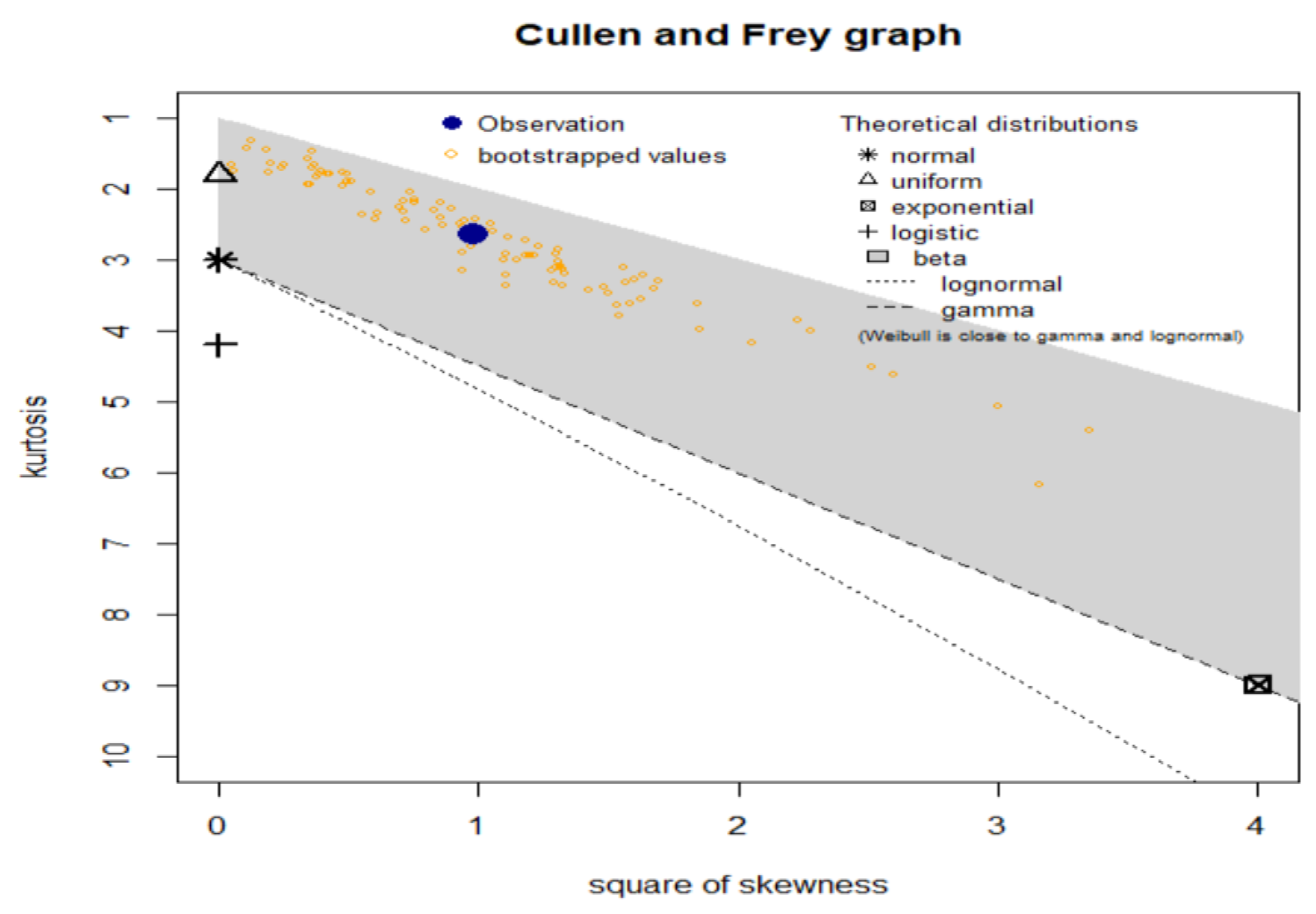



| Model | BIC | AIC | ADC | CVMT | p-Value | K.S |
|---|---|---|---|---|---|---|
| GRC | 40.492 | 37.505 | 0.2321 | 0.0402 | 0.9524 | 0.1155 |
| EWC | 40.624 | 37.632 | 0.2411 | 0.042 | 0.9525 | 0.116 |
| GC | 50.335 | 46.353 | 0.2845 | 0.046 | <0.013 | 0.992 |
| BC | 44.493 | 40.517 | 0.348 | 0.065 | 0.7688 | 0.155 |
| TC | 56.625 | 53.635 | 1.576 | 0.274 | 0.2427 | 0.233 |
| KUMC | 44.324 | 40.024 | 0.303 | 0.059 | 0.8200 | 0.140 |
| MOC | 47.877 | 44.879 | 0.848 | 0.147 | 0.7738 | 0.157 |
| Chen | 55.129 | 53.144 | 1.6666 | 0.297 | 0.2055 | 0.244 |
| Model | MLE (SEs) |
|---|---|
| ) | |
| ) | |
| ) | 1663.342, 1.1672, 0.1213 |
| (3.863), (2.4872), (5.7591) | |
| ) | 7.5914, 1.988, 5.0023, 0.534 |
| (2.091), (0.462), (1.077), (0.0030) | |
| ) | 400.01231, 2.32433, 0.4343 |
| (488.0654), (0.643), (0.082) | |
| ) | 160.07, 0.491, 2.212, 0.5234 |
| (222.413), (0.514), (0.752), (0.214) | |
| ) | 85.873, 0.481, 2.013, 0.552 |
| (103.1), (0.512), (0.69), (0.202) | |
| ) | 0.74554, 0.07144, 1.0221 |
| (0.2841), (0.034), 0.09) | |
| ) | 0.13888, 0.9453 |
| (0.05121, 0.093) |
| Model | BIC | AIC | ADC | CVMT | p-Value | K.S |
|---|---|---|---|---|---|---|
| GRC | 394.349 | 389.436 | 0.443 | 0.054 5 | 0.7617 | 0.1086 |
| EWC | 394.373 | 389.360 | 0.6021 | 0.1198 | 0.7050 | 0.1133 |
| MOC | 395.471 | 390.563 | 0.6111 | 0.0930 | 0.6892 | 0.1239 |
| GC | 398.033 | 391.480 | 1.7112 | 0.2888 | <0.010 | 0.5735 |
| Chen | 401.900 | 398.623 | 0.6465 | 0.1014 | 0.2623 | 0.1665 |
| BC | 398.761 | 392.210 | 0.7532 | 0.1219 | 0.343 | 0.1542 |
| KUMC | 397.788 | 391.236 | 0.6664 | 0.1191 | 0.4090 | 0.1451 |
| TEC | 398.290 | 391.735 | 0.7054 | 0.1111 | 0.3728 | 0.1549 |
| TC | 394.444 | 389.533 | 0.6632 | 0.1132 | 0.3825 | 0.1555 |
| EC | 394.818 | 389.912 | 0.7223 | 0.1312 | 0.3488 | 0.1513 |
| Model | MLE (SEs) |
|---|---|
| ) | 0.5443, 0.3596,8 0.0017 |
| (0.0938), (0.002), (0.013) | |
| ) | 19.79869, 0.05371, 0.24494 |
| (4.666), (0.0049), (0.00363) | |
| ) | 3.0143, 0.7741, 0.014, 0.3542 |
| (1.9013), (1.244), (0.011), (0.051) | |
| ) | 4.514, 21.1104, 0.022, 0.273 |
| (2.022), (42.855), (0.02), (0.054) | |
| ) | 3.1353, 4.364, 0.096, 0.345 |
| (1.143), (4.4), (0.02), (0.02) | |
| ) | 13.0014, 0.0232, 0.3454 |
| (18.666), (0.024), (0.044) | |
| ) | 2.85937, 0.01443, 0.3553 |
| (0.9832), (0.0045), (0.0234) | |
| ) | 2.737, −0.248, 0.01, 0.348 |
| (1.213), (0.466), (0.013), (0.023) | |
| ) | −1.00442, 0.00394, 0.3684 |
| (0.702), (0.002), (0.012) | |
| ) | 0.00323, 0.3654 |
| (0.00113), 0.0133) |
| MLE | 2995.433059 | 4275.474776 | 1,042,528.782433 | 525,539.865993 | 1280.041717 | |
| 3468.400242 | 4625.137504 | 895,045.930997 | 452,148.103003 | 1156.737262 | ||
| 4038.356035 | 5066.752664 | 744,038.824351 | 377,086.16484 | 1028.396629 | ||
| 4846.834605 | 5723.310099 | 572,400.996532 | 291,923.808365 | 876.475495 | ||
| 5521.447578 | 6292.299079 | 460,064.535012 | 236,324.566585 | 770.851502 | ||
| 6781.639964 | 7399.960377 | 207,362.181718 | 111,081.051237 | 618.320413 | ||
| 8156.146208 | 8635.322651 | 196,466.546046 | 106,868.595674 | 479.176442 | ||
| LS | 2995.79625 | 4823.79565 | 2,565,875.85054 | 1,287,761.72092 | 1827.9994 | |
| 3605.64058 | 5334.88391 | 2,366,027.27058 | 1,188,348.5192 | 1729.24334 | ||
| 4391.41575 | 6013.29109 | 2,142,778.10812 | 1,077,402.34515 | 1621.87534 | ||
| 5601.69265 | 7087.85952 | 1,856,663.30908 | 935,419.51407 | 1486.16688 | ||
| 6697.28146 | 8081.14632 | 1,641,518.22068 | 828,840.25666 | 1383.86487 | ||
| 8949.4202 | 10,160.16005 | 1,291,686.50067 | 656,003.41039 | 1210.73985 | ||
| 11,699.26883 | 12,740.63136 | 977,455.63285 | 501,468.44778 | 1041.36252 | ||
| WLS | 2993.45166 | 4368.83178 | 1,198,197.19961 | 603,467.43158 | 1375.38011 | |
| 3502.27954 | 4744.4535 | 1,026,058.03873 | 517,773.47286 | 1242.17396 | ||
| 4115.72289 | 5218.34142 | 849,786.00448 | 430,111.34366 | 1102.61853 | ||
| 4984.46424 | 5921.19761 | 649,727.92329 | 330,785.15925 | 936.73337 | ||
| 5707.04377 | 6528.38195 | 519,378.08162 | 266,217.42276 | 821.33818 | ||
| 7050.06113 | 7698.10238 | 342,283.93764 | 178,840.0712 | 648.04125 | ||
| 8505.4338 | 9010.49496 | 217,699.48623 | 117,860.23808 | 505.06116 | ||
| CVM | 2975.27503 | 4684.45314 | 2,201,083.89688 | 1,105,226.40158 | 1709.1781 | |
| 3551.76054 | 5161.13256 | 2,017,075.48552 | 1,013,698.87532 | 1609.37202 | ||
| 4289.09745 | 5790.95426 | 1,812,296.77407 | 911,939.34129 | 1501.85681 | ||
| 5415.39634 | 6782.63414 | 1,554,382.10192 | 783,973.6851 | 1367.2378 | ||
| 6427.2668 | 7694.09081 | 1,363,501.38182 | 689,444.78172 | 1266.82401 | ||
| 8489.86108 | 9589.04377 | 1,057,767.93624 | 538,473.01189 | 1099.18269 | ||
| 10,984.15414 | 11,922.07451 | 789,278.32307 | 406,561.23605 | 937.92037 | ||
| ADE | 2977.72629 | 4499.40165 | 1,593,652.26016 | 801,325.53173 | 1521.67536 | |
| 3516.26365 | 4919.35247 | 1,411,403.46935 | 710,621.08715 | 1403.08883 | ||
| 4184.76712 | 5461.36406 | 1,217,267.95014 | 614,095.33913 | 1276.59695 | ||
| 5167.3597 | 6289.28735 | 984,627.83405 | 498,603.20438 | 1121.92765 | ||
| 6016.03503 | 7026.48158 | 823,529.60842 | 418,791.28579 | 1010.44655 | ||
| 7665.33888 | 8499.81389 | 586,821.22316 | 301,910.42547 | 834.475 | ||
| 9548.8129 | 10,227.62167 | 402,428.42768 | 211,441.83551 | 678.80877 | ||
| Moment | 2938.57331 | 4201.12314 | 1,050,991.15004 | 529,696.69817 | 1262.54983 | |
| 3396.72068 | 4547.52614 | 915,340.92543 | 462,217.98885 | 1150.80546 | ||
| 3955.16777 | 4989.23409 | 774,776.31709 | 392,377.39264 | 1034.06633 | ||
| 4759.76904 | 5654.47064 | 611,475.60507 | 311,392.27317 | 894.7016 | ||
| 5442.35853 | 6238.90719 | 501,528.1582 | 257,002.98629 | 796.54866 | ||
| 6743.48259 | 7388.89619 | 346,141.988 | 180,459.89019 | 645.4136 | ||
| 8197.24619 | 8712.92223 | 229,937.55821 | 123,681.70134 | 515.67604 |
| MLE | 3018.151137 | 4228.504423 | 895,307.42374 | 451,882.216293 | 1210.353286 | |
| 3476.191406 | 4557.144289 | 755,914.936649 | 382,514.612614 | 1080.952883 | ||
| 4018.195081 | 4967.151113 | 617,382.044371 | 313,658.173299 | 948.956032 | ||
| 4771.39211 | 5568.556439 | 448,149.30637 | 229,643.209624 | 797.16433 | ||
| 5388.71247 | 6083.137469 | 369,667.951793 | 190,917.113365 | 694.424999 | ||
| 6523.604751 | 7069.40067 | 243,602.679891 | 128,870.740616 | 545.795919 | ||
| 7749.241041 | 8177.125483 | 157,453.697061 | 86,903.974013 | 427.884442 | ||
| LS | 3057.31723 | 4616.08258 | 1,572,944.00665 | 791,088.08591 | 1558.76535 | |
| 3627.94661 | 5042.87182 | 1,359,642.80998 | 684,864.27681 | 1414.92521 | ||
| 4320.48304 | 5584.35879 | 1,139,971.02561 | 575,569.8716 | 1263.87575 | ||
| 5309.58291 | 6393.90828 | 889,164.50728 | 450,976.16192 | 1084.32537 | ||
| 6140.27802 | 7100.03757 | 724,434.88826 | 369,317.4817 | 959.75955 | ||
| 7707.47013 | 8481.07818 | 498,718.1162 | 257,840.13628 | 773.60805 | ||
| 9449.44305 | 10,070.24175 | 335,705.12524 | 177,922.80437 | 620.7987 | ||
| WLS | 3016.57287 | 4357.54867 | 1,125,040.18728 | 566,877.64231 | 1340.97581 | |
| 3517.26542 | 4722.90662 | 959,163.35091 | 484,304.58208 | 1205.6412 | ||
| 4115.89338 | 5181.88499 | 791,913.74316 | 401,138.75657 | 1065.99161 | ||
| 4957.14659 | 5860.26126 | 605,455.00866 | 308,587.76559 | 903.11467 | ||
| 95% | 5653.57081 | 6445.60633 | 485,959.42745 | 249,425.32005 | 792.03552 | |
| 6947.55125 | 7576.56834 | 325,971.49602 | 170,562.31636 | 629.01709 | ||
| 8361.65005 | 8859.53398 | 214,308.30495 | 116,013.68646 | 497.88393 | ||
| CVM | 3042.58341 | 4571.44196 | 1,507,415.34803 | 758,279.11598 | 1528.85855 | |
| 3603.50313 | 4989.81522 | 1,301,028.07761 | 655,503.85402 | 1386.31208 | ||
| 80% | 4283.12424 | 5520.04414 | 1,088,976.79416 | 550,008.44122 | 1236.9199 | |
| 5252.03564 | 6311.76547 | 847,325.32097 | 429,974.42596 | 1059.72983 | ||
| 6064.47679 | 7001.50331 | 689,362.44601 | 351,682.72631 | 937.02652 | ||
| 7594.63827 | 8348.70189 | 472,931.24023 | 244,814.322 | 754.06362 | ||
| 9292.25602 | 9896.43605 | 317,706.23491 | 168,749.55351 | 604.18003 | ||
| ADE | 3025.58204 | 4382.96196 | 1,155,270.56969 | 582,018.24681 | 1357.37992 | |
| 3531.75877 | 4752.90735 | 985,824.9595 | 497,665.3871 | 1221.14858 | ||
| 4137.52807 | 5217.94783 | 814,745.39537 | 412,590.64551 | 1080.41976 | ||
| 4989.70807 | 5905.79682 | 623,720.17381 | 317,765.88372 | 916.08875 | ||
| 5695.83725 | 6499.7418 | 501,000.37295 | 256,999.92827 | 803.90455 | ||
| 7009.15169 | 7648.20733 | 336,694.11449 | 175,995.26458 | 639.05564 | ||
| 8445.96804 | 8952.25142 | 221,709.26206 | 119,806.88245 | 506.28338 | ||
| Moment | 60% | 966.65702 | 4103.34393 | 13,926,896.58904 | 6,967,551.63844 | 3136.68691 |
| 1653.56101 | 5043.53049 | 15,020,357.32578 | 7,515,222.19338 | 3389.96948 | ||
| 2811.11642 | 6476.60327 | 16,314,187.9627 | 8,163,570.58462 | 3665.48685 | ||
| 90% | 5145.63806 | 9139.30372 | 18,006,882.83894 | 9,012,580.72319 | 3993.66566 | |
| 7776.40195 | 11,987.80281 | 19,224,262.08164 | 9,624,118.84363 | 4211.40085 | ||
| 14,529.11205 | 19,024.55224 | 20,916,418.13409 | 10,477,233.61929 | 4495.4402 | ||
| 24,938.9476 | 29,594.42541 | 21,896,109.43017 | 10,977,649.14049 | 4655.47781 |
| Rank | ||||
|---|---|---|---|---|
| MLE | 1.52776 | 0.15012 | 0.02804 | 6 |
| LS | 2.31433 | 0.11868 | 0.06689 | 1 |
| WLS | 1.34353 | 0.15026 | 0.02708 | 4 |
| CVM | 2.3485 | 0.12133 | 0.06332 | 2 |
| ADE | 0.17658 | 0.13559 | 0.04256 | 3 |
| Moment | 2.17018 | 0.14186 | 0.03780 | 5 |
| Rank | |||
|---|---|---|---|
| MLE | 0.25197 | 0.00049 | 6 |
| LS | 0.23566 | 0.00121 | 2 |
| WLS | 0.24496 | 0.00074 | 5 |
| CVM | 0.23669 | 0.00116 | 3 |
| ADE | 0.24429 | 0.00077 | 4 |
| Moment | 0.15750 | 0.05048 | 1 |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.7821 | 1.14740 | 252.8311 | 1.8194 | 3.1188 | |
| 0.1020 | 0.8678 | 0.29340 | 90.97970 | 0.2563 | 2.2633 | |
| 1.4172 | 0.0437 | 0.01265 | 0.094400 | 0.0047 | 2.5657 | |
| - | - | - | 308.0258 | - | 30.4398 | |
| - | - | - | 76.06600 | - | - | |
| Distribution and bias | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.7662 | −0.9539 | 15.9007 | −1.0547 | −1.766 | |
| −0.3125 | −0.9316 | −0.0095 | 9.5383 | −0.0565 | −1.5009 | |
| −1.1904 | −0.2053 | 0.0195 | −0.3067 | 0.0247 | 1.6018 | |
| - | - | - | 17.5507 | - | 5.5172 | |
| - | - | - | 8.7156 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.5537 | 0.6893 | 250.5503 | 1.0569 | 3.0902 | |
| 0.1139 | 0.8768 | 0.0694 | 95.1393 | 0.0777 | 2.2738 | |
| 1.4408 | 0.0446 | 0.0026 | 0.09490 | 0.0014 | 1.3801 | |
| - | - | - | 305.5076 | - | 46.4741 | |
| - | - | - | 85.5873 | - | - | |
| Distribution and bias | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.7441 | −0.829 | 15.8287 | −0.9145 | −1.7579 | |
| −0.3375 | −0.9364 | 0.02116 | 9.7539 | −0.0459 | −1.5079 | |
| −1.2003 | −0.2106 | 0.0034 | -0.3081 | 0.0113 | 1.1748 | |
| - | - | - | 17.4787 | - | 6.8172 | |
| - | - | - | 9.2513 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.6478 | 0.7424 | 247.2826 | 0.8578 | 3.0847 | |
| 0.114 | 0.8663 | 0.0239 | 91.596 | 0.0362 | 2.2754 | |
| 1.4408 | 0.0433 | 0.00077 | 0.0949 | 0.0005 | 1.0698 | |
| - | - | - | 301.8983 | - | 82.8442 | |
| - | - | - | 82.4628 | - | - | |
| Distribution and bias↓ | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.8049 | −0.8616 | 15.7252 | −0.898 | −1.7563 | |
| −0.3376 | −0.9308 | −0.0054 | 9.5706 | −0.0002 | −1.5085 | |
| −1.2003 | −0.208 | 0.0022 | −0.3081 | 0.0041 | 1.0343 | |
| - | - | - | 17.3752 | - | 9.1018 | |
| - | - | - | 9.0809 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.5236 | 0.6238 | 240.3421 | 0.6534 | 2.8015 | |
| 0.1152 | 0.8663 | 0.0112 | 86.93 | 0.0196 | 2.2746 | |
| 1.4414 | 0.0485 | 0.0004 | 0.0947 | 0.0003 | 0.8668 | |
| - | - | - | 292.2038 | - | 127.32 | |
| - | - | - | 80.3590 | - | - | |
| Distribution and bias | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.6216 | −0.8507 | 15.444 | −0.8859 | −1.7497 | |
| −0.3395 | −0.9307 | 0.0074 | 9.3236 | −0.0072 | −1.5082 | |
| −1.2006 | −0.2202 | 0.0016 | −0.3078 | 0.0009 | 0.9310 | |
| - | - | - | 17.0939 | - | 11.283 | |
| - | - | - | 8.9643 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.2363 | 0.6892 | 832.8201 | 0.9754 | 1.3653 | |
| 40.6931 | 0.0448 | 125.888 | 510.6551 | 46.1623 | 3.8990 | |
| 0.02363 | 0.0022 | 0.6668 | 1.194900 | 0.1256 | 14.061 | |
| - | - | - | 894.526 | - | 33.912 | |
| - | - | - | 368.289 | - | - | |
| Distribution and bias | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.0991 | −0.7347 | 28.8586 | 0.6776 | −1.1685 | |
| 6.3791 | 0.2115 | 11.22 | 22.5977 | 6.794283 | 1.9746 | |
| −0.1534 | 0.0192 | 0.8166 | 1.09310 | 0.3545 | 3.7498 | |
| - | - | - | 29.9086 | - | 5.8234 | |
| - | - | - | 19.1888 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.0486 | 0.45580 | 832.335 | 0.8829 | 1.3531 | |
| 39.9115 | 0.0361 | 91.6124 | 521.084 | 47.0146 | 1.9761 | |
| 0.02520 | 0.0004 | 0.52890 | 1.00610 | 0.1149 | 8.1882 | |
| - | - | - | 894.023 | - | 18.522 | |
| - | - | - | 366.152 | - | - | |
| Distribution and bias↓ | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.019 | −0.6740 | 28.8502 | 0.9352 | −1.1632 | |
| 6.3176 | 0.1901 | 9.5714 | 22.8273 | 6.8567 | 1.4057 | |
| −0.1588 | 0.0090 | 0.7272 | 1.00300 | 0.339 | 2.8615 | |
| - | - | - | 29.9002 | - | 4.3038 | |
| - | - | - | 19.1351 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.0226 | 0.4749 | 832.0821 | 1.4275 | 1.3509 | |
| 39.5123 | 0.0354 | 90.4661 | 522.9859 | 47.6067 | 1.3186 | |
| 0.0251 | 0.0003 | 0.5513 | 0.9602 | 0.106 | 5.5305 | |
| - | - | - | 893.7608 | - | 12.716 | |
| - | - | - | 365.7548 | - | - | |
| Distribution and bias | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.0403 | −0.689 | 28.8458 | 1.1948 | −1.1622 | |
| 6.2859 | 0.1881 | 9.5113 | 22.8689 | 6.8998 | 1.1483 | |
| −0.1584 | 0.0105 | 0.7425 | 0.9799 | 0.3256 | 2.3517 | |
| - | - | - | 29.8958 | - | 3.5659 | |
| - | - | - | 19.1247 | - | - | |
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
|---|---|---|---|---|---|---|
| - | 0.0102 | 0.4522 | 832.152 | 1.3039 | 1.3400 | |
| 39.1249 | 0.0343 | 87.444 | 523.0877 | 47.5951 | 1.2668 | |
| 0.02578 | 0.0001 | 0.5307 | 0.943 | 0.1066 | 5.2669 | |
| - | - | - | 893.8333 | - | 12.5085 | |
| - | - | - | 365.3734 | - | - | |
| Distribution and bias | ||||||
| Estimator | Chen | GRC | GC | KUMC | MOC | TEC |
| - | −0.0218 | −0.6725 | 28.847 | 1.1419 | −1.1576 | |
| 6.255 | 0.1851 | 9.3511 | 22.8711 | 6.899 | 1.1255 | |
| −0.1606 | 0.0082 | 0.7285 | 0.9711 | 0.3265 | 2.295 | |
| - | - | - | 29.897 | - | 3.5367 | |
| - | - | - | 19.1147 | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousof, H.M.; Emam, W.; Tashkandy, Y.; Ali, M.M.; Minkah, R.; Ibrahim, M. A Novel Model for Quantitative Risk Assessment under Claim-Size Data with Bimodal and Symmetric Data Modeling. Mathematics 2023, 11, 1284. https://doi.org/10.3390/math11061284
Yousof HM, Emam W, Tashkandy Y, Ali MM, Minkah R, Ibrahim M. A Novel Model for Quantitative Risk Assessment under Claim-Size Data with Bimodal and Symmetric Data Modeling. Mathematics. 2023; 11(6):1284. https://doi.org/10.3390/math11061284
Chicago/Turabian StyleYousof, Haitham M., Walid Emam, Yusra Tashkandy, M. Masoom Ali, R. Minkah, and Mohamed Ibrahim. 2023. "A Novel Model for Quantitative Risk Assessment under Claim-Size Data with Bimodal and Symmetric Data Modeling" Mathematics 11, no. 6: 1284. https://doi.org/10.3390/math11061284
APA StyleYousof, H. M., Emam, W., Tashkandy, Y., Ali, M. M., Minkah, R., & Ibrahim, M. (2023). A Novel Model for Quantitative Risk Assessment under Claim-Size Data with Bimodal and Symmetric Data Modeling. Mathematics, 11(6), 1284. https://doi.org/10.3390/math11061284





_Masoom_Ali.png)


