VRR-Net: Learning Vehicle–Road Relationships for Vehicle Trajectory Prediction on Highways

Abstract

Vehicle trajectory prediction is an important decision-making and planning basis for autonomous driving systems that enables them to drive safely and efficiently. To accurately predict vehicle trajectories, the complex representations and dynamic interactions among the elements in a traffic scene are abstracted and modelled. This paper presents vehicle–road relationships net, a deep learning network that extracts features from vehicle–road relationships and models the effects of traffic environments on vehicles. The introduction of geographic highway information and the calculation of spatiotemporal distances with a reference not only unify heterogeneous vehicle–road relationship representations into a time series vector but also reduce the requirement for sensing transient changes in the surrounding area. A hierarchical long short-term memory network extracts environmental features from two perspectives—social interactions and road constraints—and predicts the future trajectories of vehicles by their manoeuvre categories. Accordingly, vehicle–road relationships net fully exploits the contributions of historical trajectories and integrates the effects of road constraints to achieve performance that is comparable to or better than that of state-of-the-art methods on the next-generation simulation dataset.

1. Introduction

Vehicle trajectory prediction, an essential component of an automated driving system (ADS), supports planning and decision-making for safe [1,2] and efficient resource allocation [3], especially under highway conditions [4]. In traffic scenarios, vehicles are the most dominant traffic participants and the dynamic obstacles with the greatest impact on traffic safety. If the future trajectories of vehicles are accurately predicted, intelligent systems will have the potential to build safer, more efficient and more comfortable transportation paradigms [5,6].

The trajectories of vehicles in traffic scenes are inextricably linked to the changes in their surroundings [7]. The dynamic interactions among traffic infrastructure elements (e.g., roads and traffic lights) and traffic participants (e.g., vehicles and pedestrians) make up complex and diverse traffic scenarios [8]. The traffic infrastructure constrains the movements of participants who can move freely but are constrained by the infrastructure, and accurate vehicle trajectory prediction in complex traffic environments requires considering environmental constraints and social interactions [9,10,11,12,13]. Ju et al. propose a multilayer architecture called interaction-aware Kalman neural networks (IaKNN), which involves an interaction layer for resolving high-dimensional traffic environmental observations as interaction-aware accelerations, a motion layer for transforming the accelerations to interaction-aware trajectories, and a filter layer for estimating future trajectories with a Kalman filter network [9]. Deo and Trivedi propose an LSTM encoder–decoder model that uses convolutional social pooling to learn inter-dependencies in vehicle motion and outputs a multimodal predictive distribution over future trajectories based on maneuver classes [10]. Guo et al. propose a dual-attention mechanism trajectory prediction method based on long short-term memory encoding that is coupled with the motion trend of the ego vehicle [11]. Chen et al. propose a new model structure, which uses a convolutional social pool to extract general features and uses GAN to extract confidence features of the generated trajectories, enabling the model to generate trajectories that are close to the real trajectories [12]. Malviya and Kala present a multi-behavioural social force-based particle filter to track a group of moving humans from a moving robot using a limited field-of-view monocular camera [13]. Overall, these papers contribute to the development of more accurate and robust trajectory prediction methods for various scenarios, such as complex traffic systems and human–robot interactions. The proposed methods utilise different techniques such as multilayer architecture, convolutional social pooling, dual-attention mechanism, and social heuristics to enhance the accuracy and generalizability of the prediction models.

Two difficulties are currently faced with regard to vehicle trajectory prediction. On the one hand, the combination of the elements in a traffic environment is complex, and current methods are not yet able to reliably cover all elements that have impacts on trajectories [14,15]. On the other hand, on the road, the motions of human-driven vehicles are multimodal [16,17,18,19], which means that similar inputs should produce different prediction results. In recent years, the problems concerning the social interactions between vehicles and the modelling of the relationships between vehicles and roads have received attention from researchers, who have proposed many different models and methods aimed at constructing the interactions between the vehicles to be predicted and their surroundings [20,21,22].

For highway scenarios, vehicle–road relationships (VRR)-Net, a network proposed for predicting vehicle trajectories from a vehicle–road relationship perspective, includes a data preprocessing strategy and an environment modelling framework. First, the input representations of VRR-Net are unified by the idea of serialisation. The relationships between vehicles and environments are mapped to the same representation space, thus extending the feature-capturing advantage of the model for dynamic environments. Specifically, a long short-term memory (LSTM) network with a similar structure separately extracts the interactive features of vehicles with different kinds of environmental elements and is hierarchically organised into a parallel structure. In addition, the social interactions of vehicles are abstracted from the original inputs by a spatiotemporal graph structure, which projects the social interactions into both the temporal and spatial dimensions. In the proposed spatiotemporal graph structure, the movement changes exhibited by the vehicles themselves are described by temporal edges, and the interactions between the vehicles are described by spatial edges. The experimental results show that the temporalised spatiotemporal graph reinforces the social interactions and significantly improves the utilisation of the information embedded in the historical trajectories by the social LSTM encoder.

The contributions of the proposed VRR-Net are summarised as follows.

•

A serialised vehicle–road relationship model for highway scenarios is introduced, which integrates the geometry of real highways and the relative positions of vehicles and roads. The serialised model not only preserves the spatiotemporal dependencies between vehicles and roads but also implicitly expresses the manoeuvring interaction behaviours of vehicles that are parallel and perpendicular to the road direction, making the interactions between vehicles and roads more closely related to the motion features of the target vehicle.

•

A novel intervehicle interaction model based on a spatiotemporal graph structure is studied; this model abstracts social interaction information at the spatial level and vehicle motion information at the temporal level. In cases where the instantaneous motions of the observed vehicles are not accessible in real-time, both the local and overall features of vehicle motions in dynamic traffic scenarios can be effectively extracted.

•

A novel hierarchical environment encoder module with two LSTM layers is proposed for simultaneously extracting the spatiotemporal features of the interactions of the target vehicle with the road and with the surrounding vehicles. The network integrating vehicle–road and vehicle–vehicle relationships achieves better manoeuvre and trajectory prediction accuracy in highway scenarios than competing approaches.

2. Related Work

The development of trajectory prediction methods has progressed from simple to complex processes that can be outlined in three development stages.

The first-stage approaches try to deduce the future trajectory from only the historical trajectory of the vehicle to be predicted. This approach is intuitive and consistent with vehicle motion patterns. The kinematics-based approach [23,24,25] achieves superior short-term prediction performance (within 1 s) by extracting physical quantities such as vehicle speeds, constant yaw rates and acceleration values as vehicle motion characteristics [26]. It is worth noting that vehicle manoeuvre categories are used as high-level information that reduces the complexity of the motion model. Methods such as hidden Markov models [27], random forest classifiers [28] and multilayer perceptrons [29] have considered the importance of vehicle manoeuvre categories. However, regardless of this fact, their core ideas start from the vehicle’s own motion characteristics only. When the prediction time exceeds 1 s, the associations between future trajectories and physical laws are gradually weakened by the driver’s intention, so they cannot produce reliable long-term trajectories [30] to support the planning and decision-making of intelligent systems.

The second-stage approaches build on the previous stage by considering the influence of the social interactions between the vehicles to be predicted and other traffic participants [31]. The methods in [32,33] demonstrated that considering the interactions among surrounding vehicles helps to improve the accuracy of lane-changing behaviour prediction. The effect of this influence on predicting the future trajectories of vehicles is considered significant. Deo and Trivedi [10] proposed a social pooling mechanism to extract the features of the interactions between vehicles based on recurrent neural networks and achieved better long-term trajectory predictions. Guo et al. [11], Giuliari et al. [34] and Yan et al. [35] proposed incorporating attention mechanisms into the field of trajectory prediction so that their model could autonomously select the appropriate trajectory features for prediction when training on massive historical data. Chen et al. [36] constructed a spatiotemporal graph structure for intervehicle relationships and better extracted the spatiotemporal interactions between vehicles.

In the third stage, researchers built on the second stage and started to study the influence of the surrounding traffic infrastructure on the target vehicle [37]. In real traffic scenarios, constraints and controls from traffic infrastructure, such as lane orientations, road boundaries and traffic light scheduling, play important roles in determining the outcome of trajectory prediction. However, it is still difficult to effectively model these complex additions. Trajectron++ [15] and AgentFormer [38] process a high-definition (HD) map into feature vectors via convolutional neural networks, thus giving the networks the ability to perceive their environments. Although the aforementioned methods successfully model the influence of roads on the future trajectories of vehicles using different structures, their feature extraction abilities with respect to environmental influences are still inadequate.

Furthermore, the idea of VectorNet [39], LaneGCN [40] and prediction via graph-based policy (PGP) [21] is to organise the roads contained in the input HD map into a graph structure after segmentation and then use a graph convolutional network (GCN) to extract road features, thereby effectively solving the multimodal trajectory prediction problem in intersection scenes. Although the roads in highway scenarios are relatively simple, with long sections and small turning angles, the constraining effect of roads on vehicle behaviour still cannot be ignored. To comprehensively consider the environmental effects in this scenario and achieve better trajectory prediction accuracy, our study models both the road constraints imposed on vehicles and the social interactions between vehicles. The open next-generation simulation (NGSIM) dataset [41,42] is used to validate the method proposed in this paper for a fair comparison with most existing methods.

3. Hierarchical Model with Spatiotemporal Awareness of Vehicle–Road Relationships

For an arbitrary vehicle at each time stamp on a highway, its future motion is influenced by the environment, including both the road and the surrounding vehicles. The serialised vehicle–road relationships are implemented by a vector transformation of the vehicle trajectory points on the road geometry space, and the vehicle–vehicle relationships are constructed using a spatiotemporal graph structure, including the target vehicle and its surrounding vehicles. Furthermore, the proposed encoder extracts the temporalised features of these two aspects simultaneously using LSTM networks. Therefore, the trajectories output by the decoder are the result of a combination of the local and overall interactions between the vehicle and its driving environment.

3.1. Problem Formulation

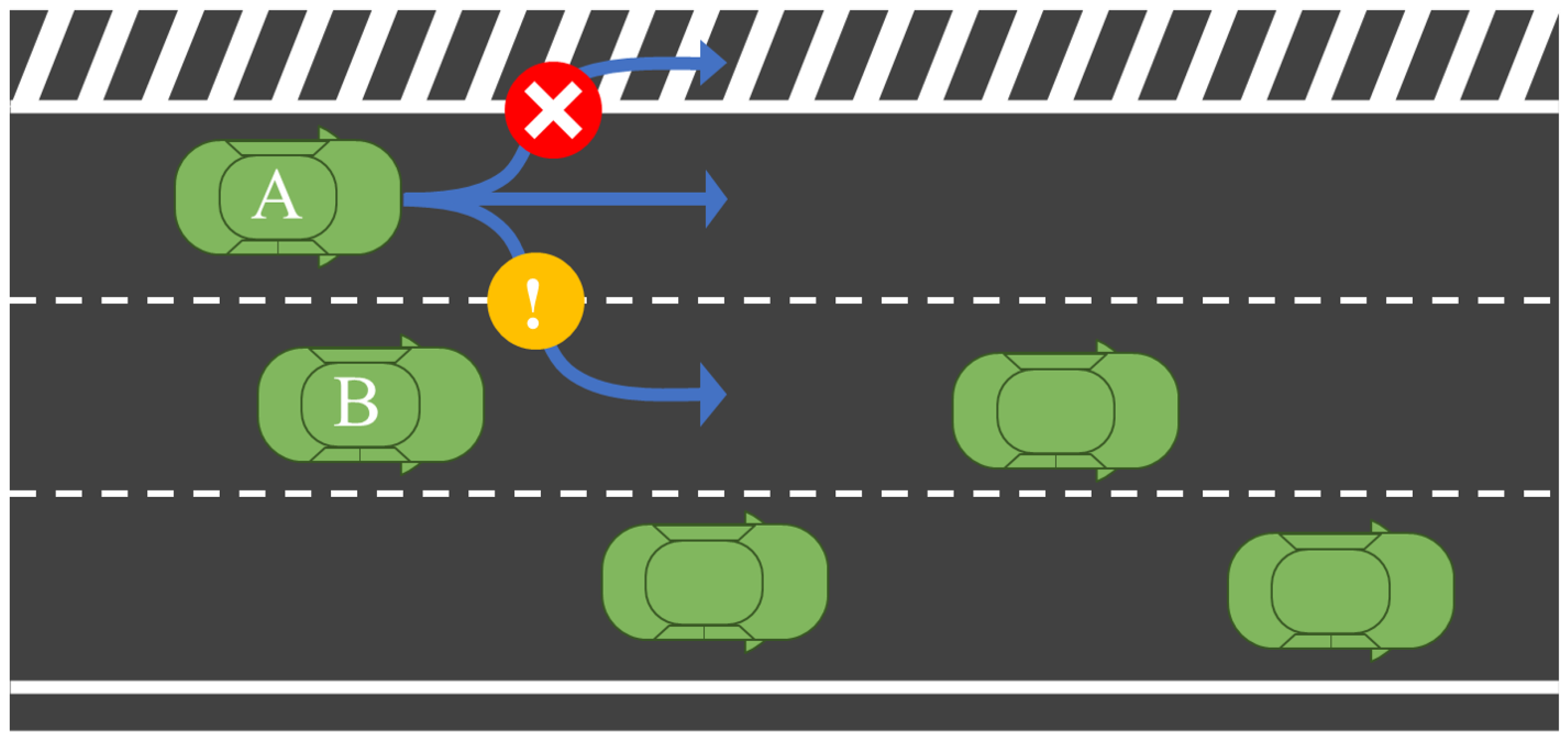
A figurative example is given in Figure 1. In this case, the traffic infrastructure is characterised by a relatively fixed location, which acts as a constraint on the movements of traffic participants; the traffic participants are characterised by the ability to move freely but are constrained by the traffic infrastructure. In addition, dynamic social interaction behaviours [9,10,11,12,13] occur among the traffic participants because of their willingness to avoid collisions. Without considering the environmental constraints and social interactions, it is impossible to accurately predict the future trajectories of vehicles in complex traffic environments. Therefore, effectively modelling the constraints and interactions in traffic scenarios is a problem that needs to be focused on for vehicle trajectory prediction.

At any time step in a freeway traffic scenario, there are two bases for predicting the future trajectory of a target vehicle. The first is based on the spatial relationship between the target vehicle and the road. Highway geometries and attributes (e.g., lane types, lane widths, and lane orientations) limit the future trajectory of the target vehicle in the long term. The second is based on the spatiotemporal interactions between the target vehicle and its surrounding vehicles. Their historical trajectories implicitly influence the future trajectory of the target vehicle as a result of their social interactions.

Both the vehicle trajectories and the geometry of the highway can be represented by combinations of position points. Let $p=(x,y)$ denote the position point in the scene, where $x,y\in \mathbb{R}$ are the lateral and vertical coordinates, respectively.

The road segments of highways are linearly distributed in the road network with a wide road surface, a long distance, less curvature and directional characteristics. We approximate the curved road segments by several straight segments; thus, the road network can be partitioned and represented as a set of straight road segments:

$$RS=\{r_j\mid j=1,\dots ,m\},$$

(1)

where m is the number of segments obtained from the partition, and each segment $r_j=\left(p_s^{r_j},p_e^{r_j}\right)$ can be labelled by a start position point $p_s^{r_j}=\left(x_s^{r_j},y_s^{r_j}\right)$ and an end position point $p_e^{r_j}=\left(x_e^{r_j},y_e^{r_j}\right)$.

Without loss of generality, let $v_0$ denote the target vehicle to be predicted, and let $v_1,\dots ,v_n$ denote the n vehicles around $v_0$. Then, the observed trajectory of each vehicle $v_i(i=0,1,\dots ,n)$ is denoted as

$$T^{v_i}=\{p_t^{v_i}\mid t=-H+1,-H+2,\dots ,0\},$$

(2)

where $H\in {\mathbb{N}}^{+}$ is the number of observed historical time steps, and $p_t^{v_i}=(x_t^{v_i},y_t^{v_i})$ is the position of vehicle $v_i$ at time step t. Correspondingly, the predicted trajectory of target vehicle $v_0$ in the future is

$$\widehat{T}=\{{\widehat{p}}_t\mid t=1,2,\dots ,F\},$$

(3)

where $F\in {\mathbb{N}}^{+}$ is the number of predicted future time steps, and ${\widehat{p}}_t=({\widehat{x}}_t,{\widehat{x}}_t)$ is the position of the target vehicle $v_0$ at time step t. Figure 2 illustrates the architecture of the proposed vehicle trajectory prediction model for learning vehicle-road relationships and vehicle-vehicle relationships in highway scenarios.

According to the classifications of manoeuvres mentioned in [10], when a vehicle is driving along a highway, the lateral manoeuvres of the vehicle in the parallel road direction are classified as braking and normal, and the longitudinal manoeuvres of the vehicle in the perpendicular road direction are classified as left lane changes (LCLs), lane keeping (KL) and right lane changes (LCRs). There are six combinations of the results in both directions, which are represented by one-hot codes.

3.2. Serialised Vehicle–Road Relationships

To represent the spatiotemporal relationships between vehicles and roads during the driving procedure, a generalised vehicle trajectory point transformation method is established based on the geometry of road segments.

As shown in Figure 3, given any trajectory point P in the $xOy$ coordinate system, let a vector r denote the segment in which P is located, where $S=p_s^r$ denotes the starting point of r, and $E=p_e^r$ denotes the ending point of r. Then, the projection point $P^{\prime }$ of P on $\overrightarrow{SE}$ can be represented by the $\overrightarrow{O{P}^{\prime }}$ vector as follows:

$$\overrightarrow{O{P}^{\prime }}=\overrightarrow{OS}+\frac{\overrightarrow{SP}·\overrightarrow{SE}}{{\left|\overrightarrow{SE}\right|}^2}·\overrightarrow{SE}.$$

(4)

According to Equation (4), the distance from point P to vector r can be expressed as:

$$d(P,r)=\left|\overrightarrow{P^{\prime }P}\right|,$$

(5)

and r denotes the element in road segment $RS$ (as shown in Equation (1)) with the shortest distance $d(P,r)$.

In this way, the vector combination with the projection point as the turn is equivalent to the original trajectory points; i.e., they satisfy the following vector relation:

$$\overrightarrow{eq:OP}=\overrightarrow{O{p_t^{v_i}}^{\prime }}+\overrightarrow{{p_t^{v_i}}^{\prime }{p}_t^{v_i}},$$

(6)

where the projection point $\overrightarrow{O{p_t^{v_i}}^{\prime }}$ reflects the position of the vehicle in the parallel road direction and $\overrightarrow{{p_t^{v_i}}^{\prime }{p}_t^{v_i}}$ reflects the position of the vehicle in the perpendicular road direction. Moreover, to eliminate the differences among the representations of points in different coordinate systems, the shift alignment method, with the projection point ${p_0^{v_i}}^{\prime }$ at the end of the trajectory as the coordinate origin, is applied for vehicle trajectory sequence alignment. Thus, the serialised vehicle–road relationships can be expressed in a form similar to Equation (2) as follows:

$$R^{v_i}=\left\{(\overrightarrow{{p_t^{v_i}}^{\prime }{p_0^{v_i}}^{\prime }},\overrightarrow{{p_t^{v_i}}^{\prime }{p}_t^{v_i}}-\overrightarrow{{p_0^{v_i}}^{\prime }{p}_0^{v_i}})\mid t=-H+1,\cdots ,0\right\},$$

(7)

where $R^{v_i}$ is the vehicle–road relationship sequence of $v_i$, $p_t^{v_i}$ and H have the same meanings as in Equation (2), ${p_t^{v_i}}^{\prime }$ denotes the projection point of $p_t^{v_i}$ on the road segment, and $\overrightarrow{{p_t^{v_i}}^{\prime }{p}_t^{v_i}}$ denotes the vector from the projection point to the original trajectory point.

3.3. Spatiotemporal Graph Construction

The historical trajectories of the target vehicle and its surrounding vehicles are used to construct a spatiotemporal graph structure centred on the spatiotemporal location of the predicted object, which highlights the local vehicle motion information and the relative spatiotemporal location relationships of the vehicle interactions while preserving the vehicle motion trends.

As shown in Figure 4, given a set of vehicle history trajectories $\{T^{v_0},T^{v_1},\dots ,T^{v_n}\}$ composed of the elements shown in Equation (2), the spatiotemporal graph structure $G=\{V,E_T,E_S\}$ is constructed, where

$$V=\left\{p_t^{v_i}\mid i\in \{0,\dots ,n\},t\in \{-H+1,\dots ,0\}\right\}$$

(8)

denotes the set of vertices composed of the vehicle trajectory points.

$$E_T=\left\{(p_t^{v_i},p_{t-1}^{v_i})\mid i\in \{0,\dots ,n\},t\in \{-H+2,\dots ,0\}\right\}$$

(9)

denotes the directed temporal edge from $p_t^{v_i}$ to $p_{t-1}^{v_i}$, which implicitly expresses the local motion information of the same vehicle with the physical meaning of the vehicle velocity.

$$E_S=\{(p_0^{v_0},p_t^{v_i})\mid i\in \{0,\dots ,n\},t\in \{-H+1,\dots ,0\}\}$$

(10)

denotes the directed spatial edge from $p_0^{v_0}$ to $p_t^{v_i}$, which portrays the relationship between the trajectory points at different spatiotemporal locations and the current position of the target vehicle.

In the proposed spatiotemporal graph, the value of each vertex is a positional coordinate such as $p=(x,y)$, so the values of the edges can be represented by vectors such as $\overrightarrow{p_0^{v_0},p_t^{v_i}}$. In addition, except for the vertex at time step $t=0$, all the vertices have two entry degrees from a time edge and a space edge. Since the time edges have the physical meaning of velocity, the time edges from $t=-1$ to $t=-2$ are replicated between $t=0$ and $t=-1$ to unify the incidences of all vertices in the graph, and the new vehicle trajectory is represented by the values of the incidence edges as follows:

$$\begin{array}{c}\hfill ST=\left\{(\overrightarrow{p_t^{v_i},p_{t-1}^{v_i}},\overrightarrow{p_0^{v_0},p_{t-1}^{v_i}})\mid i\in \{0,\dots ,n\}\right\},\\ \hfill t\in \left\{-H+2,\dots ,0\right\}\cup \left\{(\overrightarrow{p_0^{v_i},p_{-1}^{v_i}},\overrightarrow{p_0^{v_0},p_0^{v_i}})\mid i\in \{0,\dots ,n\}\right\},\end{array}$$

(11)

where $S{T}^{v_i}$ denotes the temporal representations of the relationships between the vehicles.

3.4. Hierarchical Environmental Module

To synthetically model the road and social environment information around the target vehicle, a two-layer LSTM-based architecture is used for separately extracting serialised vehicle–vehicle and vehicle–road interaction features. In highway scenarios, these two features are directly and closely related to the manoeuvring behaviour and future trajectory of the target vehicle.

According to the relationship serialisation methods elaborated on in Section 3.2 and Section 3.3, the road LSTM encoder is used to encode a sequence of relationships $R^{v_0}$ between the target vehicle $v_0$ and the roads, and the social LSTM encoder is used to encode the sequence $ST$ of the relationships between $v_0$ and its surrounding vehicles $v_1,\dots ,v_n$ based on the spatiotemporal graph. The two LSTM encoders are described in detail below.

•

Road LSTM Encoder: For the target vehicle $v_0$, at each time step t, the vector combination $R_t^{v_0}\in R^{v_0}$ with two-coordinate values, as shown in Equation (7), is embedded into a fixed-length vector $f_t^r$ for the subsequent decoding step.

$$\begin{array}{cc}\hfill e_t^r& =FC\left(R_t^{v_0},W_r^{emb}\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill h_t^r& =LSTM\left(h_{t-1}^r,e_t^r,W_r^{lstm}\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill f_t^r& =FC\left(h_t^r,W_r^{linear}\right),\hfill \end{array}$$

(14)

where $FC(·)$ is a fully connected layer employed as an input embedding function and $h_t^r$ is the hidden state generated by this layer. The capital letter W in this paper denotes the weights of the different network layers, the superscript of each weight indicates its function, and the subscript indicates that it belongs to a specific part of the network.

•

Social LSTM Encoder: For the target vehicle $v_0$ and its surrounding vehicles $v_1,\dots ,v_n$, at each time step t, their edge values $S{T}_t^{vi}\in ST$ based on the spatiotemporal graph, as shown in Equation (11), are embedded in fixed-length vectors $f_t^v$ and $f_t^s$, respectively, for the subsequent decoding process.

$$\begin{array}{cc}\hfill e_t^{v_i}& =FC\left(S{T}_t^{vi},W_s^{emb}\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill h_t^{v_i}& =LSTM\left(h_{t-1}^{v_i},e_t^{v_i},W_s^{lstm}\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill f_t^v& =FC\left(h_t^{v_0},W_s^{linear}\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill f_t^s& =CSP\left(\{h_t^{v_1},\dots ,h_0^{v_n}\},W_s^{csp}\right),\hfill \end{array}$$

(18)

where $h_t^{v_i}$ is the hidden state generated by the social LSTM layer, and $CSP(·)$ is the convolutional social pooling layer proposed in [10].

After passing through the above hierarchical network, the vehicle–road relationship feature $f_t^r$, the motion feature $f_t^v$ of the target vehicle and the social interaction feature $f_t^s$ are extracted separately from the serialised input data, and then the three features are connected and used as the historical feature $f_t$ output by this module.

3.5. Multimodel Prediction Module

The context vector outputs from the hierarchical environment module are used to decode the manoeuvres and future trajectories of vehicles. Vehicle manoeuvre estimation helps to solve multimodal problems in highway traffic scenarios, leading to more accurate trajectory prediction results.

According to the manoeuvre classification method mentioned in Section 3.1, the lateral and longitudinal manoeuvres are decoded by two fully connected layers with different output sizes and activated by the softmax function as a probability estimate of the target vehicle manoeuvre $\widehat{m}$. Furthermore, the predicted manoeuvre loss is calculated by a binary cross-entropy function.

The future trajectory prediction of the target vehicle combines the manoeuvre decoding results and the context vectors output by the hierarchical environment module. A trajectory decoder consisting of an LSTM layer and a fully connected layer is used to output the sequence of predicted trajectories.

$$\begin{array}{c}{\widehat{h}}_t=LSTM\left({\widehat{h}}_{t-1},f_t,W_{dec}^{lstm}\right),\end{array}$$

(19)

$$\begin{array}{c}\left({\mu }_{t+1},{\sigma }_{t+1},{\rho }_{t+1}\right)=FC\left({\widehat{h}}_t,W_{dec}^{linear}\right),\end{array}$$

(20)

$$\begin{array}{c}{\widehat{p}}_t\sim N\left({\mu }_t,{\Sigma }_t\right),\end{array}$$

(21)

where ${\widehat{p}}_t=\left({\widehat{x}}_t^{v0},{\widehat{y}}_t^{v0}\right)$ is the predicted trajectory coordinate of the target vehicle at time step t, and $N(·)$ is a binary Gaussian distribution function. ${\mu }_t,{\Sigma }_t$ are the mean and covariance matrix of the two variables, respectively. Therefore, the loss of predicted trajectories can be calculated by the negative log-likelihood (NLL) error.

4. Experiments

The NGSIM dataset is used to validate the performance of the proposed model, which outperforms the baseline approach and some state-of-the-art methods. Smaller root-mean-square error (RMSE) and NLL error values are achieved for the vehicle trajectory prediction task in freeway traffic scenarios due to the effective features extracted from the serialised vehicle–road and vehicle–vehicle relationships by the hierarchical environment module. In addition, the effectiveness of the vehicle–road geometry relationships and vehicle–vehicle spatiotemporal relationships for manoeuvre and trajectory prediction is demonstrated by ablation experiments.

4.1. Datasets and Model Training

NGSIM is a large open highway vehicle driving dataset that contains real vehicle travel data and corresponding geographic information system (GIS) files for the US-101 and I-80 freeways. On each of the two freeways, the NGSIM authors, the Federal Highway Administration (FHWA) in the USA, selected data collection areas of 500 and 640 m and collected vehicle driving data for 15 min each under light, moderate, and heavy traffic conditions at different times, with a temporal sampling frequency of 10 Hz. As a result, the dataset contains million-scale vehicle location information, and these data are organised into a sequence of vehicle trajectories in temporal order.

The NGSIM dataset consists of samples and is partitioned to be consistent with previous works [10,11,36]. First, the dataset is partitioned into training, validation and test sets at a ratio of 7:1:2 by time period. Second, the length of each trajectory sample is set to 8 s, where the first 3 s are used for observation and the last 5 s are used for supervised labelling. Third, vehicles within 90 feet of the target vehicle in the adjacent lane are treated as surrounding vehicles. If too many vehicles are located within the range (more than 39), e.g., the vehicles are in a congested state, the vehicles that are farthest away are discarded. Finally, for each trajectory point, the amount of data is reduced by using interval sampling, that is, using a sampling rate of 5 Hz. Thus, the observed length of each trajectory is 15 frames, and the predicted length is 25 frames.

In addition, the GIS files in NGSIM provide geometric and attribute information for the study area, where the geometric information is vectorised. As shown in Figure 5, road maps are extracted from this geometric information so that the relationships between vehicles and roads can be described in the same coordinate system. Figure 5a,b show the visualization of the road area and corresponding road lines in two different scenarios, which were used for training and testing our method.

The construction of the VRR-Net model is based on the PyTorch framework. The model is trained with a batch size of 128 and an initial learning rate of 0.001 using the Adam optimiser. In the road encoder and the social encoder, the fully connected layers are activated by a leaky rectified linear unit (Leaky-ReLU) function with an output dimensionality of 32, and the output of the social pooling layer has 80 dimensions. The output dimensions of the LSTM in the encoder and in the trajectory decoder are 64 and 128, respectively.

4.2. Evaluation Metric and Performance Comparison

In evaluations regarding highway vehicle trajectory prediction, the RMSE is widely used, and it is used as evaluation metrics in this paper to conduct a fair comparison and analysis. At each different prediction horizon t, the RMSE is calculated based on the relative errors as follows:

$$RMS{E}_t=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(\left|{\mathbf{p}}_{\mathbf{t}}-{\widehat{\mathbf{p}}}_{\mathbf{t}}\right|\right)}^2},$$

(22)

where n is the total number of samples in the test set, and ${\mathbf{p}}_{\mathbf{t}}$ and ${\widehat{\mathbf{p}}}_{\mathbf{t}}$ are the ground truth and predicted values of each target vehicle, respectively. Based on the RMSE, the method proposed in this paper outperforms the following baseline methods.

•

CS-LSTM [10]: CS-LSTM is an LSTM encoder–decoder-based model, and the proposed convolutional social pool improves the ability of the model to extract intervehicle relationships and output a multimodal predictive distribution based on manoeuvre categories.

•

ST-LSTM [36]: ST-LSTM achieves improved prediction performance by using a stacked LSTM encoder–decoder model to process the spatiotemporal graph structure containing vehicle relationships, which directly describes the relationships between the vehicle trajectory points.

•

Scale-Net [43]: The Scale-Net utilises an edge-enhanced graph convolutional neural network to solve the dynamic number input problem of the embedding layer, which is decoded by the LSTM encoder; finally, the prediction result is output by a multilayer perceptron.

•

Ego-Trand [11]: Guo’s method separately uses an attention mechanism for both the temporal and spatial dimensions and constructs an LSTM encoder–decoder structure with a dual-attention mechanism.

•

CF-LSTM [44]: CF-LSTM constructs a social force based on a physical approach to learn contextual features using a teacher–student model, which has the effect of reducing the collision rate of the trajectories generated by the LSTM encoder–decoder network.

•

MHA-LSTM [45]: MHA-LSTM also uses an attention mechanism to emphasise the importance of the surrounding vehicles, which improves the trajectory prediction performance of the LSTM encoder–decoder network.

In this paper,

Table 1. The RMSE performance of the proposed model and the existing advanced models are compared on the NGSIM dataset. The best result is marked in black.

Prediction Horizons (Second)	CS-LSTM [10]	ST-LSTM [36]	Scale-Net [43]	Ego-Trend [11]	CF-LSTM [44]	MHA-LSTM [45]	VRR-Net (Our)
1	0.61	0.51	0.46	0.50	0.55	0.41	0.47
2	1.27	1.21	1.16	1.11	1.10	1.01	1.08
3	2.09	2.01	1.97	1.78	1.78	1.74	1.79
4	3.10	3.01	2.91	2.69	2.73	2.67	2.65
5	4.37	4.31	-	3.93	3.82	3.83	3.71

is presented to showcase the accuracy comparison between our proposed methods and recent studies, with the RMSE evaluation metric. The VRR-Net model, which combines vehicle–road relationships and vehicle–vehicle relationships, significantly outperforms other models, such as CS-LSTM, ST-LSTM, and Scale-Net, all of which are similar in size but do not use attention mechanisms, for predicting the trajectories of vehicles from 0 to 5 s in the future. Despite using a graph structure to represent the relationships between vehicles, the VRR-Net model has a 12% relative reduction in prediction error in this timeframe. Compared with the LSTM encoder–decoder models, Ego-Trand and CF-LSTM, which use attention mechanisms, the VRR-Net model achieves comparable results from 0 to 3 s but has an advantage in long-term prediction errors after 3 s. Notably, the advantage of the VRR-Net model over the teacher–student model (CF-LSTM) becomes increasingly apparent in long-term prediction scenarios. The serialised representations of the vehicle–road relationships, coupled with a feature extraction process, enable the VRR-Net model to more comprehensively perceive its environmental context, thereby producing more reliable long-term prediction results. Overall, these results demonstrate that VRR-Net is a promising trajectory prediction model that can achieve superior performance, particularly for long-term prediction tasks in dynamic traffic scenarios.

4.3. Ablation Studies

The VRR-Net model is decomposed into multiple components, and comparative experiments are conducted to verify the impacts of these different components on the final prediction accuracy. To validate the effectiveness of the spatiotemporal graph-based social encoder, the spatiotemporal graph is deconstructed into the case in which only spatial edges and both spatiotemporal edges are used. The serialised vehicle–road relationships and the road encoder are treated as independent components to verify the effect of the vehicle–road relationships on the trajectory prediction results. Furthermore, the CS-LSTM and ST-LSTM approaches are used as a baseline for comparison purposes, and the experiments are performed on the same NGSIM dataset with the same parameters. Thus, the following three ablation cases are validated:

•

VRR-Net without the temporal edges and road encoders;

•

VRR-Net without the road encoder;

•

VRR-Net.

As shown in Figure 6, the social encoder of VRR-Net is able to capture the social interaction features between vehicles more effectively from the spatiotemporal graph structure, while the VRR-Net model without temporal edges and the road encoder is inferior in performance to the model that encodes both temporal and spatial edges, as well as to the two baseline approaches. The reason for this is that the historical trajectories of the surrounding vehicles are not sufficiently exploited to obtain sufficiently effective features. In contrast, the road encoder further improves the accuracy of trajectory prediction, indicating that the vehicle–road relationships and the road encoder effectively enhance the prediction network’s ability to acquire the features of vehicle surroundings.

5. Conclusions

The VRR-Net model proposed in this paper integrates the influences of traffic participants and traffic infrastructure to predict vehicles. In terms of input features, VRR-Net only uses vehicle position data to build a spatiotemporal relationship graph, avoiding the use of instantaneous velocities and instantaneous accelerations, which are difficult to obtain in real-time from the surrounding vehicles. This spatiotemporal relationship structure is easy to vectorise and serialise and can effectively extract the environmental features around the vehicle to be predicted. In terms of model structure, VRR-Net adopts a hierarchical design with high scalability. Two parallel LSTM networks are used to address vehicle–road relationships and vehicle–vehicle relationships, and a manoeuvre decoder and a trajectory decoder comprehensively consider both kinds of relationships, thereby further enhancing the model’s feature extraction capability for traffic environments. Experimental results obtained on the NGSIM dataset demonstrate that VRR-Net is able to effectively exploit the observed vehicle–road relationships and achieve improved vehicle trajectory prediction performance over that of models that also use LSTM to extract features. Thus, the model’s success is attributed to its ability to integrate the spatiotemporal dependencies between vehicles and roads, the intervehicle interaction information, and the social interaction behaviors of traffic participants, which are crucial to predicting vehicle trajectories in complex traffic scenarios. We install four cameras around the vehicle for testing on a highway, and the results show that the proposed method can effectively predict the trajectories around the vehicle. Based on the results, it is evident that the proposed VRR-Net model achieves superior trajectory prediction performance, especially in long-term prediction tasks in dynamic traffic scenarios. However, it is essential to consider the cost of implementing this solution in real-world applications. The VRR-Net model requires additional data processing and feature extraction steps, which may increase the computational cost and complexity of the system. Furthermore, the training process of the VRR-Net model may also require more time and resources than simpler models that do not incorporate attention mechanisms or vehicle–road relationships.

Indeed, other complicated influences are included in real traffic scenarios, in addition to the influences of roads and surrounding vehicles. In future work, we will consider the influences of other traffic infrastructures in high-speed traffic scenarios on vehicle trajectories. Additionally, the generalisation capability and interpretability of the proposed model will be considered in more traffic scenarios. With further research, our future trajectory prediction approach will become more accurate and practically applicable.