Dry Friction Analysis in Doped Surface by Network Simulation Method
Abstract
1. Introduction
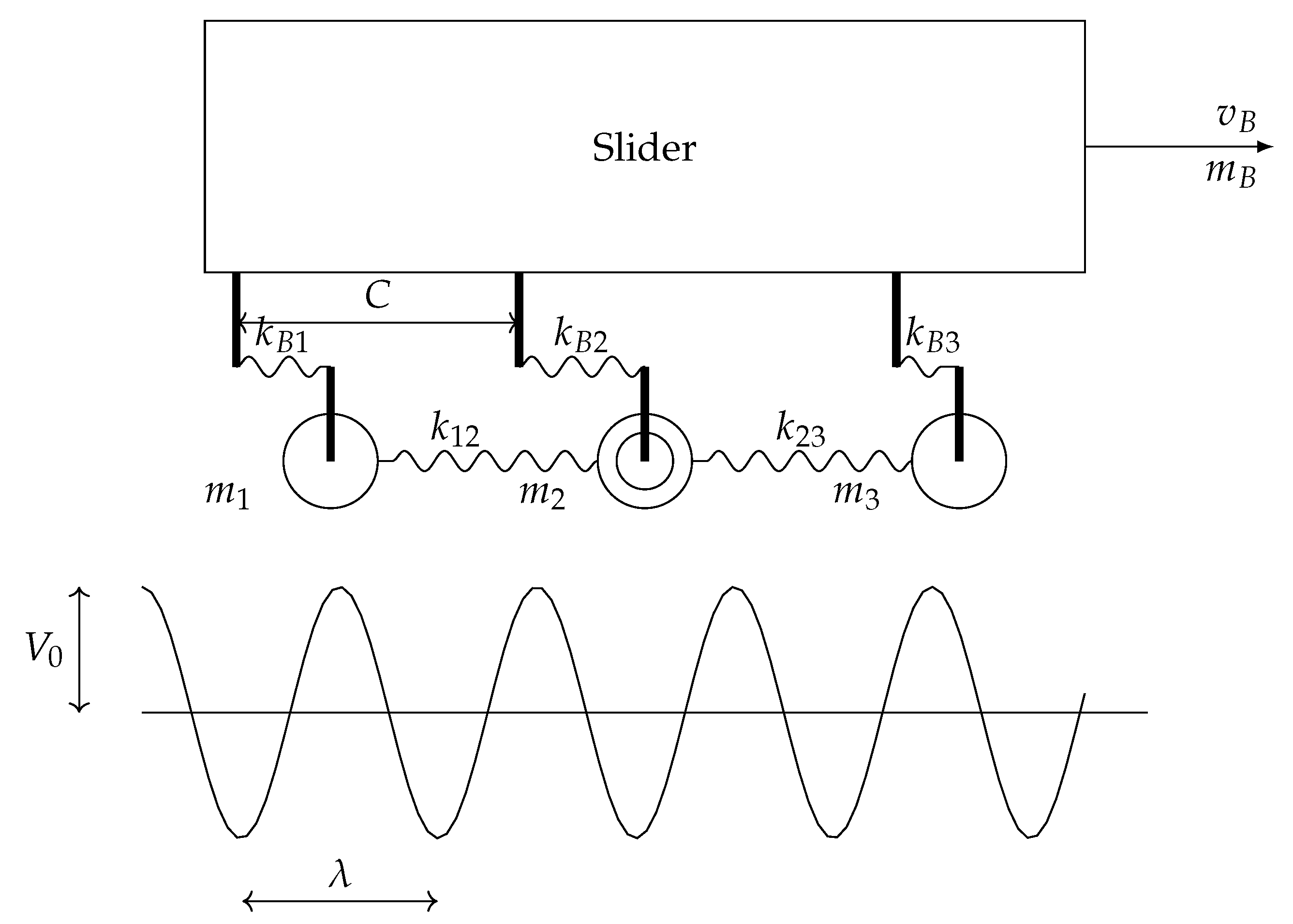
2. Surface Doping Patterns and Physical Modelling
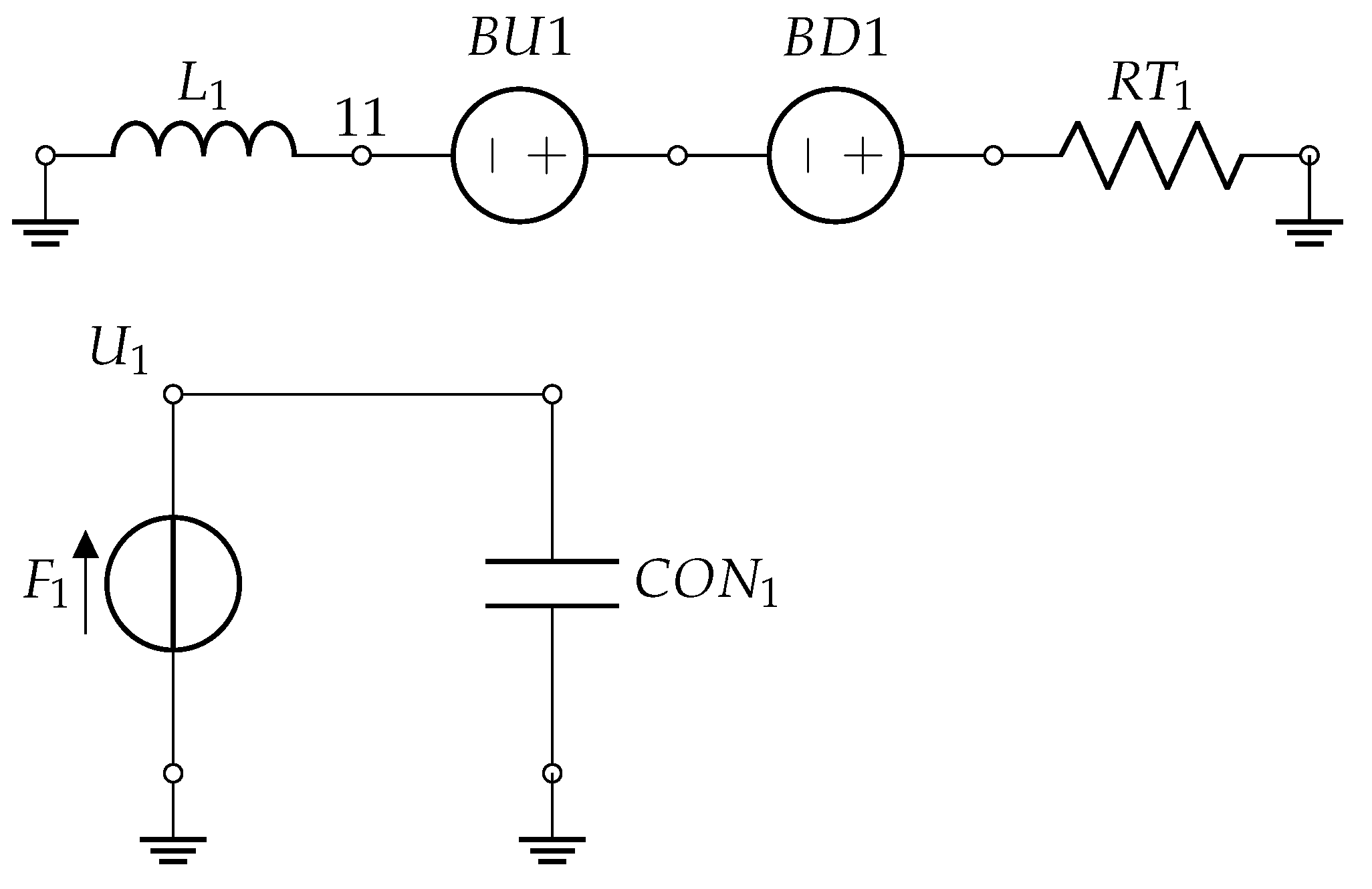
3. Network Simulation Method
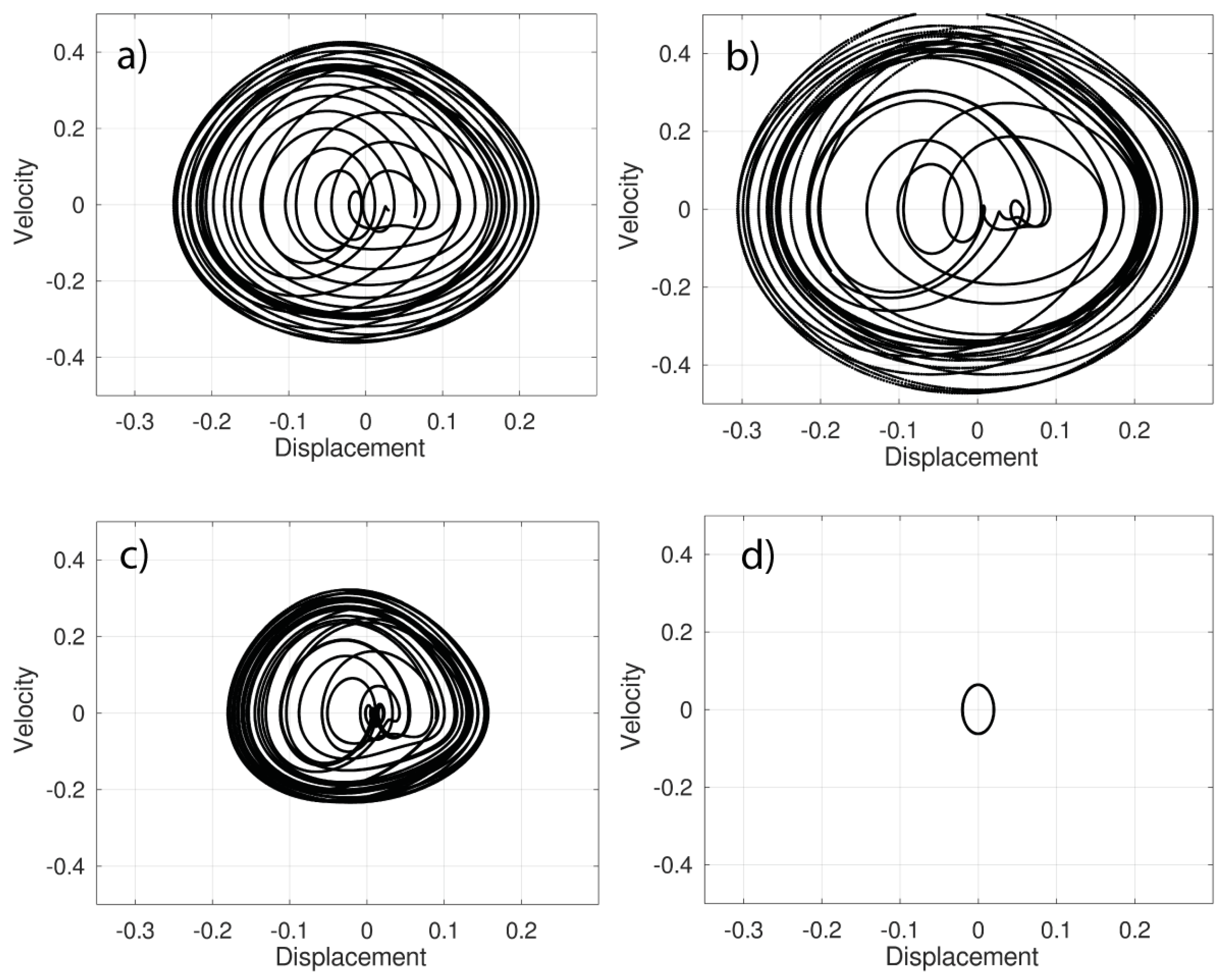
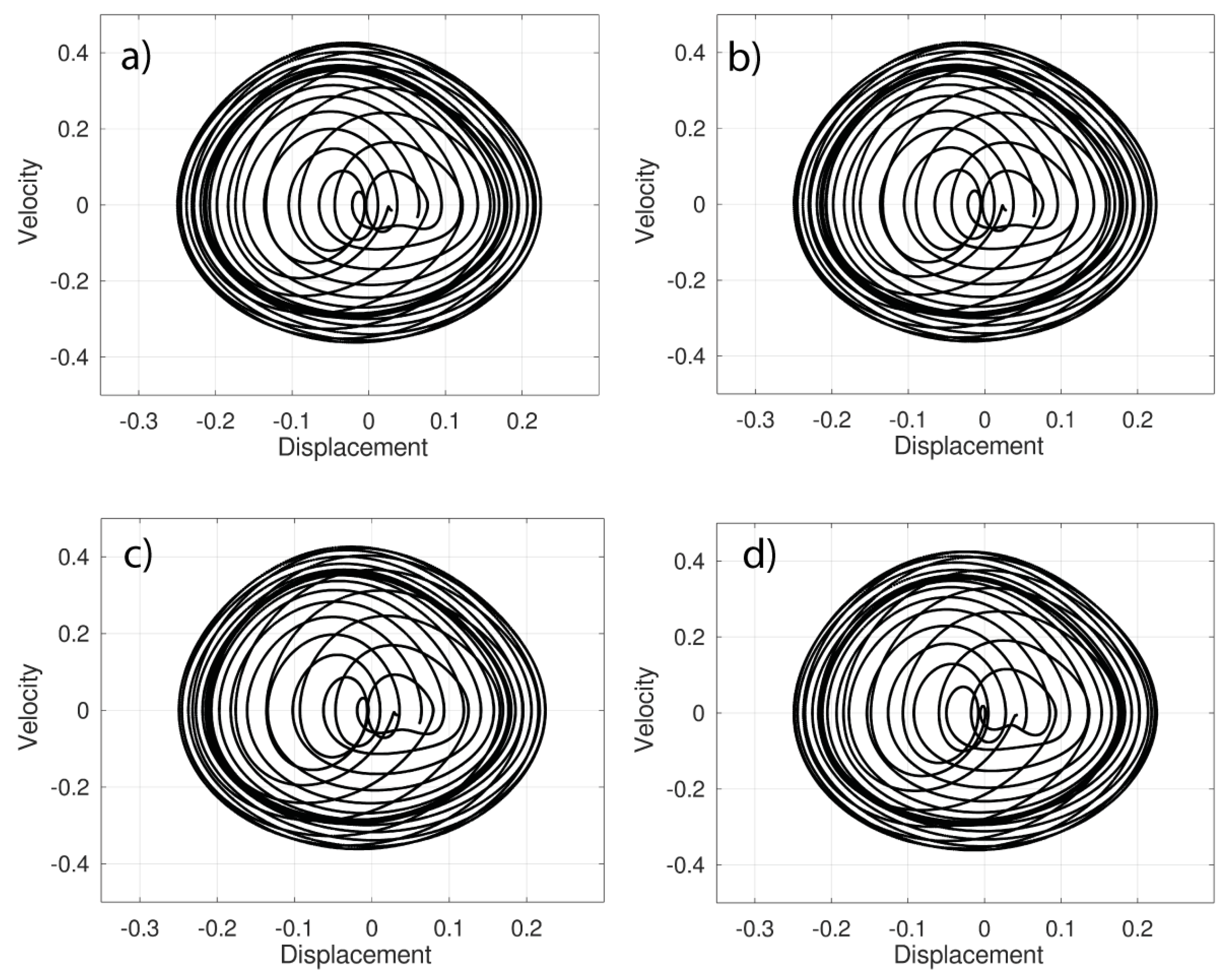
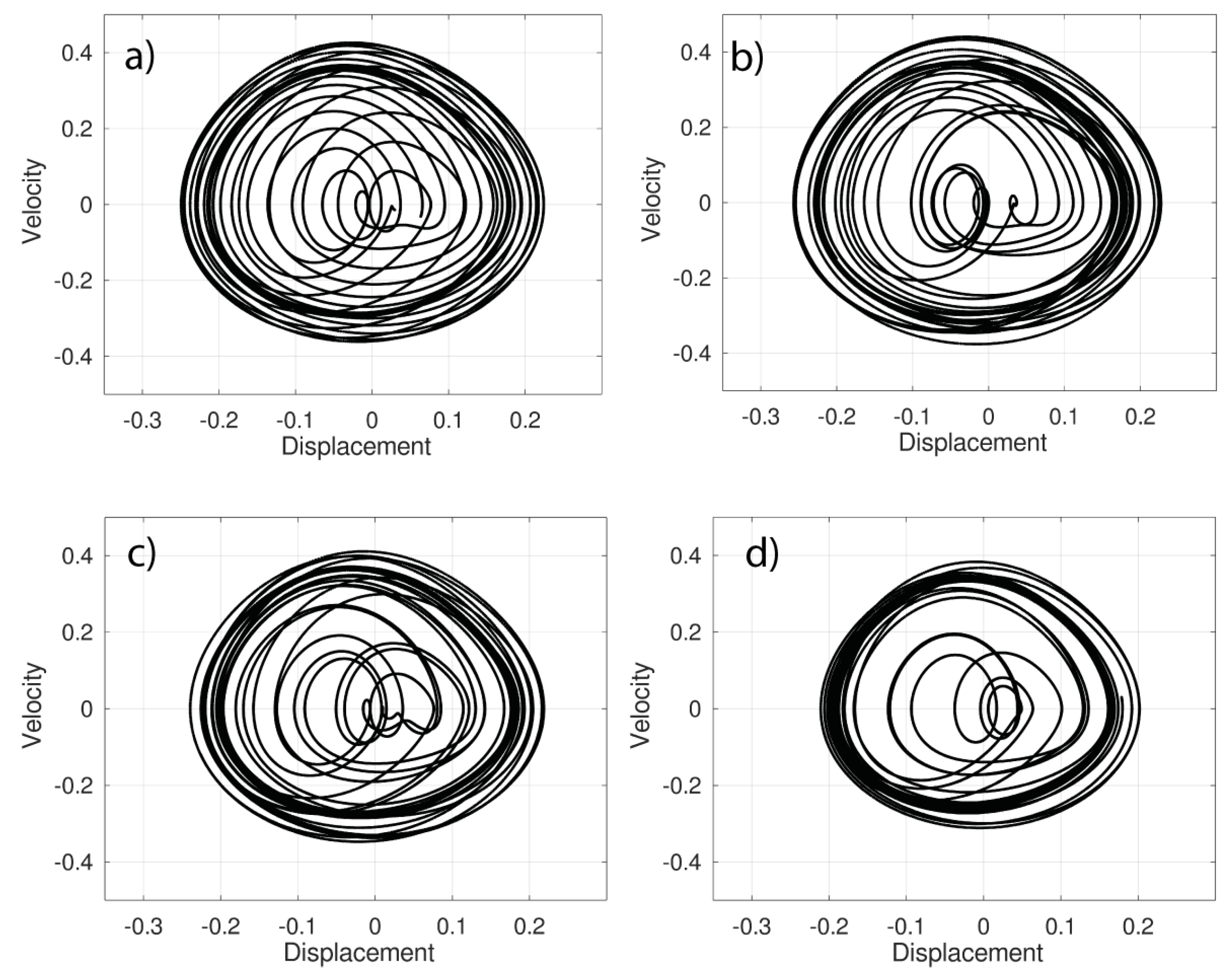
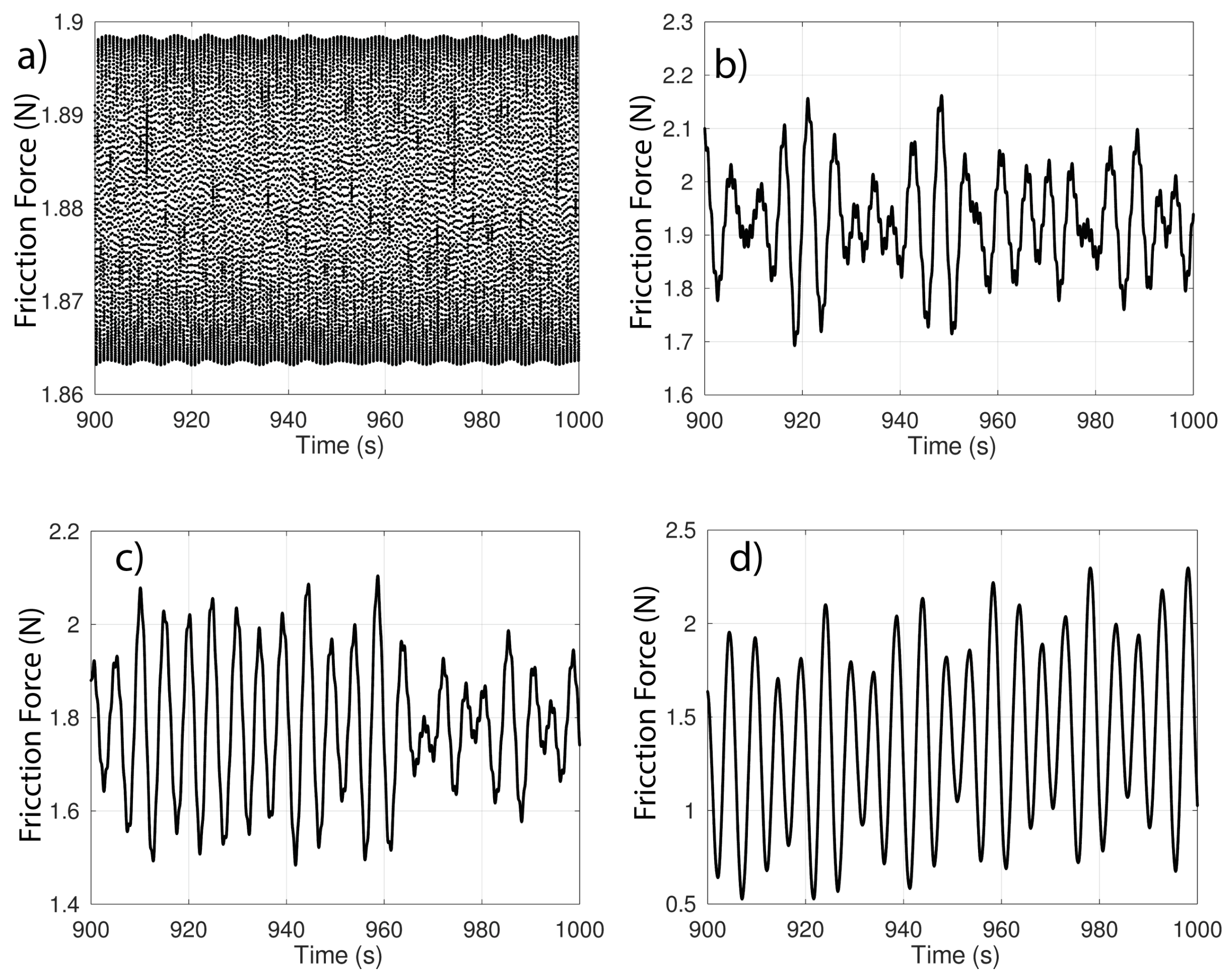
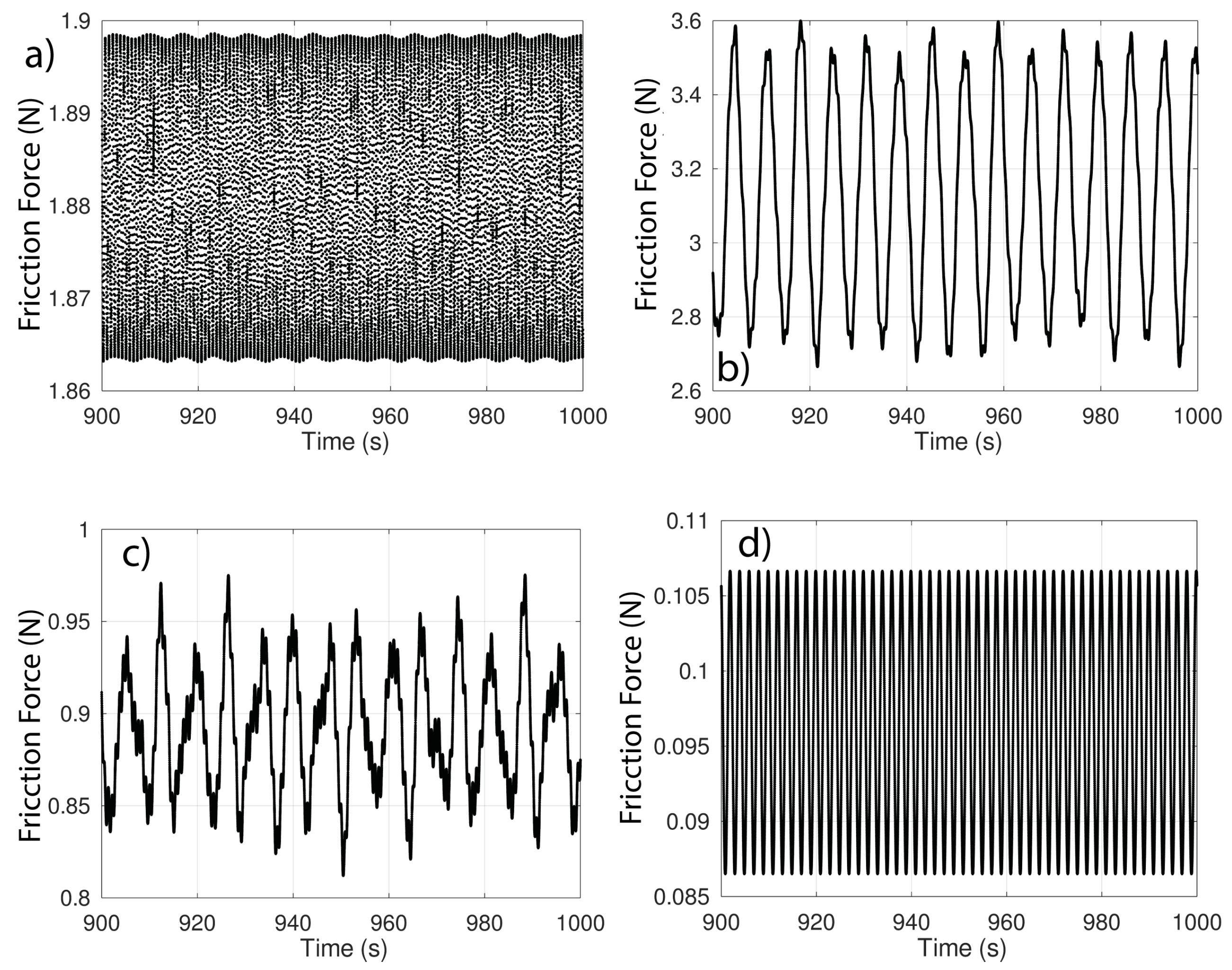
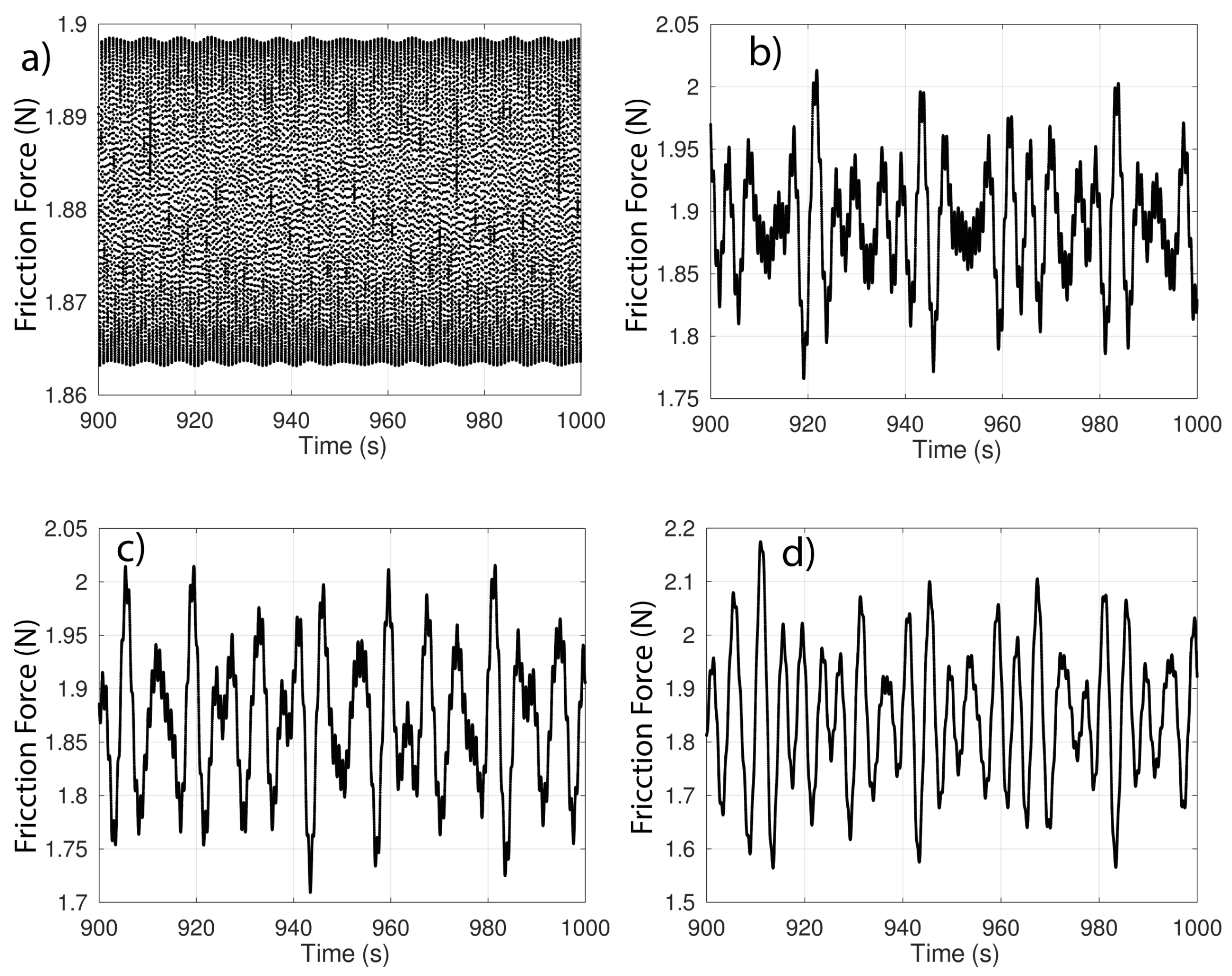
4. Simulations and Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FKT | Frenkel–Kontorova–Tomlinson model |
| PT | Prandtl–Tomlinson model |
| FK | Frenkel-Kontorova model |
| AFM | Atomic force microscope |
| SFM | Scanning force microscope |
| STM | Scanning tunneling microscope |
| PVD | Physical vapour deposition |
| VLSI | Very-large-scale integration |
| NSM | Network Simulation Method |
| FE | Forward-Euler |
| BE | Backward-Euler |
| LTE | Local truncation error |
| TR | Trapezoidal procedure |
References
- Jonsmann, J.; Sigmund, O.; Bouwstra, S. Compliant thermal microactuators. Sens. Actuators A Phys. 1999, 76, 463–469. [Google Scholar] [CrossRef]
- Mahalik, N.P. Micromanufacturing and Nanotechnology; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ouyang, X.; Tilley, D.; Keogh, P.; Yang, H.; Johnson, N.; Bowen, C.; Hopkins, P. Piezoelectric actuators for screw-in cartridge valves. In Proceedings of the 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; pp. 49–55. [Google Scholar]
- Engel, U.; Eckstein, R. Microforming—From basic research to its realization. J. Mater. Process. Technol. 2002, 125, 35–44. [Google Scholar] [CrossRef]
- Razali, A.R.; Qin, Y. A review on micro-manufacturing, micro-forming and their key issues. Procedia Eng. 2013, 53, 665–672. [Google Scholar] [CrossRef]
- Abtahi, M.; Vossoughi, G.; Meghdari, A. Dynamic Modeling of Scratch Drive Actuators. J. Microelectromech. Syst. 2015, 24, 1370–1383. [Google Scholar] [CrossRef]
- Fu, M.; Chan, W.L. A review on the state-of-the-art microforming technologies. Int. J. Adv. Manuf. Technol. 2013, 67, 2411–2437. [Google Scholar] [CrossRef]
- Singh, A.; Suh, K.Y. Biomimetic patterned surfaces for controllable friction in micro-and nanoscale devices. Micro Nano Syst. Lett. 2013, 1, 1–11. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Hu, X.; Zhang, Z.; Cheng, L.; Lin, Y.; Zhang, W. Modeling and control of piezoelectric inertia–friction actuators: Review and future research directions. Mech. Sci. 2015, 6, 95–107. [Google Scholar] [CrossRef]
- Schneider, J.; Djamiykov, V.; Greiner, C. Friction reduction through biologically inspired scale-like laser surface textures. Beilstein J. Nanotechnol. 2018, 9, 2561–2572. [Google Scholar] [CrossRef]
- Oscurato, S.L.; Salvatore, M.; Maddalena, P.; Ambrosio, A. From nanoscopic to macroscopic photo-driven motion in azobenzene-containing materials. Nanophotonics 2018, 7, 1387–1422. [Google Scholar] [CrossRef]
- Kumar, P.K.; Nithishkumar, D.; Gabriel, V.K.; Jerbin, J.; Joseph, J.J. Experimental study on frictional characteristics of alumina surface through biologically inspired catfish and shark fish scale like laser textures under dry and lubricating condition. In Proceedings of the AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2021; Volume 2417, p. 020006. [Google Scholar]
- Sharma, S.K.; Kodli, B.K.; Saxena, K.K. Micro forming and its applications: An overview. Key Eng. Mater. 2022, 924, 73–91. [Google Scholar] [CrossRef]
- Prandtl, L. Ein Gedankenmodell zur kinetischen Theorie der festen Körper. ZAMM-J. Appl. Math. Mech. Angew. Math. Und Mech. 1928, 8, 85–106. [Google Scholar] [CrossRef]
- Tomlinson, G. CVI. A molecular theory of friction. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 1929, 7, 905–939. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Marín, F.; Morales, J.; Cánovas, M.; Alhama, F. Modeling and simulation of different and representative engineering problems using Network Simulation Method. PLoS ONE 2018, 13, e0193828. [Google Scholar] [CrossRef]
- Sircar, A.; Patra, P.K. A simple generalization of Prandtl–Tomlinson model to study nanoscale rolling friction. J. Appl. Phys. 2020, 127, 135102. [Google Scholar] [CrossRef]
- Kontorova, T.; Frenkel, J. On the theory of plastic deformation and twinning. II. Zh. Eksp. Teor. Fiz. 1938, 8, 1340–1348. [Google Scholar]
- Quapp, W.; Bofill, J.M. An Analysis of Some Properties and the Use of the Twist Map for the Finite Frenkel–Kontorova Model. Electronics 2022, 11, 3295. [Google Scholar] [CrossRef]
- Alhama, F.; Marín, F.; Moreno, J. An efficient and reliable model to simulate microscopic mechanical friction in the Frenkel–Kontorova–Tomlinson model. Comput. Phys. Commun. 2011, 182, 2314–2325. [Google Scholar] [CrossRef]
- Weiss, M.; Elmer, F.J. Dry friction in the Frenkel-Kontorova-Tomlinson model: Static properties. Phys. Rev. B 1996, 53, 7539. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M.; Elmer, F.J. Dry friction in the Frenkel-Kontorova-Tomlinson model: Dynamical properties. Z. Phys. B Condens. Matter 1997, 104, 55–69. [Google Scholar] [CrossRef]
- Burridge, R.; Knopoff, L. Model and theoretical seismicity. Bull. Seismol. Soc. Am. 1967, 57, 341–371. [Google Scholar] [CrossRef]
- Carlson, J.M.; Langer, J. Properties of earthquakes generated by fault dynamics. Phys. Rev. Lett. 1989, 62, 2632. [Google Scholar] [CrossRef] [PubMed]
- Erickson, B.A.; Birnir, B.; Lavallée, D. Periodicity, chaos and localization in a Burridge–Knopoff model of an earthquake with rate-and-state friction. Geophys. J. Int. 2011, 187, 178–198. [Google Scholar] [CrossRef]
- Barbot, S. Slow-slip, slow earthquakes, period-two cycles, full and partial ruptures, and deterministic chaos in a single asperity fault. Tectonophysics 2019, 768, 228171. [Google Scholar] [CrossRef]
- Stefanou, I. Control instabilities and incite slow-slip in generalized Burridge-Knopoff models. arXiv 2020, arXiv:2008.03755. [Google Scholar]
- Awrejcewicz, J.; Olejnik, P. Stick-slip dynamics of a two-degree-of-freedom system. Int. J. Bifurc. Chaos 2003, 13, 843–861. [Google Scholar] [CrossRef]
- Galvanetto, U. Some discontinuous bifurcations in a two-block stick–slip system. J. Sound Vib. 2001, 248, 653–669. [Google Scholar] [CrossRef]
- Galvanetto, U.; Bishop, S. Characterisation of the dynamics of a four-dimensional stick-slip system by a scalar variable. Chaos Solitons Fractals 1995, 5, 2171–2179. [Google Scholar] [CrossRef]
- Van de Vrande, B.; Van Campen, D.; De Kraker, A. An approximate analysis of dry-friction-induced stick-slip vibrations by a smoothing procedure. Nonlinear Dyn. 1999, 19, 159–171. [Google Scholar] [CrossRef]
- Bishop, A. Solitons in condensed matter physics. Phys. Scr. 1979, 20, 409. [Google Scholar] [CrossRef]
- Schwarz, U.D.; Hölscher, H. Atomic-Scale Friction Studies Using Scanning Force Microscopy. In Modern Tribology Handbook, Two Volume Set; CRC Press: Boca Raton, FL, USA, 2000; pp. 671–696. [Google Scholar]
- Fan, P.; Goel, S.; Luo, X.; Upadhyaya, H.M. Atomic-scale friction studies on single-crystal gallium arsenide using atomic force microscope and molecular dynamics simulation. Nanomanuf. Metrol. 2021, 5, 39–49. [Google Scholar] [CrossRef]
- Hälg, D.; Gisler, T.; Tsaturyan, Y.; Catalini, L.; Grob, U.; Krass, M.D.; Héritier, M.; Mattiat, H.; Thamm, A.K.; Schirhagl, R.; et al. Membrane-based scanning force microscopy. Phys. Rev. Appl. 2021, 15, L021001. [Google Scholar] [CrossRef]
- Meyer, E.; Heinzelmann, H. Scanning force microscopy (SFM). In Scanning Tunneling Microscopy II; Springer: Berlin/Heidelberg, Germany, 1995; pp. 99–149. [Google Scholar]
- Ducourtieux, S.; Poyet, B. Development of a metrological atomic force microscope with minimized Abbe error and differential interferometer-based real-time position control. Meas. Sci. Technol. 2011, 22, 094010. [Google Scholar] [CrossRef]
- Greenwood, J. Fundamentals of friction. In Macroscopic and Microscopic Processes; Springer Science and Business Media, B.V.: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Myshkin, N.; Grigoriev, A.Y.; Chizhik, S.; Choi, K.; Petrokovets, M. Surface roughness and texture analysis in microscale. Wear 2003, 254, 1001–1009. [Google Scholar] [CrossRef]
- Manabe, K.-i. Metal Micro-Forming. Metals 2020, 10, 813. [Google Scholar] [CrossRef]
- Bučinskas, V.; Subačiūtė-Žemaitienė, J.; Dzedzickis, A.; Morkvėnaitė-Vilkončienė, I. Robotic micromanipulation: A) actuators and their application. Robot. Syst. Appl. 2021, 1, 2–23. [Google Scholar] [CrossRef]
- Gibbons, J.F. Ion implantation in semiconductors—Part I: Range distribution theory and experiments. Proc. IEEE 1968, 56, 295–319. [Google Scholar] [CrossRef]
- Stroscio, J.A.; Celotta, R.J. Controlling the dynamics of a single atom in lateral atom manipulation. Science 2004, 306, 242–247. [Google Scholar] [CrossRef] [PubMed]
- Manova, D.; Gerlach, J.W.; Mändl, S. Thin film deposition using energetic ions. Materials 2010, 3, 4109–4141. [Google Scholar] [CrossRef] [PubMed]
- Mundra, S.; Pardeshi, S.; Bhavikatti, S.; Nagras, A. Development of an integrated physical vapour deposition and chemical vapour deposition system. Mater. Today Proc. 2021, 46, 1229–1234. [Google Scholar] [CrossRef]
- Kizu, R.; Misumi, I.; Hirai, A.; Kinoshita, K.; Gonda, S. Development of a metrological atomic force microscope with a tip-tilting mechanism for 3D nanometrology. Meas. Sci. Technol. 2018, 29, 075005. [Google Scholar] [CrossRef]
- Misumi, I.; Sugawara, K.; Kizu, R.; Hirai, A.; Gonda, S. Extension of the range of profile surface roughness measurements using metrological atomic force microscope. Precis. Eng. 2019, 56, 321–329. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Q.J.; Zhao, N.; Zhang, M. Discrete convolution and FFT modified with double influence-coefficient superpositions (DCSS–FFT) for contact of nominally flat heterogeneous materials involving elastoplasticity. Comput. Mech. 2021, 67, 989–1007. [Google Scholar] [CrossRef]
- Peusner, L. The Principles of Network Thermodynamics: Theory and Biophysical Applications. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1970. reprinted by Entropy, Lincoln, MA, USA, 1987. [Google Scholar]
- Nagel, L.W. SPICE2: A Computer Program to Simulate Semiconductor Circuits. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1975. [Google Scholar]
- Nagel, L.; Pederson, D. Simulation program with integrated circuit emphasis. In Proceedings of the Midwest Symposium on Circuit Theory, Waterloo, ON, Canada, 12 April 1973. [Google Scholar]
- Solano, J.; Balibrea, F.; Moreno, J.A. Applications of the Network Simulation Method to Differential Equations with Singularities and Chaotic Behaviour. Mathematics 2021, 9, 1442. [Google Scholar] [CrossRef]
- Solano, J.; Balibrea, F.; Moreno, J.A.; Marín, F. Analysis of Chaotic Response of Frenkel-Kontorova-Tomlinson Model. Symmetry 2020, 12, 1413. [Google Scholar]
- Andreev, V.; Ostrovskii, V.; Karimov, T.; Tutueva, A.; Doynikova, E.; Butusov, D. Synthesis and Analysis of the Fixed-Point Hodgkin–Huxley Neuron Model. Electronics 2020, 9, 434. [Google Scholar] [CrossRef]
- Kaplun, D.I.; Tutueva, A.V.; Butusov, D.N.; Karimov, A.I.; Toming, J. Memristive Circuit Simulation Using the Semi-Implicit Multistep Method. In Proceedings of the 2019 42nd International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 1–3 July 2019; pp. 98–101. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Time-varying linearization and the Perron effects. Int. J. Bifurc. Chaos 2007, 17, 1079–1107. [Google Scholar] [CrossRef]
- Tutueva, A.; Butusov, D.; Okhota, A.; Pesterev, D.; Rodionova, E. The dynamical analysis of the modified rossler system. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 630, p. 012006. [Google Scholar]
- Vladimirescu, A. The SPICE Book; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Skowronn, D.; Li, D.; Tymerski, R. Simulation of networks with ideal switches. Int. J. Electron. 1994, 77, 715–730. [Google Scholar] [CrossRef]
- Constantinescu, F.; Gheorghe, A.G.; Nițescu, M. The energy balance error for circuit transient analysis. Rev. Roum. Sci. Techn.–Électrotechn. Énerg. 2010, 55, 243–250. [Google Scholar]




| i | |
|---|---|
| 1 | 116 |
| 3 | 58 |
| 7 | 29 |
| 28 | 8 |
| 57 | 4 |
| 115 | 2 |
| 231 | 1 |
| Type of Doping | a | b | j | |
|---|---|---|---|---|
| 1 | 114 | 5 | 1 | 1.3 |
| 114 | 5 | 1 | 1.5 | |
| 114 | 5 | 1 | 1.7 | |
| 2 | 1 | 1 | 116 | 1.3 |
| 1 | 1 | 116 | 1.5 | |
| 1 | 1 | 116 | 1.7 | |
| 3 | 116 | 1 | 1 | 1.3 |
| 116 | 1 | 1 | 1.5 | |
| 116 | 1 | 1 | 1.7 | |
| 4 | 25 | 1 | 8 | 1.3 |
| 25 | 1 | 8 | 1.5 | |
| 25 | 1 | 8 | 1.7 |
| Average Friction Force | ||
|---|---|---|
| Type of Doping | Friction Force | |
| Without doping | - | 1.880 |
| 1 | 1.3 | 1.880 |
| 1.5 | 1.880 | |
| 1.7 | 1.880 | |
| 2 | 1.3 | 3.1295 |
| 1.5 | 0.8913 | |
| 1.7 | ||
| 3 | 1.3 | 1.8885 |
| 1.5 | 1.8696 | |
| 1.7 | 1.8475 | |
| 4 | 1.3 | 1.9542 |
| 1.5 | 1.7933 | |
| 1.7 | 1.7709 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solano, J.; Balibrea, F.; Moreno, J.A.; Marín, F. Dry Friction Analysis in Doped Surface by Network Simulation Method. Mathematics 2023, 11, 1341. https://doi.org/10.3390/math11061341
Solano J, Balibrea F, Moreno JA, Marín F. Dry Friction Analysis in Doped Surface by Network Simulation Method. Mathematics. 2023; 11(6):1341. https://doi.org/10.3390/math11061341
Chicago/Turabian StyleSolano, Joaquín, Francisco Balibrea, José Andrés Moreno, and Fulgencio Marín. 2023. "Dry Friction Analysis in Doped Surface by Network Simulation Method" Mathematics 11, no. 6: 1341. https://doi.org/10.3390/math11061341
APA StyleSolano, J., Balibrea, F., Moreno, J. A., & Marín, F. (2023). Dry Friction Analysis in Doped Surface by Network Simulation Method. Mathematics, 11(6), 1341. https://doi.org/10.3390/math11061341






