Inelastic Collision Influencing the Rotational Dynamics of a Non-Rigid Asteroid (of Rubble Pile Type)
Abstract
:1. Introduction, the Dynamical Model
2. Semi-Analytical Exploration of the System of Equations (1)–(2)
3. Discussion & Conclusions
4. Highlighting Remarks
- The influence of inelastic collision on rotation of a rubble pile asteroid is studied.
- The approach stems from non-Newtonian media, applied for the first time for asteroid rotation.
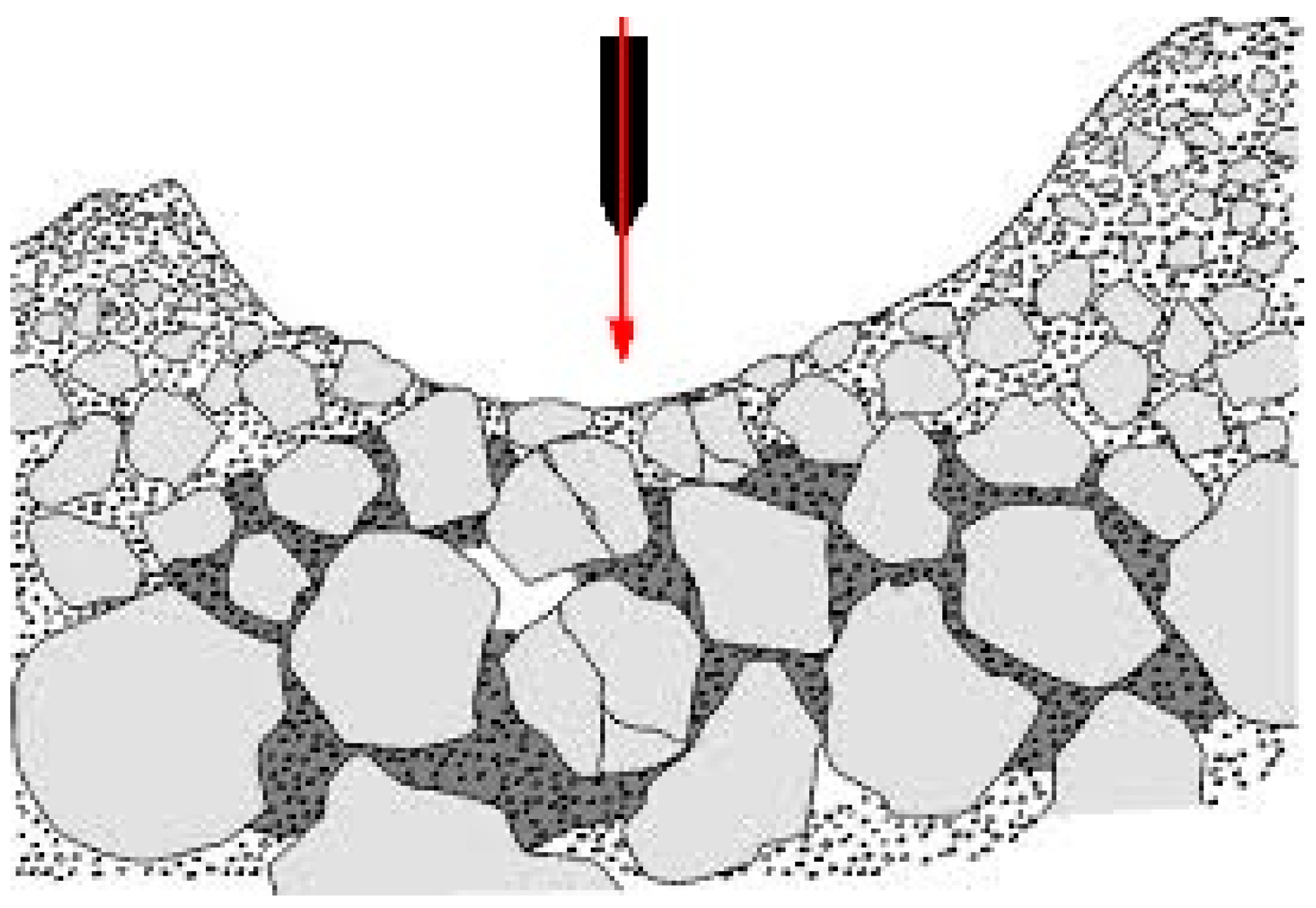
- The added mass model is presented to describe the impact of the projectile on the asteroid.
- The impact activates solidifying a plug in a rubble pile surface via dynamic hit front.
- The projectile pushes ‘rubble pile’ parts together to form a solidified plug in the crater.
- Then, the ‘solidified plug’ is pushed outside of the asteroid by centrifugal forces.
- A new solving procedure for estimation of the mass of the ‘solidified plug’ is presented.
- Changes in rotational dynamics stem from decreasing the asteroid’s mass.
- The asteroid rotates mainly along the maximal inertia axis with fixed angular momentum.
5. Clarifying Remarks Regarding the Steps of Derivation of Equation (3)
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NASA Confirms DART Mission Impact Changed Asteroid’s Motion in Space. Available online: https://www.nasa.gov/press-release/nasa-confirms-dart-mission-impact-changed-asteroid-s-motion-in-space (accessed on 8 February 2023).
- Ershkov, S.V.; Leshchenko, D. On the dynamics OF NON-RIGID asteroid rotation. Acta Astronaut. 2019, 161, 40–43. [Google Scholar] [CrossRef] [Green Version]
- Walsh, K.J. Rubble pile asteroids. Annu. Rev. Astron. Astrophys. 2018, 56, 593–624. Available online: https://arxiv.org/abs/1810.01815 (accessed on 8 February 2023). [CrossRef] [Green Version]
- Ershkov, S.V.; Shamin, R.V. The dynamics of asteroid rotation, governed by YORP effect: The kinematic ansatz. Acta Astronaut. 2018, 149, 47–54. [Google Scholar] [CrossRef] [Green Version]
- García-Gutiérrez, A.; Cubas, J.; Chen, H.; Sanz-Andrés, Á. Complex variable methods for linearized Euler rigid body rotation equations. Acta Astronaut. 2020, 170, 454–465. [Google Scholar] [CrossRef]
- Pravec, P.; Harris, A.W.; Michalowski, T. Asteroid Rotations. In Asteroids III; Bottke, W.F., Jr., Cellino, A., Paolicchi, P., Binzel, R.P., Eds.; University of Arizona Press: Tucson, AZ, USA, 2002; pp. 113–122. [Google Scholar]
- De Goede, T.C.; de Bruin, K.G.; Bonn, D. High-velocity impact of solid objects on non-Newtonian fluids. Sci. Rep. 2019, 9, 1250. [Google Scholar] [CrossRef]
- Waitukaitis, S.R.; Jaeger, H.M. Impact-activated solidification of dense suspensions via dynamic jamming fronts. Nature 2012, 487, 205–209. [Google Scholar] [CrossRef]
- Efroimsky, M.; Frouard, J. Precession Relaxation of Viscoelastic Oblate Rotators. 2016. Available online: https://arxiv.org/abs/1606.04559 (accessed on 8 February 2023).
- Efroimsky, M. Tidal evolution of asteroidal binaries. Ruled by viscosity. Ignorant of rigidity. Astron. J. 2015, 150, 98. [Google Scholar] [CrossRef]
- Meyer, A.J.; Scheeres, D.J.; Agrusa, H.F.; Noiset, G.; McMahon, J.; Karatekin, Ö.; Hirabayashi, M.; Nakano, R. Energy dissipation in synchronous binary asteroids. Icarus 2023, 391, 115323. [Google Scholar] [CrossRef]
- Asteroid Interiors. Available online: https://www.lpi.usra.edu/books/AsteroidsIII/pdf/3038.pdf (accessed on 8 February 2023).
- Ershkov, S.; Leshchenko, D.; Abouelmagd, E. About influence of differential rotation in convection zone of gaseous or fluid giant planet (Uranus) onto the parameters of orbits of satellites. Eur. Phys. J. Plus 2021, 136, 387. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Rachinskaya, A. Capture in regime of a trapped motion with further inelastic collision for finite-sized asteroid in ER3BP. Symmetry 2022, 14, 1548. [Google Scholar] [CrossRef]
- Melnikov, A.V. Rotational dynamics of asteroids approaching planets. Sol. Syst. Res. 2022, 56, 241–251. [Google Scholar] [CrossRef]
- Klavetter, J.J. Rotation of Hyperion. 2. Dynamics. Astron. J. 1989, 98, 1855. [Google Scholar] [CrossRef]
- Wisdom, J.; Peale, S.J.; Mignard, F. The chaotic rotation of Hyperion. Icarus 1984, 58, 137–152. [Google Scholar] [CrossRef] [Green Version]
- Scheeres, D.J. Orbital Motion in Strongly Perturbed Environments. Applications to Asteroid, Comet and Planetary Satellite Orbiters; Springer Praxis Publishing: Chichester, UK, 2012. [Google Scholar]
- Walsh, K.J.; Richardson, D.C.; Michel, P. Spin-up of rubble-pile asteroids: Disruption, satellite formation, and equilibrium shapes. Icarus 2012, 220, 514–529. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, B.; Yu, Y. The interactive dynamics of a binary asteroid and ejecta after medium kinetic impact. Astrophys. Space Sci. 2022, 367, 84. [Google Scholar] [CrossRef]
- Ieva, S.; Mazzotta Epifani, E.; Perna, D.; Dall’Ora, M.; Petropoulou, V.; Deshapriya, J.D.P.; Hasselmann, P.H.; Rossi, A.; Poggiali, G.; Brucato, J.R. Spectral Rotational Characterization of the Didymos System prior to the DART Impact. Planet. Sci. J. 2022, 3, 183. [Google Scholar] [CrossRef]
- Moreno, F.; Campo Bagatin, A.; Tancredi, G.; Liu, P.Y.; Domínguez, B. Ground-based observability of Dimorphos DART impact ejecta: Photometric predictions. Mon. Not. Royal Astron. Soc. 2022, 515, 2178–2187. [Google Scholar] [CrossRef]
- Yu, Y.; Michel, P.; Schwartz, S.R.; Naidu, S.P.; Benner, L.A.M. Ejecta Cloud from the AIDA Space Project Kinetic Impact on the Secondary of a Binary Asteroid: I. Mechanical Environment and Dynamical Model. Icarus 2017, 282, 313–325. [Google Scholar] [CrossRef] [Green Version]
- Rossi, A.; Marzari, F.; Brucato, J.R.; Della Corte, V.; Dotto, E.; Ieva, S.; Lambrov Ivanovski, S.; Lucchetti, A.; Mazzotta Epifani, E.; Pajola, M.; et al. Dynamical Evolution of Ejecta from the DART Impact on Dimorphos. Planet. Sci. J. 2022, 3, 118. [Google Scholar] [CrossRef]
- Fahnestock, E.G.; Cheng, A.F.; Ivanovski, S.; Michel, P.; Raducan, S.D.; Rossi, A.; Abell, P.A.; Chesley, S.; Dotto, E.; Ferrari, F.; et al. Pre-encounter Predictions of DART Impact Ejecta Behavior and Observability. Planet. Sci. J. 2022, 3, 206. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, B.; Yu, Y.; Lv, J.; Baoyin, H. Stability Analysis on the Moon’s Rotation in a Perturbed Binary Asteroid. Mathematics 2022, 10, 3757. [Google Scholar] [CrossRef]
- Agrusa, H.F.; Gkolias, I.; Tsiganis, K.; Richardson, D.C.; Meyer, A.J.; Scheeres, D.J.; Ćuk, M.; Jacobson, S.A.; Michel, P.; Karatekin, Ö.; et al. The excited spin state of Dimorphos resulting from the DART impact. Icarus 2021, 370, 114624. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Leshchenko, D. Solving procedure for 3D motions near libration points in CR3BP. Astrophys. Space Sci. 2019, 364, 207. [Google Scholar] [CrossRef] [Green Version]
- Ershkov, S.V.; Leshchenko, D. Revisiting Apophis 2029 approach to Earth (staying on shoulders of NASA’s experts) or Can we be sure in almost ricocheting fly-by of Apophis on 13 of April 2029 near the Earth? J. Space Saf. Eng. 2022, 9, 1363–1374. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Shamin, R.V. On a new type of solving procedure for Laplace tidal equation. Phys. Fluids 2018, 30, 127107. [Google Scholar] [CrossRef] [Green Version]
- Ershkov, S.V. A procedure for the construction of non-stationary Riccati-type flows for incompressible 3D Navier-Stokes equations. Rendiconti del Circolo Matematico di Palermo 2018, 65, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Ershkov, S.; Abouelmagd, E.I.; Rachinskaya, A. Perturbation of relativistic effect in the dynamics of test particle. J. Math. Anal. Appl. 2023, 524, 127067. [Google Scholar] [CrossRef]
- Ruiz-Suárez, J.C. Penetration of projectiles into granular targets. Rep. Prog. Phys. 2013, 76, 066601. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhang, X.; Chen, H.; Wang, J.; Wei, H.; Xiong, W. Experimental and theoretical study on steel long-rod projectile penetration into concrete targets with elevated impact velocities. Int. J. Impact Eng. 2020, 138, 103482. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Q.; Xue, Y.; Guo, X.; Shang, C.; Liu, W.; Ren, S.; Long, R. Hypervelocity penetration of concrete targets with long-rod steel projectiles: Experimental and theoretical analysis. Int. J. Impact Eng. 2021, 148, 103742. [Google Scholar] [CrossRef]
- Anderson, C.E., Jr. Analytical models for penetration mechanics: A Review. Int. J. Impact Eng. 2017, 108, 3–26. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ershkov, S.; Leshchenko, D. Inelastic Collision Influencing the Rotational Dynamics of a Non-Rigid Asteroid (of Rubble Pile Type). Mathematics 2023, 11, 1491. https://doi.org/10.3390/math11061491
Ershkov S, Leshchenko D. Inelastic Collision Influencing the Rotational Dynamics of a Non-Rigid Asteroid (of Rubble Pile Type). Mathematics. 2023; 11(6):1491. https://doi.org/10.3390/math11061491
Chicago/Turabian StyleErshkov, Sergey, and Dmytro Leshchenko. 2023. "Inelastic Collision Influencing the Rotational Dynamics of a Non-Rigid Asteroid (of Rubble Pile Type)" Mathematics 11, no. 6: 1491. https://doi.org/10.3390/math11061491
APA StyleErshkov, S., & Leshchenko, D. (2023). Inelastic Collision Influencing the Rotational Dynamics of a Non-Rigid Asteroid (of Rubble Pile Type). Mathematics, 11(6), 1491. https://doi.org/10.3390/math11061491






