Abstract
This research article introduces an efficient method for integrating Lane–Emden–Fowler equations of second-order singular initial value problems (SIVPs) using a pair of hybrid block methods with a variable step-size mode. The method pairs an optimized Nyström technique with a set of formulas applied at the initial step to circumvent the singularity at the beginning of the interval. The variable step-size formulation is implemented using an embedded-type approach, resulting in an efficient technique that outperforms its counterpart methods that used fixed step-size implementation. The numerical simulations confirm the better performance of the variable step-size implementation.
Keywords:
hybrid block technique; Lane–Emden–Fowler problems; optimization strategy; starting procedure; adaptive formulation MSC:
65L05; 65L06; 65L20
1. Introduction
The goal of this research paper was to find a reliable numerical approach for solving second-order SIVPs Lane–Emden–Fowler equations of the form:
where , are real numbers; and represent the initial and final points of the integration interval, respectively; and is a continuous real function. We note that the necessary conditions for the existence and uniqueness of the solution to problem (1) were established in [1,2].
Equations of the form (1) are commonly encountered in many fields, such as astrophysics, mathematical modeling, celestial mechanics, physical and social sciences, and engineering. These types of equations have also been used to model various systems, including chemical reactors, thermal behavior of gas spheres, reaction–diffusion processes in porous catalysts, stellar structure, isothermal gas spheres, and thermionic current theory (as cited in sources such as [3,4,5,6,7], etc.).
The problem under consideration becomes one of the most complex problems to integrate analytically, due to the nonlinear properties of the second order SIVP and the singularity at . Therefore, numerical methods are essential for providing an approximate and reasonable solution.
Many scholars have extensively investigated the model in (1) and similar problems and have developed various methods for solving them. These methods include the implicit Euler method, various types of spline methods, the homotopy-perturbation technique, the variational iteration techniques, the Adomian decomposition method, a Padè approximation method, various types of collocation methods, finite difference methods, the heuristics approach, the differential transform method, the pseudospectral method, Taylor wavelet techniques, hybrid block methods, Nyström methods, the Haar wavelet resolution technique, iterative methods, spectral methods, Jacobi–Gauss collocation techniques, or asymptotic numerical strategies (see [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]).
In this study, we aimed to obtain a variable step-size formulation of a pair of optimized Nyström methods (PONMs) developed in [14] to further improve their performance. The main formulas of the existing PONM are given as follows:
while the additional formulas to avoid the singularity of the existing PONM are given by
with
Note that the formulas in do not use the value , thus obtaining an approximate value for . After the formulas in and the others needed for the block formulation are applied in the first subinterval, the formulas in and the corresponding ones to form the main block method are applied in the subsequent subintervals. The reader is referred to Equations and in reference [14] to see the remaining formulas, including the complete description and theoretical analysis of the PONM method.
We remark that the main novelty of this study is a reasonable error estimation and the variable step-size implementation using embedded type approaches, which allowed us to very efficiently solve problems of the form in (1) when large integration intervals are considered.
2. Error Estimation and Mesh Selection of the PONMs
Using a fixed step-size scheme to solve a SIVP may be unreasonable because the solution rapidly changes within the integration interval. To improve efficiency, the PONM should be implemented with variable step sizes. This can be achieved by using a lower-order technique (LOT) to compute the local error at the end-point on each subinterval . In this article, an embedding approach is utilized to formulate the suggested technique in variable step-size mode; this means that in addition to the approximation provided by , an additional LOT approximation given by is still needed. The difference between and enables us to estimate the local error. A fourth-order multistep formula, given by the following Equation (4),
was used to estimate the local error at the end point, with a local truncation error of .
By following a similar strategy as the one reported in [16], the steps listed below are taken in order to increase the efficiency of the PONMs:
- Equations (2) and (3) and those in Equations (10) and (14) from [14] are used simultaneously at , using the known solution at .
- We use the multistep formula in (4) to find a second approximation to the solution of the problem under consideration at the grid point .
- We estimate the local error using the following formulawhere and are the values obtained by the fourth-order multistep formula in (4) and the PONM in (2) and (3) together with Equations and from [14], respectively.Given a user-defined tolerance, ABTOL, we proceed as follows:
- If ESTM ≤ ABTOL, the results are accepted, and the step size is increased to .
- If ESTM > ABTOL, the results are rejected, and the calculations are repeated with a new step size given bywhere is an adjustment factor to prevent failed steps, and is the order of the LOT. For more details about the choice of the variable step size strategy in (5), see [21,22].
3. Computational Details
The PONM is executed utilizing the error estimation and the mesh selection strategy presented in Section 2. The proposed PONM is written as , and the unknowns are expressed as
We use the modified Newton’s method (MNM) to solve the nonlinear systems, with a stopping criterion of 100 maximum iterations and an error from 2 subsequent estimates provided by . We write MNM as
where is the updated estimate of the solution at iteration , is the current estimate of the solution at iteration i, is the frozen Jacobian matrix of the function at the current estimate , and is the vector of residuals at the current estimate . The following initializing values were used with MNM for each iteration:
4. Numerical Experiments
In this part, we give the numerical results for the proposed PONM on different SIVPs of the form (1). We point out that the estimation and mesh selection technique described in Section 2, as well as the PONM method given in (2) and (3) and the remaining formulas presented in Equations (10) and (14) in [14], play a crucial role in determining the efficiency of the proposed method. The PONM was implemented in Mathematica 11.0 by using the constructed codes. We utilized a PC with an i7 processor, 16 GB of RAM, and the 64-bit Windows 10 operating system. To measure the accuracy of our results, we use the Maximum Absolute Error (MAE) formula, which is defined as:
In the above equation, represents the exact solution, and represents the computed result at each point on the discrete grid.
In the tables and figures, the following acronyms are used:
- PONM: The pair optimized hybrid Nyström method whose main formulas are given in (2) and (3).
- HPM: The homotopy perturbation method in [23].
- WNT: The wavelet based neural technique in [25].
- NM: The Nyström method in [26].
- BVM: The boundary value method in [27]
- NS: Number of steps.
- TFE: Total number of function evaluations.
- ABTOL: Absolute tolerance.
- CPU: Computational cost in seconds.
4.1. Problem One
We consider the SIVP from [27],
with exact solution .
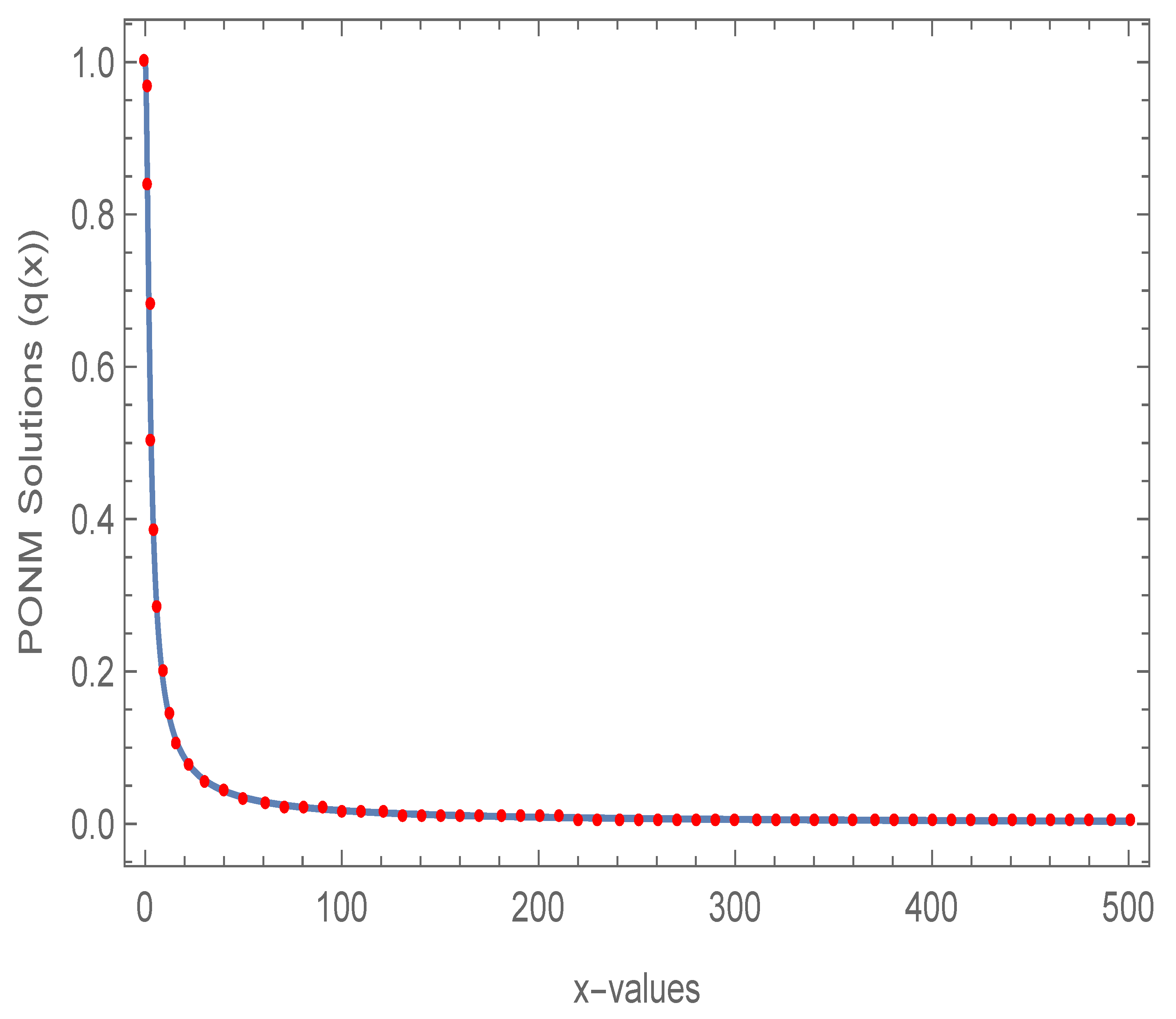
The results in Table 1 and Table 2 demonstrate the accuracy of the PONM in terms of MAE. Additionally, the comparison of the PONM and the exact solutions for (6) with ABTOL in Figure 1, shows that the PONM technique in variable step-size implementation strongly fits the analytical solution.

Table 1.
Comparison of the numerical results on Problem 6 with .

Table 2.
Numerical results for (6) with .
Figure 1.
Comparison of PONM and the exact solution for (6).
4.2. Problem Two
We consider
with exact solution .
From the data reported in Table 3 and Table 4, the proposed PONM outperforms the BVM and NM methods in terms of MAE, TFE, and CPU. Additionally, the comparison of PONM and the exact solution for (7) with ABTOL = in Figure 2, shows that the PONM method with a variable step size fits the exact solution.

Table 3.
Comparison of the numerical results for Problem 6 with .

Table 4.
Numerical results for (6) with .
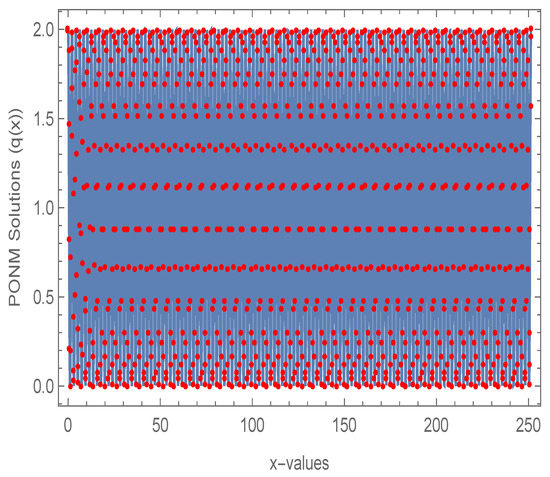
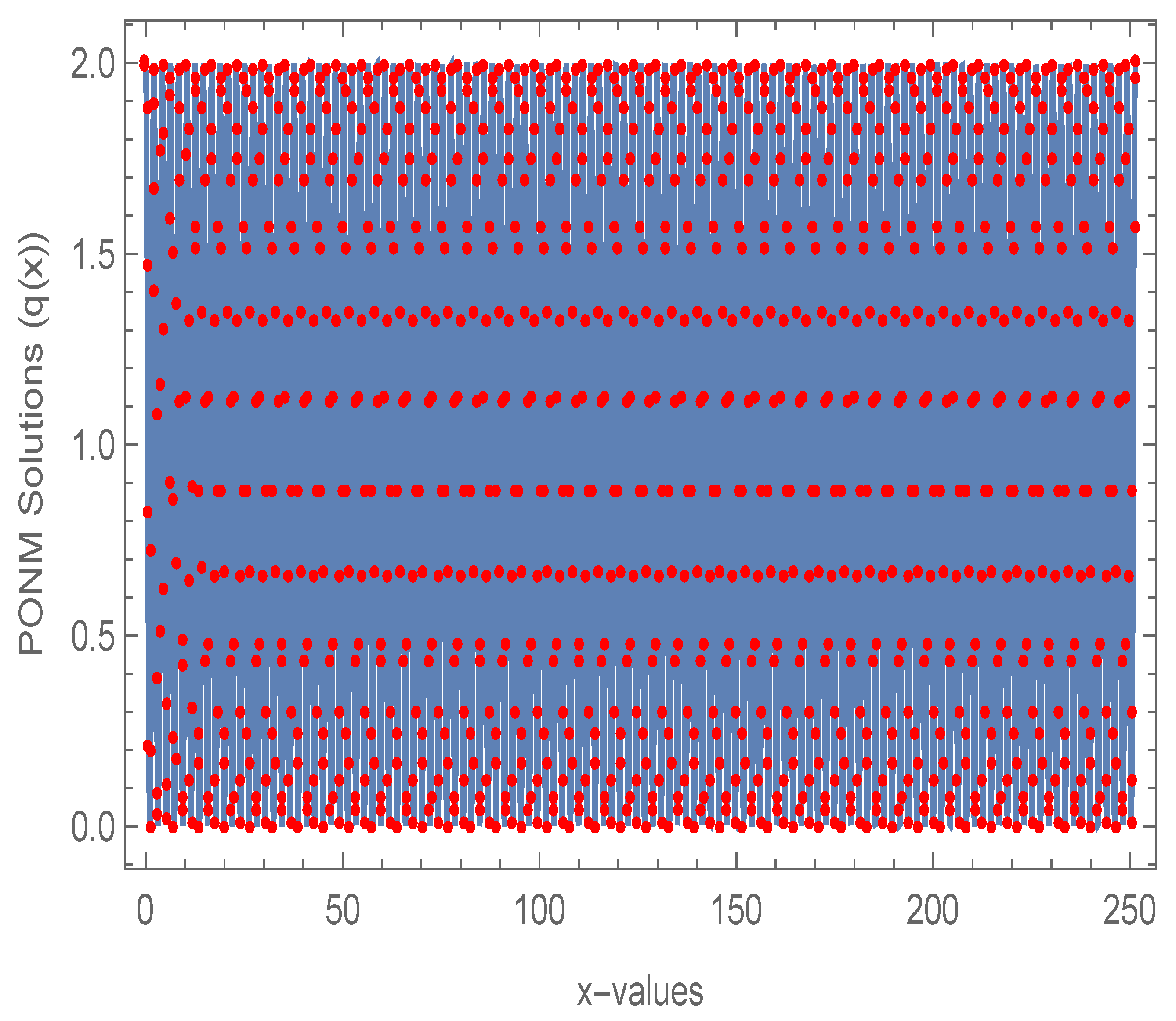
Figure 2.
Comparison of PONM and the exact solution for (7).
4.3. Problem Three
For the last problem in this research, we applied the proposed method to the following system of SIVP from [26],
with initial values
and the true solution from [26] is
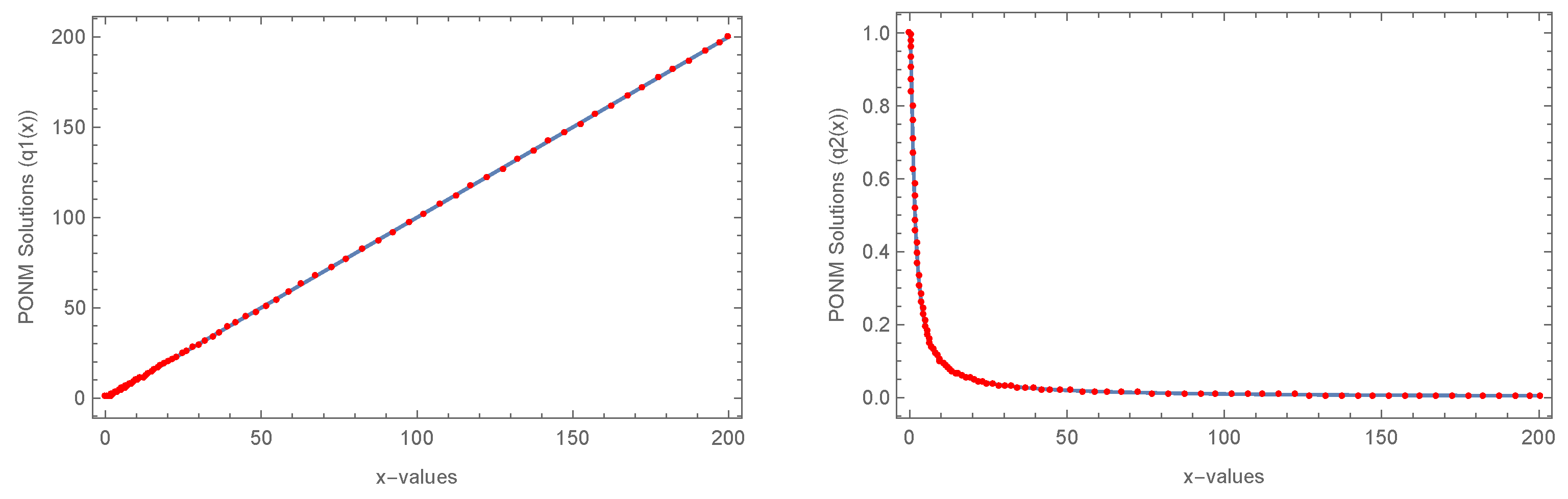
The suggested PONM surpasses the NM method in terms of MAE, TFE, and CPU, according to the data in Table 5. Furthermore, the comparison of PONM and the exact solution for (8) with ABTOL = , is shown in Figure 3; one can see that the PONM fits the exact solution.

Table 5.
Numerical results on (8) with .
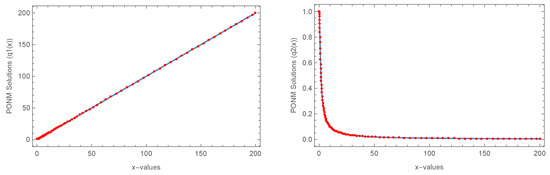
Figure 3.
Comparison of PONM and exact for (8).
5. Conclusions
In this paper, we introduced and applied a variable step-size version of a pair of optimized Nyström methods (PONM) to give numerical solutions to Lane–Emden–Fowler equations of second-order singular initial value problems. The error estimation and mesh selection of the PONM were discussed. Two scalar examples and a system of numerical experiments revealed that the variable step-size formulation using an embedded-type approach results in an efficient technique that outperforms its counterpart methods that use fixed step-size implementation. The type of strategy presented in this paper could be considered for solving time-dependent partial differential equations and fractional-order differential equations of the Lane–Emden–Fowler type in future research work.
Author Contributions
Conceptualization, M.A.R. and H.R.; Methodology, M.A.R.; Software, M.A.R.; Validation, H.R.; Formal analysis, M.A.R. and H.R.; Writing—original draft, M.A.R.; Writing—review & editing, M.A.R. and H.R.; Visualization, H.R.; Supervision, H.R.; Funding acquisition, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Agarwal, R.P.; O’Regan, D. Second order initial value problems of Lane-Emden type. Appl. Math. Lett. 2007, 20, 1198–1205. [Google Scholar] [CrossRef]
- Biles, D.C.; Robinson, M.P.; Spraker, J.S. A generalization of the Lane-Emden equation. J. Math. Anal. Appl. 2002, 273, 654–666. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Introduction to Study of Stellar Structure; Dover: New York, NY, USA, 1967. [Google Scholar]
- Rufai, M.A.; Ramos, H. Numerical integration of third-order singular boundary-value problems of Emden–Fowler type using hybrid block techniques. Commun. Nonlinear Sci. Numer. Simul. 2022, 105, 106069. [Google Scholar] [CrossRef]
- Rufai, M.A.; Ramos, H. Solving third-order Lane–Emden–Fowler equations using a variable step-size formulation of a pair of block methods. J. Comput. Appl. Math. 2023, 420, 114776. [Google Scholar] [CrossRef]
- Rufai, M.A.; Ramos, H. Numerical Solution for Singular Boundary Value Problems Using a Pair of Hybrid Nyström Techniques. Axioms 2021, 10, 202. [Google Scholar] [CrossRef]
- Shawagfeh, N.T. Nonperturbative approximate solution for Lane-Emden equation. J. Math. Phys. 1993, 34, 4364–4369. [Google Scholar] [CrossRef]
- Koch, O.; Kofler, P.; Weinmüller, E.B. The implicit Euler method for the numerical solution of singular initial value problems. Appl. Numer. Math. 2000, 34, 231–252. [Google Scholar] [CrossRef]
- Chowdhury, M.S.H.; Hashim, I. Solution of a class of singular second-order IVPs by homotopy-perturbation method. Phys. Lett. A 2007, 365, 439–447. [Google Scholar] [CrossRef]
- Mehrpouya, M.A. An efficient pseudospectral method for numerical solution of nonlinear singular initial and boundary value problems arising in astrophysics. Math. Methods Appl. Sci. 2016, 39, 3204–3214. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Alofi, A.S. A Jacobi-Gauss collocation method for solving nonlinear Lane-Emden type equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 62–70. [Google Scholar] [CrossRef]
- Swati; Singh, K.; Verma, A.K.; Singh, M. Higher order Emden–Fowler type equations via uniform Haar Wavelet resolution technique. J. Comput. Appl. Math. 2020, 376, 112836. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M. Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular Emden–Fowler equation. Eur. Phys. J. Plus 2020, 135, 410. [Google Scholar] [CrossRef]
- Rufai, M.A.; Ramos, H. Numerical solution of second-order singular problems arising in astrophysics by combining a pair of one-step hybrid block Nyström methods. Astrophys. Space Sci. 2020, 365, 96. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, J. The Adomian decomposition method with Green’s function for solving nonlinear singular boundary value problems. J. Appl. Math. Comput. 2014, 44, 397–416. [Google Scholar] [CrossRef]
- Rufai, M.A.; Ramos, H. A variable step-size fourth-derivative hybrid block strategy for integrating third-order IVPs, with applications. Int. J. Comput. Math. 2022, 99, 292–308. [Google Scholar] [CrossRef]
- Heydari, M.; Hosseini, S.M.; Loghmani, G.B. Numerical solution of singular IVPs of Lane-Emden type using integral operator and radial basis functions. Int. J. Ind. Math. 2012, 4, 135–146. [Google Scholar]
- Dong, Q.L. A new iterative method with alternated inertia for the split feasibility problem. J. Nonlinear Var. Anal. 2021, 5, 939–950. [Google Scholar]
- Zhang, J.; Shen, Y.; He, J. Some analytical methods for singular boundary value problem in a fractal space: A review. Appl. Comput. Math. 2019, 18, 225–235. [Google Scholar]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1998. [Google Scholar]
- Shampine, L.F.; Gordon, M.K. Computer Solutions of Ordinary Differential Equations: The Initial Value Problem; Freeman: San Francisco, CA, USA, 1975. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Yıldırım, A.; Özis, T. Solutions of singular IVPs of Lane-Emden type by homotopy perturbation method. Phys. Lett. A 2007, 369, 70–76. [Google Scholar] [CrossRef]
- Chawla, M.M.; Jain, M.K.; Subramanian, R. The application of explicit Nyström methods to singular second order differential equations. Comput. Math. Appl. 1990, 19, 47–51. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y. Orthonormal Bernoulli wavelets neural network method and its application in astrophysics. Comp. Appl. Math. 2021, 40, 78. [Google Scholar] [CrossRef]
- Ramos, H.; Rufai, M.A. An adaptive pair of one-step hybrid block Nyström methods for singular initial-value problems of Lane–Emden–Fowler type. Math. Comput. Simul. 2022, 193, 497–508. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C. The adapted block boundary value methods for singular initial value problems. Calcolo 2018, 55, 22. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).