Efficient Method for Derivatives of Nonlinear Stiffness Matrix
Abstract
:1. Introduction
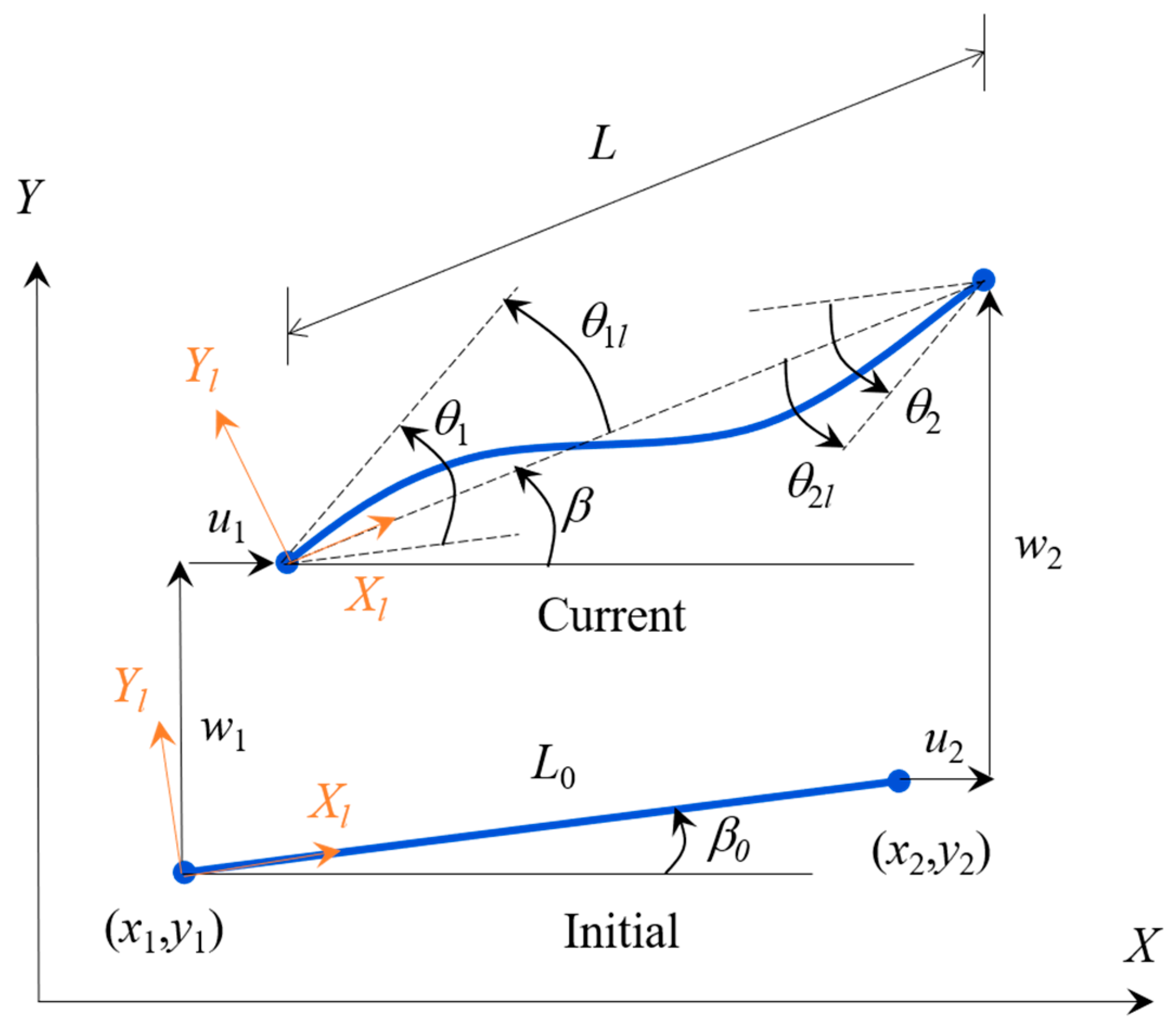
2. Analytical Formulation
2.1. Nonlinear Stiffness Matrix
2.2. Reduced Stiffness
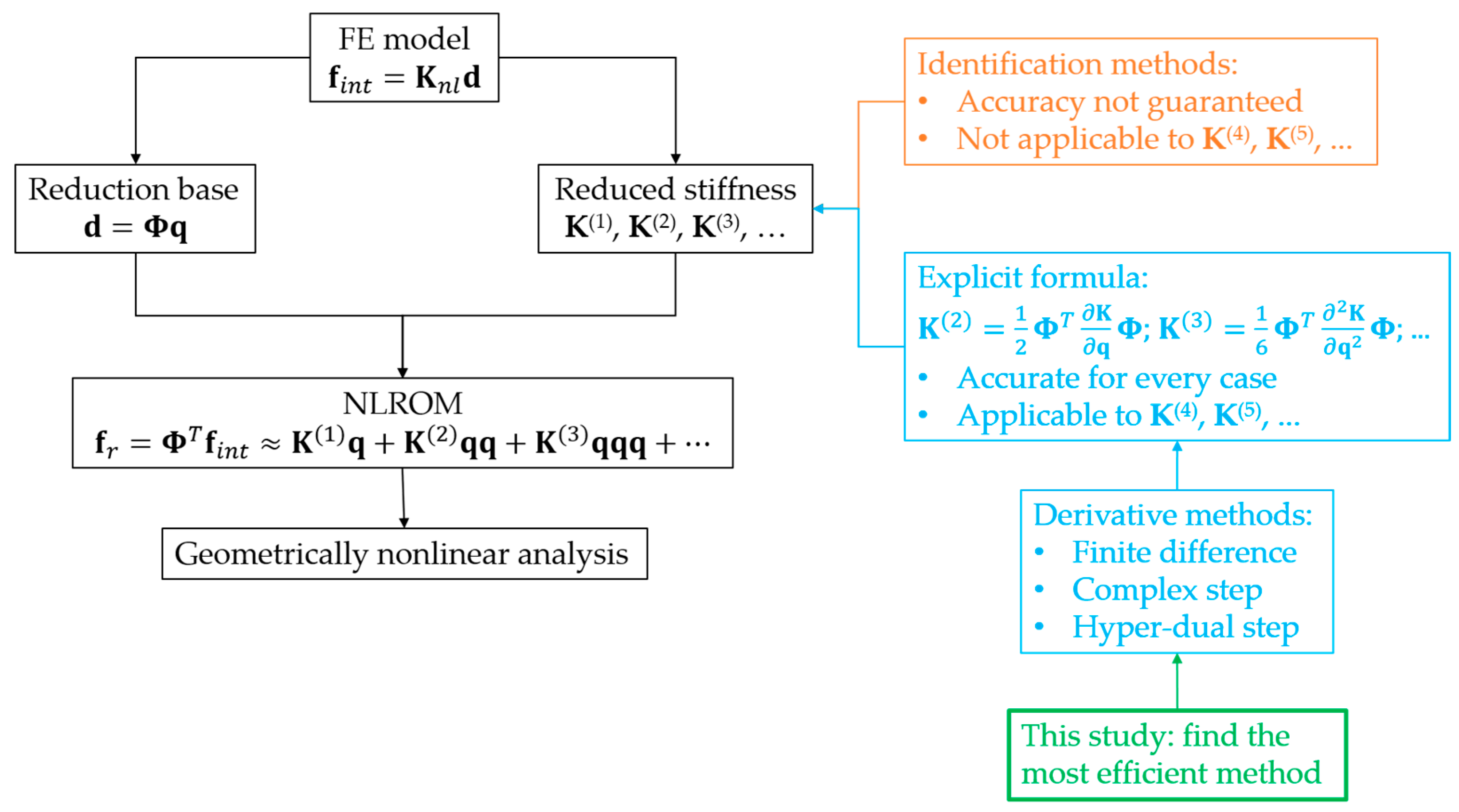
2.3. Analytical Derivative Formulation
3. Numerical Derivatives of Nonlinear Stiffness
3.1. Finite Difference Methods
| Algorithm 1 Algorithm to calculate the second-order derivative of nonlinear stiffness by forward difference method |
|
3.2. Complex Step Method
3.3. Hyper-Dual Step
4. Results
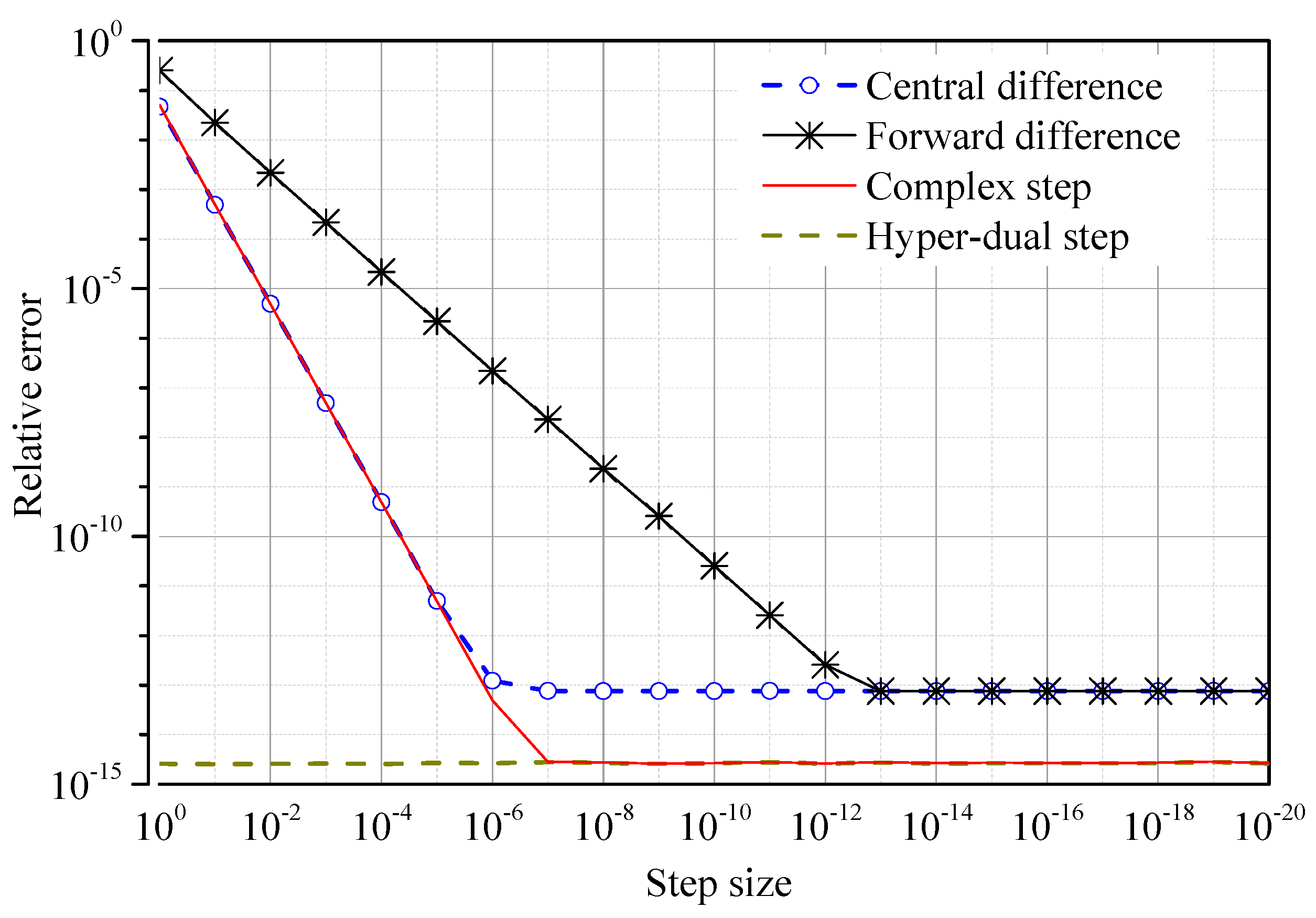
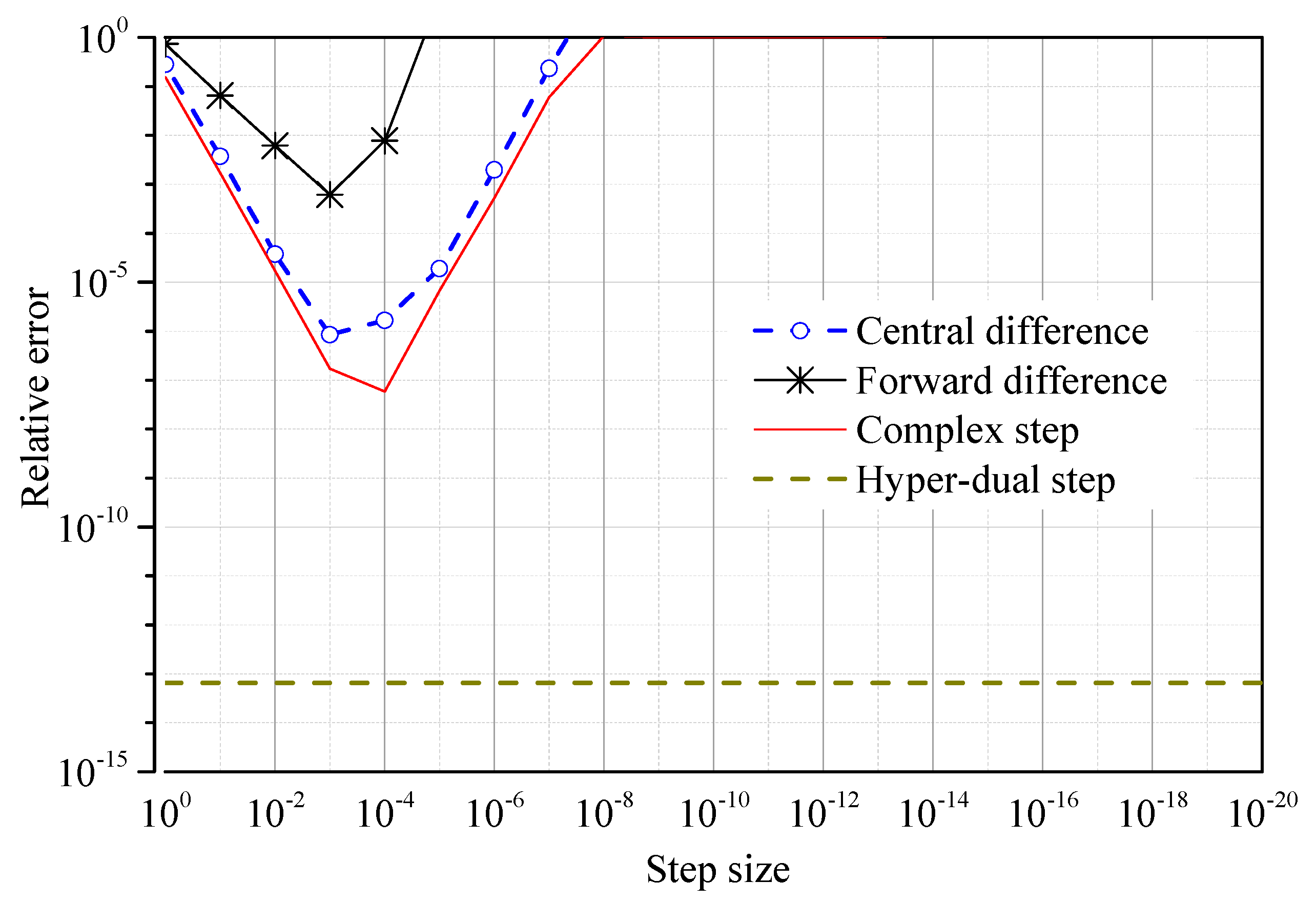
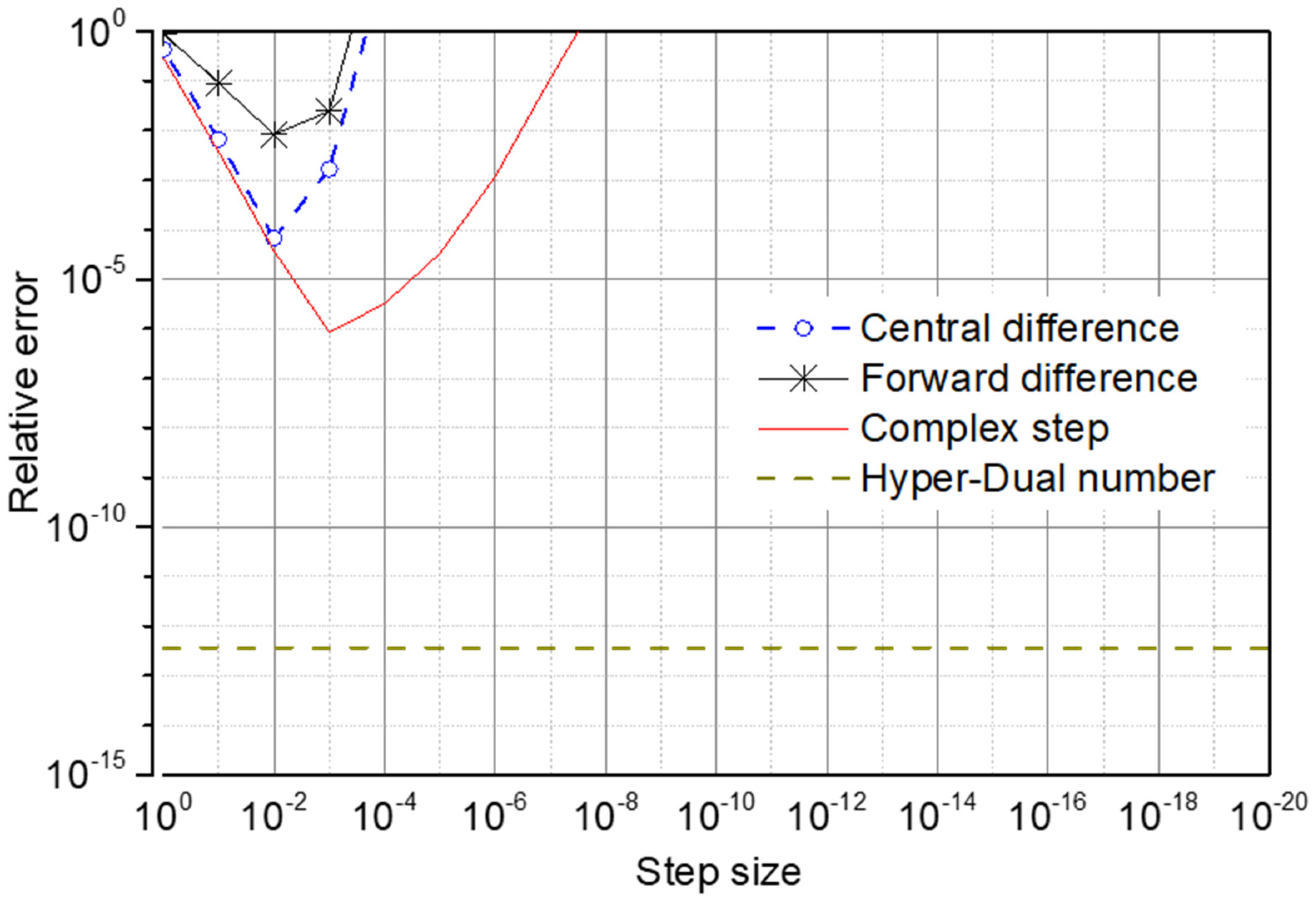
4.1. Accuracy of Derivatives of Nonlinear Stiffness
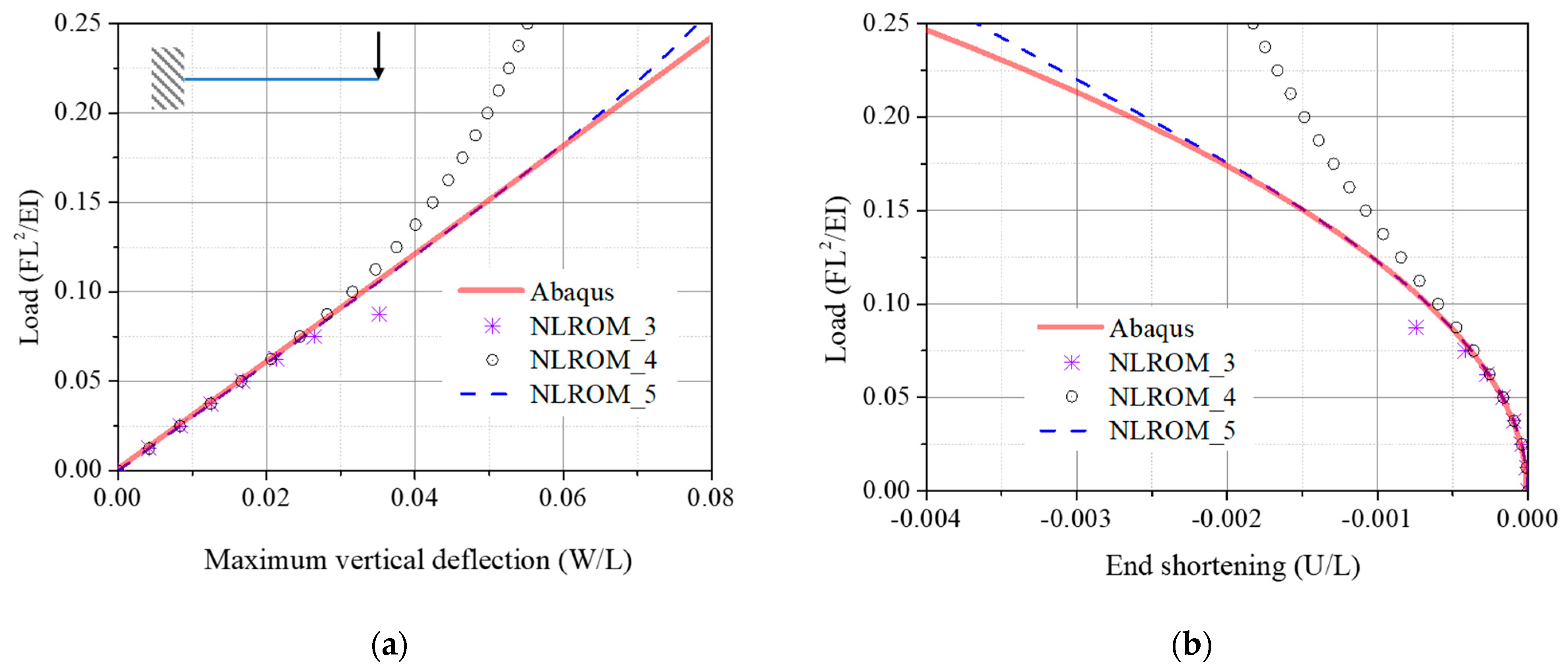
4.2. Accuracy of NLROM
4.2.1. Clamped-Clamped Beam
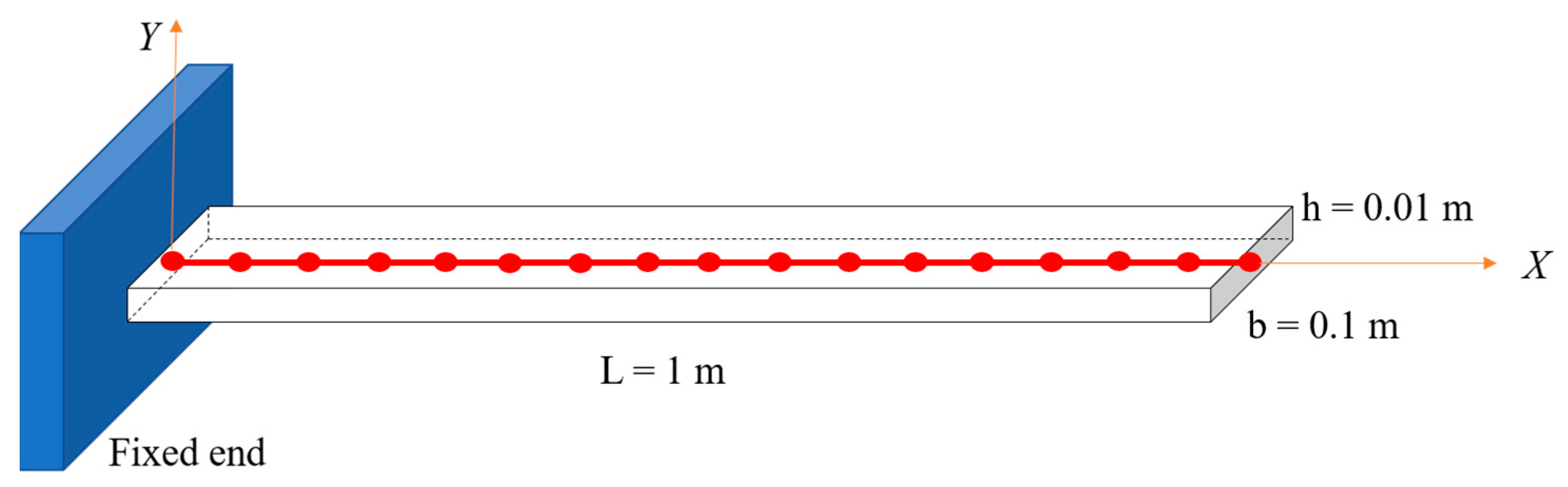
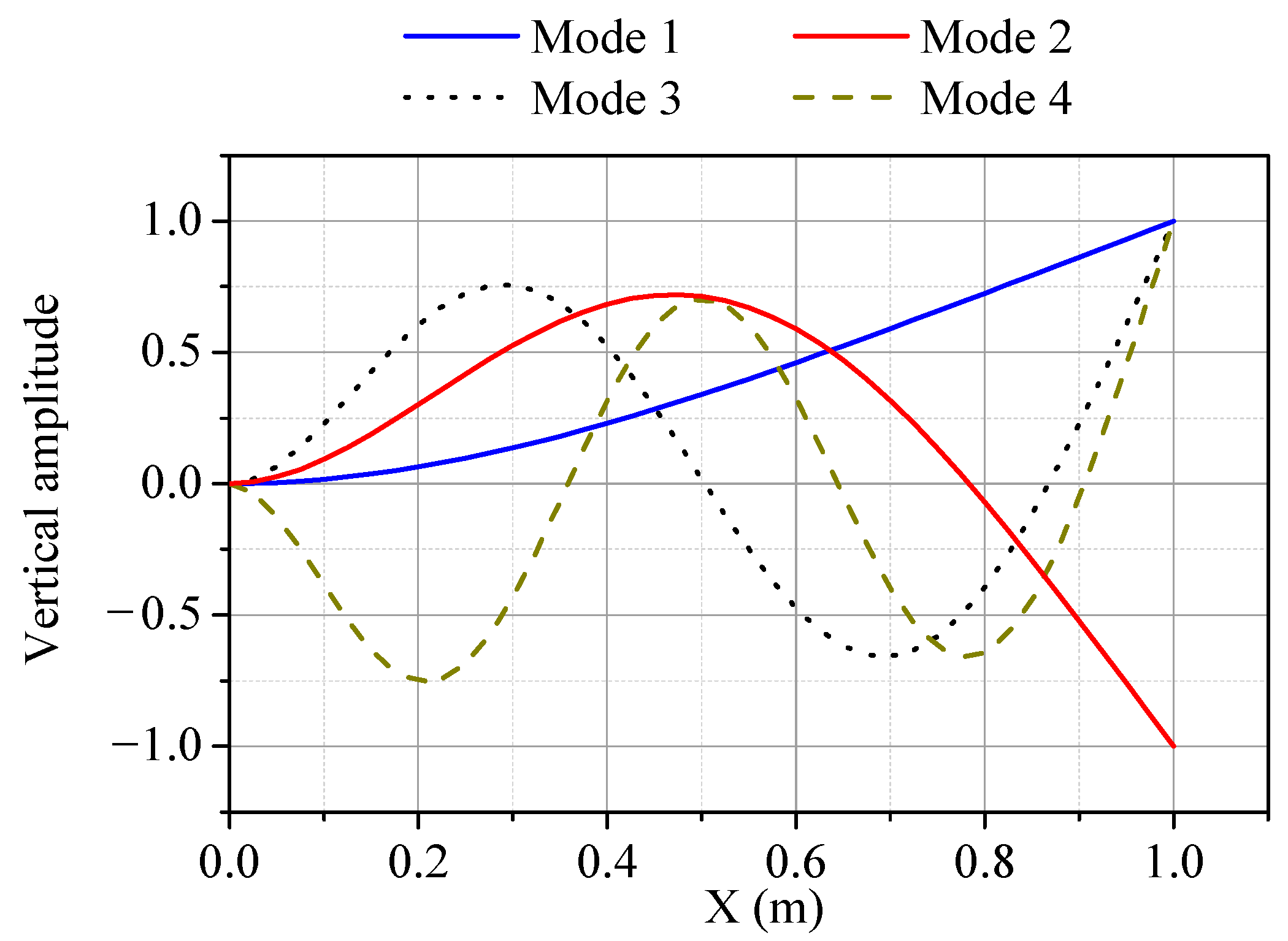
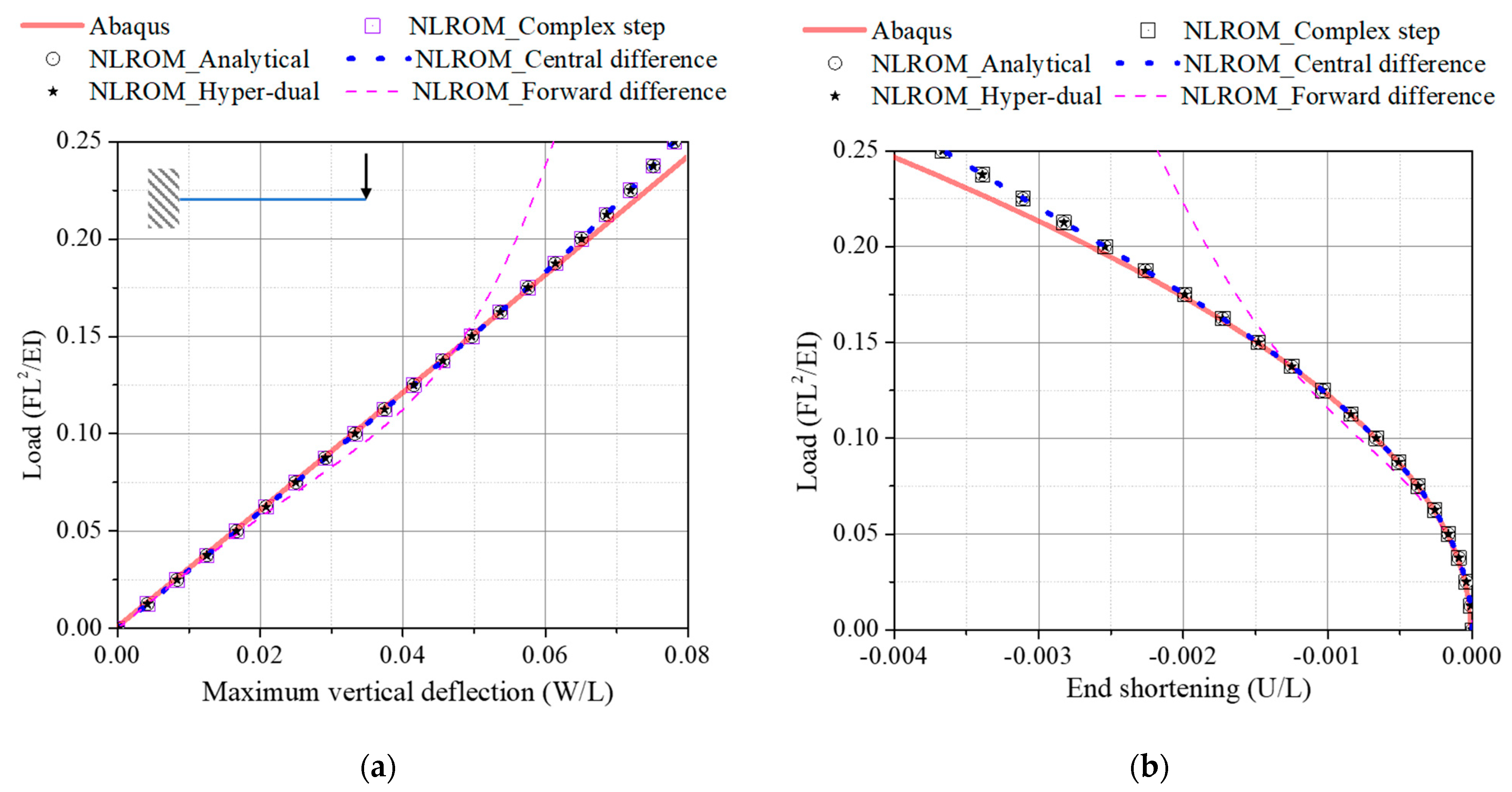
4.2.2. Cantilever Beam
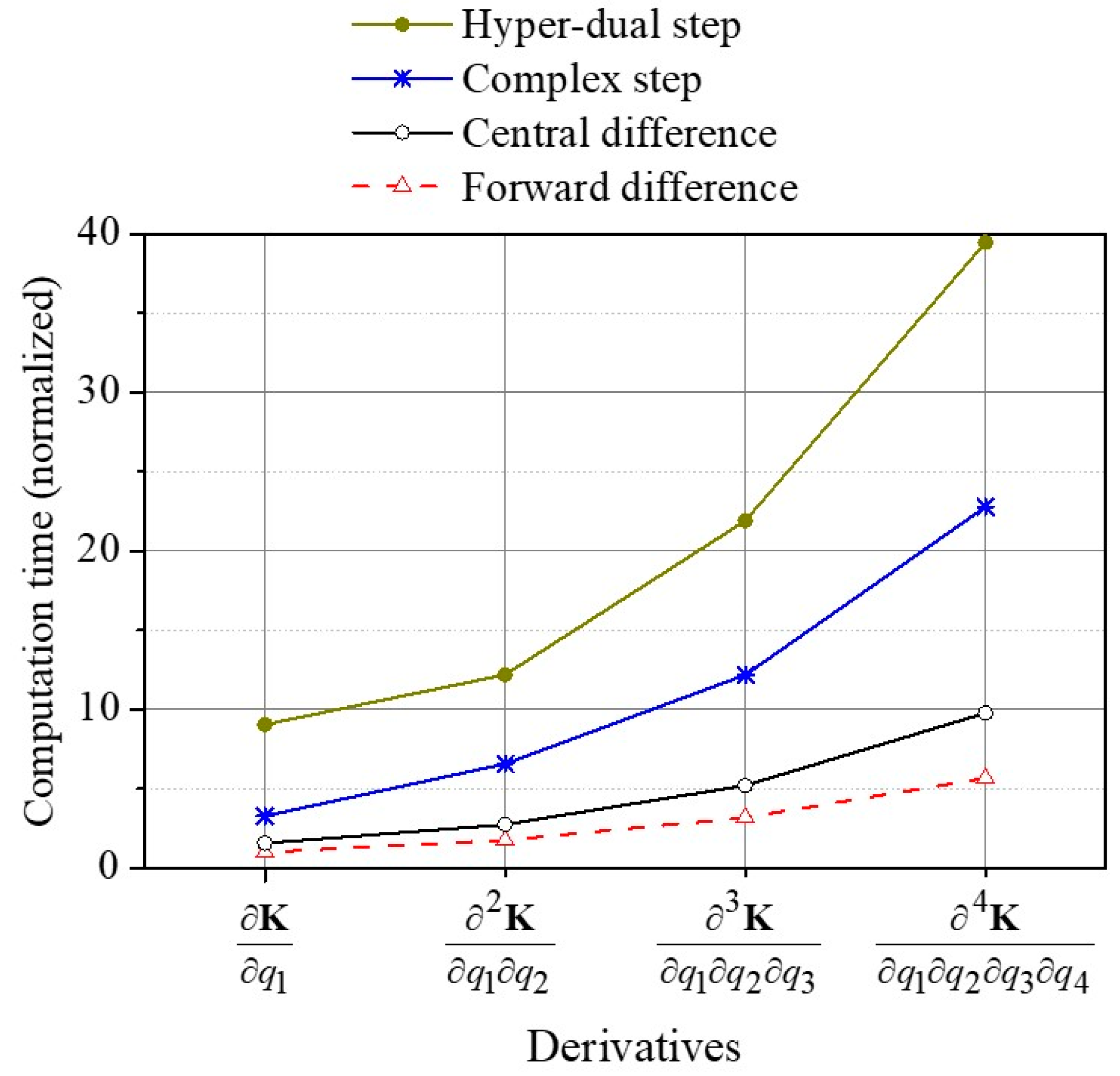
4.3. Computation Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- Rutzmoser, J. Model Order Reduction for Nonlinear Structural Dynamics. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2018. [Google Scholar]
- Muravyov, A.A.; Rizzi, S.A. Determination of nonlinear stiffness with application to random vibration of geometrically nonlinear structures. Comput. Struct. 2003, 81, 1513–1523. [Google Scholar] [CrossRef]
- Perez, R.; Wang, X.Q.; Mignolet, M.P. Nonintrusive structural dynamic reduced order modeling for large deformations: Enhancements for complex structures. J. Comput. Nonlinear Dyn. 2014, 9, 031008. [Google Scholar] [CrossRef]
- Cai, M.; Li, C. Numerical approaches to fractional integrals and derivatives: A review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef] [Green Version]
- Treanţă, S. Recent advances of constrained variational problems involving second-order partial derivatives: A review. Mathematics 2022, 10, 2599. [Google Scholar] [CrossRef]
- Kirsch, U.; Bogomolni, M.; Keulen, F.V. Efficient finite difference design sensitivities. AIAA J. 2005, 43, 399–405. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Ma, Y. Residual stress constrained self-support topology optimization for metal additive manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 389, 114380. [Google Scholar] [CrossRef]
- Lyness, J.N.; Moler, C.B. Numerical differentiation of analytic functions. SIAM J. Numer. Anal. 1967, 4, 202–210. [Google Scholar] [CrossRef]
- Lyness, J.N. Numerical algorithms based on the theory of complex variables. In Proceedings of the 22nd ACM National Conference, Washington, DC, USA, 1 January 1967. [Google Scholar] [CrossRef]
- Squire, W.; Trapp, G. Using complex variables to estimate derivatives of real functions. SIAM Rev. 1998, 10, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Lai, K.L.; Crassidis, J.L. Extensions of the first and second complex-step derivative approximations. J. Comput. Appl. Math. 2008, 219, 276–293. [Google Scholar] [CrossRef] [Green Version]
- Abreu, R.; Stich, D.; Morales, J. On the generalization of the Complex Step Method. J. Comput. Appl. Math. 2013, 241, 84–102. [Google Scholar] [CrossRef]
- Pérez-Foguet, A.; Rodríguez-Ferran, A.; Huerta, A. Numerical differentiation for local and global tangent operators in computational plasticity. Comput. Meth. Appl. Mech. Eng. 2000, 189, 277–296. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Ryu, J.; Cho, M. Numerically generated tangent stiffness matrices using the complex variable derivative method for nonlinear structural analysis. Comput. Meth. Appl. Mech. Eng. 2011, 200, 403–413. [Google Scholar] [CrossRef]
- Tanaka, M.; Fujikawa, M.; Balzani, D.; Schröder, J. Robust numerical calculation of tangent moduli at finite strains based on complex-step derivative approximation and its application to localization analysis. Comput. Meth. Appl. Mech. Eng. 2014, 269, 454–470. [Google Scholar] [CrossRef]
- Fike, J.A. Multi-Objective Optimization Using Hyper-Dual Numbers. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Tanaka, M.; Sasagawa, T.; Omote, R.; Fujikawa, M.; Balzani, D.; Schröder, J. A highly accurate 1st- and 2nd-order differentiation scheme for hyperelastic material models based on hyper-dual numbers. Comput. Meth. Appl. Mech. Eng. 2015, 283, 22–45. [Google Scholar] [CrossRef]
- Kiran, R.; Khandelwal, K. Automatic implementation of finite strain anisotropic hyperelastic models using hyper-dual numbers. Comput. Mech. 2015, 55, 229–248. [Google Scholar] [CrossRef]
- Lantoine, G.; Russell, R.P.; Dargent, T. Using multicomplex variables for automatic computation of high-order derivatives. ACM Trans. Math. Softw. 2012, 38, 1–21. [Google Scholar] [CrossRef]
- Aristizabal, M.; Ramirez-Tamayo, D.; Garcia, M.; Aguirre-Mesa, A.; Montoya, A.; Millwater, H. Quaternion and octonion-based finite element analysis methods for computing multiple first order derivatives. J. Comput. Phys. 2019, 397, 108831. [Google Scholar] [CrossRef]
- Rutzmoser, J.B.; Rixen, D.J.; Tiso, P.; Jain, S. Generalization of quadratic manifolds for reduced order modeling of nonlinear structural dynamics. Comput. Struct. 2017, 192, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2021, 103, 3335–3370. [Google Scholar] [CrossRef]
- Mahdiabadi, M.K.; Tiso, P.; Brandt, A.; Rixen, D.J. A non-intrusive model-order reduction of geometrically nonlinear structural dynamics using modal derivatives. Mech. Syst. Signal Process. 2021, 147, 107126. [Google Scholar] [CrossRef]
- Jeong, Y.M.; Kim, J.S. On the stable mode selection for efficient component mode synthesis of geometrically nonlinear beams. J. Mech. Sci. Technol. 2020, 34, 2961–2973. [Google Scholar] [CrossRef]
- Talebitooti, R.; Zarastvand, M.R. The effect of nature of porous material on diffuse field acoustic transmission of the sandwich aerospace composite doubly curved shell. Aerosp. Sci. Technol. 2018, 78, 157–170. [Google Scholar] [CrossRef]
- Seilsepour, H.; Zarastvand, M.; Talebitooti, R. Acoustic insulation characteristics of sandwich composite shell systems with double curvature: The effect of nature of viscoelastic core. J. Vib. Control 2023, 29, 1076–1090. [Google Scholar] [CrossRef]
- Yaw, L.L. 2D Corotational Beam Formulation; Walla Walla University: Washington, DC, USA, 2009. [Google Scholar]
- Sombroek, C.S.M.; Tiso, P.; Renson, L.; Kerschen, G. Numerical computation of nonlinear normal modes in a modal derivative subspace. Comput. Struct. 2018, 195, 34–46. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Radu, A.G.; Wang, X.Q.; Mignolet, M.P. Nonlinear reduced order modeling of isotropic and functionally graded plates. Int. J. Non-Linear Mech. 2013, 49, 100–110. [Google Scholar] [CrossRef]
- Rizzi, S.A.; Przekop, A. System identification-guided basis selection for reduced-order nonlinear response analysis. J. Sound Vib. 2008, 315, 467–485. [Google Scholar] [CrossRef]
- Olver, P.J. Finite Differences. In Introduction to Partial Differential Equations, 2nd ed.; Sheldon, A., Kenneth, R., Eds.; Springer: Cham, Switzerland, 2020; pp. 181–214. [Google Scholar] [CrossRef]
- Wang, X.Q.; Khanna, V.; Kim, K.; Mignolet, M.P. Nonlinear Reduced-Order Modeling of Flat Cantilevered Structures: Identification Challenges and Remedies. J. Aerosp. Eng. 2021, 34, 04021085. [Google Scholar] [CrossRef]



| Parameter | Selection |
|---|---|
| Internal force | K(1)q + K(2)qq + K(3)qqq |
| Reduction base | 4 VMs + 10 MDs |
| Derivative method | Optional |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, T.A.; Kim, J.-S.; Park, J. Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics 2023, 11, 1572. https://doi.org/10.3390/math11071572
Bui TA, Kim J-S, Park J. Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics. 2023; 11(7):1572. https://doi.org/10.3390/math11071572
Chicago/Turabian StyleBui, Tuan Anh, Jun-Sik Kim, and Junyoung Park. 2023. "Efficient Method for Derivatives of Nonlinear Stiffness Matrix" Mathematics 11, no. 7: 1572. https://doi.org/10.3390/math11071572
APA StyleBui, T. A., Kim, J.-S., & Park, J. (2023). Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics, 11(7), 1572. https://doi.org/10.3390/math11071572







