Newton’s Iteration Method for Solving the Nonlinear Matrix Equation
Abstract
1. Introduction
2. Preliminaries
3. Newton’s Iteration Method and Its Convergence Analysis for Solving (1)
3.1. Newton’s Iteration Method
3.2. Convergence Analysis
4. Numerical Experiments
- IT is the number of iterations;
- CPU means the iterations’ running times in seconds;
- In [26], the authors solve Equation (1) when by different methods:–IFI—inversion-free iteration;–BFPI—basic fixed-point iteration;
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Green, W.L.; Kamen, E.W. Stabilizability of linear systems over a commutative normed algebra with applications to spatially-distributed and parameter-dependent systems. SIAM J. Control Optim. 1985, 23, 1–18. [Google Scholar] [CrossRef]
- Anderson, W.N.; Morley, T.D.; Trapp, G.E. Ladder networks, fixpoints, and the geometric mean. Circuits Syst. Signal Process. 1983, 2, 259–268. [Google Scholar] [CrossRef]
- Pusz, W.; Woronowicz, S.L. Functional calculus for sesquilinear forms and the purification map. Rep. Math. Phys. 1975, 8, 159–170. [Google Scholar] [CrossRef]
- Anderson, W.N.; Kleindorfer, G.B.; Kleindorfer, P.R.; Woodroofe, M.B. Consistent estimates of the parameters of a linear system. Ann. Math. Stat. 1969, 40, 2064–2075. [Google Scholar] [CrossRef]
- Ouellette, D.V. Schur complements and statistics. Linear Alg. Appl. 1981, 36, 187–295. [Google Scholar] [CrossRef]
- Erfanifar, R.; Sayevand, K.; Esmaeili, H. A novel iterative method for the solution of a nonlinear matrix equation. Appl. Numer. Math. 2020, 153, 503–518. [Google Scholar] [CrossRef]
- Meini, B. Efficient computation of the extreme solutions of X + A*X−1A = Q and X − A*X−1A = Q. Math. Comput. 2001, 71, 1189–1204. [Google Scholar] [CrossRef]
- Engwerda, J.C.; Ran, A.C.M.; Rijkeboer, A.L. Necessary and sufficient conditions for the existence of a positive definite solution of the matrix equation X + A*X−1A = Q. Linear Alg. Appl. 1993, 186, 255–275. [Google Scholar] [CrossRef]
- Guo, C.H.; Lancaster, P. Iterative solution of two matrix equations. Math. Comput. 1999, 68, 1589–1603. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. On iterative solutions of general coupled matrix equations. SIAM J. Control Optim. 2006, 44, 2269–2284. [Google Scholar] [CrossRef]
- Caliò, F.; Garralda-Guillem, A.I.; Marchetti, E.; Galán, M.R. Numerical approaches for systems of Volterra–Fredholm integral equations. Appl. Math. Comput. 2013, 225, 811–821. [Google Scholar] [CrossRef]
- Marino, G.; Xu, H.K. A general iterative method for nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 2006, 318, 43–52. [Google Scholar] [CrossRef]
- Li, C.H.; Tam, P.K.S. An iterative algorithm for minimum cross entropy thresholding. Pattern Recognit. Lett. 1998, 19, 771–776. [Google Scholar] [CrossRef]
- Fital, S.; Guo, C.H. A note on the fixed-point iteration for the matrix equations X ± A*X−1A = I. Linear Alg. Appl. 2008, 429, 2098–2112. [Google Scholar] [CrossRef][Green Version]
- Ullah, M.Z. A new inversion-free iterative scheme to compute maximal and minimal solutions of a nonlinear matrix equation. Mathematics 2021, 9, 2994. [Google Scholar]
- Zhang, H. Quasi gradient-based inversion-free iterative algorithm for solving a class of the nonlinear matrix equations. Linear Alg. Appl. 2019, 77, 1233–1244. [Google Scholar]
- Zhang, H.M.; Ding, F. Iterative algorithms for X + ATX−1A = I by using the hierarchical identification principle. J. Frankl. Inst.-Eng. Appl. Math. 2016, 353, 1132–1146. [Google Scholar]
- Long, J.H.; Hu, X.Y.; Zhang, L. On the Hermitian positive definite solution of the nonlinear matrix equation X + A*X−1A + B*X−1B = I. B. Braz. Math. Soc. 2008, 39, 371–386. [Google Scholar] [CrossRef]
- Vaezzadeh, S.; Vaezpour, S.M.; Saadati, R.; Park, C. The iterative methods for solving nonlinear matrix equation X + A*X−1A + B*X−1B = Q. Adv. Differ. Equ. 2013, 2013, 229. [Google Scholar] [CrossRef]
- Sayevand, K.; Erfanifar, R.; Esmaeili, H. The maximal positive definite solution of the nonlinear matrix equation X + A*X−1A + B*X−1B = I. Math. Sci. 2022. [Google Scholar] [CrossRef]
- Hasanov, V.I.; Hakkaev, S.A. Convergence analysis of some iterative methods for a nonlinear matrix equation. Comput. Math. Appl. 2016, 72, 1164–1176. [Google Scholar] [CrossRef]
- Weng, P.C.Y. Solving two generalized nonlinear matrix equations. J. Appl. Math. Comput. 2021, 66, 543–559. [Google Scholar] [CrossRef]
- Huang, B.; Ma, C. Some iterative methods for the largest positive definite solution to a class of nonlinear matrix equation. Numer. Algorithms 2018, 79, 153–178. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- He, Y.M.; Long, J.H. On the Hermitian positive definite solution of the nonlinear matrix equation . Appl. Math. Comput. 2010, 216, 3480–3485. [Google Scholar]
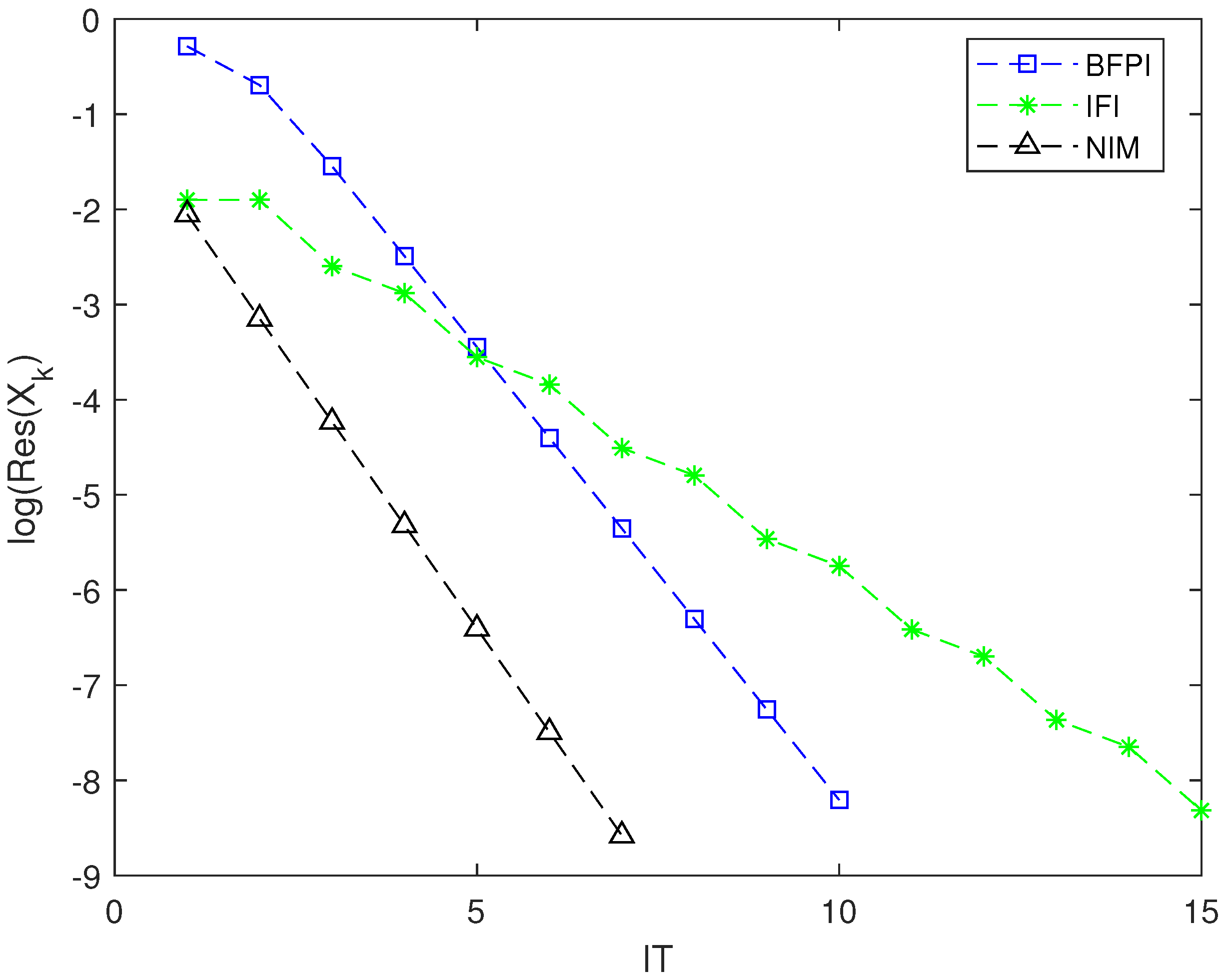

| Method | IT | CPU | Res |
|---|---|---|---|
| BFPI | 10 | 0.003025 | 6.2142 × 10 |
| IFI | 15 | 0.004163 | 4.8205 × 10 |
| NIM | 7 | 0.018660 | 2.6335 × 10 |
| Method | IT | CPU | Res |
|---|---|---|---|
| BFPI | 16 | 0.003165 | 4.1922 × 10 |
| IFI | 23 | 0.005886 | 6.9625 × 10 |
| NIM | 9 | 0.004179 | 4.3841 × 10 |
| Method | Computational Complexity |
|---|---|
| BFPI | |
| IFI | |
| NIM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.-Z.; Yuan, C.; Cui, A.-G.
Newton’s Iteration Method for Solving the Nonlinear Matrix Equation
Li C-Z, Yuan C, Cui A-G.
Newton’s Iteration Method for Solving the Nonlinear Matrix Equation
Li, Chang-Zhou, Chao Yuan, and An-Gang Cui.
2023. "Newton’s Iteration Method for Solving the Nonlinear Matrix Equation
Li, C.-Z., Yuan, C., & Cui, A.-G.
(2023). Newton’s Iteration Method for Solving the Nonlinear Matrix Equation






