Random Forest and Whale Optimization Algorithm to Predict the Invalidation Risk of Backfilling Pipeline
Abstract
:1. Introduction
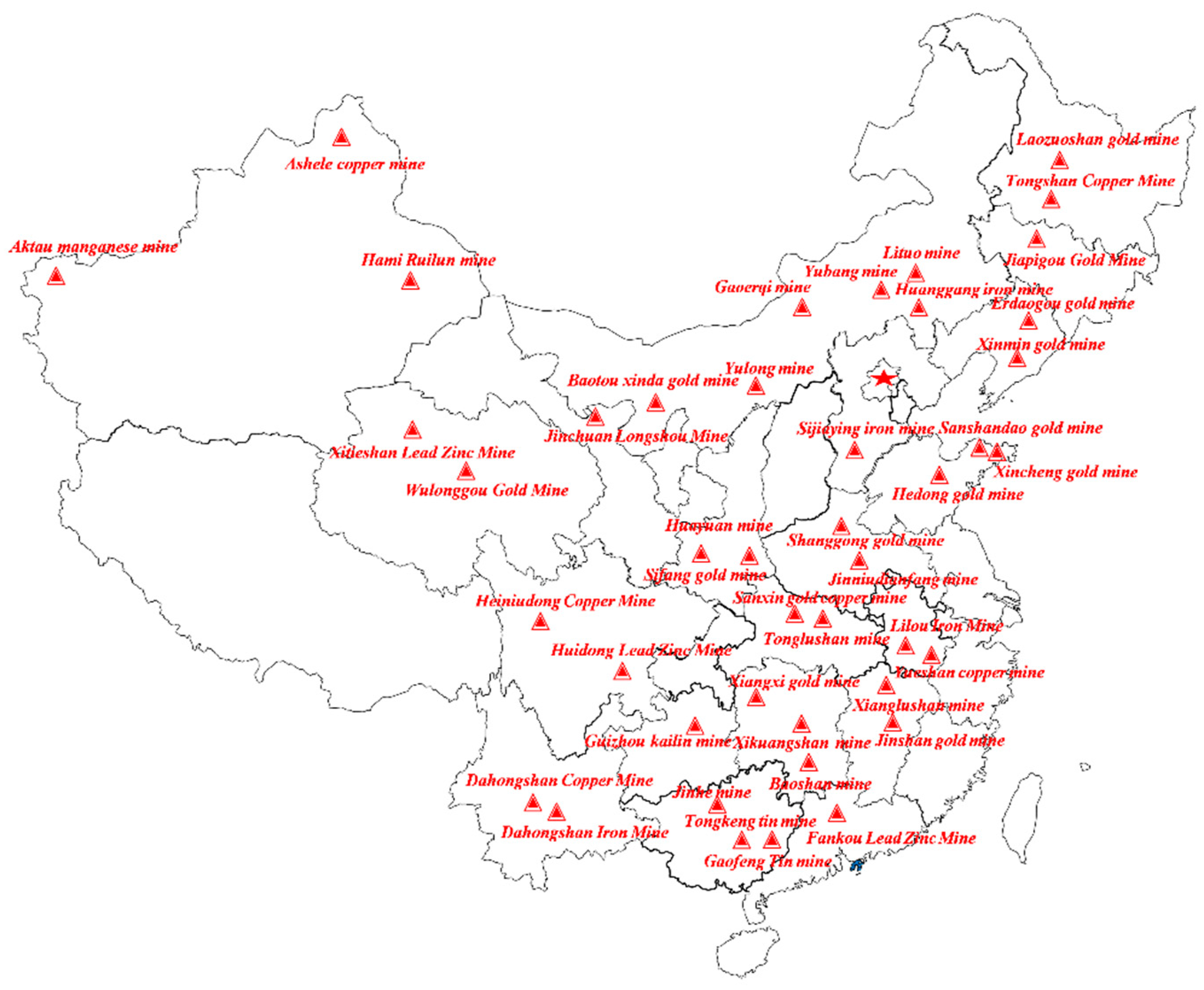
2. Engineering Background and Database Description
3. Modeling Methodology
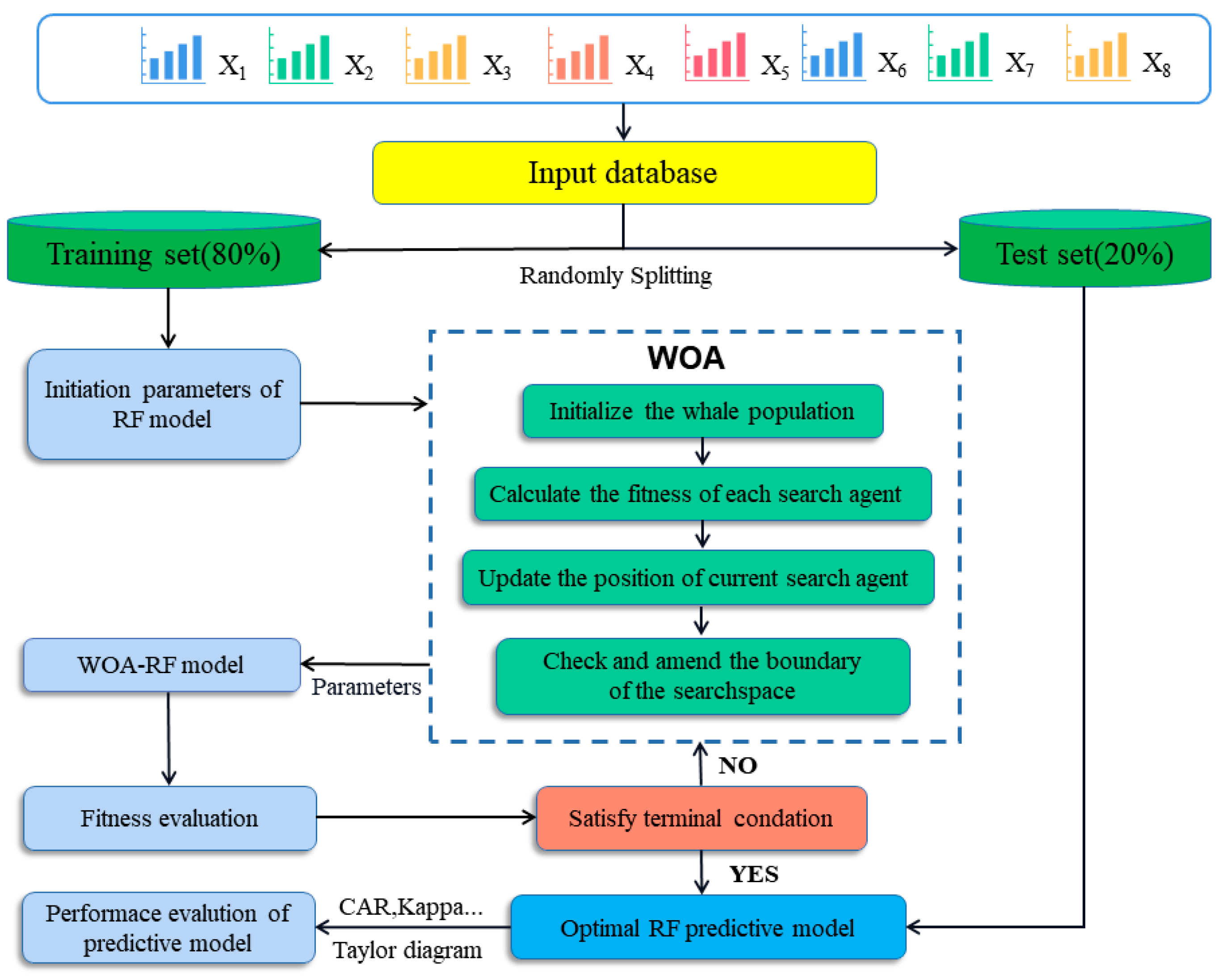
3.1. Random Forest
3.2. Whale Optimization Algorithm
4. Modeling Results and Discussion
4.1. Evaluation Indicators
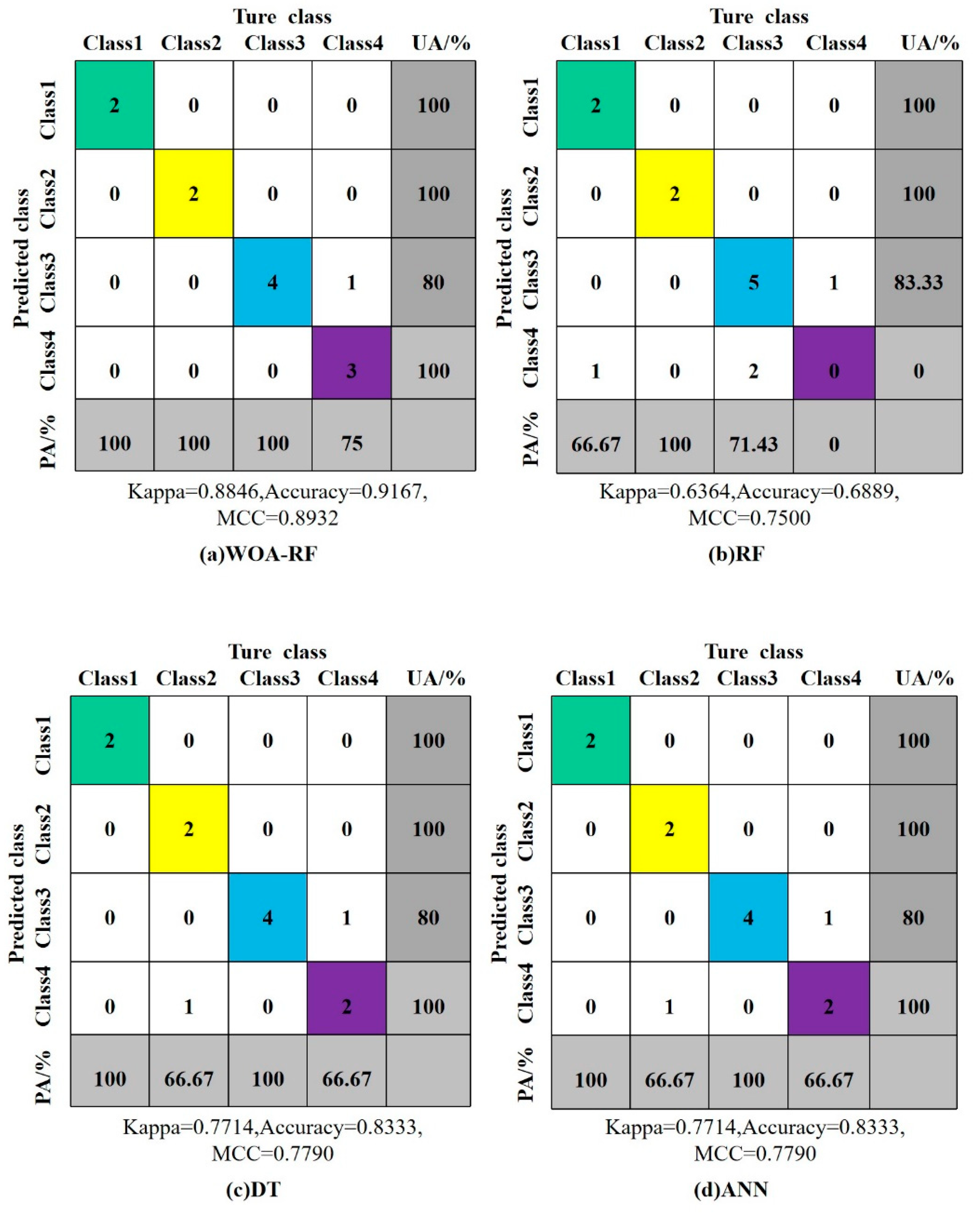
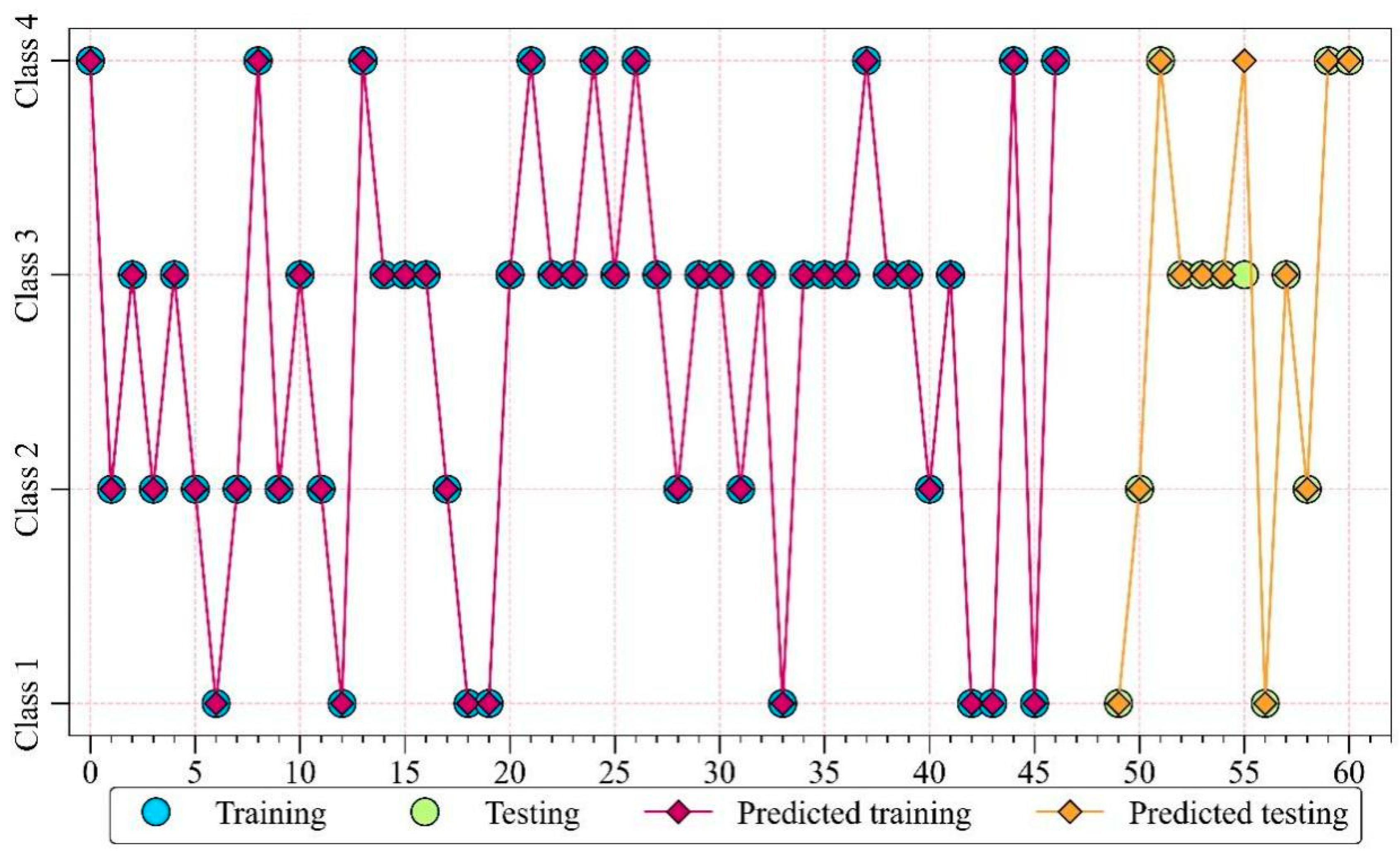
4.2. Development and Validation of the WOA–RF Model
4.3. Comparison with Other Machine Learning Models
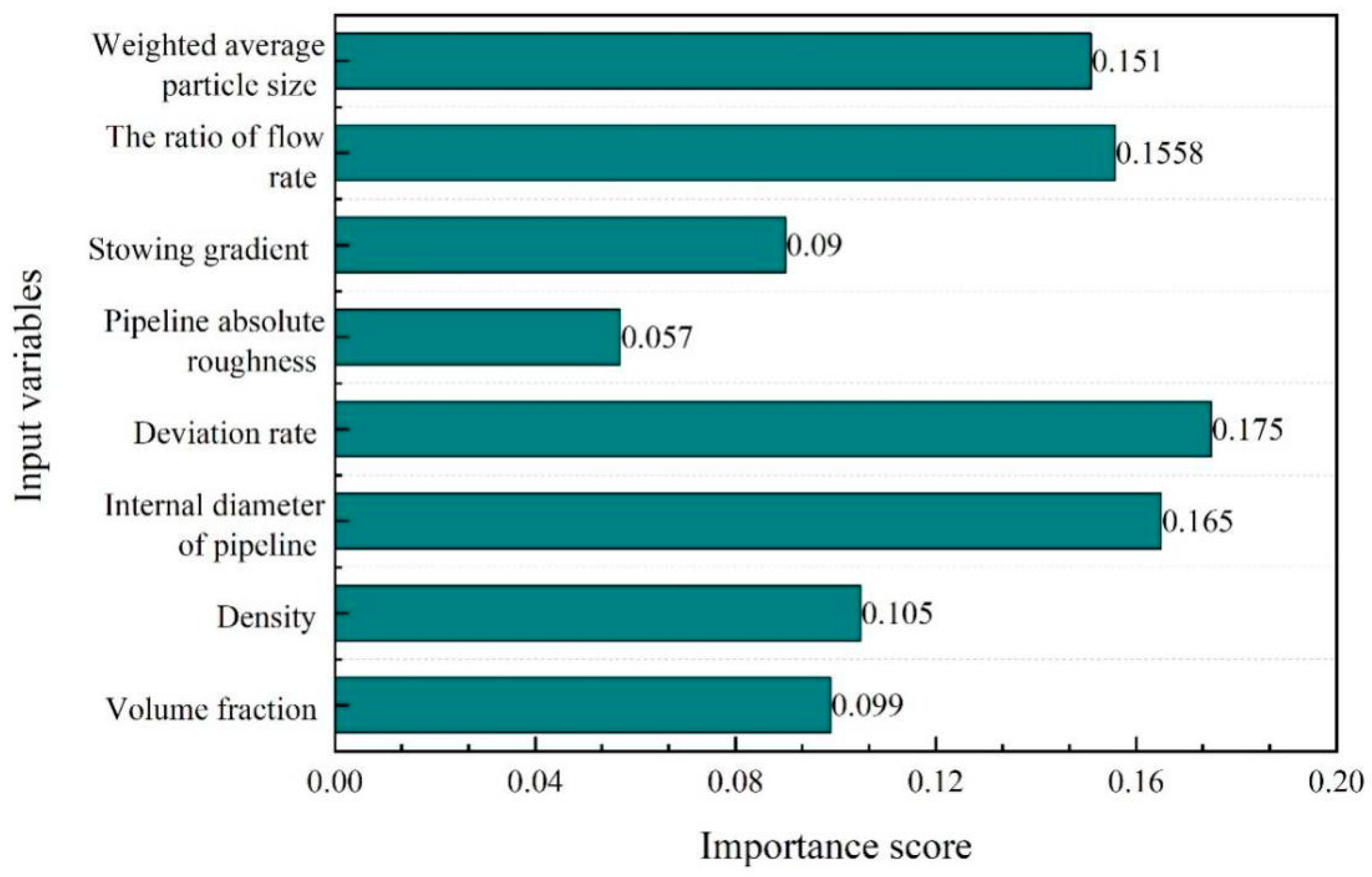
4.4. Sensitivity Analysis of Predictor Variables
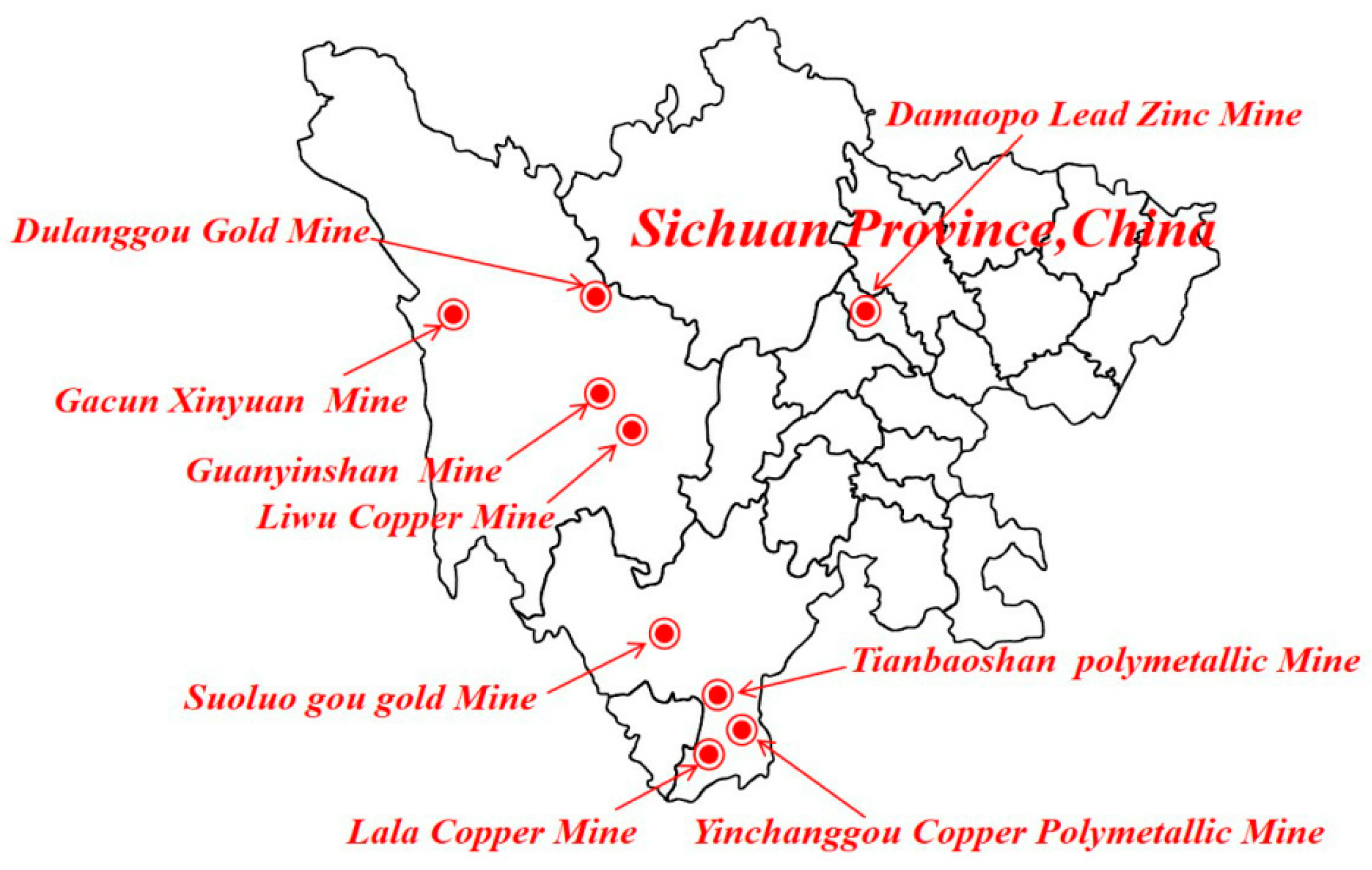
4.5. Engineering Validation
5. Study Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| RF | random forest |
| DT | decision tree |
| ANN | artificial neural network |
| AI | artificial intelligence |
| HDD | Horizontal directional drilling |
| GWO | grey wolf optimizer |
| ACOA | ant colony optimization |
| MCC | Matthews correlation coefficient |
| ROC | the receiver operating characteristic |
| TN | true negative rate |
| FP | false positive |
| FPR | false positive rate |
| TOPSIS | technique for order preference by similarity to an ideal solution methods |
| WOA | whale optimization algorithm |
| SVM | support vector machine |
| KNN | k-nearest neighbor |
| ML | machine learning |
| ANFIS | adaptive neural fuzzy reasoning system |
| BAYES | bayes classifier |
| PSO | particle swarm optimization |
| IAHP | interval-based AHP |
| AUC | area under curve |
| TP | true positive rate |
| TPR | true positive rate |
| N | the number of the samples |
References
- Aljaroudi, A.; Thodi, P.; Akinturk, A.; Khan, F.; Paulin, M. Application of Probabilistic Methods for Predicting the Remaining Life of Offshore Pipelines. In Proceedings of the 2014 10th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2014. [Google Scholar]
- Aljaroudi, A.; Khan, F.; Akinturk, A.; Haddara, M.; Thodi, P. Probability of Detection and False Detection for Subsea Leak Detection Systems: Model and Analysis. J. Fail. Anal. Prev. 2015, 15, 873–882. [Google Scholar] [CrossRef]
- Kim, S. Inverse Transient Analysis for a Branched Pipeline System with Leakage and Blockage Using Impedance Method. Procedia Eng. 2014, 89, 1350–1357. [Google Scholar] [CrossRef] [Green Version]
- Aljaroudi, A.; Khan, F.; Akinturk, A.; Haddara, M.; Thodi, P. Risk assessment of offshore crude oil pipeline failure. J. Loss Prev. Process Ind. 2015, 37, 101–109. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, G.; Li, J.; Diao, C. Risk assessment along the gas pipelines and its application in urban planning. Land Use Policy 2014, 38, 233–238. [Google Scholar] [CrossRef]
- Tabesh, A.; Najafi, M.; Kohankar, Z.; Mohammadi, M.M.; Ashoori, T. Risk Identification for Pipeline Installation by Horizontal Directional Drilling (HDD). In Proceedings of the Pipelines 2019, Nashville, TN, USA, 21–24 July 2019; pp. 141–150. [Google Scholar]
- Pillay, A. Pipeline Risk Mitigation Study. In Proceedings of the 2002 4th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2002; pp. 769–779. [Google Scholar]
- Yang, Y.; Khan, F.; Thodi, P.; Abbassi, R. Corrosion induced failure analysis of subsea pipelines. Reliab. Eng. Syst. Saf. 2017, 159, 214–222. [Google Scholar] [CrossRef]
- Lu, L.; Liang, W.; Zhang, L.; Zhang, H.; Lu, Z.; Shan, J. A comprehensive risk evaluation method for natural gas pipelines by combining a risk matrix with a bow-tie model. J. Nat. Gas Sci. Eng. 2015, 25, 124–133. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, B.; Yan, L.; Wang, C. Risk identification on hydropower project using the IAHP and extension of TOPSIS methods under interval-valued fuzzy environment. Nat. Hazards 2012, 65, 359–373. [Google Scholar] [CrossRef]
- Shin, S.; Lee, G.; Ahmed, U.; Lee, Y.; Na, J.; Han, C. Risk-based underground pipeline safety management considering corrosion effect. J. Hazard. Mater. 2018, 342, 279–289. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y. Failure risk analysis of pipelines using data-driven machine learning algorithms. Struct. Saf. 2021, 89, 102047. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Abbassi, R.; Khan, F.; Chen, G. Probabilistic fatigue failure assessment of free spanning subsea pipeline using dynamic Bayesian network. Ocean Eng. 2021, 234, 109323. [Google Scholar] [CrossRef]
- Yu, Q.Y.; Hou, L.; Li, Y.H.; Chai, C.; Yang, K.; Liu, J.Q. Pipeline Failure Assessment Based on Fuzzy Bayesian Network and AHP. J. Pipeline Syst. Eng. Pract. 2023, 14, 04022059. [Google Scholar] [CrossRef]
- Jayan, T.J.; Muthukumar, K.; Renjith, V.R.; George, P. The risk assessment of a crude oil pipeline using fuzzy and bayesian based bow-tie analysis. J. Eng. Res. 2021, 9. [Google Scholar]
- Shao, X.; Li, X.; Wang, L.; Fang, Z.; Zhao, B.; Liu, E.; Tao, Y.; Liu, L. Study on the Pressure-Bearing Law of Backfilling Material Based on Three-Stage Strip Backfilling Mining. Energies 2020, 13, 211. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhou, N.; Huang, Y.; Zhang, Q. Impact law of the bulk ratio of backfilling body to overlying strata movement in fully mechanized backfilling mining. J. Min. Sci. 2011, 47, 73. [Google Scholar] [CrossRef]
- Aslkhalili, A.; Shiri, H.; Zendehboudi, S. Probabilistic Assessment of Lateral Pipeline–Backfill–Trench Interaction. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021034. [Google Scholar] [CrossRef]
- Shukla, H.; Piratla, K.R.; Atamturktur, S. Influence of Soil Backfill on Vibration-Based Pipeline Leakage Detection. J. Pipeline Syst. Eng. Pract. 2020, 11, 04019055. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, Z.; Nie, W. Application of VMD in Pipeline Leak Detection Based on Negative Pressure Wave. J. Sens. 2021, 2021, 8699362. [Google Scholar] [CrossRef]
- Yang, K.; Zhao, X.; Wei, Z.; Zhang, J. Development overview of paste backfill technology in China’s coal mines: A review. Environ. Sci. Pollut. Res. 2021, 28, 67957–67969. [Google Scholar] [CrossRef]
- Jia, H.; Yan, B.; Yilmaz, E. A Large Goaf Group Treatment by means of Mine Backfill Technology. Adv. Civ. Eng. 2021, 2021, 3737145. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Du, X.; Tang, X. Prediction of open stope hangingwall stability using random forests. Nat. Hazards 2018, 92, 1179–1197. [Google Scholar] [CrossRef]
- Lin, Y.; Zhou, K.; Li, J.L. Prediction of Slope Stability Using Four Supervised Learning Methods. IEEE Access 2018, 6, 31169–31179. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Harandizadeh, H.; Momeni, E.; Maizir, H.; Zhou, J. An optimized system of GMDH-ANFIS predictive model by ICA for estimating pile bearing capacity. Artif. Intell. Rev. 2022, 55, 2313–2350. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Yagiz, S.; Mohamad, E.T.; Zhou, J. Prediction of TBM performance in fresh through weathered granite using empirical and statistical approaches. Tunn. Undergr. Space Technol. 2021, 118, 104183. [Google Scholar] [CrossRef]
- Xu, C.; Wang, J.; Zheng, T.; Cao, Y.; Ye, F. Prediction of prognosis and survival of patients with gastric cancer by a weighted improved random forest model: An application of machine learning in medicine. Arch. Med. Sci. 2022, 18, 1208–1220. [Google Scholar] [PubMed]
- Khandelwal, M.; Monjezi, M. Prediction of Backbreak in Open-Pit Blasting Operations Using the Machine Learning Method. Rock Mech. Rock Eng. 2013, 46, 389–396. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Jalilzadeh Yengejeh, R.; Davami, A.H. Building energy optimization using Grey Wolf Optimizer (GWO). Case Stud. Therm. Eng. 2021, 27, 101250. [Google Scholar] [CrossRef]
- Goudos, S.K.; Zaharis, Z.D.; Baltzis, K.B. Particle Swarm Optimization as Applied to Electromagnetic Design Problems. Int. J. Swarm Intell. Res. 2018, 9, 47–82. [Google Scholar] [CrossRef]
- Naadimuthu, G.; Liu, D.M.; Lee, E.S. Application of an adaptive neural fuzzy inference system to thermal comfort and group technology problems. Comput. Math. Appl. 2007, 54, 1395–1402. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.J.; Yang, G.Q.; Xiong, B.L. BP Artificial Neural Network Study on Slop Stability. Appl. Mech. Mater. 2012, 170–173, 1243–1246. [Google Scholar] [CrossRef]
- Li, F.; Wang, W.; Xu, J.; Yi, J.; Wang, Q. Comparative study on vulnerability assessment for urban buried gas pipeline network based on SVM and ANN methods. Process Saf. Environ. Prot. 2019, 122, 23–32. [Google Scholar] [CrossRef]
- Mansour, A.M. Texture Classification using Naive Bayes Classifier. Int. J. Comput. Sci. Netw. Secur. 2018, 18, 112–120. [Google Scholar]
- Otero, F.E.B.; Freitas, A.A.; Johnson, C.G. Inducing decision trees with an ant colony optimization algorithm. Appl. Soft Comput. 2012, 12, 3615–3626. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Zhu, S.; Qiu, Y.; Armaghani, D.J.; Zhou, A.; Yong, W. Predicting tunnel squeezing using support vector machine optimized by whale optimization algorithm. Acta Geotech. 2022, 17, 1343–1366. [Google Scholar] [CrossRef]
- Liu, D.; Fan, Z.R.; Fu, Q.; Li, M.; Faiz, M.A.; Ali, S.; Li, T.X.; Zhang, L.L.; Khan, M.I. Random forest regression evaluation model of regional flood disaster resilience based on the whale optimization algorithm. J. Clean. Prod. 2020, 250, 119468. [Google Scholar] [CrossRef]
- Wang, X.M.; Gao, R.W.; Hu, W.; Feng, Y.; Zhou, D.H. Risk prediction model of filling pipeline blockage. J. Cent. South Univ. 2013, 44, 4604–4610. (In Chinese) [Google Scholar]
- Li, D.Y.; Liu, Z.D.; Xiao, P.; Zhou, J.; Armaghani, D.J. Intelligent rockburst prediction model with sample category balance using feedforward neural network and Bayesian optimization. Undergr. Space 2022, 7, 833–846. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, Z.D.; Armaghani, D.J.; Xiao, P.; Zhou, J. Novel ensemble intelligence methodologies for rockburst assessment in complex and variable environments. Sci. Rep. 2022, 12, 1844. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, Z.D.; Armaghani, D.J.; Xiao, P.; Zhou, J. Novel Ensemble Tree Solution for Rockburst Prediction Using Deep Forest. Mathematics 2022, 10, 787. [Google Scholar] [CrossRef]
- Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, H.H. Optimization of parallel random forest algorithm based on distance weight. J. Intell. Fuzzy Syst. 2020, 39, 1951–1963. [Google Scholar] [CrossRef]
- Daho, M.E.; Chikh, M.A. Combining Bootstrapping Samples, Random Subspaces and Random Forests to Build Classifiers. J. Med. Imaging Health Inform. 2015, 5, 539–544. [Google Scholar] [CrossRef]
- Byeon, H. Comparing the Accuracy and Developed Models for Predicting the Confrontation Naming of the Elderly in South Korea using Weighted Random Forest, Random Forest, and Support Vector Regression. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 326–331. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Hui, G.Y.; Yang, A.M.; Zhao, Z.H. A simple and effective approach to quantitatively characterize structural complexity. Sci. Rep. 2021, 11, 1326. [Google Scholar] [CrossRef] [PubMed]
- Ben Ayed, A.; Benhammouda, M.; Ben Halima, M.; Alimi, A. Random Forest Ensemble Classification Based Fuzzy Logic; SPIE: Washington, DC, USA, 2017; Volume 10341. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Saremi, S.; Mirjalili, S. Whale Optimization Algorithm: Theory, Literature Review, and Application in Designing Photonic Crystal Filters. In Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Mirjalili, S., Song Dong, J., Lewis, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 219–238. [Google Scholar]
- Luo, J.; Shi, B.Y. A hybrid whale optimization algorithm based on modified differential evolution for global optimization problems. Appl. Intell. 2019, 49, 1982–2000. [Google Scholar] [CrossRef]
- Liang, X.D.; Xu, S.W.; Liu, Y.; Sun, L.L. A Modified Whale Optimization Algorithm and Its Application in Seismic Inversion Problem. Mob. Inf. Syst. 2022, 2022, 9159130. [Google Scholar] [CrossRef]
- Perez, I.M.; Airola, A.; Bostrom, P.J.; Jambor, I.; Pahikkala, T. Tournament leave-pair-out cross-validation for receiver operating characteristic analysis. Stat. Methods Med. Res. 2019, 28, 2975–2991. [Google Scholar] [CrossRef]
- Hand, D.J.; Till, R.J. A simple generalisation of the area under the ROC curve for multiple class classification problems. Mach. Learn. 2001, 45, 171–186. [Google Scholar] [CrossRef]
- Mourão, M.F.; Braga, A.C. Strengths and Weaknesses of Three Software Programs for the Comparison of Systems Based on ROC Curves; Springer: Cham, Switzerland, 2016; pp. 359–372. [Google Scholar]
- Pu, Y.Y.; Apel, D.; Xu, H.W. A Principal Component Analysis/Fuzzy Comprehensive Evaluation for Rockburst Potential in Kimberlite. Pure Appl. Geophys. 2018, 175, 2141–2151. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H.S. Classification of Rockburst in Underground Projects: Comparison of Ten Supervised Learning Methods. J. Comput. Civ. Eng. 2016, 30, 04016003. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.G.; Khandelwal, M.; Zhu, S.L.; Zhang, X.L. Developing a hybrid model of Jaya algorithm-based extreme gradient boosting machine to estimate blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. 2021, 145, 104856. [Google Scholar] [CrossRef]
- Chou, J.-S.; Lin, C. Predicting Disputes in Public-Private Partnership Projects: Classification and Ensemble Models. J. Comput. Civ. Eng. 2013, 27, 51–60. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, Y.; Khandelwal, M.; Monjezi, M.; Yu, Z.; Qiu, Y. Performance of Hybrid SCA-RF and HHO-RF Models for Predicting Backbreak in Open-Pit Mine Blasting Operations. Nat. Resour. Res. 2021, 30, 4753–4771. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.; Ma, G.; Yuan, Y.; Nener, B. Automating the mixture design of lightweight foamed concrete using multi-objective firefly algorithm and support vector regression. Cem. Concr. Compos. 2021, 121, 104103. [Google Scholar] [CrossRef]
- Liu, Z.; Armaghani, D.J.; Fakharian, P.; Li, D.; Ulrikh, D.V.; Orekhova, N.N.; Khedher, K.M. Rock Strength Estimation Using Several Tree-Based ML Techniques. Comput. Model. Eng. Sci. 2022, 133, 799–824. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Xu, H. Rockburst prediction in kimberlite with unsupervised learning method and support vector classifier. Tunn. Undergr. Space Technol. 2019, 90, 12–18. [Google Scholar] [CrossRef]

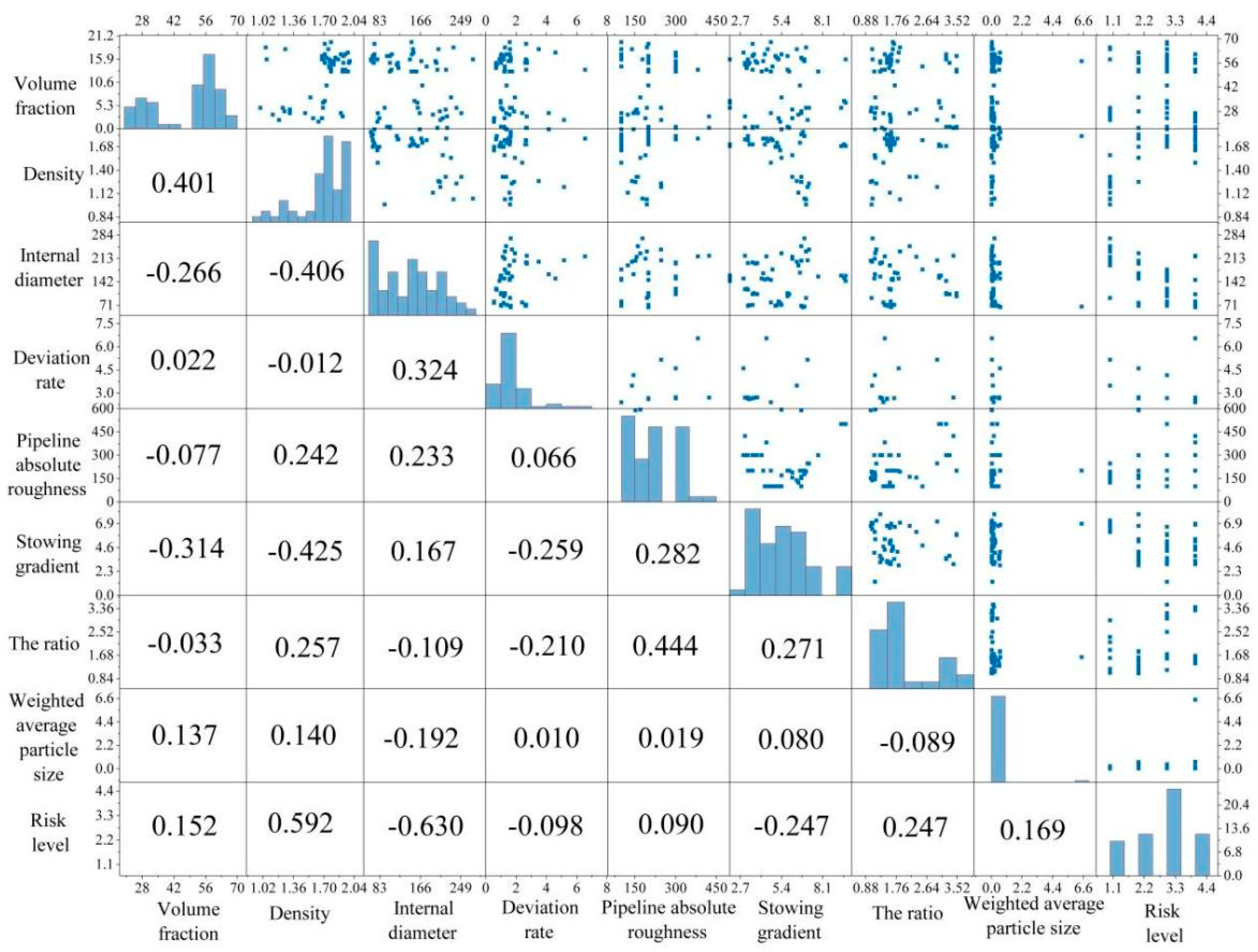





| Volume Fraction of Backfilling Slurry I1/% | Density of Backfilling Slurry I2/t.m−3 | The Internal Diameter of the Pipeline I3/mm | The Deviation Rate I4/% | Pipeline Absolute Roughness I5/um | Stowing Gradient I6 | The Ratio of Slurry Flow Rate with the Critical Velocity I7 | Weighted Average Particle Size I8/mm | Risk Level |
|---|---|---|---|---|---|---|---|---|
| ≥50 | ≥1.9 | ≤100 | ≥5 | ≥500 | ≥7 | ≤1 | ≥2.5 | 1 |
| ≥40~<50 | ≥1.7~<1.9 | >100~≤150 | ≥3~<5 | ≥300~<500 | ≥5~<7 | >1~≤1.2 | ≥0.7~<2.5 | 2 |
| ≥30~<40 | ≥1.5~<1.7 | >150~≤200 | ≥1~<3 | ≥100~<300 | ≥3~<5 | >1.2~≤1.5 | ≥0.3~<0.7 | 3 |
| <30 | <1.5 | >200 | <1 | <100 | ≥1~<3 | <1.5 | <0.3 | 4 |
| Sample of Filling Pipeline | Volume Fraction of Filling Slurry I1/% | Density of Filling Slurry I2/t.m−3 | Internal Diameter of the Pipeline I3/mm | Deviation Rate I4/% | Pipeline Absolute Roughness I5/um | Stowing Gradient I6 | The Ratio of Slurry Flow Rate with the Critical Velocity I7 | Weighted Average Particle Size I8/mm | Risk Level |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 56 | 1.98 | 199 | 2.72 | 300 | 3.8 | 1.30 | 0.58 | 2 |
| 2 | 33 | 1.69 | 160 | 0.98 | 500 | 9.6 | 3.00 | 0.05 | 3 |
| 3 | 24 | 1.68 | 82 | 0.56 | 100 | 5.2 | 1.60 | 0.21 | 4 |
| 4 | 52 | 1.94 | 107 | 1.27 | 200 | 5.8 | 3.50 | 0.11 | 3 |
| 5 | 60 | 1.92 | 104 | 1.01 | 300 | 3.5 | 3.20 | 0.05 | 3 |
| 6 | 30 | 1.76 | 69 | 2.65 | 200 | 3.2 | 1.50 | 0.05 | 4 |
| 7 | 60 | 1.68 | 69 | 1.03 | 100 | 5 | 1.57 | 0.25 | 3 |
| 8 | 56 | 1.77 | 120 | 0.69 | 300 | 3 | 1.60 | 0.13 | 3 |
| 9 | 28 | 1.86 | 65 | 1.65 | 200 | 6.8 | 1.62 | 0.65 | 4 |
| 10 | 68 | 1.78 | 148 | 1.58 | 100 | 4.7 | 1.66 | 0.05 | 3 |
| 11 | 51 | 1.93 | 152 | 1.23 | 300 | 4.1 | 1.13 | 0.26 | 2 |
| 12 | 27 | 1.49 | 79 | 2.41 | 100 | 4.7 | 1.39 | 0.17 | 4 |
| 13 | 55 | 1.77 | 120 | 0.69 | 300 | 3 | 1.60 | 0.13 | 3 |
| 14 | 43 | 1.73 | 170 | 1.37 | 200 | 6.6 | 1.72 | 0.19 | 3 |
| 15 | 51 | 1.97 | 158 | 1.74 | 300 | 7.8 | 1.30 | 0.21 | 2 |
| 16 | 26 | 1.89 | 72 | 1.37 | 100 | 5.4 | 1.43 | 0.24 | 4 |
| 17 | 57 | 1.99 | 197 | 2.71 | 300 | 3.7 | 1.30 | 0.55 | 2 |
| 18 | 34 | 1.71 | 154 | 0.99 | 500 | 9.5 | 3.00 | 0.07 | 3 |
| 19 | 22 | 1.64 | 78 | 0.54 | 100 | 5.3 | 1.60 | 0.19 | 4 |
| 20 | 51 | 1.91 | 104 | 1.25 | 200 | 5.9 | 3.50 | 0.13 | 3 |
| 21 | 61 | 1.94 | 108 | 1.03 | 300 | 3.6 | 3.20 | 0.03 | 3 |
| 22 | 56 | 1.71 | 71 | 2.61 | 200 | 3.3 | 1.50 | 0.04 | 4 |
| 23 | 59 | 1.73 | 71 | 1.01 | 100 | 5.1 | 1.57 | 0.26 | 3 |
| 24 | 55 | 1.81 | 118 | 0.72 | 300 | 3.2 | 1.60 | 0.15 | 3 |
| 25 | 27 | 1.81 | 67 | 1.63 | 200 | 6.9 | 1.62 | 6.47 | 4 |
| 26 | 64 | 1.75 | 151 | 1.61 | 100 | 4.5 | 1.66 | 0.04 | 3 |
| 27 | 53 | 1.77 | 121 | 0.69 | 300 | 3.1 | 1.56 | 0.14 | 3 |
| 28 | 61 | 1.71 | 149 | 1.58 | 100 | 4.3 | 1.63 | 0.05 | 3 |
| 29 | 52 | 1.91 | 201 | 2.66 | 300 | 3.5 | 1.35 | 0.56 | 2 |
| 30 | 30 | 1.69 | 161 | 1.02 | 500 | 9.3 | 3.05 | 0.08 | 3 |
| 31 | 56 | 1.98 | 199 | 2.72 | 300 | 3.2 | 1.30 | 0.24 | 2 |
| 32 | 33 | 1.69 | 160 | 0.98 | 500 | 9.6 | 3.00 | 0.43 | 3 |
| 33 | 24 | 1.68 | 82 | 0.56 | 100 | 5.2 | 1.60 | 0.08 | 3 |
| 34 | 52 | 1.94 | 107 | 1.27 | 200 | 5.8 | 3.50 | 0.16 | 3 |
| 35 | 62 | 1.97 | 152 | 4.6 | 300 | 2.9 | 1.83 | 0.62 | 2 |
| 36 | 54 | 1.76 | 179 | 1.25 | 100 | 4.8 | 2.52 | 0.08 | 3 |
| 37 | 31 | 1.78 | 148 | 1.58 | 200 | 4.7 | 1.66 | 0.05 | 4 |
| 38 | 57 | 1.78 | 168 | 1.5 | 200 | 4.2 | 1.80 | 0.62 | 2 |
| 39 | 58 | 1.69 | 145 | 0.91 | 500 | 9.6 | 3.20 | 0.08 | 3 |
| 40 | 59 | 1.83 | 69 | 1.65 | 100 | 6.7 | 1.50 | 0.52 | 2 |
| 41 | 56 | 1.92 | 98 | 1.19 | 200 | 5.8 | 3.50 | 0.11 | 3 |
| 42 | 56 | 1.92 | 104 | 1.01 | 300 | 3.8 | 3.30 | 0.06 | 4 |
| 43 | 67 | 1.71 | 72 | 2.67 | 200 | 3.5 | 1.70 | 0.05 | 3 |
| 44 | 58 | 1.68 | 78 | 1.18 | 100 | 5.2 | 1.60 | 0.28 | 2 |
| 45 | 69 | 1.32 | 218 | 1.12 | 156 | 6.1 | 2.34 | 0.02 | 1 |
| 46 | 68 | 1.06 | 274 | 1.65 | 178 | 6.9 | 1.08 | 0.23 | 1 |
| 47 | 27 | 1.89 | 165 | 4.16 | 145 | 1.3 | 1.15 | 0.07 | 3 |
| 48 | 64 | 1.27 | 203 | 3.49 | 139 | 6.4 | 1.07 | 0.11 | 1 |
| 49 | 36 | 1.55 | 229 | 1.93 | 170 | 5.4 | 1.16 | 0.03 | 2 |
| 50 | 30 | 1.24 | 240 | 1.72 | 246 | 7.2 | 1.19 | 0.04 | 1 |
| 51 | 25 | 1.91 | 221 | 2.71 | 423 | 3.0 | 3.41 | 0.18 | 4 |
| 52 | 66 | 1.13 | 192 | 1.57 | 124 | 6.5 | 1.58 | 0.02 | 1 |
| 53 | 28 | 1.26 | 206 | 1.88 | 152 | 6.7 | 1.03 | 0.05 | 2 |
| 54 | 67 | 1.32 | 250 | 1.34 | 161 | 6.7 | 2.15 | 0.09 | 1 |
| 55 | 65 | 1.05 | 234 | 1.27 | 194 | 7.0 | 1.87 | 0.03 | 1 |
| 56 | 27 | 1.78 | 219 | 6.55 | 382 | 4.4 | 1.43 | 0.04 | 4 |
| 57 | 60 | 0.99 | 93 | 1.60 | 194 | 7.0 | 1.05 | 0.01 | 1 |
| 58 | 63 | 1.20 | 207 | 5.16 | 247 | 7.1 | 2.94 | 0.05 | 1 |
| 59 | 64 | 1.58 | 212 | 1.24 | 189 | 6.1 | 1.14 | 0.01 | 1 |
| Precision | Recall | F1-Score | Precision | Recall | F1-Score | ||
|---|---|---|---|---|---|---|---|
| WOA–RF | RF | ||||||
| class1 | 1.00 | 1.00 | 1.00 | class1 | 1.00 | 1.00 | 1.00 |
| class2 | 1.00 | 1.00 | 1.00 | class2 | 1.00 | 1.00 | 1.00 |
| class3 | 1.00 | 0.80 | 0.89 | class3 | 1.00 | 0.80 | 0.89 |
| class4 | 0.75 | 1.00 | 0.86 | class4 | 0.75 | 1.00 | 0.86 |
| DT | ANN | ||||||
| class1 | 1.00 | 1.00 | 1.00 | class1 | 1.00 | 1.00 | 1.00 |
| class2 | 0.67 | 1.00 | 0.80 | class2 | 0.67 | 1.00 | 0.80 |
| class3 | 1.00 | 0.80 | 0.89 | class3 | 1.00 | 0.80 | 0.89 |
| class4 | 0.67 | 0.67 | 0.67 | class4 | 0.67 | 0.67 | 0.67 |
| KNN | SVM | ||||||
| class1 | 0.50 | 1.00 | 0.67 | class1 | 0.67 | 1.00 | 0.80 |
| class2 | 0.40 | 1.00 | 0.57 | class2 | 0.67 | 1.00 | 0.80 |
| class3 | 1.00 | 0.40 | 0.57 | class3 | 1.00 | 0.80 | 0.89 |
| class4 | 0.00 | 0.00 | 0.00 | class4 | 0.50 | 0.33 | 0.40 |
| Engineering | Volume Fraction of Filling Slurry I1/% | Density of Filling Slurry I2/t.m−3 | Internal Diameter of the Pipeline I3/mm | Deviation Rate I4/% | Pipeline Absolute Roughness I5/um | Stowing Gradient I6 | The Ratio of Slurry Flow Rate with the Critical Velocity I7 | Weighted Average Particle Size I8/mm | Risk Level | Predicted Level |
|---|---|---|---|---|---|---|---|---|---|---|
| Gacun Xinyuan mine | 62 | 1.94 | 205 | 5.78 | 300 | 3.5 | 1.45 | 2.65 | 1 | 1 |
| Dulang gou gold mine | 30 | 1.32 | 74 | 1.37 | 100 | 5.6 | 1.47 | 0.25 | 4 | 4 |
| Guanyinshan mine | 57 | 1.85 | 150 | 3.71 | 400 | 6.7 | 1.10 | 0.75 | 2 | 2 |
| Liwu copper mine | 45 | 1.65 | 154 | 2.10 | 250 | 4.5 | 1.42 | 0.47 | 3 | 3 |
| Suoluo Gou gold mine | 28 | 1.45 | 215 | 0.54 | 85 | 5.3 | 1.60 | 0.19 | 4 | 4 |
| Huili Lala copper mine | 51 | 1.51 | 180 | 1.25 | 200 | 5.9 | 3.50 | 0.43 | 3 | 3 |
| Damaopo Lead Zinc Mine | 66 | 2.05 | 92 | 5.57 | 524 | 7.5 | 0.78 | 2.00 | 1 | 1 |
| Tianbaoshan polymetallic Mine | 58 | 1.76 | 136 | 1.88 | 152 | 6.7 | 1.03 | 0.95 | 2 | 2 |
| Yinchanggou Copper mine | 68 | 1.98 | 90 | 1.34 | 512 | 6.7 | 2.15 | 3.09 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Liu, Z.; Liu, Z.; Xiong, S.; Zhang, S. Random Forest and Whale Optimization Algorithm to Predict the Invalidation Risk of Backfilling Pipeline. Mathematics 2023, 11, 1636. https://doi.org/10.3390/math11071636
Liu W, Liu Z, Liu Z, Xiong S, Zhang S. Random Forest and Whale Optimization Algorithm to Predict the Invalidation Risk of Backfilling Pipeline. Mathematics. 2023; 11(7):1636. https://doi.org/10.3390/math11071636
Chicago/Turabian StyleLiu, Weijun, Zhixiang Liu, Zida Liu, Shuai Xiong, and Shuangxia Zhang. 2023. "Random Forest and Whale Optimization Algorithm to Predict the Invalidation Risk of Backfilling Pipeline" Mathematics 11, no. 7: 1636. https://doi.org/10.3390/math11071636
APA StyleLiu, W., Liu, Z., Liu, Z., Xiong, S., & Zhang, S. (2023). Random Forest and Whale Optimization Algorithm to Predict the Invalidation Risk of Backfilling Pipeline. Mathematics, 11(7), 1636. https://doi.org/10.3390/math11071636






