Cross-Server End-to-End Patient Key Agreement Protocol for DNA-Based U-Healthcare in the Internet of Living Things

Abstract

(1) Background: Third-generation sequencing (TGS) technique directly sequences single deoxyribonucleic acid (DNA) molecules, enabling real-time sequencing and reducing sequencing time from a few days to a few hours. Sequencing devices can be miniaturized and DNA-reading sensors placed on the body to monitor human health and vital signs, building an “internet of living things” (IoLT) facilitating ubiquitous healthcare services. In many cases, patients may wish to directly connect to each other for purposes of sharing real-time sequencing data, medical status or trading genomic data, etc. (2) Problems: User registration for a specific service may be limited due to some reason. Registering for multiple redundant services would also result in wasted money and possible wasteful communication overhead. In addition, since medical data and health information are very sensitive, security and privacy issues in the network are of paramount importance. (3) Methods: In this article, I propose a cross-server end-to-end (CS-E2E) patient authenticated key agreement protocol for DNA-based healthcare services in IoLT networks. My work allows two patients to mutually authenticate each other through assistance of respective servers, so that they can establish a reliable shared session key for securing E2E communications. The design employs multiple cost-saving solutions and robust cryptographic primitives, including smart-card-based single sign-on, elliptic curve cryptography, biohash function, etc. (4) Results: My proposed protocol is proven to be secure against various attacks and to incur reasonable communication cost compared to its predecessor works. The protocol also provides the support for more security properties and better functionalities. (5) Conclusions: The E2E communications between the patients are properly protected using the proposed approach. This assures a secure and efficient cross-server patient conversation for multiple purposes of healthcare communication.

1. Introduction

Second-generation sequencing (SGS), also known as next-generation sequencing (NGS), is the process of identifying the sequence of millions of short deoxyribonucleic acid (DNA) fragments in parallel [1]. When sequenced data are shared with researchers, the causes of many diseases will be identified and new drugs or precision medicines developed [2]. However, the need for longer reads and shorter sequencing times, which are the drawbacks of SGS, led to the advent of third-generation sequencing (TGS) [3]. The TGS technique directly sequences single DNA molecules, enabling real-time sequencing and reducing sequencing time from a few days to a few hours. Sequencing devices can be miniaturized and DNA-reading sensors placed on the body to monitor human health and vital signs, building an “internet of living things” (IoLT) [3,4]. Taking nanopore sequencing technologies as an example, SmidgION is a very small nanopore sequencer designed to be run on smartphones or mobile devices using their batteries and dedicated apps [3]. The DNA samples are loaded into the tiny sequencer from the sensors. The data produced include FAST5 (HDF5) files and/or FASTQ files [5]; they are either stored on the phone’s memory or uploaded to the cloud. In this way, medical clinics can screen for new viruses in seconds, and researchers can obtain DNA sequences in real time for specific analysis. Ubiquitous healthcare (U-healthcare), which is a combination of electronic and mobile healthcare, is more concerned with person-centric therapy rather than traditional hospital healthcare [3]. To this end, DNA-based sequenced data are completely useful for U-healthcare, since it facilitates patient-centric service and personalized treatment process, for instance, real-time monitoring of body fluids [3].

1.1. Research Problems

In a DNA-based U-healthcare, patients communicate with service providers in order to receive medical information and analysis results on their health status through the internet. In many cases, patients may want to directly connect to each other for the purpose of sharing real-time sequencing data, medical status or trading genomic data [2,4,6], etc. However, user registration for a specific service may be limited due to some reason. Moreover, registering for multiple redundant services would result in wasted money and possible wasteful communication overhead. Therefore, a cross-server end-to-end (CS-E2E) communication solution is required in such U-healthcare scenarios for the purposes of efficiency and convenience.

In the direct communication between patients conducted with the assistance of servers, the generated shared key must only be known to the patients; this is the basic security requirement in all E2E communications. In addition, since the communication is conducted through an insecure internet channel, and personal care data and health information are very sensitive, security concerns are of paramount importance. Adversaries may launch various attacks (e.g., replay attacks), aiming to compromise patient privacy or obstruct the service system. The legitimacy of healthcare providers (e.g., doctors, physicians, etc.) during communications also needs to be considered to avoid possible fraudulent behaviors. The two-factor authentication mechanism enabled through a combination of a password and a smart card was introduced in many existing articles to alleviate the security risks present in a single-factor mechanism [7,8]. However, once the adversaries compromise the password or the smart card successfully, the system would be vulnerable to some unavoidable attacks, e.g., impersonation attacks. Upon the demand, there would be a massive number of U-healthcare services provided by different institutions or hospitals. It is not possible for the traditional single-server system to satisfy the needs of users where they may enjoy an increasing number of medical services [7]. Moreover, remembering too many credentials in order to use multiple services may cause a certain inconvenience and directly affect communication efficiency. It is necessary to provide a better authentication mechanism, which can effectively address all the above issues. In addition, concerns regarding the computation cost and communication cost must also be considered in the design.

1.2. Contributions

In this article, I propose a cross-server E2E patient authenticated key agreement protocol for DNA-based U-healthcare services in IoLT networks. Specifically, my work allows two patients to mutually authenticate each other through the assistance of respective servers, so that they can securely establish a reliable shared session key for E2E communications. The efficiency of the communications in the proposed protocol is also considered in the design. The contributions of this work can be summarized as follows.

(1)

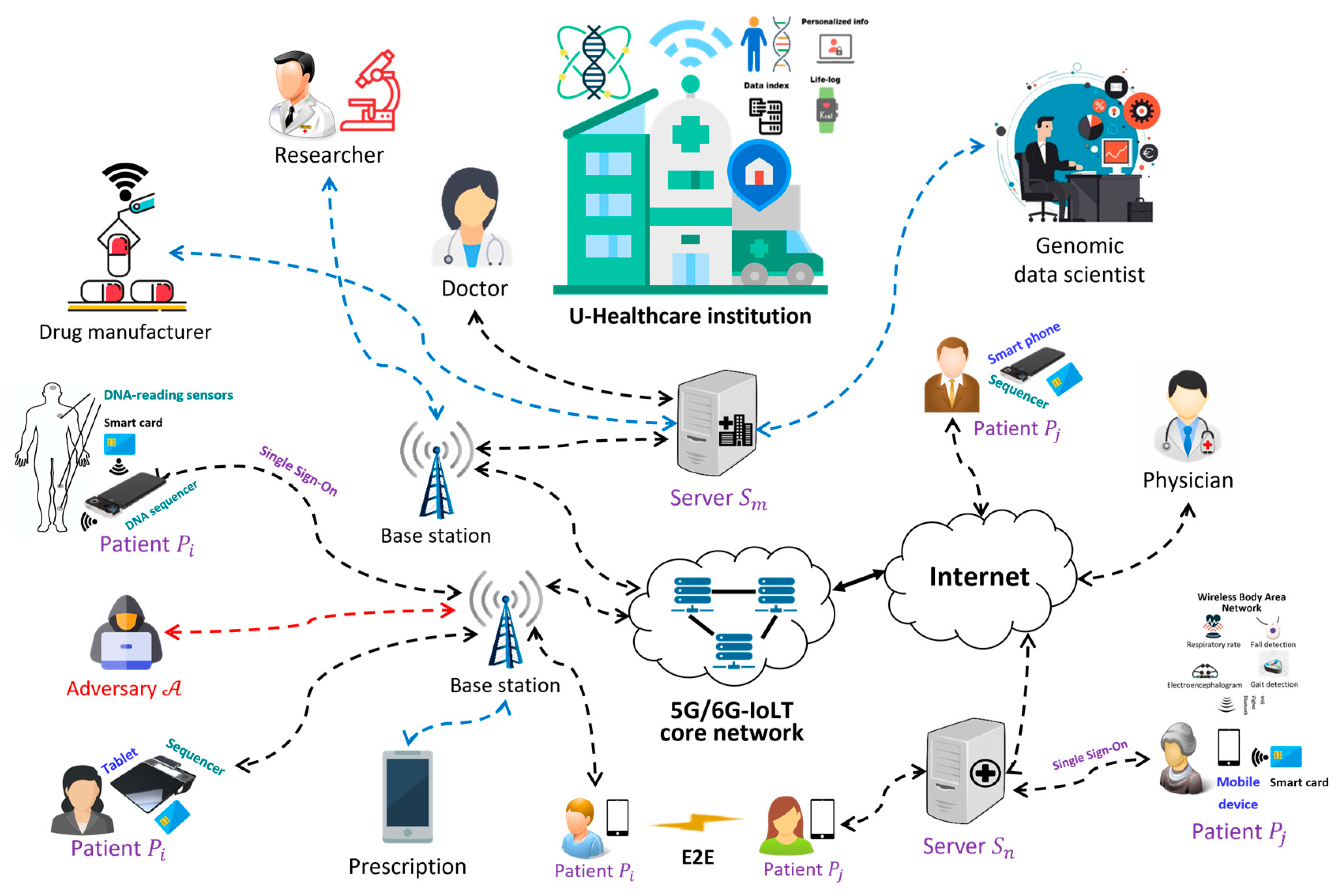
I introduce a DNA-based U-healthcare application constructed in CS-E2E communication environments. In the proposed model, multiple servers provide U-healthcare services based on real-time DNA sequencing data produced by smart tiny sequencers with TGS technology in the IoLT network. Patients are allowed to share healthcare data with each other directly.

(2)

The protocol allows the patients to store single registered credentials on a smart card and enter the credentials once per session only. They are allowed to choose specific servers of a multi-server system from a list in the device to enjoy multiple registered services. I call this solution “smart-card-based single sign-on (SC-SSO)”. Furthermore, the proposed SC-SSO is designed without a centerless solution to alleviate communication cost and reduce the security risk of third-party authority compromise.

(3)

The authentication protocol is designed using three factors, combining password, smart card and biometrics. It can guarantee higher security for communications compared to the single-factor or two-factor solutions. In the protocol, a perfect forward secrecy of shared E2E session keys is assured. Patient anonymity and untraceability are provided in the protocol. Patients can also update their passwords and biometrics to ensure higher security.

(4)

The security proof of my proposed protocol is presented using formal verification tools, including the real-or-random (RoR) model and Burrows–Abadi–Needham (BAN) logic. In addition, an informal analysis is provided to further discuss the resistance to various security attacks, e.g., replay attacks, impersonation attacks, etc.

1.3. Paper Structure

The remainder of the paper is organized as follows. In Section 2, the related works and research motivation are presented. In Section 3, some important technical preliminaries employed in the proposed protocol are explained. The problem statement in Section 4 presents the system model of the proposed protocol, adversarial capabilities and the formal security model. In Section 5, the design details of the proposed protocol are described. Section 6 and Section 7 provide the security certificate and performance analysis of the work, respectively. In Section 8 of the paper, I conclude the work and discuss some ideas regarding future research directions.

2. Related Works

E2E communication security has been discussed in many research papers. In 2012, Fereidooni et al. [9] introduced a design of E2E key exchange and encryption protocol for accelerated satellite networks. Another E2E authentication scheme for wearable health monitoring systems proposed by Jiang et al. [10] could assure a secure communication environment for patients and service providers. In Wang et al.’s [11] work, a session key agreement scheme was proposed for E2E security in time-synchronized networks. Liu et al. [12] also conducted research on E2E security authentication protocol of narrow-band internet of things (NB-IoT) for a smart grid based on the physical unclonable function. Nashwan [13] presented a two-factor authentication mechanism for E2E healthcare communications in wireless body sensor networks (WBSNs). Perez et al. [14] proposed a client-server E2E key exchange solution for IoT communications in the application layer. A multi-data multi-user E2E encryption scheme designed by Raj and Venugopalachar [15] provided an access control mechanism for electronic health records stored in clouds. In general, there was no secure cross-server solution for E2E user communications introduced in these works.

In recent years, security issues and authentication solutions in the healthcare systems have become prevalent and have attracted a lot of attention from the scientific community [16]. Deebak and Al-Turjman [17] designed a mutual authentication protocol for cloud-based medical healthcare systems, which addresses several security issues found in Ref. [18], such as smart device stolen attack, server spoofing attack, etc. In another work, a multi-factor fast authentication protocol with patient privacy protection for telecare medical information systems (TMISs) was proposed by Hsu et al. [19]. Wang et al. [20] presented an improved authentication protocol, which resolved some weaknesses of Farash et al.’s [21] scheme for smart healthcare in WBSNs. Recently, Le et al. [22] proposed a three-factor key agreement scheme for multiple healthcare services in 6G networks. Although the work was proven to withstand multiple well-known attacks, I found it was designed without the biometrics update function. The Rabin decryption operation in their protocol was no faster than the one of the RSA cryptosystem [23]. Xu et al. [24] proposed another anonymous three-factor authentication protocol with costly fuzzy extraction operation employed. Lin et al. [25] introduced a multi-server key agreement protocol with patient anonymity for 5G IoT healthcare systems. In the protocol, I found that a public parameter ($N_i$) of the first conveyed transcript was revealed to the public. There was also no timestamp employed in their work, which is not free from denial of service (DoS) attacks. Meshram et al. [26] proposed a password-based user authentication scheme using a smart card based on extended chaotic maps. The server in their protocol stores an additional value ($S{B}_i$) after the authentication procedure is complete. This would not be robust against desynchronization problems. Although Lin et al. [25] and Meshram et al. [26] can provide user anonymity, their works cannot achieve user untraceability, as the messages in their proposals contain some fixed parameters; the adversaries may guess the identity of the user based on these values. In addition, Lin et al. [25] cannot prevent lost smart card attacks, as unmasked user credentials are stored on smart cards directly. Shohaimay and Ismail [27] designed a secure ECC-based two-factor remote authentication protocol for cyber–physical system applications. The two-factor authentication mechanism in the protocol presented some security concerns that need addressing. The communication efficiency of their design is not very high considering the four message transcripts conveyed during the login and authentication process.

Given the drawbacks of the above works noted with specific concerns, I am motivated to propose a new protocol, which could address all the stated limitations while providing various communication functionalities. Furthermore, to the best of my knowledge, the proposed protocol is the first to address the security and privacy concerns in DNA-based healthcare systems enabled by onsite sequencing services.

3. Technical Preliminaries

This section discusses some important technical preliminaries, including the smart card technology, biohash function, elliptic curve cryptography, advanced encryption standard and the main cryptographic notations used in the paper.

3.1. Smart Card Technology

The modern smart card is designed with an embedded integrated circuit chip as either a secure microcontroller or an equivalent intelligence [28]. The card makes use of an internal memory; it can connect to a reader through physical contact or through the contactless radio frequency technique. Smart cards can store large amounts of data; moreover, they can carry out their own on-card functions, including data encryption or verification. For convenience, I recommend using a Bluetooth smart card token or a Bluetooth smart card reader in the design. In the proposed protocol, a smart card is the second factor (something one has) of a three-factor authentication mechanism.

3.2. Biohash Function

The biohash function maps the individuals’ biometrics to specific binary strings, providing the tolerance of noise [29]. The biohash function provides the same security as the one-way hash functions [23]. In the proposed protocol, the biohash function is employed to tolerate a noisy biometric template, which results in a flaw in some existing works, e.g., a biometric authentication protocol proposed by Wong et al. [30]. The function also addresses the efficiency problem of the related ideas, e.g., the fuzzy extractor used in the work of Zhang et al. [29].

Definition 1.

Suppose $B_i$ is the original biometric template of an individual and $B_i^{\prime }$ the newly input one. The input $B_i^{\prime }$ is not identical to $B_i$, but the difference is within an acceptable threshold. We obtain $h_{bio}\left(B_i\right)=h_{bio}\left(B_i^{\prime }\right)$ given a biohash function $h_{bio}$.

3.3. Elliptic Curve Cryptography (ECC)

The ECC is an asymmetric cryptosystem, which offers better performance compared with traditional systems because it employs a smaller key size with the same security [31]. Therefore, ECC-based authentication protocols are highly suitable for mobile devices in many applications scenarios. The security of the ECC is based on the elliptic curve discrete logarithm problem (ECDLP) and the elliptic curve computational Diffie–Hellman problem (ECCDHP), which are two security assumptions used in the proposed protocol. Suppose there is an elliptic curve over a finite field Fp $Ep\left(a, b\right): y^2=x^3+ax+b\left(mod p\right)$.

Definition 2.

Given an integer $k\in Z_p$ and a point $P_{\left(x, y\right)}\in E_p$, it is easy to compute $Q_{\left(x, y\right)}=k.P_{\left(x, y\right)}\in E_p$. However, due to the ECDLP, it is computationally difficult to find the scalar $k$, such that $Q_{\left(x, y\right)}=k.P_{\left(x, y\right)}$ given $P_{\left(x, y\right)}$ and $Q_{\left(x, y\right)}$.

Definition 3.

Given two integers $s,t\in Z_p$ and three points $P_{\left(x, y\right)},s.P_{\left(x, y\right)},t.P_{\left(x, y\right)}\in E_p$, the ECCDHP is used to find the point $s.t.P_{\left(x, y\right)}\in E_p$ given $s.P_{\left(x, y\right)}$ and $t.P_{\left(x, y\right)}$.

3.4. Advanced Encryption Standard (AES)

The AES [32] is a symmetric encryption technique, which provides a high degree of security. AES encryption converts data into an unintelligible form, called ciphertext. Conversely, the decryption converts this ciphertext into its original form, called plaintext. The AES algorithm can generate block ciphertexts of 128 bits, with three different key sizes, namely, 128, 192 and 256 bits. If the AES encryption key is an EC point in the beginning, it can be transformed into an integer (e.g., 256-bit key) through hashing the point’s $x$ and $y$ coordinates for the subsequent process.

3.5. Notations and Cryptographic Functions

Table 1. Notations and cryptographic functions used in the paper.

Notation	Description
$S_m$	$m^{th}$ server
$P_i$	$i^{th}$ patient
$pr{k}_m,pu{k}_m$	Private key, public key of $S_m$
$Cer{t}_m$	Certificate of $S_m$
${\delta }_{m,i}$	Signature of $P_i$’s message signed by $S_m$
$G_{\left(x,y\right)}$	Basic point on the curve $Ep\left(a,b\right)$
$I{D}_i$	Identity of $P_i$
$P{W}_i$	Password of $P_i$
$B_i$	Biometrics of $P_i$
$T$	Timestamp
$||$	Concatenation operation
⊕	Exclusive-or (XOR) operation
$h\left(.\right),h_{bio}\left(.\right)$	One-way hash function, biohash function
$E_k\left(.\right),D_k\left(.\right)$	Symmetric encryption, decryption algorithms using key k
${\left[.\right]}_{S{C}_i}$	Storage parameters in $P_i$’s smart card
${\left[.\right]}_{M{D}_i}$	Storage parameters in $P_i$’s mobile device

explains the notations and main cryptographic functions used in the proposed protocol.

4. Problem Statement

In this section, the system model of the proposed protocol along with the communication problem is presented. I also discuss some adversarial capabilities and describe the formal security model used in the paper.

4.1. System Model

The proposed model includes four main entities in the communication, namely patient $P_i$, server $S_m$, patient $P_j$ and server $S_n$, who are communicating in a multi-server U-healthcare environment. As depicted in Figure 1, the patient $P$ logs into and accesses services from multiple servers $S$. The DNA-based U-healthcare services include monitoring of body fluids, virus control, understanding disease mechanism at the molecular level, etc. [3]. The IoLT network consists of multiple DNA-reading sensors worn by $P$. The sensing data containing DNA samples produced by the sensors are transmitted to $P$’s mobile device with the support of a wireless technology, e.g., Bluetooth, Wi-Fi or Zigbee. Thereafter, a sequencing process is run by a tiny sequencer connected to the mobile device. Through an open internet, the sequences produced are sent to $S$ (e.g., doctors, data scientists, etc.) for further processing and analysis services. For example, in the monitoring of body fluids mentioned, $S$ is allowed to keep an eye on their $P$’s health via blood, sweat and saliva samples. The analysis results would be transmitted back to $P$ upon their specific request. Some related services, for instance, a WBSN, can be integrated to improve the overall healthcare process and possible medical treatments. It is recommended that the communications in the proposed system model are aided with 5G or 6G mobile technology to achieve a truly real-time healthcare process [22]. Mobile devices (smart phones, tablets, etc.) are now known for their simplicity, robustness and advanced connectivity, with many brands supporting 5G. They would also support 6G, which is expected to be introduced in 2030 [33].

In the model, two patients $P_i$ and $P_j$ want to share personal medical information or U-healthcare data with each other. For example, a family member may wish to know the health status of another one. Since this communication is carried out via a public channel, data security and patient privacy become prominent concerns. To this end, the proposed protocol allows $P_i$ and $P_j$ to compute an authenticated E2E session key used to protect their communicated messages. My work designs a three-factor authentication mechanism where a patient uses a mobile device and a smart card to register with respective servers. $P_i$ carries out a SC-SSO, which uses a single set of registered credentials to log into the system and directly communicate with $P_j$ through the assistance of $S_m$ and $S_n$.

4.2. Adversarial Capabilities

Possible attacks in healthcare systems may result in tremendous consequences and damage, including patient security violation, reduced service reliability, etc. The attacks may also affect the treatment processes and harm patients’ health [19]. Upon various potential risks that I have observed, an adversary 𝒜 may have the following attack capabilities.

• 𝒜 has control over the open internet. This means that 𝒜 can intercept, delete, insert or replay any transcript in each communication session.
• 𝒜 may steal the patients’ smart card and/or mobile device and then attempt to extract the secret credentials using power analysis [34].
• 𝒜 attempts to compromise the past messages communicated between patients once they have obtained secret values or even a session key of the current communication session.
• 𝒜 is a privileged insider of the system (e.g., admin) who may attempt to attack the patient’s registered information stored in $S$’s database.
• Legitimate patients or servers can behave as 𝒜 and trigger similar attacks on the system.

4.3. Formal Security Model

The real-or-random (RoR) model is employed to provide the formal security proof of this work. The model is a well-known tool used to analyze the probability of the adversary breaking the cryptographic schemes [35]. In the model concerned, there exist two communicating parties, namely patient $P$ and provider server $S$, which is consistent with the entities of the proposed protocol. They carry out the communications via an open internet channel. In the model, ℂ is a protocol challenger, and $M$ is a message communicated by $P$ and $S$. 𝒜 would execute the following queries to launch various attacks.

• Send(ℂ, $M$): 𝒜 is allowed to request $M$ to ℂ; ℂ replies to 𝒜 in accordance with the rules of the proposed protocol.
• Execute($P,S$): This passive attack allows 𝒜 to eavesdrop on the message communicated by $P$ and $S$.
• Reveal(ℂ): In this attack, 𝒜 attempts to retrieve the session key generated by ℂ based on the rules of the protocol.
• Corrupt$\left(P,x\right)$: In my proposed protocol, this query returns the password of the patient, the biometrics of the patient and the parameters stored on the smart card and the device to 𝒜 if $x=1$, $x=2$ and $x=3$, respectively.
• Test(ℂ): This query allows 𝒜 to request the session key from ℂ; ℂ replies to 𝒜 based on the probabilistic outcome of the coin $c$ tossed.

Definition 4.

Let $Ad{v}_{ℂ}^{DNAHC}$ be the advantage of 𝒜 running in polynomial time in semantically breaking the security system of the proposed protocol, where $NDAHC$ denotes the protocol (for DNA-based U-healthcare). We obtain $Ad{v}_{ℂ}^{DNAHC}=\left|2\mathit{Pr}\left[c^{\prime }=c\right]-1\right|$, where $c^{\prime }$ is the guessed bit of the session key.

5. The Proposed Protocol

Patient $P_i$ directly communicates with patient $P_j$ with the assistance of both servers $S_m$ and $S_n$. The proposed protocol consists of four phases: system initialization phase, registration phase, login and authentication phase, and password and biometrics update phase. All the parties, including $P_i$,$S_m$, $P_j$, $S_n$, participate in the communication, so that $P_i$ and $P_j$ can compute a shared E2E session key. Since the communication between $P_i$ and $S_m$ is identical with the one between $P_j$ and $S_n$, for simplicity, only the communication between $P_i$ and $S_m$ is presented in the registration phase and in the password and biometrics update phase.

5.1. System Initialization Phase

My proposed protocol employs the ECC proposed by the National Institute of Standards and Technology (NIST) [36]. The system generates a curve over a finite field Fp $Ep\left(a, b\right): y^2=x^3+ax+b\left(mod p\right)$ with the point $G_{\left(x, y\right)}$. For simplicity, two coordinates $x$ and $y$ of $G_{\left(x, y\right)}$ are ignored in the description of the protocol. $S_m$ chooses a private key $pr{k}_m$ and computes its public key $pu{k}_m=pr{k}_m.G$. Next, $S_m$ registers with a certificate authority and has the certificate, signature, public key and private key validated. The same procedure is also conducted by $S_n$.

5.2. Registration Phase

This procedure is carried out in a secure channel. $P_i$ is allowed to register with $S_m$ to become a legitimate service user. As shown in Figure 2, $P_i$ and $S_m$ perform the following steps for registration.

Step R1: $P_i$ enters the identity $I{D}_i$, password $P{W}_i$ and the biometrics $B_i$. $P_i$ selects a random number ${\sigma }_i$ and computes $A_{i,m}=h(I{D}_i\left|\left|P{W}_i\right|\right|h_{bio}\left(B_i\right)||{\sigma }_i)$. Next, $P_i$ sends $\left\{I{D}_i,A_{i,m}\right\}$ to $S_m$.

Step R2: Upon receiving $\left\{I{D}_i,A_{i,m}\right\}$, $S_m$ computes $u_{m,i}=h(I{D}_i||pr{k}_m)$ and $B_{m,i}=u_{m,i}\oplus A_{i,m}$. Next, $S_m$ sends $\left\{B_{m,i},pu{k}_m,I{D}_{S_m}\right\}$ to $P_i$.

Step R3: Upon receiving $\left\{B_{m,i},pu{k}_m\right\}$, $P_i$ computes ${\epsilon }_i={\sigma }_i\oplus h\left(I{D}_i\left|\left|P{W}_i\right|\right|h_{bio}\left(B_i\right)\right)$ and $V_i=h(h\left(I{D}_i\left|\left|P{W}_i\right|\right|{\sigma }_i\right)||h_{bio}\left(B_i\right))$. Finally, $P_i$ stores $\left\{B_{m,i},pu{k}_m,I{D}_{S_m}\right\}$ and $\left\{V_i,{\epsilon }_i,A_{i,m}\right\}$ on the mobile device $M{D}_i$ and the smart card $S{C}_i$, respectively.

5.3. Login and Authentication Phase

This phase is conducted via an unreliable channel, where $P_i$ and $P_j$ log in and mutually authenticate with $S_m$ and $S_n$, respectively. $P_i$ and $P_j$ also authenticate with each other and compute a shared session key through the assistance of $S_m$ and $S_n$. Figure 3 shows the whole procedure in this phase.

Step A1: $P_i$ inserts $S{C}_i$, enters $I{D}_i^{*},P{W}_i^{*},B_i^{*}$ and computes ${\sigma }_i={\epsilon }_i\oplus h\left(I{D}_i^{*}\left|\left|P{W}_i^{*}\right|\right|h_{bio}\left(B_i^{*}\right)\right)$. The $S{C}_i$ verifies whether $V_i\stackrel{?}{=}h(h\left(I{D}_i^{*}\left|\left|P{W}_i^{*}\right|\right|{\sigma }_i\right)||h_{bio}\left(B_i^{*}\right))$. If there is a match, this allows $P_i$ to select a server $S_m$ from an app interface for logging into a specific service and to select a $P_j$ that $P_i$ wishes to communicate with. Next, $P_i$ generates two random numbers $a_{i,m}$, $s_{i,m}$ and a timestamp $T_{i,m}$ and computes $R_{i,m}=a_{i,m}.G=\left(r_{i,m1}, r_{i,m2}\right)$, $C_{i,m1}=s_{i,m}.G$, $Y_{i,m}=\left(y_{i,m1}, y_{i,m2}\right)$ $=s_{i,m}.pu{k}_m$, $u_{m,i}=B_{m,i}\oplus A_{i,m}$, $c_{i,m21}=y_{i,m1}.(u_{m,i}||I{D}_i)\oplus T_{i,m}mod p$, $c_{i,m22}=y_{i,m2}.r_{i,m1}mod p$, $c_{i,m23}=y_{i,m2}.r_{i,m2}mod p$ and $C_{i,m2}=\left(c_{i,m21}, c_{i,m22}, c_{i,m23}\right)$. $P_i$ sends a message {$C_{i,m1},C_{i,m2},T_{i,m}$} to $S_m$ as a login request.

Step A2: Upon receiving the login request message, $S_m$ computes $Z_{m,i}=\left(z_{m,i1},z_{m,i2}\right)=pr{k}_m{C}_{i,m1}$ and $(u_{m,i}||I{D}_i)=T_{i,m}\oplus c_{i,m21}.z_{m,i1}{}^{-1}mod p$. $S_m$ then checks whether $u_{m,i}\stackrel{?}{=}h(I{D}_i||pr{k}_m)$ to confirm the authenticity of $P_i$. Next, $S_m$ generates a random number $b_{m,i}$ and computes $R_{i,m}=\left(c_{i,m22}.z_{m,i2}{}^{-1}mod p, c_{i,m23}.z_{m,i2}{}^{-1}mod p\right)$, $Y_{m,i}=R_{i,m}.b_{m,i}$ and signature ${\delta }_{m,i}=Si{g}_{pr{k}_m}\left(Y_{m,i}\right)$. Thereafter, $S_m$ sends {${\delta }_{m,i}$, certificate $Cer{t}_m$} to $S_n$ and waits for the message {${\delta }_{n,j}$, certificate $Cer{t}_n$} sent by $S_n$.

Step A3: Upon receiving the message, $S_m$ verifies $Cer{t}_n,{\delta }_{n,j}$ using the public key of $S_n$. If the verification is successful, $S_m$ computes $K_{m,i}=b_{m,i}.Y_{n,j}$, $W_{m,i}=b_{m,i}.G$, ${\beta }_{m,i}=h(Y_{m,i}\left|\left|K_{m,i}\right|\right|I{D}_i||I{D}_{S_m})$ and ciphertext ${\theta }_{m,i}=E_{R_{i,m}}\left(W_{m,i}\left|\left|K_{m,i}\right|\right|{\beta }_{m,i}\right)$. Next, $S_m$ sends {${\theta }_{m,i}$} to $P_i$.

Step A4: Upon receiving the message, $P_i$ obtains $W_{m,i},K_{m,i},{\beta }_{m,i}$ by symmetrically decrypting ${\theta }_{m,i}$ using the key $R_{i,m}$. Next, $P_i$ computes $Y_{i,m}=a_{i,m}.W_{m,i}$ and verifies whether ${\beta }_{m,i}\stackrel{?}{=}h(Y_{i,m}\left|\left|K_{m,i}\right|\right|I{D}_i||I{D}_{S_m})$.

Session key establishment: A similar procedure is carried out by $P_j$ and $S_n$, so that $P_j$ can obtain a legitimate $K_{n,j}$. Thereafter, $P_i$ and $P_j$ compute a common key $K_{i,j}=a_{i,m}.K_{m,i}=a_{j,n}.K_{n,j}=a_{i,m}.a_{j,n}.b_{m,i}.b_{n,j}.G$. In this way, a shared patient E2E session key $K_{i,j}$ is established.

5.4. Password and Biometrics Update Phase

In this phase, $P_i$ updates their password and biometrics stored in $S{C}_i$ to enhance the security. As depicted in Figure 4, the procedure is performed as follows.

Step U1: $P_i$ enters $I{D}_i^{\prime },P{W}_i^{\prime },B_i^{\prime }$ into $S{C}_i$. $S{C}_i$ computes ${\sigma }_i={\epsilon }_i\oplus h\left(I{D}_i^{\prime }\left|\left|P{W}_i^{\prime }\right|\right|h_{bio}\left(B_i^{\prime }\right)\right)$. Next, $S{C}_i$ verifies whether $V_i\stackrel{?}{=}h(h\left(I{D}_i^{\prime }\left|\left|P{W}_i^{\prime }\right|\right|{\sigma }_i\right)||h_{bio}\left(B_i^{\prime }\right))$. If there is a match, $S{C}_i$ requests $P_i$ to enter new credentials $P{W}_i^{new},B_i^{new}$.

Step U2: Upon receiving $P{W}_i^{new},B_i^{new}$, $S{C}_i$ computes ${\epsilon }_i^{new}={\sigma }_i\oplus h\left(I{D}_i^{\prime }\left|\left|P{W}_i^{new}\right|\right|h_{bio}\left(B_i^{new}\right)\right)$ and $V_i^{new}=h(h\left(I{D}_i^{\prime }\left|\left|P{W}_i^{new}\right|\right|{\sigma }_i\right)||h_{bio}\left(B_i^{new}\right))$. Finally, $S{C}_i$ replaces ${\epsilon }_i,V_i$ with ${\epsilon }_i^{new},V_i^{new}$. The new password and biometrics are provided to the smart card.

6. Security Analysis

This section provides a security evaluation of my proposed protocol. RoR model, BAN logic and an informal analysis are included in the analysis. First, the success probability of $\mathcal{A}$ in attacking the protocol is analyzed with the standard RoR model. Thereafter, a mutual authentication proof of communication between the patients is presented using the BAN logic. Finally, a semantic security analysis provides further insight into various possible attacks, which can be prevented in the protocol.

6.1. Formal Security Analysis Using RoR Model

As mentioned, I provide the formal security proof of the protocol using the widely accepted ROR model. The analysis is primarily presented for the communication between $P_i$ and $S_m$. The communication between $P_j$ and $S_n$ can also be achieved using similar arguments, so that E2E communication between $P_i$ and $P_j$ is provably secure. In this proof, several games are included where $\mathcal{A}$ makes various queries discussed in Section 4.3 in order to perform the attacks. The following are the notations used in the proof.

• $L_{hash}$: Length of a hash value.
• $L_{number}$: Length of a random number.
• $L_{biometrics}$: Length of a biometrics value.
• $q_{hash}$: Total number of hash oracle queries.
• $q_{send}$: Total number of Send queries.
• $q_{execute}$: Total number of Execute queries.
• $l_h$: List of hash oracle outputs.
• $l_o$: List of random oracle results.
• $l_m$: List of communicated messages between $P_i$ and $S_m$.
• ${\epsilon }_{biometrics}$: Probability of biometrics false positive.
• $C^{\prime },s^{\prime }$: Zipf parameters.

Definition 5.

ℂ enters an accepted state after receiving the last message in the session. All communicated messages $M_1=\left\{C_{i,m1},C_{i,m2},T_{i,m}\right\}$ and $M_2=\left\{{\theta }_{m,i}\right\}$ are concatenated, forming a session with the identification “s_id”.

Definition 6.

There are some conditions for $P_i^{T_c}$ and $S_m{}^{T_c^{*}}$, as follows: (1) they are in an accepted state; (2) they mutually authenticate each other in the same session s_id; and (3) both are mutual partners of each other. $P_i^{T_c}$ and $S_m{}^{T_c^{*}}$ are called “partners” if they simultaneously satisfy all the conditions.

Definition 7.

There are some conditions for ℂ, as follows: (1) ℂ is in an accepted state; (2) the query Reveal(ℂ) was never submitted; and (3) fewer than two Corrupt$\left(P_i,x\right)$ queries were submitted. ℂ can satisfy the freshness rule if ℂ simultaneously meets all the conditions. In fact, my protocol would still be safe even if $\mathcal{A}$ submits queries “Corrupt$\left(P_i,1\right)$ and Corrupt$\left(P_i,3\right)$ ” or “Corrupt$\left(P_i,2\right)$ and Corrupt$\left(P_i,3\right)$ ”, since $\mathcal{A}$ is not able to compromise the masked credentials stored on the smart card.

Definition 8.

Let $Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right)$ be the advantage of 𝒜 in breaking the ECDLP assumption. Since the assumption holds, $Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right)$ is defined as a negligible probability with execution time $t_{\mathcal{A}}$.

Definition 9.

Let $Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right)$ be the advantage of 𝒜 in breaking the ECCDHP assumption. Similarly, $Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right)$ is defined as a negligible probability with execution time $t_{\mathcal{A}}$.

Definition 10.

The value $max\left\{C^{\prime }.q_{send}^{s^{\prime }},q_{send}\left(\frac{1}{2^{L_{biometrics}}},{\epsilon }_{biometrics}\right)\right\}$ is sufficiently small, so that 𝒜 cannot guess the credentials of $P_i$ [19].

Theorem 1.

Since 𝒜 has the following negligible probability of breaking our security system, the proposed protocol is semantically secure.

$$\begin{gathered} Ad{v}_{ℂ}^{DNAHC} \le \frac{{\left(q_{send}+q_{execute}\right)}^3+6q_{send}}{2^{L_{number}}}+\frac{q_{hash}{}^2+14q_{hash}}{2^{L_{hash}}} \\ +2max\left\{\left(C^{\prime }.q_{send}^{s^{\prime }}\right),q_{send}\left(\frac{1}{2^{L_{biometrics}}},{\epsilon }_{biometrics}\right)\right\} \\ +6q_{hash}\left(q_{send}+q_{execute}+1\right)Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right) \\ +2q_{hash}\left(q_{send}+q_{execute}+1\right)Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right) \end{gathered}$$

(1)

Proof. 

Six simulated games are included in the proof, namely $Gam{e}_0,Gam{e}_1,Gam{e}_2,Gam{e}_3,Gam{e}_4,Gam{e}_5$, so that the success probability of 𝒜‘s attack gradually increases. The ultimate purpose of 𝒜 is to retrieve the bit $c$ with the Test query after each game finishes. $Pr\left[S_i\right]$ denotes the success probabilities where $S_i$ ($i=0,1,2,3,4,5$) are the events in different games. A protocol simulator $ℬ$ is set to play the role of the challenger ℂ.

$Gam{e}_0$: This game starts the simulation, and it is identical to the real protocol in the random oracles. $c$ is tossed by $ℬ$ to start the game. We have

$$Ad{v}_{ℂ}^{DNAHC}=\left|2\mathit{Pr}\left[S_0\right]-1\right|$$

(2)

$Gam{e}_1$: This game presents all the queries discussed in Section 4.3.

Table 2. Simulation of the Hash, Reveal, Test, Corrupt, Execute and Send oracle queries.

The Hash query is simulated as follows, where ${\mathit{M}}_{\mathit{i}}$ is a message. If the record (${\mathit{M}}_{\mathit{i}}$, $\mathit{h}\left({\mathit{M}}_{\mathit{i}}\right)$) is found in the list ${\mathit{l}}_{\mathit{h}}$, return $\mathit{h}\left({\mathit{M}}_{\mathit{i}}\right)$; otherwise, choose a ${\mathit{h}}^{\prime }\left({\mathit{M}}_{\mathit{i}}\right)\in {\mathit{Z}}_{\mathit{p}}^{*}$ and add (${\mathit{M}}_{\mathit{i}}$, ${\mathit{h}}^{\prime }\left({\mathit{M}}_{\mathit{i}}\right)$) into ${\mathit{l}}_{\mathit{h}}$; in this way, a similar procedure is performed to create ${\mathit{l}}_{\mathit{o}}$.

Simulation of the Reveal(ℂ) query is simply performed as follows. Once ℂ is in an accepted state, the session key formed by ℂ is returned.

Simulation of the Test(ℂ) query is performed as follows. ℂtosses the coin $\mathit{c}$. If $\mathit{c}=\mathbf{1}$, the query returns an available $\mathit{S}\mathit{K}$; otherwise, the query returns a random number.

The query Corrupt(${\mathit{P}}_{\mathit{i}},\mathit{x}$) is simulated as follows. If $\mathit{x}=\mathbf{1}$, the query outputs $\mathit{P}{\mathit{W}}_{\mathit{i}}$. If $\mathit{x}=\mathbf{2}$, the query outputs ${\mathit{B}}_{\mathit{i}}$. If $\mathit{x}=\mathbf{3}$, the query outputs the parameters stored in $\mathit{S}{\mathit{C}}_{\mathit{i}}$ or $\mathit{M}{\mathit{D}}_{\mathit{i}}$.

Simulation of the Execute(${\mathit{P}}_{\mathit{i}}$, ${\mathit{S}}_{\mathit{m}}$) query occurs in succession to simulation of the Send(ℂ, ${\mathit{M}}_{\mathit{i}}$) query, which is described as follows. ${\mathit{P}}_{\mathit{i}}$ sends ${\mathit{M}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathit{m}}$, and ${\mathit{S}}_{\mathit{m}}$ sends ${\mathit{M}}_{\mathbf{2}}$ to ${\mathit{P}}_{\mathit{i}}$. We have: <${\mathit{C}}_{\mathit{i},\mathit{m}\mathbf{1}},{\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{22}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{23}},{\mathit{T}}_{\mathit{i},\mathit{m}}$> ← Send(${\mathit{P}}_{\mathit{i}}$, start), <${\{{\mathit{W}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{h}({\mathit{Y}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{I}{\mathit{D}}_{\mathit{i}}||\mathit{I}{\mathit{D}}_{{\mathit{S}}_{\mathit{m}}})\}}_{{\mathit{R}}_{\mathit{i},\mathit{m}}}$> ← Send(${\mathit{S}}_{\mathit{m}}$, <${\mathit{C}}_{\mathit{i},\mathit{m}\mathbf{1}},{\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{22}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{23}},{\mathit{T}}_{\mathit{i},\mathit{m}}$>) Finally, ${\mathit{M}}_{\mathbf{1}}=〈{\mathit{C}}_{\mathit{i},\mathit{m}\mathbf{1}},{\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{22}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{23}},{\mathit{T}}_{\mathit{i},\mathit{m}}〉$ and ${\mathit{M}}_{\mathbf{2}}=〈{\{{\mathit{W}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{h}({\mathit{Y}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{I}{\mathit{D}}_{\mathit{i}}||\mathit{I}{\mathit{D}}_{{\mathit{S}}_{\mathit{m}}})\}}_{{\mathit{R}}_{\mathit{i},\mathit{m}}}〉$ are returned.

Following the rules of the proposed protocol, the Send query is executed below. 𝒜 creates a Send(${\mathit{P}}_{\mathit{i}}$, start) query; ℂ replies to 𝒜 as follows. ℂ computes ${\mathit{C}}_{\mathit{i},\mathit{m}\mathbf{1}}={\mathit{s}}_{\mathit{i},\mathit{m}}.\mathit{G}$, ${\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}={\mathit{y}}_{\mathit{i},\mathit{m}\mathbf{1}}.({\mathit{u}}_{\mathit{i},\mathit{m}}||\mathit{I}{\mathit{D}}_{\mathit{i}})\oplus {\mathit{T}}_{\mathit{i},\mathit{m}}\mathit{m}\mathit{o}\mathit{d} \mathit{p}$, ${\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{22}}={\mathit{y}}_{\mathit{i},\mathit{m}\mathbf{2}}.{\mathit{r}}_{\mathit{i},\mathit{m}\mathbf{1}}\mathit{m}\mathit{o}\mathit{d} \mathit{p}$, ${\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{23}}={\mathit{y}}_{\mathit{i},\mathit{m}\mathbf{2}}.{\mathit{r}}_{\mathit{i},\mathit{m}\mathbf{2}}\mathit{m}\mathit{o}\mathit{d} \mathit{p}$, chooses ${\mathit{T}}_{\mathit{i},\mathit{m}}$ and outputs ${\mathit{M}}_{\mathbf{1}}=〈{\mathit{C}}_{\mathit{i},\mathit{m}\mathbf{1}},{\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{22}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{23}},{\mathit{T}}_{\mathit{i},\mathit{m}}〉$. 𝒜 creates a Send(${\mathit{S}}_{\mathit{m}}$, $〈{\mathit{C}}_{\mathit{i},\mathit{m}1},{\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{22}}, {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{23}},{\mathit{T}}_{\mathit{i},\mathit{m}}〉$) query; ℂ replies to 𝒜 as follows. ℂ computes ${\mathit{Z}}_{\mathit{m},\mathit{i}}=\mathit{p}\mathit{r}{\mathit{k}}_{\mathit{m}}{\mathit{C}}_{\mathit{i},\mathit{m}\mathbf{1}}$, $({\mathit{u}}_{\mathit{i},\mathit{m}}||\mathit{I}{\mathit{D}}_{\mathit{i}})={\mathit{T}}_{\mathit{i},\mathit{m}}\oplus {\mathit{c}}_{\mathit{i},\mathit{m}\mathbf{21}}.{\mathit{z}}_{\mathit{m},\mathit{i}1}{}^{-\mathbf{1}}\mathit{m}\mathit{o}\mathit{d} \mathit{p}$, checks ${\mathit{u}}_{\mathit{m},\mathit{i}}$ and calculates the point ${\mathit{R}}_{\mathit{i},\mathit{m}}$. The session will be terminated if the check on ${\mathit{u}}_{\mathit{m},\mathit{i}}$ does not hold. Otherwise, ℂ outputs ciphertext ${\mathit{M}}_{\mathbf{2}}=〈{\{{\mathit{W}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{h}({\mathit{Y}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{I}{\mathit{D}}_{\mathit{i}}||\mathit{I}{\mathit{D}}_{{\mathit{S}}_{\mathit{m}}})\}}_{{\mathit{R}}_{\mathit{i},\mathit{m}}}〉$. 𝒜 creates a Send(${\mathit{U}}_{\mathit{i}}$, $〈{\{{\mathit{W}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{h}({\mathit{Y}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{I}{\mathit{D}}_{\mathit{i}}||\mathit{I}{\mathit{D}}_{{\mathit{S}}_{\mathit{m}}})\}}_{{\mathit{R}}_{\mathit{i},\mathit{m}}}〉$) query; ℂ replies to 𝒜 as follows. ℂ decrypts ${\{{\mathit{W}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{h}({\mathit{Y}}_{\mathit{m},\mathit{i}}\left|\left|{\mathit{K}}_{\mathit{m},\mathit{i}}\right|\right|\mathit{I}{\mathit{D}}_{\mathit{i}}||\mathit{I}{\mathit{D}}_{{\mathit{S}}_{\mathit{m}}})\}}_{{\mathit{R}}_{\mathit{i},\mathit{m}}}$, computes ${\mathit{Y}}_{\mathit{i},\mathit{m}}={\mathit{a}}_{\mathit{i},\mathit{m}}.{\mathit{W}}_{\mathit{m},\mathit{i}}$ and checks ${\mathit{\beta }}_{\mathit{i},\mathit{m}}$. If the check on ${\mathit{\beta }}_{\mathit{i},\mathit{m}}$ does not hold, ℂ terminates the session. Otherwise, a session key ${\mathit{K}}_{\mathit{i},\mathit{j}}={\mathit{a}}_{\mathit{i},\mathit{m}}.{\mathit{K}}_{\mathit{m},\mathit{i}}$ is established, and the session is terminated.

describes a simulation of the queries in accordance with the rule of the proposed protocol. $G_1$ creates three lists: $l_h$, $l_r$ and $l_m$. Because of the indistinguishability between $G_0$ and $G_1$, we obtain

$$\mathit{Pr}\left[S_1\right]=\mathit{Pr}\left[S_0\right]$$

(3)

$Gam{e}_2$: The collision probabilities of the hash oracle and random oracle queries are considered in this game for all transcripts communicated between $P_i$ and $S_m$. Based on the birthday paradox, we can obtain the highest probability of hash queries as $\frac{q_{hash}{}^2}{2^{L_{hash}+1}}$. In the login and authentication phase, there are three random numbers $a_{i,m},s_{i,m},b_{m,i}$ generated by $P_i$ and $S_m$ to construct two messages {$C_{i,m1},C_{i,m2},T_{i,m}$} and {${\theta }_{m,i}$}. Its collision probability is at most $\frac{{\left(q_{send}+q_{execute}\right)}^3}{2^{L_{number}+1}}$. As $G_1$ and $G_2$ are indistinguishable, we have

$$|\mathit{Pr}\left[S_2\right]-\mathit{Pr}\left[S_1\right]|\le \frac{{\left(q_{send}+q_{execute}\right)}^3}{2^{L_{number}+1}}+\frac{q_{hash}{}^2}{2^{L_{hash}+1}}$$

(4)

$Gam{e}_3$: This game is similar to the previous game, but the queries are executed for each specific transcript. $G_3$ consists of two cases consistent with two transcripts sent by $P_i$ and $S_m$.

+ Case 1: The query Send($S_m,M_1$) is considered in this case. The messages $C_1$ are computed from four values $C_{i,m1},c_{i,m21}, c_{i,m22}, c_{i,m23}$, which result in a probability of 4$\frac{q_{hash}}{2^{L_{hash}}}$ in total. Note that I do not consider $T_{i,m}$ in $M_1$ for the hash oracle, as the timestamp is not difficult to retrieve or generate. On the other hand, the random numbers $a_{i,m},s_{i,m}$ contained in $M_1$ have a probability of 2$\frac{q_{send}}{2^{L_{number}}}$.

+ Case 2: I consider the query Send($P_i,M_2$) in this case. Suppose the values $W_{m,i},K_{m,i}$ and the hash ${\beta }_{m,i}$ contained in messages $M_2$ are divulged to 𝒜 in order to perform the attacks. To this end, the maximum probability is up to 3$\frac{q_{hash}}{2^{L_{hash}}}$. The random number $b_{m,i}$ has a probability of $\frac{q_{send}}{2^{L_{number}}}$.

Overall, this results in the following total probability:

$$|\mathit{Pr}\left[S_3\right]-\mathit{Pr}\left[S_2\right]|\le 7\frac{q_{hash}}{2^{L_{hash}}}+3\frac{q_{send}}{2^{L_{number}}}$$

(5)

$Gam{e}_4$: I consider the guessing attacks executed by 𝒜 in this game. Four cases are presented as follows.

+ Case 1: 𝒜 executes the query Corrupt$\left(P_i,x=1\right)$ to guess the password of $P_i$. Next, 𝒜 executes the query Send($S_m,M_1$) for the attacks. In this case, the highest probability is ($C^{\prime }.q_{send}^{s^{\prime }}$).

+ Case 2: 𝒜 creates the query Corrupt$\left(P_i,x=2\right)$ to retrieve the biometrics of $P_i$. Since 𝒜 also creates the query Send($S_m,M_1$) in this case, the simulated probability is at most $max\left\{q_{send}\left(\frac{1}{2^{L_{biometrics}}},{\epsilon }_{biometrics}\right)\right\}$.

+ Case 3: 𝒜 attempts to break the ECDLP assumption (using the Hash oracle queries) to compromise the numbers $a_{i,m},s_{i,m},b_{m,i}$ based on the values $R_{i,m},C_{i,m1},Y_{m,i}$, respectively. Its maximum collision probability is up to $3q_{hash}Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right)$.

+ Case 4: 𝒜 attempts to break the ECCDHP assumption (using the Hash oracle queries) to directly compromise the key $K_{i,j}=\left(a_{i,m}.b_{m,i}\right).\left(a_{j,n}.b_{n,j}\right).G$ given the received values $Y_{m,i}=\left(a_{i,m}.b_{m,i}\right).G$ and $\left(a_{j,n}.b_{n,j}\right).G$. The maximum collision probability is up to $q_{hash}Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right)$.

Since $G_3$ and $G_4$ are identical without the above attacks, we obtain

$$\begin{gathered} \left|\mathit{Pr}\left[S_4\right]-\mathit{Pr}\left[S_3\right]\right|\le max\left\{\left(C^{\prime }.q_{send}^{s^{\prime }}\right),q_{send}\left(\frac{1}{2^{L_{biometrics}}},{\epsilon }_{biometrics}\right)\right\} \\ +3q_{hash}Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right)+q_{hash}Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right) \end{gathered}$$

(6)

$Gam{e}_5$: A forward secrecy attack scenario is simulated in this final game. 𝒜 creates the Execute, Send and Hash oracle queries to retrieve the session keys from the old transcripts sent by $P_i$ and $S_m$. The game is simulated with the advantage in breaking the ECDLP assumption and the ECCDHP assumption. To this end, the Test query is created to return the session key to 𝒜. Since 𝒜 has to break the ECDLP three times in a row or break the ECCDHP one time, we have

$$\begin{gathered} |\mathit{Pr}\left[S_5\right]-\mathit{Pr}\left[S_4\right]|\le 3q_{hash}\left(q_{send}+q_{execute}\right)Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right) \\ +q_{hash}\left(q_{send}+q_{execute}\right)Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right) \end{gathered}$$

(7)

After executing all the games, 𝒜 guesses the bit $b^{\prime }$ with the probability of the Test query as follows.

$$\mathit{Pr}\left[S_5\right]=\frac{1}{2}$$

(8)

According to Equations (3)–(8), and applying the triangular inequality, we obtain

$$\begin{gathered} |\mathit{Pr}\left[S_0\right]-\frac{1}{2}\left|=\right|\mathit{Pr}\left[S_1\right]-\mathit{Pr}\left[S_5\right]| \\ \le \left|\mathit{Pr}\left[S_1\right]-\mathit{Pr}\left[S_2\right]\right| \\ +\left|\mathit{Pr}\left[S_2\right]-\mathit{Pr}\left[S_3\right]\right| \\ +\left|\mathit{Pr}\left[S_3\right]-\mathit{Pr}\left[S_4\right]\right| \\ +\left|\mathit{Pr}\left[S_4\right]-\mathit{Pr}\left[S_5\right]\right| \end{gathered}$$

(9)

Based on Equations (2)–(9), we can achieve the following equation:

$$\begin{gathered} \frac{1}{2}Ad{v}_{ℂ}^{DNAHC}=\left|\mathit{Pr}\left[S_0\right]-\frac{1}{2}\right| \\ \le \frac{{\left(q_{send}+q_{execute}\right)}^3}{2^{L_{number}+1}}+\frac{q_{hash}{}^2}{2^{L_{hash}+1}} \\ +7\frac{q_{hash}}{2^{L_{hash}}}+3\frac{q_{send}}{2^{L_{number}}} \\ +max\left\{\left(C^{\prime }.q_{send}^{s^{\prime }}\right),q_{send}\left(\frac{1}{2^{L_{biometrics}}},{\epsilon }_{biometrics}\right)\right\} \\ +3q_{hash}\left(q_{send}+q_{execute}+1\right)Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right) \\ +q_{hash}\left(q_{send}+q_{execute}+1\right)Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right) \end{gathered}$$

(10)

The final result can be easily achieved as follows:

$$\begin{gathered} Ad{v}_{ℂ}^{DNAHC} \le \frac{{\left(q_{send}+q_{execute}\right)}^3+6q_{send}}{2^{L_{number}}}+\frac{q_{hash}{}^2+14q_{hash}}{2^{L_{hash}}} \\ +2max\left\{\left(C^{\prime }.q_{send}^{s^{\prime }}\right),q_{send}\left(\frac{1}{2^{L_{biometrics}}},{\epsilon }_{biometrics}\right)\right\} \\ +6q_{hash}\left(q_{send}+q_{execute}+1\right)Ad{v}_{\mathcal{A}}^{ECDLP}\left(t_{\mathcal{A}}\right) \\ +2q_{hash}\left(q_{send}+q_{execute}+1\right)Ad{v}_{\mathcal{A}}^{ECCDHP}\left(t_{\mathcal{A}}\right) \end{gathered}$$

(11)

Therefore, I claim Theorem 1. The proposed protocol is proven to be semantically secure, since the above probability is completely negligible. □

6.2. Authentication Proof Using BAN Logic

BAN logic is a well-known tool, which provides a mutual authentication proof of cryptographic protocols [27]. Based on the rules and analytical logic defined in the tool, I aim to prove that $P_i$ and $P_j$ believe the key $K_{i,j}$ computed as a shared secret known only to them. Some notations I use for the proof are described as follows.

• A |≡ X: A believes statement M.
• A ⊲ M: A sees statement M.
• #(M): Formula M is fresh.
• A |~ M: A once said statement M.
• (M, N): M or N is one part of formula (M, N).
• A ⟹ M: A has jurisdiction over statement M.
• $\langle M{\rangle }_N$: This represents M combined with formula N.
• $A\stackrel{K}{\leftrightarrow }B$: Value K is known only to A and B, and it is used for their communication.
• $A\stackrel{M}{\iff }B$: Formula M is a secret known only by A and B. Only A and B can use M to authenticate each other.

Based on the principle of BAN logic and the procedure of the proposed protocol, the following six authentication goals should be satisfied.

Goal 1: $S_m$ |≡ $\left(S_m\stackrel{R_{i,m}}{\leftrightarrow }{P}_i\right)$. $S_m$ believes $R_{i,m}$ is a secret value sent by $P_i$, and $R_{i,m}$ is a secret key shared by $S_m$ and $P_i$. (G1)

Goal 2: $P_i$ |≡ $\left(P_i\stackrel{R_{i,m}}{\leftrightarrow }{S}_m\right)$. $P_i$ believes $R_{i,m}$ is a secret key shared by $P_i$ and $S_m$. (G2)

Goal 3: $S_n$ |≡ $\left(S_n\stackrel{R_{j,n}}{\leftrightarrow }{P}_j\right)$. $S_n$ believes $R_{j,n}$ is a secret value sent by $P_j$, and $R_{j,n}$ is a secret key shared by $S_n$ and $P_j$. (G3)

Goal 4: $P_j$ |≡ $\left(P_j\stackrel{R_{j,n}}{\leftrightarrow }{S}_n\right)$. $P_j$ believes $R_{j,n}$ is a secret key shared by $P_j$ and $S_n$. (G4)

Goal 5: $P_i$ |≡ $\left(P_i\stackrel{K_{i,j}}{\leftrightarrow }{P}_j\right)$. $P_i$ believes $K_{i,j}$ is a secret value sent by $P_j$, and $K_{i,j}$ is a secret key shared by $P_i$ and $P_j$. (G5)

Goal 6: $P_j$ |≡ $\left(P_j\stackrel{K_{i,j}}{\leftrightarrow }{P}_i\right)$. $P_j$ believes $K_{i,j}$ is a secret value sent by $P_i$, and $K_{i,j}$ is a secret key shared by $P_j$ and $P_i$. (G6)

I consider four messages communicated in the login and authentication phase for the analysis, described as follows.

Message 1. $P_i\to S_m:(a_{i,m}.G,y_{i,m1}.(u_{i,m}||I{D}_i)\oplus T_{i,m}mod p,y_{i,m2}.r_{i,m1}mod p,y_{i,m2}.r_{i,m2}mod p,T_{i,m})$.

Message 2. $S_m\to P_i:{(b_{m,i}.G,b_{m,i}.Y_{n,j},h(Y_{m,i}\left|\left|K_{m,i}\right|\right|I{D}_i||I{D}_{S_m}))}_{R_{i,m}}$.

Message 3. $P_j\to S_n:(a_{j,n}.G,y_{j,n1}.(u_{j,n}||I{D}_j)\oplus T_{j,n}mod p,y_{j,n2}.r_{j,n1}mod p,y_{j,n2}.r_{j,n2}mod p,T_{j,n})$.

Message 4. $S_n\to P_j:{(b_{n,j}.G,b_{n,j}.Y_{m,i},h(Y_{n,j}\left|\left|K_{n,j}\right|\right|I{D}_j||I{D}_{S_n}))}_{R_{j,n}}$.

The idealized form of these messages used in the BAN logic is given below.

Message 1. $P_i\to S_m:(\langle C_{i,m1},c_{i,m21},s_{i,m},a_{i,m}{\rangle }_{X_{i,m}},T_{i,m})$.

Message 2. $S_m\to P_i:\langle b_{m,i}.G,b_{m,i}.Y_{n,j},h\left(Y_{m,i},K_{m,i},I{D}_i,I{D}_{S_m}\right){\rangle }_{X_{i,m}}$.

Message 3. $P_j\to S_n:(\langle C_{j,n1},c_{j,n21},s_{j,n},a_{j,n}{\rangle }_{X_{j,n}},T_{j,n})$.

Message 4. $S_n\to P_j:\langle b_{n,j}.G,b_{n,j}.Y_{m,i},h\left(Y_{n,j},K_{n,j},I{D}_j,I{D}_{S_n}\right){\rangle }_{X_{j,n}}$.

Some logical rules provided by the tool are specified as follows.

• $\frac{A\stackrel{K}{\iff }B,B⊲\langle M{\rangle }_K}{A\left|\equiv B\right|~M}$: Seeing rule (R1);
• $\frac{A\left|\equiv B\right|~\left(M,N\right)}{A\left|\equiv B\right|~M}$: Interpretation rule (R2);
• $\frac{A|\equiv \#\left(M\right)}{A|\equiv \#\left(M,N\right)}$: Freshness rule (R3);
• $\frac{A|\equiv \#\left(M\right),A\left|\equiv B\right|~M}{A\left|\equiv B\right|\equiv M}$: Verification rule (R4);
• $\frac{A\left|\equiv B\Rightarrow M,A\right|\equiv B|\equiv M}{A|\equiv M}$: Jurisdiction rule (R5);
• $\frac{A|\equiv \left(M,N\right)}{A|\equiv M}$: Additional rule (R6).

Based on the idealized form, the following assumptions are made for the proof of the proposed protocol.

• $S_m$ |≡ $P_i\stackrel{X_{i,m}}{\iff }{S}_m$: Assumption 1 (A1);
• $S_m$ |≡ $\#\left(T_{i,m}\right)$: Assumption 2 (A2);
• $S_m\Rightarrow \left(pr{k}_m\right)$: Assumption 3 (A3);
• $P_i$ |≡ $\#\left(Y_{n,j}\right)$: Assumption 4 (A4);
• $S_m\Rightarrow \left(b_{i,m}\right)$: Assumption 5 (A5);
• $P_i\Rightarrow \left(a_{i,m}\right)$: Assumption 6 (A6).

Based on the above rules, assumptions and protocol procedures, a mutual authentication proof of my work is performed in the following steps.

• $S_1$: According to Message 1, we have $S_m⊲(\langle C_{i,m1},c_{i,m21},s_{i,m},a_{i,m}{\rangle }_{X_{i,m}},T_{i,m})$.
• $S_2$: Based on R1 and A1, we obtain $S_m$ |≡ $P_i$ |~ $\left(C_{i,m1},c_{i,m21},s_{i,m},a_{i,m},T_{i,m}\right)$.
• $S_3$: Based on R2, we obtain $S_m$ |≡ $P_i$ |~ $\left(s_{i,m},a_{i,m},T_{i,m}\right)$.
• $S_4$: According to R3 and A2, we obtain $S_m$ |≡ #$\left(s_{i,m},a_{i,m}\right)$.
• $S_5$: Based on R4, we obtain $S_m$ |≡ $P_i$ |≡ $\left(s_{i,m},a_{i,m}\right)$.
• $S_6$: According to R5 and $S_5$, we have $S_m$ |≡ $\left(s_{i,m},a_{i,m}\right)$.
• $S_7$: Based on R6, we obtain $S_m$ |≡ $s_{i,m}$, and $S_m$ |≡ $a_{i,m}$.
• $S_8$: According to A3 and $R_{i,m}=\left(s_{i,m}.y.a_{i,m}.x mod p\right).\left(pr{k}_m.s_{i,m}.y{)}^{-1}mod p, \left(s_{i,m}.a_{i,m}.y^2 mod p\right).{\left(pr{k}_m.s_{i,m}.y\right)}^{-1}mod p\right)$, we obtain $S_m$ |≡ $\left(S_m\stackrel{R_{i,m}}{\leftrightarrow }{P}_i\right)$ (G1 achieved).
• $S_9$: According to Message 2, we have $P_i⊲\left(\langle b_{m,i}.G,b_{m,i}.Y_{n,j},{\beta }_{m,i}{\rangle }_{X_{i,m}}\right)$.
• $S_{10}$: Based on R1 and A1, we obtain $P_i$ |≡ $S_m$ |~ $\left(b_{m,i}.G,b_{m,i}.Y_{n,j},{\beta }_{m,i}\right)$.
• $S_{11}$: Based on R2, we obtain $P_i \left|\equiv S_m \right|~\left(b_{m,i}.Y_{n,j},{\beta }_{m,i}\right)$.
• $S_{12}$: Using R3, A4 and A5, we obtain $P_i |\equiv \#\left({\beta }_{m,i}\right)$.
• $S_{13}$: Based on A6, $S_{12}$ and the rule of the protocol, we obtain $P_i$ |≡ $\left(P_i\stackrel{R_{i,m}}{\leftrightarrow }{S}_m\right)$ (G2 achieved).
• $S_{14}$: Using similar arguments of $S_8$ and $S_{13}$ for Message 3 and Message 4, we can obtain $S_n$ |≡ $\left(S_n\stackrel{R_{j,n}}{\leftrightarrow }{P}_j\right)$ (G3 achieved) and $P_j$ |≡ $\left(P_j\stackrel{R_{j,n}}{\leftrightarrow }{S}_n\right)$ (G4 achieved), respectively.
• $S_{15}$: Based on A4, A5, A6, $S_{11}$ and $K_{i,j}=a_{i,m}.b_{m,i}.Y_{n,j}$, we obtain $P_i$ |≡ $\left(P_i\stackrel{K_{i,j}}{\leftrightarrow }{P}_j\right)$ (G5 achieved).
• $S_{16}$: Using similar arguments of $S_{15}$, we can obtain $P_j$ |≡ $\left(P_j\stackrel{K_{i,j}}{\leftrightarrow }{P}_i\right)$ (G6 achieved).

Therefore, the proposed protocol achieves G1, G2, G3, G4, G5 and G6. Hence, it can assure that both $P_i$ and $P_j$ mutually authenticate each other.

6.3. Informal Security Analysis

In this subsection, I further discuss the various security features of the proposed protocol and explain its resistance to multiple well-known attacks. The analysis primarily involves the communication between $P_i$ and $S_m$. Similar arguments can be used to analyze the communication between $P_j$ and $S_n$, thereby assuring $P_i$ and $P_j$ securely share an E2E common key. The details are as follows.

User anonymity, user untraceability and message unlinkability: The identity $I{D}_i$ of $P_i$ is masked in $c_{i,m21}$ of the message sent by $P_i$. The message conveyed by $S_m$ also does not make the $I{D}_i$ publicly visible. Therefore, $I{D}_i$ cannot be revealed to 𝒜 during transmission of the messages. Each value contained in message $\left\{C_{i,m1},C_{i,m2},T_{i,m}\right\}$, message $\left\{{\delta }_m,Cer{t}_m\right\}$ and message {${\theta }_{m,i}$} of each session is completely not identical, since they are computed using different random numbers and timestamps. Therefore, it is not possible for 𝒜 to identify any two transcripts conveyed by a single $P_i$. In addition, there are no constants found when linking each value of $\left\{C_{i,m1},C_{i,m2},T_{i,m},{\delta }_m,Cer{t}_m,{\theta }_{m,i}\right\}$ with each other for the purpose of tracing. Thus, the proposed protocol simultaneously achieves user anonymity, user untraceability and message unlinkability.

Robust mutual authentication: Based on the login request message $\left\{C_{i,m1},C_{i,m2},T_{i,m}\right\}$ from $P_i$, $S_m$ computes $Z_{m,i}$ using its private key $pr{k}_m$ in order to retrieve $u_{i,m},I{D}_i$. $S_m$ verifies the legitimacy of $P_i$ by checking whether $u_{m,i}=h(I{D}_i||pr{k}_m)$. On the other hand, upon receiving the message, $P_i$ decrypts ${\theta }_{m,i}$ using $R_{i,m}$. $P_i$ checks the legitimacy of $S_m$ by confirming whether ${\beta }_{i,m}=h(Y_{i,m}\left|\left|K_{m,i}\right|\right|I{D}_i||I{D}_{S_m})$. Value $Y_{n,j}$ sent from $S_n$ is also reliable upon successful checks on ${\delta }_n,Cer{t}_n$. If one of the above checks do not hold, the communication will be terminated; otherwise, it allows $P_i$ to compute the E2E key $K_{i,j}$. Furthermore, in Section 6.2, a mutual authentication proof of communication between $P_i$ and $P_j$ is provided. Thus, my protocol achieves robust mutual authentication.

Perfect forward secrecy: Suppose 𝒜 somehow obtained secret values, random numbers or even a session key communicated in the current session. 𝒜 intends to use these values to attack past communications. Since the values are completely different in each communication session, it is not possible for 𝒜 to carry out these attacks. For example, 𝒜 is not able to use the current key $K_{i,j}^{*}=a_{i,m}^{*}.a_{j,n}^{*}.b_{m,i}^{*}.b_{n,j}^{*}.G$ to decrypt a ciphertext encrypted using a past key $K_{i,j}=a_{i,m}.a_{j,n}.b_{m,i}.b_{n,j}.G$. Therefore, the conclusion is established.

E2E keysecurity: If $S_m$ acts as 𝒜 and attempts to attack the shared key of $P_i$ and $P_j$, 𝒜 needs to know the number $a_{i,m}$ randomly selected by $P_i$ used to compute $K_{i,j}=a_{i,m}.K_{m,i}$. Due to the ECDLP, it is not possible to retrieve $a_{i,m}$ from the given $R_{i,m}$, where $R_{i,m}=a_{i,m}.G$. In addition, 𝒜 will not compute the key $K_{i,j}=\left(a_{i,m}.b_{m,i}\right).\left(a_{j,n}.b_{n,j}\right).G$ successfully given the values $Y_{m,i}=\left(a_{i,m}.b_{m,i}\right).G$ and $\left(a_{j,n}.b_{n,j}\right).G$ unless 𝒜 is able to break the ECCDHP. Thus, the security of the E2E key is assured.

Resistance to DoS attacks: Defending against a DoS attack is one of the toughest tasks in cyber security, since its attack mechanism is mostly based on computer or network resources. In this analysis, I discuss the resistance of the protocol to possible risks of a DoS attack, which may affect communication performance. At first, the card $S{C}_i$ always checks the legitimacy of $P_i$ based upon $V_i$ and their input credentials $I{D}_i^{*},P{W}_i^{*},B_i^{*}$. If the verification does not hold, the system will immediately terminate the session. Therefore, 𝒜 is not able to flood the communication with subsequent steps. $S_m$ also identifies $P_i$ upon $I{D}_i$, as well as verifying the freshness of $u_{m,i}$ through some ECC-based lightweight computation steps. Repeatedly retransmitting $\left\{C_{i,m1},C_{i,m2},T_{i,m}\right\}$ to disrupt $S_m$’s services would not work efficiently considering the redundant resources on the server side. Moreover, the communication will be stopped if the check on $u_{m,i}$ fails. Hence, the conclusion is established.

Resistance to MITM attacks: In intercepting the login message, 𝒜 may use its own parameters to forge and generate a candidate message. The purpose is to act as a middle man to compromise the conveyed messages between $P_i$ and $S_m$ without being noticed. However, since 𝒜 does not know the key $pr{k}_m$ and the identity $I{D}_i$, it is not possible for 𝒜 to compute a correct $u_{i,m}$ for verification and a correct $Z_{m,i}$ for generating $R_{i,m}$. Without $R_{i,m}$, 𝒜 is also not able to create a tampered message $\left\{{\theta }_{m,i}\right\}$ sent to $P_i$. Thus, my protocol is robust against MITM attacks.

Resistance to replay attacks: Suppose 𝒜 intercepts and resends the message $\left\{C_{i,m1},C_{i,m2},T_{i,m}\right\}$ to $S_m$ in order to perform a replay attack on the subsequent communication session. In my protocol, timestamp $T_{i,m}$, which can only be used once, is employed to check whether the message is resent. Moreover, even if 𝒜 can somehow pass the timestamp challenge, the replay attack will also fail, since 𝒜 does not know $R_{i,m}$ and $a_{i,m}$ to decrypt ${\theta }_{m,i}$ and compromise $K_{i,j}$. Therefore, the conclusion is established.

Resistance to online and offline password guessing attacks: In the online login interface, 𝒜 may enter a guessed password (even with a correct identity and correct biometrics) into the system. Based on the rule of my protocol, $S{C}_i$ will check the value $V_i$ and easily decline the candidate password entered by 𝒜. Suppose 𝒜 somehow obtains values $A_{i,m}$ and $V_i$ and then 𝒜 attempts to guess $P_i$’s password based on these hash values. However, other than $P{W}_i$, $A_{i,m}$ and $V_i$ contain $I{D}_i,B_i,{\sigma }_i$. Therefore, it is not possible for 𝒜 to compute the candidate hashes $A_{i,m}^{\prime },V_i^{\prime }$ and compare them with $A_{i,m},V_i$ to guess the correct password. Thus, the conclusion is established. Along with the password, biometrics is also fully protected in my protocol during the communication process, which guarantees a strong three-factor authentication mechanism. Moreover, the password and biometrics update function is provided in the proposed protocol, which further enhances the security of $P{W}_i$ and $B_i$.

Resistance to stolen smart card attacks: Suppose the card $S{C}_i$ of $P_i$ is somehow lost and 𝒜 has obtained it; 𝒜 conducts a power analysis [34] and retrieves all the parameters stored in $S{C}_i$. Nevertheless, the password $P{W}_i$ and biometrics $B_i$ are not directly stored in $S{C}_i$; they are therefore not exposed to 𝒜 upon power analysis. Even if 𝒜 can simultaneously obtain $M{D}_i$ and $S{C}_i$, 𝒜 is not able to pass the smart card verification without $I{D}_i,P{W}_i,B_i$ when entering the credentials to the login system. With the obtained $M{D}_i$ and $S{C}_i$, it is also not possible for 𝒜 to spoof $S_m$ with $u_{m,i}=B_{m,i}\oplus A_{i,m}$, as 𝒜 does not know the $I{D}_i$ for the check $u_{m,i}\stackrel{?}{=}h(I{D}_i||pr{k}_m)$. If 𝒜 uses $V_i$ obtained from $S{C}_i$ for the verification, 𝒜 can also not compute a valid $C_{i,m21}$ for the login request without $I{D}_i$. Hence, my proposed protocol can fully prevent lost smart card attacks.

Resistance to impersonation attacks: Suppose 𝒜 has obtained the identity $I{D}_i$ and then uses it to compute a candidate login request for the purpose of impersonating $P_i$. Due to the stated resistance to online and offline password guessing attacks, $P{W}_i$ will not be revealed to 𝒜. Moreover, $B_i$ is completely protected and possessed by $P_i$ only; $M{D}_i$ and $S{C}_i$ are also carefully preserved to prevent them from being retrieved $u_{m,i}$. Therefore, upon the obtained $I{D}_i$, it is still not possible for 𝒜 to compute a correct login message $\left\{C_{i,m1},C_{i,m2},T_{i,m}\right\}$. Thus, the proposed protocol can withstand impersonation attacks.

Resistance to insider attacks: Each server $S_m$ is accepted as trustworthy during the registration procedure because $P_i$ registers their secret information to gain services from $S_m$. No sensitive values are stored in $S_m$’s database after registration. Moreover, my protocol is also designed without unmasked biometrics database or plaintext password table required. Hence, the protocol can resist insider attacks.

Resistance to desynchronization attacks: During the communication process, two acknowledgements $u_{m,i}$ and ${\beta }_{i,m}$ are generated for the verifications, which prevent user impersonation and server impersonation. These values will be deleted after the communication sessions are completed. $P_i$ and $S_m$ do not further store any redundant values after each authentication procedure finishes. Therefore, the proposed work completely withstands desynchronization attacks.

7. Performance Evaluation

In this section, a detailed comparative study of the proposed protocol and several related protocols (which are most similar to mine) discussed in Section 2 is presented. Various aspects, including functionality, communication cost and computation cost, are considered in the performance comparison.

7.1. Functionality

The results of a comparison of various functionalities achieved by the protocols are tabulated in

Table 3. Comparison of functionalities and security properties.

Functionalities	[11]	[12]	[13]	[17]	[19]	[20]	[22]	[24]	[25]	[26]	[27]	Mine
Provision of IoLT-based U-healthcare application	×	×	×	×	×	×	×	×	×	×	×	√
Provision of E2E communication	√	√	√	×	×	×	×	×	×	×	×	√
Provision of cross-server communication	×	×	×	×	×	×	×	×	×	×	×	√
Provision of three-factor authentication	×	×	×	×	√	×	√	√	×	×	×	√
Provision of centerless authentication	√	√	√	√	√	√	√	√	√	√	√	√
Provision of SC-SSO solution	×	×	×	×	√	×	√	×	√	×	×	√
Provision of user anonymity	–	√	√	√	√	√	√	√	√	√	√	√
Provision of user untraceability	–	√	√	√	√	√	√	√	×	×	√	√
Provision of message unlinkability	–	√	√	√	√	√	√	√	×	×	√	√
Provision of robust mutual authentication	–	√	√	√	√	√	√	√	√	√	√	√
Provision of perfect forward secrecy	√	√	√	√	√	√	√	√	√	√	√	√
Provision of user password update	–	–	√	–	√	√	√	√	√	√	√	√
Provision of user biometrics update	–	–	–	–	×	–	×	√	–	–	–	√
Provision of mathematical security proof	×	×	×	×	√	×	√	√	×	×	√	√
Resistance to DoS attacks	√	√	√	√	√	√	√	√	×	√	√	√
Resistance to MITM attacks	√	√	√	√	√	√	√	√	√	√	√	√
Resistance to replay attacks	√	√	√	√	√	√	√	√	√	√	√	√
Resistance to online password guessing attacks	–	–	√	–	√	√	√	√	√	√	√	√
Resistance to offline password guessing attacks	–	–	√	–	√	√	√	√	√	√	√	√
Resistance to stolen smart card attacks	–	–	√	√	√	√	√	√	×	√	√	√
Resistance to impersonation attacks	√	√	√	√	√	√	√	√	√	√	√	√
Resistance to insider attacks	√	√	√	√	√	√	√	√	–	√	√	√
Resistance to desynchronization attacks	√	√	√	√	√	√	√	√	√	×	√	√

. The √ symbol signifies that the protocol achieves a specific functionality. The × symbol signifies that the function is not achieved by the protocols. The – symbol means that a specific functionality is not available in the protocol. It is observed that my proposed protocol provides the support for more functionalities and security properties compared with the related works. Only my protocol includes a IoLT-based U-healthcare application and a cross-server E2E communication in the design. The proposed work is also the only one to provide user biometrics update for a three-factor authentication solution with the cost-saving biohash function employed.

7.2. Communication Cost

I use some parameters defined for the communicational evaluation as follows. A length of 1024 bits is assumed to be the size of the asymmetric encryptions or decryptions (e.g., RSA cryptosystem) and the Chebyshev polynomials for assuring strong security. Each block of a symmetric encryption or a symmetric decryption has a length of 256 bits. The size of an identity, a password and a biometrics value is 128 bits. The size of a random number or a hash value is 160 bits. A single elliptic curve point multiplication operation has a length of 320 bits. The size of each timestamp is 32 bits.

The total communication rounds and the length of all transcripts conveyed in each authentication session are considered as the communication cost of the protocols. In the login and authentication phase of my proposed protocol, the transcripts include $\left(C_{i,m1},c_{i,m21}, c_{i,m22}, c_{i,m23},T_{i,m}\right)$ and $\left({\theta }_{m,i}\right)$, which consume a length of (320 bits + 3*160 bits + 32 bits) and 256 bits, respectively. The total length is 1088 bits. In addition, the protocol is executed in two rounds of communication. The costs of the remaining protocols are calculated in a similar way. For a fair comparison, I do not include the communication between $S_m$ and $S_n$ of the proposed protocol in the evaluation.

Table 4. Comparison of communication cost.

Protocols	Total Communication Rounds	$\mathbf{Total} \mathbf{Cost} \mathbf{of} {\mathit{P}}_{\mathit{i}}$$\mathbf{and} {\mathit{S}}_{\mathit{m}} (\mathbf{bits})$
Le et al. [22]	2	512
Xu et al. [24]	3	1344
Lin et al. [25]	3	5736
Meshram et al. [26]	2	3072
Shohaimay and Ismail [27]	3	1376
Mine	2	1088

and Figure 5 tabulate the detailed comparison of the communication cost of different models. It is observed that my proposed work is one of the most efficient protocols. Only the work of Le et al. [22] is more efficient than mine in this evaluation. However, according to Table 3, my work provides many more functionalities and security properties compared to that of Le et al. [22].

7.3. Computation Cost

The computation cost is calculated by the execution time of all cryptographic operations in each protocol. I consider the time of computing an XOR negligible, as the operation is extremely fast. In addition, the difference between the execution times of a biohash function and a one-way hash function is too small [29]. For simplicity, they are assumed to be similar. I denote the following cryptographic functions and operations for the evaluation in this subsection.

• $T_{FE}$: Time of running fuzzy extraction function.
• $T_{CM}$: Time of running a Chebyshev chaotic polynomial mapping.
• $T_{PM}$: Time of operating an EC point multiplication.
• $T_{PA}$: Time of operating an EC point addition.
• $T_{SED}$: Time of running a symmetric encryption or symmetric decryption.
• $T_M$: Time of calculating a modular squaring.
• $T_{QR}$: Time of calculating a square root module 𝑁.
• $T_H$: Time of running a hash function.

The result of the comparison of computational cost of multiple protocols is presented in

Table 5. Comparison of computation cost.

Protocols	$\mathbf{Time} \mathbf{Complexities} \mathbf{of} {\mathit{P}}_{\mathit{i}} \mathbf{Side}$	$\mathbf{Time} \mathbf{Estimation} \mathbf{of} {\mathit{P}}_{\mathit{i}}$ Side $(\mathbf{m}\mathbf{s})$	$\mathbf{Time} \mathbf{Complexities} \mathbf{of} {\mathit{S}}_{\mathit{m}} \mathbf{Side}$	$\mathbf{Time} \mathbf{Estimation} \mathbf{of} {\mathit{S}}_{\mathit{m}}$$\mathbf{Side} (\mathbf{m}\mathbf{s})$	$\mathbf{Total} \mathbf{Time} \mathbf{Estimation} (\mathbf{m}\mathbf{s})$
Le et al. [22]	$T_M$ + $T_{SED}$ + 9$T_H$	≈0.00744	$T_{QR}$ + 2$T_{SED}$ + 8$T_H$	≈1.17560	≈1.18304
Xu et al. [24]	$T_{FE}$ + 4$T_{PM}$ + 9$T_H$	≈2.54621	3$T_{PM}$ + 5$T_H$	≈1.52745	≈4.07366
Lin et al. [25]	$2T_{CM}$$+2T_{SED}$$+7T_H$	≈0.06353	$2T_{CM}$$+2T_{SED}$$+5T_H$	≈0.06215	≈0.12568
Meshram et al. [26]	2$T_{CM}$ + 11$T_H$	≈0.06521	2$T_{CM}$ + 9$T_H$	≈0.06383	≈0.12904
Shohaimay and Ismail [27]	4$T_{PM}$ + 2$T_{PA}$ + 7$T_H$	≈2.05063	4$T_{PM}$ + $T_{PA}$ + 5$T_H$	≈2.04235	≈4.09298
Mine	$4T_{PM}$$+T_{SED}$$+4T_H$	≈2.03530	$3T_{PM}$$+T_{SED}$$+2T_H$	≈1.52592	≈3.56122

Based on Refs. [22,23], $T_{FE}$ ≈ 0.508 $\mathrm{ms}$, $T_{CM}$ ≈ 0.02881 $\mathrm{ms}$, $T_{PM}$ ≈ 0.508 $\mathrm{ms}$, $T_{PA}$ ≈ 0.0069 $\mathrm{ms}$, $T_{SED}$ ≈ 0.00054 $\mathrm{ms}$, $T_M$ ≈ 0.00069 $\mathrm{ms}$, $T_{QR}$ ≈ 1.169 $\mathrm{ms}$ and $T_H$ ≈ 0.00069 $\mathrm{ms}$.

and Figure 6. Based on the result, for each communication session, the proposed protocol is more efficient than Shohaimay and Ismail’s [27] protocol. The incurred costs in the works of Le et al. [22], Lin et al. [25] and Meshram et al. [26] are less than the ones in my protocol, Xu et al.’s [24] protocol and Shohaimay and Ismail’s [27] protocol. Nevertheless, my protocol provides support for more functional properties and is better than the ones of Le et al. [22], Lin et al. [25] and Meshram et al. [26] in terms of communicational efficiency.

Furthermore, I consider a scenario where a single patient is using multiple U-healthcare services. Since the cost-saving SC-SSO solution is employed in my work, some operations before smart card verification, such as ${\sigma }_i={\epsilon }_i\oplus h\left(I{D}_i^{*}\left|\left|P{W}_i^{*}\right|\right|h_{bio}\left(B_i^{*}\right)\right)$ and $V_i\stackrel{?}{=}h(h\left(I{D}_i^{*}\left|\left|P{W}_i^{*}\right|\right|{\sigma }_i\right)||h_{bio}\left(B_i^{*}\right))$, are only computed once for communications with multiple servers. The result is depicted in Figure 7. It is indicated that when the number of servers (s) increases, the proposed protocol incurs a more and more rational cost compared to the ones of Xu et al. [24] and Shohaimay and Ismail [27]. As a matter of fact, it incurs an acceptable computational cost considering such superiority over all related protocols in various aspects, which are discussed in Section 7.1 and Section 7.2.

8. Conclusions

In this paper, I proposed a CS-E2E patient authentication protocol for DNA-based U-healthcare services in the IoLT. The proposed protocol allows two patients to mutually authenticate each other and compute a secret shared key with the assistance of respective servers. In this way, patients can securely establish a reliable private channel for E2E healthcare communications. Based on results of the security analysis, my protocol is proven to be free from various attacks; it also provides the support for more security properties and better functionalities. Multiple cost-saving solutions, including SC-SSO, ECC, the biohash function, are employed in the design. A performance evaluation of multiple aspects, including the computational cost and communicational cost, is also presented, which indicates that the protocol incurs reasonable costs compared to related works.

In future works, I intend to design a certificateless-based E2E patient authenticated key exchange scheme for another healthcare security scenario. All credentials stored on the mobile device may be moved to the smart card in order to enable service availability on multiple devices. Here, there is a trade-off consideration between security and functionality, since the attackers only need to compromise the smart card for the attacks without obtaining the device. Furthermore, I would seek solutions, which can further reduce the computational cost and improve the whole communication efficiency of the current proposed approach—for instance, the EC point addition replacing EC point multiplication in some operations.