Diagnosing Vascular Aging Based on Macro and Micronutrients Using Ensemble Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Study Population
2.3. Variables and Measuring Instruments
2.3.1. Assessment of Carotid Intima-Media Thickness
2.3.2. Measurement of Arterial Stiffness
2.3.3. Definition of Vascular Aging
2.3.4. Adherence to the Mediterranean Diet
2.3.5. Alcohol and Tobacco Use
2.3.6. Macro and Micronutrient Intake
2.3.7. Cardiovascular Risk Factors
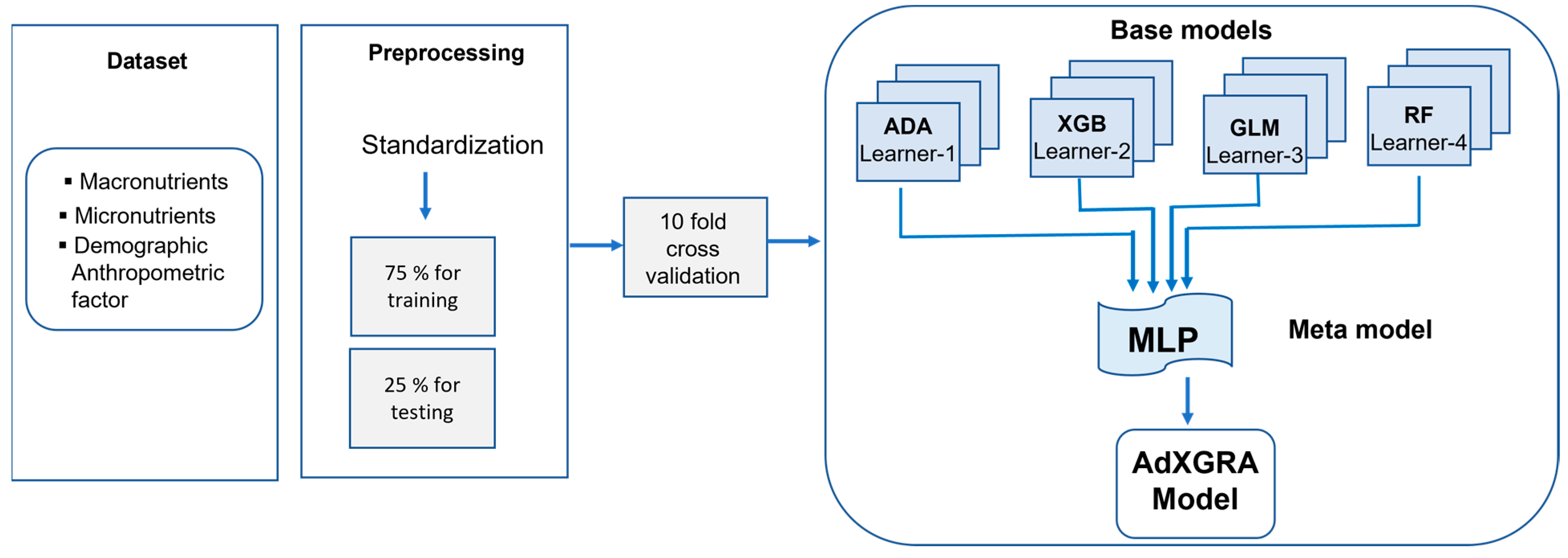
2.4. Proposed Stacked Ensemble Machine Learning Model
2.4.1. Feature Selection
2.4.2. Algorithm Flow and Data Pre-Processing
2.4.3. Employed Machine Learning Algorithms
AdaBoost
- ○
- Train weak learner using distribution .
- ○
- The whole distribution .
- ○
- Call weak hypothesis and transmit the distribution to it.
- ○
- Calculate the error rate
- ○
- Choose
- ○
- Update:
- ○
- Output the final hypothesis:
Extreme Gradient Boosting
Generalized Linear Model
- Linear predictor. The systematic component refers the independent variables. For a parameter vector and a k x p model matrix X that contains values of p independent variables for the k observations, the structure lineal is .
- Random component. This specifies the response variable and its probability distribution.
- Link function. This is a function g between random and the exploratory variables, and it is applied to each component of in the following way: .
Random Forest
- Phase 1. subsets of the training sample , , …,, are drawn from the total training sample set using the bootstrap sampling method. The sample size of subsets is the same as the total training sample set .
- Phase 2. decision trees are built based on r subsets and r classification results obtained.
- Phase 3. Each decision tree yields a single vote for the most accepted class, then optimal scores are determined.
Artificial Neural Networks
2.4.4. Scoring Metrics
2.5. Ethics Approval and Consent to Participate
3. Results
3.1. Characteristics of the Study Population
3.2. Experimental Results
3.2.1. Performances of the ML Models
3.2.2. Selection of Classifiers as Meta-Learners
3.2.3. Comparative Analysis
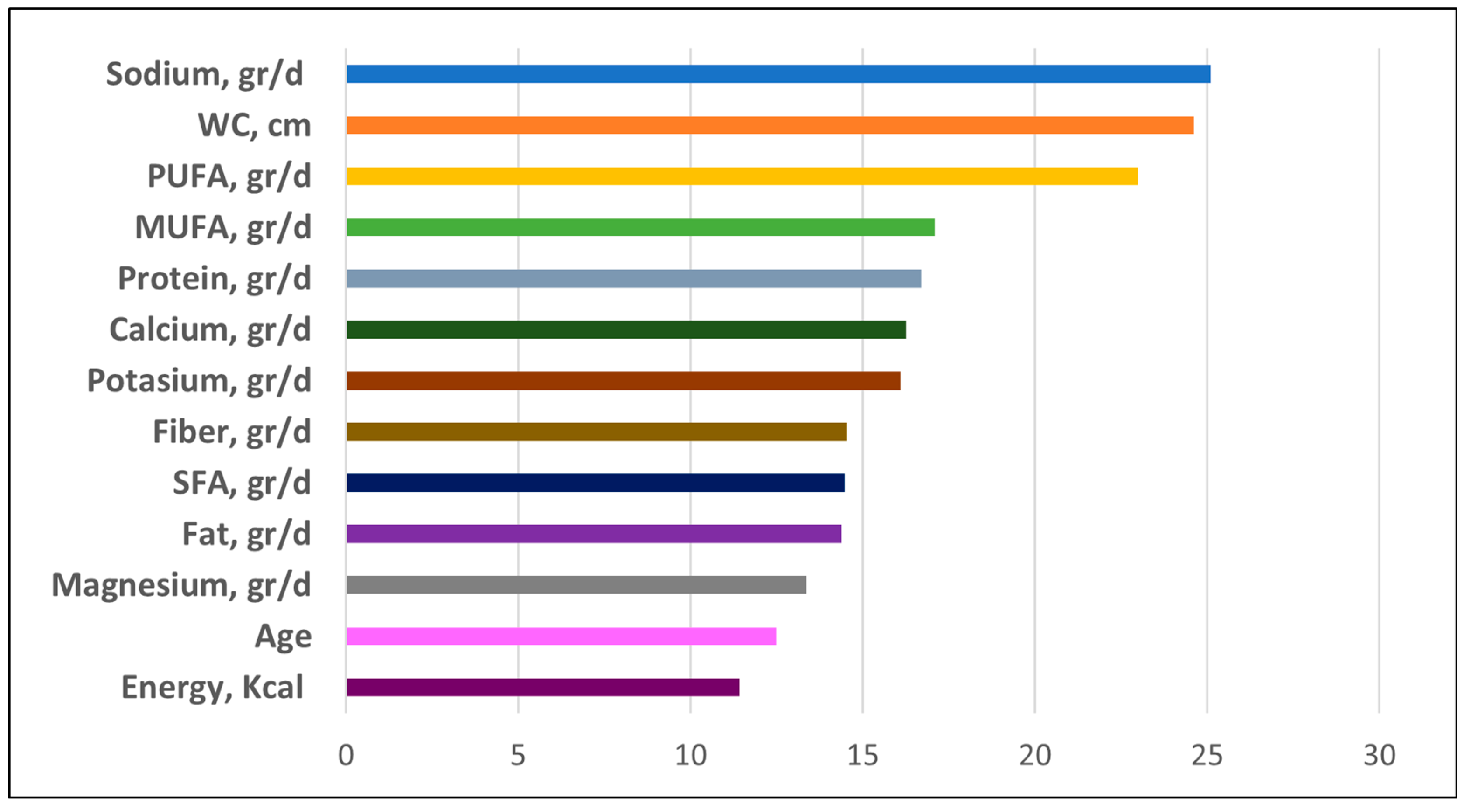
3.2.4. Importance of the Features
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rudnicka, E.; Napierała, P.; Podfigurna, A.; Męczekalski, B.; Smolarczyk, R.; Grymowicz, M. The World Health Organization (WHO) approach to healthy ageing. Maturitas 2020, 139, 6–11. [Google Scholar] [CrossRef]
- Amuthavalli Thiyagarajan, J.; Mikton, C.; Harwood, R.H.; Gichu, M.; Gaigbe-Togbe, V.; Jhamba, T.; Pokorna, D.; Stoevska, V.; Hada, R.; Steffan, G.S.; et al. The UN Decade of healthy ageing: Strengthening measurement for monitoring health and wellbeing of older people. Age Ageing 2022, 51, afac147. [Google Scholar] [CrossRef]
- Kehoe, L.; Walton, J.; Flynn, A. Nutritional challenges for older adults in Europe: Current status and future directions. Proc. Nutr. Soc. 2019, 78, 221–233. [Google Scholar] [CrossRef]
- Clegg, M.E.; Methven, L.; Lanham-New, S.A.; Green, M.A.; Duggal, N.A.; Hetherington, M.M. The Food4Years Ageing Network: Improving foods and diets as a strategy for supporting quality of life, independence and healthspan in older adults. Nutr. Bull. 2023, 48, 124–133. [Google Scholar] [CrossRef] [PubMed]
- Dorrington, N.; Fallaize, R.; Hobbs, D.A.; Weech, M.; Lovegrove, J.A. A Review of Nutritional Requirements of Adults Aged ≥65 Years in the UK. J. Nutr. 2020, 150, 2245–2256. [Google Scholar] [CrossRef] [PubMed]
- Venn, B.J. Macronutrients and human health for the 21st century. Nutrients 2020, 12, 2363. [Google Scholar] [CrossRef]
- Godswill, A.G.; Somtochukwu, I.V.; Ikechukwu, A.O.; Kate, E.C. Health Benefits of Micronutrients (Vitamins and Minerals) and their Associated Deficiency Diseases: A Systematic Review. Int. J. Food Sci. 2020, 3, 1–32. [Google Scholar] [CrossRef]
- Papadopoulou, S.K. Rehabilitation nutrition for injury recovery of athletes: The role of macronutrient intake. Nutrients 2020, 12, 2449. [Google Scholar] [CrossRef] [PubMed]
- Groenewegen, K.; den Ruijter, H.; Pasterkamp, G.; Polak, J.; Bots, M.; Peters, S.A. Vascular age to determine cardiovascular disease risk: A systematic review of its concepts, definitions, and clinical applications. Eur. J. Prev. Cardiol. 2016, 23, 264–274. [Google Scholar] [CrossRef]
- Nowak, K.L.; Rossman, M.J.; Chonchol, M.; Seals, D.R. Strategies for achieving healthy vascular aging. Hypertension 2018, 71, 389–402. [Google Scholar] [CrossRef]
- Laurent, S.; Boutouyrie, P.; Cunha, P.G.; Lacolley, P.; Nilsson, P.M. Concept of extremes in vascular aging: From early vascular aging to supernormal vascular aging. Am. Heart Assoc. 2019, 74, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Elosua-Bayés, M.; Martí-Lluch, R.; García-Gil, M.d.M.; Camós, L.; Comas-Cufí, M.; Blanch, J.; Ponjoan, A.; Alves-Cabratosa, L.; Elosua, R.; Grau, M.; et al. Association of Classic Cardiovascular Risk Factors and Lifestyles With the Cardio-ankle Vascular Index in a General Mediterranean Population. Rev. Española De Cardiol. 2018, 71, 458–465. [Google Scholar] [CrossRef]
- Laurent, S.; Marais, L.; Boutouyrie, P. The Noninvasive Assessment of Vascular Aging. Can. J. Cardiol. 2016, 32, 669–679. [Google Scholar] [CrossRef] [PubMed]
- Laurent, S. Defining vascular aging and cardiovascular risk. J. Hypertens. 2012, 30, S3–S8. [Google Scholar] [CrossRef]
- Ben-Shlomo, Y.; Spear, M.; Boustred, C.; May, M.; Anderson, S.G.; Benjamin, E.J.; Boutouyrie, P.; Cameron, J.; Chen, C.-H.; Cruickshank, J.K.; et al. Aortic pulse wave velocity improves cardiovascular event prediction: An indi-vidual participant meta-analysis of prospective observational data from 17,635 subjects. J. Am. Coll. Cardiol. 2014, 63, 636–646. [Google Scholar] [CrossRef]
- Nestel, P.J.; Beilin, L.J.; Mori, T.A. Changing dietary approaches to prevent cardiovascular disease. Curr. Opin. Lipidol. 2020, 31, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Daoud, E.; Scheede-Bergdahl, C.; Bergdahl, A. Effects of dietary macronutrients on plasma lipid levels and the consequence for cardiovascular disease. J. Cardiovasc. Dev. Dis. 2014, 1, 201–213. [Google Scholar] [CrossRef]
- Ho, F.K.; Gray, S.R.; Welsh, P.; Petermann-Rocha, F.; Foster, H.; Waddell, H.; Anderson, J.; Lyall, D.; Sattar, N.; Gill, J.M.R.; et al. Associations of fat and carbohydrate intake with cardiovascular disease and mortality: Prospective cohort study of UK Biobank participants. BMJ 2020, 368, m688. [Google Scholar] [CrossRef]
- Ge, L.; Sadeghirad, B.; Ball, G.D.C.; Da Costa, B.R.; Hitchcock, C.L.; Svendrovski, A.; Kiflen, R.; Quadri, K.; Kwon, H.Y.; Karamouzian, M.; et al. Comparison of dietary macronutrient patterns of 14 popular named dietary programmes for weight and cardiovascular risk factor reduction in adults: Systematic review and network meta-analysis of randomised trials. BMJ 2020, 369, m696. [Google Scholar] [CrossRef]
- Hosseini, B.; Saedisomeolia, A.; Skilton, M.R. Association between Micronutrients Intake/Status and Carotid Intima Media Thickness: A Systematic Review. J. Acad. Nutr. Diet. 2017, 117, 69–82. [Google Scholar] [CrossRef]
- Mazza, E.; Ferro, Y.; Lamprinoudi, T.; Gazzaruso, C.; Doldo, P. Relationship between high sodium and low PUFA intake and carotid atherosclerosis in elderly women. Exp. Gerontol. 2018, 108, 256–261. [Google Scholar] [CrossRef] [PubMed]
- Maloberti, A.; Vallerio, P.; Triglione, N.; Occhi, L.; Panzeri, F.; Bassi, I.; Pansera, F.; Piccinelli, E.; Peretti, A.; Garatti, L.; et al. Vascular Aging and Disease of the Large Vessels: Role of Inflammation. High Blood Press. Cardiovasc. Prev. 2019, 26, 175–182. [Google Scholar] [CrossRef]
- Cunha, P.G.; Boutouyrie, P.; Nilsson, P.M.; Laurent, S. Early Vascular Ageing (EVA): Definitions and Clinical Applicability. Curr. Hypertens. Rev. 2017, 13, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Laurent, S.; Briet, M.; Boutouyrie, P. Arterial Stiffness as Surrogate End Point. Hypertension 2012, 60, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Laurent, S.; Boutouyrie, P.; Cunha, P.G.; Lacolley, P.; Nilsson, P.M. Concept of Extremes in Vascular Aging. Hypertension 2019, 74, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Tao, J. Expert consensus on clinical assessment and intervention of vascular aging in China (2018). Aging Med. 2018, 1, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Xu, P. Review on Studies of Machine Learning Algorithms. J. Phys. Conf. Ser. 2019, 1187, 052103. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning, 1st ed.; McGraw-Hill, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Li, B.; Feridooni, T.; Cuen-Ojeda, C.; Kishibe, T.; de Mestral, C.; Mamdani, M.; Al-Omran, M. Machine learning in vascular surgery: A systematic review and critical appraisal. Npj Digit. Med. 2022, 5, 7. [Google Scholar] [CrossRef]
- Alqahtani, A.; Alsubai, S.; Sha, M.; Vilcekova, L.; Javed, T. Cardiovascular Disease Detection using Ensemble Learning. Comput. Intell. Neurosci. 2022, 2022, 5267498. [Google Scholar] [CrossRef] [PubMed]
- Poplin, R.; Varadarajan, A.V.; Blumer, K.; Liu, Y.; McConnell, M.V.; Corrado, G.S.; Peng, L.; Webster, D.R. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nat. Biomed. Eng. 2018, 2, 158–164. [Google Scholar] [CrossRef]
- Dall’Olio, L.; Curti, N.; Remondini, D.; Safi Harb, Y.; Asselbergs, F.W.; Castellani, G.; Uh, H.-W. Prediction of vascular aging based on smartphone acquired PPG signals. Sci. Rep. 2020, 10, 19756. [Google Scholar] [CrossRef]
- Hsiu, H.; Liu, J.-C.; Yang, C.-J.; Chen, H.-S.; Wu, M.-S.; Hao, W.-R.; Lee, K.-Y.; Hu, C.-J.; Wang, Y.-H.; Fang, Y.-A. Discrimination of vascular aging using the arterial pulse spectrum and machine-learning analysis. Microvasc. Res. 2022, 139, 104240. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Gomez-Marcos, M.A.; Martinez-Salgado, C.; Gonzalez-Sarmiento, R.; Hernandez-Rivas, J.M.; Sanchez-Fernandez, P.L.; Recio-Rodriguez, J.I.; Rodriguez-Sanchez, E.; García-Ortiz, L. Association between different risk factors and vascular accelerated ageing (EVA study): Study protocol for a cross-sectional, descriptive observational study. BMJ Open 2016, 6, e011031. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Marcos, M.A.; Recio-Rodríguez, J.I.; Patino-Alonso, M.C.; Agudo-Conde, C.; Gómez-Sanchez, L.; Gómez-Sanchez, M.; Rodríguez-Sánchez, E.; García-Ortiz, L. Protocol for measuring carotid intima-media thickness that best correlates with cardiovascular risk and target organ damage. Am. J. Hypertens. 2012, 25, 955–961. [Google Scholar] [CrossRef]
- Van Bortel, L.M.; Laurent, S.; Boutouyrie, P.; Chowienczyk, P.; Cruickshank, J.K.; De Backer, T.; Filipovsky, J.; Huybrechts, S.; Mattace-Raso, F.U.S.; Protogerou, A.D.; et al. Expert consensus document on the measurement of aortic stiffness in daily practice using carotid-femoral pulse wave velocity. J. Hypertens. 2012, 30, 445–448. [Google Scholar] [CrossRef]
- Brya, W.; Giuseppe, M.; Wilko, S.; Enrico, A.R.; Michel, A.; Michel, B.; Denis, L.C.; Antonio, C.; de Giovanni, S.; Anna, D.; et al. 2018 ESC/ESH Guidelines for the management of arterial hypertension. Eur. Heart J. 2018, 39, 3021–3104. [Google Scholar]
- Nilsson Wadström, B.; Fatehali, A.H.; Engström, G.; Nilsson, P.M. A Vascular Aging Index as Independent Predictor of Cardiovascular Events and Total Mortality in an Elderly Urban Population. Angiology 2019, 70, 929–937. [Google Scholar] [CrossRef]
- Den Ruijter, H.M.; Peters, S.A.E.; Anderson, T.J.; Britton, A.R.; Dekker, J.M.; Eijkemans, M.J.; Engström, G.; Evans, G.W.; de Graaf, J.; Grobbee, D.E.; et al. Common Carotid Intima-Media Thickness Measurements in Cardiovascular Risk Prediction. JAMA 2012, 308, 796. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Q.; Hu, M.-J.; Cui, Y.-J.; Liang, L.; Zhou, M.-M.; Yang, Y.-W.; Huang, F. Carotid–Femoral Pulse Wave Velocity in the Prediction of Cardiovascular Events and Mortality: An Updated Systematic Review and Meta-Analysis. Angiology 2018, 69, 617–629. [Google Scholar] [CrossRef]
- Schröder, H.; Fitó, M.; Estruch, R.; Martínez-González, M.A.; Corella, D.; Salas-Salvadó, J.; Lamuela-Raventós, R.; Ros, E.; Salaverría, I.; Fiol, M.; et al. A Short Screener Is Valid for Assessing Mediterranean Diet Adherence among Older Spanish Men and Women. J. Nutr. 2011, 141, 1140–1145. [Google Scholar] [CrossRef]
- Recio-Rodriguez, J.I.; Rodriguez-Martin, C.; Gonzalez-Sanchez, J.; Rodriguez-Sanchez, E.; Martin-Borras, C.; Martínez-Vizcaino, V.; Maria Soledad, A.; Olga, M.G.; Carmen, F.A.; Maderuelo-Fernandez, J.A.; et al. EVIDENT smartphone app, a new method for the dietary record: Comparison with a food frequency questionnaire. JMIR Mhealth Uhealth 2019, 7, e11463. [Google Scholar] [CrossRef]
- Salas-Salvadó, J.; Rubio Hererra, M.A.; Barbany, M.; Moreno, B. Consensus for the evaluation of overweight and obesity and the establishment of therapeutic intervention criteria. Med. Clínica 2007, 128, 184–196. [Google Scholar] [CrossRef] [PubMed]
- Moreau, K.L.; Babcock, M.C.; Hildreth, K.L. Sex differences in vascular aging in response to testosterone. Biol. Sex Differ. 2020, 11, 18. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, E.J.; Muntner, P.; Alonso, A.; Bittencourt, M.S.; Callaway, C.W.; Carson, A.P.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Das, S.R.; et al. Heart Disease and Stroke Statistics—2019 Update: A Report From the American Heart Association. Circulation 2019, 139, e56–e528. [Google Scholar] [CrossRef]
- Mohapatra, S.; Maneesha, S.; Mohanty, S.; Patra, P.K.; Bhoi, S.K.; Sahoo, K.S.; Gandomi, A.H. A stacking classifiers model for detecting heart irregularities and predicting Cardiovascular Disease. Healthc. Anal. 2023, 3, 100133. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Pan, C.; Poddar, A.; Mukherjee, R.; Ray, A.K. Impact of categorical and numerical features in ensemble machine learning frameworks for heart disease prediction. Biomed. Signal Process. Control 2022, 76, 103666. [Google Scholar] [CrossRef]
- Nelder, J.; Wedderburn, R. Generalized linear models. J. R. Stat. Soc. 1972, 135, 370. [Google Scholar] [CrossRef]
- McCullagh, P. Generalized linear-models. Eur. J. Oper. Res. 1984, 16, 285–292. [Google Scholar] [CrossRef]
- Patino-Alonso, M.C.; Molina, J.L.; Zazo, S. Multivariate linear modeling for the application in the field of hydrological engineering. In Handbook of Hydroinformatics; Elsevier: Amsterdam, The Netherlands, 2023; pp. 277–289. [Google Scholar]
- Agresti, A. Foundations of Linear and Generalized Linear Models; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-1-118-73003-4. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 1545–1588. [Google Scholar]
- Amit, Y.; Geman, D. Shape quantization and recognition with randomized trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Widiasari, I.R.; Nugroho, L.E. Widyawan Deep learning multilayer perceptron (MLP) for flood prediction model using wireless sensor network based hydrology time series data mining. In Proceedings of the 2017 International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 2–4 November 2017; pp. 1–5. [Google Scholar]
- Garson, G.D. Interpreting neural network connection weights. Artificial Intelligence Expert. Artif. Intell. Expert 1991, 6, 6–51. [Google Scholar]
- Association, W.M. World Medical Association Declaration of Helsinki: Ethical Principles for Medical Research Involving Human Subjects. JAMA 2013, 310, 2191–2194. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learnin; Springer Science+Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Radhakrishnan, P.; Ramaiyan, K.; Vinayagam, A.; Veerasamy, V. A stacking ensemble classification model for detection and classification of power quality disturbances in PV integrated power network. Measurement 2021, 175, 109025. [Google Scholar] [CrossRef]
- Juraschek, S.P.; Miller, E.R.; Weaver, C.M.; Appel, L.J. Effects of Sodium Reduction and the DASH Diet in Relation to Baseline Blood Pressure. J. Am. Coll. Cardiol. 2017, 70, 2841–2848. [Google Scholar] [CrossRef]
- Princy, R.J.P.; Parthasarathy, S.; Hency Jose, P.S.; Raj Lakshminarayanan, A.; Jeganathan, S. Prediction of Cardiac Disease using Supervised Machine Learning Algorithms. In Proceedings of the 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 13–15 May 2020; pp. 570–575. [Google Scholar]
- AlJame, M.; Ahmad, I.; Imtiaz, A.; Mohammed, A. Ensemble learning model for diagnosing COVID-19 from routine blood tests. Inform. Med. 2020, 21, 100449. [Google Scholar] [CrossRef] [PubMed]
- Ahola, A.J.; Gordin, D.; Forsblom, C.; Groop, P.H.; FinnDiane Study Group. Association between diet and measures of arterial stiffness in type 1 diabetes–Focus on dietary patterns and macronutrient substitutions. Elsevier 2018, 28, 1166–1172. [Google Scholar] [CrossRef]
- Di Pino, A.; Currenti, W.; Urbano, F.; Scicali, R.; Piro, S.; Purrello, F.; Rabuazzo, A.M. High intake of dietary advanced glycation end-products is associated with increased arterial stiffness and inflammation in subjects with type 2 diabetes. Nutr. Metab. Cardiovasc. Dis. 2017, 27, 978–984. [Google Scholar] [CrossRef]
- Firouzi, S.; Rezvani, R.; Pahlavani, N.; Jarahi, L.; Navashenaq, J.G.; Ranjbar, G.; Malekahmadi, M.; Taherzadeh, Z.; Safarian, M. Postprandial effects of macronutrient composition meals on the metabolic responses and arterial stiffness indices of lean and obese male adults: A protocol of a pilot study. Pilot Feasibility Stud. 2021, 7, 41. [Google Scholar] [CrossRef]
- Brandhorst, S.; Longo, V.D. Dietary Restrictions and Nutrition in the Prevention and Treatment of Cardiovascular Disease. Circ. Res. 2019, 124, 952–965. [Google Scholar] [CrossRef]
- Zhu, Y.; Bo, Y.; Liu, Y. Dietary total fat, fatty acids intake, and risk of cardiovascular disease: A dose-response meta-analysis of cohort studies. Lipids Health Dis. 2019, 18, 91. [Google Scholar] [CrossRef] [PubMed]
- Shay, C.M.; Stamler, J.; Dyer, A.R.; Brown, I.J.; Chan, Q.; Elliott, P.; Zhao, L.; Okuda, N.; Miura, K.; Daviglus, M.L.; et al. Nutrient and food intakes of middle-aged adults at low risk of cardiovascular disease: The international study of macro-/micronutrients and blood pressure (INTERMAP). Eur. J. Nutr. 2012, 51, 917–926. [Google Scholar] [CrossRef] [PubMed]
- Santiago, S.; Zazpe, I.; Fernandez-lazaro, C.I.; De, V.O.; Bes-rastrollo, M.; Miguel, Á. Macronutrient Quality and All-Cause Mortality in the SUN Cohort. Nutrients 2021, 13, 972. [Google Scholar] [CrossRef]
- Mizgier, M.; Jarząbek-Bielecka, G.; Wendland, N.; Jodłowska-Siewert, E.; Nowicki, M.; Alicja, B.; Witold, K.; Dorota, F.; Opydo-Szymaczek, J. Relation between Inflammation, Oxidative Stress, and Macronutrient Intakes in Normal and Excessive Body Weight Adolescent Girls with Clinical Features of Polycystic Ovary Syndrome. Nutrients 2021, 13, 896. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.M.; Nakagawa, S.; Raubenheimer, D.; Simpson, S.J. Global associations between macronutrient supply and age-specific mortality. Proc. Natl. Acad. Sci. USA 2020, 117, 30824–30835. [Google Scholar] [CrossRef] [PubMed]
- Doggui, R.; Al-jawaldeh, H.; El Ati, J.; Barham, R.; Nasreddine, L.; Alqaoud, N.; Aguenaou, H.; Ammari, L.E.; Jabbour, J.; Al-jawaldeh, A. Meta-Analysis and Systematic Review of Micro- and Macro-Nutrient Intakes and Trajectories of Macro-Nutrient Supply in the Eastern Mediterranean Region. Nutrients 2021, 13, 1515. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Migration. Nutrient Recommendations: Dietary Reference Intakes. Available online: https://ods.od.nih.gov/Health_Information/Dietary_Reference_Intakes.aspx (accessed on 28 February 2022).
| Feature Type | Feature Name | Variables |
|---|---|---|
| Continuous | Age | Demographic variable |
| Continuous | Waist Circumference | Anthropometric factor |
| Continuous | Calcium, Potassium, Magnesium, Sodium | Micronutrients |
| Continuous | Carbohydrates, Protein, Fibre, Fat, Fatty Saturated Acids (SFA), Fatty Monounsaturated Acids (MUFA), Polyunsaturated Fatty Acids (PUFA) | Macronutrients |
| Variables | Full Population, n = 484 | NVA, n = 328 | EVA, n = 156 | p |
|---|---|---|---|---|
| Cardiovascular risk factors | ||||
| Age, years | 55.86 ± 14.17 | 55.11 ± 114.14 | 57.43 ± 14.15 | 0.092 |
| WC, (cm) | 93.13 ± 12.00 | 91.83 ± 11.35 | 95.86 ± 12.87 | <0.001 |
| SBP, mmHg | 119.67 ± 17.71 | 115.64 ± 15.08 | 128.14 ± 19.77 | <0.001 |
| DBP, mmHg | 75.54 ± 10.18 | 73.33 ± 9.12 | 80.18 ± 10.75 | <0.001 |
| Total cholesterol, (mg/dL) | 194.50 ± 32.44 | 193.60 ± 33.27 | 196.40 ± 30.63 | 0.375 |
| LDL-C, mg/dL | 115.45 ± 29.42 | 114.53 ± 30.07 | 117.40 ± 27.99 | 0.319 |
| HDL-C, mg/dL | 58.51 ± 15.91 | 59.78 ± 16.09 | 55.82 ± 15.23 | 0.011 |
| Triglycerides, mg/dL | 102.89 ± 53.27 | 96.15 ± 48.68 | 117.03 ± 59.52 | <0.001 |
| Dyslipidemia, n (%) | 314 (64.9) | 199 (60.9) | 115 (74.2) | 0.004 |
| Glycemia, mg/dL | 88.17 ± 17.37 | 86.08 ± 13.30 | 92.58 ± 23.20 | <0.001 |
| HbA1c, (%) | 5.49 ± 0.56 | 5.41 ± 0.46 | 5.64 ± 0.70 | <0.001 |
| BMI, (kg/m2) | 26.47 ± 4.19 | 25.99 ± 3.86 | 27.49 ± 4.66 | 0.001 |
| CVR score, (%) | 1.15 ± 0.12 | 0.97 ± 0.10 | 1.53 ± 1.56 | <0.001 |
| cfPWV | 8.14 ± 2.54 | 7.30 ± 1.80 | 9.95 ± 2.96 | <0.001 |
| Lifestyles | ||||
| Alcohol, (g/week) | 45.65 ± 78.60 | 41.11 ± 73.13 | 55.19 ± 88.50 | 0.065 |
| Smoker | 12.93 ± 17.35 | 12.13 ± 16.50 | 14.59 ± 18.95 | 0.145 |
| Mediterranean diet | 7.15 ± 2.07 | 7.19 ± 2.04 | 7.06 ± 2.15 | 0.546 |
| Total physical activity, (METs/ min/week) | 2532.91 ± 3306.56 | 2477.69 ± 3166.41 | 1649.00 ± 3591.35 | 0.595 |
| Sedentary time, (h/week) | 42.07 ± 17.78 | 41.14 ± 18.14 | 44.04 ± 16.88 | 0.093 |
| Energy, Kcal | 2124.06 ± 555.38 | 2152.29 ± 559.96 | 2064.70 ± 542.61 | 0.105 |
| Macronutrients | ||||
| Carbohydrates gr/day | 200.500 ± 62.34 | 202.28 ± 62.90 | 196.75 ± 61.16 | 0.362 |
| Protein gr/day | 96.96 ± 25.75 | 98.53 ± 26.01 | 93.67 ± 24.96 | 0.049 |
| Fiber, gr/day | 25.82 ± 8.51 | 26.07 ± 8.71 | 25.30 ± 8.08 | 0.349 |
| Fat, gr/day | 96.74 ± 30.28 | 98.58 ± 31.05 | 92.88 ± 28.29 | 0.050 |
| SFA, gr/day | 31.31 ± 11.11 | 32.27 ± 11.36 | 29.29 ± 10.32 | 0.006 |
| MUFA, gr/day | 45.30 ± 14.51 | 45.86 ± 14.92 | 44.12 ± 13.58 | 0.217 |
| PUFA, gr/day | 12.43 ± 4.80 | 12.63 ± 4.88 | 11.99 ± 4.61 | 0.172 |
| Micronutrients | ||||
| Calcium, gr/day | 8.72 ± 2.92 | 8.81 ± 2.77 | 8.53 ± 3.22 | 0.330 |
| Potassium, gr/day | 3.59 ± 0.92 | 3.60 ± 0.91 | 3.57 ± 0.94 | 0.739 |
| Magnesium, gr/day | 3.24 ± 0.87 | 3.28 ± 0.86 | 3.16 ± 0.88 | 0.152 |
| Sodium, gr/day | 3.60 ± 1.52 | 3.71 ± 1.60 | 3.38 ± 1.32 | 0.025 |
| Model | Accuracy | Precision | Specificity | Recall | F1-Score | MCC |
|---|---|---|---|---|---|---|
| ADB | 0.6389 | 0.1304 | 0.6825 | 0.3333 | 0.1875 | 0.0113 |
| XGB | 0.6528 | 0.1522 | 0.6905 | 0.3889 | 0.2188 | 0.0563 |
| GLM | 0.6528 | 0.1304 | 0.6970 | 0.5000 | 0.2069 | 0.1168 |
| RF | 0.6597 | 0.1739 | 0.6960 | 0.4211 | 0.2462 | 0.0850 |
| Model | Accuracy | Precision | Specificity | Sensitivity |
|---|---|---|---|---|
| ADB | 0.6806 | 0.0426 | 0.6786 | 0.6667 |
| XGB | 0.6736 | 0.0435 | 0.6835 | 0.4000 |
| MLP | 0.6880 | 0.0435 | 0.6879 | 0.6667 |
| RF | 0.6667 | 0.0217 | 0.6786 | 0.2500 |
| GLM | 0.6736 | 0.0435 | 0.6835 | 0.4000 |
| Model | Accuracy | Precision | Specificity | Sensitivity | F1-Score | MCC |
|---|---|---|---|---|---|---|
| ADB | 0.6458 | 0.1957 | 0.6942 | 0.3913 | 0.2609 | 0.0672 |
| XGB | 0.5903 | 0.2826 | 0.6857 | 0.3333 | 0.3059 | 0.0182 |
| GLM | 0.6370 | 0.1489 | 0.6825 | 0.3500 | 0.2090 | 0.0239 |
| RF | 0.6042 | 0.2609 | 0.6881 | 0.3429 | 0.2963 | 0.0285 |
| Stacked classifier: AdXGRA | 0.6880 | 0.0435 | 0.6879 | 0.6667 | 0.0816 | 0.1086 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patino-Alonso, C.; Gómez-Sánchez, M.; Gómez-Sánchez, L.; Rodríguez-Sánchez, E.; Agudo-Conde, C.; García-Ortiz, L.; Gómez-Marcos, M.A. Diagnosing Vascular Aging Based on Macro and Micronutrients Using Ensemble Machine Learning. Mathematics 2023, 11, 1645. https://doi.org/10.3390/math11071645
Patino-Alonso C, Gómez-Sánchez M, Gómez-Sánchez L, Rodríguez-Sánchez E, Agudo-Conde C, García-Ortiz L, Gómez-Marcos MA. Diagnosing Vascular Aging Based on Macro and Micronutrients Using Ensemble Machine Learning. Mathematics. 2023; 11(7):1645. https://doi.org/10.3390/math11071645
Chicago/Turabian StylePatino-Alonso, Carmen, Marta Gómez-Sánchez, Leticia Gómez-Sánchez, Emiliano Rodríguez-Sánchez, Cristina Agudo-Conde, Luis García-Ortiz, and Manuel A Gómez-Marcos. 2023. "Diagnosing Vascular Aging Based on Macro and Micronutrients Using Ensemble Machine Learning" Mathematics 11, no. 7: 1645. https://doi.org/10.3390/math11071645
APA StylePatino-Alonso, C., Gómez-Sánchez, M., Gómez-Sánchez, L., Rodríguez-Sánchez, E., Agudo-Conde, C., García-Ortiz, L., & Gómez-Marcos, M. A. (2023). Diagnosing Vascular Aging Based on Macro and Micronutrients Using Ensemble Machine Learning. Mathematics, 11(7), 1645. https://doi.org/10.3390/math11071645







