1. Introduction
In the engineering computation field, nowadays, the finite element method (FEM) has made great achievements due to the fact that it has sufficient generalities and versatilities in dealing with very complex engineering problems [
1,
2]. Unfortunately, the FEM still suffers from obvious laminations in solving several specific problems, such as the wave analysis in relatively high frequency ranges [
3]. The origin of this issue is that the numerical error always arises and is not easy to effectively control when the FEM is employed for wave problems [
3,
4,
5,
6,
7,
8].
In general, the total numerical error mainly consists of two different parts [
9]. One important component of the numerical error is the interpolation error. This numerical error component usually stands for the capacities of the employed discretization to approximate the solution of the considered problems. In solving elasticity problems, the numerical error of the obtained FEM solutions is actually the interpolation error. The interpolation error usually exists locally and can be effectively suppressed by employing the smaller element sizes. In addition to the numerical interpolation error, in wave analysis the pollution error also exists and is relatively difficult to address. In contrast to the interpolation error, the pollution error usually comes from the particularity of the governing equation for wave problems (namely the Helmholtz equation). The pollution error actually represents the phase difference between the numerical and analytical solutions. More importantly, the pollution error has global feature and cannot be effectively suppressed by directly decreasing the element sizes. No matter how refined meshes are employed, in wave analysis, the pollution error still exists as long as the considered frequency values are sufficiently high. Note that the FEM always suffers from the above mentioned numerical errors for wave problems; the need of developing more powerful alternatives to FEM is quite pressing in practical engineering computation fields.
In addition to the FEM, many other numerical methods, such as the finite volume method (FVM) [
10], finite difference method (FDM) [
11,
12,
13,
14], boundary element method (BEM) [
15,
16], singular boundary method (SBM) [
17,
18,
19,
20,
21,
22,
23], and different types of meshfree numerical techniques [
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35] are also effective numerical approaches for wave problems. However, these alternative approaches also usually have their own associated advantages, disadvantages, and specificities. For example, the classical boundary element or boundary-based numerical techniques have natural advantages in dealing with the Helmholtz problems in exterior unbounded domains (such as the acoustic radiation and acoustic scattering) because the required Sommerfeld radiation at infinity can be satisfied naturally [
36,
37]. However, the resultant system matrices from these numerical approaches are always non-symmetric and full, and then the solution of the obtained system matrix equation is usually very expensive in computation cost. The meshfree numerical techniques in strong-form (such as the FDM and a variety of collocation methods [
38,
39,
40,
41,
42,
43,
44]) always have very high computation efficiency in solving Helmholtz equation. Unfortunately, these strong-form meshfree approaches usually become unstable and inaccurate when the considered Helmholtz problems have Neumann boundary conditions. The weak-form meshfree numerical techniques indeed possess relatively high computation accuracy for Helmholtz problems and the treatment of the Neumann boundary conditions is usually direct and easy to implement [
45,
46,
47,
48]. While the construction of the related numerical approximation is always quite complicated and the involved numerical integration is usually numerically expensive [
45].
Due to several preeminent and attractive features (such as rich mathematical background, symmetrical and banded system matrices, easy to solve coupled structural-acoustic problems and inhomogeneous problems) of the classical FEM, the FEM is still a very important and dominative numerical method for acoustic computation at present. Actually, the main challenge of the acoustic computation using the standard FEM is to efficaciously tackle the numerical error. With this objective in mind, many improved versions of FEMs are developed for acoustic simulation, including the smoothed FEM [
49,
50,
51,
52,
53,
54], the Galerkin/least squares FEM [
55], the generalized FEM [
56], and the mass-redistributed FEM [
57], to name a few. Unfortunately, all these methods still cannot totally remove the pollution effects for solving general two and three dimensional acoustic problems.
In addition to the above-mentioned numerical approaches, the meshfree methods, which are developed to address several inherent shortcomings of the FEM, also have great potentials in the analysis of wave problems for relatively high computation precision. One main feature of the meshfree numerical techniques is that the construction of the employed nodal shape functions is based on several scattered field nodes in the considered problem domain, while in the FEM, the pre-defined meshes are always used to construct the nodal shape functions. Note the high order numerical approximation is always quite easy to achieve in the meshfree framework; it is very reasonable to expect that the meshfree methods have more powerful capacities than the FEM in decreasing the numerical errors in wave analysis. Unfortunately, the relatively complicated formulation and implementation process always obstruct the development of the meshfree techniques. Additionally, to obtain the optimal numerical results, usually many critical parameters (such as the influence domains, the weight functions and the function bases) should be carefully determined. As a result, the meshfree techniques usually cannot outmatch the classical FEM in terms of versatility and universal nature for practical engineering computation.
The objective of the present paper is to use an extrinsic enriched finite element method (EFEM) with appropriate enrichment functions to solve the acoustic problems. In this extrinsic EFEM, the simple linear nodal interpolation functions are enriched by the polynomial and trigonometric functions, then the original linear approximation space is enriched by the specially-designed enrichment functions. Due to the use of the appropriate enrichment functions, the highly oscillating features of the Helmholtz equation in relatively large wave numbers can be effectively captured, and the numerical dispersion error can be markedly decreased. The numerical examples in this paper show that this extrinsic EFEM behaves much better than the standard FEM in suppressing the numerical dispersion effects and could provide much more accurate numerical solutions in acoustic computation. In addition, the present extrinsic EFEM also stands out as a winner in terms of the convergence rate in comparison with the standard FEM. More importantly, the extrinsic EFEM can be performed directly by using the standard triangular mesh as in the FEM and the additional nodes (such as the mid-edge-point or element centroid) are not required. In the view of these good properties of the present extrinsic EFEM, it could be a competitive alternative to the standard FEM and has great potential in acoustic computation for practical engineering applications.
In the following sections, firstly the basic formulations of the Helmholtz problems are given in
Section 2; secondly, the structure of this extrinsic EFEM for Helmholtz problems is shown in
Section 3; in
Section 4 and
Section 5, the dispersion effects of the numerical solutions for the Helmholtz equation and several typical numerical experiments are investigated in great detail; and finally, the main concluding remarks are summarized in the final section.
2. Formulation of the Helmholtz Problem
Consider a problem domain
with boundary
; the ideal acoustic fluid medium occupies the problem domain and the acoustic pressure propagation speed is
c. Following the momentum and mass conservation law as well as the ideal gas law, the following governing equation for acoustic wave propagation can be obtained:
in which
stands for the acoustic pressure variable,
represents the Laplace operator and
t is time.
If the considered pressure wave
has steady harmonic feature, we have
in which
,
represents the acoustic pressure distribution in physical space and
stands for the angular frequency.
Using Equation (2), from Equation (1) we can obtain the following reduced wave propagation equation (namely the well-known Helmholtz equation)
in which
is the wave number.
By introducing the appropriate boundary conditions, the considered Helmholtz problem governed by Equation (3) can be well posed. By using the analytical or numerical approaches, the solutions to Equation (3) can be obtained. When the involved problem domain is very simple, the analytical approach can be used to solve Equation (3). When the problem has very complicated geometry shapes, the numerical techniques are always employed to tackle Equation (3).
For the above-mentioned Helmholtz problem, the following three types of boundary conditions are usually considered
in which
stands for the acoustic fluid density,
is the Dirichlet boundary condition and the acoustic pressure
is prescribed on
,
is the Neumann boundary condition and the normal acoustic particle velocity
is prescribed on
,
is the Robin boundary condition, and
is the associated admittance coefficient which is usually employed to model the structural damping effects.
In this work, we mainly focus on the numerical techniques in weak form (such as the standard FEM) for solving the Helmholtz equation. In formulating the weak form of the Helmholtz equation, the weighted residual technique is always employed. By introducing the required boundary conditions shown in Equation (4), the following weak form of the Helmholtz equation can be obtained:
in which
stands for the employed weight functions.
According to the Gauss divergence theorem, Equation (5) can reduce to
On the purpose of solving this typical boundary-value problem described by Equation (6), the involved acoustic pressure should be discretized.
When the involved problem domain is divided into standard triangular mesh, the following numerical approximation of the acoustic pressure
p is usually employed
in which
stands for the used nodal interpolation functions for node
i,
represents the nodal unknown coefficient.
When the well-known Galerkin technique is employed here (namely the nodal interpolation functions are directly used as the weighted functions), using Equation (7) the following matrix form of Equation (6) can be obtained
in which
In Equations (8) and (9), the resultant system matrices K, M, and C correspond to the acoustical stiffness, acoustical mass and acoustical damping effects, respectively; f is a nodal vector representing the acoustical nodal excitation force, and p is a vector containing the unknown nodal acoustic pressure.
3. Structure of the Extrinsic EFEM for the Helmholtz Equation
Assuming that a scalar function
is defined in a
d-dimensional problem domain, the standard linear triangular mesh with
Ne elements and
Nn nodes is employed to perform the problem domain discretization. In this extrinsic EFEM, the numerical approximation of the defined scalar function is given by [
58,
59,
60,
61]
In the right side of Equation (10), the first term is the conventional finite element approximation, and the second term corresponds to the additional extrinsic enriched numerical approximation.
corresponds to the conventional nodal unknown coefficient in the finite element approximation which is usually the unknown nodal field variable and
is the associated additional nodal unknown coefficients.
is the standard nodal interpolation function as in the classical finite element approach, and
is a new constructed nodal interpolation function which should satisfy the partition of unity (PU) property, namely
Actually, and can be but are not necessarily chosen as the same. However, in this work = is directly used for simplicity.
From Equation (10), it is easy to observe that in this extrinsic EFEM the basic nodal unknown quantities are not the nodal unknown coefficients as in the traditional FEM, it is actually the numerical approximation of the related nodal unknown coefficients. In Equation (10), the function is a specially-designed enrichment function and it always plays a very important role in improving the numerical performance of this extrinsic EFEM. In general, the enrichment function is designed to contain the special knowledge about the solution of the considered problems. For example, in this work the trigonometric functions are incorporated into the enriched numerical approximation space to capture the highly oscillating features of the Helmholtz equation, in particular the relatively large wave numbers are considered.
Generally, the constructed numerical approximation in Equation (10) does not possess the important Kronecker-delta function property, namely the following relationship is often obtained:
Owing to the lack of the Kronecker-delta function property, the Dirichlet boundary condition is always not very easy to impose when the numerical approximation in Equation (10) is employed to build the discretized system matrix equation. To effectively address this issue, the constructed extrinsic enriched numerical approximation in Equation (10) is always modified as follows:
With the aim to further reduce the condition number of the obtained system matrices and improve the numerical stability, in practical numerical implementation, we usually employ the following shifted form of Equation (13):
in which
h is a parameter to define the characteristic length of the employed meshes.
For the Helmholtz equation considered in this work, the polynomial and trigonometric functions are exploited to create the enrichment function .
When the pure trigonometric functions are used, the enrichment function
in two dimensions has the following form [
62,
63,
64]
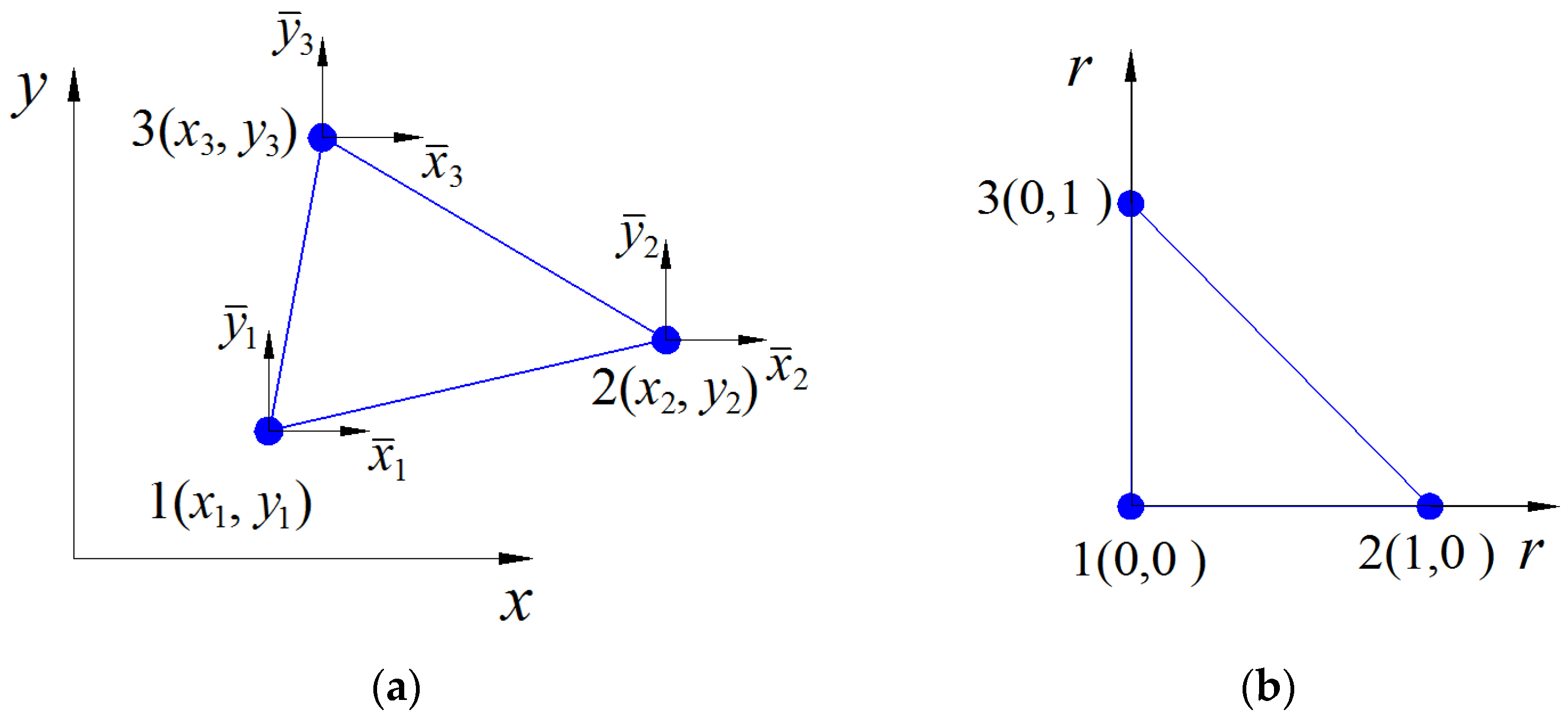
in which
and
are the relative coordinate value, as shown in
Figure 1, and
q is a parameter to denote the degree of the employed polynomial or trigonometric functions.
When the polynomial functions are combined with the trigonometric functions to create the enrichment function
, in two dimensions we have
In theory, the higher order enrichment functions can lead to higher computation accuracy, while the related numerical computation also becomes very numerically expensive. For brevity, in this work, we only employ the linear polynomial and the first order of trigonometric functions (namely q = 1) to create the enrichment function .
In addition, it should also be noted that the present extrinsic enriched numerical approximation usually suffers from the linear dependence (LD) issue when the polynomial functions are employed to create the enrichment functions [
65,
66].
This LD issue comes from the fact that the linearly dependent nodal shape functions are employed to construct the system matrix equation. Due to this LD issue, the resultant system matrices are usually singular and not positive definite, making the associated numerical computation not have sufficient numerical stability. To address this LD issue, a systematic study was performed by Gui et al., and they have proposed a simple and direct procedure to completely remove the LD issue of this extrinsic EFEM without any loss in computation accuracy [
63]. In this work, the related numerical procedures developed by Gui et al. are directly employed to tackle the possible LD issue.
4. The Dispersion Effects
It is known that the computed wave number
often differs from the exact wave number
k when the Galerkin-like numerical approaches (such as the classical FEM and several meshless techniques [
6,
9]) are employed to deal with the Helmholtz equation and a phase lag between
and
k usually exists in the numerical solutions. This non-robust numerical performance of the underlying discretization method for Helmholtz problems is called the numerical dispersion issue. It is this issue that can markedly decrease the precision of the numerical solutions. What is more, the effects of this issue always become more severe when the considered wave number gets larger. In the practical process of performing the numerical simulation, the employed mesh quality and the order of the employed numerical approximation should always be adopted to the computed wave number to ensure that the computed numerical solution quality at an acceptable level. To examine the ability of the employed numerical discretization methods from all sides and investigate how the numerical dispersion effects are affected by the mesh quality, a comprehensive dispersion analysis should be usually performed before the practical numerical simulation. The dispersion analysis can be regarded as an a priori error estimate of the obtained numerical solutions. In this section, the dispersion effects of several disparate numerical discretization approaches are compared and investigated in great detail using the regular mesh pattern shown in
Figure 2.
Without considering any boundary conditions, the constructed matrix equation in Equation (8) becomes
Clearly, the numerical solution of Equation (17) can be assumed as the following form:
in which
n is a unit vector and
x is a position vector of the interest point,
is a amplitude vector and has the following form [
63,
64,
67,
68]
in which
is a amplitude vector corresponding to each node. Since here we do not consider any types of boundary conditions, the amplitude vector
for each node should be identical; namely, this amplitude vector should repeat itself in Equation (19).
It also should be pointed out that the subscript ad in Equation (19) actually represents the number of unknown nodal degree of freedom (DoF) at each node in this extrinsic EFEM formulation. For example, when only the first order of trigonometric functions is employed to create the enriched numerical approximation space, ad = 9; when the linear polynomial and the first order of trigonometric functions are employed, ad = 11. In this work we respectively use the abbreviations EFEM-N9 and EFEM-N11 to represent different versions of this extrinsic EFEM when these two different enrichment functions are employed.
Using Equation (18), from Equation (17) we can obtain the following matrix equation:
in which
and
represent two coefficient matrices with the dimensions
and can be calculated by [
63,
64,
67,
68]
When only consider the non-trivial solutions of Equation (20), it is actually a typical eigenvalue problem and the exact wave number
k can be calculated by [
63,
64,
67,
68]
Obviously, from Equations (21) and (22) we can see that the coefficient matrices
and
are the functions of the discrete wave number
. Therefore, Equation (23) actually builds a relationship for
k and
. For any given
, we can compute the corresponding
k via Equation (23). Due to the numerical dispersion effects,
usually differs from
k. In this work the following error index is employed to measure the numerical dispersion effects of the different discretization methods in solving the Helmholtz equation [
67,
68]:
Using the regular triangular mesh pattern shown in
Figure 2, the numerical dispersion error along the varying angles of acoustic wave propagation from different discretization techniques is computed via Equation (23), and the corresponding results against the normalized wave number
are displayed in
Figure 3. It is easily seen that the dispersion errors yielded by the standard linear triangular finite element (FEM-T3) are observably larger than the extrinsic EFEM-N9 and EFEM-N11, and the numerical dispersion effects usually become larger with the increase of the considered normalized wave number
; actually, these results have also been reported in Ref. [
63].
Additionally, it is also clear that the dispersion effects from the standard FEM-T3 differs quite much when the varying wave propagation angles are considered, namely the standard FEM-T3 usually suffers from the numerical anisotropy issue in tackling the Helmholtz equation. The EFEM using the first order of trigonometric enrichment functions (EFEM-N9) is able to provide much smaller dispersion error results than the standard FEM-T3, while the EFEM-N9 still suffers from the above-mentioned numerical anisotropy issue and the numerical dispersion effects are also markedly different along different angles of wave propagation. In contrast to the standard FEM-T3 and EFEM-N9, the EFEM with linear polynomial and the first order of trigonometric enrichment functions (EFEM-N11) can yield the smallest dispersion error results which are almost zero in the computed normalized wave number range. More importantly, we also can observe that the above-mentioned numerical anisotropy issue can be basically eliminated by this EFEM-N11. The above findings show that it is quite suitable to enrich the linear numerical approximation space of the standard FEM by using the combination of the polynomial and trigonometric enrichment functions. The good performance of the EFEM-N11 in dispersion analysis indicates that the EFEM-N11 also can behave quite well in solving the practical Helmholtz problems. The related numerical experiments will be performed in the next section.
5. Numerical Results
In this section, a number of typical numerical experiments will be conducted to examine the numerical performance of all the above-mentioned numerical discretization techniques (FEM-T3, EFEM-N9, and EFEM-N11) in handling the real acoustic problems. It should be noted that all the computed numerical solutions from different methods are obtained using the totally identical mesh pattern.
5.1. Acoustic Propagation in a Two-Dimensional Tube
Here we firstly consider the acoustic propagation in a two-dimensional tube. As shown in
Figure 4, this tube is filled with water (mass density
= 1000 kg/m
3 and acoustic wave speed
c = 1500 m/s) and has a dimension with length
l = 1 m and width b = 0.1 m. The Neumann boundary condition with normal acoustic particle velocity
vn = 1 m/s is imposed on the left side of this tube, and the other three sides are rigid walls. the regular triangular elements are employed to perform the problem domain discretization and the average node space
h = 0.025 m. This is a frequently-used benchmark problem in examining the abilities of the employed numerical discretization techniques in tackling the Helmholtz problems and the exact solutions to this acoustic propagation problem can be easily obtained by
To effectively measure the quality of the obtained numerical solutions, here the following two error indexes are employed:
in which the subscript
h and
e mean that the corresponding field variables are numerical and exact, respectively;
v denotes the acoustic particle velocities and the sigh
stands for the complex conjugate of
v;
l is the order of the employed numerical approximation space; and
C1 and
C2 are two constants which are independent of the wave number
k and node space
h [
9].
From Equations (26) and (27), we can find that
is a local error index and it can examine the numerical performance of the numerical methods in local domain. On the contrary,
is a global error index and it can evaluate the solution quality in the total problem domain. For the linear numerical approximation space (such as the standard FEM using the simple linear nodal interpolation functions), Equation (27) becomes
In the right side of Equations (27) and (28), the first term is the interpolation error and the second term corresponding to the pollution error [
9].
In
Figure 5, the calculated acoustic pressure along the longitudinal direction of the tube provided by the above-mentioned numerical techniques are given together with the exact ones. To effectively assess the effects of the considered frequency values on the solution accuracy, a number of varying frequency values (
f = 1100 Hz,
f = 2200 Hz,
f = 4400 Hz and
f = 6600 Hz) are employed here. It is quite interesting that for the relatively low frequencies, all the numerical solutions produced by different methods are in very good agreement with the exact solutions. When the computed frequency value becomes higher, the standard FEM-T3 solution accuracy visibly gets worse. In contrast to the FEM-T3, the EFEM-N9 indeed behaves better and more accurate solutions can be generated. Nevertheless, among all the numerical solutions the EFEM-N11 can generate the best numerical solutions which are very close to the exact ones, even if very high frequency values are considered. These findings indicate that the enrichment functions which are constructed by the linear polynomial and the first order of trigonometric functions is indeed very suitable to enrich the original linear approximation space in the standard FEM-T3 for solving Helmholtz problems and hence very reliable numerical solutions can be obtained.
For two different frequency values (
f = 2200 Hz and
f = 4400 Hz), the relative error results, which is defined in Equation (26), are depicted in
Figure 6a and
Figure 7a. For a clear comparison and analysis, the corresponding exact acoustic particle velocity distributions along the longitudinal direction of this tube for these two frequency values are also plotted in
Figure 6b and
Figure 7b. From
Figure 6 and
Figure 7, it is again confirmed that the numerical performance of the proposed EFEM-N11 is much better than the standard FEM-T3 and EFEM-N9 in terms of computation accuracy, and it can provide the smallest relative error results. More specifically, it is quite easy to see that the relative numerical error results from the standard FEM-T3 and EFEM-N9 always exhibit obvious oscillations when the corresponding acoustic particle velocity solutions are relatively high. This means that in solving the Helmholtz problems, the numerical dispersion errors are usually larger when the acoustic gradients, which is related to the acoustic particle velocity, are relatively high. From
Figure 6 and
Figure 7, it is clearly seen that the standard FEM-T3 and EFEM-N9 cannot perform sufficiently well in capturing the high oscillating features of the Helmholtz problems in the relatively high frequency range. However, the proposed EFEM-N11 behaves quite well and almost no oscillations can be seen in the relative error results. These observations demonstrate that the effectiveness and robustness of the EFEM-N11 in tackling the Helmholtz problems.
Furthermore, we also have studied the numerical performance of different numerical approaches in addressing the global numerical error for Helmholtz problems. The global error index
from different methods versus the wave number
k is calculated and compared in
Figure 8. It is shown that the global numerical error from the standard FEM-T3 increases very fast when the computed wave number becomes larger. This means that the standard FEM-T3 is not very effective in capturing the highly oscillating features of the Helmholtz problem in the relatively large wave number range and very large numerical errors will be obtained. Compared to the standard FEM-T3, the EFEM-N9 is able to yield a much smaller global numerical error, while it still becomes larger when the computed wave number
k increases. Among the three mentioned numerical methods (FEM-T3, EFEM-N9 and EFEM-N11), the EFEM-N11 is able to yield the smallest numerical error results, which are almost zero even if the computed wave number
k is relatively large.
From Equations (27) and (28), it is shown that the numerical errors of the numerical solutions for Helmholtz problems usually contains the numerical interpolation error and numerical pollution error. Here the abilities of the three numerical techniques in controlling these two different numerical error components are investigated separately.
Figure 9 shows the calculated global numerical error from different methods by keeping the parameter
kh = constant and
k3h2 = constant. From the previous analysis, it is shown that the numerical interpolation error can be effectively controlled by keeping
kh = constant, and numerical pollution error can be effectively controlled by keeping
k3h2 = constant. These two points can be clearly confirmed by the global error results of the standard FEM-T3 in
Figure 9. The EFEM-N9 obviously performs better than the standard FEM-T3 and much lower global error results can be yielded. However, the EFEM-N11 is able to yield the lowest global error results. These observations indicate that both the numerical interpolation error and the numerical pollution error can be effectively controlled by the EFEM-N11 in solving the Helmholtz problems.
5.2. Acoustic Propagation in a Two-Dimensional Square Domain
In the second numerical experiment, a two-dimensional square domain with side length
L = 1 m is considered (see
Figure 10a). This square domain is filled with ideal acoustic fluid with mass density
= 1 kg/m
3 and acoustic wave speed
c = 1 m/s. The Robin boundary conditions with different admittance coefficients are applied on four sides of the square domains (see
Figure 10a). The Dirichlet boundary condition
p = 1 Pa is imposed at the left bottom corner of the square domain. The exact solution of this Helmholtz problem is actually the following plane wave solution:
in which
is the angle of acoustic wave propagation.
The involved problem domain is discretized into standard triangular mesh with average node space
h = 0.05 m (see
Figure 10b). For a wave propagation angle
and the varying wave numbers (
k = 2,
k = 5 and
k = 10), the calculated acoustic pressure distribution results along the defined path are plotted in
Figure 11. For comparison, the numerical solutions from the three different methods (FEM-T3, EFEM-N9, and EFEM-N11) together with the exact solutions are given in
Figure 11. The similar observations obtained from the previous numerical experiment are again confirmed here, namely the standard FEM-T3 and EFEM-N9 cannot generate sufficiently reliable numerical solutions for the Helmholtz problems, while the proposed EFEM-N11 is able to yield nearly exact solutions, even though the considered wave number is very large.
5.3. Acoustic Propagation in a Two-Dimensional Car
In the third numerical experiment, a two-dimensional section of a car is investigated. The geometry description and mesh pattern of the car is given in
Figure 12; here, the average node space of the used mesh is
h = 0.04 m. The front panel of the car is excited by the Neumann boundary condition with normal acoustic particle velocity
vn = 0.01 m/s, and the roof of this two-dimensional car is coated with absorbing material (namely the Robin boundary condition is imposed) with the admittance coefficient
An = 0.00144 m/(Pa·s). The considered acoustic fluid medium in this car is air with mass density
= 1.25 kg/m
3 and acoustic wave speed
c = 340 m/s. Note that the exact solution to this Helmholtz problem is not available, the corresponding numerical solutions from the high order elements with very refined mesh are provided as the reference solutions for comparison in this section.
For two frequency values (
f = 320 Hz and
f = 650 Hz),
Figure 13 gives the computed acoustic pressure results along the defined path. The main finding obtained from
Figure 13 is that all the employed numerical methods are able to produce acceptable numerical solutions for the relatively low frequency value (
f = 320 Hz). When it comes to the relatively high frequency value (
f = 650 Hz), the standard FEM-T3 and EFEM-N9 solutions are not very accurate, and the clear accuracy reduction can be seen in the results, while the proposed EFEM-N11 can produce very accurate and reliable numerical solutions even though the relatively high frequency value (
f = 650 Hz) is considered. These observations again show the powerful and excellent numerical performance of the EFEM-N11 in solving the Helmholtz problems. In more detail, the calculated acoustic pressure distribution results from different methods in the total problem domain are also shown in
Figure 14 and
Figure 15. We can again observe that the EFEM-N11 can obtain more accurate solutions than the standard FEM-T3 and EFEM-N9 in solving the Helmholtz problems, and the numerical error can be markedly reduced.
6. Concluding Remarks
In this work, we present the formulation and implementation of the extrinsic enriched FEM (EFEM) for solving the Helmholtz problems. In this extrinsic EFEM, the original linear polynomial approximation space in the standard FEM using linear triangular element (FEM-T3) can be enriched extrinsically by using the proper enrichment functions. To effectively reduce the numerical errors of the obtained solutions and capture the highly oscillating characteristics of the Helmholtz equation in relatively high frequency range, different types of enrichment functions are employed and their numerical performance are investigated in great detail via the dispersion analysis and several typical numerical experiments. The obtained numerical solutions show that the hybrid enrichment functions, which are constructed by the combination of the linear polynomial and the first order of trigonometric functions, are particularly suitable for solving the Helmholtz problems in relatively high frequency ranges. The explicit findings are that better control of the numerical error and much more accurate solutions can be achieved by the proposed EFEM-N11 compared to other numerical techniques (FEM-T3 and EFEM-N9). More importantly, the formulation and implementation of this proposed EFEM-N11 is as easy as in the standard FEM and can also be extended directly from the two-dimensional case to the general three-dimensional case. Therefore, the present EFEM-N11 can be regarded as a promising numerical approach in solving the complicated Helmholtz problems in practical engineering applications.
Author Contributions
Conceptualization, G.Z. and Y.C.; methodology, Y.C.; software, K.H.; validation, K.H. and Z.X.; formal analysis, K.H.; investigation, S.W.; resources, Z.X.; data curation, S.W.; writing—original draft preparation, G.Z. and K.H.; writing—review and editing, G.Z. and Y.C.; visualization, G.Z.; supervision, Y.C.; funding acquisition, Y.C. and G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Laboratory on Ship Vibration and Noise, (Grant No. 6142204210208), the Open Fund of Key Laboratory of High Performance Ship Technology (Wuhan University of Technology), the Ministry of Education (Grant No. gxnc18041401 and gxnc21112701), and the National Natural Science Foundation of China (Grant No. 51909201 and No. 52241102).
Data Availability Statement
Data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
We thank Zhang for the helpful suggestions to revise the present paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall: Watertown, MA, USA, 2014. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Zienkiewicz, O.C. Achievements and some unsolved problems of the finite element method. Int. J. Numer. Methods Eng. 2000, 47, 9–28. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Babuška, I.; Bouillard, P. Dispersion and pollution of the FEM solution for the Helmholtz equation in one, two and three dimensions. Int. J. Numer. Methods Eng. 1999, 46, 471–499. [Google Scholar] [CrossRef]
- You, X.Y.; Li, W.; Chai, Y.B. A truly meshfree method for solving acoustic problems using local weak form and radial basisfunctions. Appl. Math. Comput. 2020, 365, 124694. [Google Scholar]
- Ihlenburg, F.; Babuška, I. Finite element solution of the Helmholtz equation with high wave number. Part I: The h-version of the FEM. Comput. Math. Appl. 1995, 30, 9–37. [Google Scholar] [CrossRef]
- Liu, C.; Min, S.S.; Pang, Y.D.; Chai, Y.B. The Meshfree Radial Point Interpolation Method (RPIM) for Wave Propagation Dynamics in Non-Homogeneous Media. Mathematics 2023, 11, 523. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, G.; Gu, Q.Y.; Chai, Y.B. An enriched finite element method with interpolation cover functions for acoustic analysis in high frequencies. Eng. Anal. Bound. Elem. 2021, 129, 67–81. [Google Scholar] [CrossRef]
- Ihlenburg, F.; Babuška, I. Reliability of finite element methods for the numerical computation of waves. Adv. Eng. Softw. 1997, 28, 417–424. [Google Scholar] [CrossRef]
- Fogarty, T.R.; LeVeque, R.J. High-resolution finite-volume methods for acoustic waves in periodic and random media. J. Acoust. Soc. Am. 1999, 106, 17–28. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Li, X.L. Theoretical analysis of the generalized finite difference method. Comput. Math. Appl. 2022, 120, 1–14. [Google Scholar] [CrossRef]
- Ju, B.R.; Qu, W.Z. Three-dimensional application of the meshless generalized finite difference method for solving the extended Fisher-Kolmogorov equation. Appl. Math. Lett. 2023, 136, 108458. [Google Scholar] [CrossRef]
- Qu, W.Z.; He, H. A GFDM with supplementary nodes for thin elastic plate bending analysis under dynamic loading. Appl. Math. Lett. 2022, 124, 107664. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xie, Z.Y.; Ji, S.Y.; Tsai, C.C.; Li, A.L. Meshless generalized finite difference method for water wave interactions with multiple-bottom-seated-cylinder-array structures. Ocean Eng. 2020, 195, 106736. [Google Scholar] [CrossRef]
- Preuss, S.; Gurbuz, C.; Jelich, C.; Baydoun, S.K.; Marburg, S. Recent Advances in Acoustic Boundary Element Methods. J. Theor. Comput. Acoust. 2022, 30, 2240002. [Google Scholar] [CrossRef]
- Gu, Y.; Lei, J. Fracture mechanics analysis of two-dimensional cracked thin structures (from micro- to nano-scales) by an efficient boundary element analysis. Results Math. 2021, 11, 100172. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.J.; Li, P.W.; Qu, W. Singular boundary method for 2D and 3D acoustic design sensitivity analysis. Comput. Math. Appl. 2022, 119, 371–386. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xi, Q.; Li, Y.; Huang, H.; Rabczuk, T. Hybrid FEM–SBM solver for structural vibration induced underwater acoustic radiation in shallow marine environment. Comput. Methods Appl. Mech. Eng. 2020, 369, 113236. [Google Scholar] [CrossRef]
- Li, J.P.; Fu, Z.J.; Gu, Y.; Qin, Q.H. Recent advances and emerging applications of the singular boundary method for large-scale and high-frequency computational acoustics. Adv. Appl. Math. Mech. 2022, 14, 315–343. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xi, Q.; Gu, Y.; Li, J.P.; Qu, W.Z.; Sun, L.L.; Wei, X.; Wang, F.J.; Lin, J.; Li, W.W.; et al. Singular boundary method: A review and computer implementation aspects. Eng. Anal. Bound. Elem. 2023, 147, 231–266. [Google Scholar] [CrossRef]
- Wei, X.; Rao, C.; Chen, S.; Luo, W. Numerical simulation of anti-plane wave propagation in heterogeneous media. Appl. Math. Lett. 2023, 135, 108436. [Google Scholar] [CrossRef]
- Wei, X.; Luo, W. 2.5D singular boundary method for acoustic wave propagation. Appl. Math. Lett. 2021, 112, 106760. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W.; Wen, P.H.; Zhang, C.Z. Singular boundary method for wave propagation analysis in periodic structures. J. Sound Vib. 2018, 425, 170–188. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Lin, J.; Zhang, Y.H.; Reutskiy, S.; Feng, W.J. A novel meshless space-time backward substitution method and its application to nonhomogeneous advection-diffusion problems. Appl. Math. Comput. 2021, 398, 125964. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, L. A boundary meshless method for dynamic coupled thermoelasticity problems. Appl. Math. Lett. 2022, 134, 108305. [Google Scholar] [CrossRef]
- Cheng, S.F.; Wang, F.J.; Wu, G.Z.; Zhang, C.X. A semi-analytical and boundary-type meshless method with adjoint variable formulation for acoustic design sensitivity analysis. Appl. Math. Lett. 2022, 131, 108068. [Google Scholar] [CrossRef]
- Gu, Y.; Fan, C.M.; Fu, Z.J. Localized method of fundamental solutions for three-dimensional elasticity problems: Theory. Adv. Appl. Math. Mech. 2021, 13, 1520–1534. [Google Scholar]
- Li, J.P.; Zhang, L. High-precision calculation of electromagnetic scattering by the Burton-Miller type regularized method of moments. Eng. Anal. Bound. Elem. 2021, 133, 177–184. [Google Scholar] [CrossRef]
- Li, J.P.; Fu, Z.J.; Gu, Y.; Zhang, L. Rapid calculation of large-scale acoustic scattering from complex targets by a dual-level fast direct solver. Comput. Math. Appl. 2023, 130, 1–9. [Google Scholar] [CrossRef]
- Lin, J.; Bai, J.; Reutskiy, S.; Lu, J. A novel RBF-based meshless method for solving time-fractional transport equations in 2D and 3D arbitrary domains. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, F. Localized Method of Fundamental Solutions for Acoustic Analysis Inside a Car Cavity with Sound-Absorbing Material. Adv. Appl. Math. Mech. 2023, 15, 182–201. [Google Scholar]
- Han, Y.T.; Yan, Z.; Lin, J.; Feng, W.J. A novel model and solution on the bending problem of arbitrary shaped magnetoelectroelastic plates based on the modified strain gradient theory. J. Intell. Mater. Syst. Struct. 2022, 33, 1072–1086. [Google Scholar] [CrossRef]
- Wan, J.S.; Li, X.L. Analysis of a superconvergent recursive moving least squares approximation. Appl. Math. Lett. 2022, 133, 108223. [Google Scholar] [CrossRef]
- Qiu, L.; Ma, X.; Qin, Q.H. A novel meshfree method based on spatio-temporal homogenization functions for one-dimensional fourth-order fractional diffusion-wave equations. Appl. Math. Lett. 2023, 142, 108657. [Google Scholar] [CrossRef]
- Harari, I.; Hughes, T.J.R. GalerkinAeast-squares finite element methods for the reduced wave equation with non-reflecting boundary conditions in unbounded domains. Comput. Methods Appl. Mech. Eng. 1992, 98, 411–454. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Gong, Z.X.; Li, T.Y. Hybrid smoothed finite element method for two-dimensional underwater acoustic scattering problems. Ocean Eng. 2016, 116, 129–141. [Google Scholar] [CrossRef]
- Li, X.; Li, S. A finite point method for the fractional cable equation using meshless smoothed gradients. Eng. Anal. Bound. Elem. 2022, 134, 453–465. [Google Scholar] [CrossRef]
- Fu, Z.J.; Tang, Z.C.; Xi, Q.; Liu, Q.G.; Gu, Y.; Wang, F.J. Localized collocation schemes and their applications. Acta Mech. Sin. 2022, 38, 422167. [Google Scholar] [CrossRef]
- Fu, Z.J.; Yang, L.W.; Xi, Q.; Liu, C.S. A boundary collocation method for anomalous heat conduction analysis in functionally graded materials. Comput. Math. Appl. 2021, 88, 91–109. [Google Scholar] [CrossRef]
- Tang, Z.; Fu, Z.J.; Sun, H.; Liu, X. An efficient localized collocation solver for anomalous diffusion on surfaces. Fract. Calc. Appl. Anal. 2021, 24, 865–894. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.J.; Zhang, C.Z.; Yin, D.S. An efficient localized Trefftz-based collocation scheme for heat conduction analysis in two kinds of heterogeneous materials under temperature loading. Comput. Struct. 2021, 255, 106619. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.J.; Wu, W.J.; Wang, H.; Wang, Y. A novel localized collocation solver based on Trefftz basis for Potential-based Inverse Electromyography. Appl. Math. Comput. 2021, 390, 125604. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.J.; Rabczuk, T.; Yin, D. A localized collocation scheme with fundamental solutions for long-time anomalous heat conduction analysis in functionally graded materials. Int. J. Heat Mass Transf. 2021, 180, 121778. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. An Introduction to Meshfree Methods and Their Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Li, Y.C.; Liu, C.; Li, W.; Chai, Y.B. Numerical investigation of the element-free Galerkin method (EFGM) with appropriate temporal discretization techniques for transient wave propagation problems. Appl. Math. Comput. 2023, 442, 127755. [Google Scholar] [CrossRef]
- Zhang, Y.O.; Dang, S.N.; Li, W.; Chai, Y.B. Performance of the radial point interpolation method (RPIM) with implicit time integration scheme for transient wave propagation dynamics. Comput. Math. Appl. 2022, 114, 95–111. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Gui, Q.; Chai, Y.B. A coupled FE-Meshfree triangular element for acoustic radiation problems. Int. J. Comput. Methods 2021, 18, 2041002. [Google Scholar] [CrossRef]
- Li, W.; Gong, Z.X.; Chai, Y.B.; Cheng, C.; Li, T.Y.; Zhang, Q.F.; Wang, M.S. Hybrid gradient smoothing technique with discrete shear gap method for shell structures. Comput. Math. Appl. 2017, 74, 1826–1855. [Google Scholar] [CrossRef]
- Liu, M.Y.; Gao, G.J.; Zhu, H.F.; Jiang, C.; Liu, G.R. A cell-based smoothed finite element method (CS-FEM) for three-dimensional incompressible laminar flows using mixed wedge-hexahedral element. Eng. Anal. Bound. Elem. 2021, 133, 269–285. [Google Scholar] [CrossRef]
- Wang, T.T.; Zhou, G.; Jiang, C.; Shi, F.C.; Tian, X.D.; Gao, G.J. A coupled cell-based smoothed finite element method and discrete phase model for incompressible laminar flow with dilute solid particles. Eng. Anal. Bound. Elem. 2022, 143, 190–206. [Google Scholar] [CrossRef]
- Jiang, C.; Hong, C.; Wang, T.T.; Zhou, G. N-Side cell-based smoothed finite element method for incompressible flow with heat transfer problems. Eng. Anal. Bound. Elem. 2023, 146, 749–766. [Google Scholar] [CrossRef]
- Li, W.; You, X.Y.; Chai, Y.B.; Li, T.Y. Edge-Based Smoothed Three-Node Mindlin Plate Element. J. Eng. Mech. 2016, 142, 04016055. [Google Scholar] [CrossRef]
- Chai, Y.B.; Gong, Z.X.; Li, W.; Li, T.Y.; Zhang, Q.F.; Zou, Z.H.; Sun, Y.B. Application of smoothed finite element method to two dimensional exterior problems of acoustic radiation. Int. J. Comput. Methods 2018, 15, 1850029. [Google Scholar] [CrossRef]
- Thompson, L.L.; Plnsky, P.M. A Galerkin least-squares finite element method for the two-dimensional Helmholtz equation. Int. J. Numer. Methods Eng. 1995, 38, 371–397. [Google Scholar] [CrossRef]
- Babuška, I.; Ihlenburg, F.; Paik, E.T.; Sauter, S.A. A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution. Comput. Methods Appl. Mech. Eng. 1995, 128, 325–359. [Google Scholar] [CrossRef]
- He, Z.C.; Li, E.; Liu, G.R.; Li, G.Y.; Cheng, A.G. A mass-redistributed finite element method (MR-FEM) for acoustic problems using triangular mesh. J. Comput. Phys. 2016, 323, 149–170. [Google Scholar] [CrossRef]
- Kim, J.; Bathe, K.J. The finite element method enriched by interpolation covers. Comput. Struct. 2013, 116, 35–49. [Google Scholar] [CrossRef]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Strouboulis, T.; Copps, K.; Babuška, I. The generalized finite element method: An example of its implementation and illustration of its performance. Int. J. Numer. Methods Eng. 2000, 47, 1401–1417. [Google Scholar] [CrossRef]
- Li, Y.C.; Dang, S.N.; Li, W.; Chai, Y.B. Free and Forced Vibration Analysis of Two-Dimensional Linear Elastic Solids Using the Finite Element Methods Enriched by Interpolation Cover Functions. Mathematics 2022, 10, 456. [Google Scholar] [CrossRef]
- Kim, K.T.; Zhang, L.; Bathe, K.J. Transient implicit wave propagation dynamics with overlapping finite Elements. Comput. Struct. 2018, 199, 18–33. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Liu, Z.Y. Analysis of transient wave propagation dynamics using the enriched finite element method withinterpolation cover functions. Appl. Math. Comput. 2022, 412, 126564. [Google Scholar]
- Chai, Y.B.; Bathe, K.J. Transient wave propagation in inhomogeneous media with enriched overlapping triangular elements. Comput. Struct. 2020, 237, 106273. [Google Scholar] [CrossRef]
- Tian, R.; Yagawa, G.; Terasaka, H. Linear dependence problems of partition of unity-based generalized FEMs. Comput. Methods Appl. Mech. Eng. 2006, 195, 4768–4782. [Google Scholar] [CrossRef]
- Duarte, C.A.; Babuška, I.; Oden, J.T. Generalized finite element methods for three-dimensional structural mechanics problems. Comput. Struct. 2000, 77, 215–232. [Google Scholar] [CrossRef]
- Kim, K.T.; Bathe, K.J. Transient implicit wave propagation dynamics with the method of finite spheres. Comput. Struct. 2016, 173, 50–60. [Google Scholar] [CrossRef]
- Sun, T.T.; Wang, P.; Zhang, G.J.; Chai, Y.B. Transient analyses of wave propagations in nonhomogeneous media employingthe novel finite element method with the appropriate enrichment function. Comput. Math. Appl. 2023, 129, 90–112. [Google Scholar] [CrossRef]
Figure 1.
The employed coordinate system in this extrinsic EFEM: (a) the global coordinate and relative coordinate system for a triangular element; (b) the natural coordinate system for an isoparameter triangular element.
Figure 1.
The employed coordinate system in this extrinsic EFEM: (a) the global coordinate and relative coordinate system for a triangular element; (b) the natural coordinate system for an isoparameter triangular element.
Figure 2.
The employed regular triangular mesh pattern to investigate the dispersion effects.
Figure 2.
The employed regular triangular mesh pattern to investigate the dispersion effects.
Figure 3.
The numerical dispersion error along the varying angles of acoustic wave propagation from different discretization techniques: (a) FEM-T3; (b) EFEM-N9; (c) EFEM-N11.
Figure 3.
The numerical dispersion error along the varying angles of acoustic wave propagation from different discretization techniques: (a) FEM-T3; (b) EFEM-N9; (c) EFEM-N11.
Figure 4.
The acoustic propagation in a two-dimensional tube: (a) the geometry parameters of this tube and (b) the employed spatial discretization pattern.
Figure 4.
The acoustic propagation in a two-dimensional tube: (a) the geometry parameters of this tube and (b) the employed spatial discretization pattern.
Figure 5.
The calculated acoustic pressure provided by various numerical techniques for different frequency values: (a) f = 1100 Hz; (b) f = 2200 Hz; (c) f = 4400 Hz; (d) f = 6600 Hz.
Figure 5.
The calculated acoustic pressure provided by various numerical techniques for different frequency values: (a) f = 1100 Hz; (b) f = 2200 Hz; (c) f = 4400 Hz; (d) f = 6600 Hz.
Figure 6.
The calculated relative error results from different numerical techniques for the frequency value f = 2200 Hz: (a) the relative error results and (b) the corresponding exact acoustic particle velocity distributions.
Figure 6.
The calculated relative error results from different numerical techniques for the frequency value f = 2200 Hz: (a) the relative error results and (b) the corresponding exact acoustic particle velocity distributions.
Figure 7.
The calculated relative error results from different numerical techniques for the frequency value f = 4400 Hz: (a) the relative error results and (b) the corresponding exact acoustic particle velocity distributions.
Figure 7.
The calculated relative error results from different numerical techniques for the frequency value f = 4400 Hz: (a) the relative error results and (b) the corresponding exact acoustic particle velocity distributions.
Figure 8.
Comparison of the calculated global error results from different methods versus the wave number k.
Figure 8.
Comparison of the calculated global error results from different methods versus the wave number k.
Figure 9.
Comparison of the numerical performance of different methods in controlling the different numerical error components: (a) keeping kh = constant; (b) keeping k3h2 = constant.
Figure 9.
Comparison of the numerical performance of different methods in controlling the different numerical error components: (a) keeping kh = constant; (b) keeping k3h2 = constant.
Figure 10.
The acoustic propagation in a two-dimensional square domain: (a) the geometry parameters of this square domain and the related boundary conditions and (b) the employed spatial discretization pattern.
Figure 10.
The acoustic propagation in a two-dimensional square domain: (a) the geometry parameters of this square domain and the related boundary conditions and (b) the employed spatial discretization pattern.
Figure 11.
Thecalculated acoustic pressure distribution results along the defined path for the varying wave numbers: (a) k = 2; (b) k = 5; (c) k = 10.
Figure 11.
Thecalculated acoustic pressure distribution results along the defined path for the varying wave numbers: (a) k = 2; (b) k = 5; (c) k = 10.
Figure 12.
The acoustic propagation in a two-dimensional car: (a) the geometry parameters of this two-dimensional car and (b) the employed spatial discretization pattern.
Figure 12.
The acoustic propagation in a two-dimensional car: (a) the geometry parameters of this two-dimensional car and (b) the employed spatial discretization pattern.
Figure 13.
Comparisons the computed numerical acoustic pressure results along the defined path for two different frequency values: (a) the frequency value f = 320 Hz and (b) the frequency value f = 650 Hz.
Figure 13.
Comparisons the computed numerical acoustic pressure results along the defined path for two different frequency values: (a) the frequency value f = 320 Hz and (b) the frequency value f = 650 Hz.
Figure 14.
Comparisons the calculated acoustic pressure distribution results from different methods in the total problem domain for the frequency value f = 320 Hz: (a) FEM-T3; (b) EFEM-N9; (c) EFEM-N11; (d) reference solution.
Figure 14.
Comparisons the calculated acoustic pressure distribution results from different methods in the total problem domain for the frequency value f = 320 Hz: (a) FEM-T3; (b) EFEM-N9; (c) EFEM-N11; (d) reference solution.
Figure 15.
Comparisons the calculated acoustic pressure distribution results from different methods in the total problem domain for the frequency value f = 650 Hz: (a) FEM-T3; (b) EFEM-N9; (c) EFEM-N11; (d) reference solution.
Figure 15.
Comparisons the calculated acoustic pressure distribution results from different methods in the total problem domain for the frequency value f = 650 Hz: (a) FEM-T3; (b) EFEM-N9; (c) EFEM-N11; (d) reference solution.
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).