A Study on Electric Potential and Electric Field Distribution for Optimal Design of Lightning Rod Using Finite Element Method
Abstract
:1. Introduction
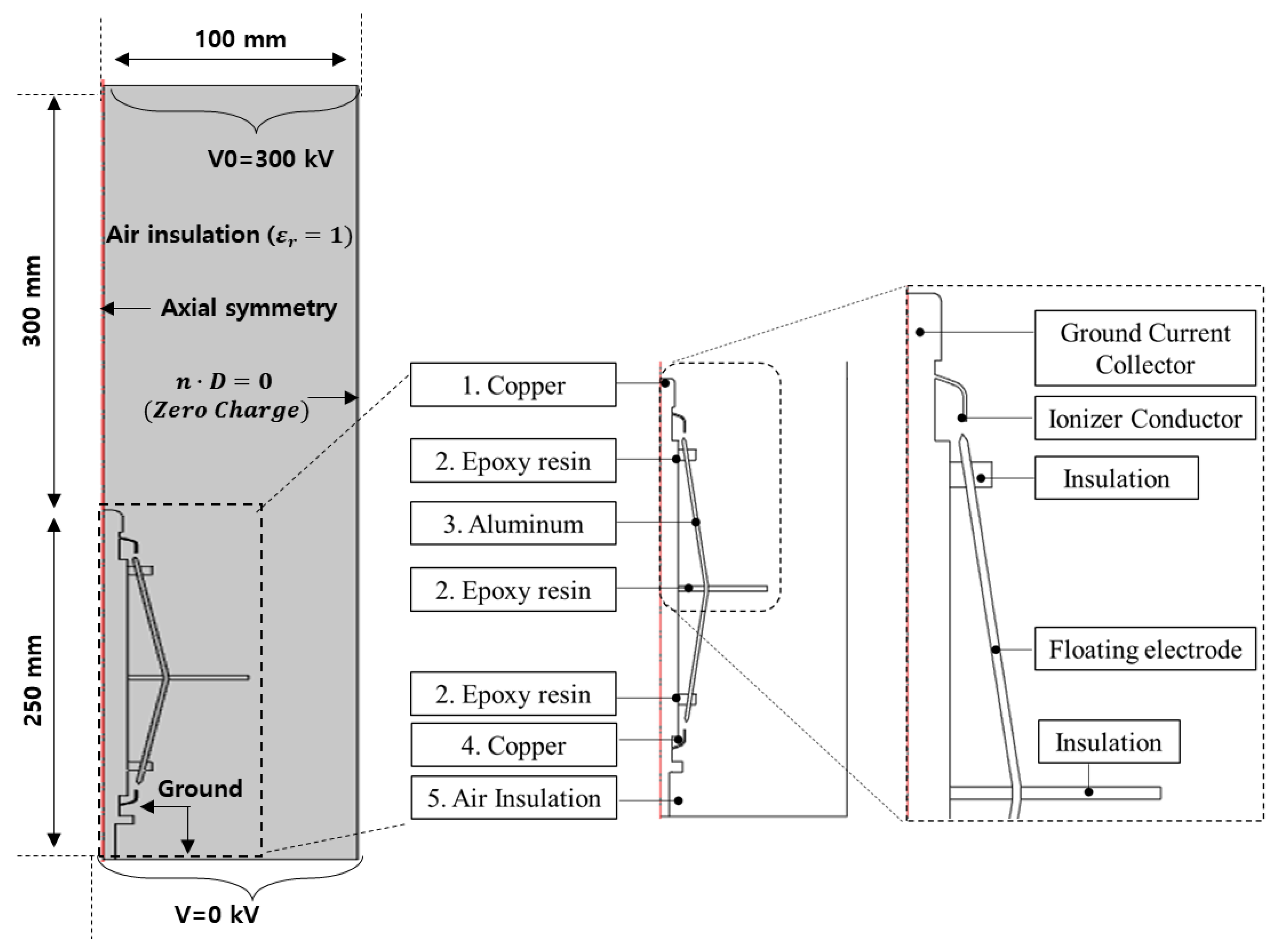
2. Modeling for Electric Field Analysis
3. Results and Discussion
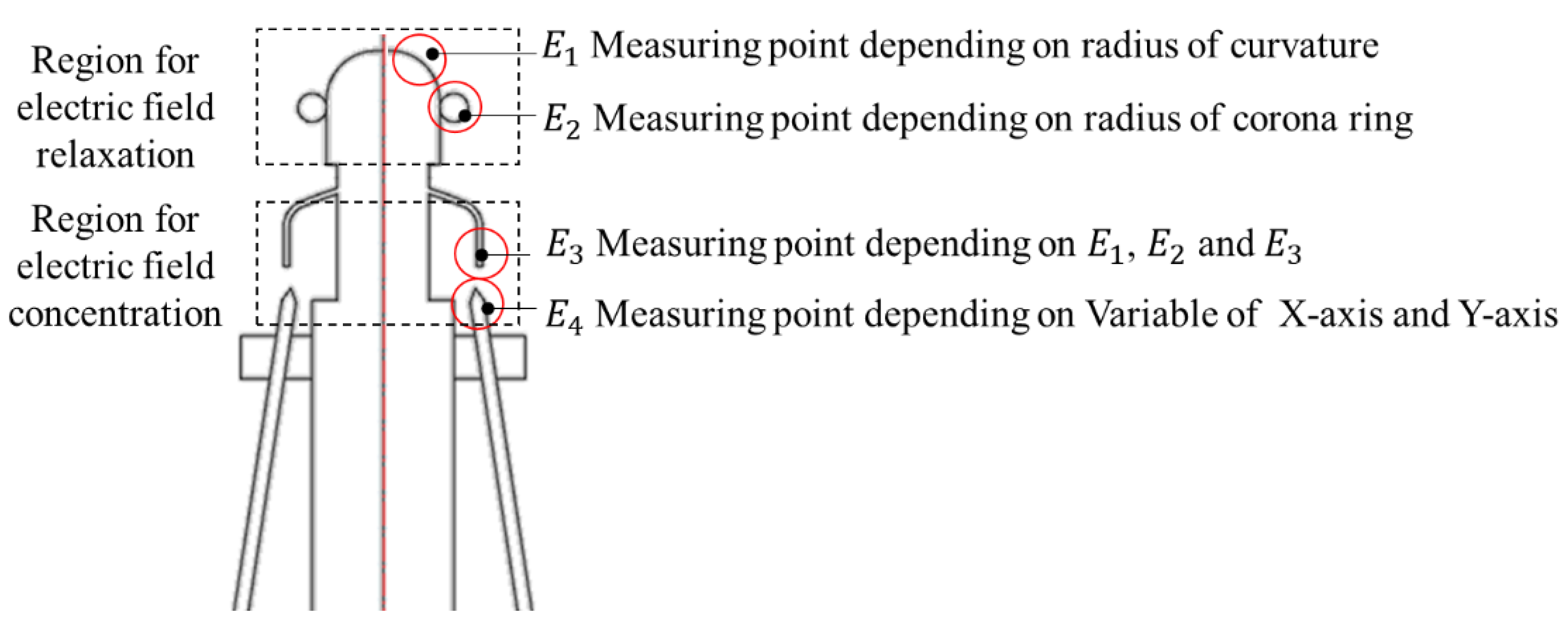
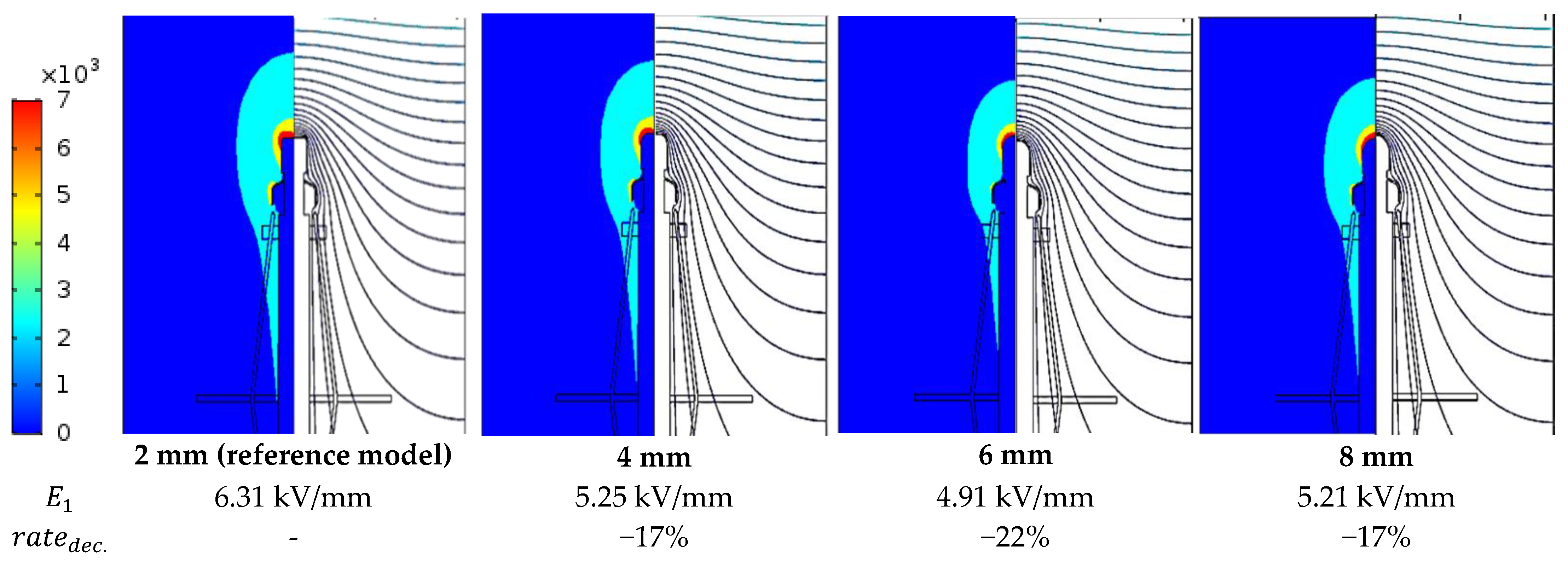
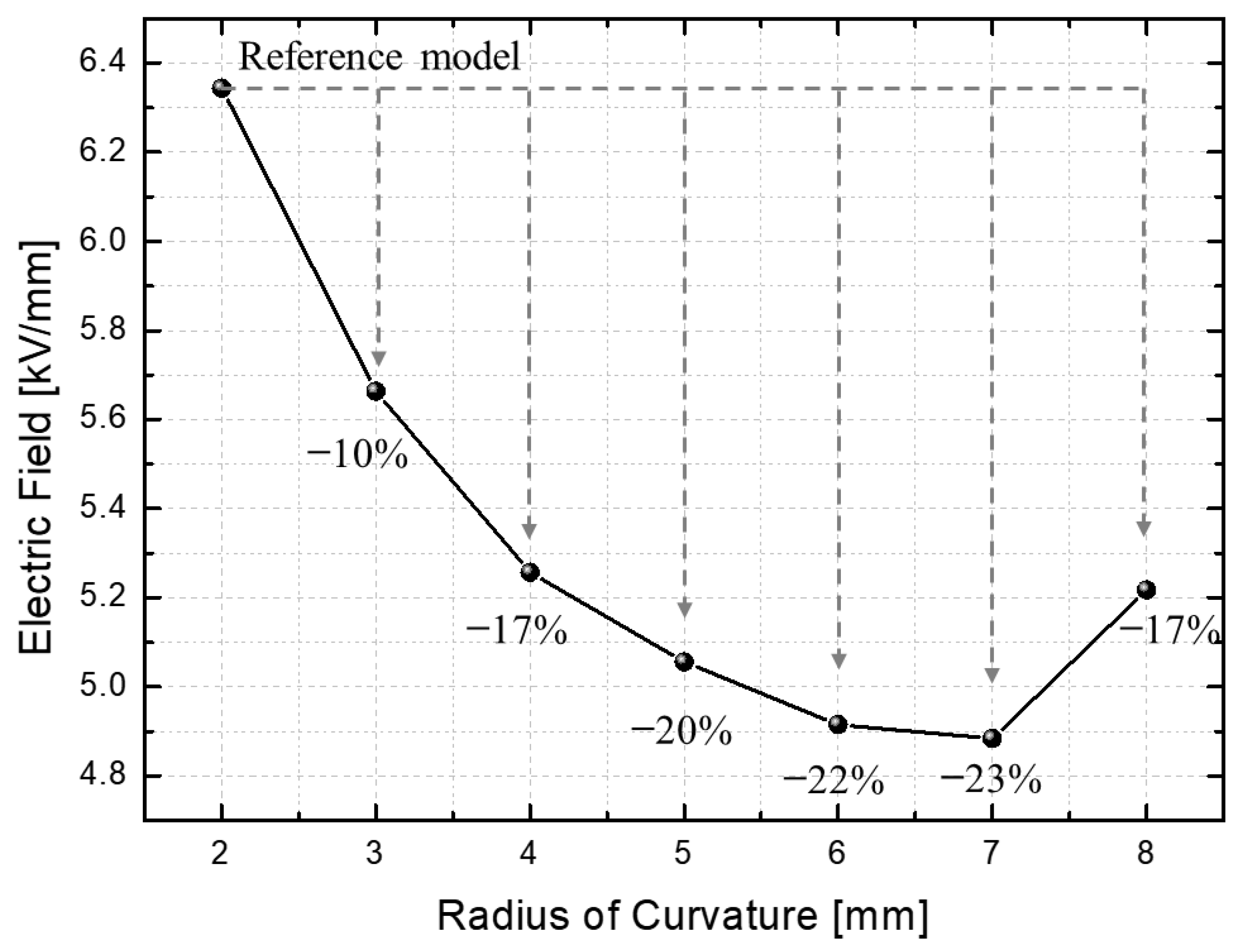
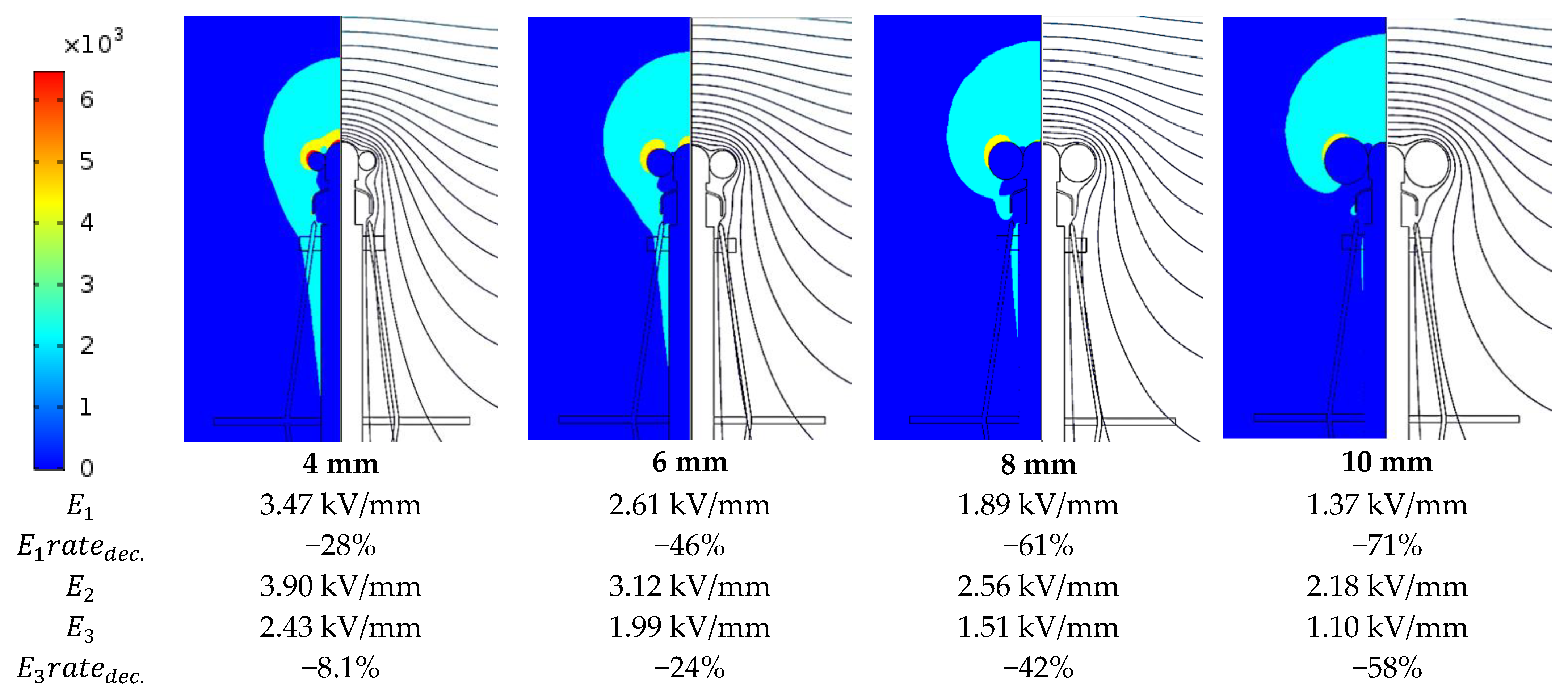
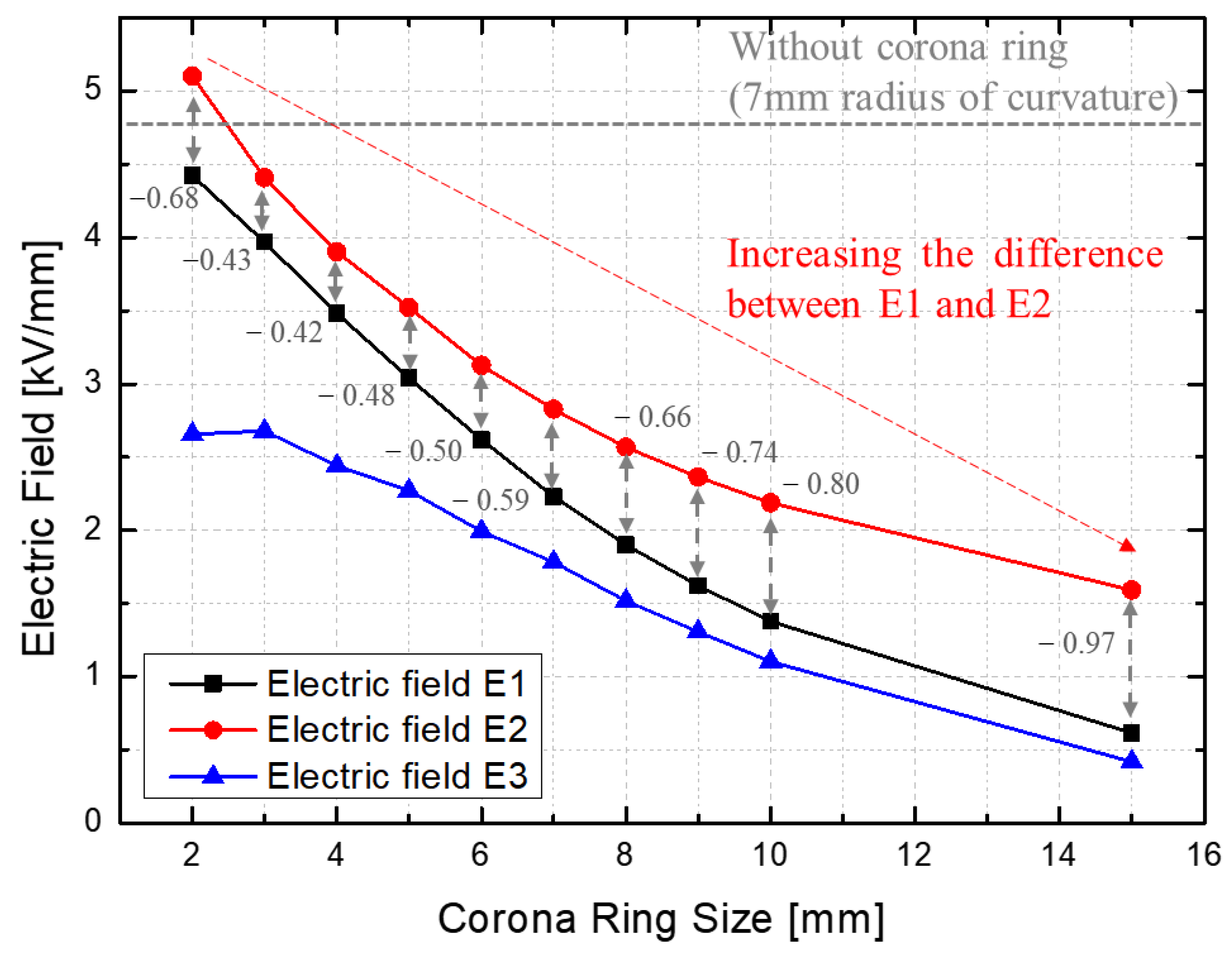
3.1. Electric Field Relaxation Part
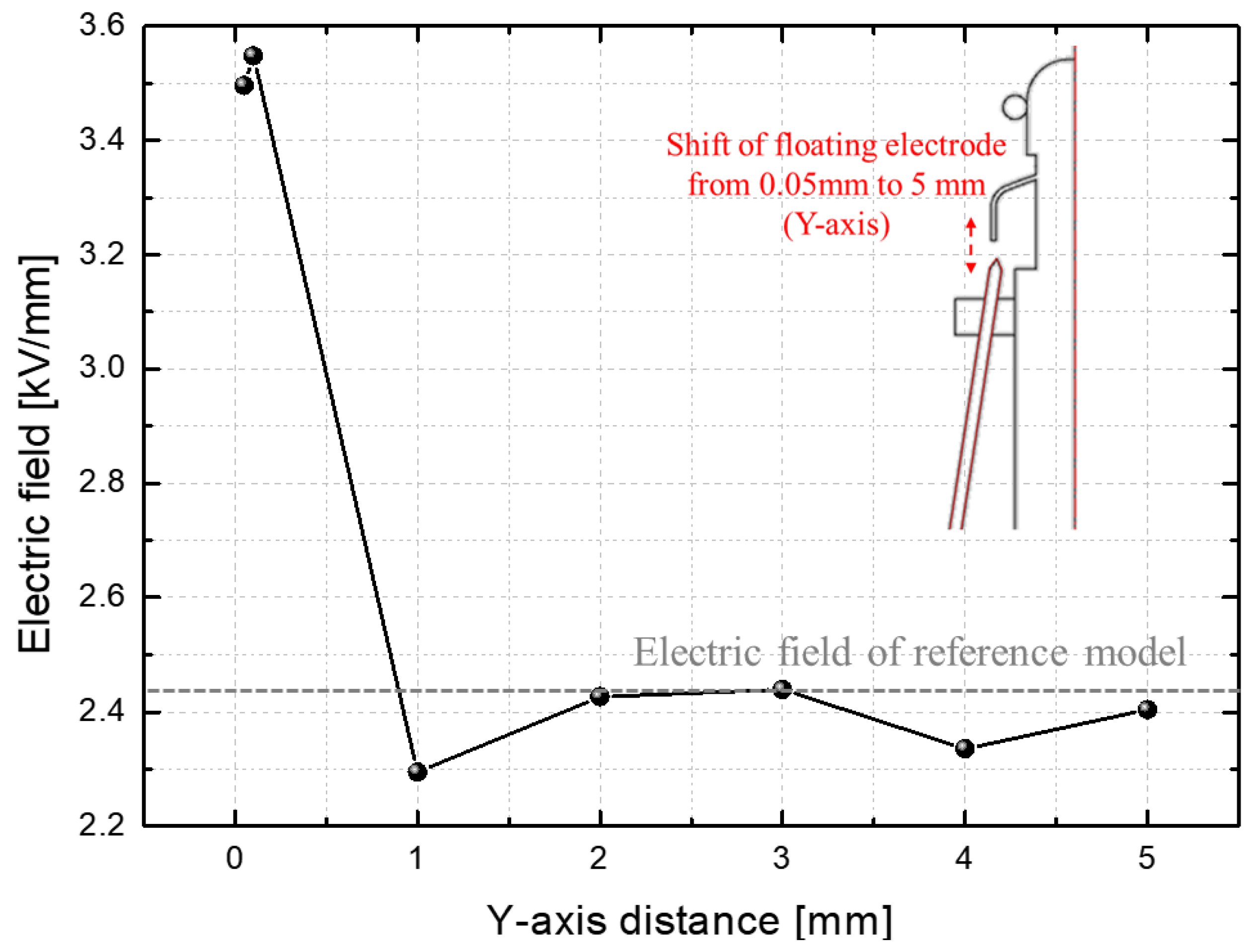
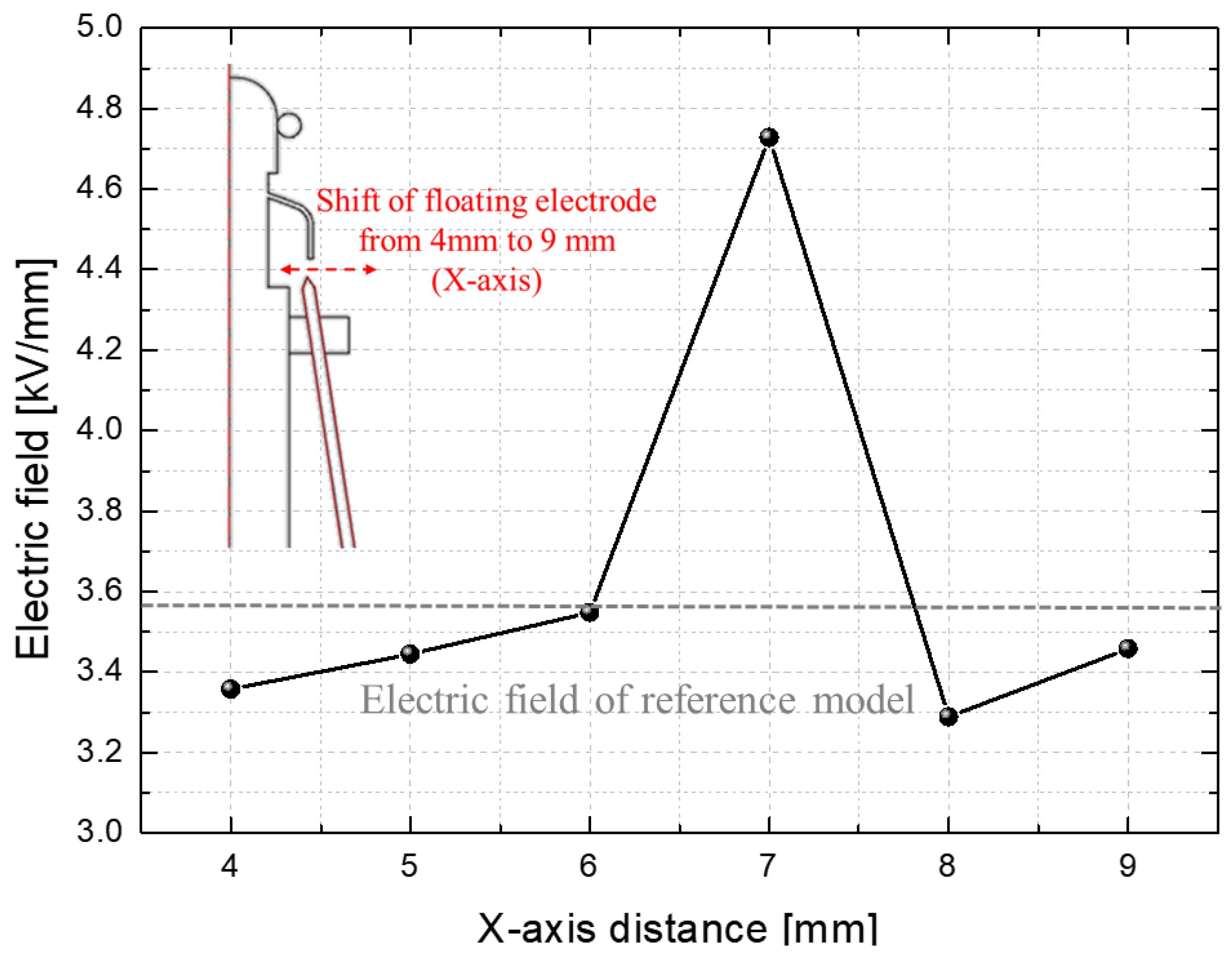
3.2. Local Electric Field Concentration Part
4. Conclusions
- (1)
- Radius of curvature (electric field relaxation)
- (2)
- Corona ring size (electric field relaxation)
- (3)
- The position of the floating electrode in the direction of the X-axis (electric field concentration)
- (4)
- The position of the floating electrode in the direction of the Y-axis (electric field concentration)
- (1)
- Uniform electric field formation, both at the corona ring and tip part of the grounding current collector.
- (2)
- The reduction in the electric field of the ionizer conductor due to the increase in corona ring size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lightning Costs and Losses from Attributed Sources, Lightning Costs and Losses from Attributed Sources—National Lightning Safety Institute. 2020. Available online: https://lightningelectricity.com/ (accessed on 22 March 2020).
- Facts + Statistics: Lightning. 2022. Available online: https://www.iii.org/fact-statistic/facts-statistics-lightning (accessed on 22 March 2020).
- History.com Editors. Benjamin Franklin. A&E Television Networks, 2022 (Last Updated). Available online: https://www.history.com/topics/american-revolution/benjamin-franklin (accessed on 22 March 2022).
- Kim, H.-G.; Lee, K.-S. The Change of Lightning Air Terminal and Trend of the World. In Proceedings of the International Symposium on High Voltage Engineering, Hannover, Germany, 22–26 August 2011. [Google Scholar]
- Cooray, V. The Similarity of the Action of Franklin and ESE Lightning Rods under Natural Conditions. Atmosphere 2018, 9, 225. [Google Scholar] [CrossRef] [Green Version]
- Cooray, V. Non-Conventional Lightning Protection System. In Proceedings of the 30th International Conference on Lightning Protection (ICLP), Cagliari, Italy, 13–17 September 2010. [Google Scholar]
- Kim, D.-J. A Study on the HEC (Hybrid ESE Conductor) Method for Lightning Protection of Buildings. Trans. Korean Inst. Electr. Eng. 2008, 57, 2. [Google Scholar]
- Mladen, B. Early Streamer Emission Vs Conventional Lightning Protection Systems. B&H Electr. Eng. 2019, 13, 24–34. [Google Scholar]
- Becerra, M.; Cooray, V. The Early Streamer Emission Principle Does Not Work Under Natural Lightning. In Proceedings of the International Symposium on Lightning Protection, Foz do Iguaçu, Brazil, 26–30 November 2007. [Google Scholar]
- Baek, M.K.; Chung, Y.K.; Park, I.H. Experiment and Analysis for Effect of Floating Conductor on Electric Discharge Characteristic. IEEE Trans. Magn. 2013, 49, 5. [Google Scholar] [CrossRef]
- Lee, B.-H. Effect of the Corona Shield of the OMNI Bipolar Conventional Air Terminals. In Proceedings of the 2016 International Conference on ElectroMagnetic Interference & Compatibility (INCEMIC), Bengaluru, India, 8–9 December 2016. [Google Scholar]
- Lee, B.-H. Analysis and Test on Electric Field Concentration Effect of Bipolar Conventional Air Terminal. In Proceedings of the International Conference on Lightning Protection (ICLP), Shanghai, China, 11–18 October 2014. [Google Scholar]
- Produit, T. The Laser Lightning Rod Project. Eur. Phys. J. Appl. Phys. 2020, 92, 30501. [Google Scholar] [CrossRef]
- Jang, K.-H. Corona Discharge Behaviors with Presence of Floating Electrode in Air Insulation using Numerical Model Analysis. J. Mater. Sci. Manuf. Res. 2023, 4, 1–4. [Google Scholar] [CrossRef]
- Jang, K.-H. Numerical Simulation Analysis on Non-Conventional Lightning Protection System. In Proceedings of the IEEE 4th Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 28–30 October 2022. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Benguesmia, H.; M’ziou, N. Simulation of the Potential and Electric Field Distribution on High Voltage Insulator using the Finite Element Method. Diagnostyka 2018, 19, 2. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, G.; Wang, Q. Simulation Analysis and Calculation of Electric Field Distribution Characteristics of UHV Wall Bushing. In Proceedings of the 4th International Conference on Electrical Engineering and Green Energy CEEGE, Munich, Germany, 10–13 June 2021. [Google Scholar]
- Liao, L.; Xue, T.; Xiong, J.; Lu, B. Research on the Influence of the Relative Permittivity of the Reinforced Insulation of the Cable Intermediate Joint on the Electric Field Intensity. J. Phys. Conf. Ser. 2021, 1815, 012037. [Google Scholar] [CrossRef]
- Jang, K.-H.; Seo, S.-W.; Kim, D.-J. Electric Field Analysis on the Corona Discharge Phenomenon according to the Variable Air Space between the Ionizer and Ground Current Collector. Appl. Syst. Innov. 2023, 6, 10. [Google Scholar] [CrossRef]
- Lee, J.-H. Local Electric Field Analysis for Evaluation of Charge Transfer System Using Sequential Subwindow Technique. IEEE Trans. Magn. 2004, 40, 2. [Google Scholar] [CrossRef]

| Symbol | Meaning |
|---|---|
| D | Electric flux density |
| V | Electric potential |
| εr | Relative permittivity |
| ρ | Charge density |
| J | Current density |
| σ | Electric conductivity |
| Name | Material | Functions of the Main Component | Relative Permittivity (εr) | Conductivity (S/m) | |
|---|---|---|---|---|---|
| 1 | Tip part of the ground current collector | Copper | Electric field relaxation part | 1 | 1.6 × 107 |
| 2 | Insulation support | Epoxy resin | Insulation support for fixing a floating electrode | 4.2 | 3.8 × 1015 |
| 3 | Floating electrode | Aluminum | Electric field concentration between the ionizer conductor and floating electrode | 1 | 3.5 × 107 |
| 4 | Ionizer conductor | Copper | Electric field concentration between the ionizer conductor and floating electrode | 1 | 1.6 × 107 |
| 5 | Air insulation | Air | - | 1 | 2.6 × 10−17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, K.-H.; Seo, S.-W.; Kim, D.-J. A Study on Electric Potential and Electric Field Distribution for Optimal Design of Lightning Rod Using Finite Element Method. Mathematics 2023, 11, 1668. https://doi.org/10.3390/math11071668
Jang K-H, Seo S-W, Kim D-J. A Study on Electric Potential and Electric Field Distribution for Optimal Design of Lightning Rod Using Finite Element Method. Mathematics. 2023; 11(7):1668. https://doi.org/10.3390/math11071668
Chicago/Turabian StyleJang, Kyung-Hoon, Sang-Won Seo, and Dong-Jin Kim. 2023. "A Study on Electric Potential and Electric Field Distribution for Optimal Design of Lightning Rod Using Finite Element Method" Mathematics 11, no. 7: 1668. https://doi.org/10.3390/math11071668
APA StyleJang, K. -H., Seo, S. -W., & Kim, D. -J. (2023). A Study on Electric Potential and Electric Field Distribution for Optimal Design of Lightning Rod Using Finite Element Method. Mathematics, 11(7), 1668. https://doi.org/10.3390/math11071668








