Financial Volatility Modeling with the GARCH-MIDAS-LSTM Approach: The Effects of Economic Expectations, Geopolitical Risks and Industrial Production during COVID-19

Abstract

Forecasting stock markets is an important challenge due to leptokurtic distributions with heavy tails due to uncertainties in markets, economies, and political fluctuations. To forecast the direction of stock markets, the inclusion of leading indicators to volatility models is highly important; however, such series are generally at different frequencies. The paper proposes the GARCH-MIDAS-LSTM model, a hybrid method that benefits from LSTM deep neural networks for forecast accuracy, and the GARCH-MIDAS model for the integration of effects of low-frequency variables in high-frequency stock market volatility modeling. The models are being tested for a forecast sample including the COVID-19 shut-down after the first official case period and the economic reopening period in in Borsa Istanbul stock market in Türkiye. For this sample, significant uncertainty existed regarding future economic expectations, and the period provided an interesting laboratory to test the forecast effectiveness of the proposed LSTM augmented model in addition to GARCH-MIDAS models, which included geopolitical risk, future economic expectations, trends, and cycle industrial production indices as low-frequency variables. The evidence suggests that stock market volatility is most effectively modeled with geopolitical risk, followed by industrial production, and a relatively lower performance is achieved by future economic expectations. These findings imply that increases in geopolitical risk enhance stock market volatility further, and that industrial production and future economic expectations work in the opposite direction. Most importantly, the forecast results suggest suitability of both the GARCH-MIDAS and GARCH-MIDAS-LSTM models, and with good forecasting capabilities. However, a comparison shows significant root mean squared error reduction with the novel GARCH-MIDAS-LSTM model over GARCH-MIDAS models. Percentage decline in root mean squared errors for forecasts are between 39% to 95% in LSTM augmented models depending on the type of economic indicator used. The proposed approach offers a key tool for investors and policymakers.

1. Introduction

The forecasting of the direction of financial markets has always been of interest to researchers, investors, and policymakers. Due to the volatile structure of these markets, a large set of generalized autoregressive conditional heteroskedasticity (GARCH) models with different architectures has been developed to achieve various aspects of financial markets, including volatility clustering, asymmetry, leverage effects, in addition to heavy tails and leptokurtic distribution. A portion of the literature further integrated nonlinear econometric approaches with various GARCH models to achieve regime-dependent models, including Markov-Switching GARCH (MS-GARCH), Smooth Transition GARCH (ST-GARCH) and, further, recent advances in machine learning, which also led to the introduction of the Neural Networks' GARCH (NN-GARCH) family of models, Support Vector GARCH (SV-GARCH), and more recently, the MS-NN-GARCH model as a hybrid model to capture improved forecast capabilities. Lastly, recent advances in machine learning models, particularly in the field of deep neural networks, have led to LSTM-based deep neural network hybrid models to achieve forecast accuracy improvements for the GARCH model.

The above-mentioned models are univariate in nature; however, the inclusion of exogenous variables in the models is also possible. To this end, a typical model is the GARCH-M model, which allows exogenous variables to enter the explanatory parts of the GARCH-type volatility models. However, all models necessitate equal frequencies for the data used, and this puts a common burden on all models of volatility. The volatility modeling generally necessitates data with highly frequent time series repetitions, such as daily or intra-day stock market returns. In contrast, the exogeneous indicators are generally in less frequent time frequencies, and the majority are variables measured in typically monthly frequency, such as the inflation rates, industrial production, unemployment rates, and various indicators including the Baltic Dry Index (BDI), which is generally accepted as producing effective results in monthly frequency [1,2]. As a general variable with quarterly frequency, GDP is effective in providing information regarding the current state of the economy. Economic data exists in higher frequencies such as the number of weekly unemployment applications, which could be taken as leading economic indicators. In short, it is a challenging task to model volatility and to include leading indicators in volatility models due to the frequency mismatch of the variables. The data frequency mismatch problem affects all volatility models including the single-regime GARCH and the nonlinear GARCH counterparts.

To this end, Engle et al. [3] proposed the integration of Ghysels et al.’s mixed data sampling (MIDAS) strategy of [4] to achieve the GARCH-MIDAS model. The GARCH-MIDAS model benefits from a set of functions (which will be discussed) to transform the low-frequency variable to higher frequencies within a smoothed transformation achieved with various functions. The aim is to solve the frequency mismatch problem in addition to including the effects of lower frequency variables to the GARCH specification of conditional volatility. Though the MIDAS approach to GARCH allows for a solution to overcome the frequency mismatch and provides important information regarding the effects of macroeconomic and leading indicators, the forecast accuracy of such models is evaluated in the studies, and questions have emerged with regard to this respect. Therefore, our study assumes a method to integrate Long-Short-Term-Memory (LSTM) deep neural networks to the GARCH-MIDAS method. To this end, our paper suggests that the GARCH-MIDAS-LSTM model be used to explore the possibility of augmenting the forecast capabilities of GARCH-MIDAS models with deep learning architectures. As will be shown, the proposed method benefits from the GARCH-MIDAS method in the integration of lower frequency variables to the volatility modelling of higher frequency variables. By utilizing a selected set of economic fundamentals, the proposed model is tested for forecasting effectiveness for a sample covering the early period of the COVID-19 pandemic in an emerging stock market in the context of the Borsa Istanbul stock market. The forecast period included lock-down policies followed by the reopening of the economy in the following month. Therefore, the out-of-sample period provides a good laboratory with distinguished characteristics from the in-sample period to evaluate forecast performances of the GARCH-MIDAS and the GARCH-MIDAS-LSTM models. The last section of the in-sample and, most importantly, the out-of-sample period also include a high level of uncertainty regarding the future of the economic activity due to uncertainties about the new-normal policies introduced in May and followed thereafter.

In this paper, the sample selection for in-sample modeling and out-of-sample forecast practice is of crucial importance. The selected periods play a crucial role in testing the model performances during the pandemic in various aspects. The first official COVID-19 case was announced on 13 March 2020 in Türkiye. This date followed various health measures which ended with the economic shut-down followed by lockdown periods in the months that followed. Towards the end of the spring of 2020, the measures were relaxed and economic policies followed a controlled economic reopening period. As a result, the sample selection serves an important laboratory in which to test the LSTM augmented model, in addition to its non-LSTM variant, the GARCH-MIDAS model. The last portion of the in-sample dataset includes the first case following the economic shut-down and the early reopening policies. On the other hand, the out-of-sample forecast period covers a period that is characterized by the opening of the economy coupled with the elimination of the controlled lock-down period. Therefore, the differences in the economic dynamics in the forecast sample and the training sample is expected to play an important role on the effectiveness of the models. Furthermore, the period was also characterized by a significant level of uncertainty with regard to future economic performance, in addition to geopolitical uncertainty, as captured with the indices to be discussed below. Due to these different dynamics, the forecast performances of both GARCH-MIDAS and the proposed GARCH-MIDAS-LSTM will be explored in the study to determine the effects of economic factors in addition to the LSTM algorithm on forecast performances.

In both the GARCH-MIDAS and the GARCH-MIDAS-LSTM model, the volatility is decomposed into short run and long run components. The latter is captured with MIDAS sampling that also integrates the impact of the macroeconomic variable to the conditional variance process of the daily stock market. Similar to the GARCH-MIDAS model, the GARCH-MIDAS-LSTM is allowed to be modeled with fixed and rolling window specifications. In the empirical analysis, a total of four monthly macroeconomic indicators are considered as leading indicators by various agencies, including the Central Bank of the Republic of Türkiye (CBRT) and the Organization of Economic Cooperation and Development (OECD). These indicators are utilized by including their influence on the conditional volatility of the Borsa Istanbul 100 stock market. The selection of the economic indicators is due to their leading indicator potential. Among the four indicators, the first two are the leading production indicators announced by the CBRT, which are announced as representing the cycle and trend of monthly industrial production. These indicators, to be denoted as IPI-cycle and IPI-trend throughout the text, are two series that are announced as ‘leading’ indicators of CBRT which correspond to the cycles and trends of the industrial production indices for Türkiye.

In addition to CBRT’s IPI-cycle and IPI-trend indicators, the paper aims to analyze two additional economic fundamentals as the drivers of volatility. Among these two additional indicators, first is the Composite Leading Indicator (CLI) of OECD. CLI is a monthly index created by the OECD as an index of mainly future expectations regarding various economic factors [5,6]. The CLI index is country-specific and is also announced monthly on the CBRT webpage. The last index other than the IPI-cycle, IPI-trend and CLI indices is the Geopolitical Risk Indicator (GPR) of Caldara and Iocaviello [7]. GPR is calculated with the use of news-based analytics and text mining strategies [7]. In the formation of GPR, a vocabulary set of keywords related to the geopolitical tensions published in the major newspapers is of central importance [7].

The contributions of this paper are designed to be two-fold. First, it proposes the novel model GARCH-MIDAS-LSTM. The model aims at the augmentation of the forecast capabilities of the GARCH-MIDAS method and the benefits from the LSTM and MIDAS methods. Therefore, the model allows for the simultaneous modeling of variables at lower and higher frequencies in an LSTM setting for forecast capabilities. The second aim is to determine the influence of the economic fundamentals in the GARCH-MIDAS and GARCH-MIDAS-LSTM settings. To this end, monthly industrial production fundamentals, composite leading indicator as a proxy of future economic performance expectations, and geopolitical risk is utilized in modeling daily stock market volatility. Furthermore, the GARCH-MIDAS and GARCH-MIDAS-LSTM models are compared in terms of the effectiveness of forecasting both with multivariate and univariate specifications. The proposed model is also allowed to be modeled without exogenous factors following the realized variance (RV) strategy of GARCH-MIDAS models adapted to LSTM. Forecast evaluation is conducted for a sample that corresponds to the economic reopening period during COVID-19 in Türkiye. As noted, the test sample is expected to provide an interesting laboratory to test the effectiveness of models. Forecast performances of models are evaluated under various specifications, including rolling windows and fixed sampling strategies. In the empirical section, the daily stock market volatility of BIST100 is modeled with a total set of five fundamentals determining the long-run components of volatility: RV, IPI-cycle, IPI-trend, GPR, and CLI, with two specifications, fixed and rolling window strategies. This led to an estimation and forecast practice with a total of 20 models: ten GARCH-MIDAS and ten GARCH-MIDAS-LSTM, with the aim being the evaluation of forecast performances and the determination of the effects of the fundamentals.

If an overview of the results is provided, the empirical findings are as follows: (i) in terms of RMSE forecast error criteria, the novel LSTM augmented model leads to a percentage decrease in forecast error criteria with a minimum of around 40% over its GARCH-MIDAS variants depending on the fundamental factor used for the long-run component. Therefore, LSTM GARCH-MIDAS-LSTM improves the forecasting capability of the GARCH-MIDAS models. (ii) The RV-based GARCH-MIDAS-LSTM model also performs quite well in terms of forecasting. The model provides an improvement in forecasts over all GARCH-MIDAS models that are modeled in a univariate or a multivariate setting. The results suggest the forecast capabilities of the GARCH-MIDAS-LSTM model under a univariate RV setting. (iii) Inclines in IPI and future economic performance expectations lower the volatility in the market, while geopolitical risks work in the opposite direction in the GARCH-MIDAS models, which are confirmed by the GARCH-MIDAS-LSTM models. (iv) As an economic policy perspective, the geopolitical risk is the most influential factor on stock market volatility among all factors analyzed for the sample period and for the market analyzed.

The paper is organized as follows. The literature review is undertaken in Section 2. The methodology is given in Section 3. The empirical analysis is reported in Section 4. Lastly, the discussion and conclusions are found in Section 5.

2. Literature Review

The time series properties of a financial series include volatility clustering and heavy tails, which are subject to asymmetry and volatility. The GARCH model has been the major workhorse of volatility models, which led to continuous research on new variants of the GARCH model to incorporate and to better capture the aspects the conditional variance processes. In this respect, the model family is undergoing research in econometrics, and a glossary for GARCH provides the contributions [8]. The majority of the models focus on univariate modelling in addition to recent advancements in multivariate modeling. Furthermore, there is also a study that focus on the advancement of models for forecasting with a selected set of Machine Learning (ML) and Neural Network (NN) approaches to GARCH. The literature review will be conducted in two sections, (i) the literature on ML and the NN integration to GARCH, and (ii) Mixed Frequency Data Sampling (MIDAS) integration into GARCH models.

2.1. Neural Networks, Machine Learning and GARCH

In the last decade, volatility models in econometrics have been generalized to NN models with a single hidden layer, such as the GARCH-NN model [9], which augments the GARCH model with a single-layer Multilayer Perceptron (MLP). After the popularization and development of deep learning (DL) models in early 2010s, the single-layer NN models were also referred to as ‘shallow neural networks’. Though the deep neural networks (DNN) allow for the modeling of NN’s with more than a single layer at first, the DNN models also bring about a developing field of learning algorithms, newer activation functions, and newer model architectures. Such developments are also in line with advancements in computer technologies, cloud computing, and parallel processing. Donaldson and Kamstra’s 1997 paper is an important step for NN’s to be integrated into GARCH models [9]. The generalization of GARCH-NN to a broader family of GARCH models with learning algorithm updates were developed by Bildirici and Ersin in 2009 [10]. The proposed GARCH-NN family of models benefits from single-layer MLP. In the field of ML, Support Vector Regressions (SVR) provided a generalization of Support Vector Machines (SVM) to regression problems. The proposed SVR-GARCH method delivers a solution to the financial volatility forecasting problems [11]. Bildirici and Ersin further extend the SVR-GARCH model to fractional integration and asymmetric power terms to achieve SVR-APGARCH and SVR-FIGARCH models [12,13]. The SVR-GARCH family of models allows for the utilization of famous kernel functions, including polynomial and Radial Basis Function (RBF) kernels. Further studies emphasize the capabilities of these models as effective predictors in volatility modeling. The fruitful generalization of SVR to GARCH in addition to the effectiveness of model hybridization with econometric techniques are demonstrated [14,15].

Deep Learning (DL) methodologies have been shown to capture the nonlinear and leptokurtic properties of financial returns. Among DL models, LSTM is a DNN model developed by Hochrider and Sxhmidhuber, which was shown to produce significant improvements in time series data modeling and forecasting problems [16]. Sezer et al., after providing an extensive literature review, stressed the efficiency of DNN models at forecasting compared to many forms of Machine Learning (ML) models [17]. Kumbure et al. reviewed ML model usage in the financial literature and for stock market prediction, and they emphasized the efficiency of ML methods and underlined the effectiveness of the LSTM model over convolutional NN and other recurrent NN models [18]. As an example, Li et al. proposed Deep Belief NN to predict stock price time series [19]. Krauss et al. suggested DNN models in addition to Random Forests (RF) and Gradient-Boosted-Trees (GBT) to achieve arbitrage effectiveness in the S&P stock market [20]. Jeong and Kim emphasize the increase in success in financial decision making using a deep Q DL method [21]. Troiano et al. show that LSTM models are capable of improving the trading strategies in financial markets [22].

Following the DNN and LSTM applications in time series, the integration of LSTM into the GARCH model has also attracted interest. Liu et al. modeled carbon price forecasting with the hybrid decomposition technique, and models including GARCH, LSTM, BPNN and SVR, and showed the effectiveness of hybridization [23]. Hu et al. propose a hybrid model that benefits from LSTM and Bi-LSTM DNN models with GARCH, and they stress the efficiency of the hybrid model in forecasting copper prices over various forms of GARCH models [24]. These models combined the DNN models to NN-GARCH models, and their tests confirm the efficiency of Bi-LSTM in three-week forecasts and LSTM in other tested forecast horizons [24]. Lastly, Bildirici et al. employed the logistic smooth transition autoregressive (LSTAR) model [25] to hybridize with the GARCH-LSTM model to achieve LSTAR-GARCH-LSTM [26]. The model captures nonlinear volatility dynamics in conditional mean and variance with LSTAR type nonlinearity and augment forecast performance with LSTM [26].

Various studies utilize hybrid methodologies that integrate DNN models. In addition, the inclusion of macroeconomic or other types of exogeneous variables in such models are emphasized in order to achieve improved forecast performances. Wex et al. developed an early warning mechanism for oil price shocks by including news with text mining [27]. By using topic modeling based on latent Dirichlet allocation, text mining and convolutional NNs are hybridized in modeling and forecasting [28]. Yu et al. provide a seminal approach to text mining and NN model incorporation [29]. Chen et al. emphasize DNN and LSTM’s capacity in capturing the complex nonlinear dynamics of crude oil prices [30]. Khodayar et al. propose that stacked autoencoder and denoising encoders be integrated into DNNs to further achieve forecast improvements in wind speed forecasting [31]. Zhao et al. suggest an ensemble of DL and LSTM DNN methods for efficiency in forecasting [32]. Xu et al. emphasize the efficiency of convolutional DNN and combining text mining in stock market prediction [33]. BiLSTM and stacked LSTM are emphasized in terms of effectiveness in stock market prediction and in overcoming vanishing gradient problems in various DNN models [34]. The effectiveness of LSTM models are highlighted [35,36], and LSTM and GARCH model hybridization are suggested in order to forecast financial and stock market returns [37].

Fabbri and Moro showed that recurrent neural networks (RNN) outperform traditional ML methods, and in Dow Jones stock market modeling, the relative gain in forecast accuracy is 50% higher than those for other selected DNN models [38]. To model stock prices during COVID-19, media chatter on COVID-19 in addition to macroeconomic fundamentals are integrated to MAP-LSTM and ISOMAP-GB models for feature extraction in daily stock price movements in Indian company stocks [39]. The effects of sentiment of sociological and political issues, wars, and, recently, the COVID-19 pandemic on stock markets in the USA and India are modeled using LSTM models that have more accurate forecasts over traditional time series models [40]. The effectiveness of LSTM models in predicting stock markets are shown to increase with exogeneous factors included in models through the calculation of technical analysis indicators [41]. Selvin et al. emphasize augmentation with sliding windows estimation and LSTM, RNN and CNN models in stock price forecasting over the ARCH, GARCH, ARMA, and NN models [42]. Bhandari et al. show that the recent advancements in information technology and investor behavior altered the stock market in the direction of complexity, volatility, and nonlinear dynamics. Furthermore, the utilization of LSTM DNN models with the integration of macroeconomic variables in addition to fundamental and technical stock market data has proved to be effective in stock market forecasting [43].

2.2. MIDAS and GARCH-MIDAS

Compared to the discussion above, various papers suggest methods to integrate the effects of low frequency variables, i.e., economic fundamentals, to the volatility forecast problems. In the ML literature, various studies have suggested methods in this regard. Feng et al. (2018) highlight the importance of the inclusion of fundamentals in DNN models [44]. Accordingly, including macroeconomic indicators such as the inflation rate and stock-specific fundamentals such as the dividends, earnings, and book-to-market ratios are effective inputs for DNN models [44]. Such fundamental features have been shown to improve the forecast capabilities of modeling techniques in the context of LSTM models [44]. The inclusion of Google trends and stock market keywords as exogeneous variables have been shown to improve the forecast capabilities of DNN models in stock market modelling [45]. However, in the discussion given above, the modeling generally assumes the variables to be matched in terms of a common frequency (such as hourly, daily, or monthly) for all variables in the input and output layers of models.

In the econometrics literature, Ghysels et al. [4] suggest mixed data sampling (MIDAS) in order to combine variables in different frequencies in a setting in which the variables in the later input are in lower frequencies in terms of sampling relative to the higher frequency target variable. Engle et.al. [3] utilize the MIDAS approach to generalize the volatility modeling with the proposed GARCH-MIDAS model. The GARCH-MIDAS approach of [3] transforms the low frequency variable through beta or exponential polynomial functions. For this purpose, polynomial functions provide a parametric transformation of monthly economic fundamentals into daily frequency to be incorporated in GARCH type conditional volatilities. The resulting GARCH-MIDAS method allows conditional volatility to be decomposed into long-run and short-run dynamics, and the total variance could be recovered in a multiplicative manner. In the literature, Ghysels et al. [4] propose a mixed frequency methodology for economic modelling, while Clements and Galvao and Andreou et al. provide early applications of MIDAS regressions to model and forecast various economic variables [46,47]. Ferrara and Marsilli show the effectiveness of financial variables in economic data forecasting for French data with MIDAS regressions [48]. Pettenuzzo et al. propose the Bayesian generalization to obtain a Bayesian-MIDAS model [49]. Kuzin, et al. apply and extend MIDAS with MIDAS-VAR [50]. Raza et al. utilize the economic policy uncertainty (EPU) index, another index that follows the newspaper headings-based index formation strategy utilized for the GPR index [51]. Raza et al. showed the importance of EPU as a news-based index to measure volatility in modeling and in forecasting precious metal price volatility with GARCH-MIDAS models [51]. Ersin et al. utilized a large set of GARCH-MIDAS models to model the effects of EPU in addition CLI on G7 stock market volatility [52]. By estimating 42 different models and forecast comparisons, Ersin et al. showed that no a-priori decision should be made regarding the selection of model types between rolling windows, and that fixed sampling and decision requires the evaluation of forecast performances of all models with different specifications to decide on the type of fundamental and the type of model specification [52]. Furthermore, their findings indicate strong forecast improvement in the CLI index in GARCH-MIDAS models for G7 stock markets. Liu and Chen examine the effects of CLI on stock market volatility, and their findings confirm the significance of CLI in improving forecast and prediction performances on large and small stock returns and volatility [53]. Segnon et al. utilized the GPR indicator and its influence on stock market volatility within a GARCH-MIDAS setting [54]. They suggest a Markov switching GARCH-MIDAS model and an augmentation of the GARCH-MIDAS model with regime-switching dynamics in order to capture the effects of nonlinearities in addition to the influence of geopolitical risk on stock market volatility [54]. In Segnon et al., their empirical findings indicate no significant forecast improvement by modeling the long-run component of volatility of the Dow-Jones Industrial Average index with GPR and Markov-Switching. GARCH was already shown to capture nonstationarities in data for a sample covering 122 years [54]. As a result, Segnon et al. question the effectiveness of GPR in terms of forecast improvement with regime switching GARCH-MIDAS, and they highlight that GPR improves forecasts depending on the forecast period selected within the entire sample. Zhang et al. examined the influence of GPR on stock market volatility [55]. In their research, Zhang et al. included various GPR factors, namely geopolitical risk threats, geopolitical risk acts, and GPR [55]. Their findings are in favor of forecast and modeling performance improvement in their GJR-GARCH-MIDAS models, which benefit from MIDAS sampling to evaluate the effects of economic fundamentals at different frequencies [55]. In contrast to Segnon et al., the findings of Zhang et al. indicate strong forecast capability improvement due to GPR through the GJR-GARCH-MIDAS model, and the contrasting results for GPR’s effectiveness will provide a basis for the evaluation of GPR in the GARCH-MIDAS and GARCH-MIDAS-LSTM models in our study. Among other studies, typical macroeconomic fundamentals are evaluated including the effects of economic performance including IPI and other macroeconomic variables such as the inflation rates and the unemployment rates in the literature. Among these studies, Chuang et al. show the effects of macroeconomic variables on volatility modeling and the forecasting of crude oil [56]. Andreani et al. modelled the effects of various low frequency factors to this end during COVID-19 on the volatility of high frequency energy prices using GARCH-MIDAS and Double-Asymmetric GARCH-MIDAS [57]. Their findings also indicate the significance of GARCH-MIDAS modeling with economic fundamentals in addition to spillover effects [57].

3. Method

Given the discussion above, the paper aims to make a contribution with a hybridization of the GARCH-MIDAS and LSTM models. Similar to the GARCH-MIDAS, the proposed GARCH-MIDAS-LSTM model integrates exogenous indicators at a lower-frequency to the volatility modeling of higher-frequency target variables. The modeling of the GARCH-MIDAS-LSTM model consists of two steps: the first is the GARCH-MIDAS filtering, and the second is the LSTM modeling [3,4].

The GARCH-MIDAS model [3] integrates a mixed data sampling transformation (MIDAS) in MIDAS regressions [4]. The model extends MIDAS regressions to the generalized autoregressive conditional heteroskedasticity (GARCH) model [58]. With this characteristic, the GARCH-MIDAS model effectively mixes the effects of economic factors and fundamentals at lower-frequency to the volatility equations for a financial time series at higher-frequencies, such as the daily stock returns.

The conditional mean process of $y_{i,t}$ daily stock returns in the GARCH-MIDAS model is defined as [53],

$$y_{i,t}-E_{i-1,t}\left(y_{i,t}\right)=\sqrt{{\tau }_t·g_{i,t}}{\epsilon }_{i,t}$$

(1)

and

$${\epsilon }_{i,t}|{\mathsf{\Phi }}_{i-1,t}~N(\mathrm{0,1})$$

(2)

where $y_{i,t}$ represents the daily returns on ith day of tth month, E_i−1,t($y_{i,t}$) is the expected value or the mean; therefore, the demeaned stock return on the left-hand-side follows a heteroskedastic process which could be decomposed into three factors: (i) the ${\tau }_{,t}$ secular component, influencing the long-run volatility dynamics, (ii) $g_{i,t}$ is the short-run component of volatility, and (iii) ${\epsilon }_{i,t}$ is the normally distributed white noise portion conditional on ${\mathsf{\Phi }}_{i-1,t}$ available information at the i − 1 previous business day of month t. Hence, the multiplication of three factors lead to the total variance. Interestingly, the model suggests the short run component $g_{i,t}$ as,

$$g_{i,t}=\left(1-\alpha -\beta \right)+\alpha \frac{{\left(y_{i-1,t}-E_{i-1,t}\left(y_{i,t}\right)\right)}^2}{{\tau }_t}+\beta g_{i-1,t}$$

(3)

suggesting the GARCH (1,1) process, where α and β are the ARCH and GARCH parameters, with the effects of secular component ${\tau }_{,t}$ being included in the ARCH portion of the model. Furthermore, $\left(\alpha +\beta \right)<1$ is the stability condition [58]. The secular component, also known as the long-run component of volatility, is derived from the monthly economic variables with MIDAS transformation. The model assumes two different strategies to define ${\tau }_{,t}$ [3]. The first is called realized variance modeling (RV) of ${\tau }_{,t}$, which is the univariate approach,

$${\tau }_t=m+\theta {{\displaystyle \sum }}_{k=1}^K{\phi }_k({\omega }_1,{\omega }_2){RV}_{t-k}$$

(4)

since the extraction of the long-run component ${\tau }_{,t}$ is via the daily stock market return itself,

$${RV}_t={{\displaystyle \sum }}_{i=1}^{N^{\prime }}{y}_{i,t}^2$$

(5)

Due to the derivation of ${\tau }_{,t}$ from RV_t, the model follows a univariate approach for both short and long-run volatilities and excludes multivariate settings [3]. Here, RV_t is a sum of $y_{i,t}^2$ for a selected lag length, N′, suggested to be equal to 22, which corresponds to the total number of business days in the average month [53]. For the quarterly fundamental variable, N′ = 65 [59].

In contrast to the RV approach, the following specification suggests ${\tau }_{,t}$ to be modeled from exogeneous economic factor X_t−k at t with lag k,

$${\tau }_t=m+\theta {{\displaystyle \sum }}_{k=1}^K{\phi }_k({\omega }_1,{\omega }_2)X_{t-k}.$$

(6)

In the specification given in Equation (6), the GARCH-MIDAS assumes a multivariate form in which ${\tau }_{,t}$ is a function of ${\phi }_k({\omega }_1,{\omega }_2)$ and m is the constant term. K is known as MIDAS lags. As for the MIDAS method [4], two functions are used for ${\phi }_k({\omega }_1,{\omega }_2)$, the beta polynomial and the exponential [3]. The beta polynomial is,

$${\phi }_k({\omega }_1,{\omega }_2)=\frac{{\left(k/K\right)}^{{\omega }_1-1}{\left(1-k/K\right)}^{{\omega }_2-1}}{{\displaystyle \sum }_{j=1}^K{\left(j/K\right)}^{{\omega }_1-1}{\left(1-j/K\right)}^{{\omega }_2-1}}$$

(7)

and the exponential function is,

$${\phi }_k\left(\omega \right)={\omega }^k/{{\displaystyle \sum }}_{j=1}^K{\omega }^j.$$

(8)

In the first function, w₁ and w₂ are weight parameters to be estimated with non-negativity through w₁, w₂ > 0. Similarly, w defines the weights in Equation (8). As a result, both functions follow strictly non-negative paths ${\phi }_k({\omega }_1,{\omega }_2)\ge 0$ and ${\phi }_k\left(\omega \right)\ge 0$. In addition, in the case of two weight parameters, w₁ + w₂ = 1. Engle et al. stress that both functions lead to similar results [3]. Since w₁ + w₂ = 1, w₂ = 1 − w₁, the estimation of a single weight parameter is adequate, and the beta polynomial function is used with a single weight parameter [53]. It is adequate to achieve a monotonically decaying weighting process in this respect [59]. Furthermore, two sampling specifications for the GARCH-MIDAS model are possible, and ${\tau }_{,t}$ specifications in Equations (4) and (6) attain fixed (f) sampling [60]. The rolling-windows, rw, specifications are given below,

$${\tau }_t^{\left(rw\right)}=m^{\left(rw\right)}+{\theta }^{\left(rw\right)}{{\displaystyle \sum }}_{k=1}^K{\phi }_k({\omega }_1,{\omega }_2){RV}_{t-k}^{\left(rw\right)}$$

(9)

$${\tau }_t^{\left(rw\right)}=m^{\left(rw\right)}+{\theta }^{\left(rw\right)}{{\displaystyle \sum }}_{k=1}^K{\phi }_k({\omega }_1,{\omega }_2)X_{t-k}^{\left(rw\right)}.$$

(10)

Here, Equations (9) and (10) represent rw generalizations of the long-run component ${\tau }_{,t}$ with univariate RV specification in Equation (4) and the multivariate X_t−k specification given in Equation (6) [60]. In GARCH-MIDAS with rw specification, ${\tau }_{,t}$ the long-run component follows a dynamic process which changes over time at each i and t due to the rolling-windows sampling of the total sample [3,53].

In this study, the GARCH-MIDAS model is augmented with LSTM to achieve GARCH-MIDAS-LSTM. The proposed model benefits from the forecasting capabilities of LSTM DNNs which exploit the short-term and long-term dependencies of time series datasets. Therefore, the LSTM provides an efficient tool that is in line with GARCH-MIDAS modeling.

In the initial LSTM model, multiplicative gate units are assumed to achieve a constant error stream [43,61]. In this respect, LSTM achieves stability in the constant error carousel unit to prevent the loss of error signals flowing backward in time [16,26]. The model utilizes feature vectors extracted from the datasets to produce efficent answers to forecasting problems [34]. Afterwards, the LSTM is further augmented in terms of its basic architecture, with adaptive forget gates to prevent the internal state from growing indefinitely by enabling the LSTM cell to learn to reset itself when its contents become outdated [61].

The GARCH model is augmented with LSTM units, and GARCH-LSTM is proposed in the literature [24]. Furthermore, the model is augmented with logistic smooth transition autoregressive processes for nonlinearity in the mean proceses [26]. In our study, the GARCH-MIDAS-LSTM model is suggested as a hybrid model with MIDAS mixed sampling. The model accepts inputs produced by the GARCH-MIDAS sampling method to generate the short and long-run volatility components to the LSTM unit below.

$$m_{i,t}=f_{i,t}{⨀}_{*}{m}_{i,t-1}+j_{i,t}{⨀}_{*}{\tilde{m}}_{i,t}$$

(11)

$${\tilde{m}}_{i,t}=\mathit{tanh}\left(V_m{x}_{i,t}+Q_m{g}_{i,t-1}+a_m\right)$$

(12)

$$j_{i,t}=\sigma \left(V_j{x}_{i,t}+Q_j{g}_{i,t-1}+a_j\right)$$

(13)

$$f_{i,t}=\sigma \left(V_f{x}_{i,t}+Q_f{g}_{i,t-1}+a_f\right)$$

(14)

$$o_{i,t}=\sigma \left(V_o{x}_{i,t}+Q_o{g}_{i,t-1}+a_o\right)$$

(15)

$$g_{i,t}=o_{i,t}{⨀}_{*}tanh\left(m_{i,t}\right)$$

(16)

where Q and V are weight matrices, a is a bias vector, σ(·) denotes the activation function, and ${⨀}_{*}$ symbolizes element-wise multiplication. In the specification given above, LSTM has a memory cell that has three gates, and as noted, $m_{i,t}$ is the cell state vector, and the activation vectors of the three gates are initiated according to Equations (11)–(16), the input and output vectors are $g_{i,t-1}$, $x_{i,t}$, and a is the bias vectors which are passed through the activation function to generate activation, which is assumed as the sigmoid activation function. Therefore, activation values are bounded between [0, 1] [26]. An activation value of one at each of these gates causes the information at the input to that gate to completely pass through, whereas a value of zero forces all the information at the input to be entirely filtered out [26].

In Equation (11), the input gate $j_{i,t}$ functions as a decision gate on the part regarding the new information to be stored in the current cell state ($m_{i,t}$). $f_{i,t}$ is the forget gate acting as a decision maker regarding the information in the most recent cell state ($m_{i,t-1}$) to be passed to the current cell state or not [61]. Equation (12) computes the new information ${\tilde{m}}_{i,t}$ at time i,t as a weighted sum of $x_{i,t}$ and $g_{i,t-1}$, and the bias where the output of the hyperbolic tangent (tanh) activation function is bounded in the range of [−1, 1] [60]. Finally, the normalized output value $g_{i,t}$ in Equation (16) is determined by filtering the tanh function to be normalized to the range of [−1, 1] at cell state $m_{i,t}$ by using the output gate $o_{i,t}$ activations determined as in Equation (15). This process separates the necessary information from unnecessary information to yield the output vector $g_{i,t}$ [26].

The proposed GARCH-MIDAS-LSTM modelling is in line with the GARCH and LSTM hybrid models. In the case of excluding the MIDAS transformation, the model nests hybrid LSTM-GARCH [24]. Furthermore, if the model was generalized to LSTAR type nonlinearity, LSTM-GARCH would be extended to LSTAR-GARCH-LSTM [26]. Different from these methods, the proposed GARCH-MIDAS-LSTM has an interesting property, in that it allows for the integration of mixed frequency modeling and the inclusion of lower frequency exogeneous variables, leading indicators, and their influence on conditional volatility. Furthermore, the GARCH-MIDAS-LSTM also allows univariate modeling by extracting the long-run component from the high frequency daily stock return series itself following the RV method of GARCH-MIDAS models, as outlined above.

4. Results

4.1. Dataset

The sample period covers 2 January 2002 to 10 June 2020, and consists of a mix of daily and monthly time series. Since the daily dataset includes working days, the holidays are removed from the sample and the sample size (n) for daily data is 4812. XU100_t represents the daily Borsa İstanbul Stock Market 100 index, and is obtained from the Central Bank of the Republic of Türkiye’s (CBRT) electronic database. A set of monthly explanatory variables correspond to economic leading indicators in this study. Therefore, while the target variable is daily, the economic fundamentals are in monthly frequency, for which the sample covers January 2002 to June 2020. For the monthly dataset, the sample size is 222. The data descriptions and sources are given in

Table 1. Variable Description and Sources.

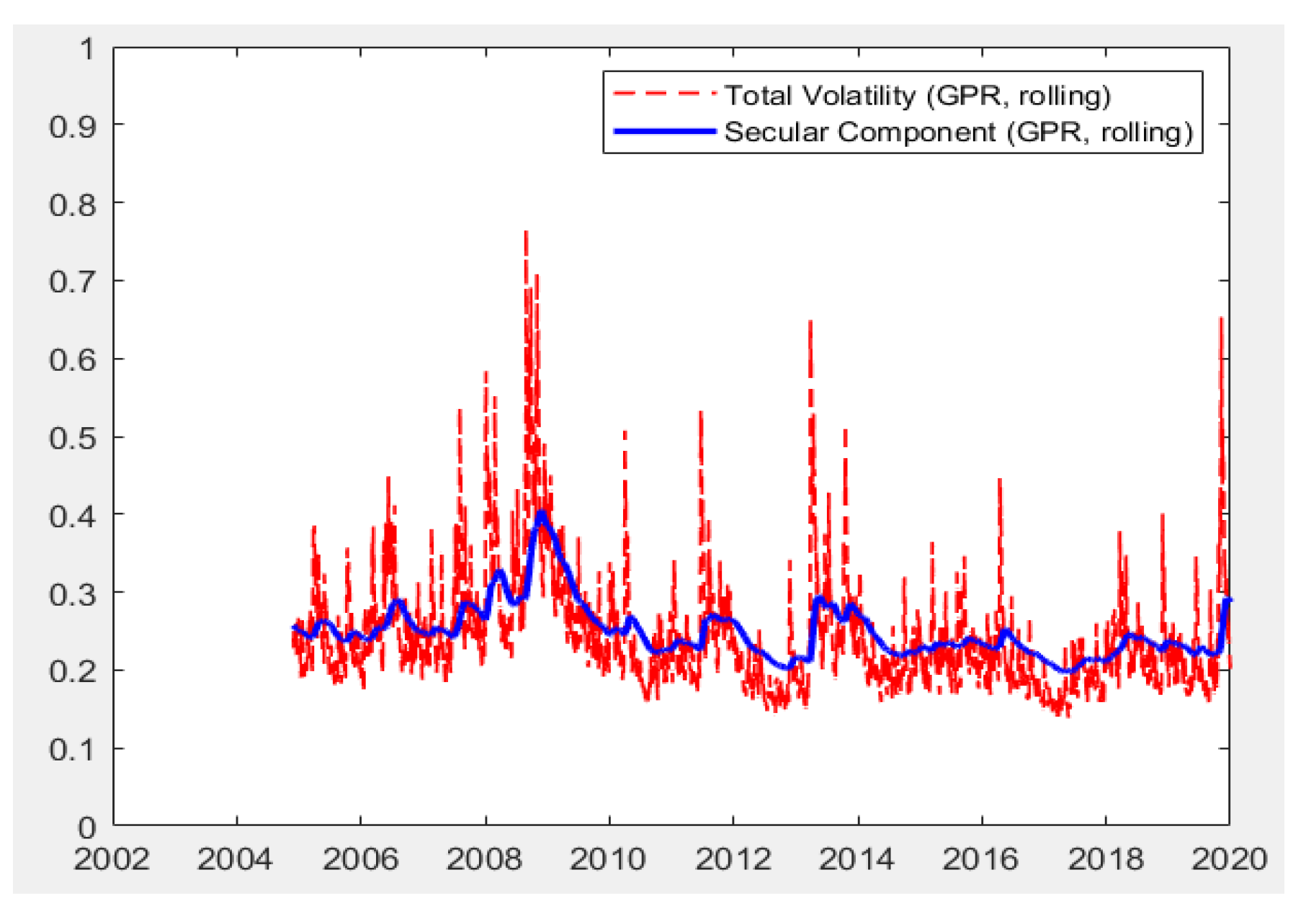
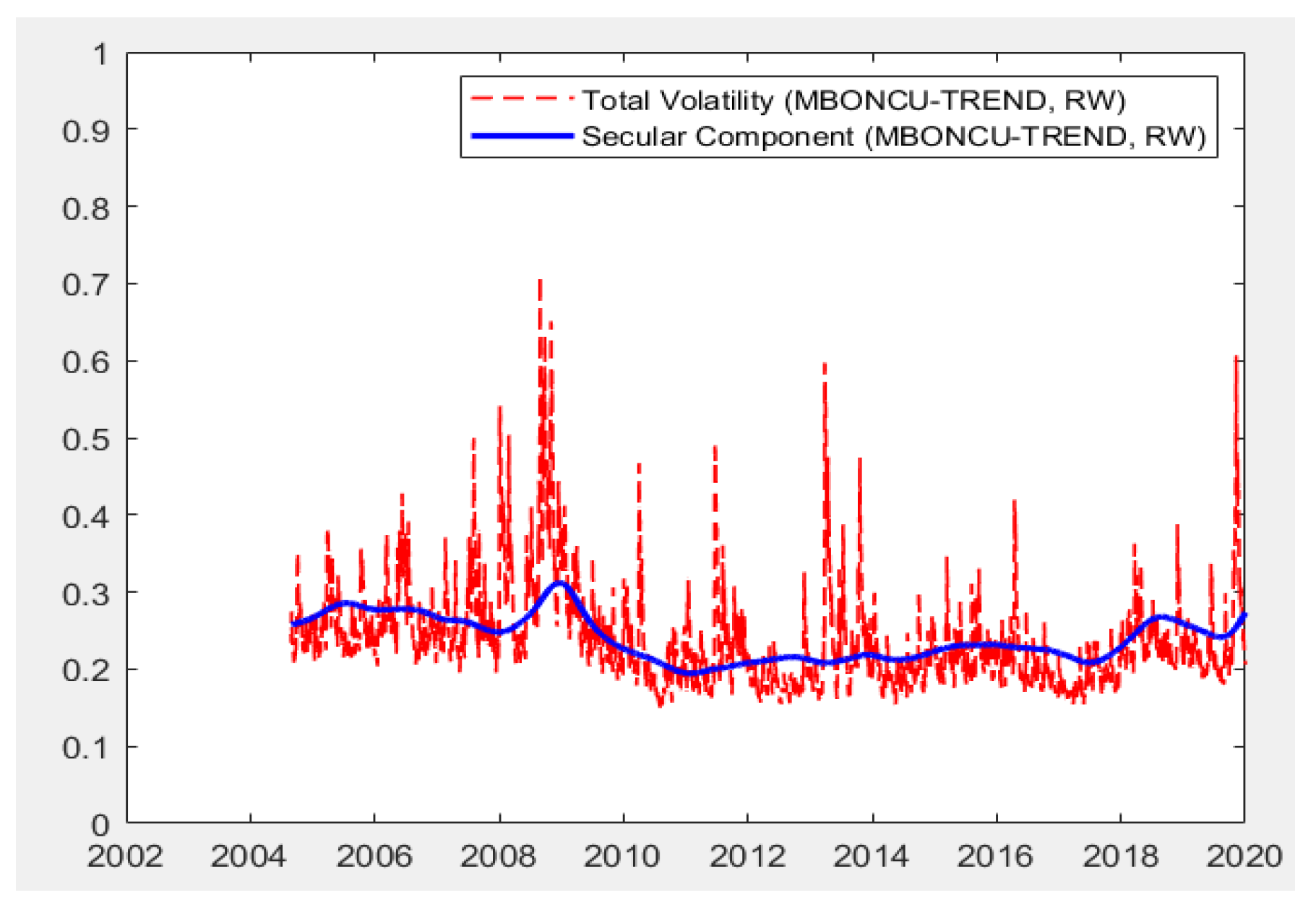
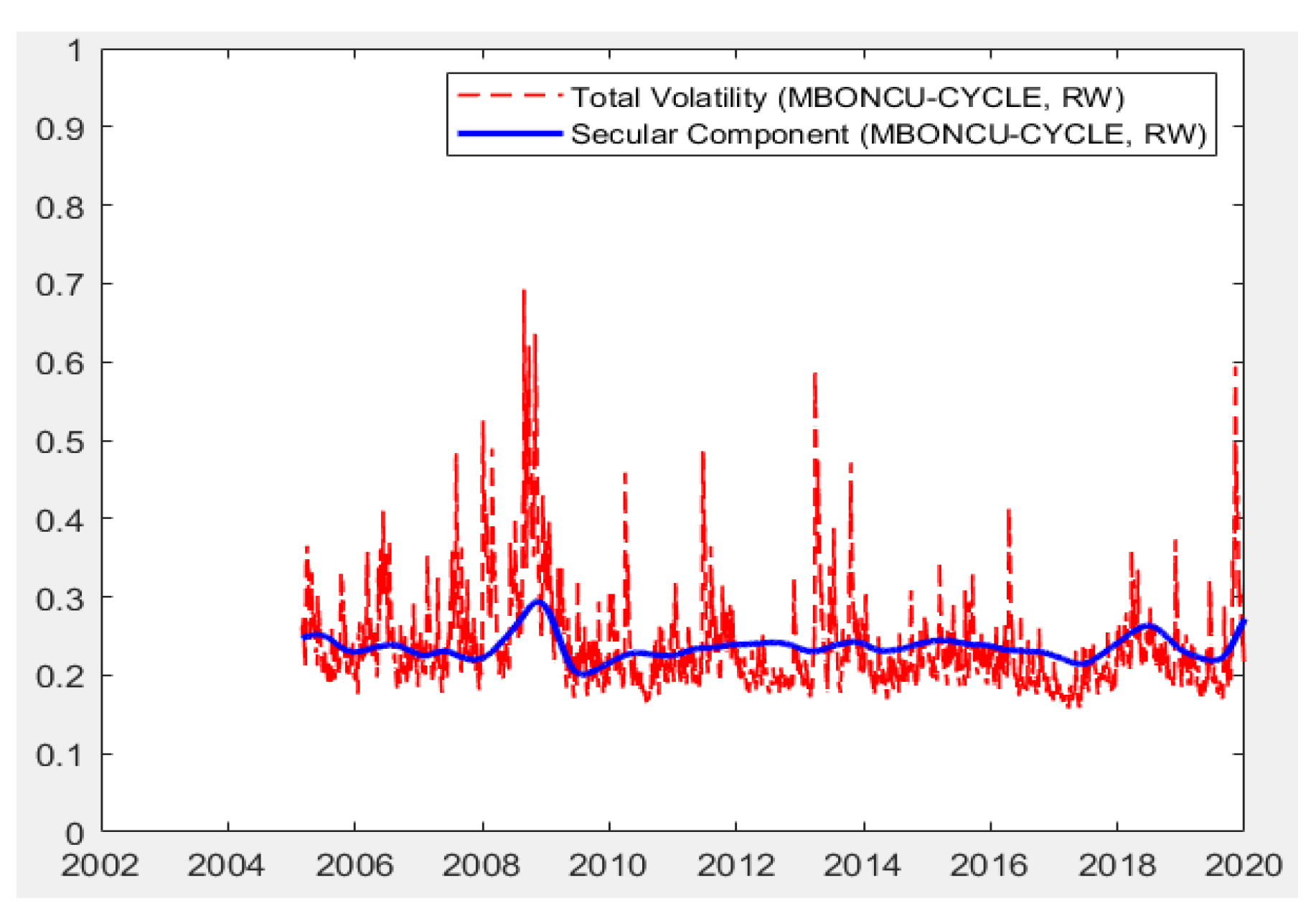
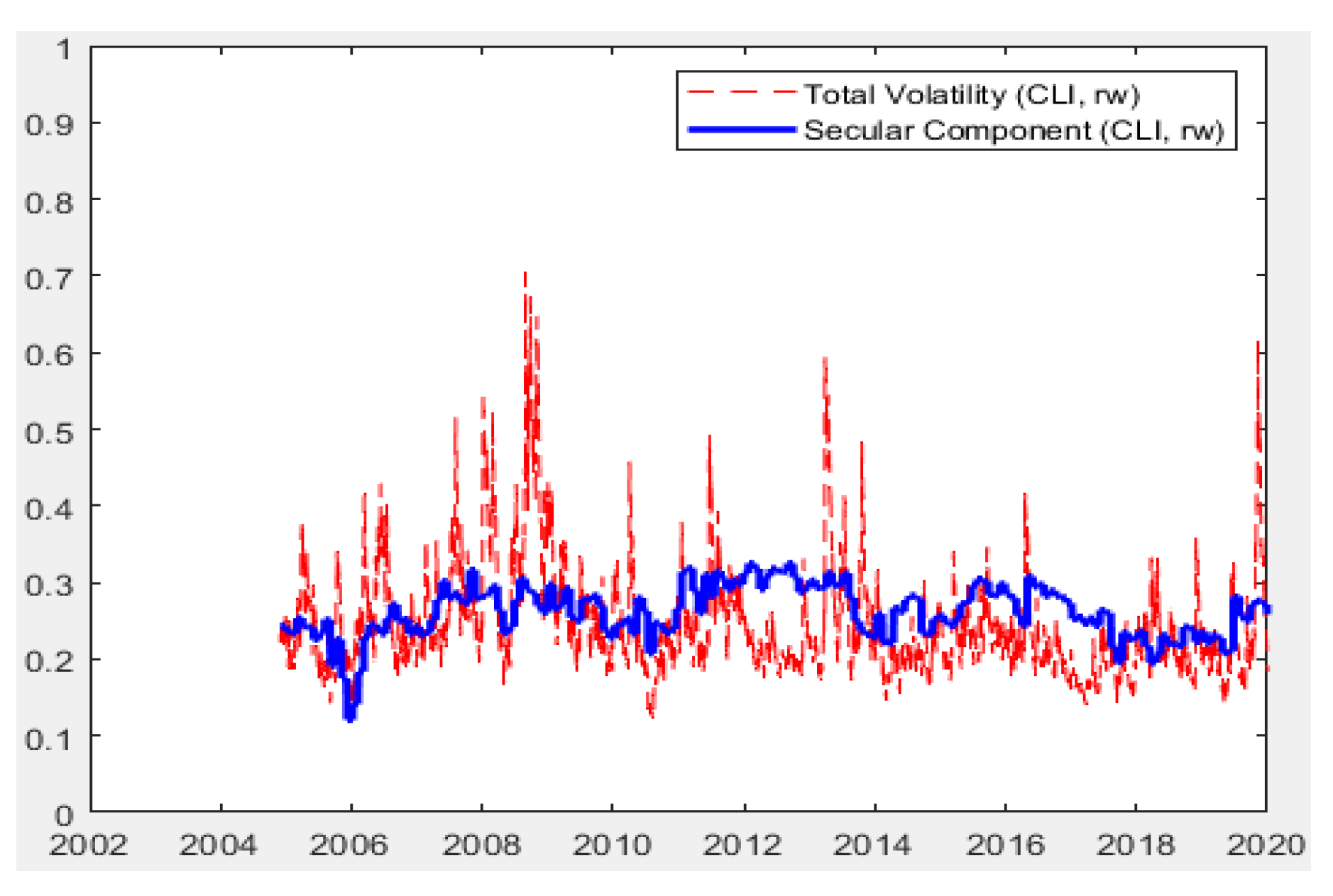
Variable	Description	Source	Frequency	n
XU100	Borsa İstanbul 100 Stock Market Index (BIST100)	CBRT EVDS Database	Daily	4812
IPIC	Industrial production leading indicator index, cycle series	CBRT EVDS Database	Monthly	22
IPIT	Industrial production leading indicator index, trend series	CBRT EVDS Database	Monthly	22
CLI	Composite leading indicator (Amplitude) for Türkiye	OECD Database	Monthly	222
GPR	Geopolitical Risk Index, Türkiye	Policyuncertainty.com	Monthly	222

.

IPIC and IPIT are the cycle and trend industrial production index announced monthly by the CBRT, and the data source is the CBRT EVDS database. CBRT assumes these two variables as the foremost leading economic indicators for economic performance. Additional variables are globally accepted indicators. CLI is the Composite Leading Index published by the OECD and obtained from the OECD database. Three versions of CLI were deemed to exist by the OECD: the amplitude, trend and normalized CLI. In our analysis, we utilize amplitude-CLI data from the OECD for Türkiye. With this respect, the study follows the literature and the financial markets which consider amplitude-CLI as the headline CLI indicator of OECD. GPR is the country-specific Geopolitical Risk Index for Türkiye and was acquired from policyuncertainty.com, which publishes GPR following the proposed methodology in the construction of the GPR index [7].

Both daily and monthly variables are subject to natural logarithms. Furthermore, as will be seen in the next section, the series are first differenced following the unit root test findings to achieve stationarity, as reported in

Table 2. Descriptive Statistics.

	Mean	Min.	Max.	SD	SKW	KR	JB	ARCH
Daily Dataset, n = 4812
XU100	10.788	9.063	11.725	0.683	−0.921	2.859	660.5 [0.00]	430,658 [0.00]
ΔXU100	0.0004	−0.133	0.1212	0.018	−0.209	7.932	4740.4 [0.00]	57.18 [0.00]
Monthly Dataset, n = 390
IPIC	4.605	4.535	4.673	0.019	−0.813	4.689	12.4 [0.00]	39,996.2 [0.00]
ΔIPIC	0.026	−0.015	0.015	0.494	−1.164	4.835	142.4 [0.00]	2653.4 [0.00]
IPIT	4.847	4.301	5.411	0.293	0.274	2.317	89.3 [0.00]	9853.80 [0.00]
ΔIPIT	−0.029	−0.019	0.012	0.462	−1.299	5.984	253.7 [0.00]	2877.9 [0.00]
CLI	4.604	4.374	4.718	0.034	−1.704	10.174	1024.9 [0.00]	36.63 [0.00]
ΔCLI	−0.027	−0.032	0.022	0.747	−1.129	6.521	283.5 [0.00]	1976.7 [0.00]
GPR	4.675	3.787	5.769	0.357	0.229	2.837	31.8 [0.00]	21.31 [0.00]
ΔGPR	0.105	−0.009	0.015	0.296	0.644	4.633	70.1 [0.00]	4.94 [0.03]

Notes. All variables without Δ are in natural logarithms, where Δ denotes first differencing. SD is the standard deviation, SK. and KR are skewness and kurtosis, and JB is the Jarque-Bera test of normality, ARCH is the ARCH-LM test of no autoregressive conditional heteroskedasticity at orders 1 to 5 for the daily variables. For monthly variables, ARCH-LM is conducted at the order of 1 to 2. For both JB and ARCH-LM tests, the p values are given in brackets.

. After logarithms and first differencing, following series are utilized. They also reflect the percentage (%) growth rates. The target variable ΔXU100 is the daily % change in the BIST100 stock market; in other words, the daily % stock returns, equivalent to r_t in the methodology section. ΔIPIC and ΔIPIT are the monthly % change of cycle and trend industrial production indicators. ΔGPR is the monthly % change in the GPR indicator. ΔCLI is the monthly % change in the CLI indicator reflecting economic expectations for future economic performance. For the included subindices in the calculation of expectations, readers are referred to Section 1. The descriptive statistics for daily and monthly variables are reported in Table 2.

According to the JB test of normality, all daily series, and XU100 and ΔXU100, the logarithmic daily stock market index and daily % stock market returns have non-normal distributions. ARCH-LM test results indicate the existence of ARCH type heteroskedasticity at conventional significance levels for daily stock market variables. For all monthly series, similar results are obtained with the JB and ARCH tests. All monthly economic indicators and their first differenced counterparts are not normally distributed, and ARCH type heteroskedasticity cannot be rejected in all series. Once investigated, their skewed distributions in addition to excess kurtosis is revealed, especially for the first differenced series. Exceptions exist for the level series only, which were found to be non-stationary in the next section. Among all level series, the GPR and IPI cycle series are exceptions with no excess kurtosis; however, they also possess strong deviation from normality due to skewness. Overall results in Table 2 signify the existence of heteroskedasticity, with heavy-tails and leptokurtic distribution for all first differenced series. In the next stage, the variables are examined for unit root behavior with selected linear and nonlinear unit root tests.

4.2. Linear and Nonlinear Unit Root Test Results

The test results that are reported in Table 3 cover linear unit root tests, in addition to a set of tests which are robust to certain forms of nonlinearity and structural breaks.

The augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) tests [62] assume unit root under the null hypothesis. A Dickey-Fuller Generalized Least Squares (DF-GLS) test [63] was utilized for confirmatory analysis. The non-parametric Kwiatkowski–Phillips–Schmidt–Shin (KPSS) stationarity test [64] is known for being robust to various forms of nonlinearity. In contrast to ADF and PP, the KPSS test tests the stationarity of a series under the null. Furthermore, the test was also shown to be robust against fractionally integrated long memory processes [65]. In a STAR type nonlinear setting, the Kapetanios-Shin-Snell (KSS) test assumes that the series follows a STAR-type nonlinear unit root process under the null against the alternative of stationarity [66]. The KSS test benefits from Taylor expansions for the exponential STAR type nonlinear process, and is a nonlinear generalization of the ADF test. According to both linear ADF and PP tests, all series follow the integration of order one I(1) processes at conventional significance levels, which was also confirmed with the DF-GLS test results under heteroskedasticity. The findings of the KPSS and KSS tests confirm this result under nonlinearity, since KPSS is known to be robust for a set of nonlinear processes, and KSS is robust for STAR type nonlinearity, which also covers threshold type nonlinear processes. Therefore, they are all nonstationary at levels and become stationary once they are first differenced. The findings suggest the necessity of the use of the first differenced series in the model estimations reported in the following section.

Table 3. Linear and Nonlinear Unit Root and Stationarity Tests.

	ADF	PP	DF-GLS	KPSS	KSS
XU100	−2.1215 [t + i]	−2.1699 [t + i]	−1.9838 [t + i]	1.0726 ** [t + i]	−2.4479 [t + i]
ΔXU100	−67.6468 ** [i]	−67.6479 ** [i]	−67.6146 ** [i]	0.0810 [i]	−33.9307 ** [i]
IPIC	−0.4662 [i]	−1.0528 [i]	−0.4533 [i]	0.2864 ** [t + i]	1.9882 [i]
ΔIPIC	−6.5866 ** [i]	−3.7754 ** [i]	−7.5985 ** [i]	0.0425 [i]	−2.9479 * [i]
IPIT	−0.5839 [i]	−0.1208 [i]	2.3620 [i]	1.9448 ** [i]	0.2453 [i]
ΔIPIT	−6.5589 ** [i]	−3.5518 ** [i]	−5.2453 ** [i]	0.0907 [i]	−3.2002 * [i]
CLI	−1.3632 [t + i]	−1.9904 [t + i]	−1.8346 [t + i]	0.8120 [t + i]	−0.0542 ** [t + i]
ΔCLI	−5.0547 ** [i]	−4.6978 ** [t + i]	−3.1916 * [t + i]	0.0778 ** [t + i]	−27.2008 ** [t + i]
GPR	−3.1087 [t + i]	−6.9208 ** [t + i]	−1.5647 [t + i]	0.1635 ** [t + i]	−2.0759 [t + i]
ΔGPR	−26.6857 ** [i]	−26.6865 ** [i]	−2.9227 * [t + i]	0.1132 * [t + i]	−3.9118 ** [i]

Notes. * and ** denote significance at 5% and 1% significance levels, respectively. [i] and [t + i] denote intercept and trend + intercept assumptions. ADF and PP are the augmented Dickey-Fuller and Phillips-Perron unit root tests. For the ADF and PP tests, the McKinnon critical values at 5% and 1% significance levels are −2.87 and −3.44 for i and −3.42 and −3.98 for intercept and trend (i + t) [67]. KSS is the nonlinear unit root test of [66]. The critical values at 5% are −2.93 and −3.40 for i and i + t assumptions, and −3.40 and −3.93 for 1% [66]. DF-GLS is the Elliot-Rothenberg-Stock DF-GLS test [63]. The critical values at 5% for i and i + t are −1.94 and −2.89; and the critical values at 1% are −2.89 and −3.48 [63]. KPSS is the Kwiatkowski-Phillips-Schmidt-Shin stationarity test [64]. The critical values at 5% (1%) are 0.46 and 0.15 (0.74 and 0.22) for i and i + t, respectively [64].

Table 3. Linear and Nonlinear Unit Root and Stationarity Tests.

	ADF	PP	DF-GLS	KPSS	KSS
XU100	−2.1215 [t + i]	−2.1699 [t + i]	−1.9838 [t + i]	1.0726 ** [t + i]	−2.4479 [t + i]
ΔXU100	−67.6468 ** [i]	−67.6479 ** [i]	−67.6146 ** [i]	0.0810 [i]	−33.9307 ** [i]
IPIC	−0.4662 [i]	−1.0528 [i]	−0.4533 [i]	0.2864 ** [t + i]	1.9882 [i]
ΔIPIC	−6.5866 ** [i]	−3.7754 ** [i]	−7.5985 ** [i]	0.0425 [i]	−2.9479 * [i]
IPIT	−0.5839 [i]	−0.1208 [i]	2.3620 [i]	1.9448 ** [i]	0.2453 [i]
ΔIPIT	−6.5589 ** [i]	−3.5518 ** [i]	−5.2453 ** [i]	0.0907 [i]	−3.2002 * [i]
CLI	−1.3632 [t + i]	−1.9904 [t + i]	−1.8346 [t + i]	0.8120 [t + i]	−0.0542 ** [t + i]
ΔCLI	−5.0547 ** [i]	−4.6978 ** [t + i]	−3.1916 * [t + i]	0.0778 ** [t + i]	−27.2008 ** [t + i]
GPR	−3.1087 [t + i]	−6.9208 ** [t + i]	−1.5647 [t + i]	0.1635 ** [t + i]	−2.0759 [t + i]
ΔGPR	−26.6857 ** [i]	−26.6865 ** [i]	−2.9227 * [t + i]	0.1132 * [t + i]	−3.9118 ** [i]

Notes. * and ** denote significance at 5% and 1% significance levels, respectively. [i] and [t + i] denote intercept and trend + intercept assumptions. ADF and PP are the augmented Dickey-Fuller and Phillips-Perron unit root tests. For the ADF and PP tests, the McKinnon critical values at 5% and 1% significance levels are −2.87 and −3.44 for i and −3.42 and −3.98 for intercept and trend (i + t) [67]. KSS is the nonlinear unit root test of [66]. The critical values at 5% are −2.93 and −3.40 for i and i + t assumptions, and −3.40 and −3.93 for 1% [66]. DF-GLS is the Elliot-Rothenberg-Stock DF-GLS test [63]. The critical values at 5% for i and i + t are −1.94 and −2.89; and the critical values at 1% are −2.89 and −3.48 [63]. KPSS is the Kwiatkowski-Phillips-Schmidt-Shin stationarity test [64]. The critical values at 5% (1%) are 0.46 and 0.15 (0.74 and 0.22) for i and i + t, respectively [64].

4.3. Estimation Results

Following the findings regarding heteroskedastic and leptokurtic distributions of the series analyzed, the GARCH-MIDAS and GARCH-MIDAS-LSTM models were estimated. In all models, the economic fundamental set includes IPIT, IPIC, CLI and GPR to investigate the effects of the trend and the cycle of industrial production, future economic expectations measured with the composite leading index and, lastly, the geopolitical risk. These economic fundamentals are taken as exogenous factors affecting the long-run components of stock market volatility. In addition, estimations also include models with RV, the realized variance, to capture the secular component within a univariate setting. The RV-based univariate results will be taken as the baseline estimation results. Given that there are four economic indicators and RV, there are five factors determining the long-run component of volatility in the study. Furthermore, the models were estimated with fixed and rolling windows specifications. As a result, a total of 20 models consisting of 10 GARCH-MIDAS and 10 GARCH-MIDAS-LSTM models were estimated.

In the model estimation, the last 23 days corresponding to the 11 May 2020 to 10 June 2020 period is left out of the out-of-sample forecast analysis. The sample size for daily stock returns is 4812; for estimation, the sample reduces to 4789. As a result, the in-sample dataset is n = 1, 2, …, 4789, and the forecast horizon is h = n + 1, n + 2, …, n + 23 days ahead. As noted in the methodology section, the model architectures assume beta polynomial functions with one weight parameter, which satisfies the desired property of achieving a monotonically decaying weight function.

4.3.1. GARCH-MIDAS Estimation Results

The estimation results for the GARCH-MIDAS models are presented in

Table 4. GARCH-MIDAS Parameter Estimation Results.

Model:	1	2	3	4	5	6	7	8	9	10
X:	RV	RV	IPIT	IPIT	IPIC	IPIC	GPR	GPR	CLI	CLI
type:	f	rw	f	rw	f	Rw	f	rw	f	rw
Parameter estimates:
µ	0.00093 ** (4.5026)	0.00094 ** (4.5345)	0.00095 ** (4.3601)	0.00095 ** (4.3819)	0.00092 ** (4.085)	0.00092 ** (4.0917)	0.0009 ** (4.0563)	0.0010 ** (4.6432)	0.0009 ** (4.0545)	0.0009 ** (4.4027)
α	0.11566 ** (15.282)	0.11662 ** (15.17)	0.09716 ** (13.536)	0.09794 ** (13.683)	0.09193 ** (13.337)	0.09238 ** (13.359)	0.0871 ** (14.745)	0.1176 ** (13.486)	0.0931 ** (13.395)	0.1109 * (15.471)
β	0.80705 ** (62.064)	0.80072 ** (58.97)	0.80802 ** (56.775)	0.81186 ** (58.328)	0.8172 ** (61.533)	0.8177 ** (61.988)	0.8807 ** (112.08)	0.7967 ** (45.809)	0.8098 ** (59.727)	0.8413 ** (82.098)
θ	0.03111 ** (12.348)	0.03183 ** (12.776)	−0.0209 ** (−6.8337)	−0.0211 ** (−6.6477)	−0.0099 ** (−3.2215)	−0.0108 ** (−3.2082)	0.0052 ** (8.6137)	0.0247 ** (6.3436)	−0.008 * (−2.329)	−0.0334 (1.0056)
ω	3.64030 ** (4.575)	4.77050 ** (4.5963)	2.7006 ** (4.3842)	2.5853 ** (4.282)	11.758 * (2.3582)	10.205 * (2.5122)	1.2624 ** (13.103)	9.245 ** (3.2151)	4.8722 * (2.3151)	1.0056 ** (5.0055)
m	0.00009 ** (6.8231)	0.00008 ** (6.91)	0.00029 ** (20.307)	0.00029 ** (19.659)	0.00022 ** (32.902)	0.00022 ** (32.558)	0.0003 ** (13.949)	0.0001 ** (6.4681)	0.0002 ** (33.977)	0.0003 ** (16.553)
Diagnostics:
LogL	12,621.2	12,622.7	11,123.2	11,123.9	10,740	10,740.4	10,913.4	10,945.6	10,736.2	10,750.8
AIC	−25,230.4	−25,233.4	−22,234.4	−22,235.8	−21,468	−21,468.8	−21,814.8	−21,879.2	−21,460.4	−21,489.6
BIC	−25,191.6	−25,194.6	−22,195.6	−22,197	−21,429.2	−21,430	−21,776	−21,840.4	−21,421.6	−21,450.8
HQ	−25,140.7	−25,143.7	−22,144.7	−22,146.1	−21,378.3	−21,379.1	−21,725.1	−21,789.5	−21,370.7	−21,399.9

Notes. X represents variables entering the secular component of volatility. RV is realized variance and is univariate. The RV based models present baseline models. IPIT and IPIC are the industrial production trend and cycle indexes. GPR is a geopolitical risk indicator. CLI stands for Composite Leading Indicator. f and rw denote the fixed and rolling window sampling type. t statistics are in parentheses. LogL is the log-likelihood, and AIC, BIC and HQ refer to Akaike, Bayesian and Hannan-Quinn information criteria. * is the statistical significance at 5% and ** is at 1% significance levels.

.

If an overlook is presented to the estimation results for GARCH-MIDAS models in Table 4, considering the diagnostics of the Log-likelihood, Akaike (AIC), Bayesian (BIC), and Hannan-Quinn information criteria, the findings show that the models have the ability to predict daily stock market returns effectively for in-sample estimations. If the parameters of all models are evaluated for statistical significance, the parameters are statistically significant generally at 1% and 5% significance levels. Furthermore, for all models, the θ parameter estimates, their statistical significance, and their signs play a crucial role in the long-run component of volatility, ${\tau }_{,t}$. For instance, for models specified with RV, the sign and size of θ determines the direction of the effect of the long-run component on the volatility of the series modeled. Similarly, θ determines the direction of the effect of the macroeconomic variable and, therefore, the effect of the long-run volatility component on short-run (daily) volatility. If the signs of θ parameters are evaluated, for RV models, inclines in the long-run component leads to inclines in daily conditional stock market volatility. The GARCH-MIDAS model is capable of including the effects of the macroeconomic indicators on the volatility of daily stock markets, an important characteristic compared to the GARCH models.

According to the estimation results, the findings confirm that increases in industrial production reduce stock market volatility. Furthermore, increases in geopolitical risk have a positive effect on daily stock market volatility in the BIST100 daily returns. In contrast, the CLI is an index for which inclines in CLI represent positive expectations regarding the economy, and the findings suggest that, similar to the results for IPI production indices, inclines in CLI leads to declines in daily stock market volatility. However, it should be noted that the θ parameters are statistically significant for all models except for Model X, which assumes CLI as the exogeneous factor, and although the parameter estimate is −0.0334, the parameter is statistically insignificant, suggesting no effect of CLI on stock market volatility for the period analyzed. Furthermore, in the first CLI—based model, the θ parameter is statistically significant for Model 9 in contrast to Model 10. However, the parameter estimate is too close to zero, leading to the questioning of the efficiency of CLI as an effective economic indicator for in-sample estimation results. Even though this is the case in 9 out of 10 models, the long-run component functions are effective with statistically significant m, w and θ parameters. Nonetheless, the performance of the models will be particularly crucial for model comparisons in out-of-sample forecasts. As a result, all models including Model 10 will be used for forecasting purposes. One additional finding is that, for in-sample results, the best fit of the models is obtained for the GARCH-MIDAS model with RV, the baseline model, which is a univariate model in nature. Nevertheless, such findings do not necessitate similar conclusions for out-of-sample forecast accuracy.

4.3.2. GARCH-MIDAS-LSTM Estimation Results

In the estimation of the GARCH-MIDAS-LSTM model, similar to the GARCH-MIDAS results, the last 23 observations were left out of the out-of-sample forecasts. The remaining sample was split into training, validation and test samples, with 80–10–10 percentages during the model estimation. After estimation, the left-out sample was used for forecast analysis, similar to the GARCH-MIDAS models, for comparative purposes. The GARCH-MIDAS-LSTM model estimation results are reported in Table 4 below.

The same GARCH-MIDAS architectures selected for each GARCH-MIDAS model is maintained for their LSTM counterparts, and all models utilize beta polynomial functions and the single weight parameter, w. This is because the weight parameter w₂ = 1 − w₁; therefore, the reported w is w₂. The estimated models will be evaluated for forecast performances in the next section. The LSTM augmented models provide the opportunity to investigate the possibility whether further information could be extracted from the macroeconomic indicators utilized in the study.

In

Table 5. GARCH-MIDAS-LSTM Estimation Results.

Model:	11	12	13	14	15	16	17	18	19	20
X:	RV	RV	IPIT	IPIT	IPIC	IPIC	GPR	GPR	CLI	CLI
type:	f	rw	f	rw	f	rw	f	rw	f	rw
Parameter estimates:
µ	0.0008 ** (3.4121)	0.0008 ** (3.4277)	0.0009 ** (4.1590)	0.001 ** (4.2306)	0.0010 ** (4.2021)	0.0001 ** (1.2004)	0.0009 ** (4.0472)	0.0009 ** (4.1255)	0.0009 (1.5904)	0.001 ** (4.3932)
α	0.1134 ** (15.178)	0.1133 ** (16.0142)	0.0970 ** (13.574)	0.0978 ** (13.692)	0.0911 ** (12.985)	0.0910 ** (12.849)	0.0903 ** (14.540)	0.1006 ** (14.649)	0.0899 ** (13.448)	0.0972 ** (14.041)
β	0.8144 ** (52.673)	0.8151 ** (49.916)	0.8106 ** (51.768)	0.8106 ** (53.022)	0.8196 ** (54.058)	0.8181 ** (61.094)	0.8841 ** (101.65)	0.8004 ** (39.905)	0.8105 ** (57.954)	0.8295 ** (79.881)
θ	0.0304 ** (14.802)	0.0303 ** (13.109)	−0.0211 ** (−9.6581)	−0.0240 ** (−6.7843)	−0.0103 ** (−7.4490)	−0.0139 ** (−8.4522)	0.0031 ** (10.4062)	0.0307 ** (10.7601)	−0.029 ** (−6.001)	−0.0301 ** (−6.1583)
ω	3.4504 ** (4.692)	3.8941 ** (4.9470)	2.6826 ** (5.2351)	2.6756 ** (5.377)	12.002 ** (5. 2676)	11.870 ** (6.5513)	8.2547 ** (14.5063)	9.0499 ** (11.6502)	5.2190 ** (3.6774)	4.79411 ** (4.07101)
m	0.0001 ** (4.7440)	0.0001 ** (4.8913)	0.0003 ϯ (1.93491)	0.0003 * (1.9625)	0.0003 ** (21.876)	0.0003 ** (17.4662)	0.0002 * (1.9672)	0.00027 * (2.02486)	0.00026 ** (19.503)	0.00025 ** (19.8474)
Diagnostics:
LogL	11,998.3	12,001.6	12,806.8	12,839.7	12,661.4	12,058.02	12,105.8	11,174.5	10,796.9	11,027.5
AIC	−23,984.6	−23,991.2	−25,601.6	−25,667.4	−25,310.8	−24,104	−24,199.6	−22,337	−21,581.8	−22,043
BIC	−23,945.8	−23,952.4	−25,562.8	−25,628.6	−25,272	−24,065.2	−24,160.8	−22,298.2	−21,543	−22,004.2
HQ	−23,894.9	−23,901.5	−25,511.9	−25,577.7	−25,221.1	−24,014.4	−24,109.9	−22,247.3	−21,492.1	−21,953.3

Notes. X represents variables entering as the secular component of volatility. f and rw denote the fixed and rolling window sampling type. t statistics are in parentheses. LogL is the log-likelihood, AIC, BIC and HQ refer to Akaike, Bayesian and Hannan-Quinn information criteria. * is statistical significance at 5% and ** at 1% and ^ϯ denotes significance at 10% significance level.

, similar to Models 1 to 10 in Table 4, a total of 10 GARCH-MIDAS-LSTM models are estimated. These models are numbered as models 11 to 20. Furthermore, we noted that certain aspects observed in the models in Table 4 have changed for the LSTM model estimations in Table 5. First, the RV was no longer the model that provided the best fit for in-sample estimation. The AIC, BIC and HQ information criteria are no longer the lowest for Models 11 and 12, the models with RV. Second, the θ parameters are statistically significant for both GARCH-MIDAS-LSTM models with rolling windows and fixed sampling strategies. Both models confirm the increases in CLI, i.e., positive expectations about the economy in the future, having negative effects on stock market volatility in the BIST100 daily stock market returns.

Overall, all LSTM augmented models confirm the positive effects of geopolitical risk, the negative effects of industrial production increases, in addition to the negative effects of CLI on stock market volatility. Hence, these findings have important implications. In light of CLI, the included variables in the index a play crucial role in defining it as being largely based on forward looking expectations regarding the economy. According to the OECD, the CLI index was formed to produce early signals regarding the turning points of business cycles by measuring deviations in the short-run versus long-run economic trends [5]. To this end, the OECD has a set of variables that provide early signals about the Turkish economy. These include monthly electricity production, three manufacturer surveys on new domestic orders of final inventories, and survey results regarding the likelihood of employing new employees in the upcoming months. The CLI for Türkiye also includes exports and import trends n in addition to survey data on expectations in the service sector [6]. If weights are evaluated, the CLI is largely influenced by the forecasters’ expectations regarding future economic performance. From an economic policy perspective, in the context of CLI and IPI cycle and trend indices, positive economic expectations and increases in industrial production have a significant effect on stock market volatility. In addition, increases in both expectations of future economic performance and in economic performance measured with two IPI indices result in the reduction of stock market volatility in Türkiye. In contrast, the geopolitical risk indicator, GPR, is a weighted index based on the text mining of the major newspapers for words related to geopolitical tensions. In addition, GPR has been shown to increase during political disputes and tensions, and the largest hikes in GPR were shown to have occurred during World Wars I and II, following 9/11, and in many various forms of political tensions that affect geographical boundaries [7]. Our findings confirm the positive θ parameter estimates, which are statistically significant considering the relevant t-tests in Models 17 and 18. Therefore, the findings emphasize the significant and positive effects of geopolitical risk on enhancing volatility in financial markets of an emerging market in the context of the BIST100 in Türkiye. In addition, the findings obtained with GARCH-MIDAS-LSTM models also confirm the negative effects of CLI, and the positive effects of IPIC and IPICT as observed for the GARCH-MIDAS models considering the signs of parameter estimates for both model types, although the size of parameter estimates are subject to slight differences.

4.3.3. Out-of-Sample Forecast Performance Analysis

Following in-sample estimation results, the out-of-sample performances of models were evaluated. The out-of-sample forecast results are given in

Table 6. Out-of-Sample Forecast Results, 23 Days Ahead.

Model No:	I	II	III	IV	V	VI	VII	VIII	IX	X
X:	RV	RV	IPIT	IPIT	IPIC	IPIC	GPR	GPR	CLI	CLI
type:	f	rw	f	rw	f	rw	f	rw	f	rw
Group 1: GARCH-MIDAS models
RMSE:	0.000172	0.000181	0.000191	0.0001812	0.000174	0.000174	0.000192	0.000161	0.000227	0.000227
Rank in Group 1:	9	4	5	10	2	3	6	1	8	7
Group 2: GARCH-MIDAS-LSTM models
Model No:	XI	XII	XIII	XIV	XV	XVI	XVII	XVIII	XIX	XX
X:	RV	RV	IPIT	IPIT	IPIC	IPIC	GPR	GPR	CLI	CLI
type:	f	rw	f	rw	f	rw	f	rw	f	rw
RMSE:	0.000076	0.000093	0.000049	0.000036	0.000073	0.000079	0.000091	0.000034	0.000138	0.000078
Rank in Group 2:	5	9	3	2	4	7	8	1	10	6
Comparative analysis of GARCH-MIDAS and GARCH-MIDAS-LSTM models
Rel.RMSE *	0.44	0.52	0.26	0.20	0.42	0.46	0.21	0.28	0.61	0.34
RMSE%Δ **	−55.81	−48.46	−74.38	−95.55	−58.23	−54.35	−78.88	−71.90	−39.23	−65.62

Notes. The volatility forecast horizon consists of 23 working days ahead (the equivalent of 1 month). rw and f are the rolling window and fixed specifications in GARCH-MIDAS models. RMSE values are reported for comparisons within the GARCH-MIDAS group. The rank denotes the rank of the model from the highest performance (lowest RMSE) to the lowest (with the highest RMSE). Typically, GARCH-MIDAS with the geopolitical risk (GPR) and the rw specification produces the lowest RMSE among the GARCH-MIDAS models, followed by the model with rw specification and the industrial production index cycle (IPI, cycle) assumed as to be providing information regarding the secular component of the total volatility in the stock returns. * Rel. RMSE is the relative value of the RMSE of the LSTM based model over its baseline model (the non-LSTM variant). Typically, 0.10 in the 1st column with regard to the RMSE of GARCH-MIDAS-LSTM is one-tenth of the RMSE of GARCH-MIDAS, with RV taken as the long-run component. ** RMSE %Δ is the percentage change in RMSE of the LSTM-based model over its no LSTM counterpart.

. If an overview of the in-sample results obtained in the previous section is to be evaluated, it is seen that the LSTM augmented GARCH-MIDAS-LSTM models provided a slight improvement. Compared to GARCH-MIDAS models, the AIC, HQ and BIC information criteria have changed and are relatively lower (i.e., more negative) for the majority of GARCH-MIDAS-LSTM models in the majority of cases.

Relative to GARCH-MIDAS models in Table 4, the GARCH-MIDAS-LSTM results in Table 5 confirmed the statistical significance of CLI as being effective on stock market volatility. The RV-based models’ performance is slightly lower for the LSTM augmented model compared to non-LSTM models with RV. Even so, such conclusions should be taken lightly, since they are restricted to in-sample fit. The out-of-sample forecast performances of models will play a crucial role in the determination of the effectiveness of models.

The forecast performance of the models is examined for a horizon h = 23 days ahead. This constitutes almost 5 weeks, given that the data is for working days. The forecast performances are evaluated with root mean squared forecast errors (RMSFE) calculated for forecast errors covering h = 1, 2, …, 23. The results are reported in Table 6, where two different model groups are provided in two subsections.

Group 1 represents GARCH-MIDAS models with rolling window and fixed specifications for the economic fundamental set of the study. Group 2 represents the GARCH-MIDAS-LSTM models and the LSTM augmented variants of models in Group 1. Lastly, the final rows present a comparative forecast analysis for models used in the study. The RMSE’s for GARCH-MIDAS models reported under Group 1 signify that these models provided good forecast performances for the GARCH-MIDAS models with selected economic fundamentals and leading indicators.

The models are ranked from 1 to 10, from lowest RMSE to highest, and the lowest is achieved as 0.000161 for the GARCH-MIDAS model with rolling windows specification and with a geopolitical risk index (GPR) being utilized as the economic indicator. Furthermore, an overview of the ranks shows that though the models that use GPR are followed with two models that use the industrial production cycle indicator (IPIC) as the economic fundamental, taking the second and third places. The fourth and fifth places were taken by the RV-based univariate model, closely followed by the model with trend production (IPIT). Sixth place went to the model with a GPR index and with a fixed window specification. Seventh and eighth place went to GARCH-MIDAS models utilizing CLI as the leading indicator. The ninth and tenth places went to the RV-based model with a fixed window and the IPIT based model with a rolling window. The findings lead to interesting results: (i) Although models are ranked from 1 to 10, the RMSEs of all models are very low and very close. Therefore, although the models are ranked, the lowest and highest RMSEs for models are 0.000161 and 0.0001812, signifying the significant forecast capabilities of all models. In the literature, the generally accepted cutoff point for RMSFE is assumed to be 0.08, and all GARCH-MIDAS and GARCH-MIDAS-LSTM type models provided a significant improvement in forecasts. (ii) There is a tendency for rolling window-specified models to perform better than fixed window- specified ones; however, no clear distinction could be made. This is because the model with IPI performed better with fixed windows. As a result, future research should be cautious about making a-priori decisions for GARCH-MIDAS models in terms of rw and f specifications, and it is necessary to take the out-of-sample forecasts first. (iii) The results for GARCH-MIDAS models suggest geopolitical risk followed by industrial production, and lastly by future expectations (proxied with CLI) with regard to playing crucial roles in stock market volatility forecasts. The GARCH-MIDAS results show that CLI-included models performed badly when compared to other economic indicators in the Turkish stock market case. As will be shown, the LSTM augmented GARCH-MIDAS-LSTM estimations showed a forecast improvement for models with CLI over all GARCH-MIDAS models without LSTM. However, among all LSTM augmented models, we cannot conclude that models that utilize CLI are among the top models in forecasting BIST100 stock market volatility. Furthermore, it should be noted that there are variations in the variables and their weights in the CLI index. In fact, the CLI index uses country-specific variables and weights due to the different availability of the expectations related to variables at the nation level [6]. Therefore, the findings cannot be generalized to other stock markets, and this should be evaluated as country-specific. In contrast, a recent study showed a clear forecast improvement in GARCH-MIDAS models with CLI for the modeling of the different stock market volatilities of the G7 countries [53].

The GARCH-MIDAS-LSTM forecast results are reported in the second section under Group 2. In addition to Group 1 models, RMSE values and ranks of models are reported. The overall investigation of GARCH-MIDAS-LSTM models show that RMSE’s obtained are significantly lower than those obtained for GARCH-MIDAS models. The lowest RMSE was achieved for the GARCH-MIDAS-LSTM model with a geopolitical risk indicator (RMSE = 0.000034), and the models have the first rank among all other models. The relative change in RMSE is a −71.90% reduction from the GARCH-MIDAS models with GPR again, which had taken first place among all GARCH-MIDAS models in Group 1. Therefore, LSTM augmentation has the potential to further improve the forecast performances of GARCH-MIDAS models. If the performances are compared for models in Group 2 models with the LSTM specification, second and third place are taken by models utilizing IPI cycle and IPI trend indicators, followed by fourth place again being taken by the model with IPI cycle. On the other hand, RV- based models take the fifth and ninth places, and CLI-based models take the sixth and tenth places. Again, one could conclude that the general tendency favors the rolling window specification; however, such generalizations would be incorrect for two reasons. First, it shouldn’t be forgotten that GARCH-MIDAS-LSTM with the IPIT indicator is among the first three models with the lowest RMSE within Group 2. Second, it is in fact not the fixed or rolling window specification but rather the LSTM architecture and modeling which led to significantly lower RMSE’s in the forecasts.

In addition to RMSE statistics, we calculated the relative improvement of LSTM augmented models over their non-LSTM counterparts with two different measures, Rel. RMSE and RMSE%Δ, which are reported in the last two rows. Rel.RMSE represents the ratio of RMSE of the LSTM augmented model in Group 2 to its non-LSTM variant in Group 1. Typically, Rel.RMSE = 0.44 in column 1 is the ratio of RMSE of the GARCH-MIDAS-LSTM with RV to RMSE of GARCH-MIDAS with RV and without LSTM. As long as Rel.RMSE < 1, the evidence favors the improvement of forecasts in the given out-of-sample forecast horizon. Otherwise, Rel.RMSE > 1 indicates a performance loss in forecasts for the LSTM augmented models. The second index we calculated is the RMSE%Δ, which calculates the % change in RMSE after LSTM specifications. Typically, −RMSE%Δ = −55.81 for GARCH-MIDAS-LSTM with the RV specification indicates a 55.81% decline in the RMSE of forecasts after augmenting the GARCH-MIDAS model with the LSTM architecture.

The findings in the last section of Table 6 clearly indicate the ability of the LSTM specification for the GARCH-MIDAS-LSTM models in forecast accuracy improvement. The relative RMSE, the ratio of RMSE of GARCH-MIDAS-LSTM models to non-LSTM models, ranges between 0.20 to 0.61, with all being less than 1. Furthermore, the relative % change in RMSE accounts for the negative 39% to 95% reduction in RMSE in forecasts for the various forms of GARCH-MIDAS-LSTM models over the non-LSTM, GARCH-MIDAS counterparts.

5. Discussion

The proposed models serve two purposes. First, by utilizing the GARCH-MIDAS architecture, the models effectively capture the effect of the economic indicator included in the model, in addition to the direction and size of the effect on stock market volatility. Second, by benefiting from LSTM methods, the models estimated provide a significant improvement in the forecasts. The summary of these findings is presented in

Table 7. Out-of-Sample Forecast Accuracy Comparison and Ranks, 23 Days Ahead.

Forecast Rank	RMSE (Ascending)	Economic Indicator	Effect *	Model Name:	Spec.
1	0.000034	GPR	+	GARCH-MIDAS-LSTM	rw
2	0.000036	IPI, trend	-	GARCH-MIDAS-LSTM	rw
3	0.000049	IPI, trend	-	GARCH-MIDAS-LSTM	f
4	0.000073	IPI, cycle	-	GARCH-MIDAS-LSTM	f
5	0.000076	RV	+	GARCH-MIDAS-LSTM	f
6	0.000078	CLI	-	GARCH-MIDAS-LSTM	rw
7	0.000079	IPI, cycle	-	GARCH-MIDAS-LSTM	rw
8	0.000091	GPR	+	GARCH-MIDAS-LSTM	f
9	0.000093	RV	+	GARCH-MIDAS-LSTM	rw
10	0.000138	CLI	-	GARCH-MIDAS-LSTM	f
11	0.000161	GPR	+	GARCH-MIDAS	rw
12	0.000174	IPI, cycle	-	GARCH-MIDAS	f
13	0.000174	IPI, cycle	-	GARCH-MIDAS	rw
14	0.000172	RV	+	GARCH-MIDAS	f
15	0.000181	RV	+	GARCH-MIDAS	rw
16	0.000191	IPI, trend	-	GARCH-MIDAS	f
17	0.000192	GPR	+	GARCH-MIDAS	f
18	0.000227	CLI	-	GARCH-MIDAS	f
19	0.000227	CLI	-	GARCH-MIDAS	rw
20	0.000812	IPI, trend	-	GARCH-MIDAS	rw

Notes. rw and f denote rolling window and fixed. * signifies the direction of the effect of the indicator on volatility. It is determined by the sign of the θ estimate in the model estimations. The estimated direction of the effect is given as + or - reflecting positive and negative effect of the indicator on volatility of stock market returns.

.

The findings in Table 7 highlight that the LSTM specification clearly improves the out-of-sample forecasts for the GARCH-MIDAS-LSTM models regardless of the type of economic indicator included. In addition, the decrease in out-of-sample forecast RMSE with the RV based the LSTM model also point to the improvement in forecast capability of the model after LSTM specification, since the models utilizing RV do not assume an exogeneous economic indicator. Moreover, all leading indicators utilized in the models provide enhancement in forecast effectiveness. However, the highest performance is achieved by the inclusion of geopolitical risk (GPR), followed by two models with industrial production trend indicators (IPIT). These models are followed again by another LSTM model with an industrial production cycle indicator. It is noted that the GARCH-MIDAS-LSTM model with the composite leading indicator (CLI) achieved an improvement in forecast performance with a relatively lower RMSE compared to all GARCH-MIDAS models, which includes the GPR, IPIC and IPIT indicators of industrial production. However, the CLI specified models took the sixth and tenth places among all 20 models.

In addition, RV specified models, though univariate in nature, took the fifth and ninth places, which is close to the CLI based models but with one rank higher, and passed all GARCH-MIDAS models, even those with monthly economic indicators. Therefore, if the results are evaluated together, the relative contribution of the geopolitical risk indicator in volatility forecasting is highest, and models with industrial production indicators follow close behind. The RV- and CLI-based models also led to the improvement in the prediction of the direction of volatility in LSTM specifications in addition to the non-LSTM GARCH-MIDAS models.

Moreover, the models are capable of producing total volatilities decomposed into short-run and long-run components. As presented in the methodology section, total volatility is the multiplication of short-run and long-run components. The Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 below present the total volatility (red, dashed) and the long-run component of volatility (blue line) modeled with realized variance, geopolitical risk, industrial production trend, and cycle indices and composite leading indicators, respectively. To save space, a selected set of results are reported, which cover all economic indicators and the univariate RV-based findings.

Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 indicate the following: In all specifications, the long-run components follow a relatively smooth process, which goes through the central tendency of total volatility. However, the CLI-based model results provide an exception. The CLI based long-run component is clearly more volatile than those reported for all other indicators. This is because the CLI is an index of future expectations and is likely to uncouple from stock volatility in uncertain times such as the period analyzed, with significant uncertainty about future expectations during COVID-19. This also becomes evident in the figure during the economic recovery period after 2009 global crisis. In all models, the sharp incline in the long-run coupled with the incline in the total volatility is clearly evident for the period that started in early 2020. A relatively higher level of variance is noted towards the last observations of the figure. Such findings indicate the efficiency of the proposed models in integrating the effects of economic indicators to volatility modelling, especially in terms of GPR, IPIC, IPIT, and, lastly, CLI indicators.

The effects of the long-run components were summarized in Table 7. If evaluated together with the findings regarding the path followed by the long-run components of stock market volatility, the long-run components and their effects are in line with those reported. The overall findings confirmed the following: (i) positive effects of increases in geopolitical risk lead to the further acceleration of total volatility. (ii) Increases in both cycle and trend industrial production lower the long-run volatility and the total volatility in the stock market. (iii) In the context of CLI, positive economic expectations lower the long-run and, in return, the total stock market volatility. The economic expectations in terms of CLI are more volatile, and the nature of these explanations play a crucial role in stock market volatility. (iv) Based on RV, in all models, univariate modeling is capable of producing effective modeling and forecasting. It is also evident that increases in the RV-based long-run component affect stock market volatility positively in the emerging stock market in the context of the BIST100 stock market index of Türkiye.

As a policy perspective, the geopolitical tensions and leading economic indicators clearly provide vital information regarding the stock market volatility in an emerging market in the context of the BIST100 example. The findings emphasize the integration of the GPR and IPI cycle and trend indices and the CLI indicator into the toolboxes of investors and policy makers. However, the uncertainty in the economic factors and in the financial markets lead to forecast problems which cannot be disregarded. For this purpose, the LSTM and deep neural networks-augmented hybrid models provide effective forecasts for the near future, and are shown to improve the forecast performances of the GARCH-MIDAS models. Lastly, the proposed model shows that the integration of the parametric specification of the implications of macroeconomic factors on volatility could lead to the improvement of the determination of the influences of leading indicators, such as the CLI, on the direction of stock markets and stock market volatility. Though the findings are obtained for various different economic indicators through 20 different models, the results are specific to the sample and to the economy covered. The findings also underlined the distinct volatility dynamics and the effects of selected economic fundamentals during the COVID-19 period. Future studies are expected to further test the effectiveness of the proposed GARCH-MIDAS-LSTM model in other markets for the investigation of the model under different conditions. It should also be noted that the overall findings indicated that important information could be gathered from the economic factors in terms of their effects on stock market volatility. Such findings are clearly in favor of deviations from the well-known Efficient Market Hypothesis (EMH). Future studies are encouraged to evaluate financial markets with EMH testing methods coupled with the GARCH-MIDAS and GARCH-MIDAS-LSTM models.

6. Conclusions

Our paper focuses on the hybrid modeling of LSTM deep learning and GARCH-MIDAS models to achieve the GARCH-MIDAS-LSTM model, which addresses the volatility modeling and forecasting problem of the stock market in daily frequency, with a set of monthly frequency fundamental indicators. The proposed GARCH-MIDAS-LSTM model benefited from the mixed data sampling (MIDAS) framework borrowed from the GARCH-MIDAS models, and from the LSTM architecture and algorithms to achieve forecast improvement. In the exercise in this study, the selected sample provides an interesting laboratory in which to test the model for forecast accuracy.

The in-sample dataset was selected as 1 January 2002 to 8 May 2020, a period that included the COVID-19 pandemic lock-down after the first case was discovered on 13 March 2020. The in-sample is also unique in that it includes the lockdown and partial opening policies. Most interestingly, the out-of-sample forecast period for models covers 9 May 2020 to 10 June 2020, a period that also coincides with reopening policies in the Turkish economy. In the paper, the GARCH-MIDAS and GARCH-MIDAS-LSTM models were utilized to forecast the volatility in daily BIST100 stock market returns with four different monthly economic indicators being applied to models exogenously; Geopolitical Risk (GPR), Composite Leading (CLI) Indicator of OECD, Industrial Production Trend (IPIT), and Industrial Production Cycle (IPIC) early indicators. Therefore, the study tested the performance of the GARCH-MIDAS and the GARCH-MIDAS-LSTM models in a comparative perspective in terms of their efficiency in extracting information to achieve forecast improvement from the four economic indicators, in addition to an RV-based univariate architecture. A total of 20 models were estimated. Among these, 10 of them were LSTM-augmented, and the other ten were non-LSTM models with both fixed and rolling window sampling strategies.

Among these indicators, the IPI-related indices were published as leading indicators by the CBRT in addition to the CLI, which is measured with manufacturer expectations of future economic activity. In contrast, when results were evaluated, the GPR was observed to lead to the most significant results in all settings; therefore, GPR is the most influential indicator among the indicators analyzed in terms of forecast performance. GPR is an index of political uncertainties, and thus it has a strong influence on the financial volatility of the Turkish BIST100 stock market index.

The CLI, as an indicator of future expectations, which did not provide such a significant improvement in forecasting for the COVID-19 period Even though this is the case, the GARCH-MIDAS-LSTM models that utilized CLI as the economic indicator provided improvement over the GARCH-MIDAS models. Instead of econometric reasons, the relatively lower contribution of CLI is evaluated as being a result of the increased future uncertainty at the specific period analyzed in this study, which hindered the leading potential of CLI. Is is observed that the relative decline in performance of the models with CLI is due to the uncertainty regarding future economic expectations in the forecast practice specifically conducted for the selected COVID-19 period with controlled reopening policies after a period of lock-down.

In addition to the four economic monthly indicators, the models were estimated with Realized Variance (RV) within a univariate setting. The approach extracts the long-run component from the daily stock market returns as a moving average process. The RV based GARCH-MIDAS-LSTM modeling also showed strong potential in forecast accuracy relative to all GARCH-MIDAS models with exogeneous economic fundamental variables.

The estimation results showed that all models provided a good fit for in-sample predictions. If the non-LSTM models are compared with the LSTM augmented models for in-sample modeling, the GARCH-MIDAS models also led to low AIC, BIC and HQ indicators, although the LSTM augmented GARCH-MIDAS models performed better in many cases. However, the most striking gain of LSTM modeling was in out-of-sample forecasting for the 23 days ahead forecasts. By augmenting the GARCH-MIDAS model with LSTM, the empirical findings indicated a significant improvement in forecast effectiveness. In this study, once the GARCH-MIDAS models are augmented with LSTM, the proposed GARCH-MIDAS-LSTM models achieved a relative RMSE ratio in forecasts ranging between 0.20 to 0.61 over their GARCH-MIDAS counterparts, depending on model specification. The relative % change in the RMSE of LSTM augmented models are calculated as ranging from minus 39% to minus 95.5%. These findings confirmed the effectiveness of the proposed models over their non-LSTM counterparts. Furthermore, LSTM augmented models which utilized RV instead of an exogenous economic indicator also performed significantly better than all GARCH-MIDAS models, including the GARCH-MIDAS models utilizing GPR, IPIT, IPIC and CLI economic indicators as exogeneous variables. Therefore, the findings demonstrated strong forecasting capabilities of the proposed models not only with all utilized economic indicators, but also in a univariate setting without exogeneous economic factors used in modeling the long-run drivers of volatility. The improvement of forecasts is especially important, since the coverage of data includes the COVID-19 lockdown followed by the opening of the economy in the out-of-sample period in the context of the BIST100 stock market.

In addition to the forecast results, the paper also determined the influence of economic indicators through the statistical significance of θ parameters. Among all non-LSTM models estimated, the increase in geopolitical risk in the country has negative effects on stock market volatility by enhancing the volatility in the BIST100 stock market. Furthermore, both trend and cycle economic indicators for industrial production lower volatility and therefore uncertainty. In this respect, industrial production and therefore the increase in economic growth performance in the Turkish economy lessens the volatility in stock markets. In the context of CLI, the improvement in expectations regarding future economic activity further mitigates the volatility in the stock market. Although the finding for CLI could only be partially accepted in the GARCH-MIDAS models, the GARCH-MIDAS-LSTM model confirmed the statistically significant effect of CLI on stock markets. Furthermore, the LSTM-augmented models confirm the negative effects of geopolitical risk, the positive effects of industrial production, and the negative effects of worsened future economic expectations in all model settings. Lastly, the proposed GARCH-MIDAS-LSTM modeling with the univariate RV approach was shown to be capable of performing even better than the GARCH-MIDAS models with the selected economic indicators in their long-run components.

The overall findings indicated that the proposed model offered a key tool for investors and policymakers to forecast the direction of the stock markets. Furthermore, policymakers focusing on policies aiming at lowering financial uncertainty should also focus on lowering geopolitical risks in addition to policies encouraging industrial production. In addition, lowering future uncertainties in terms of economic expectations is of crucial importance in reducing stock market volatility.