Fatigue Characteristics of Long-Span Bridge-Double Block Ballastless Track System
Abstract
1. Introduction
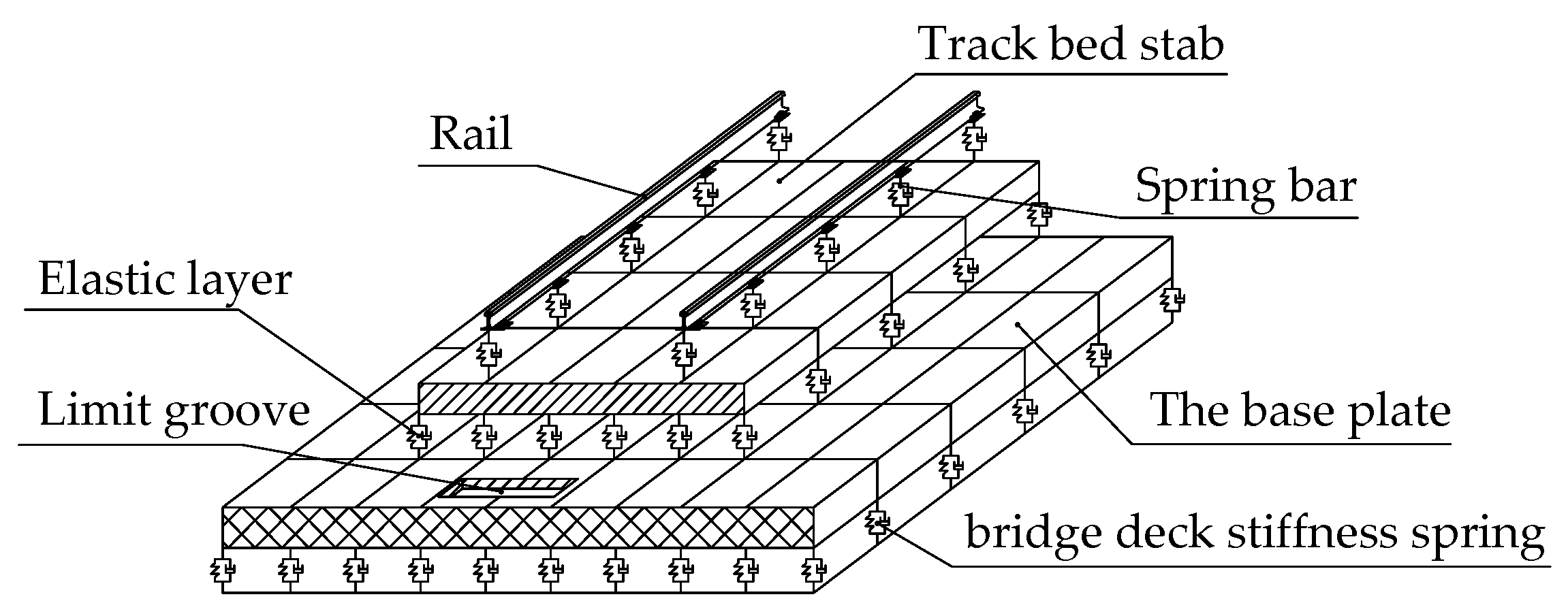
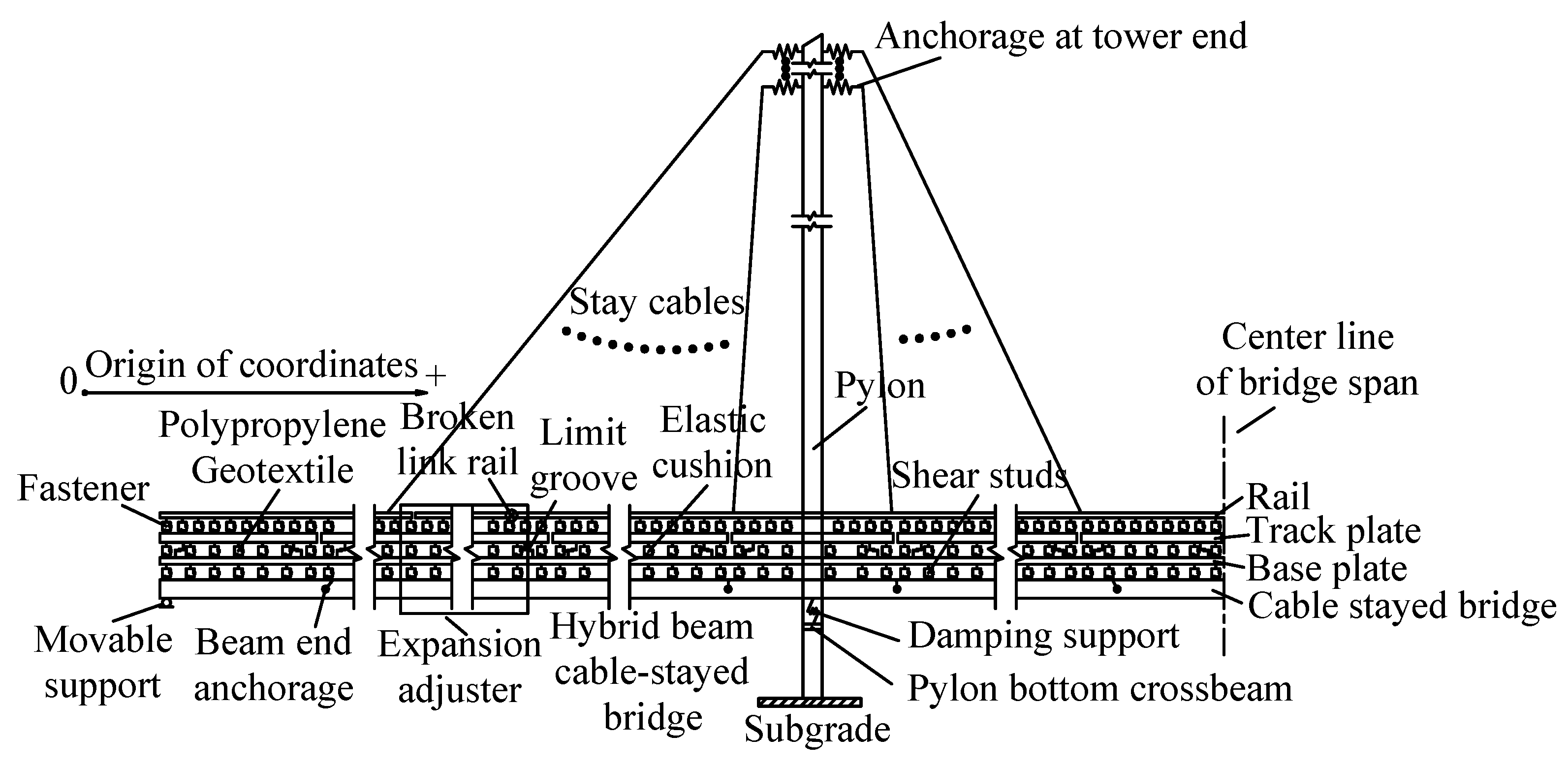
2. Simulation Model of Double Block Ballastless Track System on Bridge
2.1. Ballastless Track Structure
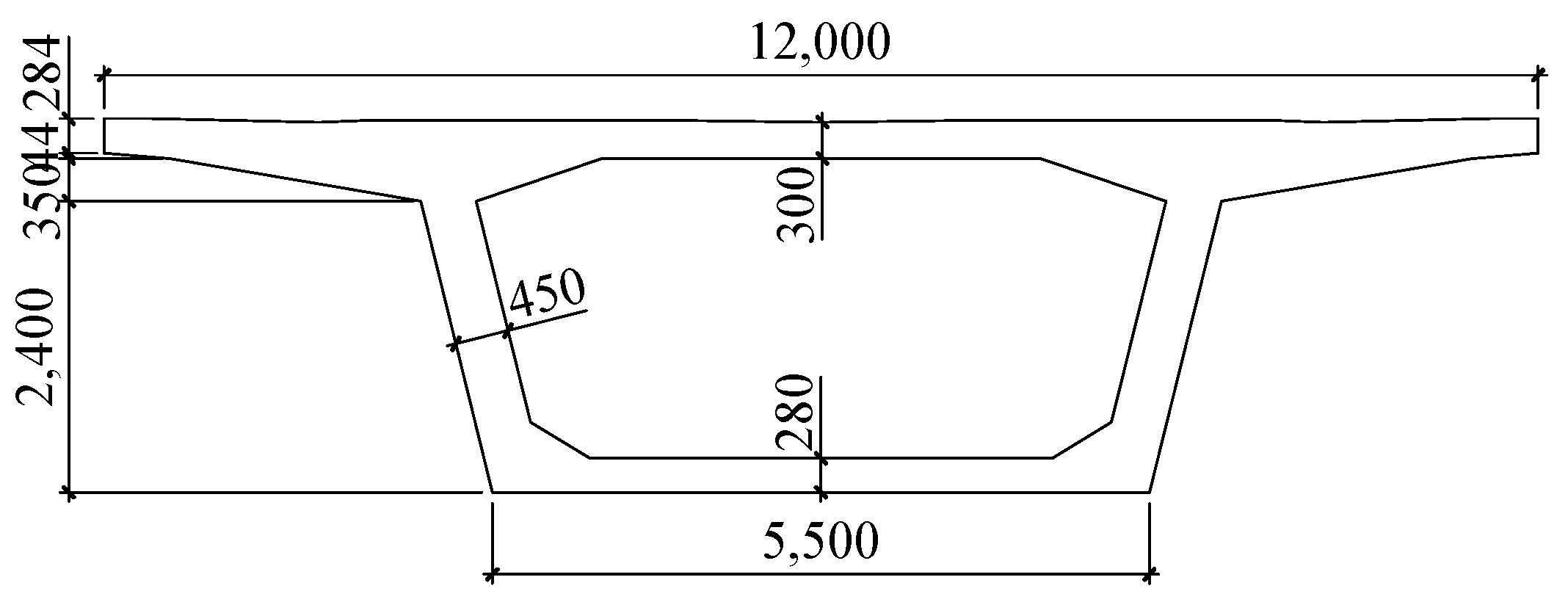
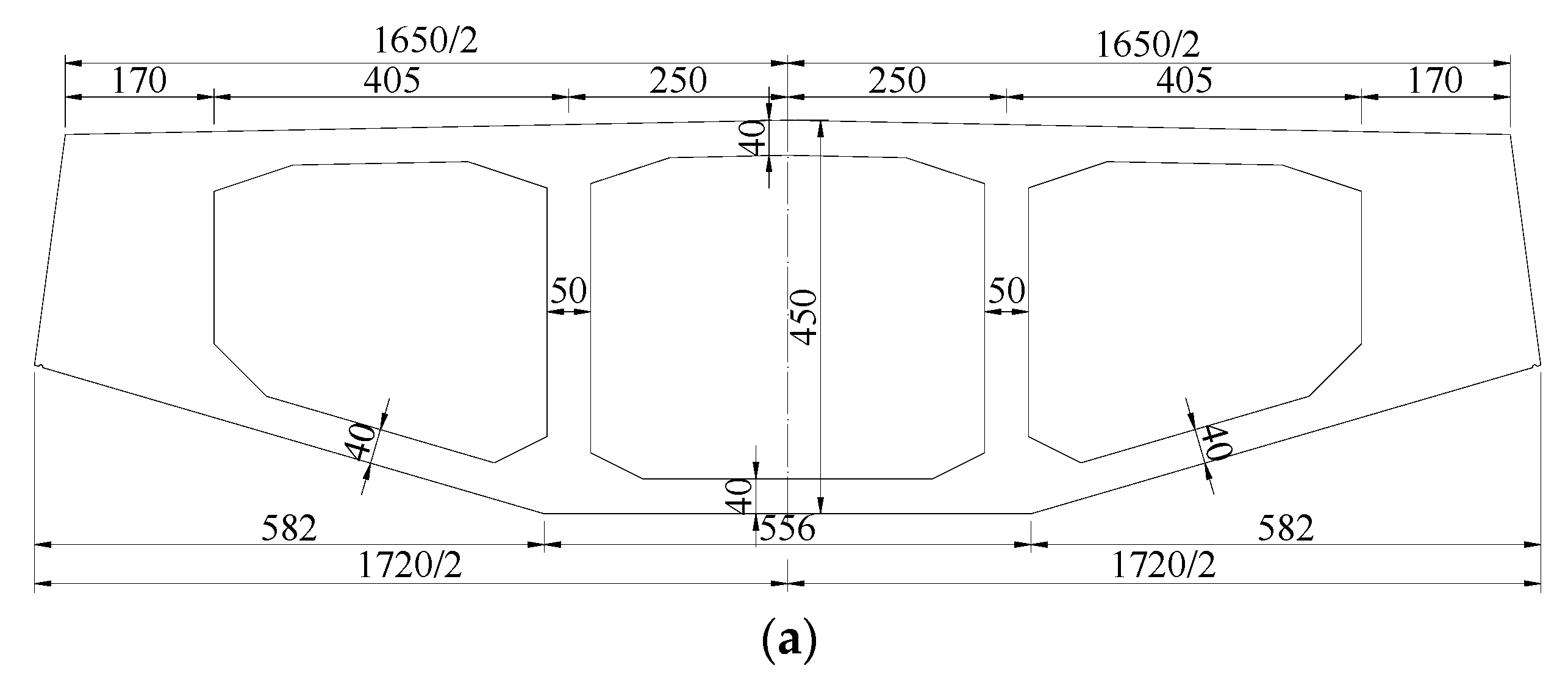
2.2. Continuous Beam Structure and Finite Element Model
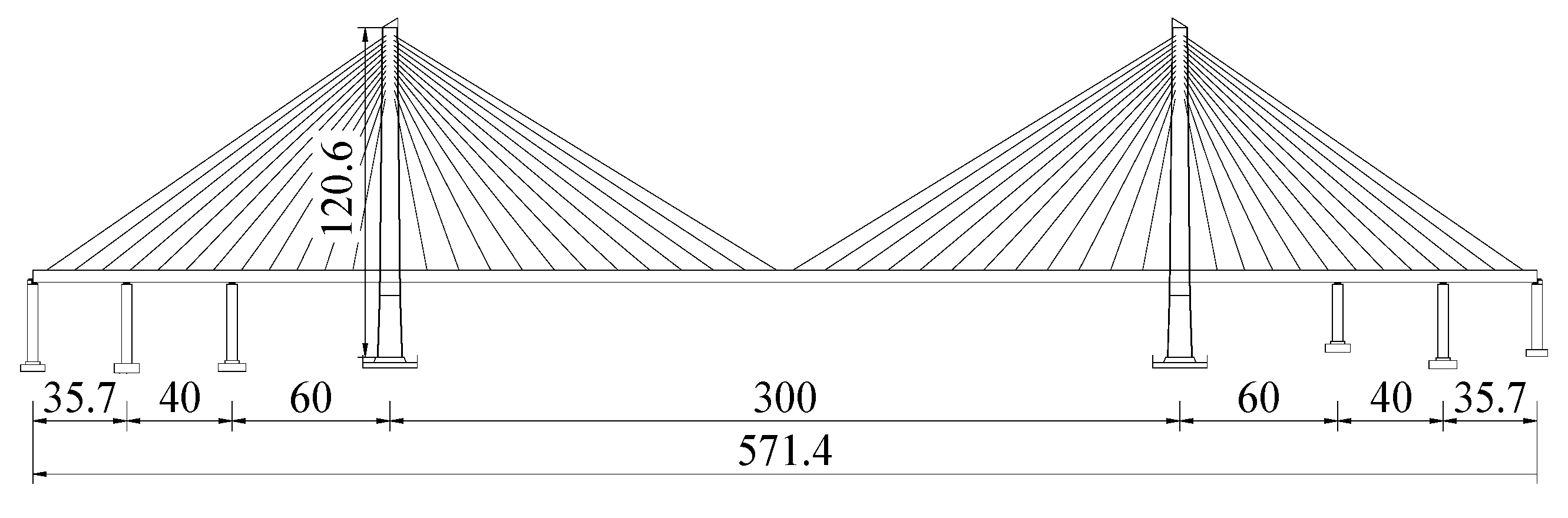
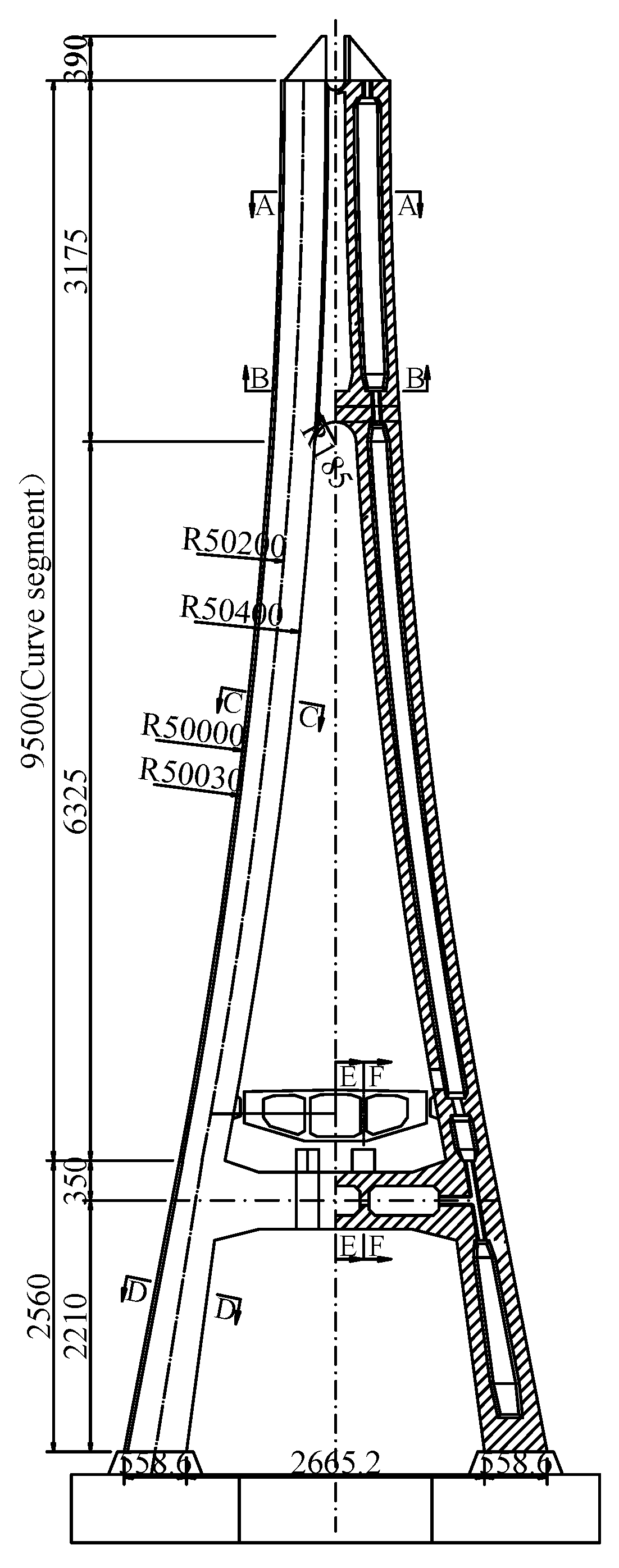
2.3. Structure and Finite Element Model of Cable-Stayed Bridge
2.4. Finite Element Model Verification
3. Calculation Method of Fatigue Life of Ballastless Track Structure
3.1. Calculation Method of Fatigue Life of Ballastless Track Structure
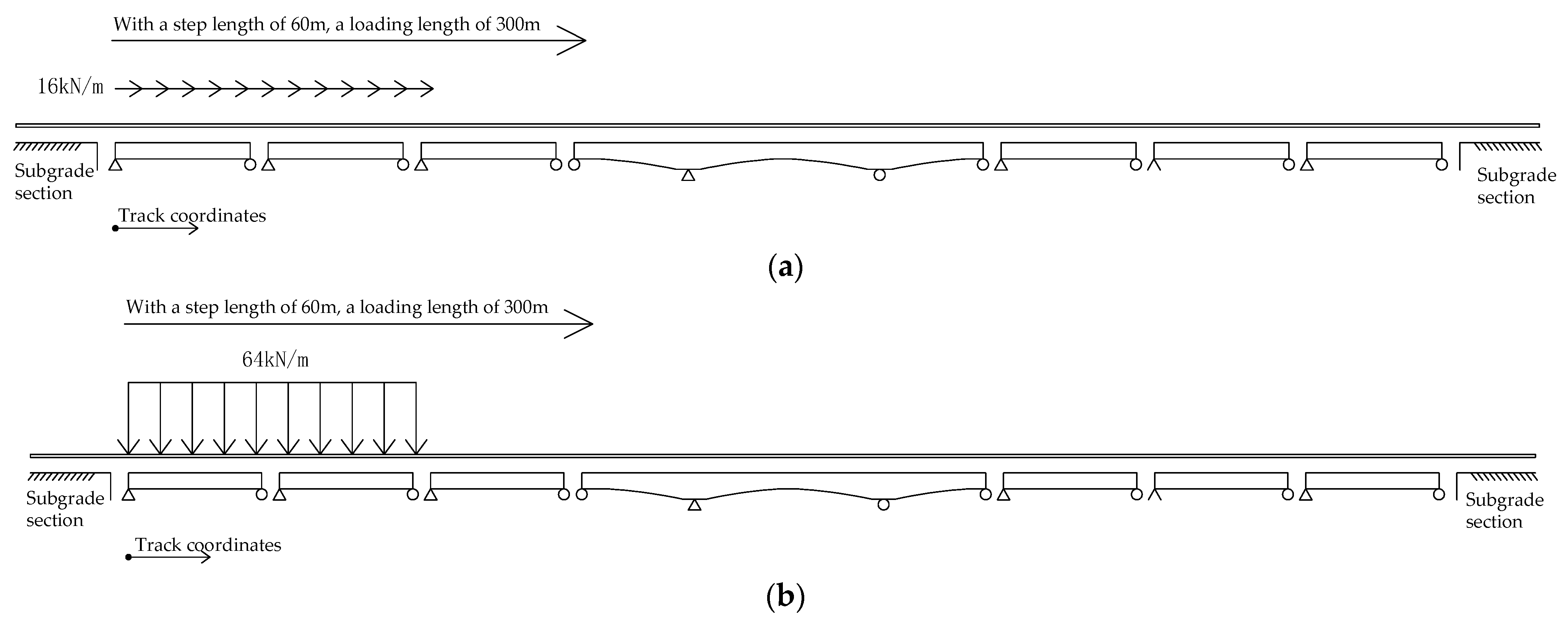
3.2. Traffic Load Spectrum
4. Fatigue Characteristics of Continuous Beam-CRTS I Double Block Ballastless Track System
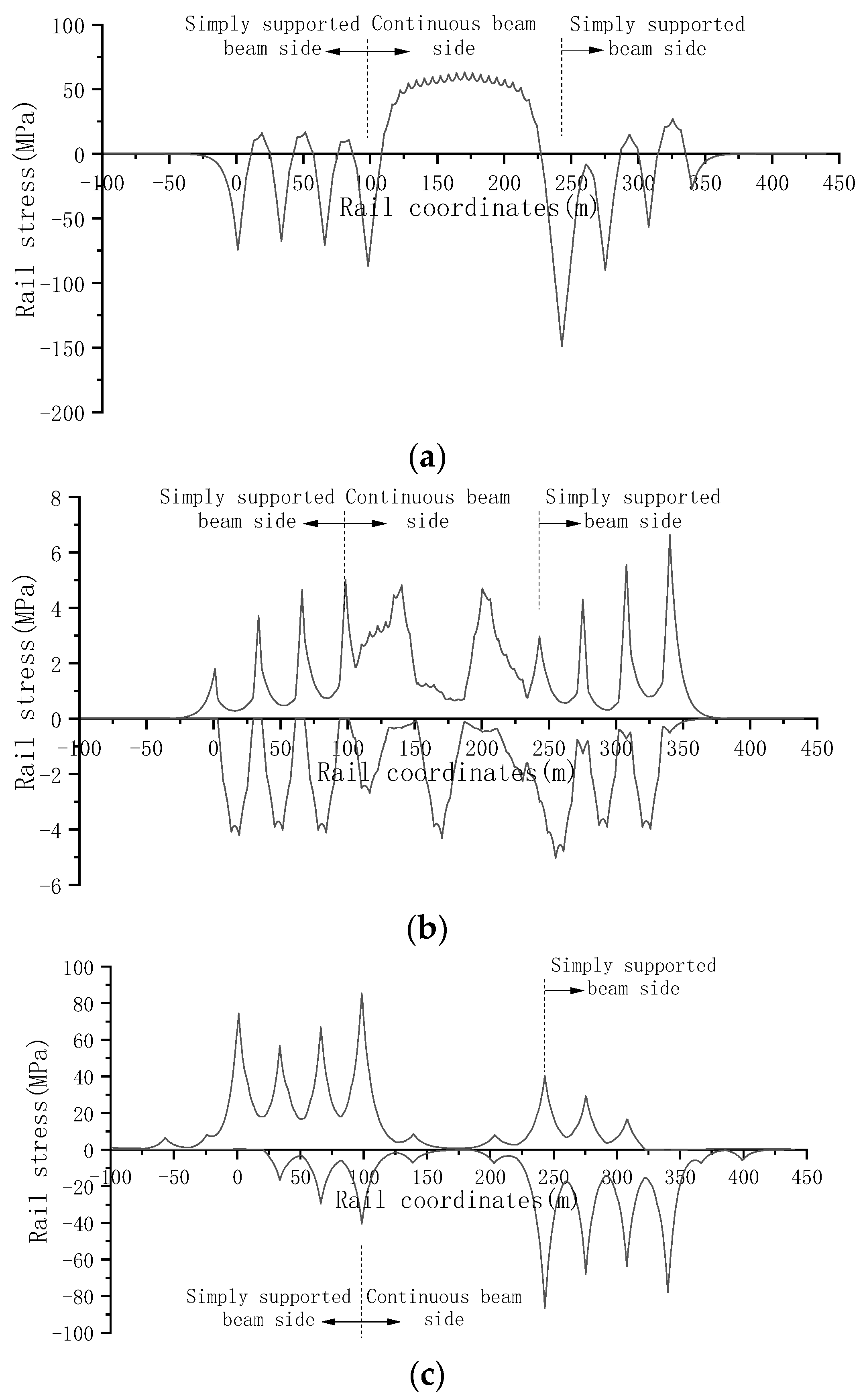
4.1. Additional Stress of Seamless Rail on Continuous Beam Bridge
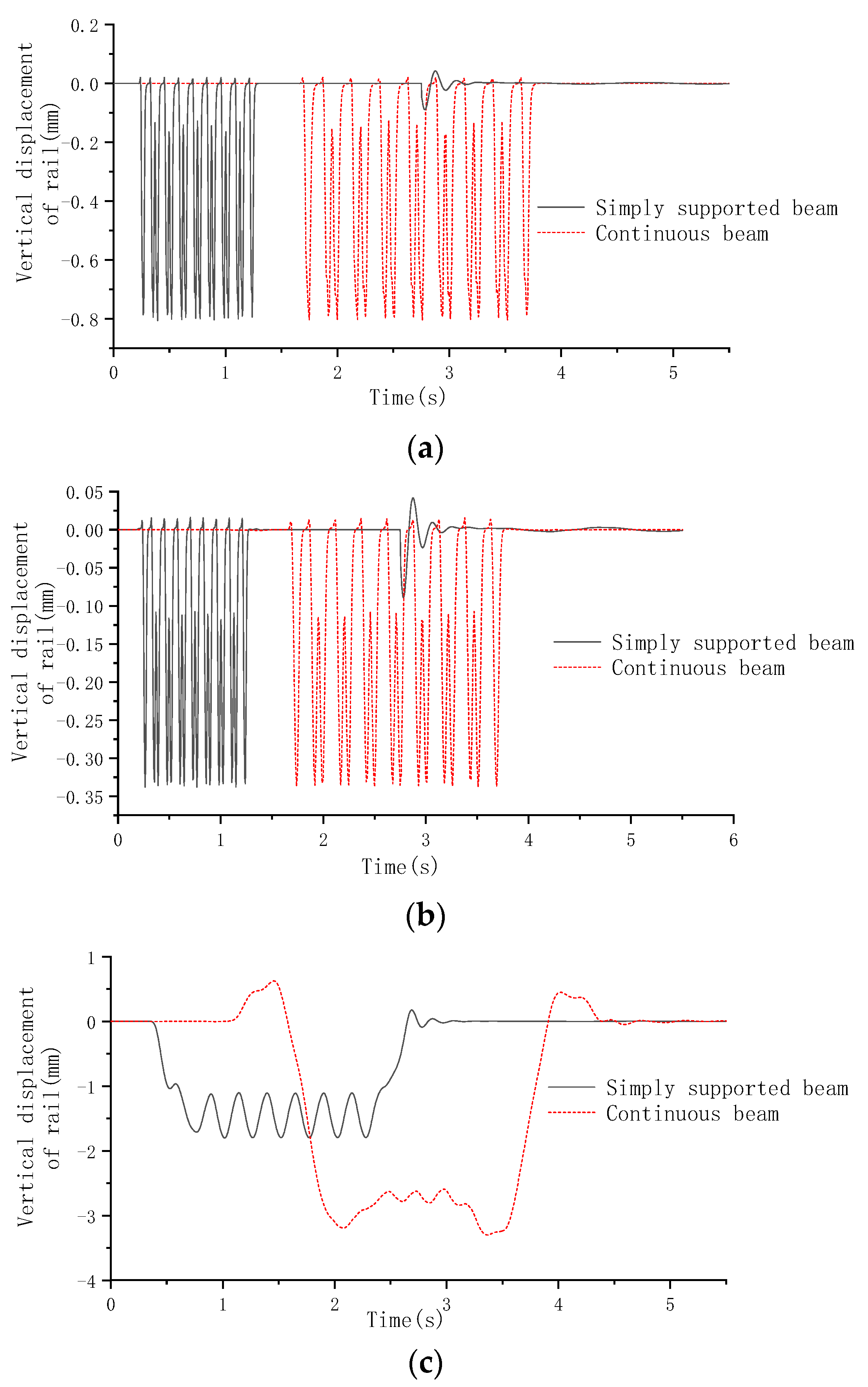
4.2. Dynamic Characteristics of Ballastless Track Structural System on Continuous Beam Bridge
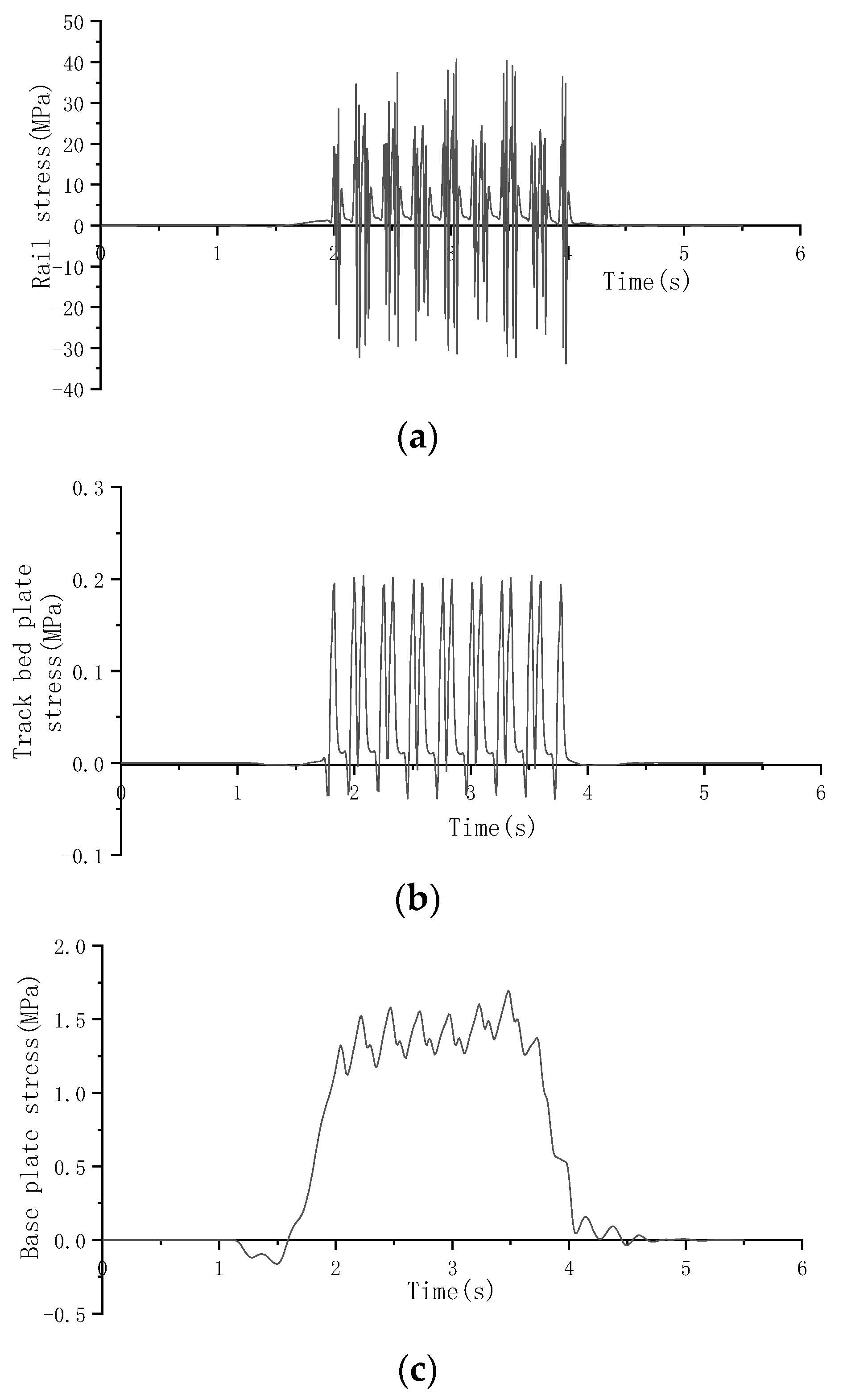
4.3. Fatigue Characteristics of Ballastless Track System on Continuous Beam Bridge
5. Fatigue Characteristics of Cable Stayed Bridge CRTS I Double Block Ballastless Track System
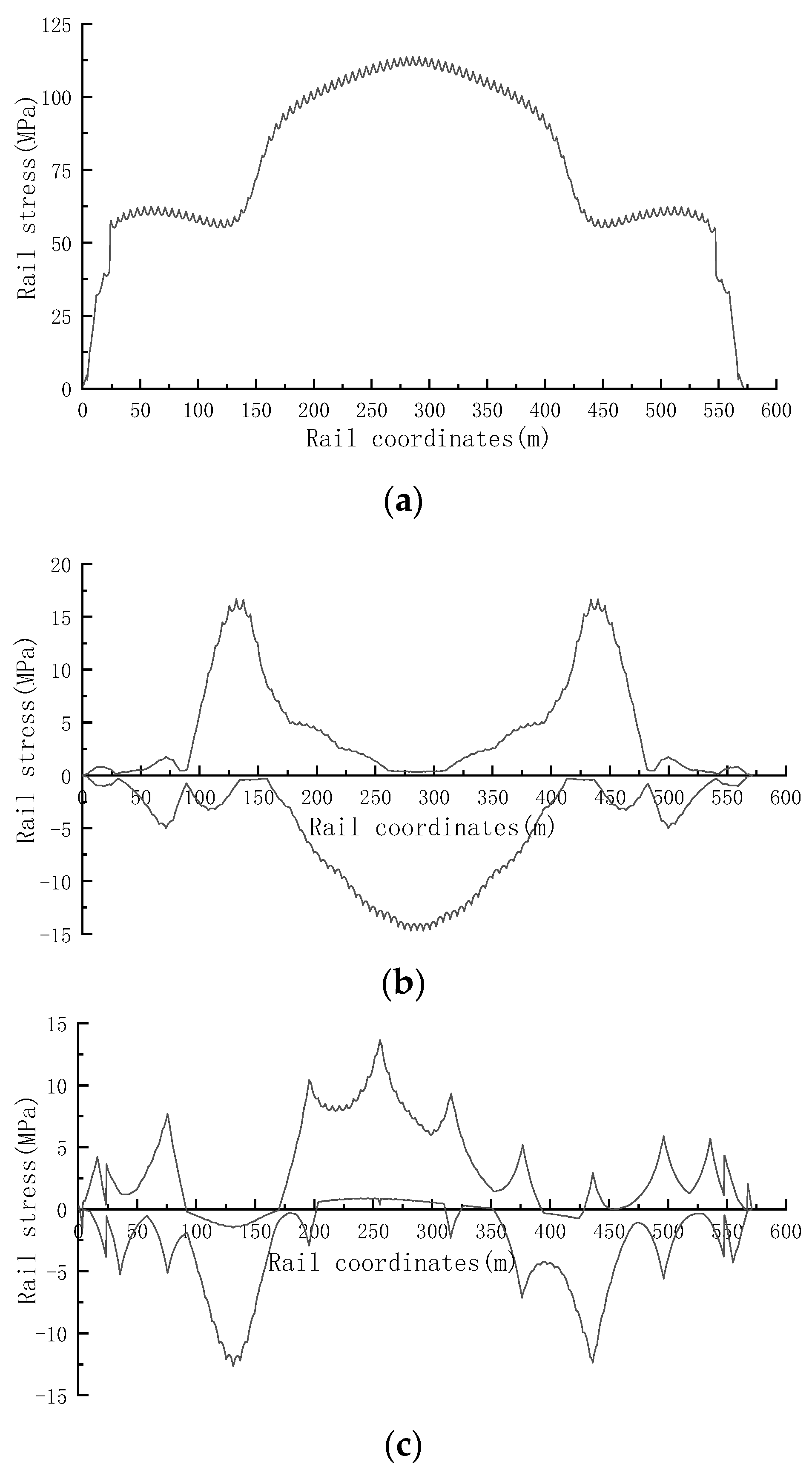
5.1. Additional Stress of CWR Rail on Cable-Stayed Bridge
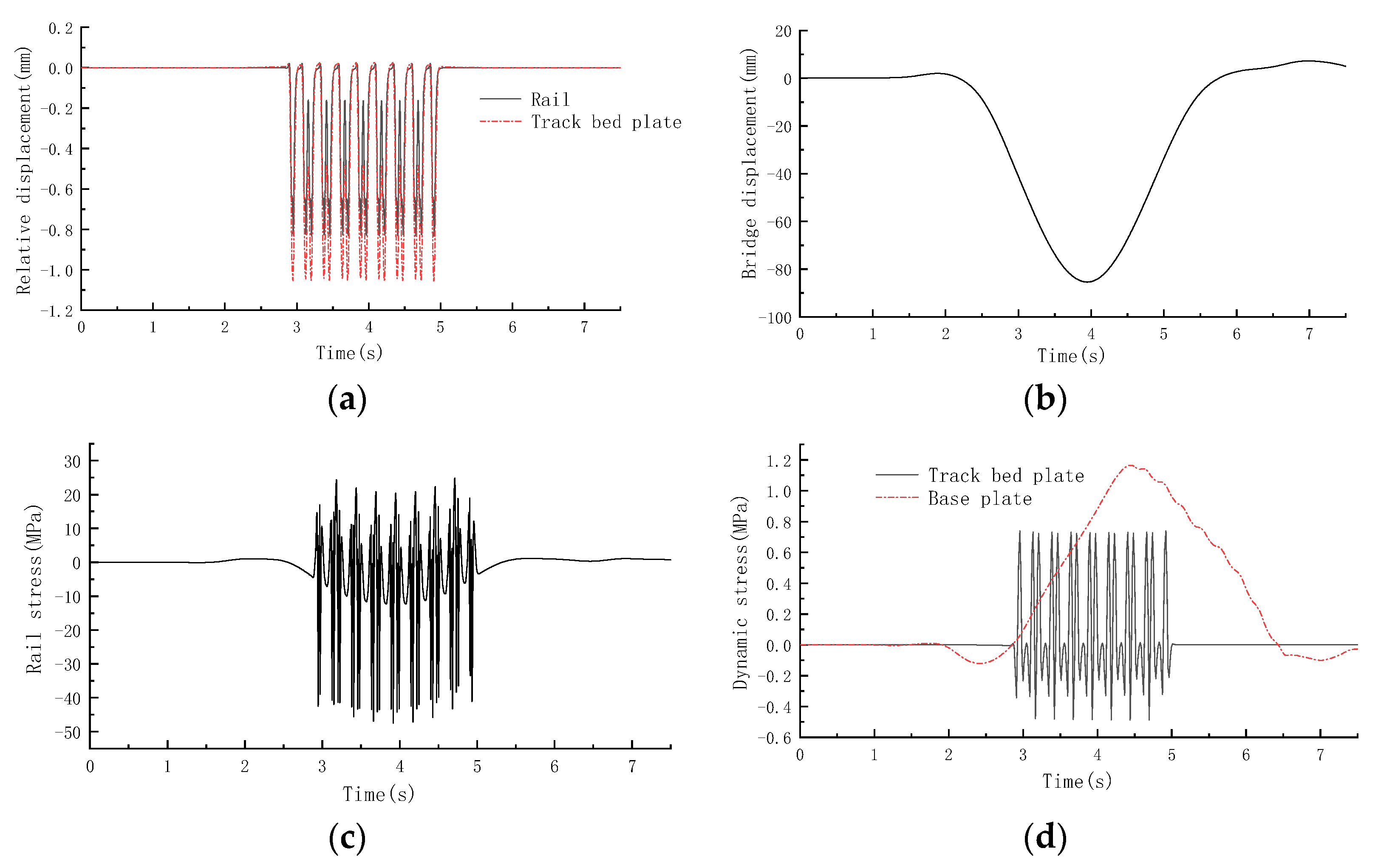
5.2. Dynamic Characteristics of Ballastless Track System on Cable-Stayed Bridge
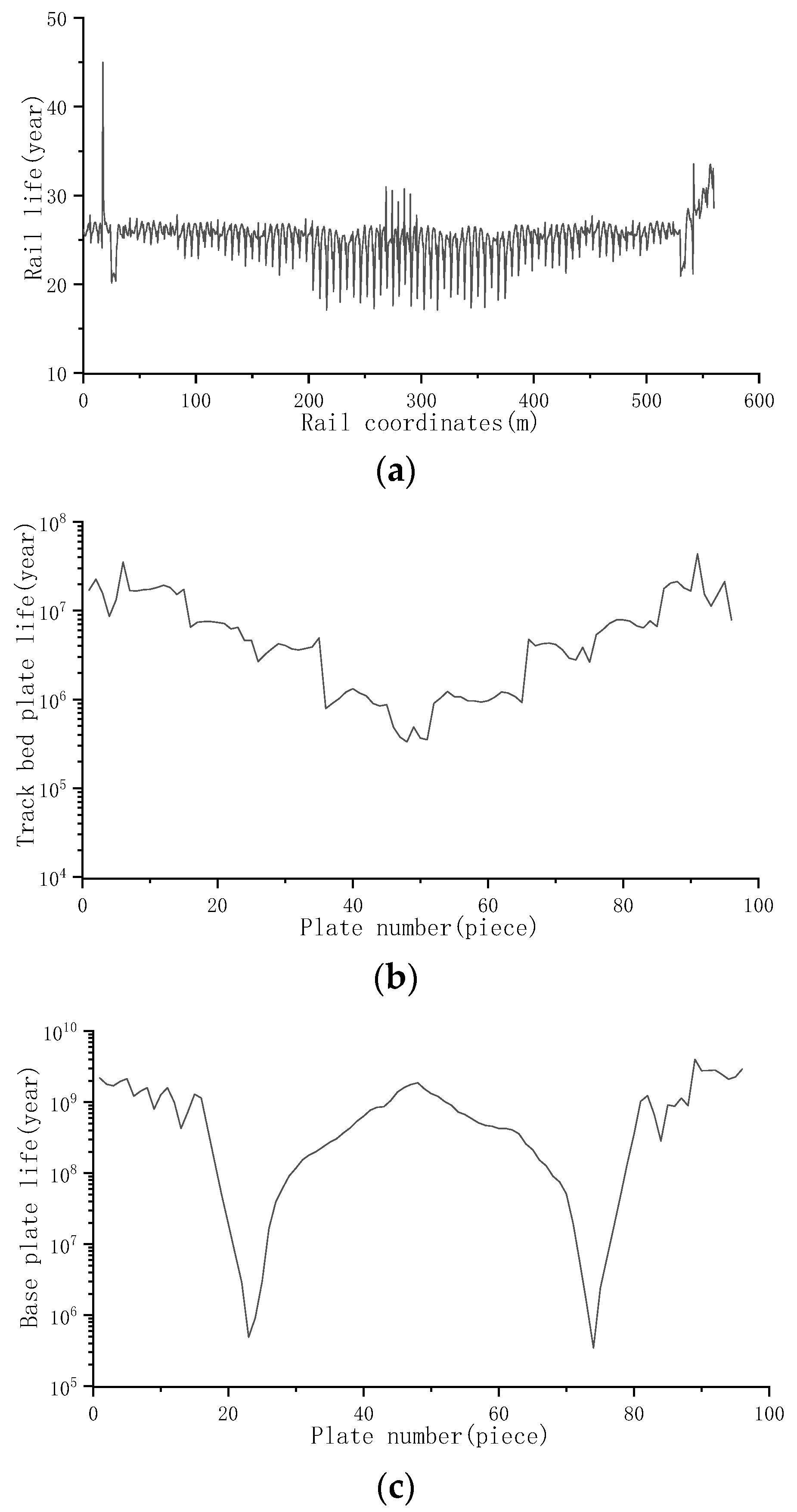
5.3. Fatigue Characteristics of Ballastless Track System on Cable-Stayed Bridge
6. Influence of Key Parameters of Ballastless Track System on Fatigue Characteristics
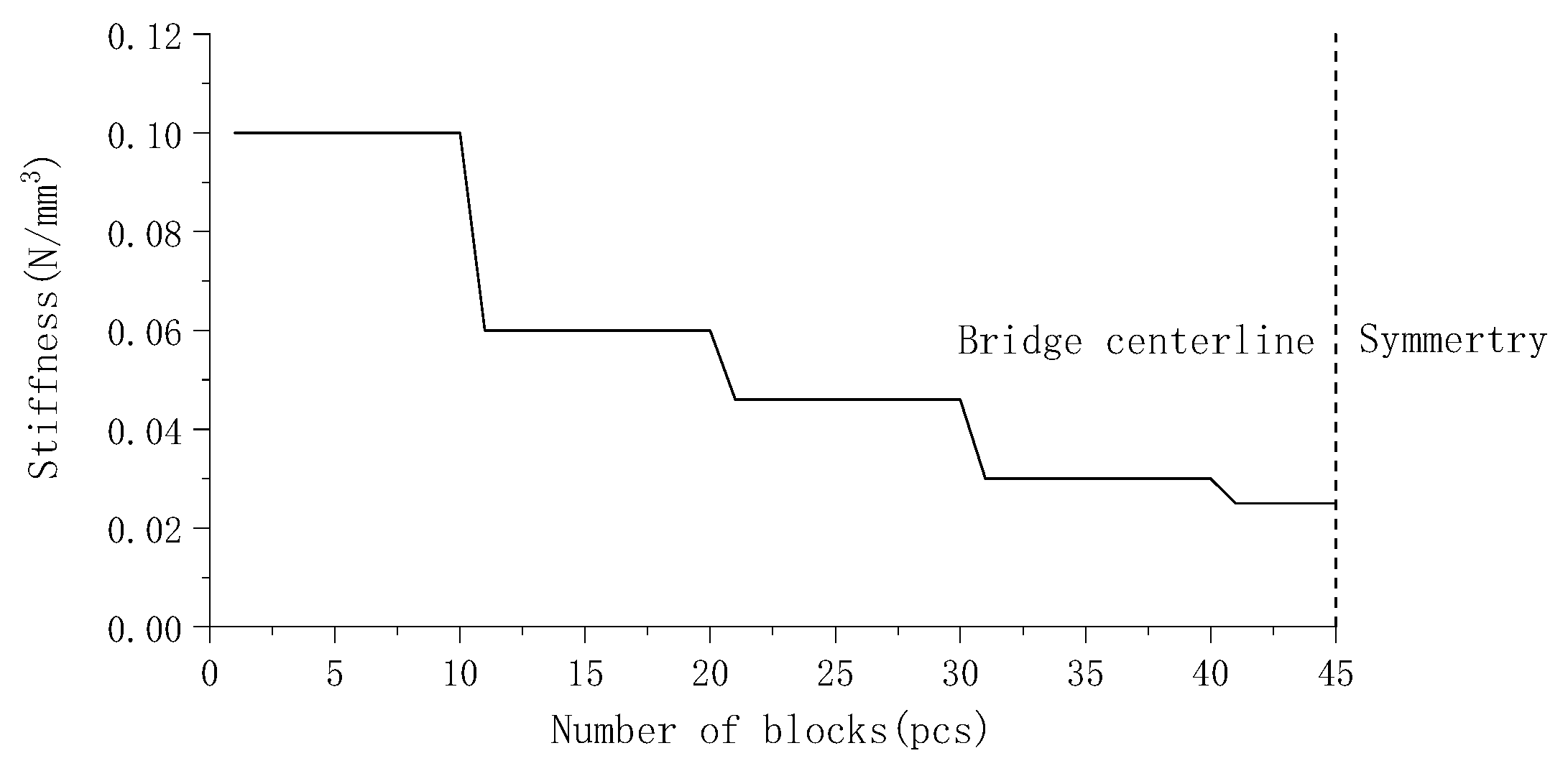
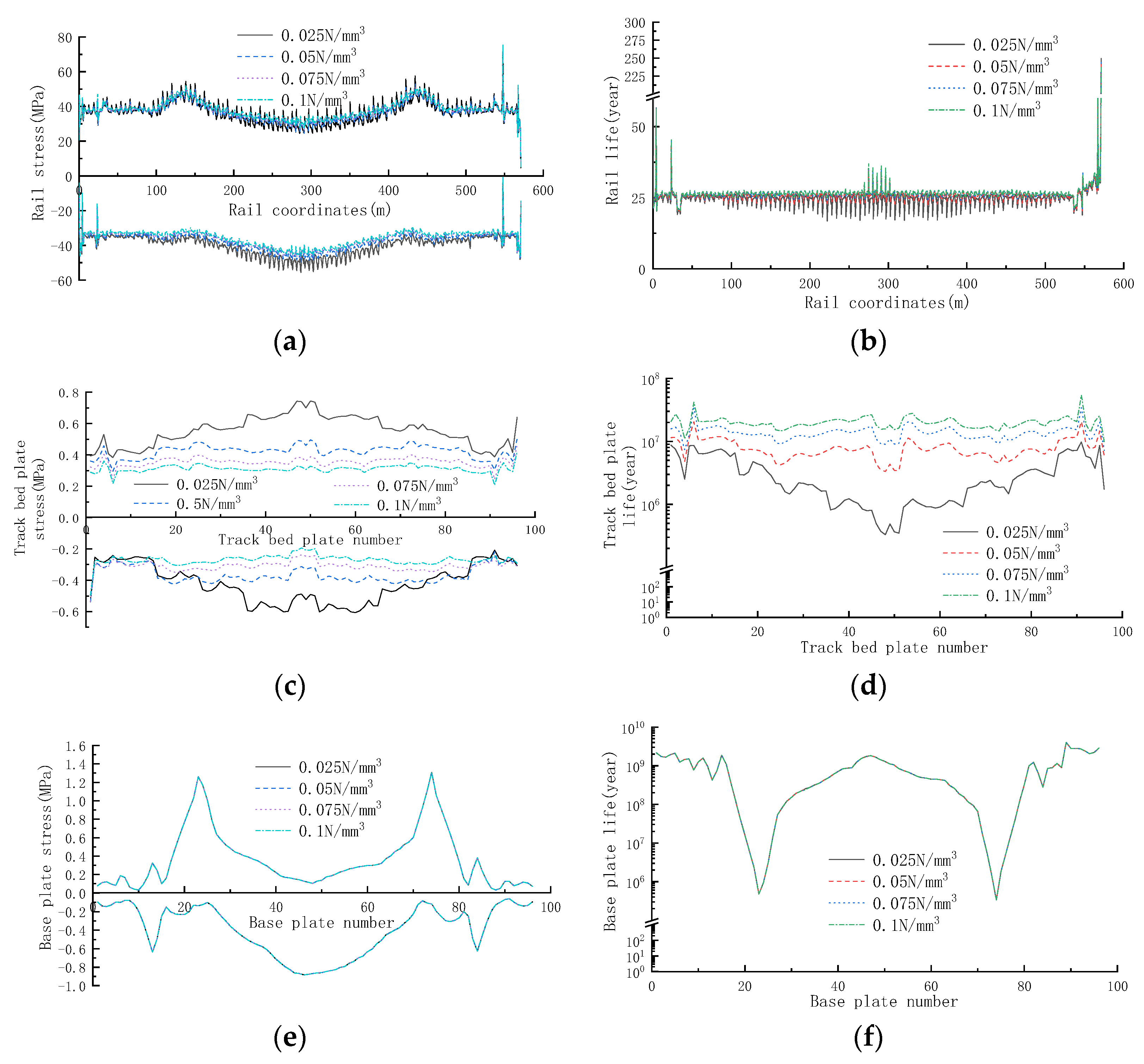
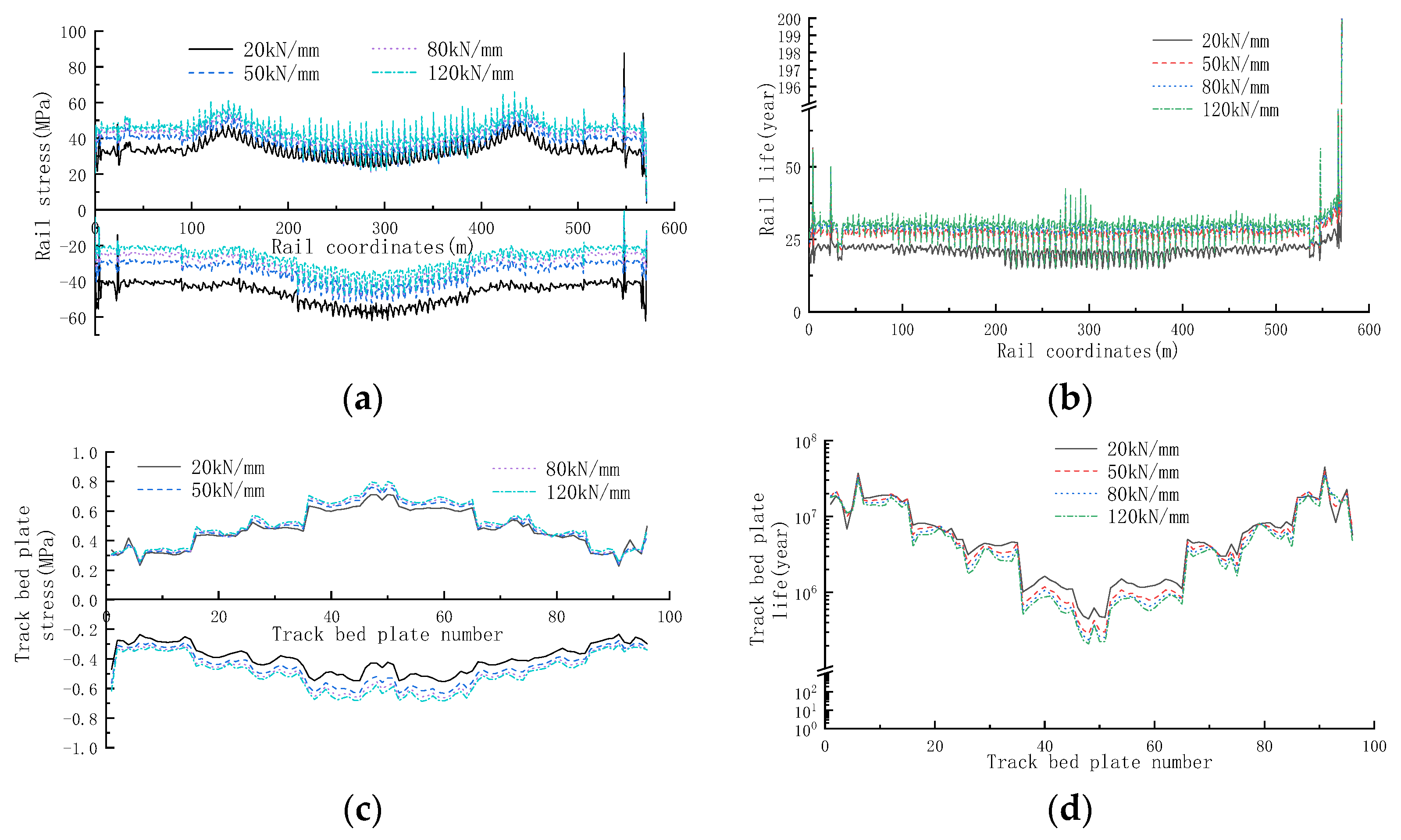
6.1. Stiffness of Elastic Cushion
6.2. Vertical Stiffness of Fastener
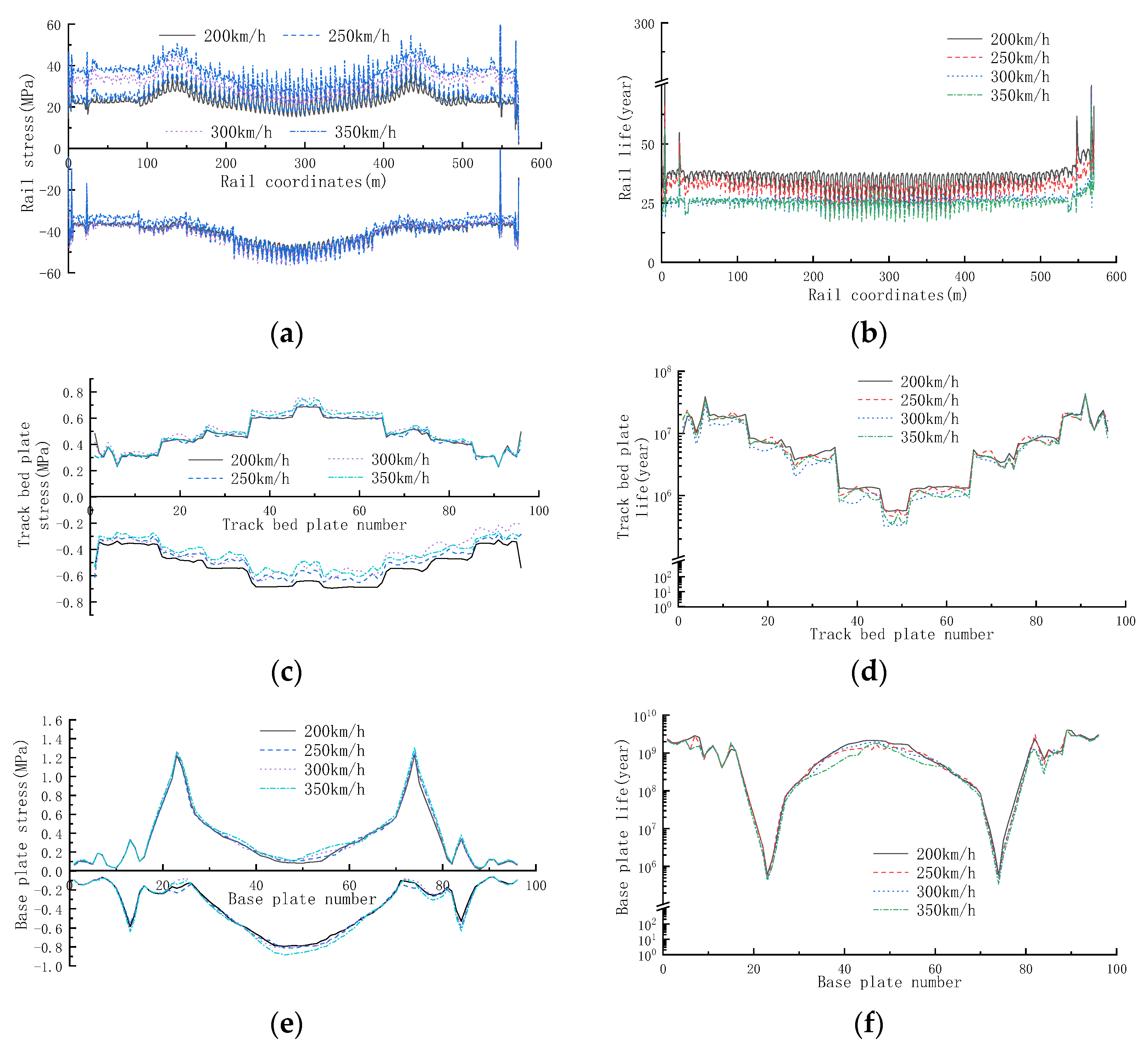
6.3. Train Speed
7. Conclusions
- (1)
- For the bridge ballastless track system, under the action of temperature load, the maximum compressive stress of the steel rail expansion force on the simply supported beam and continuous beam is located near the bridge support, and the maximum tensile stress of the steel rail on the simply supported beam, continuous beam and cable-stayed bridge appears in the middle of the bridge span; Under flexure load, the extreme value of tensile stress of rail flexure is located near the bridge support, and the extreme value of compressive stress is located in the middle of the bridge span; Under the action of braking load, the extreme positions of the tensile and compressive stress of the rail braking force on the simple supported beam and continuous beam are located near the bridge support. The maximum tensile stress of the rail on the cable-stayed bridge appears in the middle of the main beam span, and the maximum compressive stress appears near the bridge tower support.
- (2)
- Under the action of train dynamic load, the service life curve of steel rails on simply supported beams, continuous beams and cable-stayed bridges is relatively smooth. Because the structural system of cable-stayed bridges is relatively flexible, the minimum service life of steel rails is reduced from 27.1 years on continuous beams to 17 years on cable-stayed bridges.
- (3)
- Under the action of train dynamic load, the service life curves of rails and track bed plates on simply supported beams and continuous beams are relatively smooth, and the service life is basically the same. The service life curves of track bed plates on cable-stayed bridges are related to the stiffness of elastic cushion, which decreases step by step. Meanwhile, the track bed plates will not be fatigue damaged during the service period. The life curve of the base plate is related to the bridge. The minimum life occurs near the bridge bearing, and the base plate will not be fatigue damaged during the service period.
- (4)
- The fatigue life of track bed slab can be effectively improved by appropriately increasing the stiffness of elastic cushion. Properly increasing the vertical fastener stiffness can enhance the connection between the rail and the track bed slab, and can improve the rail life but reduce the fatigue life of the track bed slab. The increase of train speed will increase the dynamic stress amplitude of track structure and reduce the fatigue life.
- (1)
- In practical situations, the nonlinear characteristics and uncertainties of the bridge and track system may affect the accuracy of the model. Therefore, it is necessary to further optimize and improve the analysis model to improve the accuracy and reliability of the research.
- (2)
- Reliability analysis can consider uncertain factors and provide more comprehensive and accurate results for the evaluation of the fatigue characteristics of ballastless track structures. However, this paper lacks research on reliability, and thus future research should consider using reliability analysis to evaluate the service life of ballastless track structures and provide reliability design methods.
- (3)
- This paper only considers the dynamic response characteristics of components such as the bridge, ballast mat, base plate, fasteners, and steel rails, while the effects of external environmental factors such as wind and temperature also play an important role. Future research can further explore the impact of multi-field coupling on the fatigue characteristics of ballastless track structures.
- (4)
- In the study of the fatigue characteristics of the long-span bridge-double-block ballastless track system, continuous beam bridges and cable-stayed bridges are chiefly under consideration. Therefore, the research types of long-span bridges can be expanded.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, Y.; Liu, Z.G.; Ronnquist, A.; Navik, P.; Liu, Z.D. Contact Wire Irregularity Stochastics and Effect on High-Speed Railway Pantograph-Catenary Interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Liu, C.; Thompson, D.; Griffin, M.J.; Entezami, M. Effect of train speed and track geometry on the ride comfort in high-speed railways based on ISO 2631-1. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2020, 234, 765–778. [Google Scholar] [CrossRef]
- Dai, G.; Ge, H.; Qiu, Y.; Liu, W. Study on stress of broken slab of ballastless track on long-span continuous beam bridge of high-speed railway. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2015, 43, 100. (In Chinese) [Google Scholar]
- Li, Y.; Su, Y.; Xia, F.; Zhang, N. Vertical dynamic response of the ballastless track on long-span plate-truss cable-stayed bridges. Sci. China-Technol. Sci. 2015, 58, 236–247. [Google Scholar] [CrossRef]
- Wenner, M.; Marx, S.; Koca, M. Additional rail stresses due to long-term deformations of railway viaducts with ballastless track—Model and reality. Bautechnik 2019, 96, 674. [Google Scholar] [CrossRef]
- Yan, B.; Gan, R.; Zhang, G.; Zeng, Z. Study on longitudinal force distribution law of jointless track on kilometer level railway suspension bridge. Railw. Trans. 2021, 43, 130–135. (In Chinese) [Google Scholar]
- Xu, Q.; Lin, Q.; Fang, Z.; Zhang, Z. Fatigue characteristics of longitudinal slab ballastless track on bridge under combined load. China Railw. Sci. 2017, 38, 37. (In Chinese) [Google Scholar]
- Zhu, Z.; Feng, Q.; Gong, W.; Yu, Z. Local fatigue analysis of heavy haul railway steel bridge considering vehicle bridge coupling. J. Railw. Eng. 2019, 36, 36–42, 78. (In Chinese) [Google Scholar]
- Li, S.; Yang, R. Study on fatigue life of CRTS-I slab ballastless track. Railw. Stand. Des. 2016, 60, 34–37. (In Chinese) [Google Scholar]
- Shan, Y.; Wang, B.; Zhang, J.; Zhou, S. The influence of dynamic loading and thermal conditions on tram track slab damage resulting from subgrade differential settlement. Eng. Fail. Anal. 2021, 128, 105610. [Google Scholar] [CrossRef]
- Ren, J.; Tian, G.; Xu, J.; Deng, S.; Xie, P. Load action characteristics and fatigue life prediction of passenger freight mixed unit slab ballastless track. J. Railw. 2019, 41, 110–116. (In Chinese) [Google Scholar]
- Poveda, E.; Rena, C.; Lancha, J.; Ruiz, G. A numerical study on the fatigue life design of concrete slabs for railway tracks. Eng. Struct. 2015, 100, 455–467. [Google Scholar] [CrossRef]
- Qu, C. Research on Design Theory and Method of Ballastless Track Jointless Track for High-Speed Railway Long Bridge. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2013; p. 42. (In Chinese). [Google Scholar]
- Ren, J. Design and Maintenance Theory of Ballastless Track on Bridge; Science Press: Beijing, China, 2015; p. 79. (In Chinese) [Google Scholar]
- Liu, Z.; Wen, W.; Chen, L. Design Innovation and Practice of Railway Hybrid Girder Cable stayed Bridge. J. Railw. Eng. 2019, 36, 30–36. (In Chinese) [Google Scholar]
- Yan, B. Study on the Interaction between Medium and Small Span Bridges and Tracks of High-Speed Railway. Ph.D. Thesis, Central South University, Changsha, China, 2013; p. 24. (In Chinese). [Google Scholar]
- Zhai, W.; Xia, H. Theory and Engineering Application of Train Track Bridge Dynamic Interaction; Science Press: Beijing, China, 2011; p. 174. (In Chinese) [Google Scholar]
- Liu, J.; Wei, Q. Fatigue life prediction of high-speed railway rails. J. Railw. Eng. 2000, 30–34. (In Chinese) [Google Scholar]
- Gong, J. Basic Theory and Application of Modern Concrete Structure; China Architecture Press: Beijing, China, 2009; p. 4. (In Chinese) [Google Scholar]
- TB 10002-2017; Code for Design of Railway Bridges and Culverts. China Railway Press: Beijing, China, 2017; p. 132. (In Chinese)
- Yan, B.; Xie, H.; Pan, W.; Dai, G. Dynamic characteristics of train ballastless track bridge system considering track damage. J. Vib. Eng. 2020, 33, 807–814. (In Chinese) [Google Scholar]
- TB 10082-2017; Code for Design of Railway Track. China Railway Press: Beijing, China, 2017; p. 26. (In Chinese)
- TB 10015-2012; Code for Design of Railway Seamless Track. China Railway Press: Beijing, China, 2013; p. 59. (In Chinese)



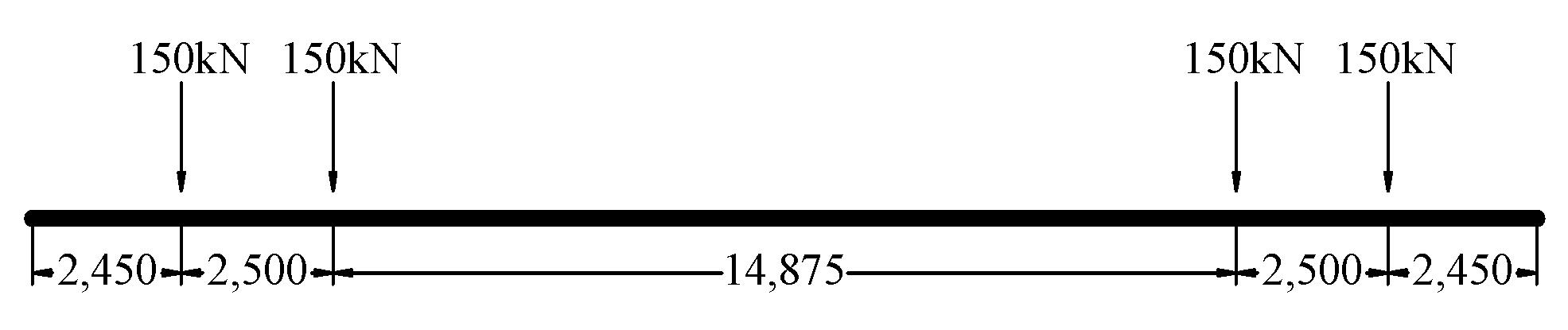

| Item | Expansion Force | Flexural Force | Braking Force | ||||||
|---|---|---|---|---|---|---|---|---|---|
| UIC | Example | Error | UIC | Example | Error | UIC | Example | Error | |
| Track stress at fixed support (MPa) | 8.00 | 7.83 | 2.13% | 30.60 | 30.71 | 0.36% | 28.00 | 27.36 | 2.29% |
| Track stress at sliding support (MPa) | −26.00 | −25.62 | 1.46% | −10.80 | −10.29 | 4.72% | −28.00 | −27.83 | 0.61% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, B.; Tian, J.; Huang, J.; Lou, P. Fatigue Characteristics of Long-Span Bridge-Double Block Ballastless Track System. Mathematics 2023, 11, 1792. https://doi.org/10.3390/math11081792
Yan B, Tian J, Huang J, Lou P. Fatigue Characteristics of Long-Span Bridge-Double Block Ballastless Track System. Mathematics. 2023; 11(8):1792. https://doi.org/10.3390/math11081792
Chicago/Turabian StyleYan, Bin, Jianghao Tian, Jie Huang, and Ping Lou. 2023. "Fatigue Characteristics of Long-Span Bridge-Double Block Ballastless Track System" Mathematics 11, no. 8: 1792. https://doi.org/10.3390/math11081792
APA StyleYan, B., Tian, J., Huang, J., & Lou, P. (2023). Fatigue Characteristics of Long-Span Bridge-Double Block Ballastless Track System. Mathematics, 11(8), 1792. https://doi.org/10.3390/math11081792







