Heat Transfer Enhancement of MHD Natural Convection in a Star-Shaped Enclosure, Using Heated Baffle and MWCNT–Water Nanofluid
Abstract
1. Introduction
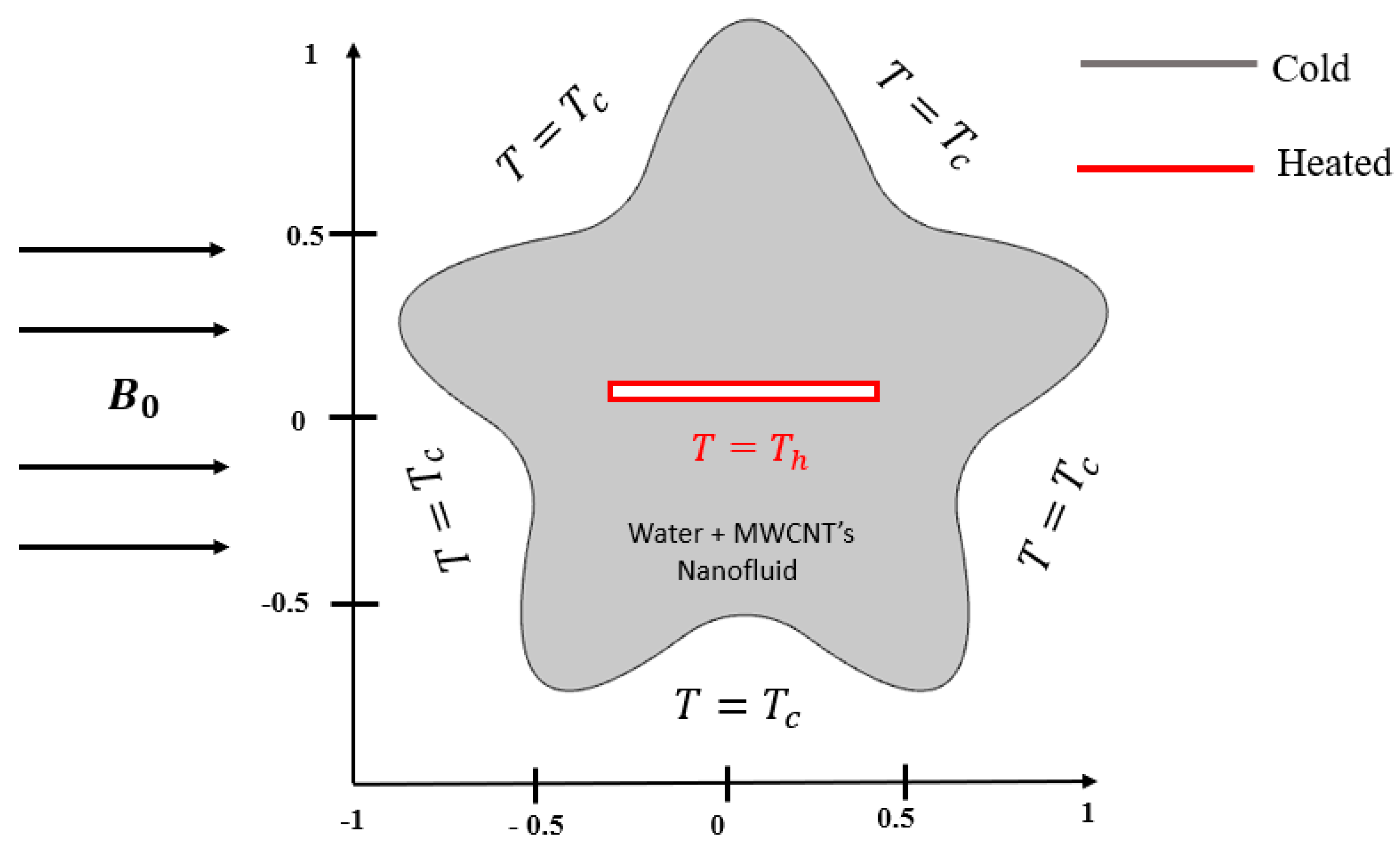
2. Problem Formulation
Mathematical Formulation
3. Solution Methodology
3.1. Discretization of Modeled Equations
3.2. Weak Formulation
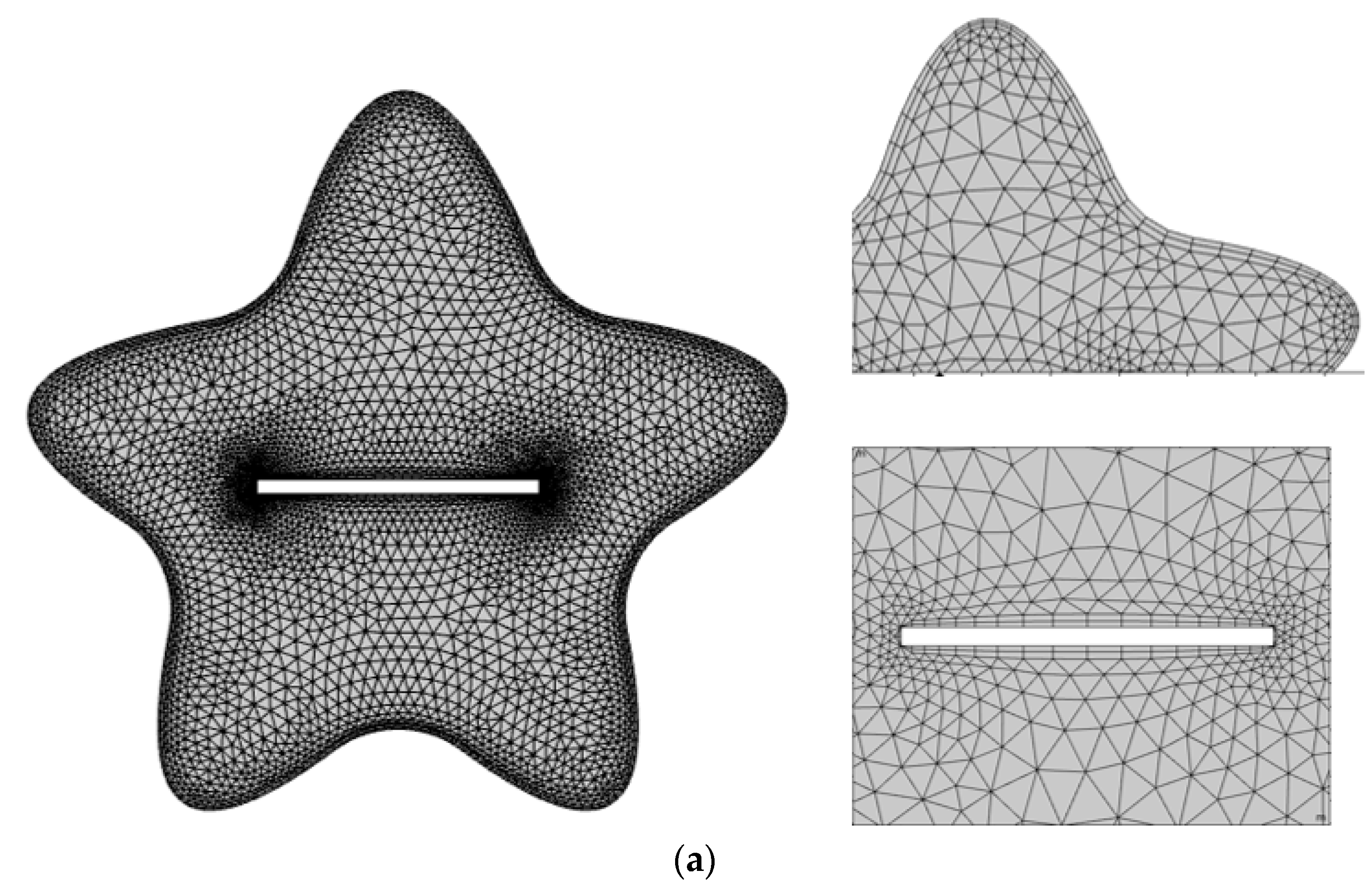
3.3. Grid Generation
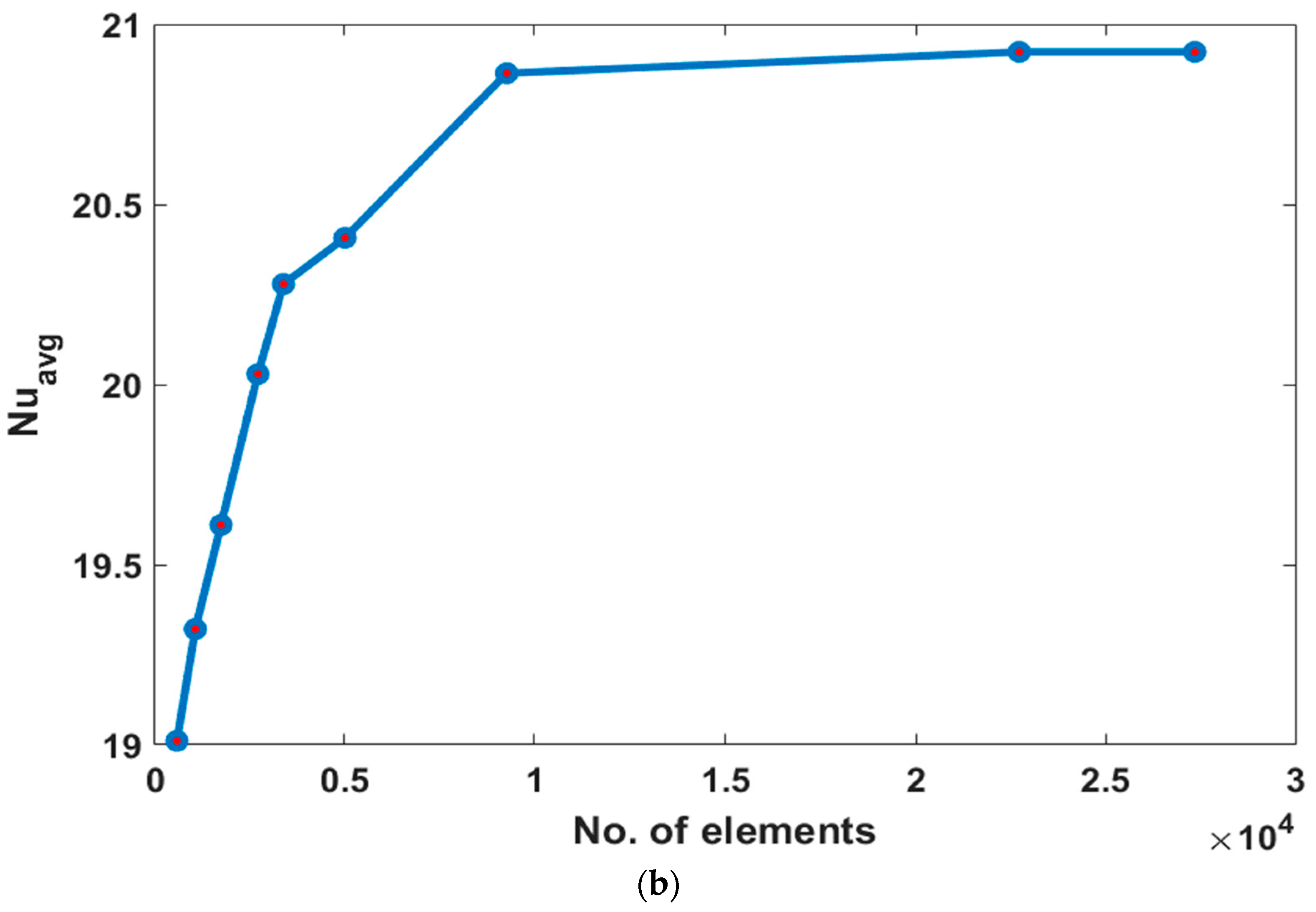
Grid Independence Test
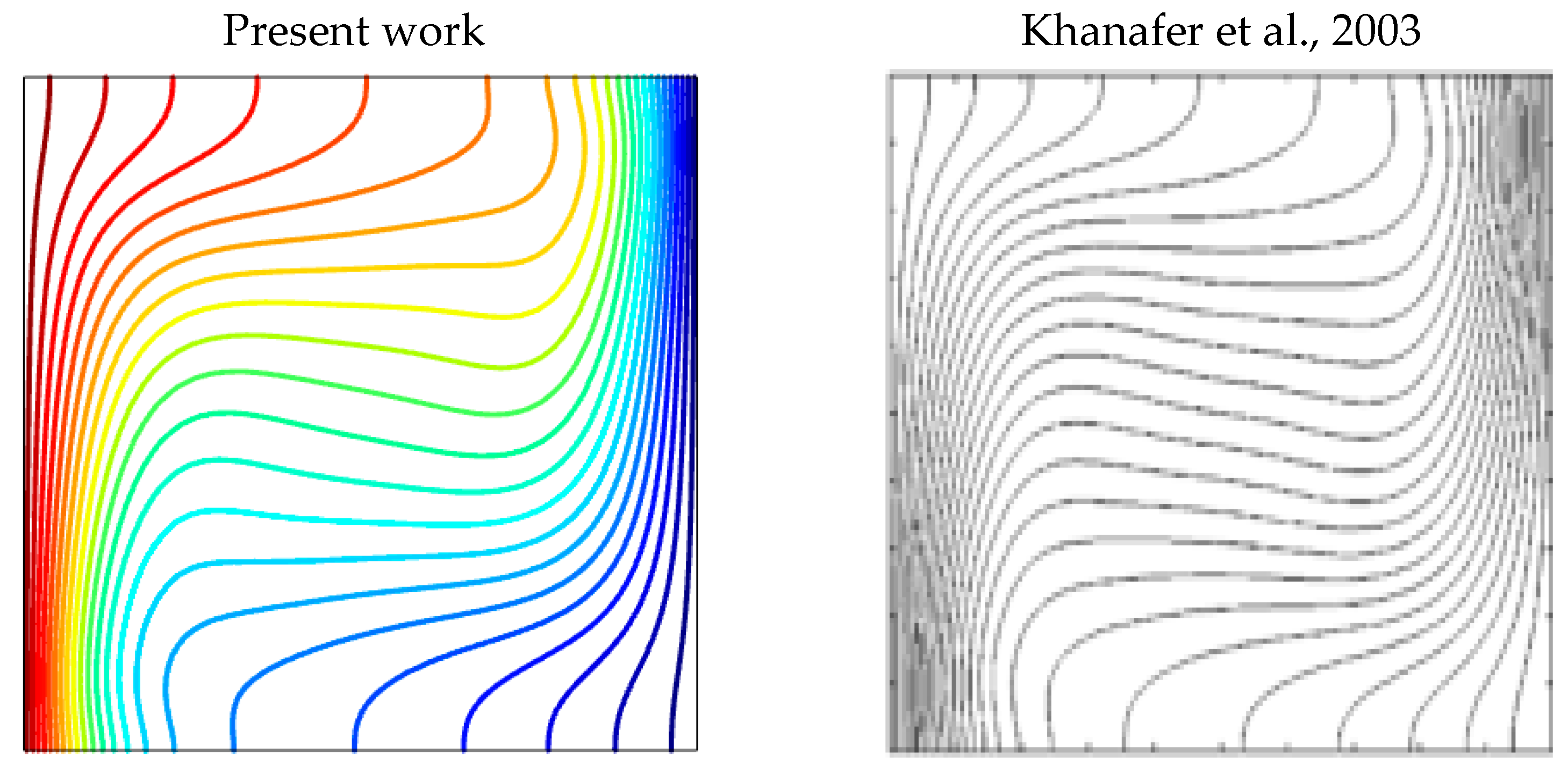
3.4. Verification of the Numerical Model
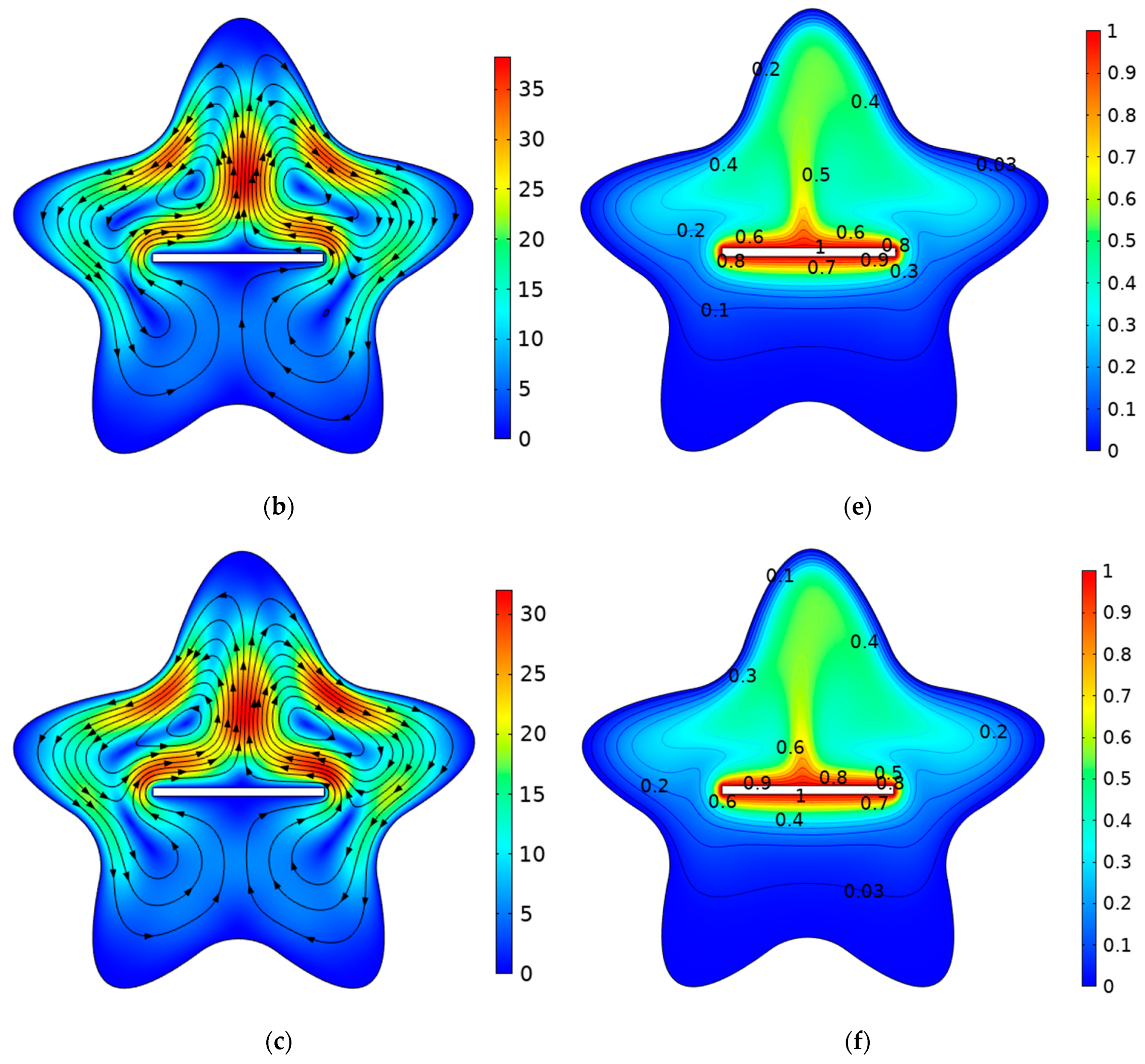
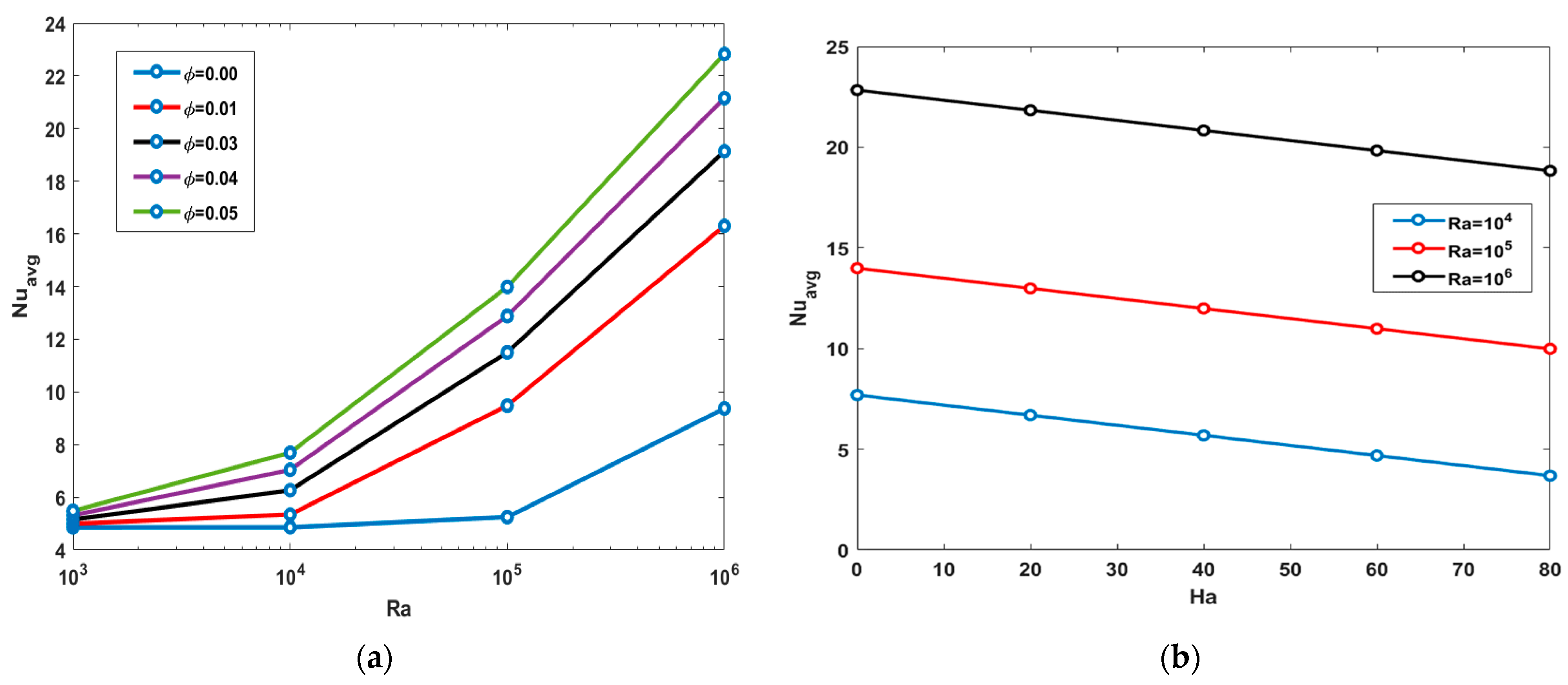
4. Results and Discussions
5. Conclusions
- An intensification in flow circulation occurs when increasing the Rayleigh number due to the enhancement of the convective heat transfer.
- The increase in the magnitude of the magnetic field causes a reduction in the velocity of the fluid due to the generated Lorentz force, which opposes the convective flow.
- The addition of nanoparticles augments the heat transfer rate due to the enhancement of the thermophysical properties, and the highest value of the average Nusselt number occurs for .
- The use of the MWCNTs increases the flow intensity due to the enhancement of the buoyancy force.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Laboratory (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Das, S.K.; Choi, S.U.; Patel, H.E. Heat transfer in nanofluids—A review. Heat Transf. Eng. 2006, 27, 3–19. [Google Scholar] [CrossRef]
- Ho, C.; Chen, M.; Li, Z. Numerical simulation of natural convection of nanofluid in a square enclosure: Effects due to uncertainties of viscosity and thermal conductivity. Int. J. Heat Mass Transf. 2008, 51, 4506–4516. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Bouchoucha, A.E.M.; Bessaïh, R. Natural convection in a square cavity filled with nanofluids. Fluid Dyn. Mater. Process. 2015, 11, 279–300. [Google Scholar]
- Duangthongsuk, W.; Wongwises, S. Heat transfer enhancement and pressure drop characteristics of TiO2–water nanofluid in a double-tube counter flow heat exchanger. Int. J. Heat Mass Transf. 2009, 52, 2059–2067. [Google Scholar] [CrossRef]
- Tasnim, S.H.; Collins, M.R. Numerical analysis of heat transfer in a square cavity with a baffle on the hot wall. Int. Commun. Heat Mass Transf. 2004, 31, 639–650. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Numerical investigation of MHD effects on Al2O3–water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy 2013, 60, 501–510. [Google Scholar] [CrossRef]
- Boulahia, Z.; Wakif, A.; Sehaqui, R. Numerical Investigation of Mixed Convection Heat Transfer of Nanofluid in a Lid Driven Square Cavity with Three Triangular Heating Blocks. Int. J. Comput. Appl. 2016, 143, 37–45. [Google Scholar] [CrossRef]
- Mejri, I.; Mahmoudi, A.; Abbassi, M.A.; Omri, A. Magnetic field effect on entropy generation in a nanofluid-filled enclosure with sinusoidal heating on both side walls. Powder Technol. 2014, 266, 340–353. [Google Scholar] [CrossRef]
- Garoosi, F.; Hoseininejad, F.; Rashidi, M.M. Numerical study of natural convection heat transfer in a heat exchanger filled with nanofluids. Energy 2016, 109, 664–678. [Google Scholar] [CrossRef]
- Armaghani, T.; Kasaeipoor, A.; Alavi, N.; Rashidi, M. Numerical investigation of water-alumina nanofluid natural convection heat transfer and entropy generation in a baffled L-shaped cavity. J. Mol. Liq. 2016, 223, 243–251. [Google Scholar] [CrossRef]
- Motlagh, S.Y.; Taghizadeh, S.; Soltanipour, H. Natural convection heat transfer in an inclined square enclosure filled with a porous medium saturated by nanofluid using Buongiorno’s mathematical model. Adv. Powder Technol. 2016, 27, 2526–2540. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Jafari, M.; Farhadi, M.; Akbarzade, S.; Ebrahimi, M. Lattice Boltzmann simulation of natural convection heat transfer of SWCNT-nanofluid in an open enclosure. Ain Shams Eng. J. 2015, 6, 913–927. [Google Scholar] [CrossRef]
- Arani, A.A.A.; Akbari, O.A.; Safaei, M.R.; Marzban, A.; Alrashed, A.A.; Ahmadi, G.R.; Nguyen, T.K. Heat transfer improvement of water/single-wall carbon nanotubes (SWCNT) nanofluid in a novel design of a truncated double-layered microchannel heat sink. Int. J. Heat Mass Transf. 2017, 113, 780–795. [Google Scholar] [CrossRef]
- Ben Said, L.; Kolsi, L.; Ben Khedher, N.; Alshammari, F.; Malekshah, E.; Hussein, A. Numerical Study of the Fluid-Structure Interaction During CNT-Water Nanofluid Mixed Convection in a Micro-Channel Equipped with Elastic Fins Under Periodic Inlet Velocity Conditions. Exp. Tech. 2021, 47, 7–15. [Google Scholar] [CrossRef]
- Farooq, W.; Abbasi, A.; Al-Khaled, K.; Ghachem, K.; Khan, S.U.; Ahmad, I.; Kolsi, L. Thermal aspect of boron nitride nanotubes (BNNT) and multiwall carbon nanotubes (MWCNT) with distinct physical features: Keller Box simulations. J. Appl. Math. Mech. (ZAMM-Z. Fur Angew. Math. Und Mech.) 2022, 102, e202100560. [Google Scholar] [CrossRef]
- Cao, Y.; Ayed, H.; Jarad, F.; Togun, H.; Alias, H.; Issakhov, A.; Dahari, M.; Wae-Hayee, M.; El Ouni, M.H. MHD natural convection nanofluid flow in a heat exchanger: Effects of Brownian motion and thermophoresis for nanoparticles distribution. Case Stud. Therm. Eng. 2021, 28, 101394. [Google Scholar] [CrossRef]
- Haritha, C.; Shekar, B.C.; Kishan, N. MHD Natural Convection Heat Transfer in a Porous Square Cavity Filled by Nanofluids with Viscous Dissipation. J. Nanofluids 2018, 7, 928–938. [Google Scholar] [CrossRef]
- Redouane, F.; Jamshed, W.; Devi, S.; Prakash, M.; Nasir, N.A.A.M.; Hammouch, Z.; Eed, E.M. Heat flow saturate of Ag/MgO-water hybrid nanofluid in heated trigonal enclosure with rotate cylindrical cavity by using Galerkin finite element. Sci. Rep. 2022, 12, 1–20. [Google Scholar] [CrossRef]
- Sannad, M.; Hussein, A.K.; Abidi, A.; Homod, R.Z.; Biswal, U.; Ali, B.; Kolsi, L.; Younis, O. Numerical Study of MHD Natural Convection inside a Cubical Cavity Loaded with Copper-Water Nanofluid by Using a Non-Homogeneous Dynamic Mathematical Model. Mathematics 2022, 10, 2072. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Dogonchi, A.; Ganji, D. Magnetohydrodynamic Nanofluid Natural Convection in a Cavity under Thermal Radiation and Shape Factor of Nanoparticles Impacts: A Numerical Study Using CVFEM. Appl. Sci. 2018, 8, 2396. [Google Scholar] [CrossRef]
- Hussam, W.K.; Khanafer, K.; Salem, H.J.; Sheard, G.J. Natural convection heat transfer utilizing nanofluid in a cavity with a periodic side-wall temperature in the presence of a magnetic field. Int. Commun. Heat Mass Transf. 2019, 104, 127–135. [Google Scholar] [CrossRef]
- Vijay, N.; Sharma, K. Magnetohydrodynamic hybrid nanofluid flow over a decelerating rotating disk with Soret and Dufour effects. Multidiscip. Model. Mater. Struct. 2023, 19, 253–276. [Google Scholar] [CrossRef]
- Sharma, K. FHD flow and heat transfer over a porous rotating disk accounting for Coriolis force along with viscous dissipation and thermal radiation. Heat Transf. 2022, 51, 4377–4392. [Google Scholar] [CrossRef]
- Ram, P.; Kumar, V. Revolving Ferrofluid Flow in Porous Medium with Rotating Disk. Int. J. Aerosp. Mech. Eng. 2013, 7, 1664–1669. [Google Scholar]
- Hussain, S.H.; Hussein, A.K. Numerical investigation of natural convection phenomena in a uniformly heated circular cylinder immersed in square enclosure filled with air at different vertical locations. Int. Commun. Heat Mass Transf. 2010, 37, 1115–1126. [Google Scholar] [CrossRef]
- Bararnia, H.; Soleimani, S.; Ganji, D. Lattice Boltzmann simulation of natural convection around a horizontal elliptic cylinder inside a square enclosure. Int. Commun. Heat Mass Transf. 2011, 38, 1436–1442. [Google Scholar] [CrossRef]
- De, A.K.; Dalal, A. A numerical study of natural convection around a square, horizontal, heated cylinder placed in an enclosure. Int. J. Heat Mass Transf. 2006, 49, 4608–4623. [Google Scholar] [CrossRef]
- Lee, J.; Ha, M.; Yoon, H. Natural convection in a square enclosure with a circular cylinder at different horizontal and diagonal locations. Int. J. Heat Mass Transf. 2010, 53, 5905–5919. [Google Scholar] [CrossRef]
- Kim, B.; Lee, D.; Ha, M.; Yoon, H. A numerical study of natural convection in a square enclosure with a circular cylinder at different vertical locations. Int. J. Heat Mass Transf. 2008, 51, 1888–1906. [Google Scholar] [CrossRef]
- Kim, M.; Doo, J.H.; Park, Y.G.; Yoon, H.S.; Ha, M.Y. Natural convection in a square enclosure with a circular cylinder according to the bottom wall temperature variation. J. Mech. Sci. Technol. 2014, 28, 5013–5025. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Sabour, M.; Pop, I.; Wen, D. Free convection heat transfer of MgO-MWCNTs/EG hybrid nanofluid in a porous complex shaped cavity with MHD and thermal radiation effects. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4349–4376. [Google Scholar] [CrossRef]
- Izadi, M.; Mohebbi, R.; Karimi, D.; Sheremet, M.A. Numerical simulation of natural convection heat transfer inside a┴ shaped cavity filled by a MWCNT-Fe3O4/water hybrid nanofluids using LBM. Chem. Eng. Process.-Process Intensif. 2018, 125, 56–66. [Google Scholar] [CrossRef]
- Ghasemi, B. Magnetohydrodynamic Natural Convection of Nanofluids in U-shaped Enclosures. Numer. Heat Transf. Part A Appl. 2013, 63, 473–487. [Google Scholar] [CrossRef]
- Pirmohammadi, M.; Ghassemi, M.; Sheikhzadeh, G.A. The effect of a magnetic field on buoyancy-driven convection in differentially heated square cavity. In Proceedings of the 2008 14th Symposium on Electromagnetic Launch Technology, Victoria, BC, Canada, 10–13 June 2008; pp. 1–6. [Google Scholar]
- Corcione, M. Heat transfer features of buoyancy-driven nanofluids inside rectangular enclosures differentially heated at the sidewalls. Int. J. Therm. Sci. 2010, 49, 1536–1546. [Google Scholar] [CrossRef]
- Haddad, Z.; Oztop, H.F.; Abu-Nada, E.; Mataoui, A. A review on natural convective heat transfer of nanofluids. Renew. Sustain. Energy Rev. 2012, 16, 5363–5378. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873; Volume 1. [Google Scholar]
- Brinkman, H.C. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 1952, 20, 571. [Google Scholar] [CrossRef]
- Lyster, P.; Bergman, L.; Li, P.; Stanfill, D.; Crippe, B.; Blom, R.; Okaya, D. CASA gigabit supercomputing network: CALCRUST three-dimensional real-time multi-dataset rendering. Proc. Supercomput. 1992, 16, 3–37. [Google Scholar] [CrossRef]




| Pure water | 997.1 | 4179 | 0.613 | ||
| MWCNT | 2100 | 711 | 3000 |
| Present Work | Khanafer et al. [4] | |
|---|---|---|
| 4.0921 | 4.0975 | |
| .04 | 4.4598 | 4.4634 |
| 4.6938 | 4.6829 |
| ϕ | % | |
|---|---|---|
| 0 | 4.8425 | --- |
| 0.01 | 5.3400 | 10.27% |
| 0.03 | 7.0387 | 31.81% |
| 0.04 | 9.6903 | 37.45% |
| 0.05 | 14.2643 | 47.85% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, S.; Shah, I.A.; Ghachem, K.; Aydi, A.; Kolsi, L. Heat Transfer Enhancement of MHD Natural Convection in a Star-Shaped Enclosure, Using Heated Baffle and MWCNT–Water Nanofluid. Mathematics 2023, 11, 1849. https://doi.org/10.3390/math11081849
Bilal S, Shah IA, Ghachem K, Aydi A, Kolsi L. Heat Transfer Enhancement of MHD Natural Convection in a Star-Shaped Enclosure, Using Heated Baffle and MWCNT–Water Nanofluid. Mathematics. 2023; 11(8):1849. https://doi.org/10.3390/math11081849
Chicago/Turabian StyleBilal, Sardar, Imtiaz Ali Shah, Kaouther Ghachem, Abdelkarim Aydi, and Lioua Kolsi. 2023. "Heat Transfer Enhancement of MHD Natural Convection in a Star-Shaped Enclosure, Using Heated Baffle and MWCNT–Water Nanofluid" Mathematics 11, no. 8: 1849. https://doi.org/10.3390/math11081849
APA StyleBilal, S., Shah, I. A., Ghachem, K., Aydi, A., & Kolsi, L. (2023). Heat Transfer Enhancement of MHD Natural Convection in a Star-Shaped Enclosure, Using Heated Baffle and MWCNT–Water Nanofluid. Mathematics, 11(8), 1849. https://doi.org/10.3390/math11081849







