Coordinated Slip Control of Multi-Axle Distributed Drive Vehicle Based on HLQR
Abstract
:1. Introduction
- (1)
- The HLQR method is expanded to a 12 × 12 MADD vehicle, where the 12-wheel driving system is decoupled according to the static wheel load and simplified to a double local subsystem. The front four wheels with a small vertical load are simplified to a local system, and the rear eight wheels with a large vertical load are simplified to another local system. The complexity of the longitudinal dynamics system for 12 wheels is reduced significantly;
- (2)
- The coordination of anti-slip control and torque distribution is proposed. By adopting the wheel-slipping state as a constraint, the torque distribution can be regulated based on the feedback.
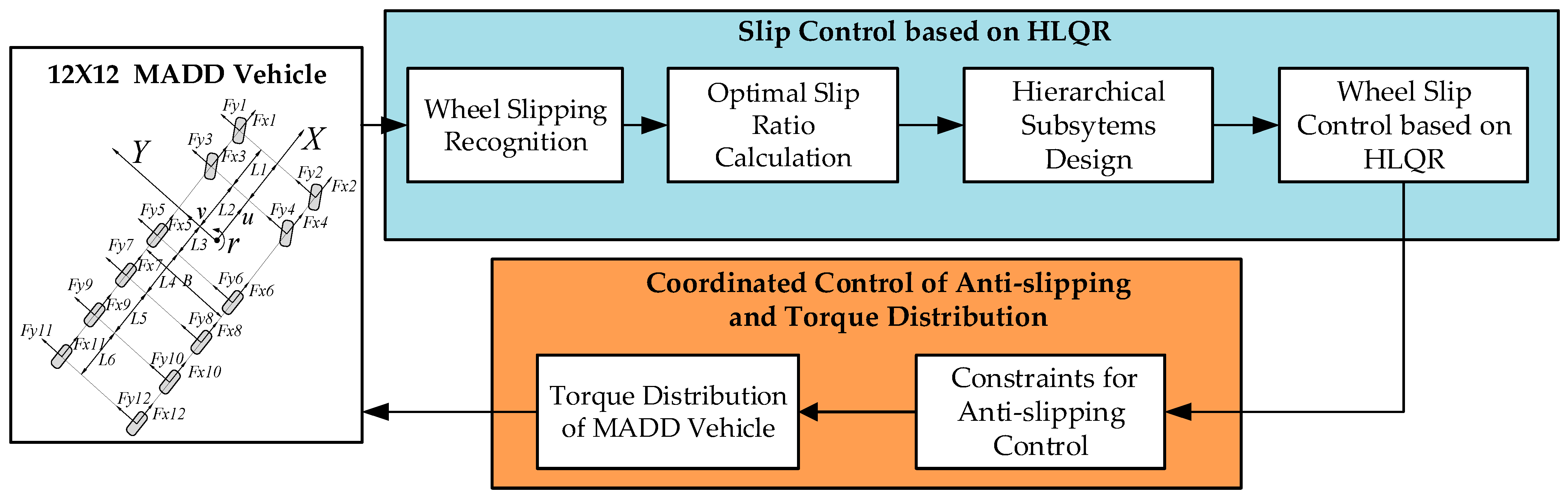
2. Control Framework and MADD Vehicle Model
2.1. Framework of Coordinated Slip Control
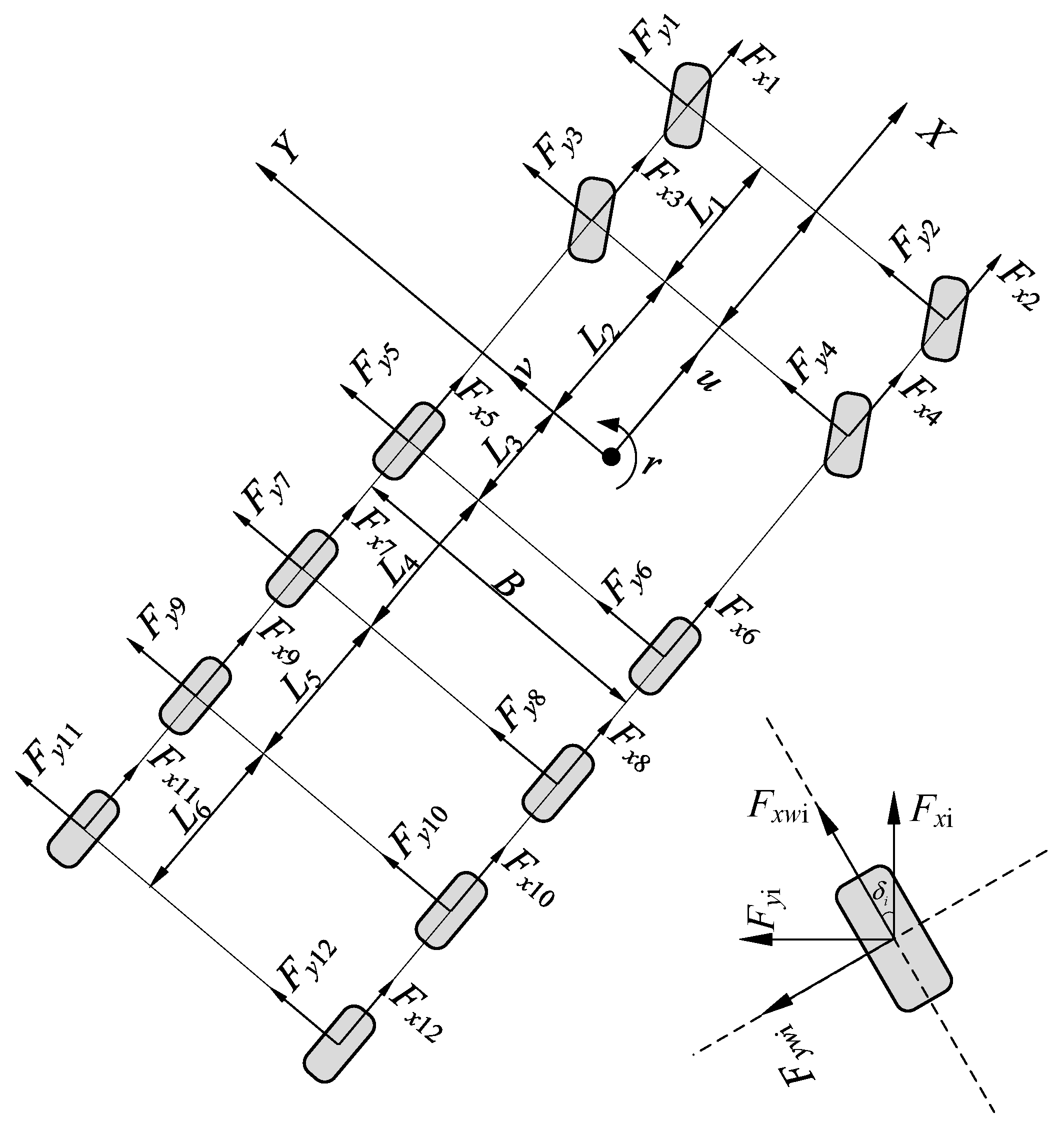
2.2. Modeling of the MADD Vehicle
3. Slip Control Based on HLQR
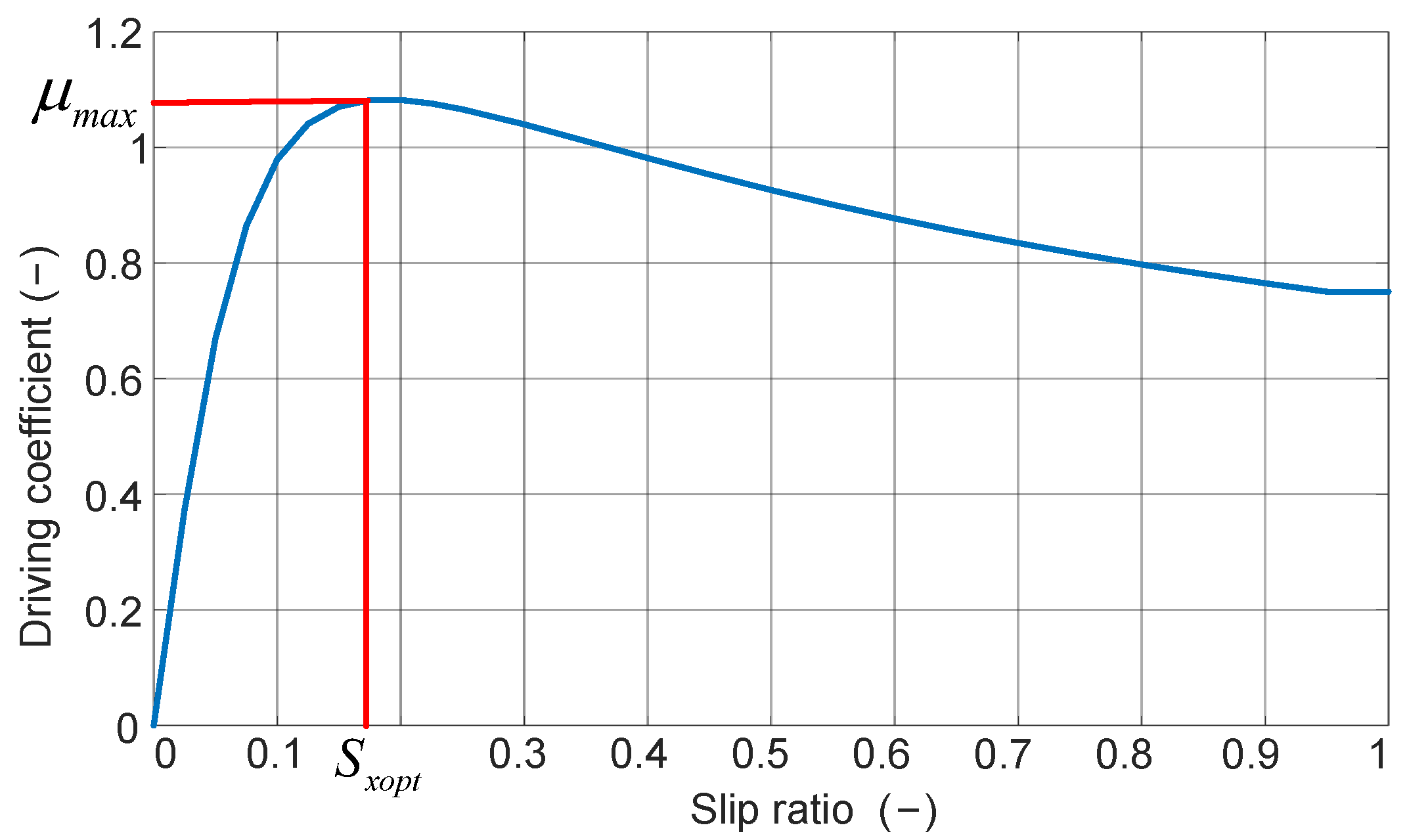
3.1. Calculation of the Optimal Slip Ratio
3.2. Modeling of MADD Driving System
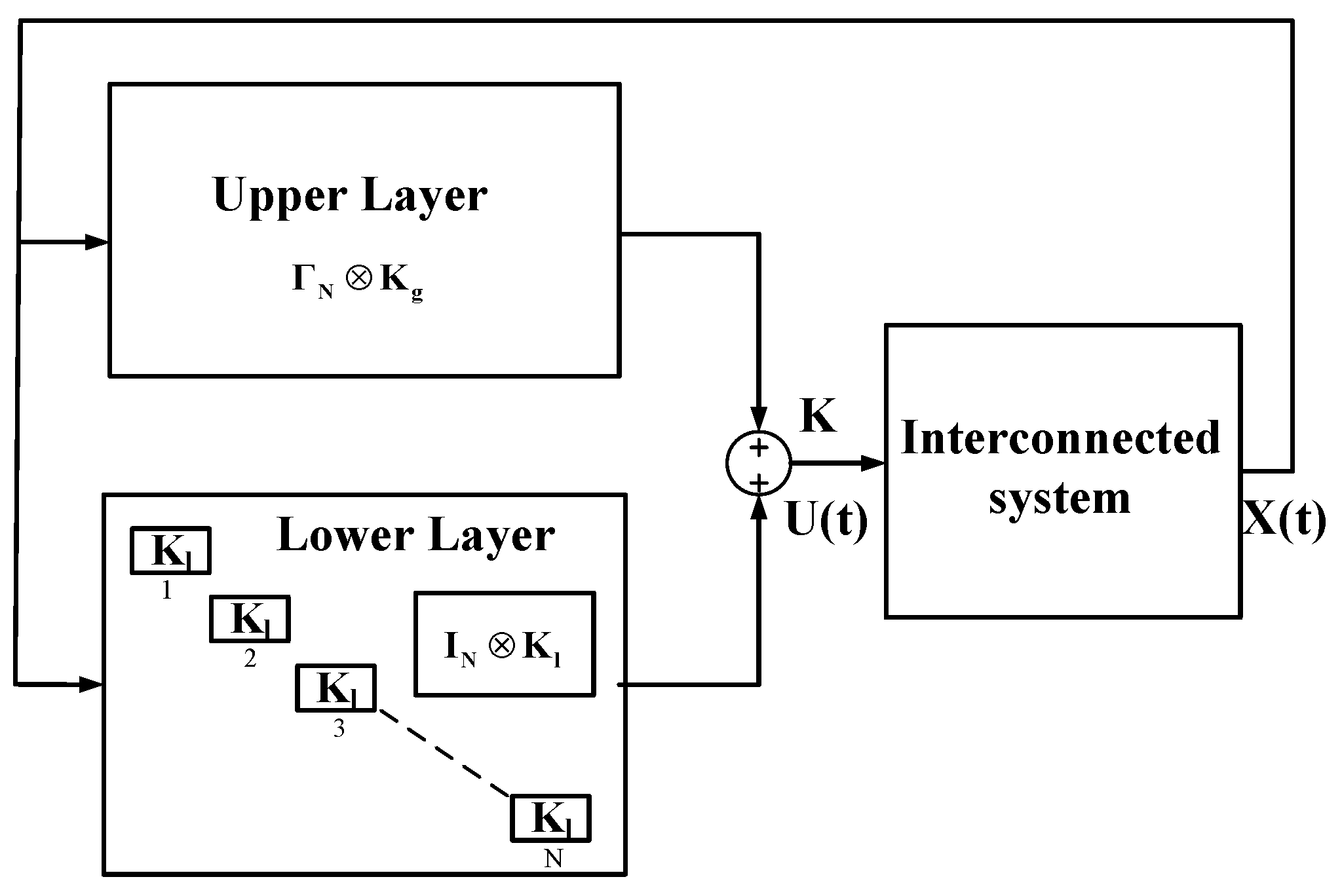
3.3. Design of the HLQR Control System
| Algorithm 1: HLQR Algorithm |
|
|
|
|
| Return: ,. |
4. Torque Control Allocation Based on QP
4.1. Cost Function of Torque Control Allocation Problem
4.2. Constraints for Coordinated Control with HLQR
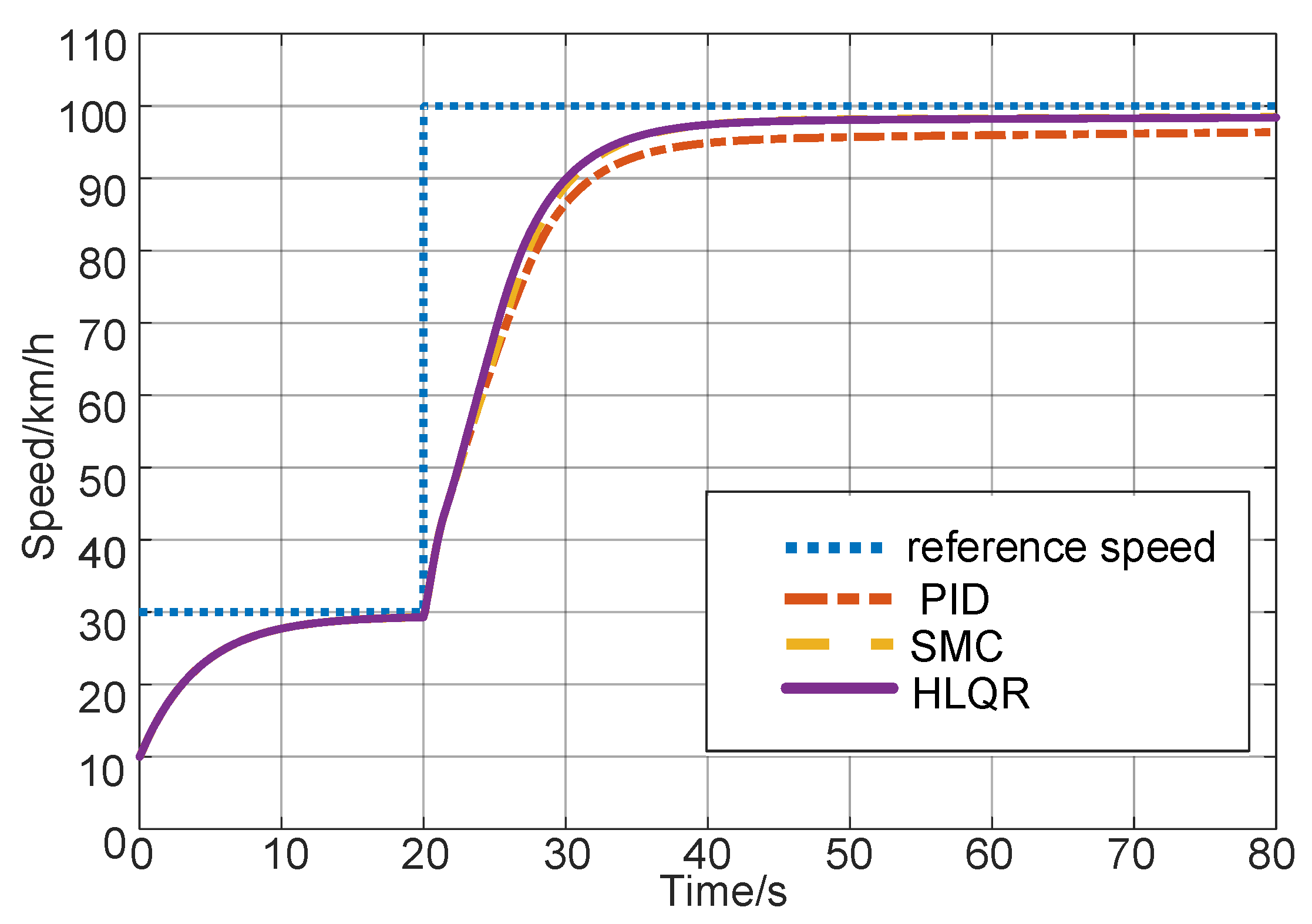
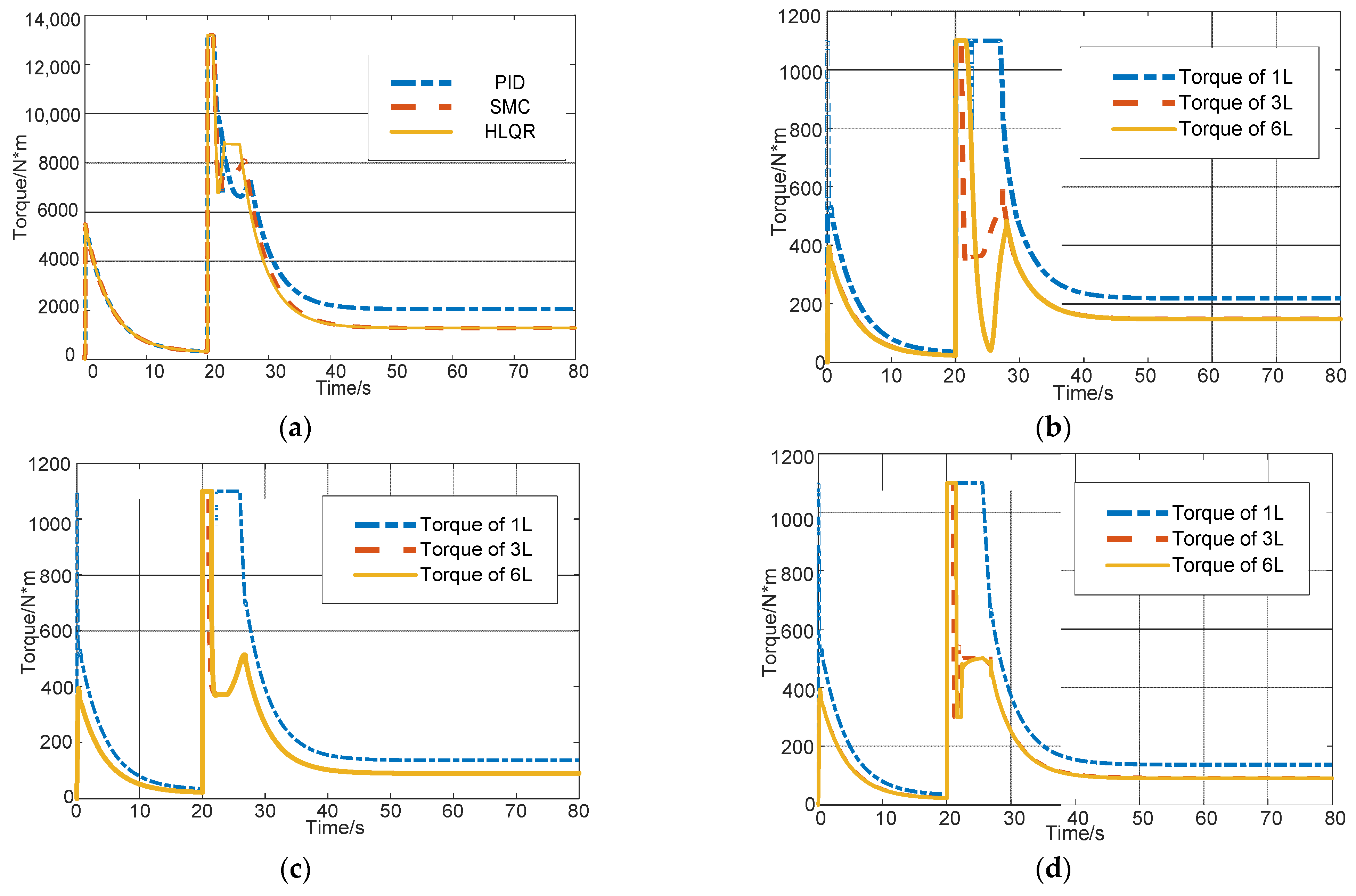
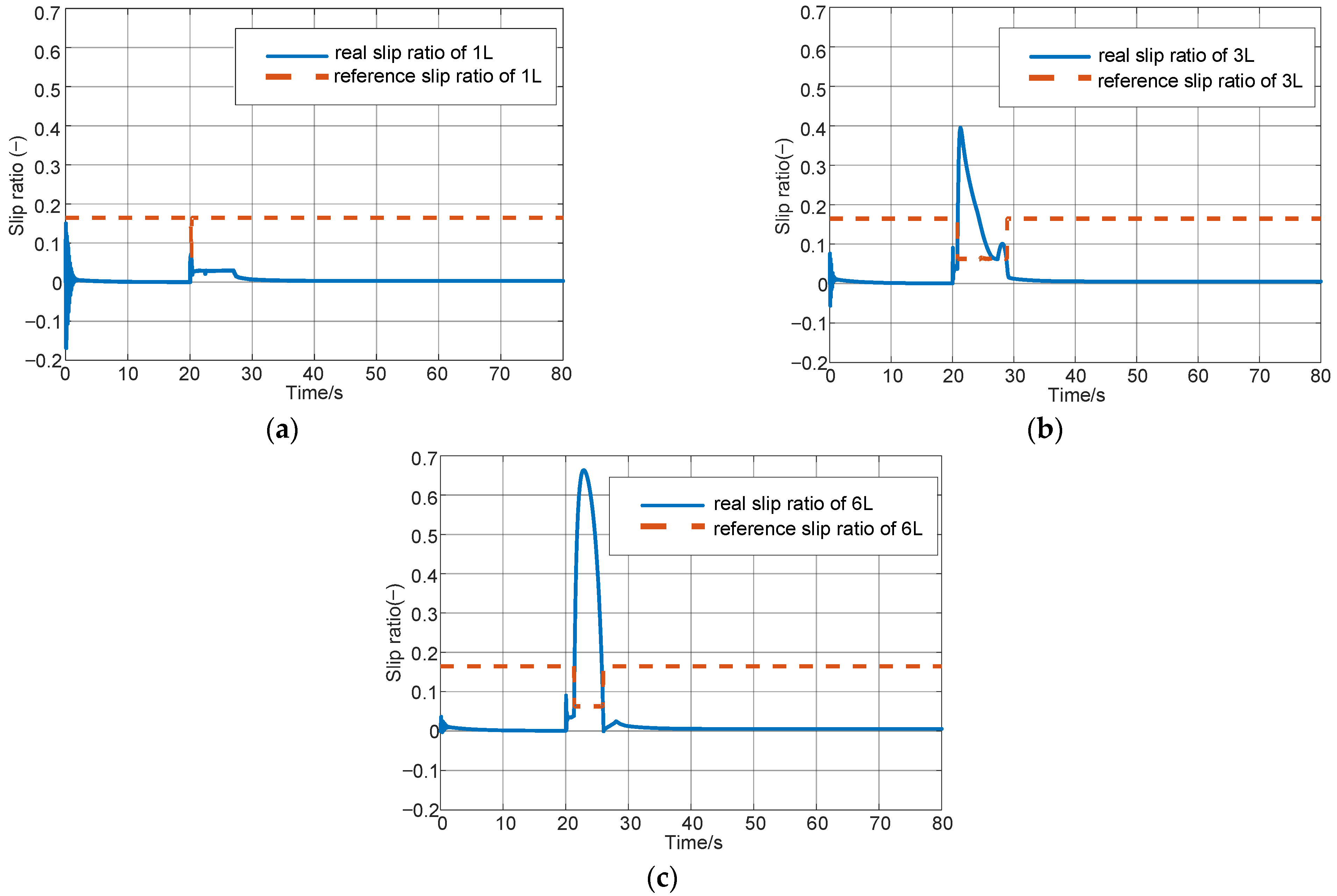
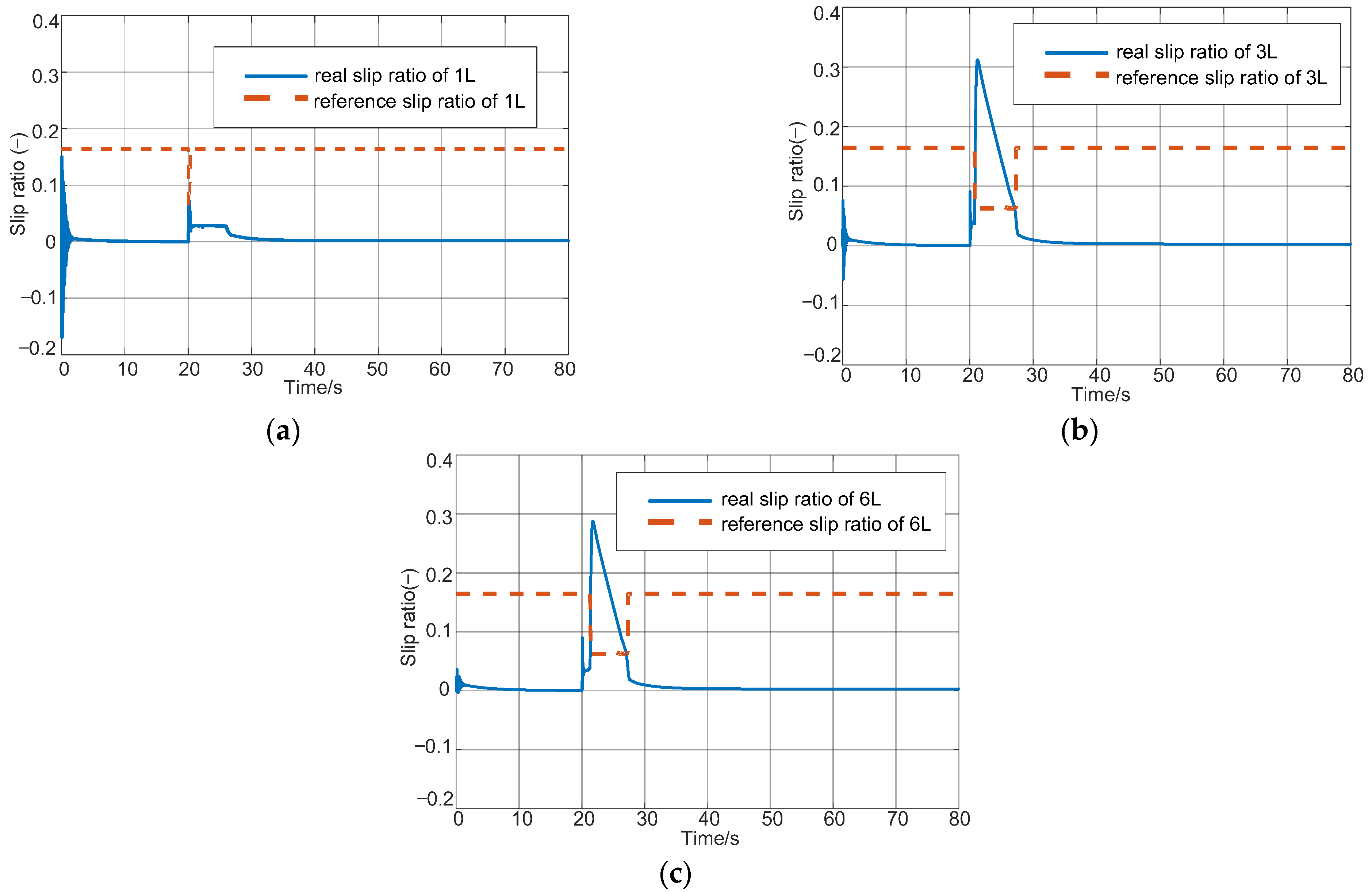
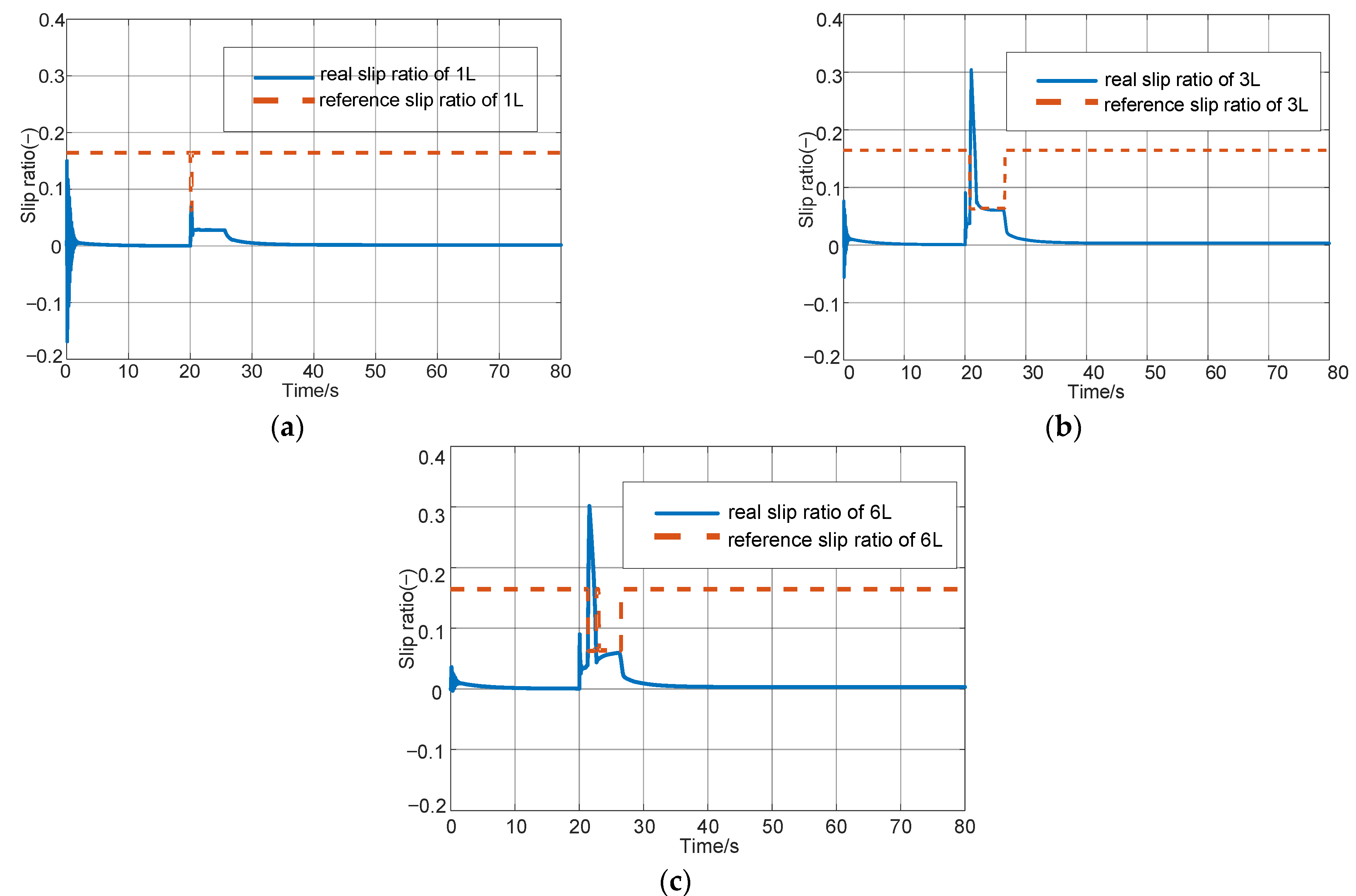
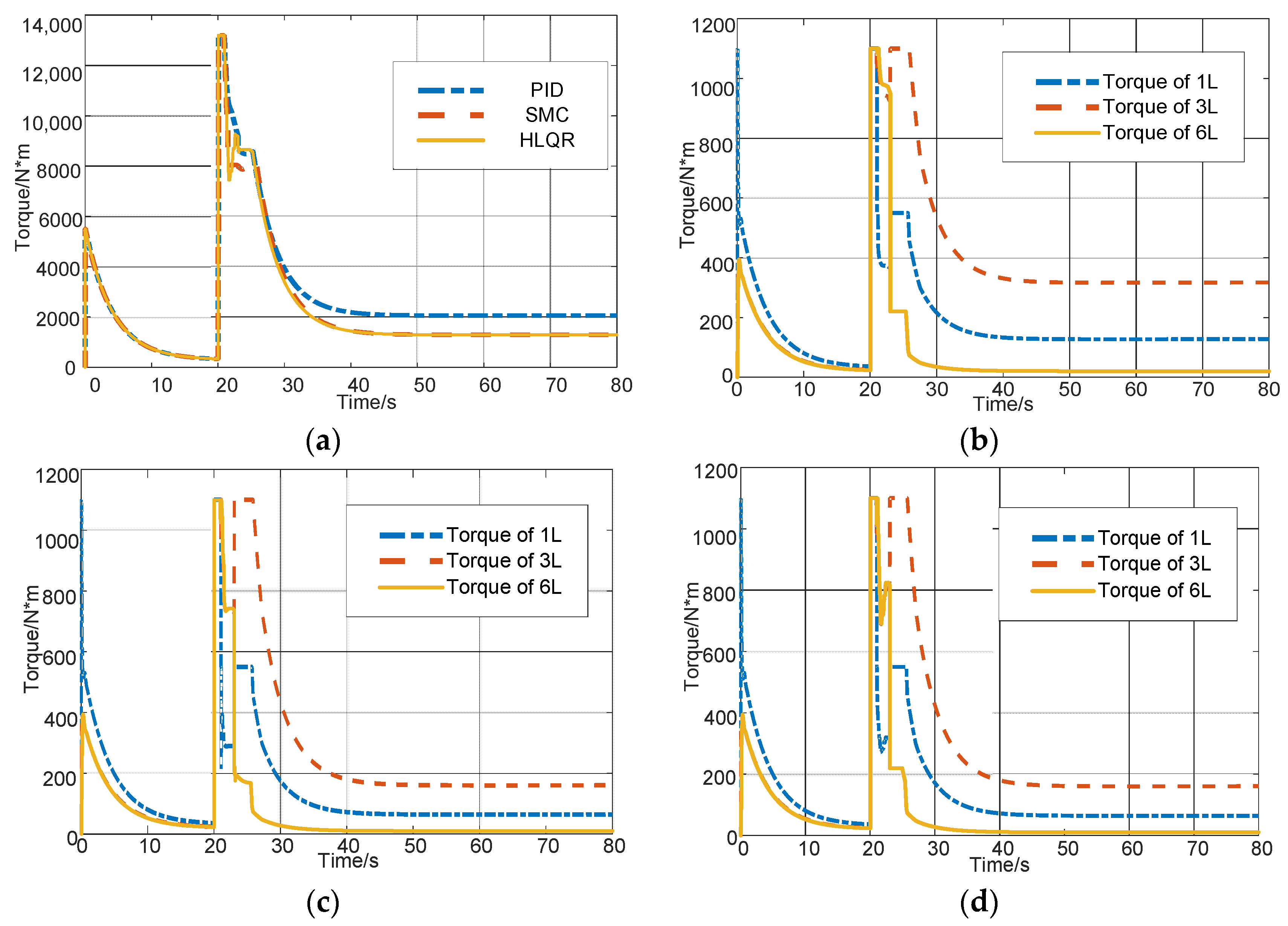
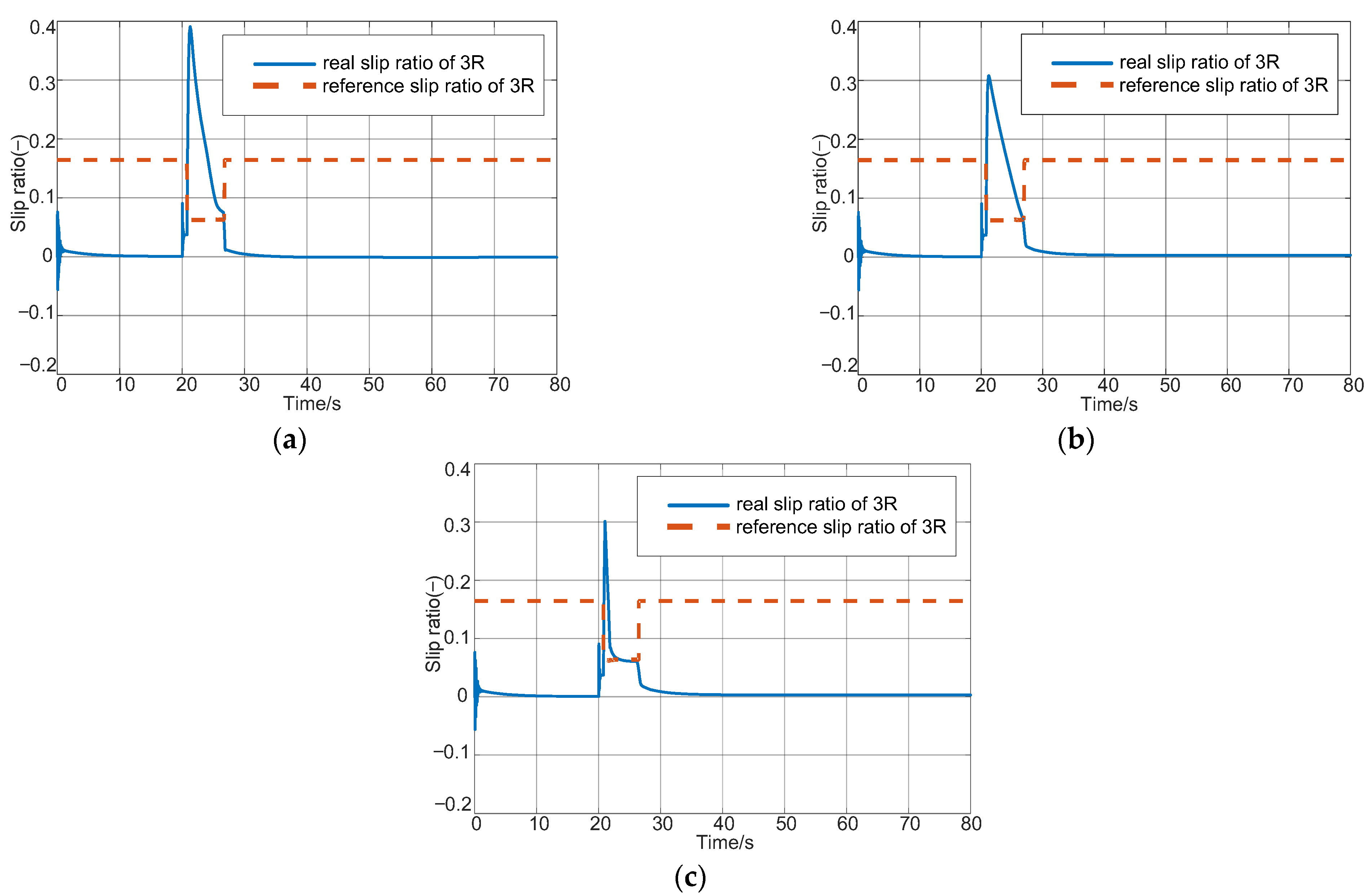
5. Simulation Results
5.1. Simulation for Changed Road Surface Coefficient
5.2. Simulation on Split Road Surface with the Electric Motor Failure
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Gong, M.-D.; Zhao, D.-X.; Liu, W.-B.; Jia, G.-Y. Coordination Control of Multi-Axis Steering and Active Suspension System for High-Mobility Emergency Rescue Vehicles. Mathematics 2022, 10, 3562. [Google Scholar] [CrossRef]
- Hamouda, M.; Al-Amyal, F.; Odinaev, I.; Ibrahim, M.N.; Számel, L. A Novel Universal Torque Control of Switched Reluctance Motors for Electric Vehicles. Mathematics 2022, 10, 3833. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, F.; Xi, J.; Cao, D. Mixed-Integer Optimal Design and Energy Management of Hybrid Electric Vehicles with Automated Manual Transmissions. IEEE Trans. Veh. Technol. 2020, 69, 12705–12715. [Google Scholar] [CrossRef]
- Gao, L.; Xiong, L.; Xia, X.; Lu, Y.; Yu, Z.; Khajepour, A. Improved Vehicle Localization Using On-Board Sensors and Vehicle Lateral Velocity. IEEE Sens. J. 2022, 22, 6818–6831. [Google Scholar] [CrossRef]
- Chen, H.; Lian, X.; Lyu, C. Piecewise integral-proportional wheel slip control for an in-wheel motor driven vehicle. Veh. Syst. Dyn. 2022, 1–21. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, H.; Huang, Y.; Wang, P.; Guo, K. Human-Centered Torque Vectoring Control for Distributed Drive Electric Vehicle Considering Driving Characteristics. IEEE Trans. Veh. Technol. 2021, 70, 7386–7399. [Google Scholar] [CrossRef]
- Hua, M.; Chen, G.; Zhang, B.; Huang, Y. A hierarchical energy efficiency optimization control strategy for distributed drive electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 233, 605–621. [Google Scholar] [CrossRef]
- George, A.D.; Besselink, I. Rear suspension design for an in-wheel-drive electric car. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 230, 147–159. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, F.; Tian, L. Normalized coupling method for speed synchronization of multi-axis driving vehicles. Int. J. Adv. Robot. Syst. 2012, 9, 50. [Google Scholar]
- Trikande, M.; Karve, N.; Rajamohan, V.; Jagirdar, V.; Vasudevan, R. Semi-active vibration control of an 8x8 armored wheeled platform. J. Vib. Control 2016, 24, 283–302. [Google Scholar] [CrossRef]
- Hashemi, E.; Jalali, M.; Khajepour, A.; Kasaiezadeh, A.; Chen, S.-K. Vehicle Stability Control: Model Predictive Approach and Combined-Slip Effect. IEEE/ASME Trans. Mechatron. 2020, 25, 2789–2800. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Vehicle sideslip angle estimation by fusing inertial measurement unit and global navigation satellite system with heading alignment. Mech. Syst. Signal Process. 2021, 150, 107290. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Leng, B.; Yu, Z. Vehicle stability control based on driver’s emergency alignment intention recognition. Int. J. Automot. Tech. 2017, 18, 993–1006. [Google Scholar]
- Kim, W.; Yi, K.; Lee, J. An optimal traction, braking, and steering coordination strategy for stability and manoeuvrability of a six-wheel drive and six-wheel steer vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 226, 3–22. [Google Scholar] [CrossRef]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip Angle Estimation Based on Consensus Kalman Filter. IEEE Trans. Control. Syst. Technol. 2022, 31, 179–192. [Google Scholar] [CrossRef]
- Liu, M.C.; Zhang, C.N. Development of an optimal control system for longitudinal and lateral stability of an individual eight-wheel-drive electric vehicle. Int. J. Veh. Des. 2015, 69, 132. [Google Scholar] [CrossRef]
- Hu, J.; Li, J.; Hu, Z.; Zhang, B.; Xu, L.; Ouyang, M. Energy-efficient torque-allocation strategy for a 6 × 6 vehicle using electric wheels. Etransportation 2021, 5, 100136. [Google Scholar] [CrossRef]
- Han, Z.; Xu, N.; Chen, H.; Huang, Y.; Zhao, B. Energy-efficient control of electric vehicles based on linear quadratic regulator and phase plane analysis. Appl. Energy 2018, 213, 639–657. [Google Scholar] [CrossRef]
- Grechi, S.; Caiti, A. Comparison between Optimal Control Allocation with Mixed Quadratic & Linear Programming Techniques. IFAC-PapersOnLine 2016, 49, 147–152. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, X.; Zhang, L. Overview on Key Technologies of Acceleration Slip Regulation for Four-wheel·independently·actuated Electric Vehicles. J. Mech. Eng. Chin. Ed. 2019, 55, 99–120. [Google Scholar]
- Chen, G.; He, L.; Zhang, B.; Hua, M. Dynamics integrated control for four-wheel independent control electric vehicle. Int. J. Heavy Veh. Syst. 2019, 3–4, 515–534. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Y.; Yan, N. Researchon acceleration slip regulation of 6x6 electrically—driven wheeled vehicle. Acta Armamentarii 2014, 35, 1335–1343. [Google Scholar]
- Chen, G.; Hua, M.; Zong, C.; Zhang, B.; Huang, Y. Comprehensive chassis control strategy of FWIC-EV based on sliding mode control. IET Intell. Transp. Syst. 2019, 13, 703–713. [Google Scholar] [CrossRef]
- Liu, L.; Fei, J.; Yang, X. Adaptive Interval Type-2 Fuzzy Neural Network Sliding Mode Control of Nonlinear Systems Using Improved Extended State Observer. Mathematics 2023, 11, 605. [Google Scholar] [CrossRef]
- Cai, L.; Liao, Z.; Wei, S.; Li, J. Improvement of Maneuverability and Stability for Eight Wheel Independently Driven Electric Vehicles by Direct Yaw Moment Control; ICEMS: Gyeongju, Republic of Korea, 2021. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Huang, Y.; Lu, Y.; Gao, L.; Xu, N.; Yu, Z. Estimation on IMU yaw misalignment by fusing information of automotive onboard sensors. Mech. Syst. Signal Process. 2021, 162, 107993. [Google Scholar] [CrossRef]
- Nguyen, D.-H.; Hara, S. Hierarchical Decentralized Controller Synthesis for Heterogeneous Multi-Agent Dynamical Systems by LQR. SICE J. Control. Meas. Syst. Integr. 2015, 8, 295–302. [Google Scholar] [CrossRef]
- Sadamoto, T.; Ishizaki, T.; Imura, J.-I. Hierarchical Distributed Control for Networked Linear Systems; CDC: Los Angeles, CA, USA, 2014; pp. 2447–2452. [Google Scholar] [CrossRef]
- Nguyen, B.-M.; Hara, S.; Fujimoto, H.; Hori, Y. Slip control for IWM vehicles based on hierarchical LQR. Control Eng. Pract. 2019, 93, 104179. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated vehicle sideslip angle estimation considering signal measurement characteristic. IEEE Sens. J. 2021, 19, 21675–21687. [Google Scholar] [CrossRef]
- Liu, W.; Quijano, K.; Crawford, M.M. YOLOv5-Tassel: Detecting tassels in RGB UAV imagery with improved YOLOv5 based on transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8085–8094. [Google Scholar] [CrossRef]
- Burckhardt, M. Wheel Slip Control Systems; Vogel Verlag: Würzburg, Germany, 1993. [Google Scholar]

| Parameters | Value |
|---|---|
| Vehicle mass(no load) (kg) | 6310 |
| Number of driving wheel (–) | 12 |
| Rated torque of each wheel (Nm) | 1100 |
| Effective rolling radius (mm) | 550 |
| Height of mass center (mm) | 1407 |
| Distance between axles (L1–L6) (mm) | 2600, 2500, 2300, 1800, 1800, 2400 |
| Algorithm | 3L Changed Road | 6L Changed Road | 3R Split Road |
|---|---|---|---|
| PID | 0.1751 | 0.4451 | 0.1634 |
| SMC | 0.1502 | 0.1372 | 0.1156 |
| HLQR | 0.0675 | 0.0872 | 0.0983 |
| 61.4 | 80.4 | 39.8 | |
| 55.1 | 36.4 | 14.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Du, C.; Wu, D.; Liu, H.; Liu, W.; Li, J. Coordinated Slip Control of Multi-Axle Distributed Drive Vehicle Based on HLQR. Mathematics 2023, 11, 1964. https://doi.org/10.3390/math11081964
Bao Y, Du C, Wu D, Liu H, Liu W, Li J. Coordinated Slip Control of Multi-Axle Distributed Drive Vehicle Based on HLQR. Mathematics. 2023; 11(8):1964. https://doi.org/10.3390/math11081964
Chicago/Turabian StyleBao, Yutong, Changqing Du, Dongmei Wu, Huan Liu, Wei Liu, and Jun Li. 2023. "Coordinated Slip Control of Multi-Axle Distributed Drive Vehicle Based on HLQR" Mathematics 11, no. 8: 1964. https://doi.org/10.3390/math11081964
APA StyleBao, Y., Du, C., Wu, D., Liu, H., Liu, W., & Li, J. (2023). Coordinated Slip Control of Multi-Axle Distributed Drive Vehicle Based on HLQR. Mathematics, 11(8), 1964. https://doi.org/10.3390/math11081964






