Dynamic Learning Rate of Template Update for Visual Target Tracking

Abstract

The trackers based on discriminative correlation filter (DCF) have achieved remarkable performance in visual target tracking in recent years. Since the targets are usually affected by various factors such as deformation, rotation, motion blur and so on, the trackers have to update the templates for tracking online. The purpose of template update is to adapt to the target changes, the magnitude of which is closely related to the motion state of the target. Actually, the learning rate of template update indicates the weight of the historical sample, and its value is fixed in most existing trackers, which will decrease the precision of the tracker or make the tracker unstable. In this study, a new dynamic learning rate method for template update is proposed for visual target tracking. The motion state of the target is defined by the difference in target center position between the frames. Then, the learning rate is adjusted dynamically according to the motion state of the target instead of the fixed value, which could achieve better performance. Experiments on the popular datasets OTB100 and UAV123 show that with the proposed dynamic learning rate for template update, the DCF-based trackers can improve tracking accuracy and obtain better tracking stability in scenarios such as fast movement and motion blur.

1. Introduction

Visual target tracking is one of the main challenges in computer vision and has a wide range of application scenarios. At the current stage, there are two main aspects that make the task of visual target tracking difficult. One includes the rotation and deformation of the target itself, scale changes and other factors; the other one is that the interference of complex environments can also produce tracking drift, background occlusion and other problems. Therefore, the performance of real-time target tracking still needs to be improved in complex environments with high accuracy. Due to increasing improvements in datasets and benchmarks, such as OTB50 [1], OTB100 [2], VOT2016 [3], UAV123 [4], etc., many algorithms with high accuracy and robustness have been proposed. The current research in visual target tracking focuses on two main areas: correlation filtering [5,6] and deep learning [7]. While some deep learning-based target tracking algorithms [8,9,10] are more accurate than the correlation filtering algorithms, they typically do not guarantee real-time performance or require hardware performance to support. The discriminative correlation filter (DCF) can guarantee a certain accuracy and at the same time achieve the real-time requirements.

Bolme et al. [11] introduced the first correlation filter, the sum of minimum output squared errors (MOSSE) filter, to the field of target tracking. Correlation and convolution are closely related to each other. The convolution theorem can be used to transform the complex and time-consuming convolution operation in the time domain into a dot product operation in the frequency domain by Fourier transformation. This increases the computational speed of the algorithm. MOSSE can achieve tracking rates of up to 669 fps while ensuring high accuracy, demonstrating the potential of correlation filtering in the field of target tracking. Henriques et al. [12] proposed the circulant structure with kernels (CSK) to achieve dense sampling of samples using a circular shift structure. The closed solution of the associated filtering template is obtained by ridge regression, and the nature of the circular matrix is exploited to simplify the operation by matrix diagonalization, which reduces the computational burden associated with the dense sampling strategy while expanding the samples. The kernel function is also introduced to map the linearly indistinguishable target features in the low-dimensional space to a high-dimensional space to speed up sample classification. In CSK, the tracker chooses the histogram of gradients (HOG) to describe the target, which has better performance compared to grayscale features. Then, Henriques et al. [13] proposed the kernelized correlation filter (KCF), which replaces the features in CSK with multi-channel HOG features. During the target tracking process, the size of the target usually changes, and the traditional correlation filtering algorithm has a fixed detection region and template size that cannot adapt to the scale change of the target. Danelljan et al. [14] proposed an efficient discriminative scale space tracker (DSST). This algorithm adopts a stepwise optimal strategy, which trains two filters, including a two-dimensional filter responsible for target localization and a one-dimensional filter responsible for determining the target size. Mueller et al. [15] took contextual information into account and derived a closed-form solution that significantly improved the performance of many correlation filter-based trackers. Danelljan et al. [16] proposed efficient convolution operators (ECO) for tracking. ECO defined the decomposition convolution operation, which makes the model reduce the number of parameters by about 80%. It also optimizes the sample set construction strategy to remove redundant and invalid samples and increase sample richness. A sparse update strategy is used to avoid sample overfitting and improve the stability of the template. Dai et al. [17] proposed a novel adaptive spatial regularization correlation filter (ASRCF). Unlike SRDCF [18], its spatial regularization adaptively adjusts as the target changes, and it uses shallow features in estimating the target scale, thus improving the efficiency of the algorithm. Li et al. [19] proposed the AutoTrack algorithm for adaptive spatio-temporal regularization. The algorithm finds that the response maps obtained by correlation operations between filter templates and candidate regions reflect the reliability of the current sample and its similarity to the real target. The adaptive spatio-temporal regularization is achieved by the local as well as the global response values of the response maps. An end-to-end trainable deep network has a greater advantage in model optimization [20]. Valmadre et al. [21] proposed the CFNet, which uses the correlation filter as a layer in the neural network. This achieves a combination of correlation filtering and deep learning.

Trackers such as KCF and ECO only consider a fixed learning rate for template update, but we find that better performance can be obtained when the learning rate varies appropriately with the target motion. In this paper, the learning rate of template update is dynamically adjusted by describing the target’s motion in terms of its inter-frame center position offset. Experiments conducted on popular benchmarks show that the dynamic learning rate improves the accuracy of trackers.

The main contributions of this paper are as follows:

• A new learning rate adjustment strategy is proposed. The learning rate of template update is dynamically adjusted by the motion state of the target. The effectiveness and portability of the method were demonstrated in the experiments.
• The method demonstrates that the motion state of the target contains a wealth of potential information and that this information has a positive impact on the performance of the tracker.

The rest of this paper is arranged as follows. Section 2 reviews some related works on correlation filter-based visual target tracking and briefly introduces some existing correlation filter-based trackers. In Section 3, our new tracker is described in detail from three aspects. In Section 4 the related experiments and results are presented for the proposed tracker. In Section 5 the conclusion and future work are given.

2. Related Work

2.1. The Strategy of Template Update

Visual tracking algorithms commonly use a template update strategy to adapt to changes in the target’s appearance. Most correlation filters update the initial filter through filters obtained in the subsequent frames according to an exponential moving average (EMA) strategy, i.e., with a fixed learning rate. In addition, LMCF [22] uses a confidence update strategy to update the tracking template only when the tracking confidence is relatively high to avoid contamination of the target model and to improve speed simultaneously. The first confidence metric is the maximum response fraction F_max, which is the maximum response value. The second confidence metric is the average peak-to-correlation energy (APCE), which refers to the degree of fluctuation of the response graph and the confidence level of the detection target. One of the crucial changes in the accelerated version of ECO based on C-COT [23] is the sparser updating scheme, which updates the tracking template every five frames, which not only enhances the speed of the algorithm but also maintains its stability against sudden changes, occlusions, and other situations.

2.2. The Application of Motion State

Both optical flow and Kalman filtering, the two conventional tracking algorithms, considered the motion information of the target in tracking.

The concept of optical flow, first introduced by Gibson in 1950 [24], is the motion of a target, scene or camera caused by the target’s motion between two consecutive frames. It is the instantaneous velocity of the motion of a spatially moving object in pixel motion on the observation imaging plane. Therefore, the change in pixels in continuous images could represent the correspondence between the previous frame and the current frame, and the correlation between adjacent frames accounts for the motion information of the object.

In 1960, Kalman filtering was first introduced [25]. It is an algorithm that uses the state equation of a linear system to optimally estimate the system state from system input and output observations. The main idea is to use the known information to estimate the unknown information. A recursive approach is used to achieve the optimal estimation of the system state by continuously updating the state estimates and the covariance matrix. A typical application of the Kalman filter is to estimate the target position, which uses dynamic information about the target to eliminate the effect of noise on target position estimation.

In view of optical flow and the Kalman filter, we can find the potential value of the motion state in target tracking. In addition, Chen et al. [26] proposed to use the acceleration of the target to adjust the size of the search window during target tracking, which also improved the performance of target trackers. These validate the positive effect of target motion state on target tracking. In our study we found through extensive experiments that the learning rate of template update is related to the motion state of the target.

3. Method

In order to reasonably establish the relation between the target motion state and the learning rate of template update, the center position inter-frame difference of the target is used to reflect the motion state. Firstly, a discriminative correlation filter-based tracker is introduced, and the learning rate of template update is explained. Secondly, the center position inter-frame difference of the target is used to define the motion velocity of the target as a representation of the motion state. Finally, it is presented that the learning rate of template update adjusts dynamically with the motion state.

3.1. Preview of DCF Based Tracker

MOSSE first introduced correlation filtering to the field of target tracking and was the first DCF tracker. Its basic idea is that correlation is a measurement of the similarity value of two signals; if two signals are more similar, then their correlation value will be higher. In the application of target tracking, the task is that a filter template needs to be designed so that when it acts on the tracking target, the maximal response is obtained and the position with the maximal response value is the position of the target. It is expressed by the following equation:

$$G=F\odot H^{*}$$

(1)

where F is the Fourier transform of the input image and G is the Fourier transform of the output response. After the target passing through the filter, the response at the location of the target is maximum, and when the target is in the center of the image, we can set the response G as a two-dimensional Gaussian function with the peak position in the center of the image. H* denotes the complex conjugate of H. The specific principle of correlation filtering applied to target tracking is shown in Figure 1.

Using multiple images F_i to find the optimal H*, the criterion proposed in the MOSSE is to minimize the sum of squared errors between the results calculated for each image and the Gaussian template, expressed as follows:

$$\underset{H^{*}}{\min }{\displaystyle \sum }_{\mathrm{i}}{\left|F_i\odot H^{*}-G_i\right|}^2$$

(2)

The closed solution is obtained by taking the partial derivative of the formula and taking the derivative to zero to obtain the extreme value as follows:

$$H=\frac{{\sum }_i{F}_i\odot G_i^{*}}{{\sum }_i{F}_i\odot F_i^{*}}$$

(3)

The subsequent KCF is proposed to define the basic framework of DCF, which introduced circular shifts, fast Fourier transforms, and multi-channel features compared to MOSSE. The change brought with it is the loss function for solving the objective:

$$\underset{w}{\min }\parallel X_w-y{\parallel }_2^2+\lambda \parallel w{\parallel }_2^2$$

(4)

Here, the correlation filter template of the required solution is changed from the previous H to $w$, which is denoted as the weight vector of the classifier; X is obtained by circularly shifting the original image x; y denotes the ideal Gaussian response of the corresponding samples; λ is the penalty coefficient of the regular term, which is used to prevent overfitting.

The closed solution is obtained as follows:

$$w={\left(X^{T}X+ \mathsf{\lambda }\mathrm{I}\right)}^{-1}{X}^{T}y$$

(5)

Using the properties of circular matrices, X can be diagonalized in Fourier space using a discrete Fourier matrix (DFT), which is useful for reducing the computational burden; the specific form is as follows:

$$X=Fdiag\left(\widehat{x}\right)F^H$$

(6)

where F is the constant matrix of the discrete Fourier transform, $\widehat{x}$ represents the offline Fourier transform of the generating vector x of X, and $\mathrm{diag}\left(\widehat{x}\right)$ represents the diagonal matrix constructed in terms of $\widehat{x}$.

Equations (5) and (6) can be converted to the following form:

$$\widehat{w}=\frac{{\widehat{x}}^{*}\odot \widehat{y}}{x^{*}\odot \widehat{x}+\lambda }$$

(7)

To improve the accuracy of the classifier and solve the linear indistinguishability problem, KCF uses a kernel trick to map data that are indistinguishable in a low-dimensional space to a high-dimensional space. The filter template $\mathrm{w}$ consists of a linear combination of nonlinear transformations $\mathsf{\Psi }\left(x\right)$ of the samples. The specific form is:

$$w=\sum {\alpha }_i{x}_i$$

(8)

In this case the solution about the filter changes from $\mathrm{w}$ to $\mathsf{\alpha }$, and the classifier has the form $\mathrm{f}\left(z\right)=wz$ to $\mathrm{f}\left(z\right)=\sum {\alpha }_i\mathsf{\Psi }\left(x\right)\mathsf{\Psi }\left(z\right)$, noted $K\left(x_i,y_i\right)=\mathsf{\Psi }\left(x_i\right)\mathsf{\Psi }\left(y_i\right)$, called the kernel function, at which point the solution of $\mathsf{\alpha }$ is:

$$\alpha ={\left(K+\lambda I\right)}^{-1}y$$

(9)

where K denotes the kernel matrix, which also has the properties of a circular matrix and can be diagonalized by the discrete Fourier transform, at which point the formula can be reduced to:

$$\alpha =\frac{y}{k^{xx}+\lambda }$$

(10)

where the generation vector k^xx is the first row of the kernel cycle matrix.

Eventually, after obtaining the solution of the filter template, most other DCF trackers use EMA as the update strategy, as follows:

$$X_t=\eta X_t+\left(1-\eta \right)X_{t-1}$$

(11)

where η is the learning rate, X_t is the template at frame t, and X_t−1 is the template at frame t−1.

As far as we know, for most DCF based trackers, the learning rate of template update is fixed or changes less. The method proposed in this paper uses the motion state of the target to adjust the learning rate of template update in order to improve the accuracy and stability of the tracker.

3.2. Definition of Motion State

Most trackers maintain a fixed learning rate for template update. No tracker otherwise dynamically adjusts the learning rate of template update. However, if the target or camera is moving rapidly, the target will typically experience motion blur or larger deformations. Thus, a fixed learning rate for template update can lead to untimely update or the accumulation of background errors. It can be seen that the speed of the target affects the tracking performance. The offset of the target’s center position between each frame is designed to define the target’s velocity, which can be obtained as follows:

$$v_t=\frac{\sqrt{{\left(c_{t_x}-c_{t-1_x}\right)}^2+{\left(c_{t_y}-c_{t-1_y}\right)}^2}}{\Delta t}$$

(12)

where c_t is the center position of the target bounding box in the current frame and c_t−1 is that in the previous frame. x denotes the horizontal pixel distance to the left edge of the target rectangle border. y denotes the vertical pixel distance to the top edge of the target rectangle border. Except for the first frame, where the position c_t is determined, p_t in subsequent frames is predicted by the tracker, and its accuracy is consistent with the tracking effectiveness of the tracker. Δt denotes the time interval between adjacent frames of the video. Its specific value is determined by the video frame rate. All videos do not have exactly the same frame rate and at the same time do not affect each other. In this paper, Δt is set as a constant, Δt = 1.

Usually, our tracking task does not go to track the complete motion of a target, and the initial motion state of the target is unknown. We define the target motion state with a default initial frame target motion velocity of 0 m/s. To reduce the effect of this factor, the average velocity of the target in the previous k frames is considered as the velocity of the target in the current frame, in the form shown below:

$$\overline{v_t}=\frac{v_t+v_{t-1}+v_{t-2}+\dots v_{t-k}}{k}$$

(13)

where v_t−k is the velocity of the target in the previous k frame and v_t is the velocity in the current frame.

3.3. Strategy of Dynamic Learning Rate

During tracking, targets often change their appearance by changing their rotation, scale, pose, by moving under different lighting conditions, or even by undergoing non-rigid deformations. Therefore, the tracker needs to adapt quickly in order to track the object. For this reason, the template update strategy chosen by most DCF trackers is EMA, or exponential weighted moving average (EWMA). It can be used to estimate the local mean of a variable so that the update of the variable is related to the historical values taken over a period of time. The EMA is developed from the moving average, which has the advantages of sliding averages and reducing the number of data stored during the operation, while also taking into account the different roles played by data during different periods. The crucial step to using EMA is to determine the value of parameter η in Equation (11).

When the tracker is evaluated in some benchmark dataset, the learning rate η is set to be the same for all sequences. However, the target motion states in different sequences are not the same, and there are differences in the requirements for the learning rate of template update. On the other hand, for individual sequences, the target motion state also changes continuously over time, which requires the learning rate of template update to be adjusted continuously as well. For all baseline trackers, the optimal learning rate η for each sequence is determined by the sequence itself, not by the tracker.

The magnitude of η in EMA is related both to the capability to reflect recent data and to the data fluctuation condition. When it is applied to template update in the target tracking process, the relationship between the η value and the data capability, as well as the data fluctuation condition, can be reflected as the relationship between the learning rate η and the target motion state. As a result, a new method is proposed to dynamically adjust the learning rate of template update by considering the speed of the target to obtain better performance.

Many factors such as fast motion and camera shake can affect the learning rate of template update. Obviously, if the learning rate is too large, more information is retained for the current frame and less for the historical information. In partial or brief occlusion and any inaccurate detection, the model learns the background information, which accumulates to a point where the model follows the background drift and can never recover. If the learning rate is too small and the target has changed while the template is still the same as before, it will fail to identify the target, resulting in tracking failure. For some of the videos in OTB-100 (BlurCar1, Soccer, etc.), blurring or larger deformation occurs when the target is moving rapidly, as shown in Figure 2.

Inspired by this, the speed of the target is calculated in each sequence by Equation (12), and the learning rate of the template update will be adjusted by the value of the speed of the target as follows:

$${\eta }_t={\eta }_{t-1}\times \left(1+{\mathsf{\lambda }}_{\eta }v\right)$$

(14)

where η_t is the weight of the current sample, ${\eta }_{t-1}$ is the weight of the previous one, ${\lambda }_{\eta }$ is the canonical coefficient, and ${\eta }_t$ is adjusted on the basis of ${\eta }_{t-1}$ according to the motion speed $v$ of the target.

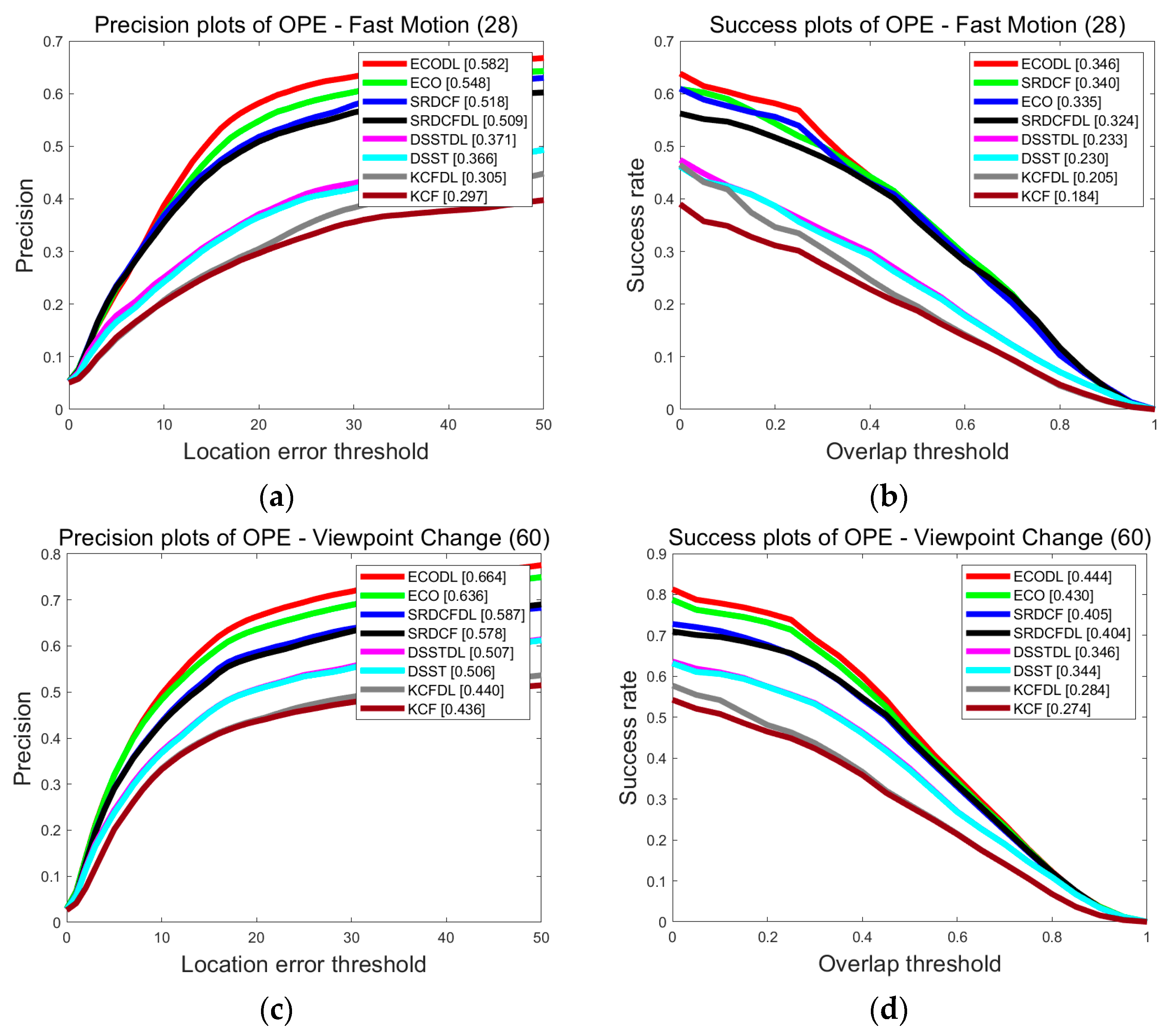
4. Experiment Results

To verify the effectiveness of the dynamic learning rate, it was applied to four baseline trackers. Moreover, the popular visual object tracking datasets OTB100 and UAV123 were used to evaluate its performance.

4.1. Baseline Trackers

The proposed method is adaptive to trackers with learning rate updating templates, which are satisfied by most DCF-based trackers. In order to obtain objective and reliable experimental results, several typical trackers were selected. These trackers are summarized in

Table 1. Baseline tracker information for comparison experiments.

Tracker	Learning Rate	Published
KCF [13]	Static	2014 (CVPR)
SRDCF [18]	Static	2015 (ICCV)
DSST [14]	Static	2016 (CVPR)
ECO [16]	Static	2017 (CVPR)

, while the improved comparison trackers using the dynamic learning rates for template update are called KCFDL, DSSTDL, SRDCFDL, and ECODL. To ensure experimental rigor, the standard parameters of the comparison tracker are aligned with the corresponding baseline tracker. In addition, the value of the constant k in Equation (13) is set to 10, and the canonical coefficient ${\lambda }_{\eta }$ in Equation (14) is set to −6 × 10².

In Table 1, learning rate is static, meaning the η value of the template update remains constant during the whole tracking process.

4.2. Test on OTB100

In OTB100, the performance of the tracker is evaluated using two metrics, precision rate and success rate. Precision rate represents the proportion of images in which the center error between the tracker’s bounding box and ground truth is less than a certain threshold among all images. Success rate is measured as the intersection over union (IoU) of the tracker bounding box and the ground-truth bounding box, which is expressed as the area under the curve (AUC).

The test results for all sequences of OTB100 are shown in Figure 3. Overlap success and distance precision are plotted using one-pass evaluation (OPE). It can be found that all comparison trackers have improved success as well as precision with respect to the baseline trackers. The greatest improvement in success rate was achieved with the DSST, at 2.5 percent, and the smallest improvement with ECO, at 0.63 percent. The improvement effect of all comparison trackers is shown in

Table 2. Comparison results of the success and precision rate of all algorithms on OTB100.

Tracker	Precision	Improvement	Success	Improvement
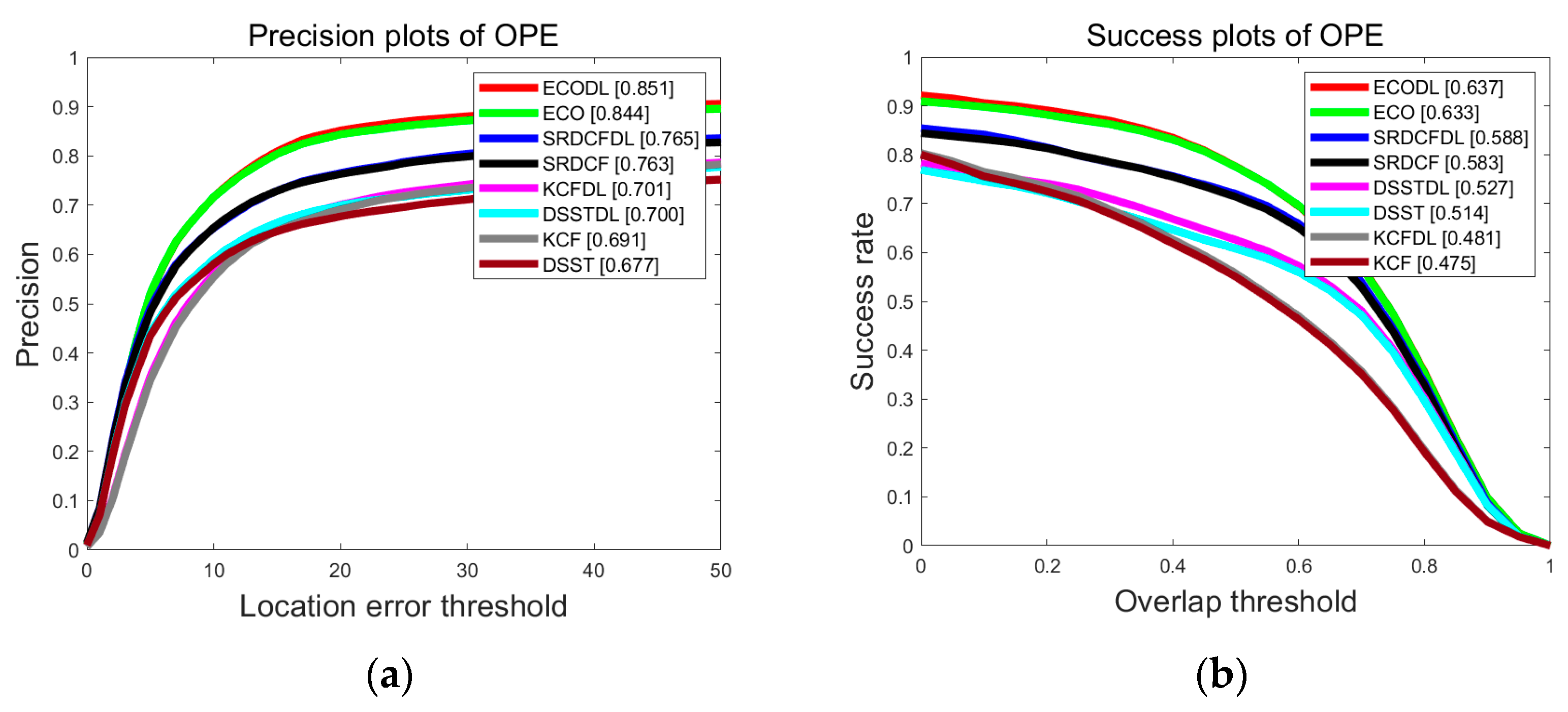
ECODL	85.1	0.83%	63.7	0.63%
ECO	84.4	—	63.3	—
SRDCFDL	76.5	0.26%	58.8	0.85%
SRDCF	76.3	—	58.3	—
DSSTDL	70.0	3.4%	52.7	2.5%
DSST	67.7	—	51.4	—
KCFDL	70.1	1.4%	48.1	1.2%
KCF	69.1	—	47.5	—

.

In Table 2, improvement shows the improvement effect of the precision and success rate of the comparison tracker on the corresponding baseline tracker, ‘—’ indicate the baseline tracker.

The OTB100 has eleven different attribute classifications for video sequences.

Table 3. Success rate under all attribute classifications of OTB100.

Attribute	ECO	SRDCF	DSST	KCF
IV	62.7/61.5	59.8/58.4	56.5/56.2	47.3/47.6
OPR	60.6/59.7	54.0/53.7	48.1/47.0	44.9/45.0
IPR	57.0/56.2	52.7/52.0	51.7/49.9	47.1/46.5
SV	61.0/60.1	54.9/54.5	48.3/46.6	40.0/39.2
OV	57.6/55.7	46.3/44.5	41.4/39.2	38.7/38.9
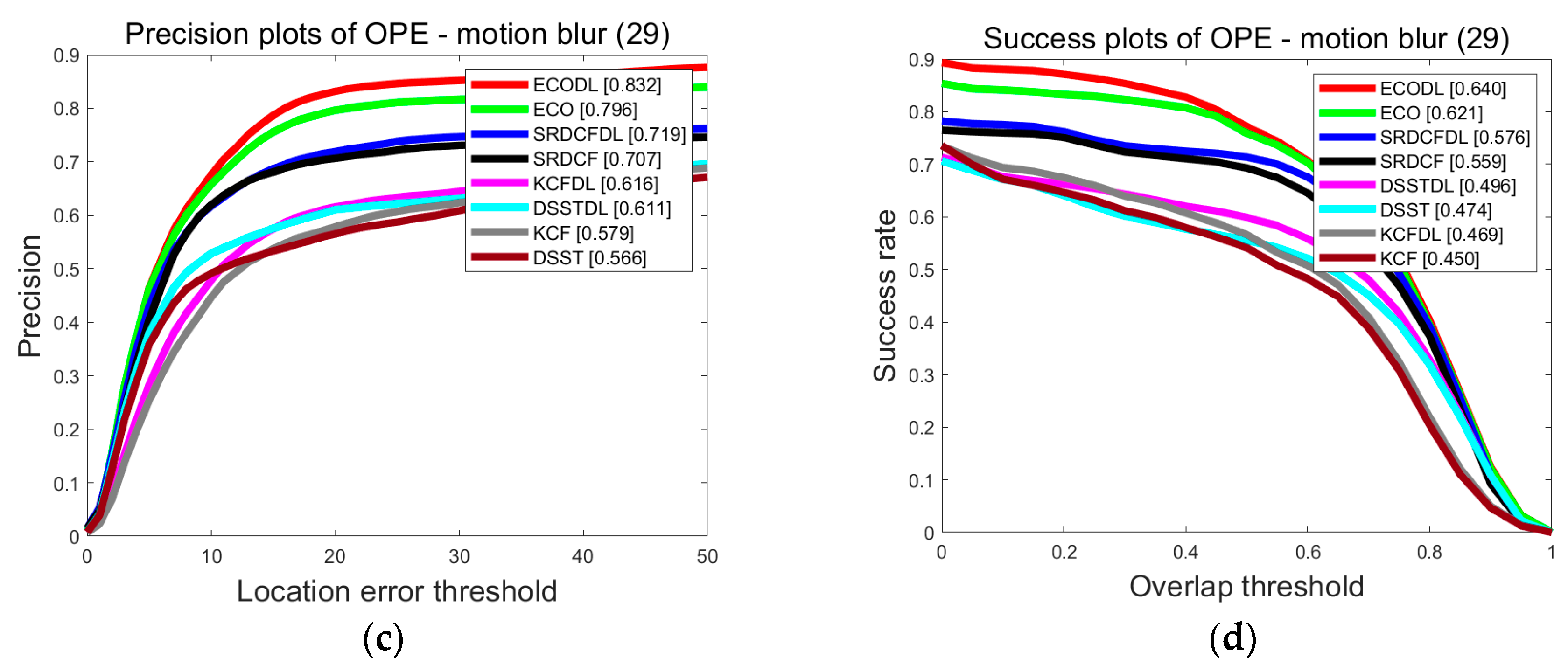
MB	64.0/62.1	57.6/55.9	49.6/47.4	46.9/45.0
DEF	59.3/59.6	53.4/53.2	44.3/42.0	44.5/43.9
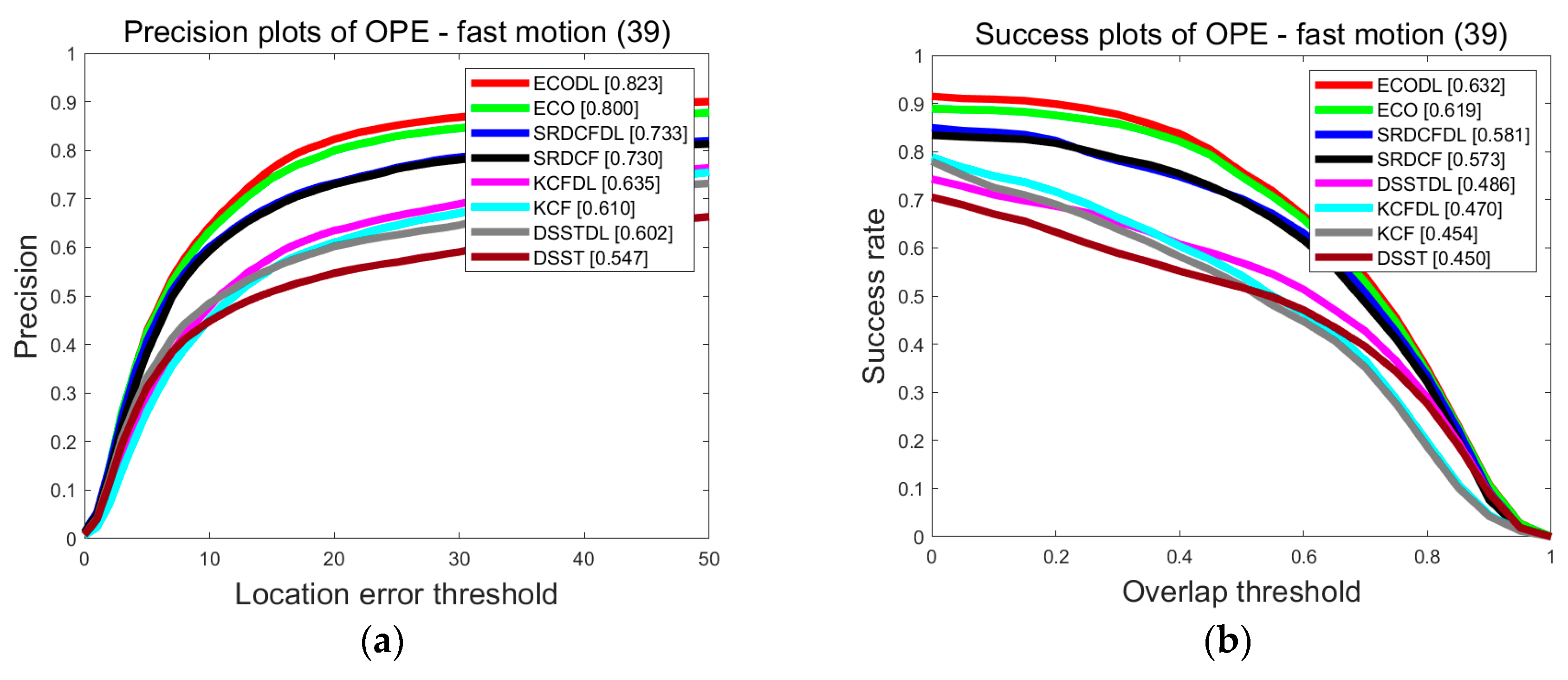
FM	63.2/61.9	58.1/57.3	48.6/45.0	47.0/45.4
OCC	62.1/61.2	54.4/53.8	46.2/45.0	43.8/44.0
BC	62.2/61.8	55.5/54.9	52.5/53.1	49.2/49.0
LR	56.0/53.4	49.0/49.2	40.0/39.8	30.7/30/7

presents the comparison results of success rate under all attribute classifications. The most significant improvements are achieved in the cases of fast motion and motion blur (see Figure 4). In these cases, the target position changes drastically, which means that the acceleration of the target can be significant.

In Table 3, the red numbers represent the performance improvement of the comparison tracker compared to the baseline tracker. Attribute explanation: IV (illumination variation), OPR (out-of-plane rotation), IPR (in-plane rotation), SV (scale variation), OV (out of view), MB (motion blur), DEF (deformation), FM (fast motion), OCC (occlusion), BC (background clutter), LR (low resolution).

4.3. Test on UAV123

In UAV123, the tracker’s evaluation metrics are consistent with OTB100. The test results for all sequences of UAV123 are shown in Figure 5. The experimental results in the figure show that the comparison trackers with dynamic learning rate have the same improved precision and success rates compared to the baseline trackers. The improvement effect of all comparison trackers is shown in

Table 4. Comparison results of success and precision rate of all algorithms on UAV123.

Tracker	Precision	Improvement	Success	Improvement
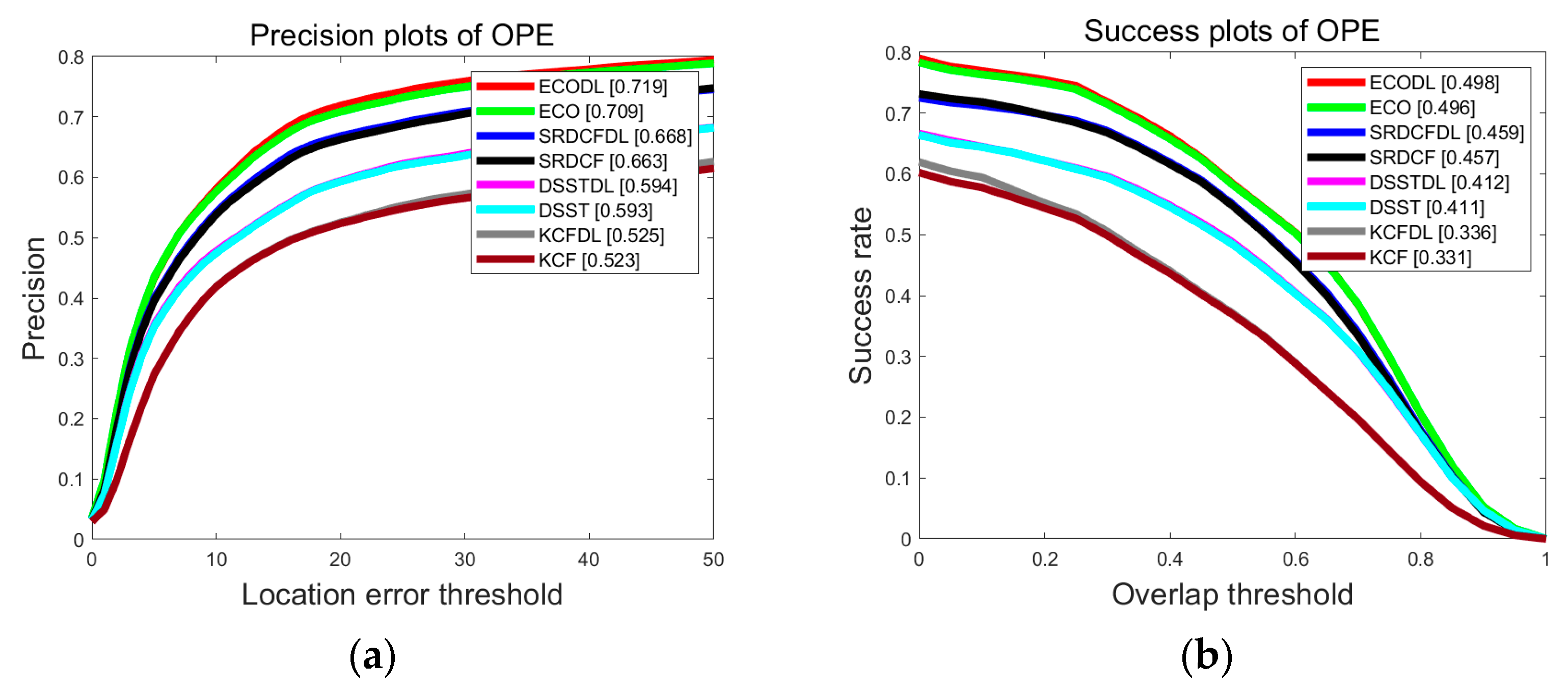
ECODL	71.9	1.4%	49.8	0.40%
ECO	70.9	—	49.6	—
SRDCFDL	66.8	0.75%	45.9	0.44%
SRDCF	66.3	—	45.7	—
DSSTDL	59.4	0.17%	41.2	0.24%
DSST	59.3	—	41.1	—
KCFDL	52.5	0.38%	33.6	1.5%
KCF	52.3	—	33.1	—

.

UAV123 also classifies different attributes for video sequences, and there are twelve in total. The performance is outstanding in the case of video sequence attribute classification with fast motion and viewpoint changes. The specific results are shown in Figure 6.

Table 5. Success rate under all attribute classifications of UAV123.

Attribute	ECO	SRDCF	DSST	KCF
ARC	42.4/42.4	38.4/38.2	33.6/33.4	27.4/26.7
BC	35.7/35.7	31.2/30.7	30.4/30.5	27.2/27.2
CM	47.6/47.3	43.9/44.6	37.9/37.7	31.9/31.0
FM	34.6/33.5	32.4/34.0	23.3/23.0	20.5/18.4
FO	27.7/28.1	24.8/24.8	20.9/21.0	18.5/18.5
IV	40.9/41.6	39.6/39.5	35.6/35.0	28.3/27.0
LR	35.6/35.6	30.9/30.1	26.4/26.4	18.0/18.0
OV	41.6/40.2	38.3/39.7	33.7/33.7	25.7/25.6
PO	43.4/43.0	38.7/38.4	34.4/34.2	28.4/28.2
SO	49.1/48.8	44.2/44.1	42.2/42.2	35.0/34.2
SV	46.6/46.4	42.8/42.7	37.4/37.3	29.6/29.1
VC	44.4/43.0	40.4/40.5	34.6/34.4	28.4/27.4

presents the comparison results of success rates under all attribute classifications.

In Table 5, the red numbers represent the performance improvement of the comparison tracker compared to the baseline tracker. Attribute explanation: ARC (aspect ratio change), BC (background clutter), CM (camera motion), FM (fast motion), FO (full occlusion), IV (illumination variation), LR (low resolution), OV (out of view), PO (partial occlusion), SO (similar object), SV (scale variation), VC (viewpoint change).

4.4. Discussion

Experimental results on OTB100 as well as UAV123 show that the comparison trackers with a dynamic learning rate strategy achieve better performance compared to the baseline trackers. The enhancement effect is more prominent in some specific scenarios, such as fast motion, motion blur, and viewpoint change. The dynamic learning rate strategy can benefit more from the more pronounced changes in the target motion state in these scenarios.

In addition, the test results on UAV123 show a slightly reduced boosting effect compared with OTB100. This is mainly due to the longer length of the video sequence in UAV123, which requires more robustness for the tracker, and more experimental tests are needed to adjust the parameter settings regarding the dynamic learning rate strategy.

Since the main purpose of template update in the tracking process is to enable the tracker to adapt to the changes of the target, and the motion state of the target reflects the change magnitude of the target to a certain extent, the strategy of adjusting the learning rate of template update based on the motion state of the target can better adapt to the changes of the target.

In conclusion, the above experimental results can fully prove that the dynamic learning rate strategy in this paper has a positive impact on target tracking and can improve the performance of most trackers.

5. Conclusions and Future Work

A new method named dynamic learning rate is proposed for the optimization of template update for visual target tracking. It employs the target center position difference between adjacent frames to calculate target motion velocity, which defines the target motion state. The learning rate is adjusted dynamically by the change in the target velocity. This establishes the relationship between template update and target motion state, which enables the template to adapt to the target changes more efficiently. Comparative experiments on datasets OTB100 and UAV123 show that the proposed method can improve their accuracy compared to most baseline trackers with fixed learning rates and perform better in scenarios such as fast movement and motion blur.

In the future, we plan to apply the target motion state to other parameters of the tracker for optimization, so as to take full advantage of the intrinsic information contained in the target motion state. The definition of the target motion state can also be further improved, for example, by taking into account the scale change and rotational attitude of the target.