Sustainable Supplier Selection and Order Allocation Using an Integrated ROG-Based Type-2 Fuzzy Decision-Making Approach
Abstract
1. Introduction
2. Literature Review
3. Methodology
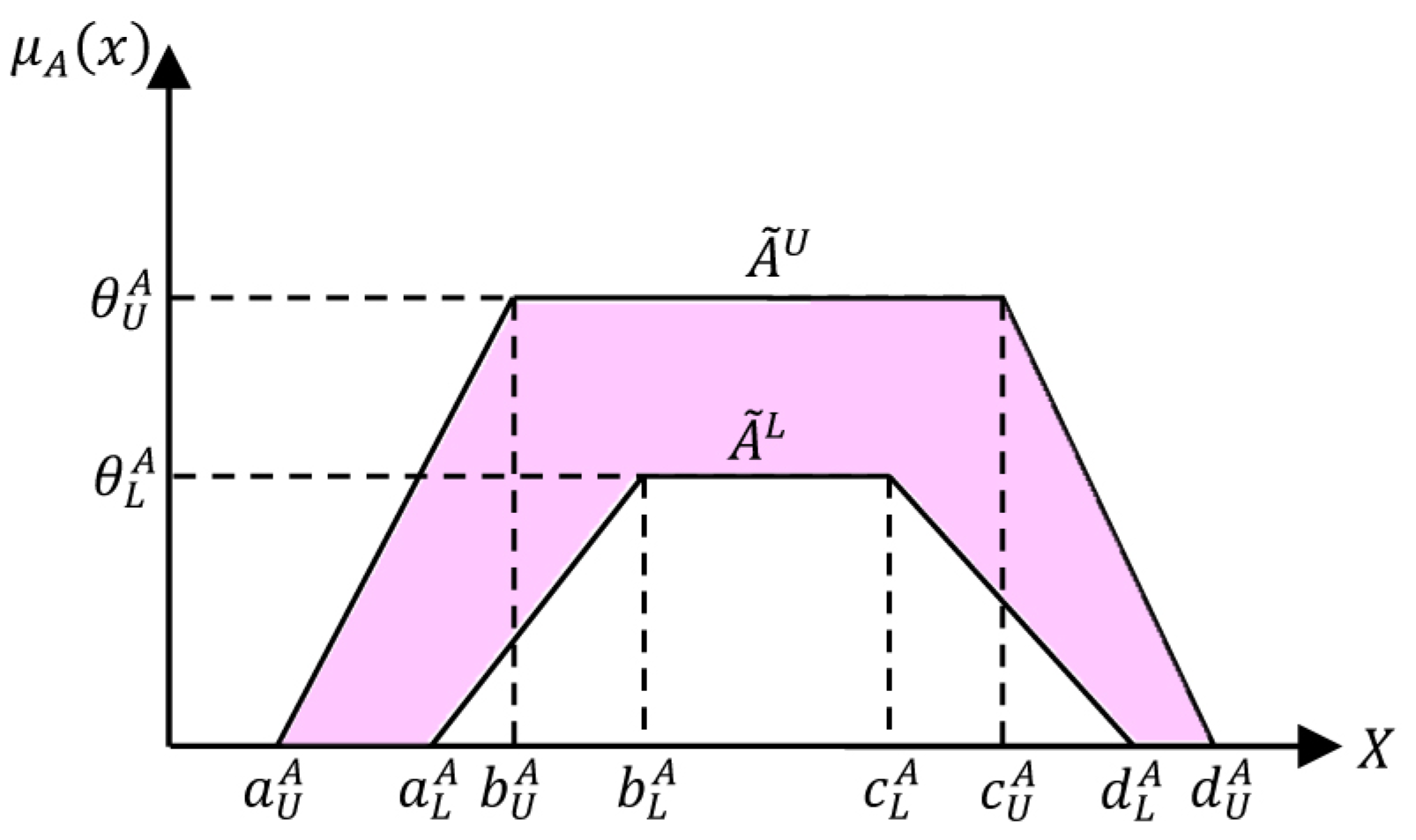
3.1. Interval Type-2 Fuzzy Sets
3.2. Comparative Ranking of Trapezoidal IT2FSs Based on ROG
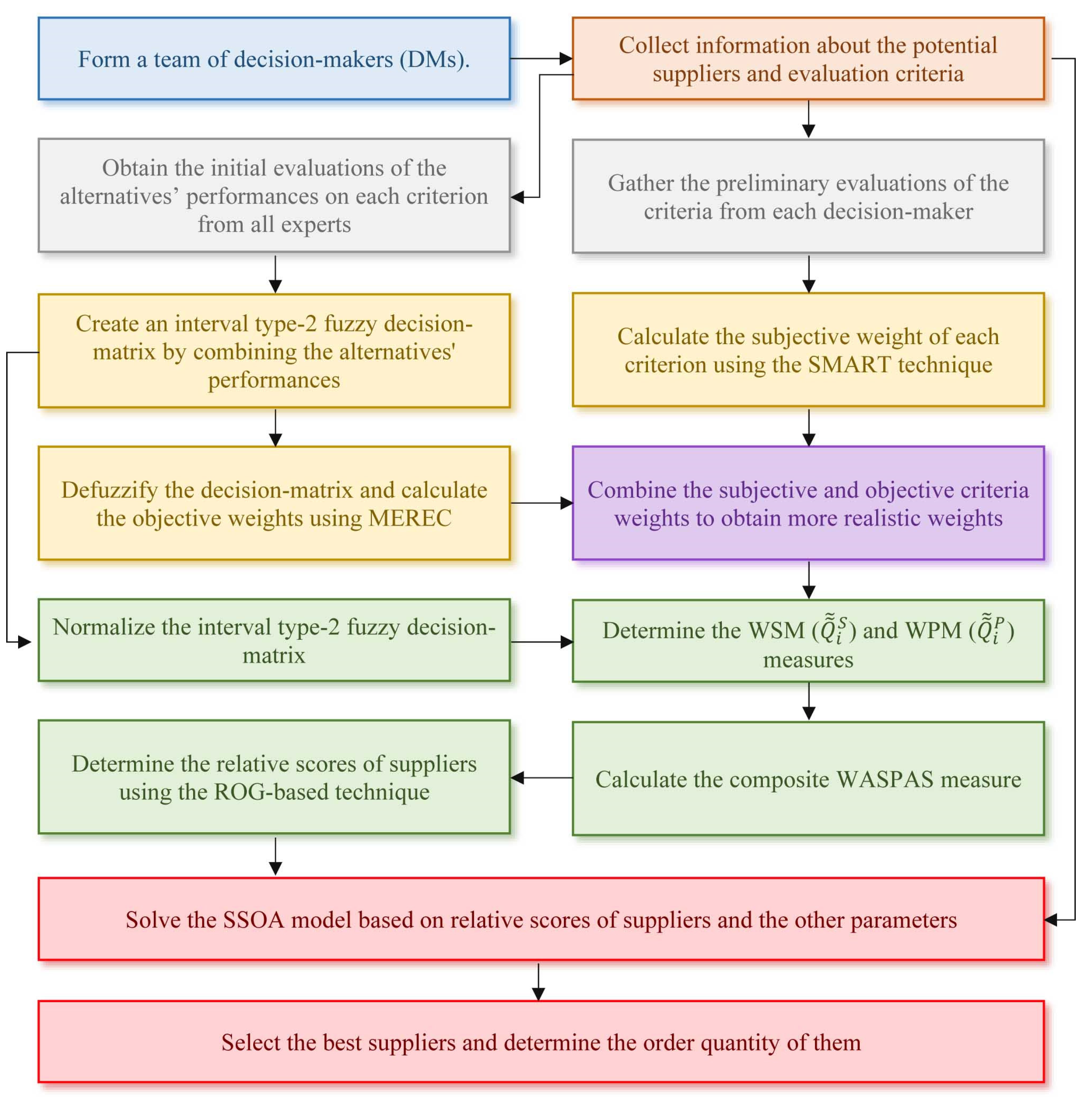
3.3. The Proposed MCDM Approach
3.4. A Mathematical Model for the SSOA Problem
4. Results and Discussion
4.1. The Application of the Methodology in Sustainable SSOA
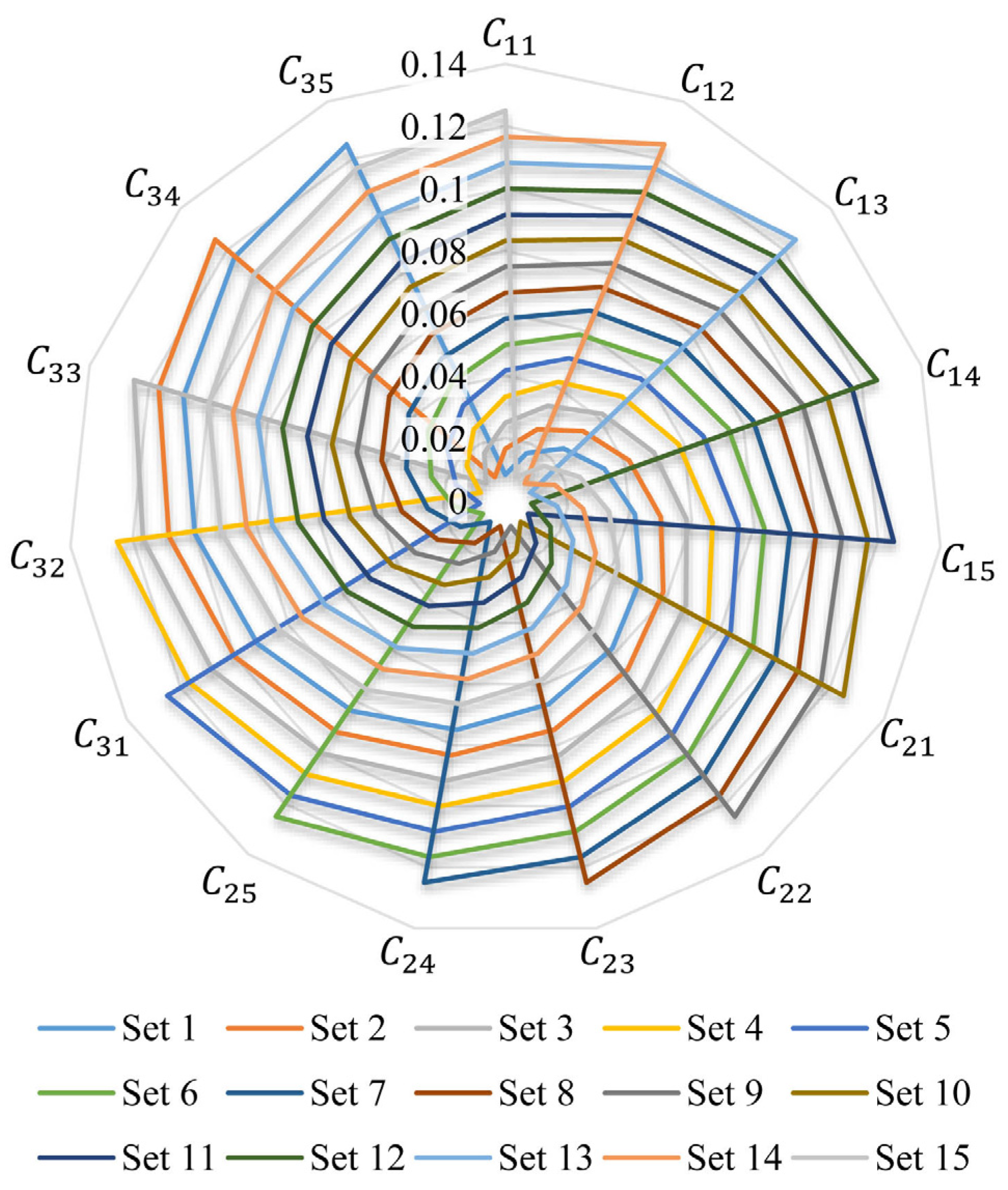
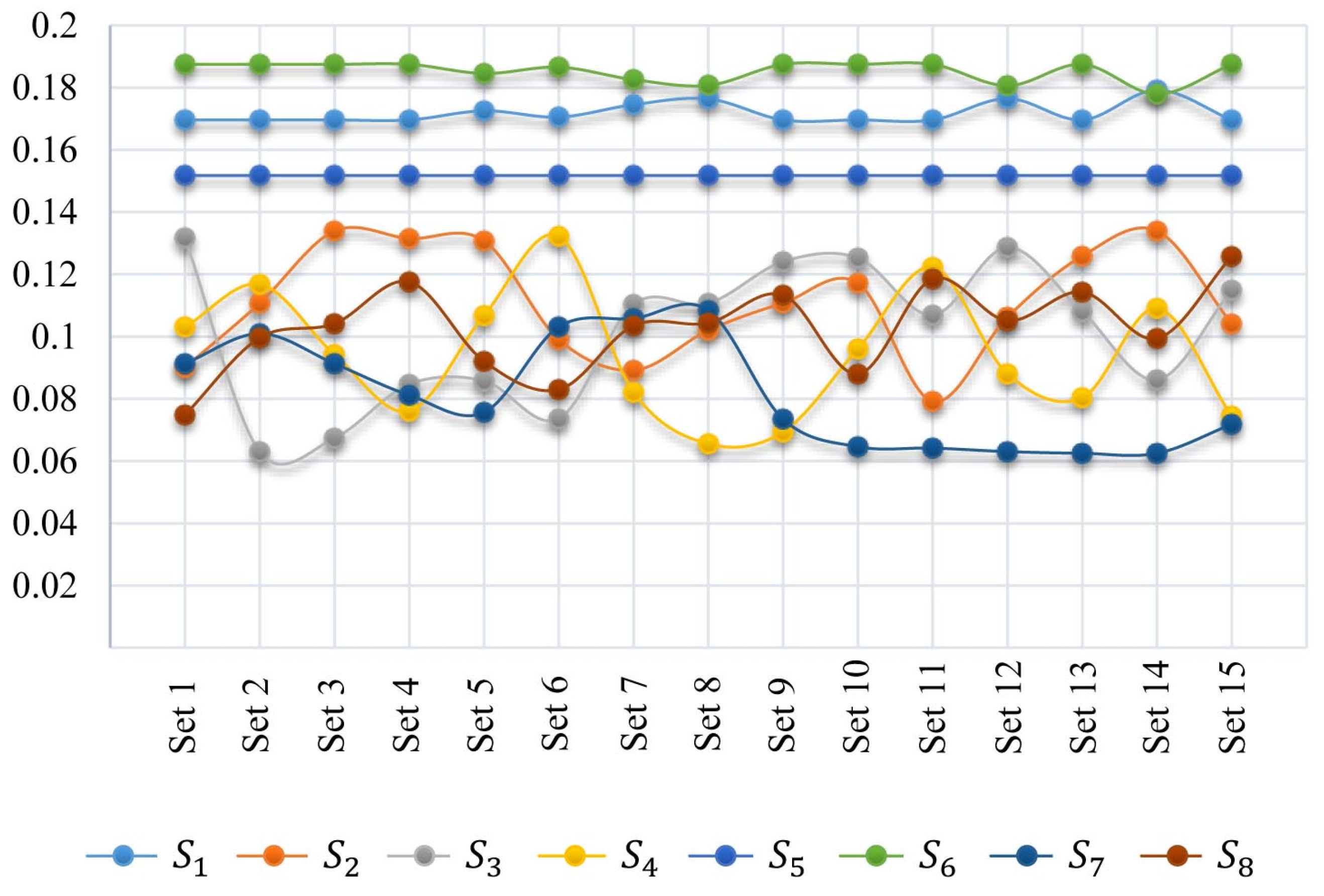
4.2. Sensitivity Analysis
4.3. Comparative Analysis
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vahidi, F.; Torabi, S.A.; Ramezankhani, M.J. Sustainable supplier selection and order allocation under operational and disruption risks. J. Clean. Prod. 2018, 174, 1351–1365. [Google Scholar] [CrossRef]
- Ghadimi, P.; Ghassemi Toosi, F.; Heavey, C. A multi-agent systems approach for sustainable supplier selection and order allocation in a partnership supply chain. Eur. J. Oper. Res. 2018, 269, 286–301. [Google Scholar] [CrossRef]
- Ashby, A.; Leat, M.; Hudson-Smith, M. Making connections: A review of supply chain management and sustainability literature. Supply Chain. Manag. Int. J. 2012, 17, 497–516. [Google Scholar] [CrossRef]
- Giri, B.C.; Molla, M.U.; Biswas, P. Pythagorean fuzzy DEMATEL method for supplier selection in sustainable supply chain management. Expert Syst. Appl. 2022, 193, 116396. [Google Scholar] [CrossRef]
- Yadav, S.; Choi, T.-M.; Kumar, A.; Luthra, S.; Naz, F. A meta-analysis of sustainable supply chain practices and performance: The moderating roles of type of economy and innovation. Int. J. Oper. Prod. Manag. 2023, 43, 802–845. [Google Scholar] [CrossRef]
- Acerbi, F.; Rocca, R.; Fumagalli, L.; Taisch, M. Enhancing the cosmetics industry sustainability through a renewed sustainable supplier selection model. Prod. Manuf. Res. 2023, 11, 2161021. [Google Scholar] [CrossRef]
- Wilhelm, M.M.; Blome, C.; Bhakoo, V.; Paulraj, A. Sustainability in multi-tier supply chains: Understanding the double agency role of the first-tier supplier. J. Oper. Manag. 2016, 41, 42–60. [Google Scholar] [CrossRef]
- Manupati, V.K.; Schoenherr, T.; Ramkumar, M.; Wagner, S.M.; Pabba, S.K.; Inder Raj Singh, R. A blockchain-based approach for a multi-echelon sustainable supply chain. Int. J. Prod. Res. 2020, 58, 2222–2241. [Google Scholar] [CrossRef]
- Zeballos, L.J.; Méndez, C.A.; Barbosa-Povoa, A.P.; Novais, A.Q. Multi-period design and planning of closed-loop supply chains with uncertain supply and demand. Comput. Chem. Eng. 2014, 66, 151–164. [Google Scholar] [CrossRef]
- Rösner, T. Supplier selection and order allocation in purchasing and supply management: A systematic literature review. Int. J. Procure. Manag. 2022, 16, 31–74. [Google Scholar] [CrossRef]
- Gören, H.G. A decision framework for sustainable supplier selection and order allocation with lost sales. J. Clean. Prod. 2018, 183, 1156–1169. [Google Scholar] [CrossRef]
- Tronnebati, I.; El Yadari, M.; Jawab, F. A Review of Green Supplier Evaluation and Selection Issues Using MCDM, MP and AI Models. Sustainability 2022, 14, 16714. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antuchevičienė, J. Ranking of Bridge Design Alternatives: A TOPSIS-FADR Method. Balt. J. Road Bridge Eng. 2018, 13, 209–237. [Google Scholar] [CrossRef]
- Resende, C.H.L.; Geraldes, C.A.S.; Lima, F.R. Decision Models for Supplier Selection in Industry 4.0 Era: A Systematic Literature Review. Procedia Manuf. 2021, 55, 492–499. [Google Scholar] [CrossRef]
- Paul, A.; Shukla, N.; Paul, S.K.; Trianni, A. Sustainable Supply Chain Management and Multi-Criteria Decision-Making Methods: A Systematic Review. Sustainability 2021, 13, 7104. [Google Scholar] [CrossRef]
- Gupta, P.; Govindan, K.; Mehlawat, M.K.; Kumar, S. A weighted possibilistic programming approach for sustainable vendor selection and order allocation in fuzzy environment. Int. J. Adv. Manuf. Technol. 2016, 86, 1785–1804. [Google Scholar] [CrossRef]
- De Capua, C.; Morello, R.; Carbone, R. Measurement uncertainty in decision-making: How to take reliable decisions under uncertainty. Int. J. Meas. Technol. Instrum. Eng. 2011, 1, 40–52. [Google Scholar] [CrossRef]
- Chen, K.-S.; Chang, T.-C.; Huang, C.-C. Supplier Selection by Fuzzy Assessment and Testing for Process Quality under Consideration with Data Imprecision. Mathematics 2020, 8, 1420. [Google Scholar] [CrossRef]
- Xie, Y.; He, L.; Xiang, W.; Peng, Z.; Ming, X.; Goh, M. Prioritizing risk factors in sustainable supply chain using fuzzy Kano and interval-valued intuitionistic fuzzy QFD. Kybernetes 2022. [Google Scholar] [CrossRef]
- Smets, P. Imperfect Information: Imprecision and Uncertainty. In Uncertainty Management in Information Systems: From Needs to Solutions; Motro, A., Smets, P., Eds.; Springer: Boston, MA, USA, 1997; pp. 225–254. [Google Scholar] [CrossRef]
- Gonzalez, A.; Pons, O.; Vila, M.A. Dealing with uncertainty and imprecision by means of fuzzy numbers. Int. J. Approx. Reason. 1999, 21, 233–256. [Google Scholar] [CrossRef]
- Kaya, I.; Çolak, M.; Terzi, F. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Farid, H.M.A.; Bouye, M.; Riaz, M.; Jamil, N. Fermatean Fuzzy CODAS Approach with Topology and Its Application to Sustainable Supplier Selection. Symmetry 2023, 15, 433. [Google Scholar] [CrossRef]
- Hailiang, Z.; Khokhar, M.; Islam, T.; Sharma, A. A model for green-resilient supplier selection: Fuzzy best–worst multi-criteria decision-making method and its applications. Environ. Sci. Pollut. Res. 2023, 30, 54035–54058. [Google Scholar] [CrossRef] [PubMed]
- Kaya, S.K. A novel two-phase group decision-making model for circular supplier selection under picture fuzzy environment. Environ. Sci. Pollut. Res. 2023, 30, 34135–34157. [Google Scholar] [CrossRef] [PubMed]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. Supplier evaluation and selection in fuzzy environments: A review of MADM approaches. Econ. Res.-Ekon. Istraz. 2017, 30, 1073–1118. [Google Scholar] [CrossRef]
- Güneri, B.; Deveci, M. Evaluation of supplier selection in the defense industry using q-rung orthopair fuzzy set based EDAS approach. Expert Syst. Appl. 2023, 222, 119846. [Google Scholar] [CrossRef]
- Celik, E.; Gul, M. Hazard identification, risk assessment and control for dam construction safety using an integrated BWM and MARCOS approach under interval type-2 fuzzy sets environment. Autom. Constr. 2021, 127, 103699. [Google Scholar] [CrossRef]
- Liu, P.; Gao, H.; Ma, J. Novel green supplier selection method by combining quality function deployment with partitioned Bonferroni mean operator in interval type-2 fuzzy environment. Inf. Sci. 2019, 490, 292–316. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Amiri, M.; Antucheviciene, J. Evaluation by an area-based method of ranking interval type-2 fuzzy sets (EAMRIT-2F) for multi-criteria group decision-making. Transform. Bus. Econ. 2016, 15, 76–95. [Google Scholar]
- Ecer, F. Multi-criteria decision making for green supplier selection using interval type-2 fuzzy AHP: A case study of a home appliance manufacturer. Oper. Res. 2022, 22, 199–233. [Google Scholar] [CrossRef]
- Yucesan, M.; Mete, S.; Serin, F.; Celik, E.; Gul, M. An Integrated Best-Worst and Interval Type-2 Fuzzy TOPSIS Methodology for Green Supplier Selection. Mathematics 2019, 7, 182. [Google Scholar] [CrossRef]
- Hoseini, S.A.; Hashemkhani Zolfani, S.; Skačkauskas, P.; Fallahpour, A.; Saberi, S. A Combined Interval Type-2 Fuzzy MCDM Framework for the Resilient Supplier Selection Problem. Mathematics 2022, 10, 44. [Google Scholar] [CrossRef]
- Boral, S.; Chaturvedi, S.K.; Howard, I.; Naikan, V.N.A.; McKee, K. An integrated interval type-2 fuzzy sets and multiplicative half quadratic programming-based MCDM framework for calculating aggregated risk ranking results of failure modes in FMECA. Process Saf. Environ. Prot. 2021, 150, 194–222. [Google Scholar] [CrossRef]
- Boral, S.; Chakraborty, S. Failure analysis of CNC machines due to human errors: An integrated IT2F-MCDM-based FMEA approach. Eng. Fail. Anal. 2021, 130, 105768. [Google Scholar] [CrossRef]
- Celik, E.; Gul, M.; Aydin, N.; Gumus, A.T.; Guneri, A.F. A comprehensive review of multi criteria decision making approaches based on interval type-2 fuzzy sets. Knowl. Based Syst. 2015, 85, 329–341. [Google Scholar] [CrossRef]
- Zardari, N.H.; Ahmed, K.; Shirazi, S.M.; Yusop, Z.B. Weighting Methods and their Effects on Multi-Criteria Decision Making Model Outcomes in Water Resources Management; Springer: New York, NY, USA, 2014. [Google Scholar]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of Objective Weights Using a New Method Based on the Removal Effects of Criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektron. Ir. Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, E.; Fallah Nezhad, M.S.; Pourmohammadi, H.; Honarvar, M.; Vahdatzad, M.A. A joint supplier selection and order allocation model with disruption risks in centralized supply chain. Comput. Ind. Eng. 2019, 127, 734–748. [Google Scholar] [CrossRef]
- Moheb-Alizadeh, H.; Handfield, R. Sustainable supplier selection and order allocation: A novel multi-objective programming model with a hybrid solution approach. Comput. Ind. Eng. 2019, 129, 192–209. [Google Scholar] [CrossRef]
- Hosseini, S.; Morshedlou, N.; Ivanov, D.; Sarder, M.D.; Barker, K.; Khaled, A.A. Resilient supplier selection and optimal order allocation under disruption risks. Int. J. Prod. Econ. 2019, 213, 124–137. [Google Scholar] [CrossRef]
- Kellner, F.; Utz, S. Sustainability in supplier selection and order allocation: Combining integer variables with Markowitz portfolio theory. J. Clean. Prod. 2019, 214, 462–474. [Google Scholar] [CrossRef]
- Duan, C.-Y.; Liu, H.-C.; Zhang, L.-J.; Shi, H. An Extended Alternative Queuing Method with Linguistic Z-numbers and Its Application for Green Supplier Selection and Order Allocation. Int. J. Fuzzy Syst. 2019, 21, 2510–2523. [Google Scholar] [CrossRef]
- Mohammed, A.; Harris, I.; Govindan, K. A hybrid MCDM-FMOO approach for sustainable supplier selection and order allocation. Int. J. Prod. Econ. 2019, 217, 171–184. [Google Scholar] [CrossRef]
- Safaeian, M.; Fathollahi-Fard, A.M.; Tian, G.; Li, Z.; Ke, H. A multi-objective supplier selection and order allocation through incremental discount in a fuzzy environment. J. Intell. Fuzzy Syst. 2019, 37, 1435–1455. [Google Scholar] [CrossRef]
- Alegoz, M.; Yapicioglu, H. Supplier selection and order allocation decisions under quantity discount and fast service options. Sustain. Prod. Consum. 2019, 18, 179–189. [Google Scholar] [CrossRef]
- Mari, S.I.; Memon, M.S.; Ramzan, M.B.; Qureshi, S.M.; Iqbal, M.W. Interactive Fuzzy Multi Criteria Decision Making Approach for Supplier Selection and Order Allocation in a Resilient Supply Chain. Mathematics 2019, 7, 137. [Google Scholar] [CrossRef]
- Laosirihongthong, T.; Samaranayake, P.; Nagalingam, S. A holistic approach to supplier evaluation and order allocation towards sustainable procurement. Benchmarking Int. J. 2019, 26, 2543–2573. [Google Scholar] [CrossRef]
- Feng, J.; Gong, Z. Integrated linguistic entropy weight method and multi-objective programming model for supplier selection and order allocation in a circular economy: A case study. J. Clean. Prod. 2020, 277, 122597. [Google Scholar] [CrossRef]
- Khoshfetrat, S.; Rahiminezhad Galankashi, M.; Almasi, M. Sustainable supplier selection and order allocation: A fuzzy approach. Eng. Optim. 2020, 52, 1494–1507. [Google Scholar] [CrossRef]
- Jia, R.; Liu, Y.; Bai, X. Sustainable supplier selection and order allocation: Distributionally robust goal programming model and tractable approximation. Comput. Ind. Eng. 2020, 140, 106267. [Google Scholar] [CrossRef]
- Wong, J.-T. Dynamic procurement risk management with supplier portfolio selection and order allocation under green market segmentation. J. Clean. Prod. 2020, 253, 119835. [Google Scholar] [CrossRef]
- You, S.-Y.; Zhang, L.-J.; Xu, X.-G.; Liu, H.-C. A New Integrated Multi-Criteria Decision Making and Multi-Objective Programming Model for Sustainable Supplier Selection and Order Allocation. Symmetry 2020, 12, 302. [Google Scholar] [CrossRef]
- Rezaei, A.; Rahiminezhad Galankashi, M.; Mansoorzadeh, S.; Mokhatab Rafiei, F. Supplier Selection and Order Allocation with Lean Manufacturing Criteria: An Integrated MCDM and Bi-objective Modelling Approach. Eng. Manag. J. 2020, 32, 253–271. [Google Scholar] [CrossRef]
- Kaviani, M.A.; Peykam, A.; Khan, S.A.; Brahimi, N.; Niknam, R. A new weighted fuzzy programming model for supplier selection and order allocation in the food industry. J. Model. Manag. 2020, 15, 381–406. [Google Scholar] [CrossRef]
- Rezaei, S.; Ghalehkhondabi, I.; Rafiee, M.; Namdar Zanganeh, S. Supplier selection and order allocation in CLSC configuration with various supply strategies under disruption risk. OPSEARCH 2020, 57, 908–934. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Q.; Dai, S. Supplier Selection and Order Allocation under a Carbon Emission Trading Scheme: A Case Study from China. Int. J. Environ. Res. Public Health 2020, 17, 111. [Google Scholar] [CrossRef] [PubMed]
- Çalık, A. A hybrid approach for selecting sustainable suppliers and determining order allocation based on interval type-2 fuzzy sets. J. Enterp. Inf. Manag. 2020, 33, 923–945. [Google Scholar] [CrossRef]
- Khalili Nasr, A.; Tavana, M.; Alavi, B.; Mina, H. A novel fuzzy multi-objective circular supplier selection and order allocation model for sustainable closed-loop supply chains. J. Clean. Prod. 2021, 287, 124994. [Google Scholar] [CrossRef]
- Kaur, H.; Prakash Singh, S. Multi-stage hybrid model for supplier selection and order allocation considering disruption risks and disruptive technologies. Int. J. Prod. Econ. 2021, 231, 107830. [Google Scholar] [CrossRef]
- Islam, S.; Amin, S.H.; Wardley, L.J. Machine learning and optimization models for supplier selection and order allocation planning. Int. J. Prod. Econ. 2021, 242, 108315. [Google Scholar] [CrossRef]
- Rezaei, A.; Aghsami, A.; Rabbani, M. Supplier selection and order allocation model with disruption and environmental risks in centralized supply chain. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 1036–1072. [Google Scholar] [CrossRef]
- Firouzi, F.; Jadidi, O. Multi-objective model for supplier selection and order allocation problem with fuzzy parameters. Expert Syst. Appl. 2021, 180, 115129. [Google Scholar] [CrossRef]
- Li, F.; Wu, C.-H.; Zhou, L.; Xu, G.; Liu, Y.; Tsai, S.-B. A model integrating environmental concerns and supply risks for dynamic sustainable supplier selection and order allocation. Soft. Comput. 2021, 25, 535–549. [Google Scholar] [CrossRef]
- Yousefi, S.; Jahangoshai Rezaee, M.; Solimanpur, M. Supplier selection and order allocation using two-stage hybrid supply chain model and game-based order price. Oper. Res. 2021, 21, 553–588. [Google Scholar] [CrossRef]
- Beiki, H.; Mohammad Seyedhosseini, S.; Ponkratov, V.; Olegovna Zekiy, A.; Ivanov, S.A. Addressing a sustainable supplier selection and order allocation problem by an integrated approach: A case of automobile manufacturing. J. Ind. Prod. Eng. 2021, 38, 239–253. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, E.; Azad, N.; Saber Fallah Nezhad, M. Risk-averse supplier selection and order allocation in the centralized supply chains under disruption risks. Expert Syst. Appl. 2021, 175, 114691. [Google Scholar] [CrossRef]
- Mohammed, A.; Harris, I.; Soroka, A.; Naim, M.; Ramjaun, T.; Yazdani, M. Gresilient supplier assessment and order allocation planning. Ann. Oper. Res. 2021, 296, 335–362. [Google Scholar] [CrossRef]
- Hosseini, Z.S.; Flapper, S.D.; Pirayesh, M. Sustainable supplier selection and order allocation under demand, supplier availability and supplier grading uncertainties. Comput. Ind. Eng. 2022, 165, 107811. [Google Scholar] [CrossRef]
- Ali, H.; Zhang, J.; Liu, S.; Shoaib, M. An integrated decision-making approach for global supplier selection and order allocation to create an environment-friendly supply chain. Kybernetes 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Goodarzi, F.; Abdollahzadeh, V.; Zeinalnezhad, M. An integrated multi-criteria decision-making and multi-objective optimization framework for green supplier evaluation and optimal order allocation under uncertainty. Decis. Anal. J. 2022, 4, 100087. [Google Scholar] [CrossRef]
- Liaqait, R.A.; Warsi, S.S.; Agha, M.H.; Zahid, T.; Becker, T. A multi-criteria decision framework for sustainable supplier selection and order allocation using multi-objective optimization and fuzzy approach. Eng. Optim. 2022, 54, 928–948. [Google Scholar] [CrossRef]
- Gai, L.; Liu, H.-C.; Wang, Y.; Xing, Y. Green supplier selection and order allocation using linguistic Z-numbers MULTIMOORA method and bi-objective non-linear programming. Fuzzy Optim. Decis. Mak. 2022. [Google Scholar] [CrossRef]
- Aouadni, S.; Euchi, J. Using Integrated MMD-TOPSIS to Solve the Supplier Selection and Fair Order Allocation Problem: A Tunisian Case Study. Logistics 2022, 6, 8. [Google Scholar] [CrossRef]
- Galankashi, M.R.; Rezaei, A.; Keyvanpazhooh, M.; Rafiei, F.M. Assessment of suppliers and optimum order allocation in agile automotive manufacturing companies. Int. J. Ind. Syst. Eng. 2022, 42, 245–276. [Google Scholar] [CrossRef]
- Liu, P.; Hendalianpour, A.; Fakhrabadi, M.; Feylizadeh, M. Integrating IVFRN-BWM and Goal Programming to Allocate the Order Quantity Considering Discount for Green Supplier. Int. J. Fuzzy Syst. 2022, 24, 989–1011. [Google Scholar] [CrossRef]
- Bai, C.; Zhu, Q.; Sarkis, J. Supplier portfolio selection and order allocation under carbon neutrality: Introducing a “Cool”ing model. Comput. Ind. Eng. 2022, 170, 108335. [Google Scholar] [CrossRef]
- Ahmad, M.T.; Firouz, M.; Mondal, S. Robust supplier-selection and order-allocation in two-echelon supply networks: A parametric tolerance design approach. Comput. Ind. Eng. 2022, 171, 108394. [Google Scholar] [CrossRef]
- Chen, S.-M.; Lee, L.-W. Fuzzy multiple attributes group decision-making based on the interval type-2 TOPSIS method. Expert Syst. Appl. 2010, 37, 2790–2798. [Google Scholar] [CrossRef]
- Celik, E.; Bilisik, O.N.; Erdogan, M.; Gumus, A.T.; Baracli, H. An integrated novel interval type-2 fuzzy MCDM method to improve customer satisfaction in public transportation for Istanbul. Transp. Res. Part E Logist. Transp. Rev. 2013, 58, 28–51. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Salehi Sadaghiani, J.; Zavadskas, E.K. Multi-criteria project selection using an extended VIKOR method with interval type-2 fuzzy sets. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 993–1016. [Google Scholar] [CrossRef]
- Kahraman, C.; Öztayşi, B.; Uçal Sarı, İ.; Turanoğlu, E. Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowl. Based Syst. 2014, 59, 48–57. [Google Scholar] [CrossRef]
- Lee, E.S.; Li, R.J. Comparison of fuzzy numbers based on the probability measure of fuzzy events. Comput. Math. Appl. 1988, 15, 887–896. [Google Scholar] [CrossRef]
- Cheng, C.-H. A new approach for ranking fuzzy numbers by distance method. Fuzzy Sets Syst. 1998, 95, 307–317. [Google Scholar] [CrossRef]
- Chu, T.-C.; Tsao, C.-T. Ranking fuzzy numbers with an area between the centroid point and original point. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Deng, Y.; Zhenfu, Z.; Qi, L. Ranking fuzzy numbers with an area method using radius of gyration. Comput. Math. Appl. 2006, 51, 1127–1136. [Google Scholar] [CrossRef]
- Xu, Z. Algorithm for priority of fuzzy complementary judgment matrix. J. Syst. Eng. 2001, 16, 311–314. [Google Scholar]
- Chen, S.-M.; Lee, L.-W. Fuzzy multiple attributes group decision-making based on the ranking values and the arithmetic operations of interval type-2 fuzzy sets. Expert Syst. Appl. 2010, 37, 824–833. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zakuan, N.; Loganathan, N.; Soheilirad, S.; Saman, M.Z.M.; Ibrahim, O. A systematic review and meta-Analysis of SWARA and WASPAS methods: Theory and applications with recent fuzzy developments. Appl. Soft. Comput. 2017, 57, 265–292. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Schramm, V.B.; Cabral, L.P.B.; Schramm, F. Approaches for supporting sustainable supplier selection—A literature review. J. Clean. Prod. 2020, 273, 123089. [Google Scholar] [CrossRef]
- Zimmer, K.; Fröhling, M.; Schultmann, F. Sustainable supplier management—A review of models supporting sustainable supplier selection, monitoring and development. Int. J. Prod. Res. 2016, 54, 1412–1442. [Google Scholar] [CrossRef]
- Rashidi, K.; Noorizadeh, A.; Kannan, D.; Cullinane, K. Applying the triple bottom line in sustainable supplier selection: A meta-review of the state-of-the-art. J. Clean. Prod. 2020, 269, 122001. [Google Scholar] [CrossRef]
- Koberg, E.; Longoni, A. A systematic review of sustainable supply chain management in global supply chains. J. Clean. Prod. 2019, 207, 1084–1098. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M. Supplementary data for “Sustainable supplier selection and order allocation using an integrated ROG-based type-2 fuzzy decision-making approach”. Figshare 2023. [Google Scholar] [CrossRef]
- Walters, S.J. Quality of Life Outcomes in Clinical Trials and Health-Care Evaluation: A Practical Guide to Analysis and Interpretation; Wiley: New York, NY, USA, 2009. [Google Scholar]


| No. | Author(s) and Reference | Year of Publication | Description of the Approach for SSOA |
|---|---|---|---|
| 1 | Esmaeili-Najafabadi et al. [40] | 2019 | An MINLP model that incorporates two precautionary measures aimed at mitigating disruption risks |
| 2 | Moheb-Alizadeh and Handfield [41] | 2019 | An MODM model considering multiple periods, products, and transportation modes |
| 3 | Hosseini et al. [42] | 2019 | A graphical model to obtain the likelihood of disruption scenarios for SSOA |
| 4 | Kellner and Utz [43] | 2019 | An MODM model for evaluation of supplier sustainability based on costs and supply risk. |
| 5 | Duan et al. [44] | 2019 | An integrated model for SSOA by combining AQM, linguistic Z-numbers, and an MODM model |
| 6 | Mohammed et al. [45] | 2019 | A hybrid approach based on AHP, fuzzy TOPSIS and an MODM model |
| 7 | Safaeian et al. [46] | 2019 | An MODM model based on the Zimmermann fuzzy approach and NSGA |
| 8 | Alegoz and Yapicioglu [47] | 2019 | A hybrid approach based on trapezoidal type-2 fuzzy AHP, fuzzy TOPSIS and goal programming |
| 9 | Mari et al. [48] | 2019 | A possibilistic fuzzy MODM model and an interactive fuzzy optimization methodology |
| 10 | Laosirihongthong et al. [49] | 2019 | An approach based on the fuzzy AHP and a cost-minimization model |
| 11 | Feng and Gong [50] | 2020 | An integrated approach using MODM and the linguistic entropy weight method |
| 12 | Khoshfetrat et al. [51] | 2020 | An integrated approach based on AHP and MODM model in a fuzzy environment |
| 13 | Jia et al. [52] | 2020 | A robust MODM model based on four conflicting objectives |
| 14 | Wong [53] | 2020 | A fuzzy goal programming model that considered various factors like suppliers’ dynamic risk |
| 15 | You et al. [54] | 2020 | A framework that employed Double Hierarchy Hesitant Linguistic Term Sets |
| 16 | Rezaei et al. [55] | 2020 | An integrated approach using the AHP method and MODM model |
| 17 | Kaviani et al. [56] | 2020 | An approach that combined fuzzy multi-objective optimization and intuitionistic fuzzy AHP |
| 18 | Rezaei et al. [57] | 2020 | A two-stage model based on stochastic programming that uses a conditional value-at-risk |
| 19 | Wang et al. [58] | 2020 | A model based on ANP and integer programming |
| 20 | Çalık [59] | 2020 | An approach based on the AHP method, interval type-2 fuzzy sets and MODM model |
| 21 | Khalili Nasr et al. [60] | 2021 | A two-stage model based on a fuzzy BWM and a linear MODM model |
| 22 | Kaur and Prakash Singh [61] | 2021 | An integrated approach based on DEA, fuzzy AHP, and TOPSIS |
| 23 | Islam et al. [62] | 2021 | A new two-stage approach based on a Relational Regressor Chain, ε-constraint and weighted-sum methods |
| 24 | Rezaei et al. [63] | 2021 | A framework based on MINLP models, risk reduction strategies and FMEA technique |
| 25 | Firouzi and Jadidi [64] | 2021 | A fuzzy MODM model that could manage the uncertainties brought about by disasters |
| 26 | Li et al. [65] | 2021 | An approach based on the risk value assessed and an MODM model |
| 27 | Yousefi et al. [66] | 2021 | A two-stage hybrid approach that employed DEA and an MODM model |
| 28 | Beiki et al. [67] | 2021 | A new approach by combining an MODM model with the language entropy weight method |
| 29 | Esmaeili-Najafabadi et al. [68] | 2021 | A multi-objective approach based on VaR, CVaR, and PSO |
| 30 | Mohammed et al. [69] | 2021 | An integrated approach based on AHP, TOPSIS, and the ε-constraint method |
| 31 | Hosseini et al. [70] | 2022 | An approach based on the evidential reasoning, BWM, stochastic programming and dynamic programming |
| 32 | Ali et al. [71] | 2022 | A hybrid approach using fuzzy AHP, fuzzy TOPSIS and an MODM model |
| 33 | Goodarzi et al. [72] | 2022 | A framework based on fuzzy Delphi, Gray Correlation method, TOPSIS and MODM models |
| 34 | Liaqait et al. [73] | 2022 | Fuzzy MCDM techniques, demand forecasting, and MODM mathematical models |
| 35 | Gai et al. [74] | 2022 | A two-stage approach that incorporated linguistic Z-Numbers, MULTIMOORA, and an MODM model |
| 36 | Aouadni and Euchi [75] | 2022 | A hybrid methodology based on BWM, TOPSIS and bi-objective programming |
| 37 | Galankashi et al. [76] | 2022 | An integrated approach based on a fuzzy AHP and an MODM model with multiple periods |
| 38 | Liu et al. [77] | 2022 | An approach based on a modified BWM method and goal programming |
| 39 | Bai et al. [78] | 2022 | An MODM mathematical model that can assess various procurement policies |
| 40 | Ahmad et al. [79] | 2022 | An integrated approach based on an MINLP model and the Taguchi Method of Tolerance Design |
| Linguistic Variables | Trapezoidal IT2FSs |
|---|---|
| Very Poor (VP) | ((0, 0, 0, 1; 1), (0, 0, 0, 0.5; 0.9)) |
| Poor (P) | ((0, 1, 1.5, 3; 1), (0.5, 1, 1.5, 2; 0.9)) |
| Medium Poor (MP) | ((1, 3, 3.5, 5; 1), (2, 3, 3.5, 4; 0.9)) |
| Fair (F) | ((3, 5, 5.5, 7; 1), (4, 5, 5.5, 6; 0.9)) |
| Medium Good (MG) | ((5, 7, 7.5, 9; 1), (6, 7, 7.5, 8; 0.9)) |
| Good (G) | ((7, 8.5, 9, 10; 1), (8, 8.5, 9, 9.5; 0.9)) |
| Very Good (VG) | ((9, 10, 10, 10; 1), (9.5, 10, 10, 10; 0.9)) |
| Parameters/Variables | Description |
|---|---|
| Unit purchasing cost of the th supplier for th production center | |
| Distance between th supplier and th production center | |
| The relative score of th supplier | |
| Minimum quantity to be ordered from th supplier | |
| Supply capacity of th supplier | |
| Demand of th production center | |
| Minimum number of suppliers that need to be selected | |
| Variable: order quantity of the th supplier for th production center | |
| Binary variable: = 1 if th supplier is selected; = 0 otherwise | |
| Total purchasing cost | |
| Minimum value of | |
| Maximum value of | |
| Total distance-based measure | |
| Minimum value of | |
| Maximum value of | |
| Total relative score of selected suppliers | |
| Minimum value of | |
| Maximum value of |
| Expert | Department | Job Title | Years of Experience | Gender | Academic Degree |
|---|---|---|---|---|---|
| Procurement department | Purchasing Director | 8 | Male | PhD in Management | |
| Procurement department | Sourcing Specialist | 6 | Female | MA in Business Management | |
| Operations department | Operations Manager | 7 | Male | PhD in Operations Research | |
| Operations department | Supply Chain Analyst | 2 | Female | BA in Industrial Engineering | |
| Finance department | Finance manager | 8 | Female | MA in Accounting & Finance | |
| Finance department | Risk analyst | 4 | Male | BA in Accounting & Finance | |
| Marketing department | Chief marketing officer | 7 | Male | MA in Marketing | |
| R&D department | Project manager | 10 | Male | PhD in Industrial Engineering |
| Dimension | Criteria | Description |
|---|---|---|
| Environmental sustainability | Climate change mitigation () | This involves reducing greenhouse gas emissions and implementing measures to mitigate the effects of climate change, such as investing in renewable energy, improving energy efficiency, and adopting low-carbon transportation options. |
| Resource conservation () | This involves reducing the consumption of non-renewable resources and conserving natural resources such as water, land, and forests. Companies can achieve this by implementing sustainable sourcing practices, using recycled materials, and minimizing waste. | |
| Pollution prevention () | This involves minimizing or eliminating the release of harmful substances into the environment, such as toxic chemicals or air pollutants. Companies can achieve this by implementing pollution prevention measures, such as using clean production processes, reducing emissions, and properly disposing of hazardous waste. | |
| Biodiversity conservation () | This involves protecting and conserving biodiversity and ecosystem services, such as pollination, soil fertility, and water quality. Companies can achieve this by using sustainable land management practices, protecting endangered species and habitats, and reducing deforestation. | |
| Adoption of circular economy principles () | This involves moving away from the traditional linear model of “take-make-dispose” and instead adopting a circular economy model where waste is minimized and resources are kept in use for as long as possible. This can be achieved by implementing recycling programs, designing products for reuse, and finding ways to extend the lifespan of products. | |
| Social sustainability | Labor standards () | This involves ensuring fair wages, safe working conditions, and other labor standards throughout the supply chain. Companies can achieve this by implementing codes of conduct for suppliers, auditing their supply chains for compliance, and providing training and support to suppliers to help them meet these standards. |
| Human rights () | This involves respecting and promoting human rights, including freedom from discrimination, the right to privacy, and the right to freedom of association. Companies can achieve this by implementing human rights policies, engaging with stakeholders to understand their concerns, and monitoring their supply chains to identify and address human rights abuses. | |
| Community engagement () | This involves engaging with local communities in a respectful and transparent manner, and taking their concerns into account in decision-making processes. Companies can achieve this by implementing community engagement strategies, conducting impact assessments to understand the potential impacts of their operations on local communities, and providing support to local communities to help build their capacity and improve their well-being. | |
| Health and safety () | This involves ensuring that the health and safety of workers and local communities are protected from harm. Companies can achieve this by implementing health and safety policies and procedures, providing training and support to workers and suppliers, and conducting risk assessments to identify and address potential health and safety hazards. | |
| Diversity and inclusion () | This involves promoting diversity and inclusion throughout the supply chain, including ensuring that women and other underrepresented groups have equal opportunities to participate in economic activities. Companies can achieve this by implementing diversity and inclusion policies and programs, providing training and support to suppliers, and monitoring their supply chains for compliance. | |
| Economic sustainability | Cost-efficiency () | This involves reducing costs while maintaining or improving the quality of products and services. Companies can achieve this by implementing efficiency measures, such as improving production processes, reducing waste, and optimizing logistics and transportation. |
| Innovation () | This involves developing and implementing new products, services, or business models that create value for the company and its stakeholders. Companies can achieve this by investing in research and development, collaborating with other organizations to share knowledge and expertise, and exploring new markets or opportunities. | |
| Resilience () | This involves building resilience into the supply chain to ensure that it can withstand disruptions, such as natural disasters, political instability, or economic downturns. Companies can achieve this by diversifying their suppliers, implementing risk management strategies, and maintaining adequate inventory levels. | |
| Responsible investment () | This involves investing in companies or projects that have a positive impact on the environment, society, or economy. Companies can achieve this by implementing responsible investment policies, conducting due diligence on potential investments, and engaging with stakeholders to understand their concerns. | |
| Long-term perspective () | This involves taking a long-term perspective when making business decisions, and considering the potential impacts of those decisions on future generations. Companies can achieve this by implementing sustainability strategies that consider the environmental, social, and economic impacts of their operations over the long term. |
| Sum | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 35 | 45 | 50 | 30 | 30 | 40 | 40 | 310 | 0.0665 | |
| 40 | 45 | 50 | 40 | 35 | 40 | 30 | 30 | 310 | 0.0665 | |
| 30 | 40 | 40 | 40 | 45 | 45 | 50 | 30 | 320 | 0.0687 | |
| 20 | 25 | 25 | 20 | 10 | 20 | 30 | 20 | 170 | 0.0365 | |
| 30 | 20 | 30 | 35 | 40 | 20 | 30 | 20 | 225 | 0.0483 | |
| 40 | 50 | 60 | 30 | 30 | 40 | 45 | 50 | 345 | 0.0740 | |
| 25 | 20 | 20 | 30 | 35 | 25 | 20 | 25 | 200 | 0.0429 | |
| 30 | 30 | 40 | 40 | 30 | 40 | 30 | 30 | 270 | 0.0579 | |
| 30 | 40 | 40 | 45 | 35 | 40 | 20 | 25 | 275 | 0.0590 | |
| 15 | 10 | 10 | 15 | 20 | 10 | 10 | 20 | 110 | 0.0236 | |
| 60 | 70 | 60 | 80 | 80 | 70 | 75 | 70 | 565 | 0.1212 | |
| 40 | 50 | 50 | 40 | 30 | 40 | 45 | 50 | 345 | 0.0740 | |
| 40 | 30 | 50 | 45 | 35 | 50 | 45 | 45 | 340 | 0.0730 | |
| 50 | 60 | 60 | 50 | 70 | 60 | 70 | 60 | 480 | 0.1030 | |
| 45 | 50 | 55 | 60 | 45 | 40 | 60 | 40 | 395 | 0.0848 |
| VG | G | P | MG | P | G | MP | MG | VG | F | G | G | VG | MG | VG | ||
| MP | MG | F | MP | P | MG | P | MP | P | MG | G | MG | MP | P | VP | ||
| MP | P | MP | P | VP | MG | F | VP | MP | P | F | F | MP | F | F | ||
| P | MG | P | F | MG | VP | MP | MP | P | F | P | MP | MP | F | VP | ||
| MG | P | MP | F | MP | MG | MG | F | P | MP | MG | P | MG | F | F | ||
| G | MP | F | MP | F | G | G | P | G | MG | MG | VG | VG | MG | G | ||
| VP | P | P | MG | MP | MP | MP | F | VP | MP | VP | F | P | F | VP | ||
| MG | P | F | MP | F | P | MP | VP | MP | P | MG | MG | MP | P | P | ||
| MG | G | P | MG | MP | VG | MP | MG | MG | F | G | G | MG | F | MG | ||
| MP | G | MP | P | VP | G | MP | P | P | F | F | MP | P | VP | VP | ||
| P | P | MG | F | P | F | MP | MP | P | P | MG | F | VP | MP | F | ||
| VP | G | MP | MP | MP | VP | P | F | P | F | VP | P | F | F | P | ||
| F | P | F | P | MP | MP | MG | MG | F | MP | MG | F | F | MG | MP | ||
| G | F | MG | F | MG | G | MG | MP | G | F | VG | VG | G | MG | G | ||
| VP | P | P | MP | MP | MP | P | MP | VP | MP | VP | F | MP | MP | MP | ||
| G | MP | MP | VP | MP | P | MP | P | MP | P | MP | F | VP | MP | P | ||
| MG | G | P | MG | MP | VG | MP | MG | MG | F | G | G | MG | F | MG | ||
| MP | G | MP | P | VP | G | MP | P | P | F | F | MP | P | VP | VP | ||
| P | P | MG | F | P | F | MP | MP | P | P | MG | F | VP | MP | F | ||
| VP | G | MP | MP | MP | VP | P | F | P | F | VP | P | F | F | P | ||
| F | P | F | P | MP | MP | MG | MG | F | MP | MG | F | F | MG | MP | ||
| G | F | MG | F | MG | G | MG | MP | G | F | VG | VG | G | MG | G | ||
| VP | P | P | MP | MP | MP | P | MP | VP | MP | VP | F | MP | MP | MP | ||
| G | MP | MP | VP | MP | P | MP | P | MP | P | MP | F | VP | MP | P |
| 6.25 | 7.94 | 8.31 | 9.38 | 1 | 7.13 | 7.94 | 8.31 | 8.69 | 0.9 | |
| 5.75 | 7.5 | 8 | 9.25 | 1 | 6.75 | 7.5 | 8 | 8.5 | 0.9 | |
| 1.25 | 2.75 | 3.25 | 4.75 | 1 | 2 | 2.75 | 3.25 | 3.75 | 0.9 | |
| 3.75 | 5.75 | 6.25 | 7.75 | 1 | 4.75 | 5.75 | 6.25 | 6.75 | 0.9 | |
| 0.38 | 1.5 | 1.88 | 3.25 | 1 | 0.94 | 1.5 | 1.88 | 2.38 | 0.9 | |
| 2.5 | 4.5 | 5 | 6.5 | 1 | 3.5 | 4.5 | 5 | 5.5 | 0.9 | |
| 4.75 | 6.63 | 7.13 | 8.5 | 1 | 5.75 | 6.63 | 7.13 | 7.63 | 0.9 | |
| 0.25 | 1.13 | 1.44 | 2.75 | 1 | 0.69 | 1.13 | 1.44 | 1.94 | 0.9 | |
| 1.5 | 3.25 | 3.75 | 5.25 | 1 | 2.38 | 3.25 | 3.75 | 4.25 | 0.9 | |
| 0 | 0.38 | 0.56 | 1.75 | 1 | 0.19 | 0.38 | 0.56 | 1.06 | 0.9 |
| 8.04 | 3.92 | 1.70 | 0.85 | 5.67 | 9.00 | 1.27 | 6.86 | 0.0811 | 0.0738 | |
| 7.69 | 7.94 | 2.48 | 7.05 | 2.48 | 4.67 | 2.01 | 2.71 | 0.0418 | 0.0542 | |
| 2.98 | 3.45 | 5.92 | 1.79 | 2.96 | 6.55 | 1.32 | 5.42 | 0.0556 | 0.0621 | |
| 5.92 | 1.09 | 3.45 | 3.21 | 2.49 | 3.70 | 5.42 | 1.79 | 0.0608 | 0.0486 | |
| 1.70 | 0.85 | 1.32 | 4.42 | 1.41 | 5.42 | 1.70 | 3.21 | 0.0544 | 0.0514 | |
| 9.29 | 7.44 | 5.17 | 1.18 | 4.92 | 8.76 | 4.92 | 1.09 | 0.0795 | 0.0768 | |
| 4.67 | 2.71 | 3.21 | 0.80 | 7.11 | 6.61 | 3.20 | 4.67 | 0.0883 | 0.0656 | |
| 7.69 | 1.70 | 0.94 | 2.96 | 7.49 | 2.32 | 4.67 | 1.56 | 0.0660 | 0.0620 | |
| 8.23 | 0.85 | 1.56 | 2.48 | 3.45 | 9.15 | 1.18 | 1.56 | 0.0596 | 0.0593 | |
| 4.17 | 4.67 | 1.78 | 6.99 | 4.17 | 5.42 | 3.68 | 2.74 | 0.0482 | 0.0359 | |
| 9.29 | 6.30 | 4.92 | 1.47 | 5.92 | 8.95 | 1.56 | 4.67 | 0.0645 | 0.0929 | |
| 7.69 | 6.17 | 4.67 | 2.23 | 3.20 | 9.44 | 4.92 | 6.80 | 0.0496 | 0.0618 | |
| 8.57 | 3.45 | 0.94 | 3.70 | 5.67 | 9.29 | 2.71 | 1.32 | 0.0748 | 0.0739 | |
| 6.61 | 0.94 | 3.68 | 5.17 | 7.44 | 7.11 | 4.17 | 3.45 | 0.0894 | 0.0962 | |
| 8.95 | 1.03 | 6.99 | 1.00 | 3.70 | 8.85 | 1.41 | 0.56 | 0.0862 | 0.0855 |
| 0.69 | 0.88 | 0.92 | 1.04 | 1 | 0.79 | 0.88 | 0.92 | 0.97 | 0.9 | |
| 0.72 | 0.94 | 1.01 | 1.17 | 1 | 0.85 | 0.94 | 1.01 | 1.07 | 0.9 | |
| 0.19 | 0.42 | 0.5 | 0.73 | 1 | 0.31 | 0.42 | 0.5 | 0.57 | 0.9 | |
| 0.63 | 0.97 | 1.06 | 1.31 | 1 | 0.8 | 0.97 | 1.06 | 1.14 | 0.9 | |
| 0.07 | 0.28 | 0.35 | 0.6 | 1 | 0.17 | 0.28 | 0.35 | 0.44 | 0.9 | |
| 0.27 | 0.48 | 0.54 | 0.7 | 1 | 0.38 | 0.48 | 0.54 | 0.59 | 0.9 | |
| 0.5 | 0.7 | 0.76 | 0.9 | 1 | 0.61 | 0.7 | 0.76 | 0.81 | 0.9 | |
| 0.03 | 0.12 | 0.15 | 0.3 | 1 | 0.07 | 0.12 | 0.15 | 0.21 | 0.9 | |
| 0.2 | 0.44 | 0.5 | 0.71 | 1 | 0.32 | 0.44 | 0.5 | 0.57 | 0.9 | |
| 0 | 0.04 | 0.06 | 0.2 | 1 | 0.02 | 0.04 | 0.06 | 0.12 | 0.9 |
| 0.63 | 0.83 | 0.89 | 1.03 | 1 | 0.74 | 0.83 | 0.89 | 0.94 | 0.9 | |
| 0.22 | 0.39 | 0.45 | 0.62 | 1 | 0.31 | 0.39 | 0.45 | 0.51 | 0.9 | |
| 0.21 | 0.4 | 0.46 | 0.64 | 1 | 0.31 | 0.4 | 0.46 | 0.52 | 0.9 | |
| 0.17 | 0.34 | 0.4 | 0.57 | 1 | 0.26 | 0.34 | 0.4 | 0.46 | 0.9 | |
| 0.35 | 0.57 | 0.63 | 0.81 | 1 | 0.46 | 0.57 | 0.63 | 0.69 | 0.9 | |
| 0.67 | 0.87 | 0.93 | 1.06 | 1 | 0.78 | 0.87 | 0.93 | 0.98 | 0.9 | |
| 0.16 | 0.35 | 0.4 | 0.58 | 1 | 0.25 | 0.35 | 0.4 | 0.46 | 0.9 | |
| 0.21 | 0.39 | 0.44 | 0.62 | 1 | 0.3 | 0.39 | 0.44 | 0.5 | 0.9 | |
| 1.61 | 1.82 | 1.87 | 2.02 | 1 | 1.72 | 1.82 | 1.87 | 1.93 | 0.9 | |
| 1.21 | 1.37 | 1.42 | 1.59 | 1 | 1.29 | 1.37 | 1.42 | 1.48 | 0.9 | |
| 1.2 | 1.39 | 1.44 | 1.62 | 1 | 1.29 | 1.39 | 1.44 | 1.5 | 0.9 | |
| 1.16 | 1.32 | 1.37 | 1.54 | 1 | 1.24 | 1.32 | 1.37 | 1.43 | 0.9 | |
| 1.33 | 1.55 | 1.61 | 1.8 | 1 | 1.44 | 1.55 | 1.61 | 1.68 | 0.9 | |
| 1.65 | 1.86 | 1.91 | 2.06 | 1 | 1.76 | 1.86 | 1.91 | 1.97 | 0.9 | |
| 1.15 | 1.33 | 1.38 | 1.56 | 1 | 1.24 | 1.33 | 1.38 | 1.44 | 0.9 | |
| 1.19 | 1.37 | 1.42 | 1.59 | 1 | 1.28 | 1.37 | 1.42 | 1.48 | 0.9 | |
| 0.78 | 0.95 | 1 | 1.12 | 1 | 0.87 | 0.95 | 1 | 1.04 | 0.9 | |
| 0.45 | 0.59 | 0.63 | 0.77 | 1 | 0.52 | 0.59 | 0.63 | 0.68 | 0.9 | |
| 0.44 | 0.6 | 0.64 | 0.79 | 1 | 0.52 | 0.6 | 0.64 | 0.69 | 0.9 | |
| 0.4 | 0.54 | 0.59 | 0.73 | 1 | 0.48 | 0.54 | 0.59 | 0.64 | 0.9 | |
| 0.55 | 0.73 | 0.78 | 0.93 | 1 | 0.64 | 0.73 | 0.78 | 0.84 | 0.9 | |
| 0.81 | 0.99 | 1.03 | 1.15 | 1 | 0.91 | 0.99 | 1.03 | 1.07 | 0.9 | |
| 0.4 | 0.55 | 0.59 | 0.74 | 1 | 0.47 | 0.55 | 0.59 | 0.64 | 0.9 | |
| 0.43 | 0.58 | 0.62 | 0.77 | 1 | 0.51 | 0.58 | 0.62 | 0.68 | 0.9 |
| Supplier | (Tons) | (Tons) | ( IRR) | ( IRR) | (Km) | (Km) | |
|---|---|---|---|---|---|---|---|
| 0.1696 | 5000 | 40,000 | 200 | 260 | 45 | 150 | |
| 0.1155 | 7000 | 25,000 | 260 | 270 | 30 | 120 | |
| 0.1230 | 4500 | 26,000 | 250 | 260 | 35 | 110 | |
| 0.0717 | 5500 | 26,000 | 260 | 280 | 20 | 80 | |
| 0.1518 | 4000 | 20,000 | 280 | 260 | 40 | 60 | |
| 0.1875 | 5800 | 35,000 | 290 | 200 | 80 | 20 | |
| 0.0711 | 3900 | 15,000 | 280 | 230 | 100 | 25 | |
| 0.1097 | 4200 | 25,000 | 270 | 240 | 130 | 35 | |
| = 50,000 | = 40,000 | = 2 | |||||
| Supplier | Objective Functions | ||||
|---|---|---|---|---|---|
| 34,079.12 | 0 | 1 | = 0.1865 × 108 | = 0.1927956 × 108 | |
| 9705.485 | 0 | 1 | = 0.2541 × 108 | ||
| 0 | 0 | 0 | = 2,065,000 | = 2,948,341 | |
| 0 | 0 | 0 | = 0.1155 × 108 | ||
| 6215.396 | 0 | 1 | = 8445.527 | = 14,956.37 | |
| 0 | 35,000 | 1 | = 15,625 | ||
| 0 | 0 | 0 | = 0.9069 | ||
| 0 | 5000 | 1 | |||
| Set 1 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 |
| Set 2 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 |
| Set 3 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 |
| Set 4 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 |
| Set 5 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 |
| Set 6 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 |
| Set 7 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 |
| Set 8 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 |
| Set 9 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 |
| Set 10 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 |
| Set 11 | 0.092 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 |
| Set 12 | 0.100 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 |
| Set 13 | 0.108 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 |
| Set 14 | 0.117 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 |
| Set 15 | 0.125 | 0.008 | 0.017 | 0.025 | 0.033 | 0.042 | 0.050 | 0.058 | 0.067 | 0.075 | 0.083 | 0.092 | 0.100 | 0.108 | 0.117 |
| Supplier | SAW | COPRAS | TOPSIS | VIKOR | EDAS | MULTIMOORA | Proposed Approach |
|---|---|---|---|---|---|---|---|
| 2 | 2 | 2 | 1 | 2 | 2 | 2 | |
| 5 | 5 | 5 | 6 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 7 | 7 | 7 | 8 | 8 | 7 | 7 | |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| 1 | 1 | 1 | 2 | 1 | 1 | 1 | |
| 8 | 8 | 8 | 7 | 7 | 8 | 8 | |
| 6 | 6 | 6 | 5 | 6 | 6 | 6 | |
| 1 | 1 | 1 | 0.929 | 0976 | 1 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshavarz-Ghorabaee, M. Sustainable Supplier Selection and Order Allocation Using an Integrated ROG-Based Type-2 Fuzzy Decision-Making Approach. Mathematics 2023, 11, 2014. https://doi.org/10.3390/math11092014
Keshavarz-Ghorabaee M. Sustainable Supplier Selection and Order Allocation Using an Integrated ROG-Based Type-2 Fuzzy Decision-Making Approach. Mathematics. 2023; 11(9):2014. https://doi.org/10.3390/math11092014
Chicago/Turabian StyleKeshavarz-Ghorabaee, Mehdi. 2023. "Sustainable Supplier Selection and Order Allocation Using an Integrated ROG-Based Type-2 Fuzzy Decision-Making Approach" Mathematics 11, no. 9: 2014. https://doi.org/10.3390/math11092014
APA StyleKeshavarz-Ghorabaee, M. (2023). Sustainable Supplier Selection and Order Allocation Using an Integrated ROG-Based Type-2 Fuzzy Decision-Making Approach. Mathematics, 11(9), 2014. https://doi.org/10.3390/math11092014






