Numerical Solution of Fractional Models of Dispersion Contaminants in the Planetary Boundary Layer
Abstract
:1. Introduction
2. Preliminaries
3. Maximum Principle
4. A Priori Estimates for the Solutions
5. Finite Difference Scheme
5.1. Semidiscretization
5.2. Full Discretization
6. Properties of the Numerical Scheme
7. 2D Problem
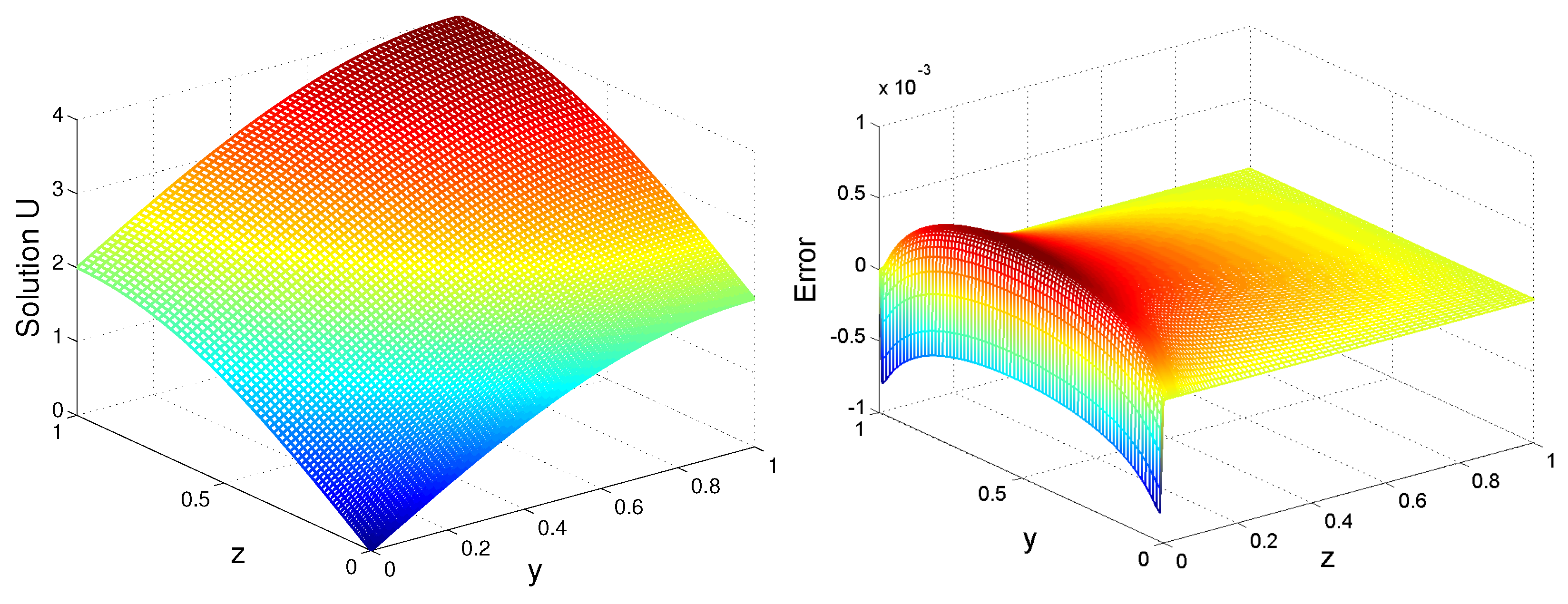
8. Numerical Experiments
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arya, S.P. Air Pollution Meteorology and Disperision; Oxford University Press: New York, NY, USA, 1999; 310p. [Google Scholar]
- Blackadar, A.K. Turbulence and Diffusion in the Atmosphere: Lectures in Environmental Science; Springer: Berlin, Germany, 1997; 185p. [Google Scholar]
- Goulart, A.G.O.; Lazo, M.J.; Suarez, J.M.S.; Moreira, D.M. Fractional derivative models for atmospheric dispersion of pollutants. Phys. A Stat. Mech. Its Appl. 2017, 477, 9–19. [Google Scholar] [CrossRef]
- Marchuk, G.I. Mathematical modelling in environmental problems. Stud. Math. Its Appl. 1986, 16, 1986. [Google Scholar]
- Goulart, A.G.O.; Lazo, M.J.; Suarez, J.M.S. A new parameterization for the concentration flux using the fractional calculus to model the dispersion of contaminants in the Planetary Boundary Layer. Phys. A Stat. Mech. Its Appl. 2019, 518, 38–49. [Google Scholar] [CrossRef]
- Moreira, D.; Moret, M. A new direction in the atmospheric pollutant dispersion inside the planetary boundary layer. J. Appl. Meteorol. Climatol. 2018, 57, 185–192. [Google Scholar] [CrossRef]
- Moreira, D.M.; Santos, C.A.G. New approach to handle gas-particle transformation in air pollution modelling using fractional derivatives. Atmos. Pollut. Res. 2019, 10, 1577–1587. [Google Scholar] [CrossRef]
- Sylvain, T.T.A.; Patrice, E.A.; Marie, E.E.J.; Pierrea, O.A.; Huberta, B.-B.G. A three-dimensional fractional solution for air contaminants dispersal in the planetary boundary layer. Heliyon 2021, 7, e07005. [Google Scholar]
- Sylvain, T.T.A.; Patrice, E.A.; Marie, E.E.J.; Pierre, O.A.; Hubert, B.B.G. Analytical solution of the steady-state atmospheric fractional diffusion equation in a finite domain. Pramana-J. Phys. 2021, 95, 1. [Google Scholar] [CrossRef]
- Golant, E.I. Conjugate families of difference schemes for equations of parabolic type with lowest terms. Zh. Vychisl. Mat. Mat. Fiz. 1978, 18, 1162–1169. [Google Scholar] [CrossRef]
- Hosseini, B.; Stockie, J.M. Estimating airborne particulate emissions using a finite-volume forward solver coupled with a Bayesian inversion approach. Comput. Fluids 2017, 154, 27–43. [Google Scholar] [CrossRef]
- Moreira, D.M.; Rizza, U.; Vilhena, M.T.; Goulart, A. Semi-analytical model for pollution dispersion in the planetary boundary layer. Atmos. Environ. 2005, 39, 2673–2681. [Google Scholar] [CrossRef]
- Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Boundary-Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Vulkov, L.G. Well-posedness for initial value problems of atmospheric flow models with degenerate vertical diffusion. AIP Conf. Proc. 2022, 2505, 030003. [Google Scholar]
- Albani, R.A.S.; Albani, V.V.L.; Neto, A.J.S. Genetic algorithm optimization applied to source estimation in the atmosphere. In Proceedings of the 18th Brazilian Congress of Thermal Sciences and Engineering, Online, 16–20 November 2020. [Google Scholar] [CrossRef]
- Albani, R.A.S.; Duda, F.P.; Pimentel, L.C.G. On the modeling of atmospheric pollutant dispersion during a diurnal cycle: A finite element study. Atmos. Environ. 2015, 118, 19–27. [Google Scholar] [CrossRef]
- Stockie, J.M. The mathematics of atmospheric dispersion modeling. SIAM Rev. 2011, 53, 349–372. [Google Scholar] [CrossRef]
- Kandilarov, J.; Vulkov, L. Determination of concentration source in a fractional derivative model of atmospheric pollution. AIP Conf. Proc. 2021, 2333, 090014. [Google Scholar]
- Caputo, M. Vibrations of infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Klibas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; p. 540. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Arora, U.; Gakkhar, S.; Gupta, R.S. Removal model suitable for air pollutants from an elevated source. Appl. Math. Model. 1991, 15, 386–389. [Google Scholar] [CrossRef]
- Bhaskar, C.; Lakshminarayanachari, K. Numerical model for primary and secondary air pollutants emitted from an area and point source in an urban area with chemical reaction and removal mechanisms. Mater. Today 2021, 37, 2961–2967. [Google Scholar] [CrossRef]
- Blottner, F.G.; Lopez, A.R. Determination of Solution Accuracy of Numerical Scheme as Part Code and Calculation Verification; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 1998; 77p.
- Chernogorova, T.P.; Koleva, M.N.; Vulkov, L.G. Exponential finite difference scheme for transport equations with discontinuous coefficients in porous media. Appl. Math. Comput. 2021, 392, 125691. [Google Scholar]
- Dang, Q.A.; Ehrhardt, M. Adequate numerical solution of air pollution problems by positive difference schemes on unbounded domains. Math. Comput. Model. 2006, 44, 834–856. [Google Scholar] [CrossRef]
- Dang, Q.A.; Ehrhardt, M.; Tran, G.L.; Le, D. On the numerical solution of some problems ofenvironmental pollution. In Air Pollution Research Advances; Bodine, C.G., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2007. [Google Scholar]
- Koleva, M.N.; Vulkov, L.G. Positivity-preserving finite volume difference schemes for atmospheric dispersion models with degenerate vertical diffusion. Comp. Appl. Math. 2022, 41, 406. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Tr. Akad. Nauk. SSSR Geophiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Dimov, I.T.; Kandilarov, J.D.; Vulkov, L.G. Numerical Identification of the Time Dependent Vertical Diffusion Coefficient in a Model of Air Pollution. In Advanced Computing in Industrial Mathematics; Studies in Computational Intelligence; Georgiev, I., Kostadinov, H., Lilkova, E., Eds.; Springer: Cham, Switzerland, 2021; Volume 961. [Google Scholar]
- Koleva, M.N. Numerical method for space degenerate fractional derivative problems of atmospheric pollution. AIP Conf. Proc. 2022, 2505, 080024. [Google Scholar]
- Fazio, R.; Jannelli, A.; Agreste, S. A Finite Difference Method on Non-Uniform Meshes for Time-Fractional Advection–Diffusion Equations with a Source Term. Appl. Sci. 2018, 8, 960. [Google Scholar] [CrossRef]
- Shiri, B.; Baleanu, D. A general fractional pollution model for lakes. Commun. Appl. Math. Comput. 2022, 4, 1105–1130. [Google Scholar]
- Mahsud, Y.; Shah, N.A.; Vieru, D. Influence of time-fractional derivatives on the boundary layer flow of Maxwell fluids. Chin. J. Phys. 2017, 55, 1340–1351. [Google Scholar] [CrossRef]
- Van Bockstal, K. Uniqueness for inverse source problems of determining a space-dependent source in time-fractional equations with non-smooth solutions. Fractal Fract. 2021, 5, 169. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical identification of external boundary conditions for time fractional parabolic equations on disjoint domains. Fractal Fract. 2023, 7, 326. [Google Scholar] [CrossRef]
- Long, L.D.; Zhou, Y.; Thanh Binh, T.; Can, N. A mollification regularization method for the inverse source problem for a time fractional diffusion equation. Mathematics 2019, 7, 1048. [Google Scholar] [CrossRef]
- Ozbilge, E.; Kanca, F.; Ozbilge, E. Inverse problem for a time fractional parabolic equation with nonlocal boundary conditions. Mathematics 2022, 10, 1479. [Google Scholar] [CrossRef]
- Yang, F.; Gao, Y.-X.; Li, D.-G.; Li, X.-X. Identification of the initial value for a time-fractional diffusion equation. Symmetry 2022, 14, 2569. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. Numerical and analytical investigations for solving the inverse tempered fractional diffusion equation via interpolating element-free Galerkin (IEFG) method. J. Therm. Anal. Calorim. 2021, 143, 1917–1933. [Google Scholar] [CrossRef]
- Kinash, N.; Janno, J. An inverse problem for a generalized fractional derivative with an application in reconstruction of time- and space-dependent sources in fractional diffusion and wave equations. Mathematics 2019, 7, 1138. [Google Scholar] [CrossRef]
- Kinash, N.; Janno, J. Inverse problems for a generalized subdiffusion equation with final overdetermination. Math. Model. Anal. 2019, 24, 236–262. [Google Scholar]
- Koleva, M.N.; Vulkov, L.G. Analytical and computational analysis of space degenerate time fractional parabolic model of atmospheric dispersion of pollutants. AIP Conf. Proc. 2023; accepted. [Google Scholar]
- Alikhanov, A.A. A priori estimates for solutions of boundary value problems for fractional-order equations. Differ. Equ. 2010, 46, 660–666. [Google Scholar] [CrossRef]
- Luchko, Y. Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation. Comput. Math. Appl. 2010, 59, 1766–1772. [Google Scholar] [CrossRef]
- Brunner, H.; Han, H.; Yin, D. The Mmaximum principle for time-fractional diffusion equations and its application. Numer. Funct. Optim. 2015, 36, 1307–1321. [Google Scholar] [CrossRef]
- Popov, I.V. On monotonic differential schemes. Matem. Mod. 2019, 31, 21–43. [Google Scholar]
- Samarskii, A.A. Theory of Finite Difference Schemes; Marcel Decker: New York, NY, USA, 2001; 786p. [Google Scholar]
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Zhanga, Y.; Sun, Z.; Liao, H. Finite difference methods for the time fractional diffusion equation on non-uniform meshes. J. Comput. Phys. 2014, 265, 195–210. [Google Scholar] [CrossRef]
- Chen, H.; Stynes, M. Error analysis of a second-order method on fitted meshes for a time-fractional diffusion problem. J. Sci. Comput. 2019, 79, 624–647. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, X.; Li, D. Nonuniform Alikhanov Linearized Galerkin Finite Element Methods for Nonlinear Time-Fractional Parabolic Equations. J. Sci. Comput. 2020, 85, 39. [Google Scholar] [CrossRef]
- Faragó, I.; Horváth, R.; Korotov, S. Discrete maximum principle for linear parabolic problems solved on hybrid meshes. Appl. Numer. Math. 2005, 53, 249–264. [Google Scholar] [CrossRef]
- Ulke, A.G. New turbulent parameterization for a dispersion model in the atmospheric boundary layer. Atmos. Environ. 2000, 34, 1029–1042. [Google Scholar] [CrossRef]
- Chen, H.; Stynes, M. A high order method on graded meshes for a time-fractional diffusion problem. In Finite Difference Methods. Theory and Applications; Lecture Notes in Computer, Science; Dimov, I., Farago, I., Vulkov, M.L., Eds.; Springer: Cham, Switzerland, 2019; p. 11386. [Google Scholar]
- Tangerman, G. Numerical Simulations of Air Pollutant Dispersion in a Stratified Planetary Boundary Layer. Atmos. Environ. 1978, 12, 1365–1369. [Google Scholar] [CrossRef]


| num | 1 | ||||||||
| 1.814 | 1.901 | 1.947 | 1.973 | 1.986 | |||||
| um | 1 | ||||||||
| 0.938 | 0.956 | 0.970 | 0.980 | 0.986 | |||||
| num | −1 | ||||||||
| 1.828 | 1.901 | 1.946 | 1.971 | 1.983 | |||||
| um | −1 | ||||||||
| 0.786 | 0.872 | 0.920 | 0.948 | 0.965 | |||||
| num | 1 | ||||||||
| 1.496 | 1.511 | 1.535 | 1.547 | 1.679 | |||||
| um | 1 | ||||||||
| 0.926 | 0.946 | 0.961 | 0.971 | 0.984 |
| 0.25 | |||||||
| 1.682 | 1.714 | 1.730 | 1.740 | 1.744 | |||
| 0.5 | |||||||
| 1.409 | 1.446 | 1.468 | 1.481 | 1.489 | |||
| 0.85 | |||||||
| 0.997 | 1.038 | 1.093 | 1.108 | 1.124 |
| 𝖳𝖾𝗌𝗍 | |||||||
|---|---|---|---|---|---|---|---|
| (𝖠) | |||||||
| 1.838 | 1.848 | 1.889 | 1.927 | 1.953 | |||
| (𝖡) | 2.440 | ||||||
| 1.637 | 1.685 | 1.740 | 1.842 | 2.130 | |||
| (𝖢) | 1.917 | ||||||
| 1.319 | 1.567 | 1.696 | 1.777 | 1.833 |
| 𝖳𝖾𝗌𝗍 | |||||||
|---|---|---|---|---|---|---|---|
| (𝖠) | |||||||
| 1.838 | 1.848 | 1.889 | 1.928 | 1.971 | |||
| (𝖡) | |||||||
| 1.616 | 1.665 | 1.727 | 1.792 | 1.824 | |||
| (𝖢) | |||||||
| 1.341 | 1.576 | 1.700 | 1.779 | 1.857 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koleva, M.N.; Vulkov, L.G. Numerical Solution of Fractional Models of Dispersion Contaminants in the Planetary Boundary Layer. Mathematics 2023, 11, 2040. https://doi.org/10.3390/math11092040
Koleva MN, Vulkov LG. Numerical Solution of Fractional Models of Dispersion Contaminants in the Planetary Boundary Layer. Mathematics. 2023; 11(9):2040. https://doi.org/10.3390/math11092040
Chicago/Turabian StyleKoleva, Miglena N., and Lubin G. Vulkov. 2023. "Numerical Solution of Fractional Models of Dispersion Contaminants in the Planetary Boundary Layer" Mathematics 11, no. 9: 2040. https://doi.org/10.3390/math11092040





