Combined Micro-Structural Effects of Linearly Increasing Reynolds Number and Mean Inflow Velocity on Flow Fields with Mesh Independence Analysis in Non-Classical Framework
Abstract
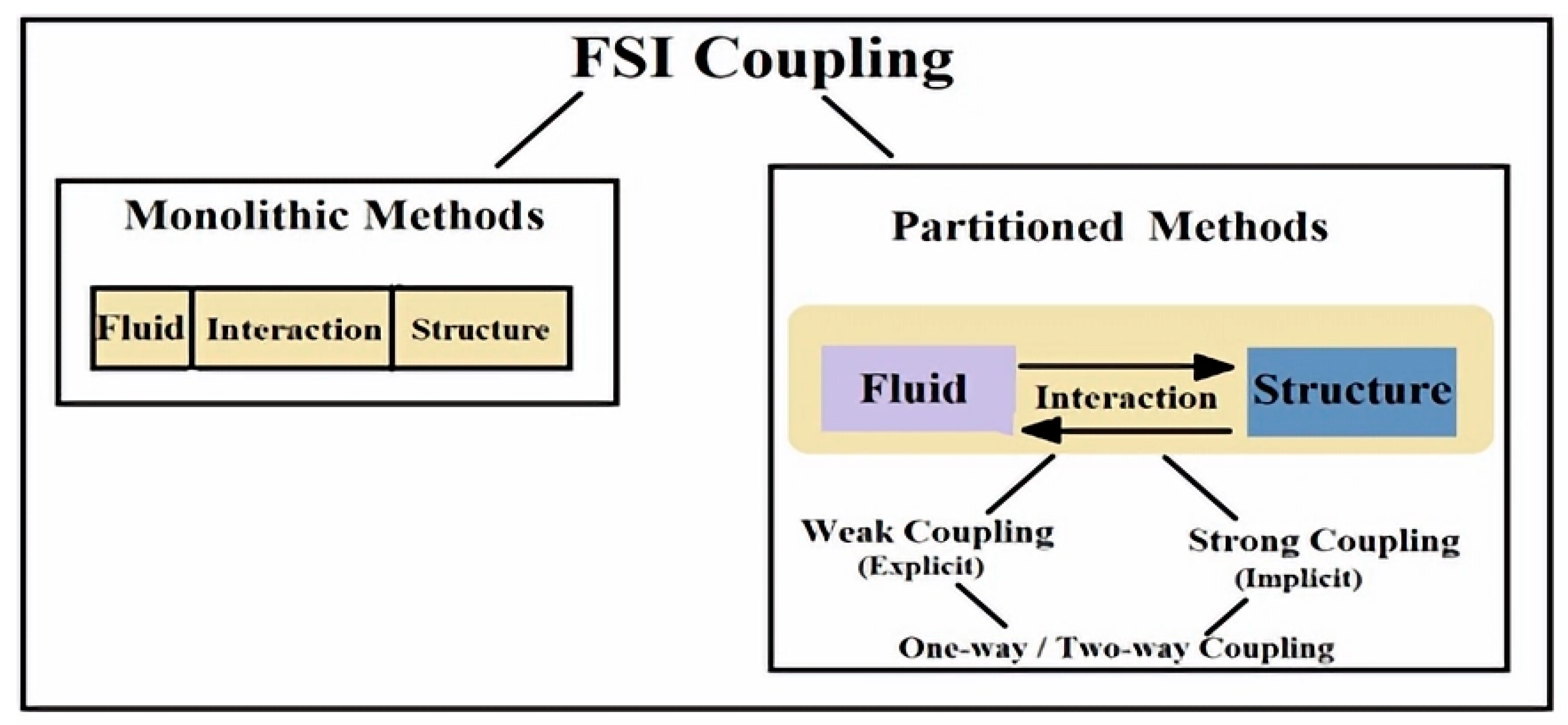
1. Introduction
Contribution of the Study
- ➢
- Analysis of different micro-structural characteristics of fluid flow for FSI problem in a non-classical framework.
- ➢
- Use of the Cosserat theory of fluids.
- ➢
- Employing a monolithic Eulerian formulation for solving the coupling problem of finite deformation in a non-classical framework.
- ➢
- Computation and validation of the results using the prominent classical benchmark FSI test FLUSTRUK-FSI-3*‘flow around a cylinder.
- ➢
- Implementation of algorithmic description with FreeFEM ++.
- ➢
- Verification of the convergence of the results using mesh independence analysis in a non-classical framework.
- ➢
- Section 2 presents the mathematical modeling of the CFSI problem to be studied. This section includes an overview of the fundamental notations for continuum description, and then the complete derivation of the governing equations for fluid and solid structure from conservation laws using constitutive relations in a monolithic Eulerian frame is presented.
- ➢
- Section 3 presents a monolithic variational formulation of the governing CFSI model in the Eulerian frame.
- ➢
- Section 4 presents the discretization schemes, where the semi-implicit and the finite-element method are used for discretizing time and space domains, respectively.
- ➢
- Section 5 describes the description, configuration, boundary conditions, and initial conditions of the benchmark test problem.
- ➢
- Section 6 discusses the results of the study obtained from computer simulations.
- ➢
- Section 7 concludes the present study with some of its future developments.
2. Cosserat Fluid–Structure Interaction Modeling
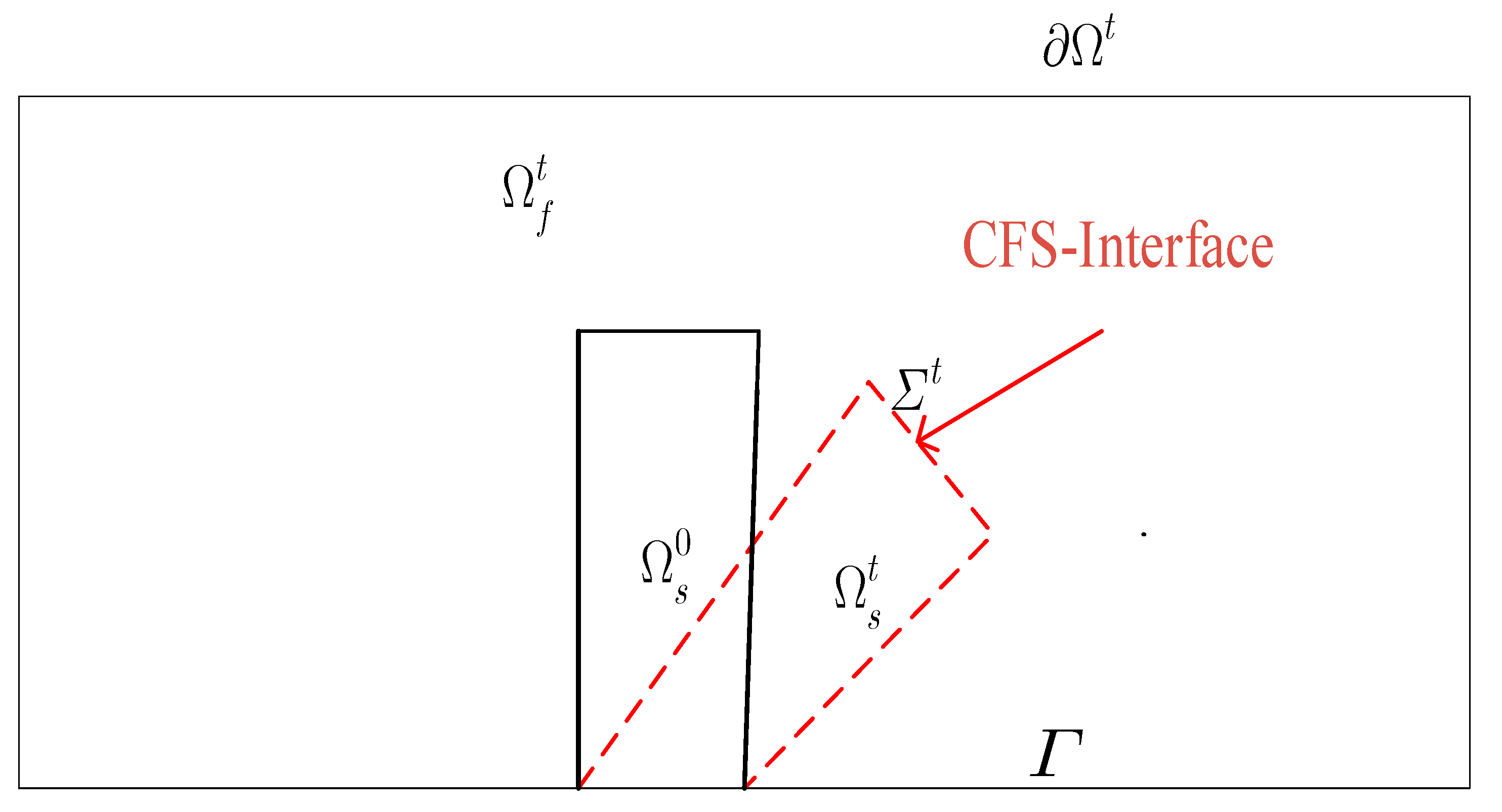
2.1. Fluid–Structure Interaction Problem Description
2.2. Coupling Conditions
2.2.1. Kinematic Condition
2.2.2. Dynamic Condition
2.2.3. Geometric Condition
2.3. Field Variables and Tensors
- ➢
- is the material location at time of (i.e., a material point at at is transported to at time by the motion).
- ➢
- is the displacement field.
- ➢
- is the velocity field.
- ➢
- is the micro-rotation velocity field.
- ➢
- is the transposed deformation gradient tensor.
- ➢
- is the Jacobian of deformation gradient tensor.
- ➢
- is the density.
- ➢
- is the stress tensor.
2.4. Conservation Laws
2.5. Constitutive Relations
- ➢
- For incompressible viscous Cosserat fluids:where , , and are the non-symmetric stress tensor, the couple stress tensor, and the identity tensor, respectively. The pressure field and coefficient of dynamic viscosity are denoted by and , respectively. The micro-viscosity coefficients and the Levi–Civita tensor are represented by , , ,, and .
- ➢
- For an hyper-elastic incompressible solid structural material:where is the Helmholtz potential, which, in the case of two-dimensional Mooney–Rivlin material [79], is defined as
2.6. Derivation of the Mooney–Rivlin Stress Tensor
2.7. Mathematical Formulation of Cosserat Fluids Theory
3. Variational Formulation
4. Discretization
4.1. Monolithic Semi-Implicit Time Discretization
4.2. Monolithic Finite Elements Space-Discretization
4.3. Finite-Element Mesh Updating Strategy
5. Numerical Tests
5.1. Description of Benchmark Test
5.2. Configuration, Boundary, and Initial Conditions
6. Results and Discussion
6.1. Validation of Benchmark Test
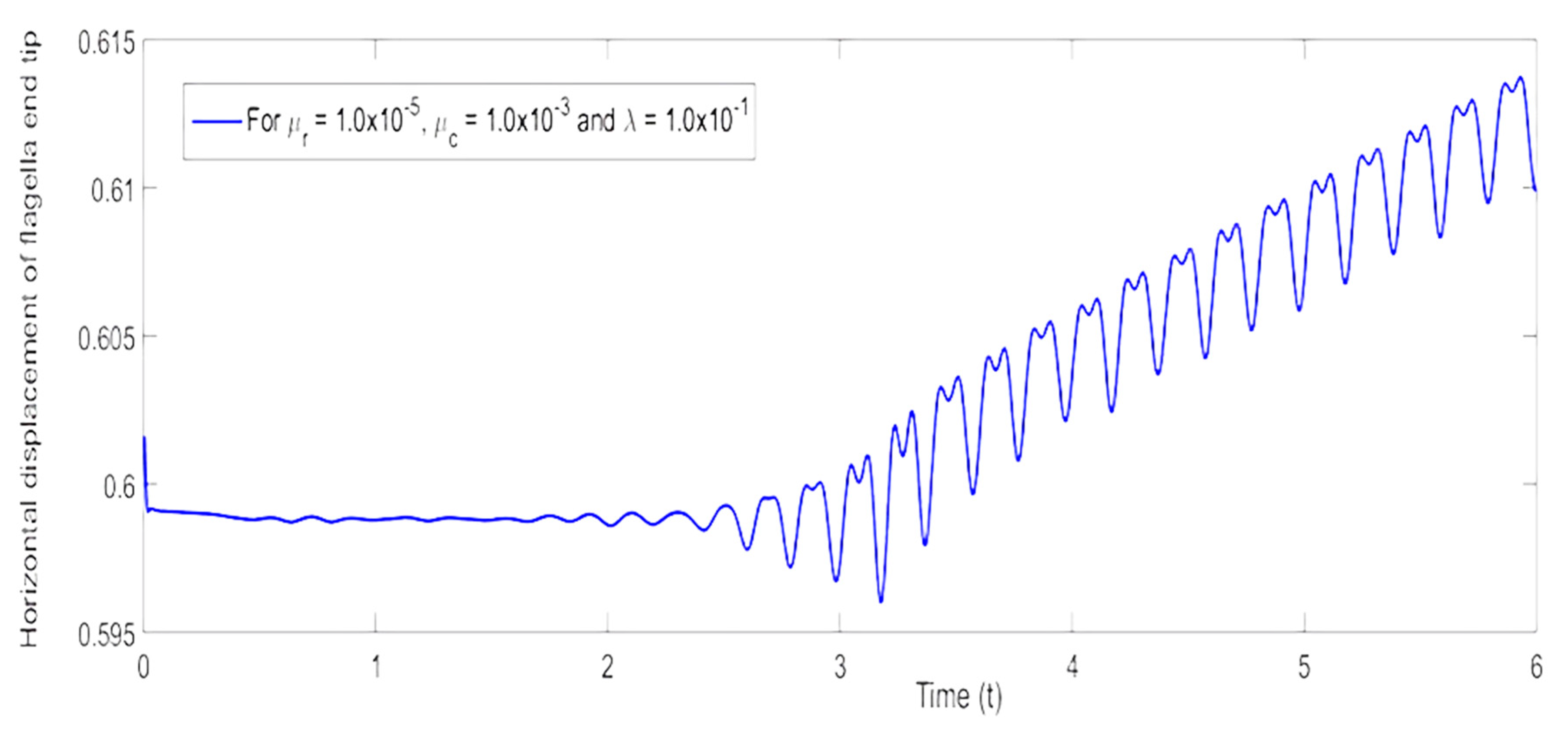
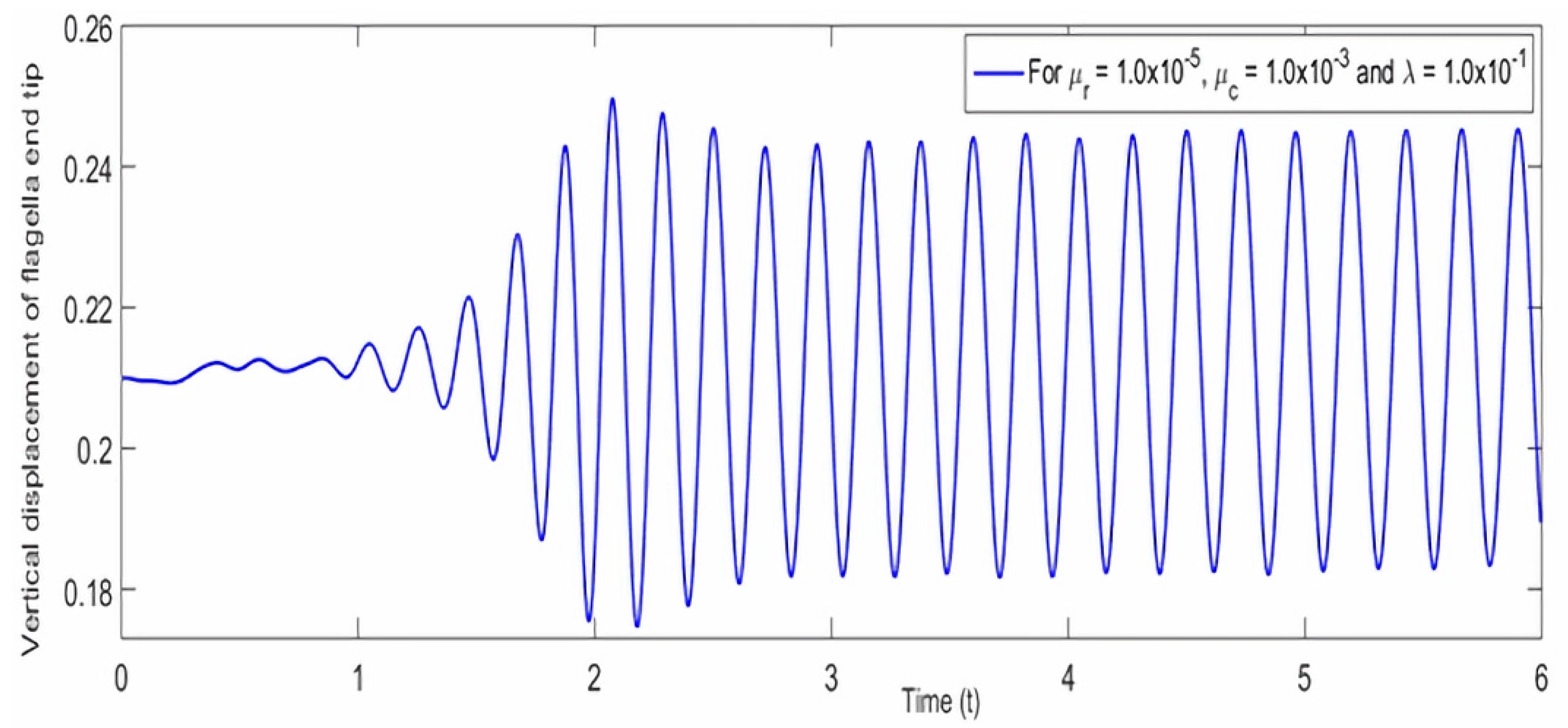
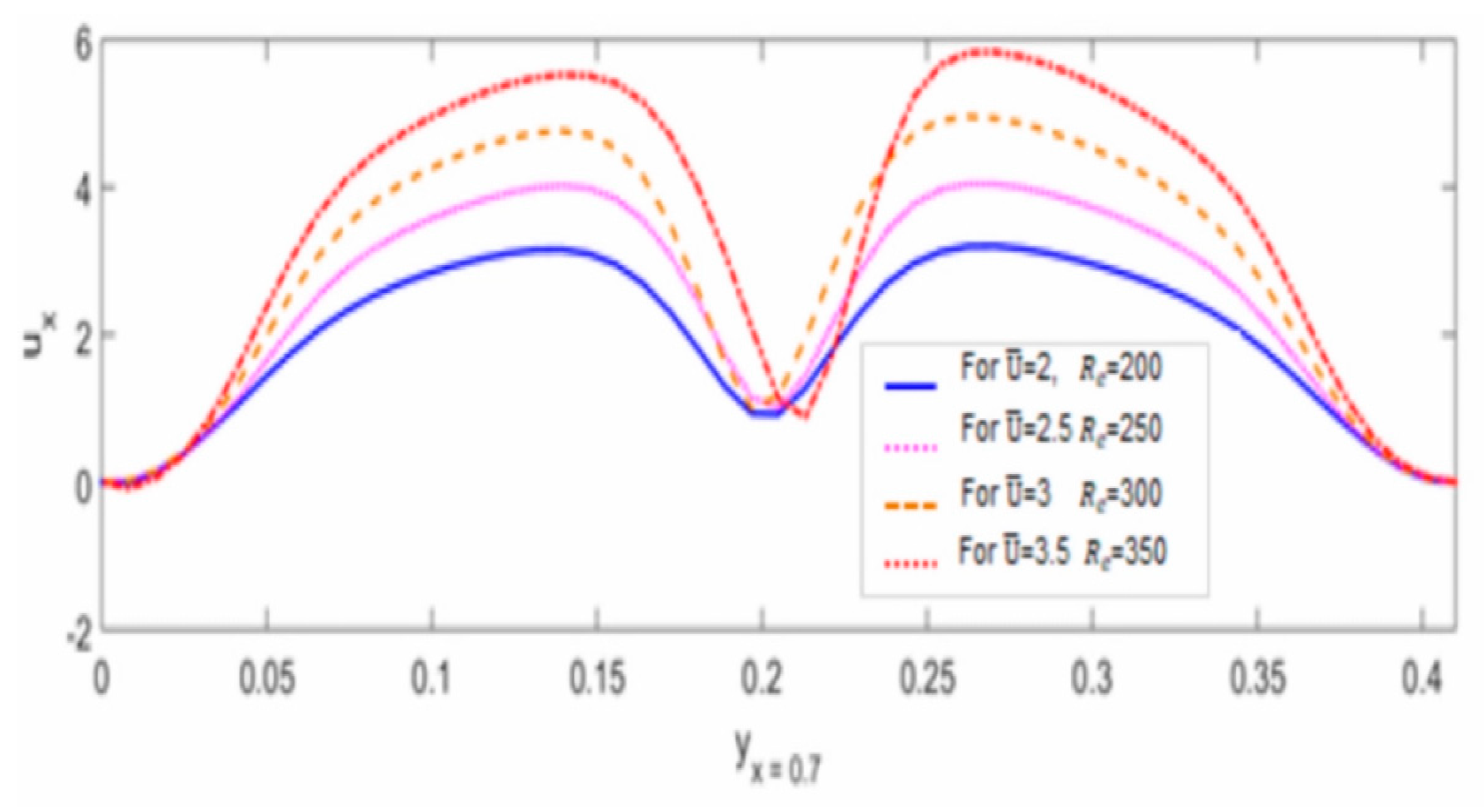
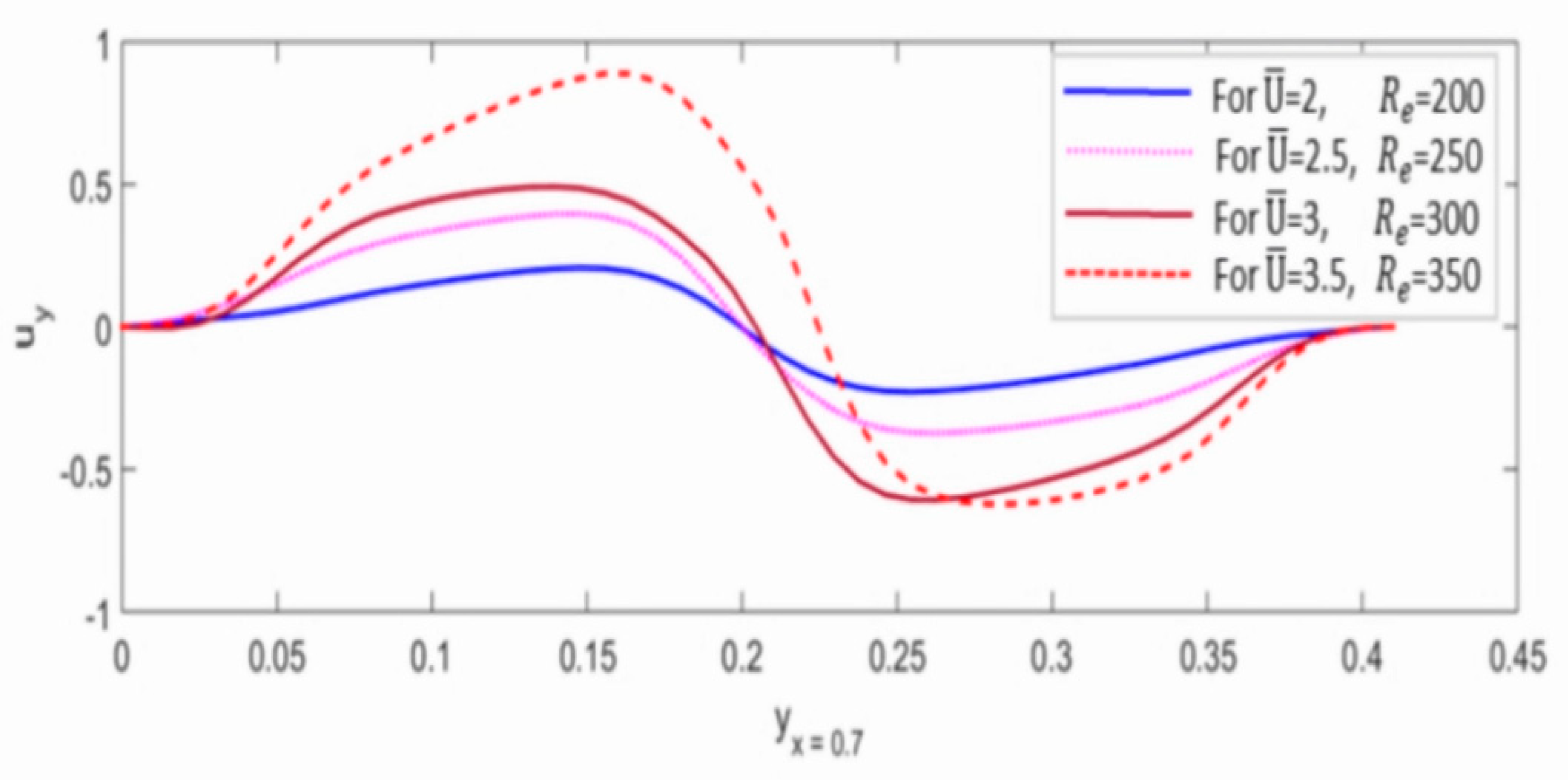
6.2. Analysis of Combined Effects of Linearly Increasing Reynolds Number and Mean Inflow Velocity
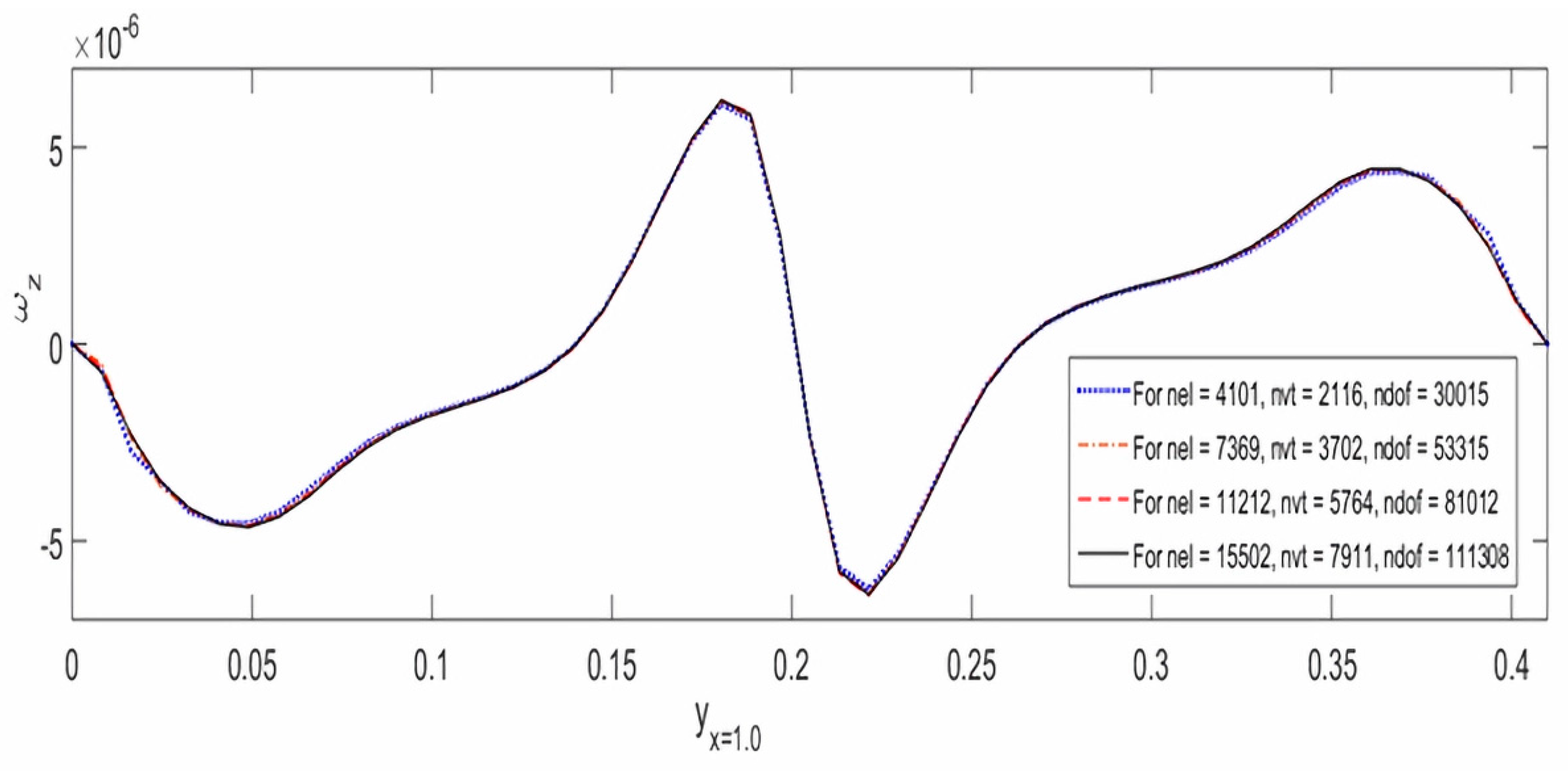
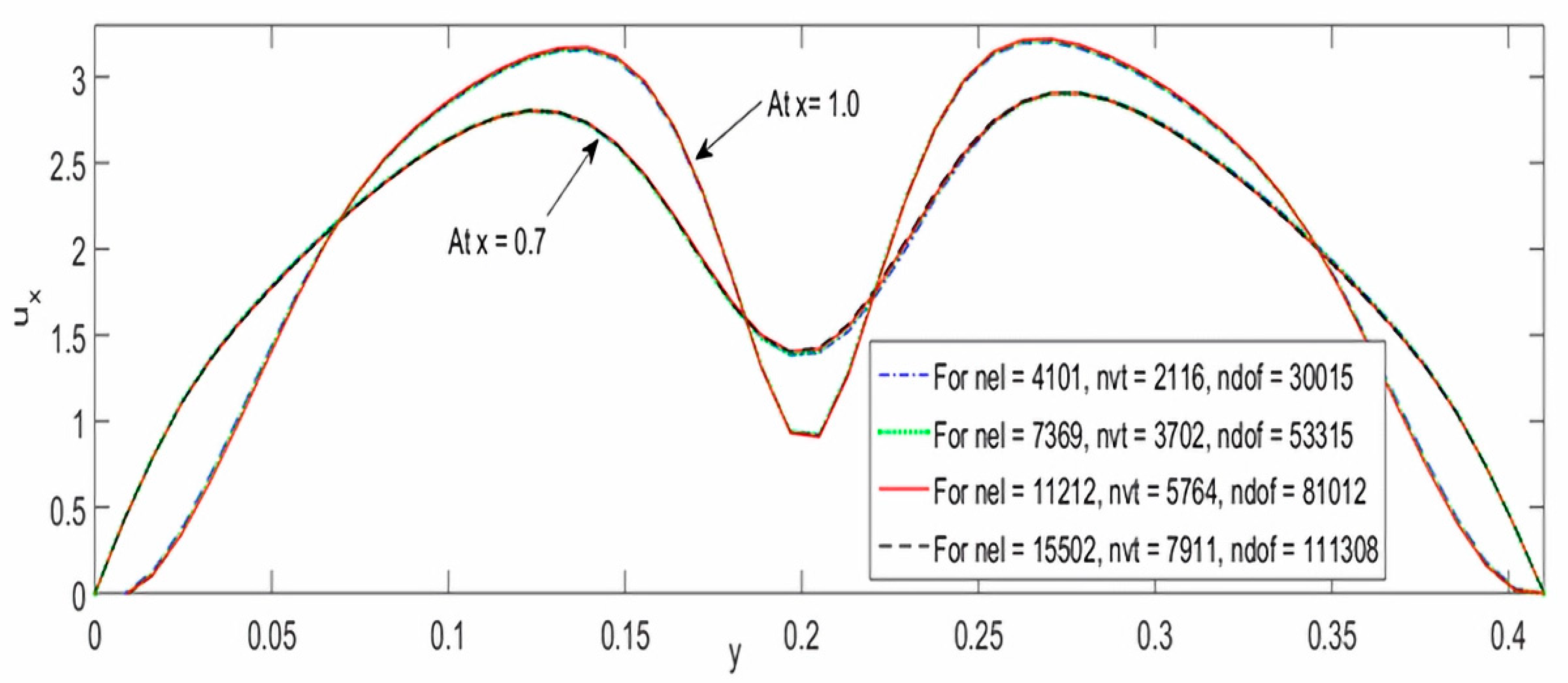
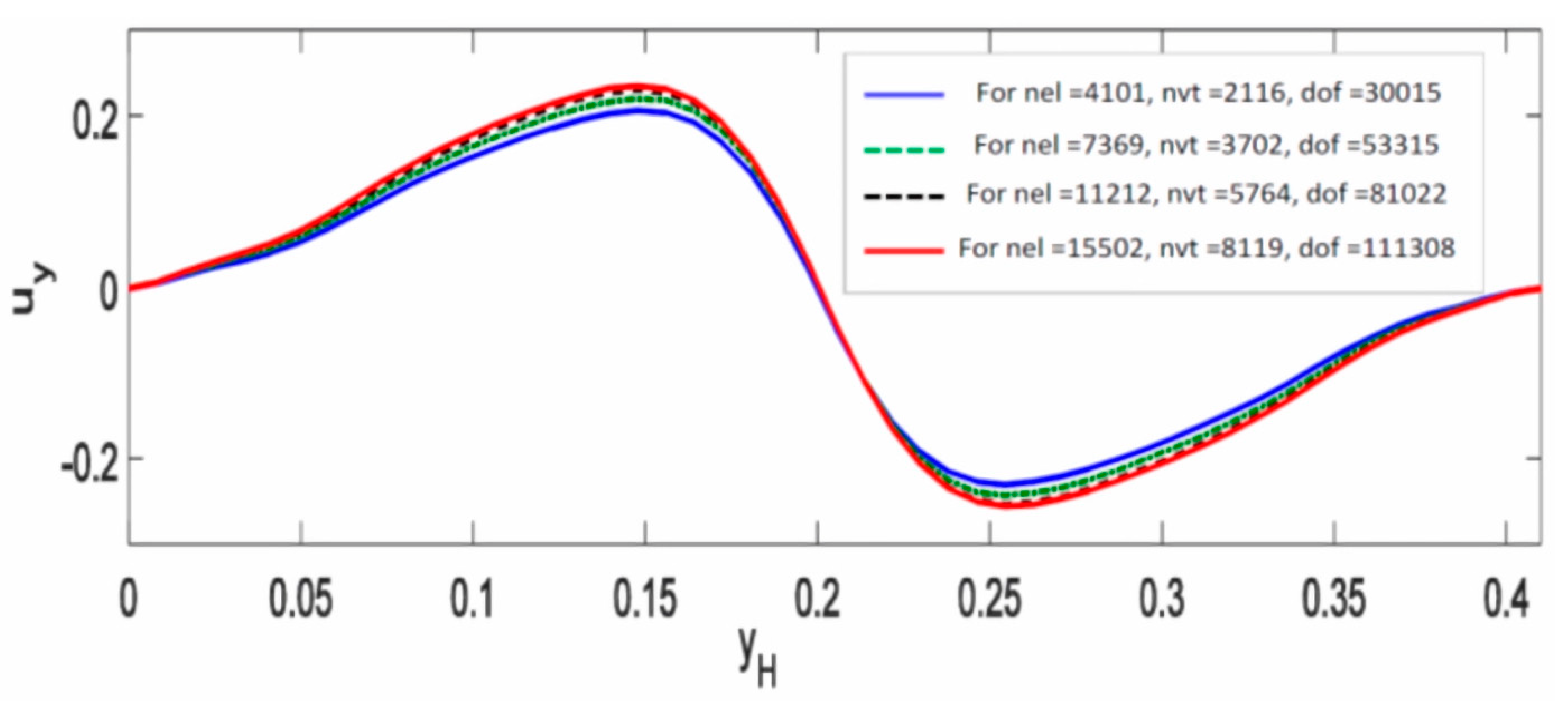
6.3. Mesh Independence Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morab, S.R.; Sharma, A. An Overview of Computational Fluid Structure Interaction: Methods and Applications. arXiv 2020, arXiv:2006.04068. [Google Scholar]
- Faizollahzadeh Ardabili, S.; Najafi, B.; Shamshirband, S.; Minaei Bidgoli, B.; Deo, R.C.; Chau, K.W. Computational intelligence approach for modeling hydrogen production: A review. Eng. Appl. Comput. Fluid Mech. 2018, 12, 438–458. [Google Scholar] [CrossRef]
- Akbarian, E.; Najafi, B.; Jafari, M.; Faizollahzadeh Ardabili, S.; Shamshirband, S.; Chau, K.W. Experimental and computational fluid dynamics-based numerical simulation of using natural gas in a dual-fueled diesel engine. Eng. Appl. Comput. Fluid Mech. 2018, 12, 517–534. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Takizawa, K. Advances in Computational Fluid-Structure Interaction and Flow Simulation; Birkhäuser: Basel, Switzerland, 2017. [Google Scholar]
- Bodnár, T.; Galdi, G.P.; Nečasová, Š. (Eds.) Fluid-Structure Interaction and Biomedical Applications; Springer: Basel, Switzerland, 2014. [Google Scholar]
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E. Computational Fluid-Structure Interaction: Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid-structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Formaggia, L.; Quarteroni, A.; Veneziani, A. (Eds.) Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Springer Science & Business Media: Berlin, Germany, 2010; Volume 1. [Google Scholar]
- Ryzhakov, P.B.; Rossi, R.; Idelsohn, S.R.; Onate, E. A monolithic Lagrangian approach for fluid–structure interaction problems. Comput. Mech. 2010, 46, 883–899. [Google Scholar] [CrossRef]
- Hron, J.; Turek, S. A monolithic FEM solver for an ALE formulation of fluid-structure interaction with configuration for numerical benchmarking. In Proceedings of the European Conference on Computational Fluid Dynamics, ECCOMAS CFD 2006, Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- Hübner, B.; Walhorn, E.; Dinkler, D. A monolithic approach to fluid–structure interaction using space–time finite elements. Comput. Methods Appl. Mech. Eng. 2004, 193, 2087–2104. [Google Scholar] [CrossRef]
- Michler, C.; Hulshoff, S.J.; Van Brummelen, E.H.; De Borst, R. A monolithic approach to fluid–structure interaction. Comput. Fluids 2004, 33, 839–848. [Google Scholar] [CrossRef]
- Dunne, T. An Eulerian approach to fluid–structure interaction and goal-oriented mesh adaptation. Int. J. Numer. Methods Fluids 2006, 51, 1017–1039. [Google Scholar] [CrossRef]
- Heil, M.; Hazel, A.L.; Boyle, J. Solvers for large-displacement fluid–structure interaction problems: Segregated versus monolithic approaches. Comput. Mech. 2008, 43, 91–101. [Google Scholar] [CrossRef]
- Wang, Y.; Jimack, P.K.; Walkley, M.A.; Pironneau, O. An energy stable one-field monolithic arbitrary Lagrangian–Eulerian formulation for fluid–structure interaction. J. Fluids Struct. 2020, 98, 103117. [Google Scholar] [CrossRef]
- Takahashi, T.; Batty, C. Monolith: A Monolithic Pressure-Viscosity-Contact Solver for Strong Two-Way Rigid-Rigid Rigid-Fluid Coupling; UWSpace: Waterloo, ON, Canada, 2020. [Google Scholar]
- Zimmerman, A.G.; Kowalski, J. Monolithic Simulation of Ice-Shelf/Ocean Interaction with an Extended Enthalpy-Porosity Method for Convection-Coupled Phase-Change. In Proceedings of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019. [Google Scholar]
- Murea, C.M. Three-Dimensional Simulation of Fluid–Structure Interaction Problems Using Monolithic Semi-Implicit Algorithm. Fluids 2019, 4, 94. [Google Scholar] [CrossRef]
- Schott, B.; Ager, C.; Wall, W.A. A monolithic approach to fluid-structure interaction based on a hybrid Eulerian-ALE fluid domain decomposition involving cut elements. Int. J. Numer. Methods Eng. 2019, 119, 208–237. [Google Scholar] [CrossRef]
- Pironneau, O. An energy stable monolithic Eulerian fluid-structure numerical scheme. Chin. Ann. Math. Ser. B 2018, 39, 213–232. [Google Scholar] [CrossRef]
- Sauer, R.A.; Luginsland, T. A monolithic fluid–structure interaction formulation for solid and liquid membranes including free-surface contact. Comput. Methods Appl. Mech. Eng. 2018, 341, 1–31. [Google Scholar] [CrossRef]
- Langer, U.; Yang, H. Numerical simulation of fluid–structure interaction problems with hyperelastic models: A monolithic approach. Math. Comput. Simul. 2018, 145, 186–208. [Google Scholar] [CrossRef]
- Hecht, F.; Pironneau, O. An energy stable monolithic Eulerian fluid-structure finite element method. Int. J. Numer. Methods Fluids 2017, 85, 430–446. [Google Scholar] [CrossRef]
- Chiang, C.Y.; Pironneau, O.; Sheu, T.W.; Thiriet, M. Numerical study of a 3D Eulerian monolithic formulation for incompressible fluid-structures systems. Fluids 2017, 2, 34. [Google Scholar] [CrossRef]
- Ata, K.; Sahin, M. A Monolithic Approach for the Incompressible Magneto-Hydrodynamics Equations. In Proceedings of the International Conference on Computational Methods for Coupled Problems in Science and Engineering (COUPLED), Rhodes Island, Greece, 12–14 June 2017. [Google Scholar]
- Gatin, I.; Jasak, H.; Vukcevic, V. Monolithic coupling of rigid body motion and the pressure field in foam-extend. In Proceedings of the VII International Conference on Computational Methods in Marine Engineering, MARINE VII, Nantes, France, 15–17 May 2017; CIMNE: Barcelona, Spain, 2017; pp. 663–669. [Google Scholar]
- Pironneau, O. Numerical study of a monolithic fluid–structure formulation. In Variational Analysis and Aerospace Engineering; Springer: Cham, Switzerland, 2016; pp. 401–420. [Google Scholar]
- Langer, U.; Yang, H. Robust and efficient monolithic fluid-structure-interaction solvers. Int. J. Numer. Methods Eng. 2016, 108, 303–325. [Google Scholar] [CrossRef]
- Langer, U.; Yang, H. Recent development of robust monolithic fluid-structure interaction solvers. Fluid-Structure Interaction. Modeling, Adaptive Discretization and Solvers. Radon Ser. Comput. Appl. Math. 2017, 20, 169–192. [Google Scholar]
- Dunne, T.; Rannacher, R. Adaptive finite element approximation of fluid-structure interaction based on an Eulerian variational formulation. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 110–145. [Google Scholar]
- Richter, T. A fully Eulerian formulation for fluid–structure-interaction problems. J. Comput. Phys. 2013, 233, 227–240. [Google Scholar] [CrossRef]
- Wick, T. Fully Eulerian fluid–structure interaction for time-dependent problems. Comput. Methods Appl. Mech. Eng. 2013, 255, 14–26. [Google Scholar] [CrossRef]
- Rannacher, R.; Richter, T. An adaptive finite element method for fluid-structure interaction problems based on a fully eulerian formulation. In Fluid Structure Interaction II; Springer: Berlin/Heidelberg, Germany, 2011; pp. 159–191. [Google Scholar]
- Richter, T.; Wick, T. Finite elements for fluid–structure interaction in ALE and fully Eulerian coordinates. Comput. Methods Appl. Mech. Eng. 2010, 199, 2633–2642. [Google Scholar] [CrossRef]
- Formaggia, L.; Gerbeau, J.F.; Nobile, F.; Quarteroni, A. On the coupling of 3D and 1D Navier–Stokes equations for flow problems in compliant vessels. Comput. Methods Appl. Mech. Eng. 2001, 191, 561–582. [Google Scholar] [CrossRef]
- Nobile, F. Numerical Approximation of Fluid-Structure Interaction Problems with Application to Haemodynamics. Ph.D. Thesis, EPFL, Milan, Italy, 2001. [Google Scholar]
- Le Tallec, P.; Mouro, J. Fluid structure interaction with large structural displacements. Comput. Methods Appl. Mech. Eng. 2001, 190, 3039–3067. [Google Scholar] [CrossRef]
- Gerbeau, J.F.; Vidrascu, M. A quasi-Newton algorithm based on a reduced model for fluid-structure interaction problems in blood flows. ESAIM Math. Model. Numer. Anal. 2003, 37, 631–647. [Google Scholar] [CrossRef]
- Fernández, M.A.; Moubachir, M. A Newton method using exact Jacobians for solving fluid–structure coupling. Comput. Struct. 2005, 83, 127–142. [Google Scholar] [CrossRef]
- Dettmer, W.; Perić, D. A computational framework for fluid–structure interaction: Finite element formulation and applications. Comput. Methods Appl. Mech. Eng. 2006, 195, 5754–5779. [Google Scholar] [CrossRef]
- Murea, C.M. Numerical simulation of a pulsatile flow through a flexible channel. ESAIM Math. Model. Numer. Anal. 2006, 40, 1101–1125. [Google Scholar] [CrossRef]
- Mbaye, I.; Murea, C.M. Numerical procedure with analytic derivative for unsteady fluid–structure interaction. Commun. Numer. Methods Eng. 2008, 24, 1257–1275. [Google Scholar] [CrossRef]
- Kuberry, P.; Lee, H. A decoupling algorithm for fluid-structure interaction problems based on optimization. Comput. Methods Appl. Mech. Eng. 2013, 267, 594–605. [Google Scholar] [CrossRef]
- Schafer, G.S.; Sieber, R.; Teschauer, I. Coupled Fluid-Solid Problems: Examples and Reliable Numerical Simulation. In Proceedings of the Trend in Computational Structural Mechanics; International Center for Numerical Methods in Engineering CIMNE: Barcelona, Spain, 2001. [Google Scholar]
- Piperno, S.; Farhat, C.; Larrouturou, B. Partitioned procedures for the transient solution of coupled aroelastic problems Part I: Model problem, theory and two-dimensional application. Comput. Methods Appl. Mech. Eng. 1995, 124, 79–112. [Google Scholar] [CrossRef]
- Piperno, S. Explicit/implicit fluid/structure staggered procedures with a structural predictor and fluid subcycling for 2D inviscid aeroelastic simulations. Int. J. Numer. Methods Fluids 1997, 25, 1207–1226. [Google Scholar] [CrossRef]
- Mok, D.P.; Wall, W.A.; Ramm, E. Accelerated iterative substructuring schemes for instationary fluid-structure interaction. Comput. Fluid Solid Mech. 2001, 2, 1325–1328. [Google Scholar]
- Richter, T. Numerical Methods for Fluid-Structure Interaction Problems; Institute for Applied Mathematics, University of Heidelberg: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Donea, J. Arbitrary Lagrangian-Eulerian finite element analysis. Comput. Methods Transient Anal. 1983, 474–516. [Google Scholar]
- Quarteroni, A.; Formaggia, L. Mathematical modelling and numerical simulation of the cardiovascular system. Handb. Numer. Anal. 2004, 12, 3–127. [Google Scholar]
- Nobile, F.; Vergara, C. An effective fluid-structure interaction formulation for vascular dynamics by generalized Robin conditions. SIAM J. Sci. Comput. 2008, 30, 731–763. [Google Scholar] [CrossRef]
- Formaggia, L.; Quarteroni, A.; Veneziani, A. Cardiovascular Mathematics, Volume 1 of MS&Modeling, A; Simulation and Applications; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Le Tallec, P.; Hauret, P. Energy conservation in fluid structure interactions. Numer. Methods Sci. Comput. Var. Probl. Appl. 2003, 94–107. [Google Scholar]
- Basting, S.; Quaini, A.; Čanić, S.; Glowinski, R. Extended ALE method for fluid–structure interaction problems with large structural displacements. J. Comput. Phys. 2017, 331, 312–336. [Google Scholar] [CrossRef]
- Liu, J. A second-order changing-connectivity ALE scheme and its application to FSI with large convection of fluids and near contact of structures. J. Comput. Phys. 2016, 304, 380–423. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Coupez, T.; Silva, L.; Hachem, E. Implicit boundary and adaptive anisotropic meshing. In New Challenges in Grid Generation and Adaptivity for Scientific Computing; Springer: Cham, Switzerland, 2015; pp. 1–18. [Google Scholar]
- Robinson-Mosher, A.; Shinar, T.; Gretarsson, J.; Su, J.; Fedkiw, R. Two-way coupling of fluids to rigid and deformable solids and shells. ACM Trans. Graph. TOG 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Boffi, D.; Cavallini, N.; Gastaldi, L. The finite element immersed boundary method with distributed Lagrange multiplier. SIAM J. Numer. Anal. 2015, 53, 2584–2604. [Google Scholar] [CrossRef]
- Wang, Y.; Jimack, P.K.; Walkley, M.A. A one-field monolithic fictitious domain method for fluid–structure interactions. Comput. Methods Appl. Mech. Eng. 2017, 317, 1146–1168. [Google Scholar] [CrossRef]
- Afra, B.; Delouei, A.A.; Mostafavi, M.; Tarokh, A. Fluid-structure interaction for the flexible filament’s propulsion hanging in the free stream. J. Mol. Liq. 2021, 323, 114941. [Google Scholar] [CrossRef]
- Hajano, N.H.; Khan, M.S.; Liu, L. Increasing Micro-Rotational Viscosity Results in Large Micro-Rotations: A Study Based on Monolithic Eulerian Cosserat Fluid–Structure Interaction Formulation. Mathematics 2022, 10, 4188. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Theorie des Corps Déformables; A. Hermann et Fils: Paris, France, 1909. [Google Scholar]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Condiff, D.W.; Dahler, J.S. Fluid mechanical aspects of antisymmetric stress. Phys. Fluids 1964, 7, 842–854. [Google Scholar] [CrossRef]
- Bazdar, H.; Toghraie, D.; Pourfattah, F.; Akbari, O.A.; Nguyen, H.M.; Asadi, A. Numerical investigation of turbulent flow and heat transfer of nanofluid inside a wavy microchannel with different wavelengths. J. Therm. Anal. Calorim. 2020, 139, 2365–2380. [Google Scholar] [CrossRef]
- Arasteh, H.; Mashayekhi, R.; Goodarzi, M.; Motaharpour, S.H.; Dahari, M.; Toghraie, D. Heat and fluid flow analysis of metal foam embedded in a double-layered sinusoidal heat sink under local thermal non-equilibrium condition using nanofluid. J. Therm. Anal. Calorim. 2019, 138, 1461–1476. [Google Scholar] [CrossRef]
- Oveissi, S.; Toghraie, D.; Eftekhari, S.A. Longitudinal vibration and stability analysis of carbon nanotubes conveying viscous fluid. Phys. E Low-Dimens. Syst. Nanostructures 2016, 83, 275–283. [Google Scholar] [CrossRef]
- Lukaszewicz, G. Micropolar Fluids: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 1999. [Google Scholar]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- Kim, C.; Jung, M.; Yamada, T.; Nishiwaki, S.; Yoo, J. Freefem++ code for reaction-diffusion equation–based topology optimization: For high-resolution boundary representation using adaptive mesh refinement. Struct. Multidiscip. Optim. 2020, 62, 439–455. [Google Scholar] [CrossRef]
- Dapogny, C.; Frey, P.; Omnès, F.; Privat, Y. Geometrical shape optimization in fluid mechanics using FreeFem++. Struct. Multidiscip. Optim. 2018, 58, 2761–2788. [Google Scholar] [CrossRef]
- Krivovichev, G.V. A computational approach to the modeling of the glaciation of sea offshore gas pipeline. Int. J. Heat Mass Transf. 2017, 115, 1132–1148. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Batra, R.C. Elements of Continuum Mechanics; AIAA: Reston, VA, USA, 2006. [Google Scholar]
- Bath, K.J. Finite Element Procedures; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Marsden, J.; Hughes, T.J.R. Mathematical Foundations of Elasticity; Dover Publications: New York, NY, USA, 1993. [Google Scholar]
- Ciarlet, P.G. Mathematical Elasticity: Volume 1: Three-Dimensional Elasticity; North Holland Publishing Company: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Schafer, M.; Turek, S. Benchmark computations of laminar flow around a cylinder. Notes Numer. Fluid Mech. 1996, 52, 547–566. [Google Scholar]
- Turek, S.; Hron, J. Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow. In Fluid-Structure Interaction; Springer: Berlin, Heidelberg, 2006; pp. 371–385. [Google Scholar]
- American Society of Mechanical Engineers. Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer: An American National Standard; American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar]


| Configuration | Boundary Conditions | Initial Conditions |
|---|---|---|
|
|
|
| Material Constant | Value |
|---|---|
| Computation of FSI Tests | No. of Vertices | Amplitude | ||
|---|---|---|---|---|
| Present Study | 2199 | 4.5 | 0.03 | 0.005 |
| Hecht and Pironneau (2017) | 2200 | 5.4 | 0.03 | 0.005 |
| Dunne and Rannacher (2006) | 2082 | 0.02226 | 1.92 | 0.005 |
| 200 | 2 |
| 250 | 2.5 |
| 300 | 3 |
| 350 | 3.5 |
| Number of Elements (nel) | Number of Vertices (nvt) | Number of Degrees of Freedom (ndof) |
|---|---|---|
| 4101 | 2116 | 30,015 |
| 7369 | 3702 | 53,315 |
| 11,212 | 5764 | 81,012 |
| 15,502 | 7911 | 111,308 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajano, N.H.; Khan, M.S.; Liu, L.; Kaloi, M.A.; Mei, H. Combined Micro-Structural Effects of Linearly Increasing Reynolds Number and Mean Inflow Velocity on Flow Fields with Mesh Independence Analysis in Non-Classical Framework. Mathematics 2023, 11, 2074. https://doi.org/10.3390/math11092074
Hajano NH, Khan MS, Liu L, Kaloi MA, Mei H. Combined Micro-Structural Effects of Linearly Increasing Reynolds Number and Mean Inflow Velocity on Flow Fields with Mesh Independence Analysis in Non-Classical Framework. Mathematics. 2023; 11(9):2074. https://doi.org/10.3390/math11092074
Chicago/Turabian StyleHajano, Nazim Hussain, Muhammad Sabeel Khan, Lisheng Liu, Mumtaz Ali Kaloi, and Hai Mei. 2023. "Combined Micro-Structural Effects of Linearly Increasing Reynolds Number and Mean Inflow Velocity on Flow Fields with Mesh Independence Analysis in Non-Classical Framework" Mathematics 11, no. 9: 2074. https://doi.org/10.3390/math11092074
APA StyleHajano, N. H., Khan, M. S., Liu, L., Kaloi, M. A., & Mei, H. (2023). Combined Micro-Structural Effects of Linearly Increasing Reynolds Number and Mean Inflow Velocity on Flow Fields with Mesh Independence Analysis in Non-Classical Framework. Mathematics, 11(9), 2074. https://doi.org/10.3390/math11092074










