The Grad–Shafranov Equation in Cap-Cyclide Coordinates: The Heun Function Solution
Abstract
:1. Introduction
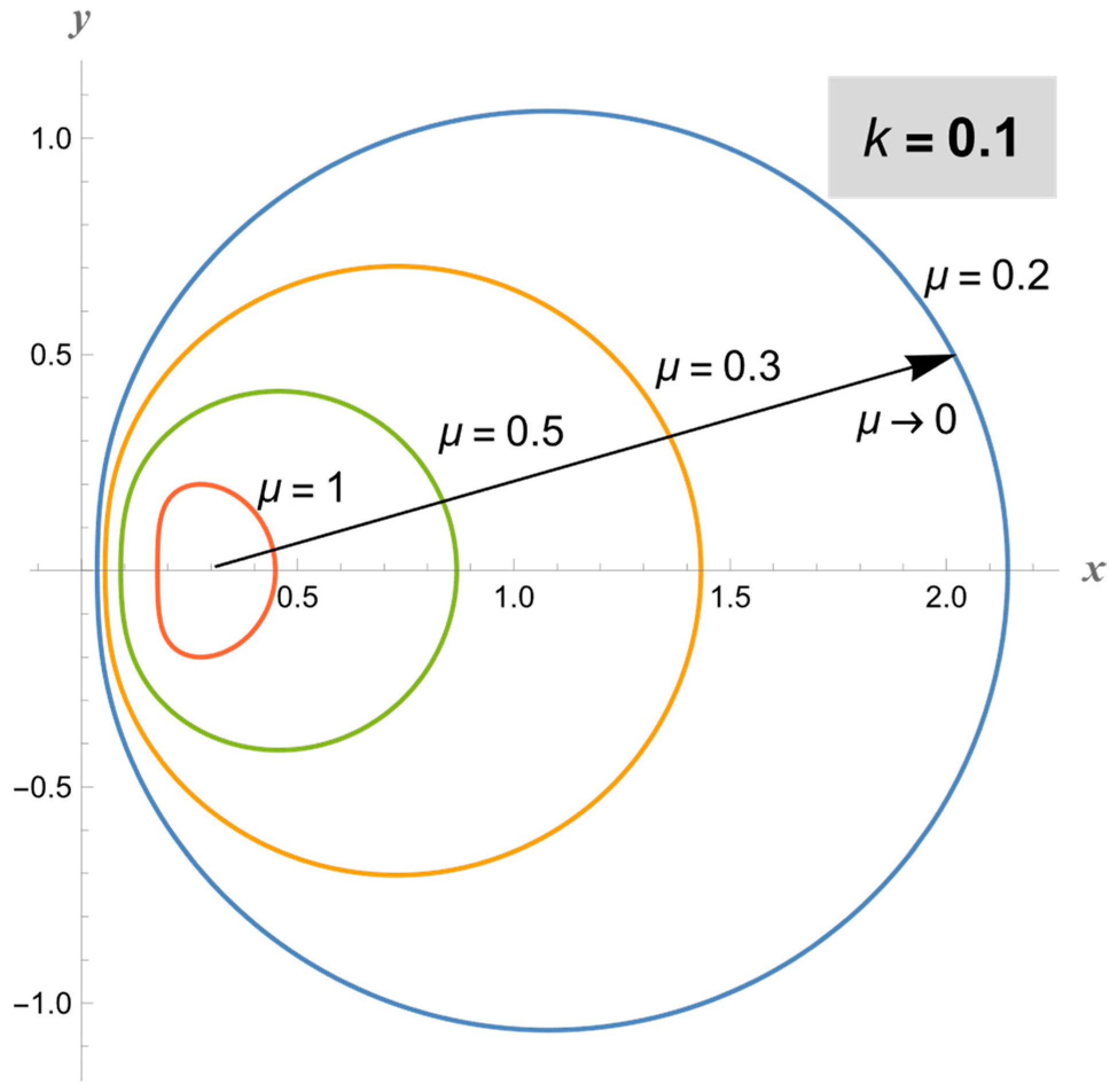
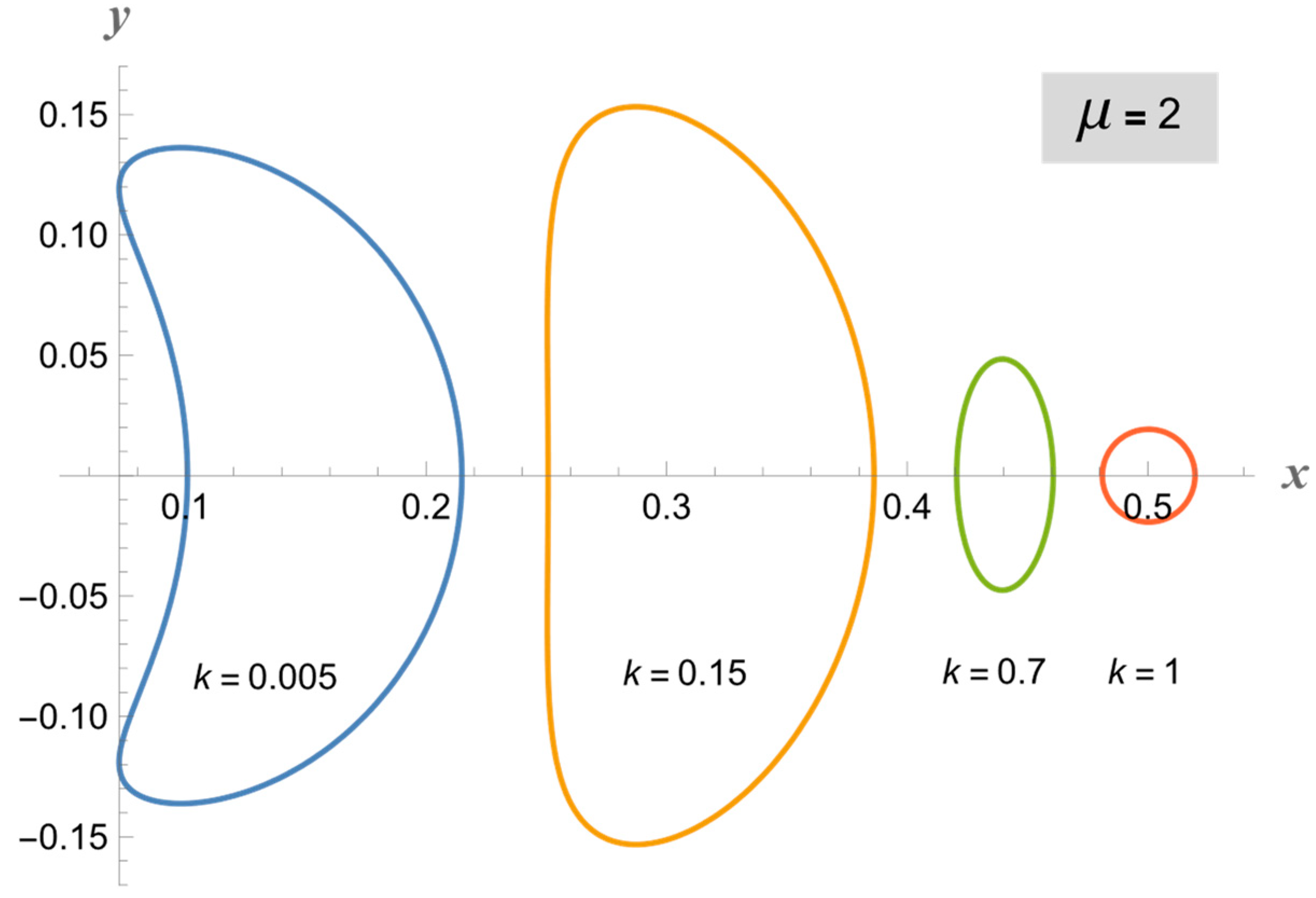
2. Cap-Cyclide Coordinates
3. The Generalized Laplace Equation
4. Solution in Bipolar Coordinates
5. Solution in Cap-Cyclide Coordinates
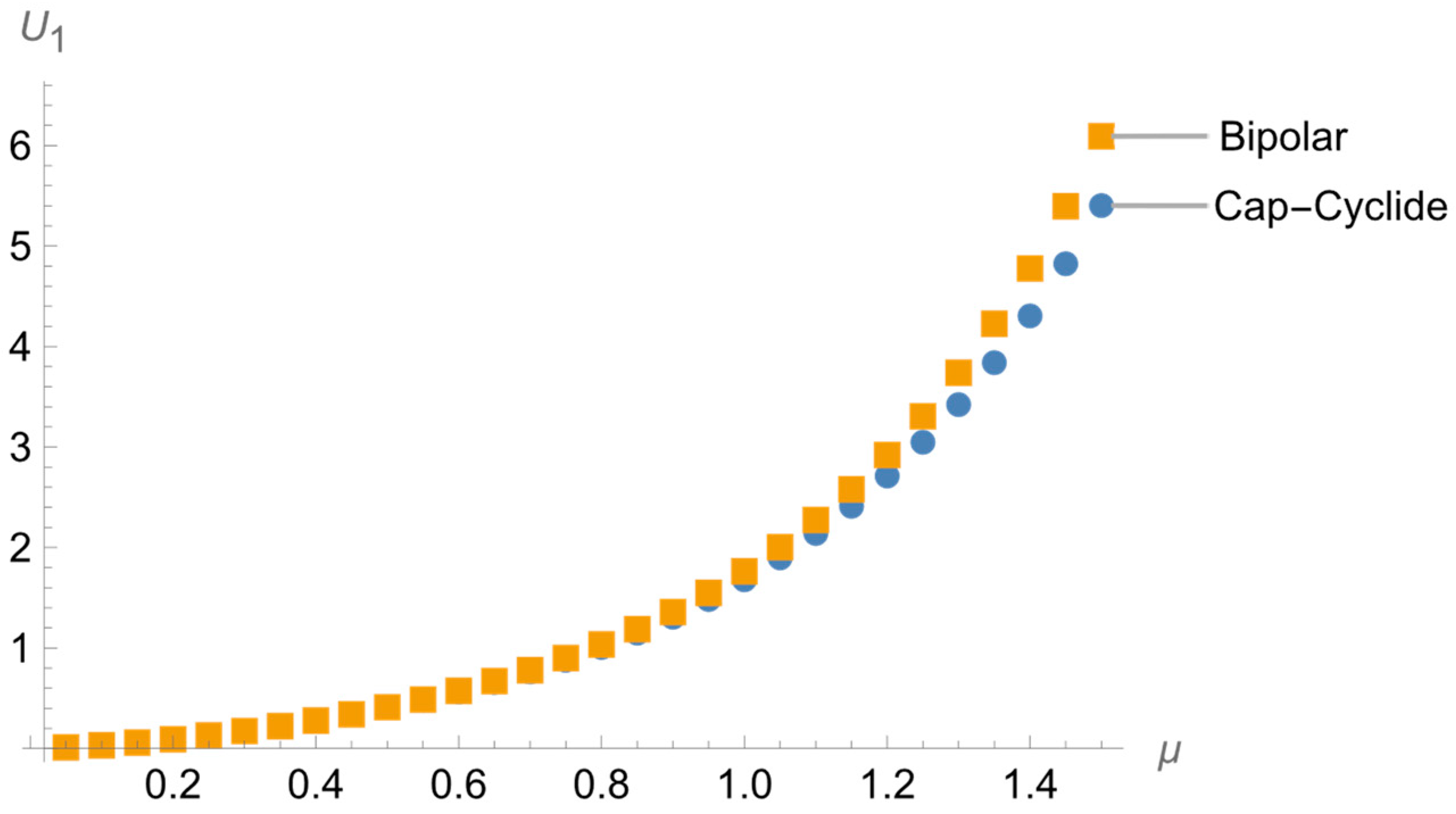
6. Bipolar Limit of Cap-Cyclide Coordinates for the Grad–Shafranov Equation
6.1. Radial Solution
6.2. Angular Solution
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grad, H.; Rubin, H. Hydromagnetic equilibria and force free fileds. J. Nucl. Energy 1958, 7, 284. [Google Scholar]
- Shafranov, V.D. Equilibrium of a plasma toroid in a magnetic field. Sov. Phys. JETP 1960, 37, 775. [Google Scholar]
- Mukhovatov, V.S.; Shafranov, V.D. Plasma equilibrium in a Tokamak. Nucl. Fusion 1971, 11, 605. [Google Scholar] [CrossRef]
- Bateman, G. MHD Instabilities; MIT Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Neumann, C. Theorie der Elektricitäts—Und Wärme-Vertheilung in einem Ringe; Verlag der buchhdlg des Weisenhauses: Halle, Germany, 1864. [Google Scholar]
- Böcher, M. Üeber Die Reihenentwickelungen Der Potential Theorie; Druck und Verlag von B. G. Teubner: Leipzig, Germany, 1894. [Google Scholar]
- Wangerin, A. Theorie des Potentials und der Kugelfunktionen; G. J. Gfischen’sche Verlagshandlung: Leipzig, Germany, 1909. [Google Scholar]
- Moon, P.; Spencer, D.E. Field Theory Handbook: Including Coordinate Systems, Differential Equations and Their Solutions; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fock, V.A. Skin effect in a ring. Fiz. Zh. Sov. 1932, 1, 215. [Google Scholar]
- Lebedev, N. The functions associated with a ring of oval cross-section. Tekh. Fiz. 1937, 4, 3. [Google Scholar]
- Honma, T.; Kito, M.; Kaji, I.; Seki, M. The vacuum poloidal flux functions satisfying of the Grad–Shafranov equation in the flat-ring cyclide coordinate system. Hokkaido Daigaku Kogakubu Kenkyu Hokoku 1979, 94, 123. [Google Scholar]
- Aikawa, I.K.; Takahara, M. Wangerin Functions; Report of Faculty of Engineering 26; Yamanashi University: Yamanashi, Japan, 1975; p. 126. [Google Scholar]
- Crisanti, F. Analytical solution of the Grad Shafranov equation in an elliptical prolate geometry. J. Plasma Phys. 2019, 85, 905850210. [Google Scholar] [CrossRef]
- Lupica, A.; Cesarano, C.; Crisanti, F.; Ishkhanyan, A. Analitical solution of the three-dimensional Laplace equation in terms of linear combinations of hypergeometric functions. Mathematics 2021, 9, 3316. [Google Scholar] [CrossRef]
- Ronveaux, A. Heun’s Differential Equations; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Slavyanov, S.Y.; Lay, W. Special Functions; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Ishkhanyan, A.M. Generalized hypergeometric solutions of the Heun equation. Theor. Math. Phys. 2020, 202, 1. [Google Scholar] [CrossRef]
- Letessier, J. Co-recursive associated Jacobi polynomials. J. Comput. Appl. Math. 1995, 57, 203. [Google Scholar] [CrossRef]
- Ishkhanyan, T.A.; Shahverdyan, T.A.; Ishkhanyan, A.M. Expansions of the solutions of the general Heun equation governed by two-term recurrence relations for coefficients. Adv. High Energy Phys. 2018, 2018, 4263678. [Google Scholar] [CrossRef]
- Ishkhanyan, A.M. Appell hypergeometric expansions of the solutions of the general Heun equation. Constr. Approx. 2019, 49, 445–459. [Google Scholar] [CrossRef]
- Alladio, F.; Crisanti, F. Analysis of MHD equilibria by toroidal multipolar expansions. Nucl. Fusion 1986, 26, 1143. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Wolfram, S. In Less than a Year, so Much New: Launching Version 12.1 of Wolfram Language & Mathematica. Available online: https://writings.stephenwolfram.com/2020/03/in-less-than-a-year-so-much-new-launching-version-12-1-of-wolfram-language-mathematica/ (accessed on 19 March 2023).
- Albanese, R.; Villone, F. The linearized CREATE-L plasma response model for the control of current, position and shape in tokamaks. Nucl. Fusion 1998, 38, 723. [Google Scholar] [CrossRef]
- Lao, L.L.; John, H.S.; Stambaugh, R.; Kellman, A.; Pfeiffer, W. Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 1985, 25, 1611. [Google Scholar] [CrossRef]
- Albanese, R.; Ambrosino, R.; Mattei, M. CREATE-NL+: A robust control-oriented free boundary dynamic plasma equilibrium solver. Fusion Eng. Des. 2015, 664, 96–97. [Google Scholar] [CrossRef]
- Mahariq, I.; Kuzuoglu, M.; Tarman, H.; Kurt, H. Photonic Nanojet Analysis by Spectral Element Method. IEEE Photonic J. 2014, 6, 5. [Google Scholar] [CrossRef]
- Mahariq, I. On the application of the spectral element method in electromagnetic problems involving domain decomposition. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 1059–1069. [Google Scholar] [CrossRef]
- Atanasiu, C.V.; Günter, S.; Lackner, K.; Miron, I.G. Analytical solutions to the Grad–Shafranov equation. Phys. Plasmas 2004, 11, 3510. [Google Scholar] [CrossRef]
- Guazzotto, L.; Freidberg, J.P. A family of analytic equilibrium solutions for the Grad–Shafranov equation. Phys. Plasmas 2007, 14, 112508. [Google Scholar] [CrossRef]
- Alladio, F.; Crisanti, F.; Lazzaro, E.; Tanga, A. Observation High βp Effect in JET Discharge. Bull. Am. Phys. Soc. 1984, F11, 3. [Google Scholar]
- Alladio, F.; Crisanti, F.; Marinucci, M.; Micozzi, P.; Tanga, A. Analysis of tokamak configurations using the toroidal multipole method. Nucl. Fusion 1991, 31, 739. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crisanti, F.; Cesarano, C.; Ishkhanyan, A. The Grad–Shafranov Equation in Cap-Cyclide Coordinates: The Heun Function Solution. Mathematics 2023, 11, 2087. https://doi.org/10.3390/math11092087
Crisanti F, Cesarano C, Ishkhanyan A. The Grad–Shafranov Equation in Cap-Cyclide Coordinates: The Heun Function Solution. Mathematics. 2023; 11(9):2087. https://doi.org/10.3390/math11092087
Chicago/Turabian StyleCrisanti, Flavio, Clemente Cesarano, and Artur Ishkhanyan. 2023. "The Grad–Shafranov Equation in Cap-Cyclide Coordinates: The Heun Function Solution" Mathematics 11, no. 9: 2087. https://doi.org/10.3390/math11092087






