An Implicit Finite Difference Scheme and Neural Network Approach for Non-Newtonian Nanofluid Flow Using Induced Magnetic Field
Abstract
1. Introduction
2. Numerical Scheme
3. Stability Analysis
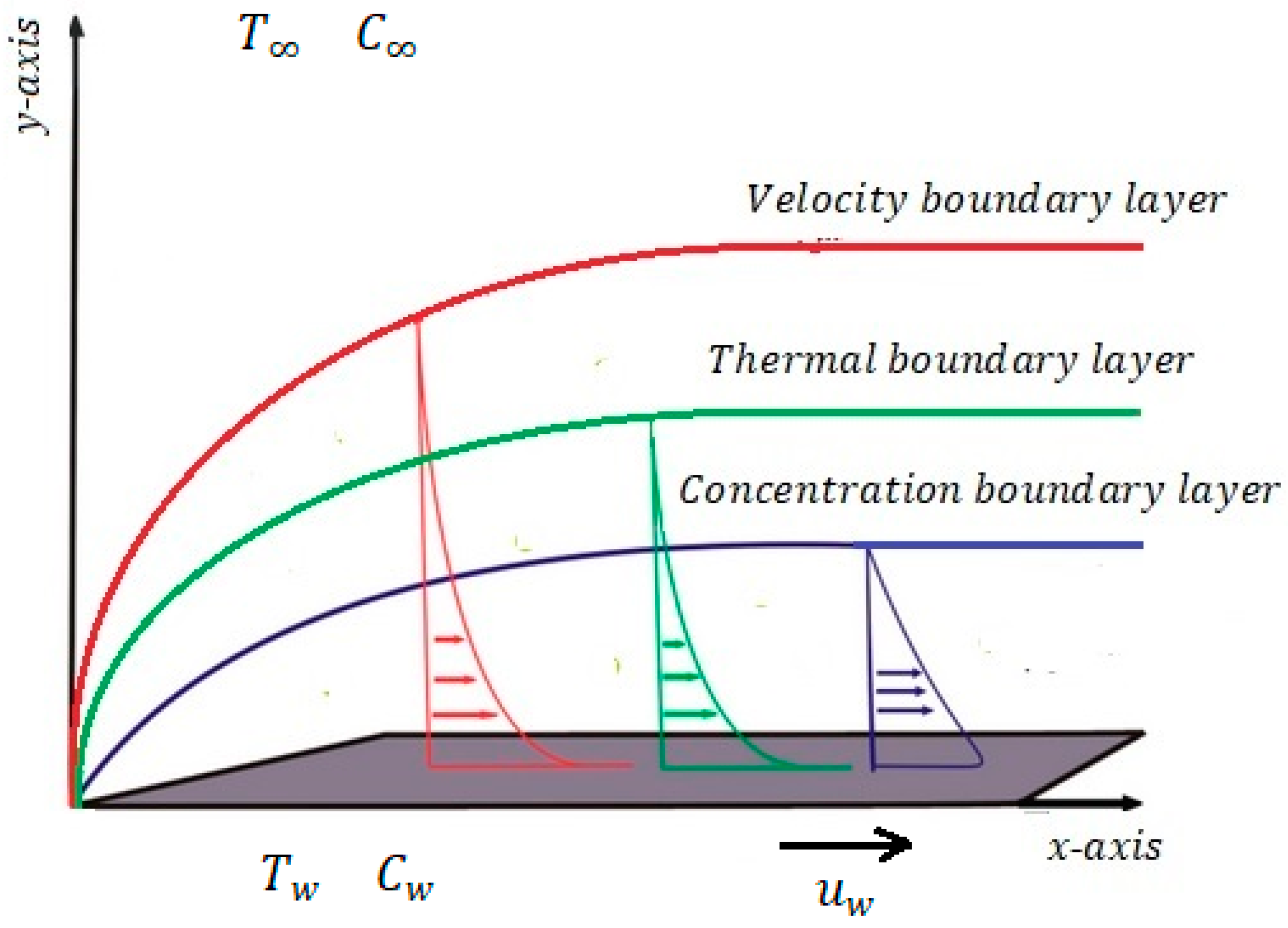
4. Problem Formulation
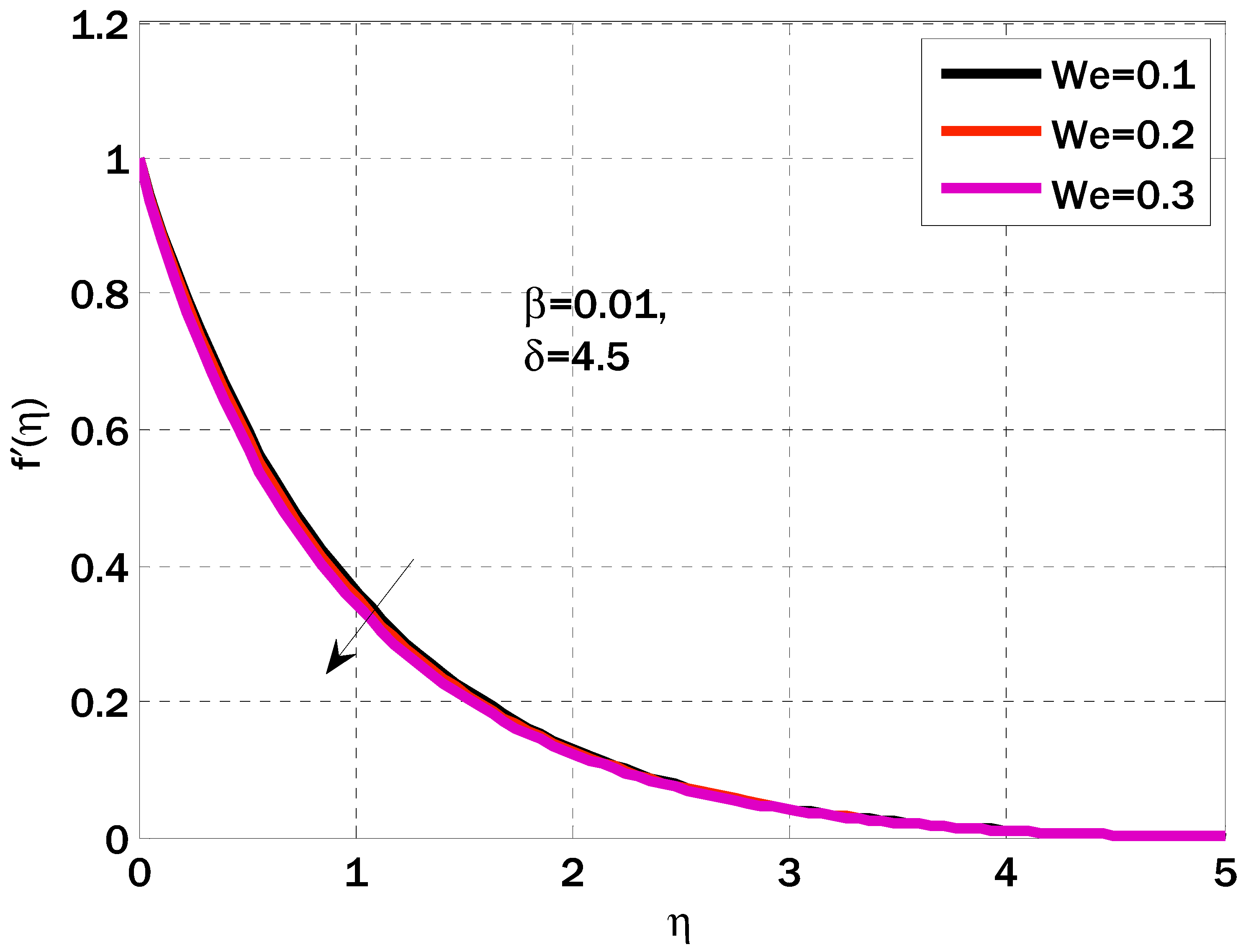
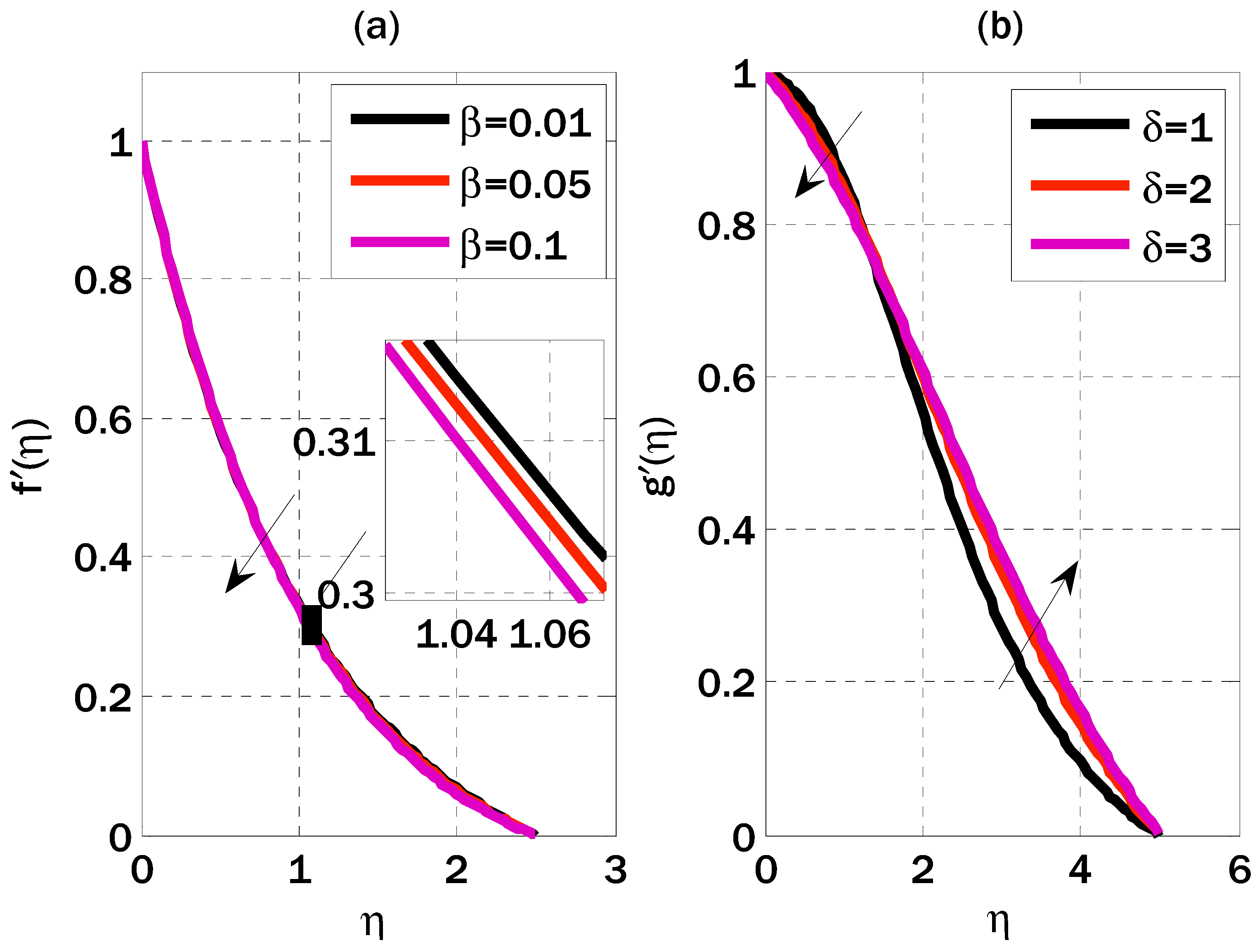
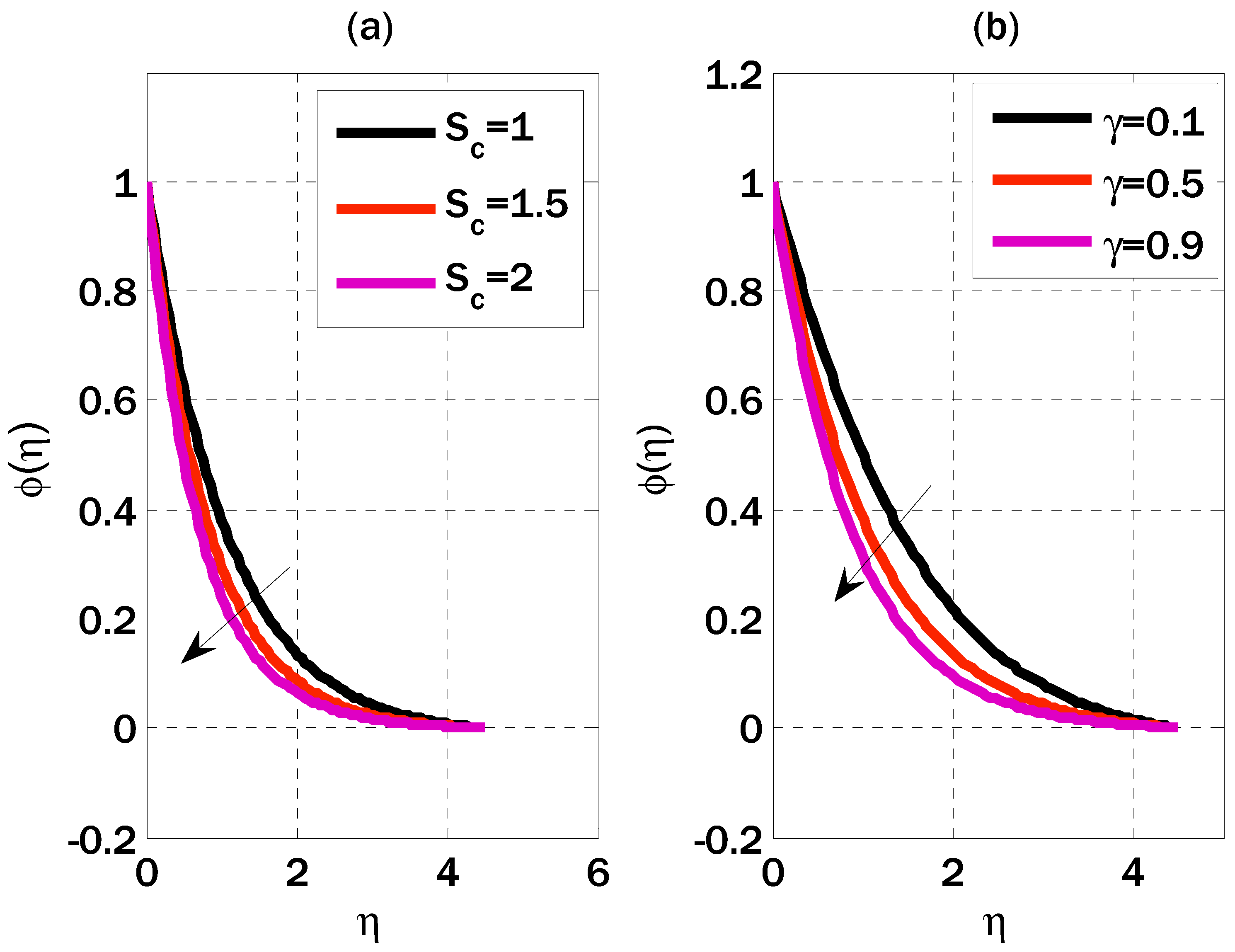
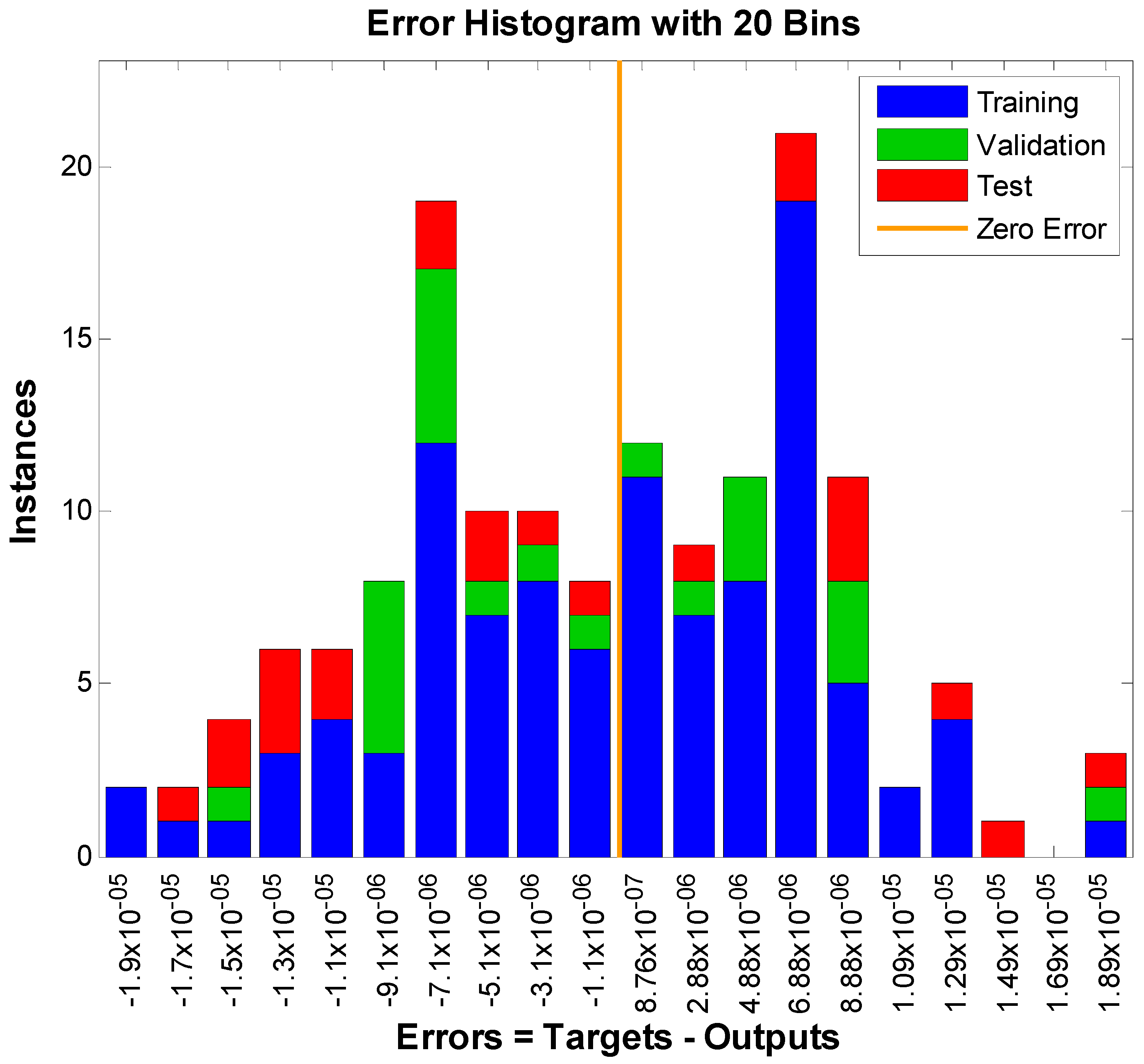
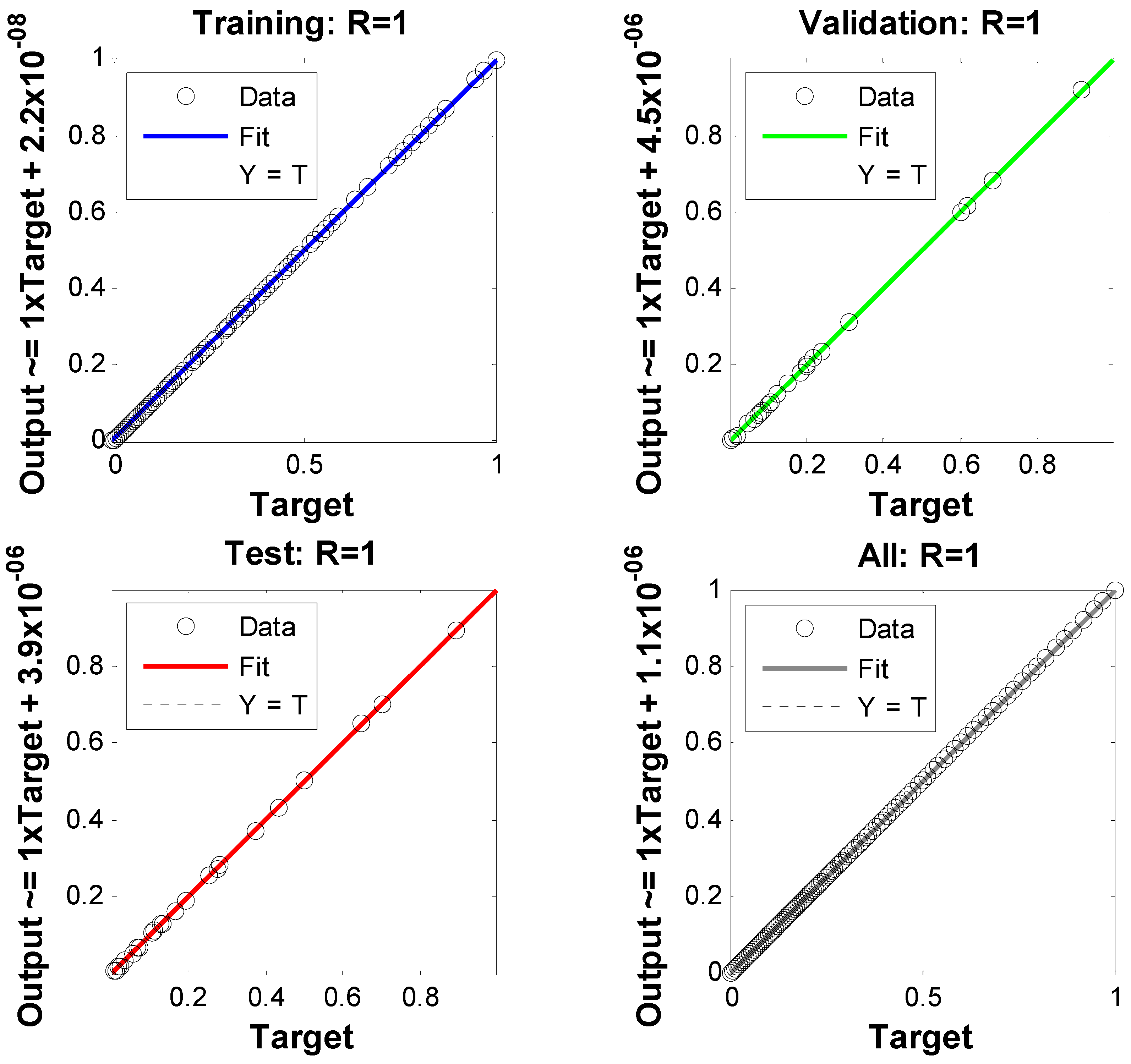
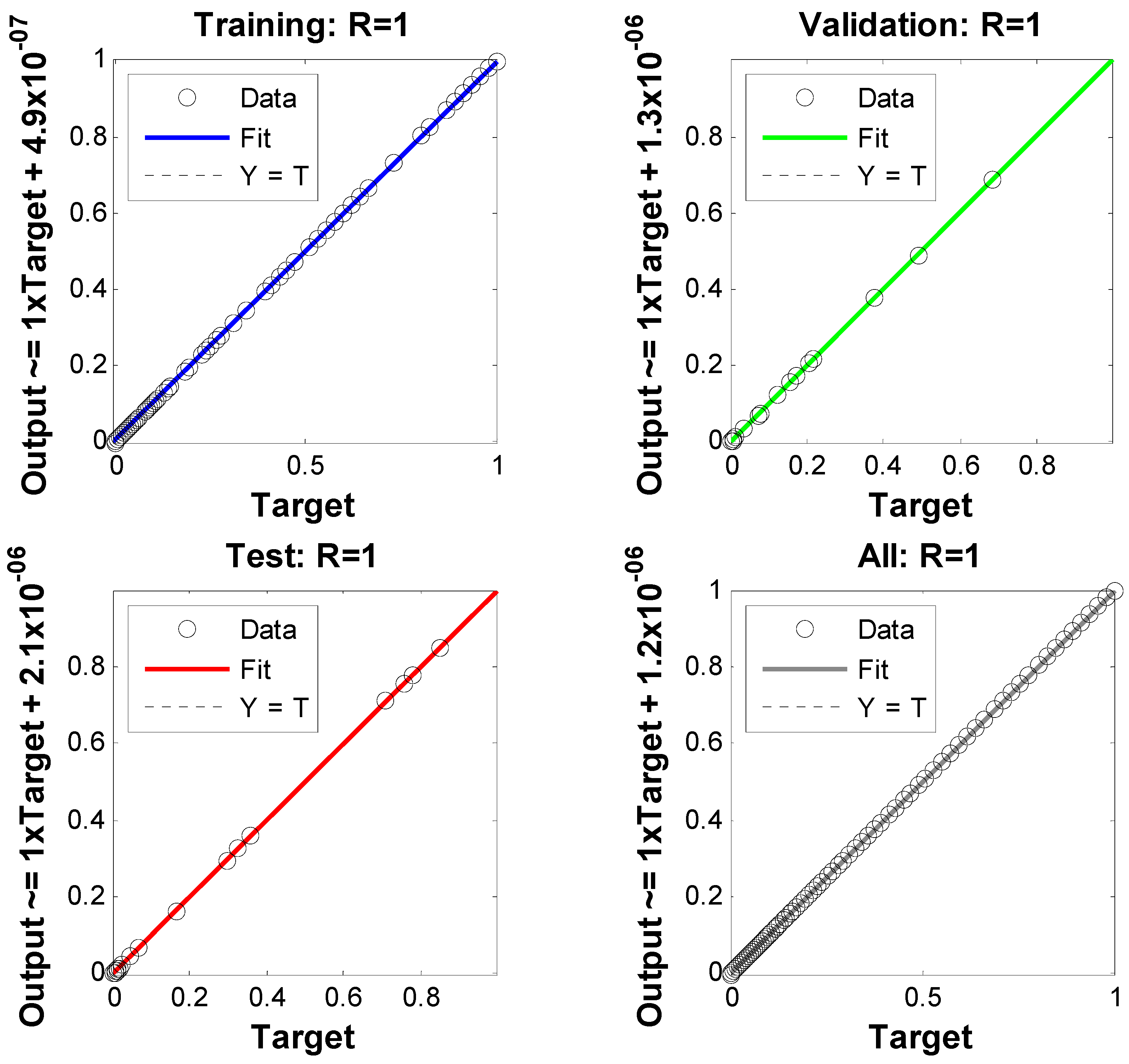
5. Results and Discussions
6. Conclusions
- It has been seen that velocity profile decayed with an enhancing of Weissenberg number;
- The horizontal component of velocity has a dual behavior with rising reciprocal of magnetic Prandtl number;
- The temperature profile declined and raised with enhancing Prandtl number and Eckert number, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Horizontal components of velocity | Electrical conductivity of the fluid | ||
| Cartesian co-ordinate | Temperature of fluid | ||
| Kinematic viscosity | Temperature of fluid at the wall | ||
| Density of fluid | Ambient temperature of the fluid | ||
| Concentration of fluid | Concentration on the wall | ||
| Brownian diffusion coefficient | Ambient concentration | ||
| Specific heat capacity | Thermophoresis coefficient | ||
| Horizontal component of induced magnetic field | Vertical component of induced magnetic field | ||
| Reaction rate | Thermal diffusivity | ||
| Reaction rate parameter | Dynamic viscosity | ||
| Time constant (s) | Effective heat capacity of fluid | ||
| Magnetic diffusivity | Eckert number | ||
| Prandtl number | Thermophoresis variable | ||
| Brownian motion variable | Schmidt number | ||
| Magnetic parameter | Weissenberg number | ||
| Reciprocal of magnetic Prandtl number |
References
- Iqbal, M.S.; Malik, F.; Mustafa, I.; Khan, I.; Ghaffari, A.; Riaz, A.; Nisar, K. Impact of induced magnetic field on thermal enhancement in gravity driven Fe3O4 ferrofluid flow through vertical non-isothermal surface. Results Phys. 2020, 19, 103472. [Google Scholar] [CrossRef]
- Kumar, D. Radiation effect on magnetohydrodynamic flow with induced magnetic field and Newtonian heating/cooling: An analytic approach. Propuls. Power Res. 2021, 10, 303–313. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Waini, I.; Pop, I.; Elattar, S.; Abed, A.M. Stagnation point flow of a water-based graphene-oxide over a stretching/shrinking sheet under an induced magnetic field with homogeneous-heterogeneous chemical reaction. J. Magn. Magn. Mater. 2023, 565, 170287. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Khan, M.I.; Alsaedi, A. Melting heat transfer and induced magnetic field effects on flow of water based nanofluid over a rotating disk with variable thickness. Results Phys. 2018, 9, 1618–1630. [Google Scholar] [CrossRef]
- Hayat, T.; Razaq, A.; Khan, S.A.; Alsaedi, A. Radiative flow of rheological material considering heat generation by stretchable cylinder. Case Stud. Therm. Eng. 2023, 44, 102837. [Google Scholar] [CrossRef]
- Khan, S.A.; Hayat, T.; Alsaedi, A. Entropy generation in chemically reactive flow of Reiner-Rivlin liquid conveying tiny particles considering thermal radiation. Alex. Eng. J. 2023, 66, 257–268. [Google Scholar] [CrossRef]
- Hayat, T.; Fatima, A.; Khan, S.A.; Alsaedi, A. Thermo-diffusion and diffusion thermo analysis for Darcy Forchheimer flow with entropy generation. Ain Shams Eng. J. 2022, 13, 101530. [Google Scholar] [CrossRef]
- Alsaedi, A.; Muhammad, K.; Hayat, T. Numerical study of MHD hybrid nanofluid flow between two coaxial cylinders. Alex. Eng. J. 2022, 61, 8355–8362. [Google Scholar] [CrossRef]
- Muhammad, K.H.; Hayat, T.; Momani, S.; Asghar, S. FDM analysis for squeezed flow of hybrid nanofluid in presence of Cattaneo-Christov (C-C) heat flux and convective boundary condition. Alex. Eng. J. 2022, 61, 4719–4727. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Al-Khaled, K.; Khan, N.; Khan, M.I.; Khan, S.U.; Hashmi, M.S.; Iqbal, M.A.; Tlili, I. Study of Buongiorno’s nanofluid model for flow due to stretching disks in presence of gyrotactic microorganisms. Ain Shams Eng. J. 2021, 12, 3975–3985. [Google Scholar] [CrossRef]
- Alblawi, A.; Malik, M.Y.; Nadeem, S.; Abbas, N. Buongiorno’s Nanofluid Model over a Curved Exponentially Stretching Surface. Processes 2019, 7, 665. [Google Scholar] [CrossRef][Green Version]
- Khatun, S.; Nasrin, R. Numerical Modeling Of Buongiorno’s Nanofluid On Free Convection: Thermophoresis And Brownian Effects. J. Nav. Archit. Mar. Eng. 2021, 18, 217–239. [Google Scholar] [CrossRef]
- Akram, S.; Athar, M.; Saeed, K.; Razia, A.; Muhammad, T.; Hussain, A. Hybrid double-diffusivity convection and induced magnetic field effects on peristaltic waves of Oldroyd 4-constant nanofluids in non-uniform channel. Alex. Eng. J. 2023, 65, 785–796. [Google Scholar] [CrossRef]
- Hasibi, A.; Gholami, A.; Asadi, Z.; Ganji, D.D. Importance of induced magnetic field and exponential heat source on convective flow of Casson fluid in a micro-channel via AGM. Theor. Appl. Mech. Lett. 2022, 12, 100342. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High performance heat sinking for VLSI. IEEE Electron. Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Liu, Y.; Rao, X.; Zhao, H.; Zhan, W.; Xu, Y.; Liu, Y. Generalized finite difference method based meshless analysis for coupled two-phase porous flow and geomechanics. Eng. Anal. Bound. Elem. 2023, 146, 184–203. [Google Scholar] [CrossRef]
- Rao, X.; Liu, Y.; Zhao, H. An upwind generalized finite difference method for meshless solution of two-phase porous flow equations. Eng. Anal. Bound. Elem. 2022, 137, 105–118. [Google Scholar] [CrossRef]
- Cocoon, E.T.; Moulton, D.; Kikinzon, E.; Berndt, M.; Manzini, G.; Garimella, R.; Lipnikov, K.; Painter, S.L. Coupling surface flow and subsurface flow in complex soil structures using mimetic finite differences. Adv. Water Resour. 2020, 144, 103701. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Tran. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Srinivasulu, T.; Goud, B.S. Effect of inclined magnetic field on flow, heat and mass transfer of Williamson nanofluid over a stretching sheet. Case Stud. Therm. Eng. 2021, 23, 100819. [Google Scholar] [CrossRef]
- Shyam, S.; Banerjee, U.; Mondal, P.K.; Mitra, S.K. Impact dynamics of ferrofluid droplet on a PDMS substrate under the influence of magnetic field. Colloids Surf. A Physicochem. Eng. Asp. 2023, 661, 130911. [Google Scholar] [CrossRef]
- Sarma, R.; Shukla, A.K.; Gaikwad, H.S.; Mondal, P.K.; Wongwises, S. Effect of conjugate heat transfer on the thermo-electro-hydrodynamics of nanofluids: Entropy optimization analysis. J. Therm. Anal. Calorim. 2022, 147, 599–614. [Google Scholar] [CrossRef]
- Mehta, S.K.; Mondal, P.K. Free convective heat transfer and entropy genreration characterisitcs of the nanofluid flow inside a wavy solar power plant. Microsyst. Technol. 2022. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Simulation of combined convective-radiative heat transfer of hybrid nanofluid flow inside an open trapezoidal enclosure considering the magnetic force impacts. J. Magn. Magn. Mater. 2023, 567, 170354. [Google Scholar] [CrossRef]


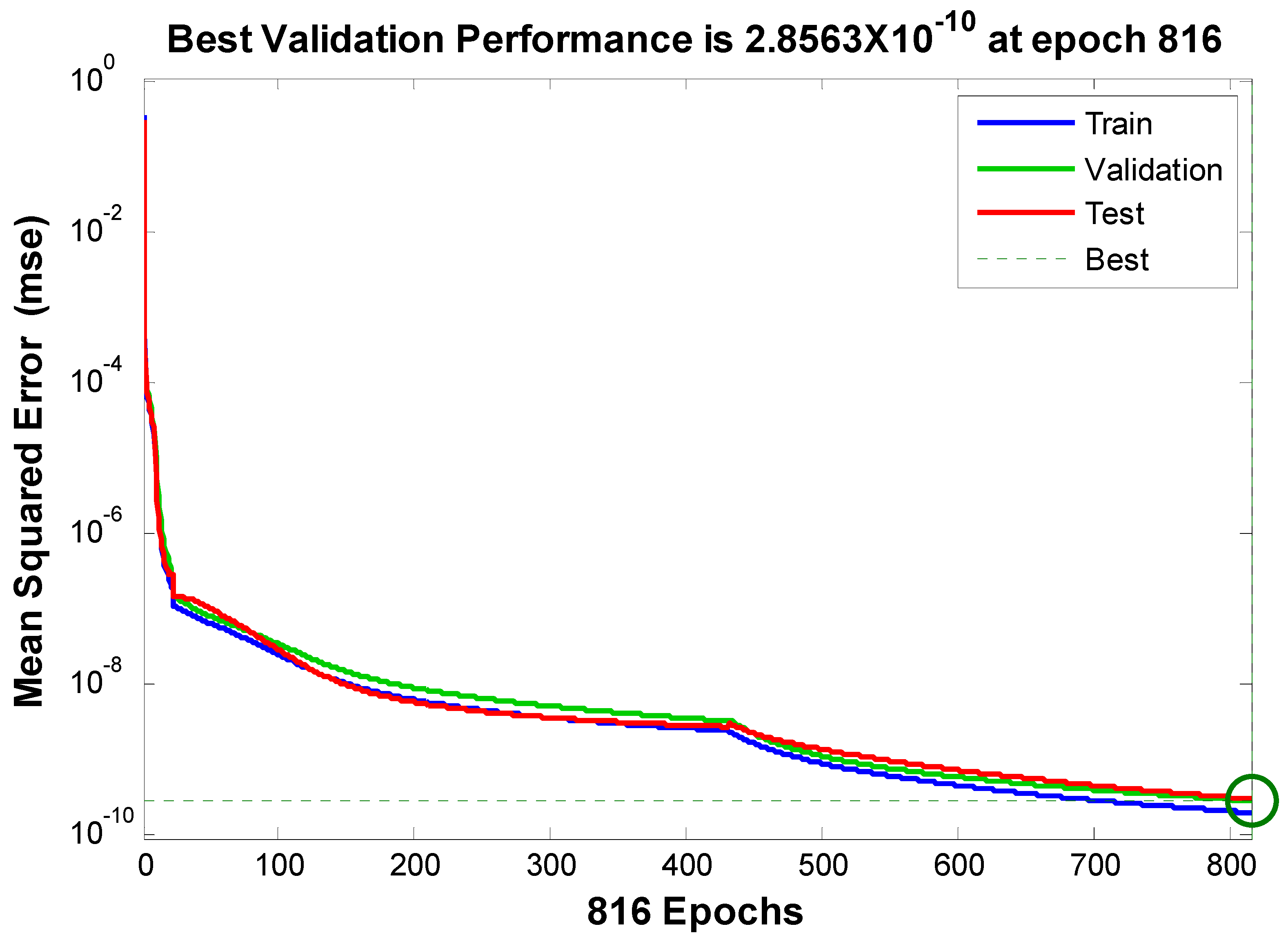
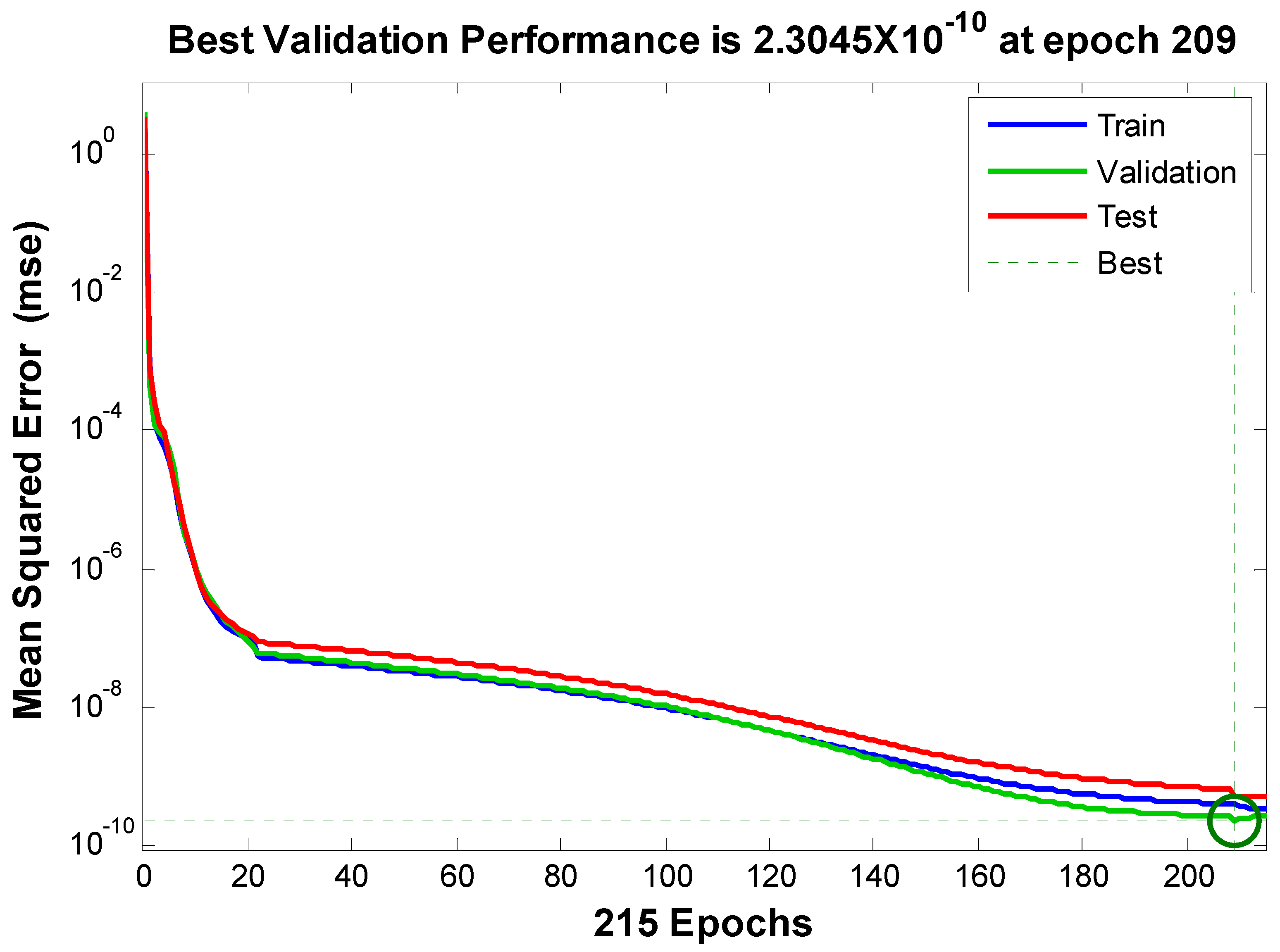
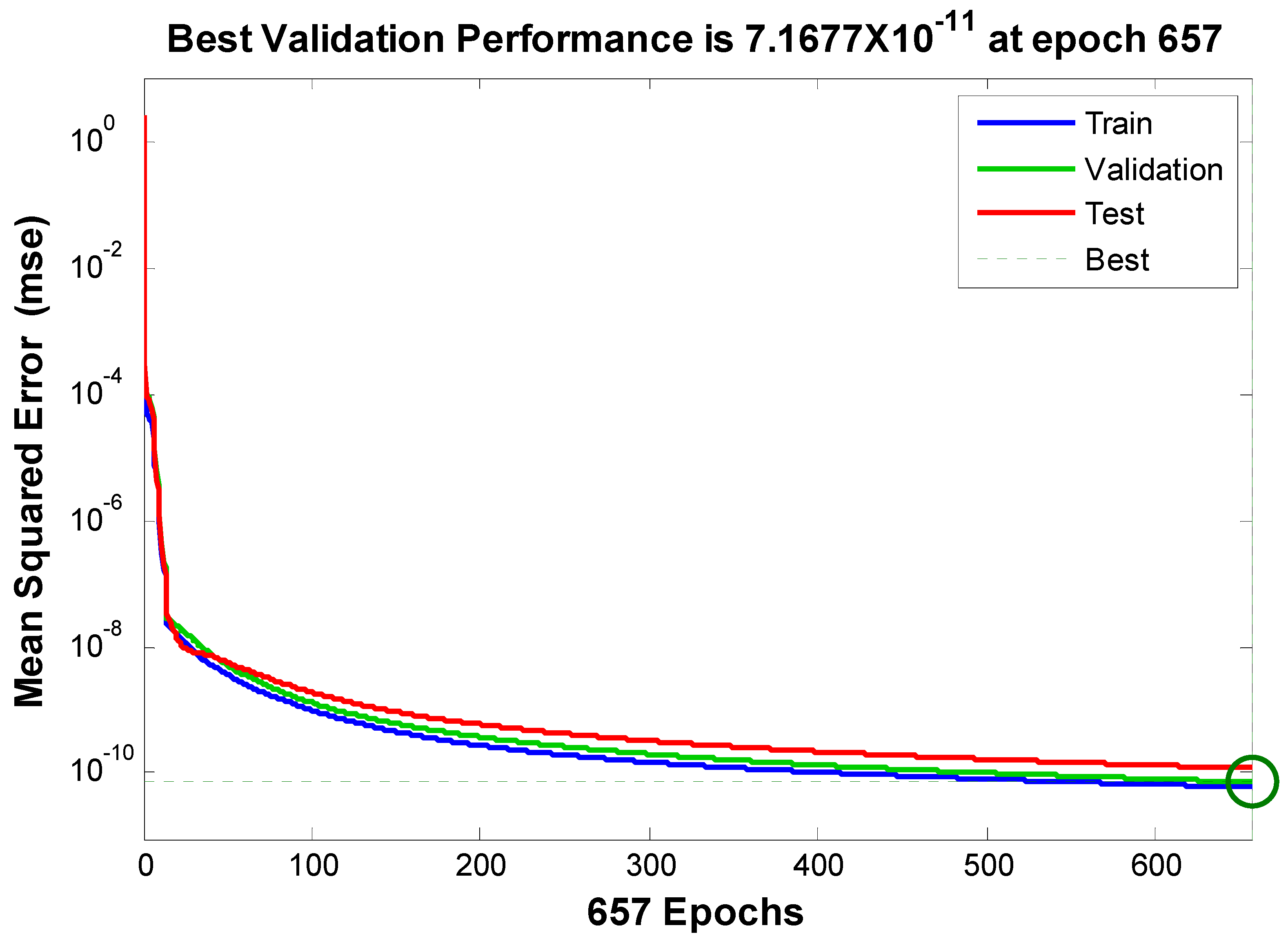

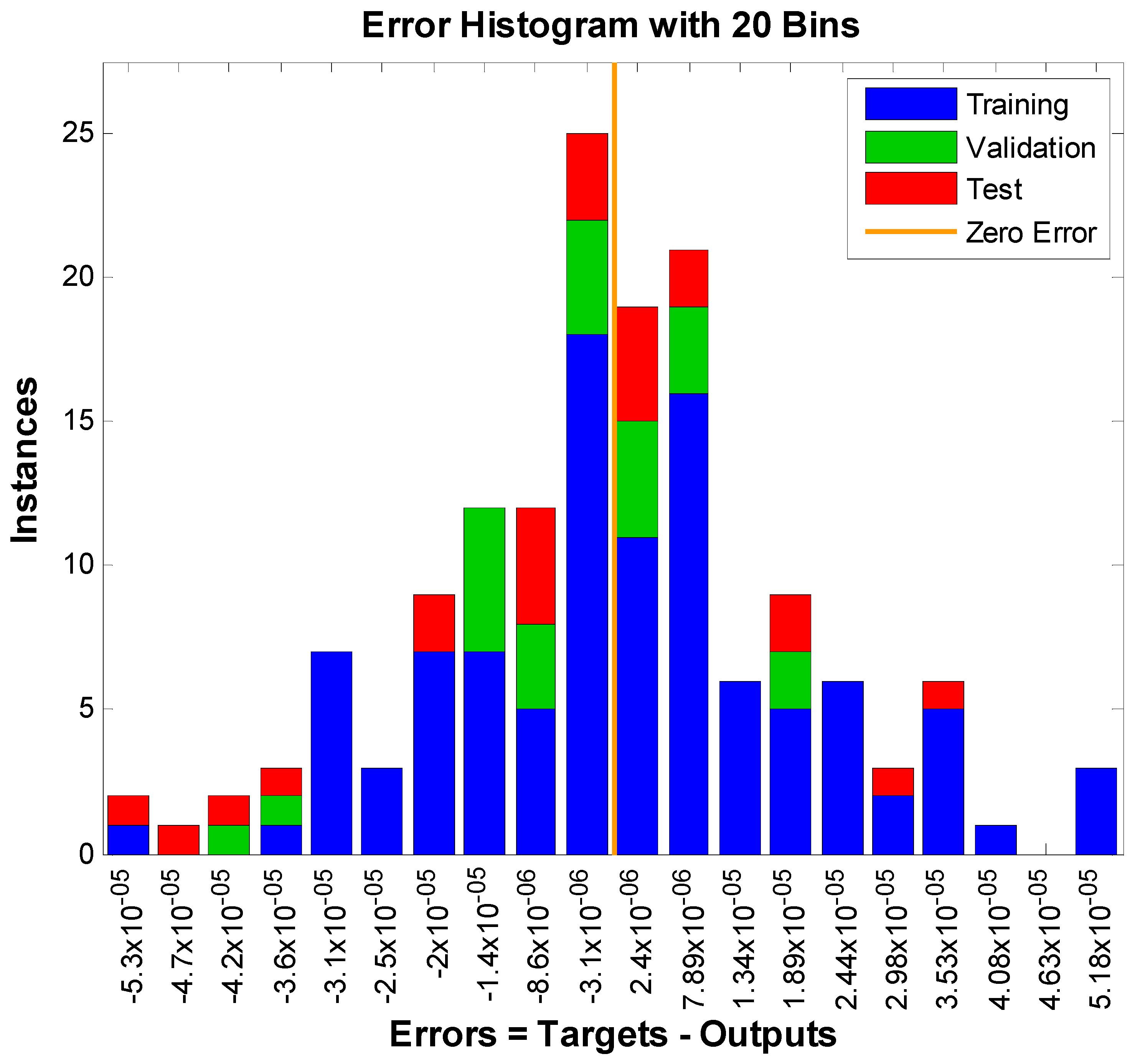

| [20] | [21] | Proposed | |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Salman, H.J.; Nawaz, Y.; Al Ghafli, A.A. An Implicit Finite Difference Scheme and Neural Network Approach for Non-Newtonian Nanofluid Flow Using Induced Magnetic Field. Mathematics 2023, 11, 2089. https://doi.org/10.3390/math11092089
Al Salman HJ, Nawaz Y, Al Ghafli AA. An Implicit Finite Difference Scheme and Neural Network Approach for Non-Newtonian Nanofluid Flow Using Induced Magnetic Field. Mathematics. 2023; 11(9):2089. https://doi.org/10.3390/math11092089
Chicago/Turabian StyleAl Salman, Hassan J., Yasir Nawaz, and Ahmed A. Al Ghafli. 2023. "An Implicit Finite Difference Scheme and Neural Network Approach for Non-Newtonian Nanofluid Flow Using Induced Magnetic Field" Mathematics 11, no. 9: 2089. https://doi.org/10.3390/math11092089
APA StyleAl Salman, H. J., Nawaz, Y., & Al Ghafli, A. A. (2023). An Implicit Finite Difference Scheme and Neural Network Approach for Non-Newtonian Nanofluid Flow Using Induced Magnetic Field. Mathematics, 11(9), 2089. https://doi.org/10.3390/math11092089






